Performance Analysis of NB-IoT Uplink in Low Earth Orbit Non-Terrestrial Networks †
Abstract
:1. Introduction
1.1. Research Background
1.2. Related Work
1.3. Contributions and Organization
2. System Model
2.1. NTN Architecture
2.2. NB-IoT Uplink Transmission Scheme
2.3. Channel Model
3. Problem Statement
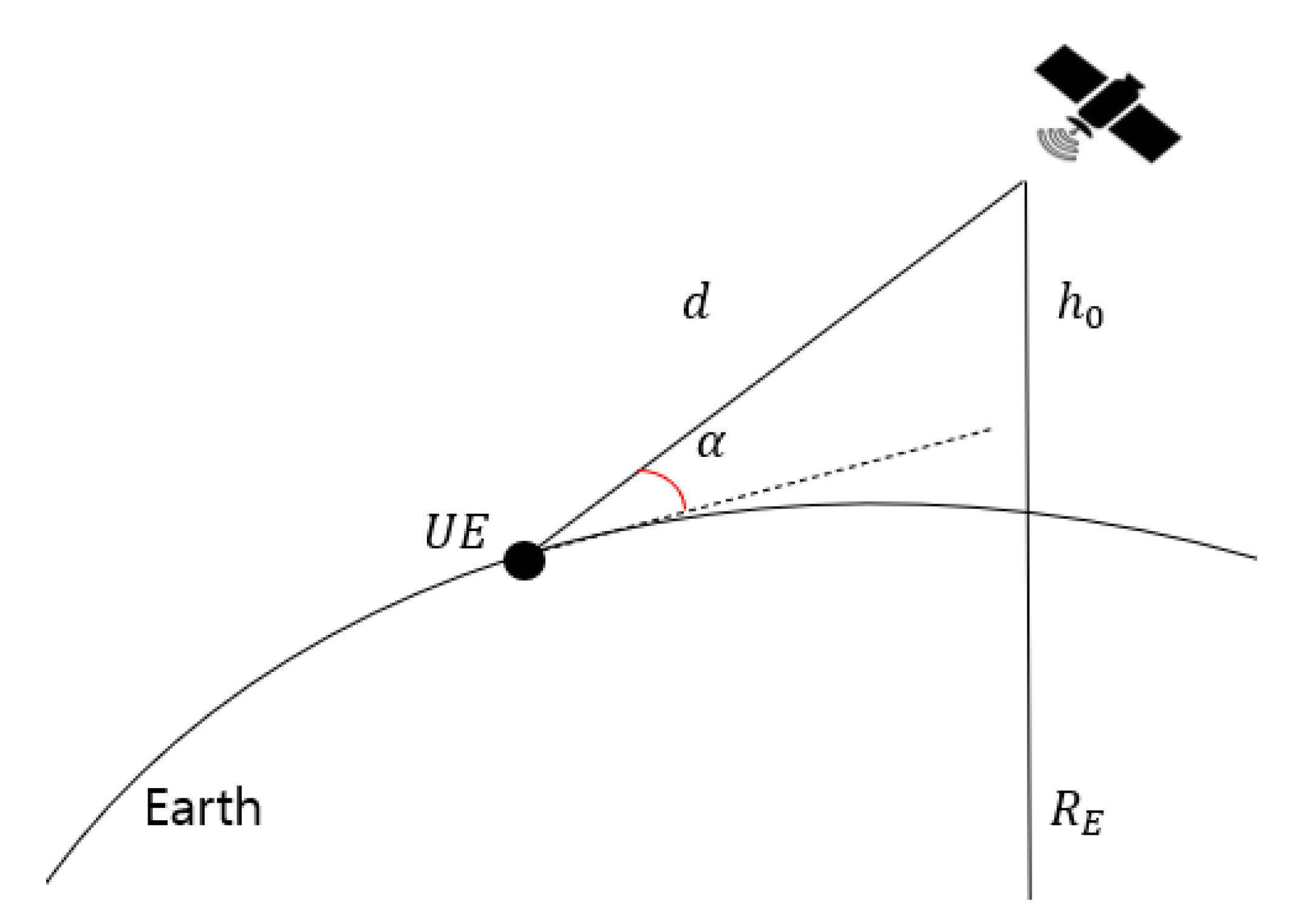
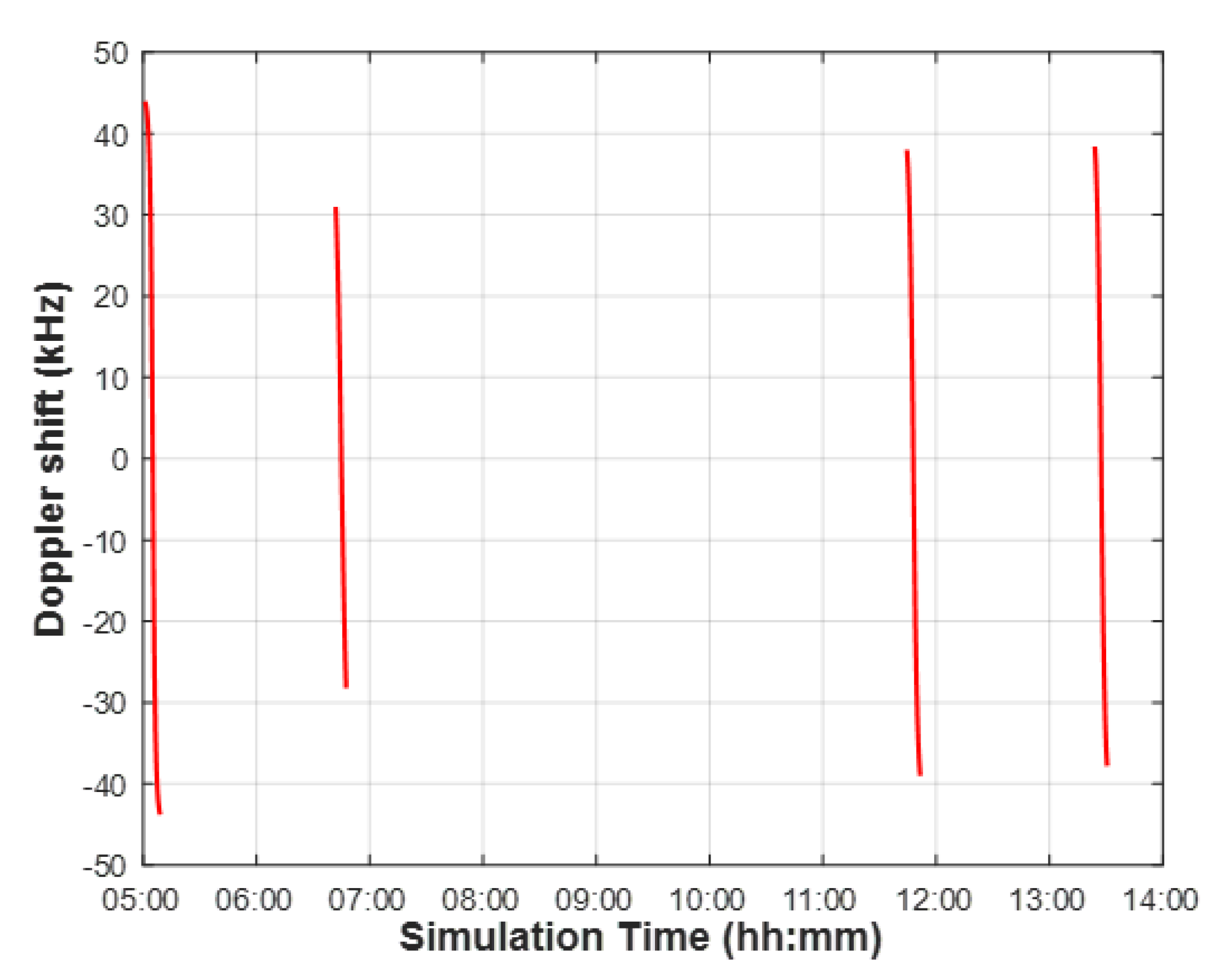
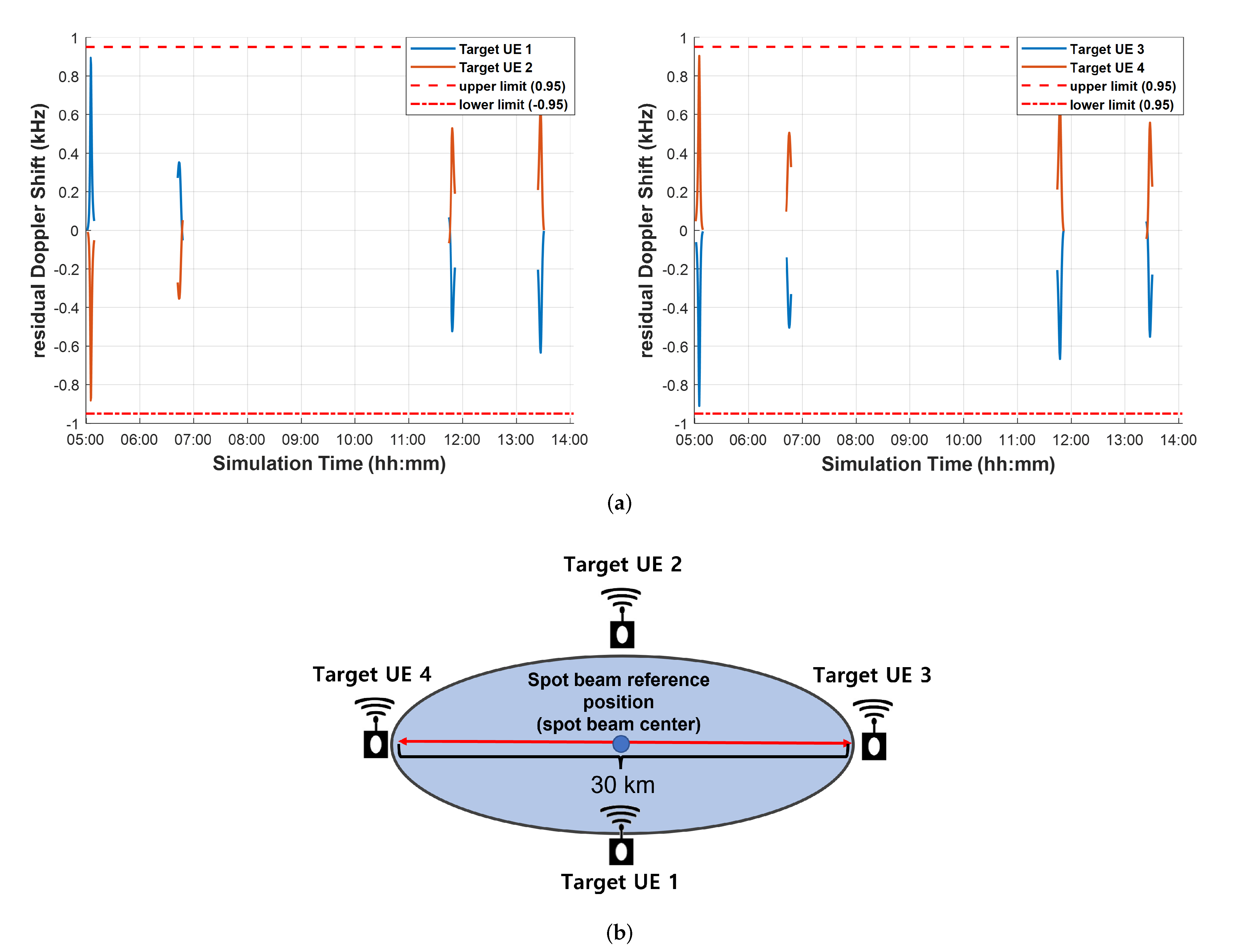
3.1. Residual Doppler Shift
3.2. Link Performance
4. Proposed Solution
4.1. Reduction in Beam Coverage
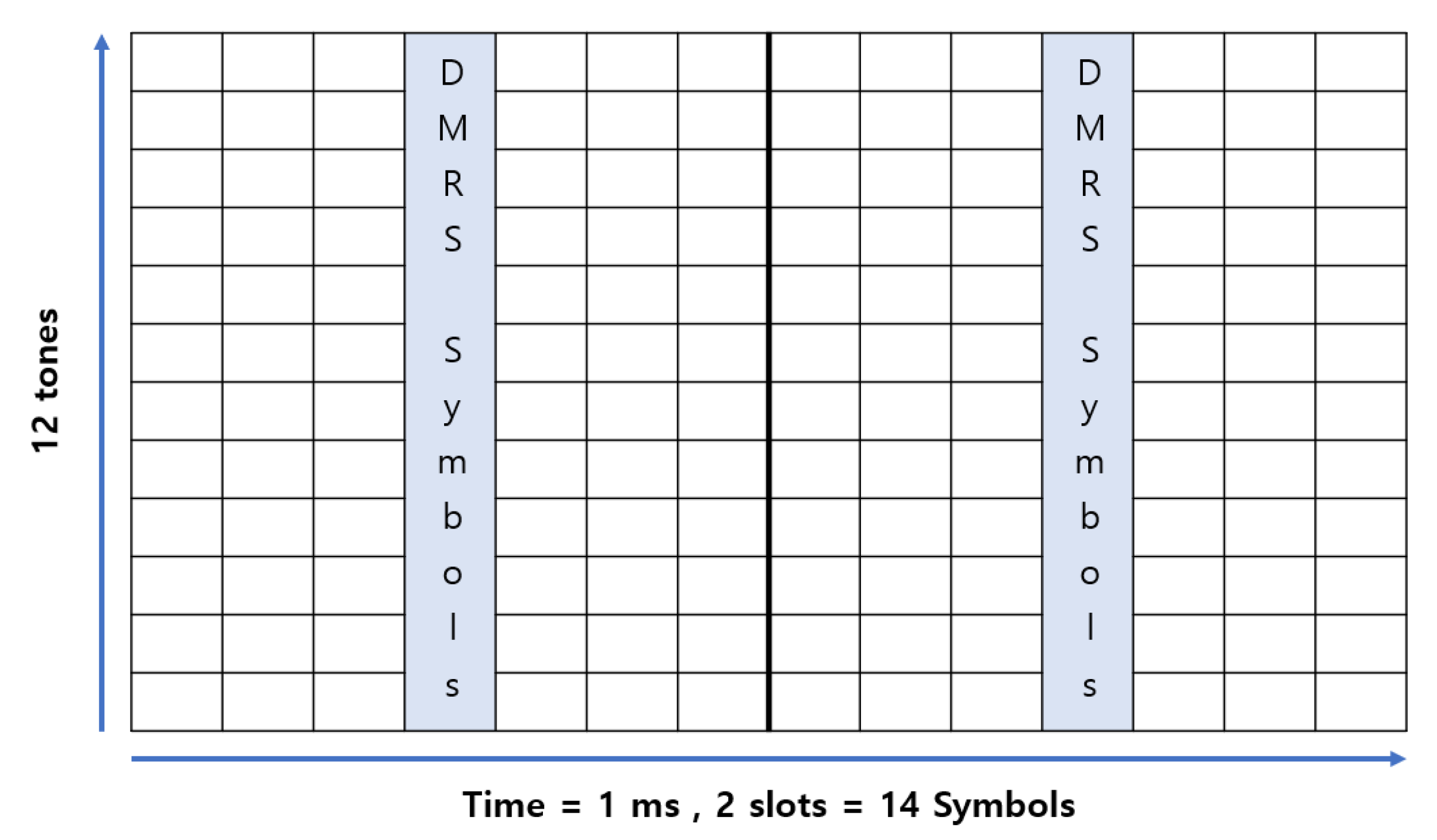
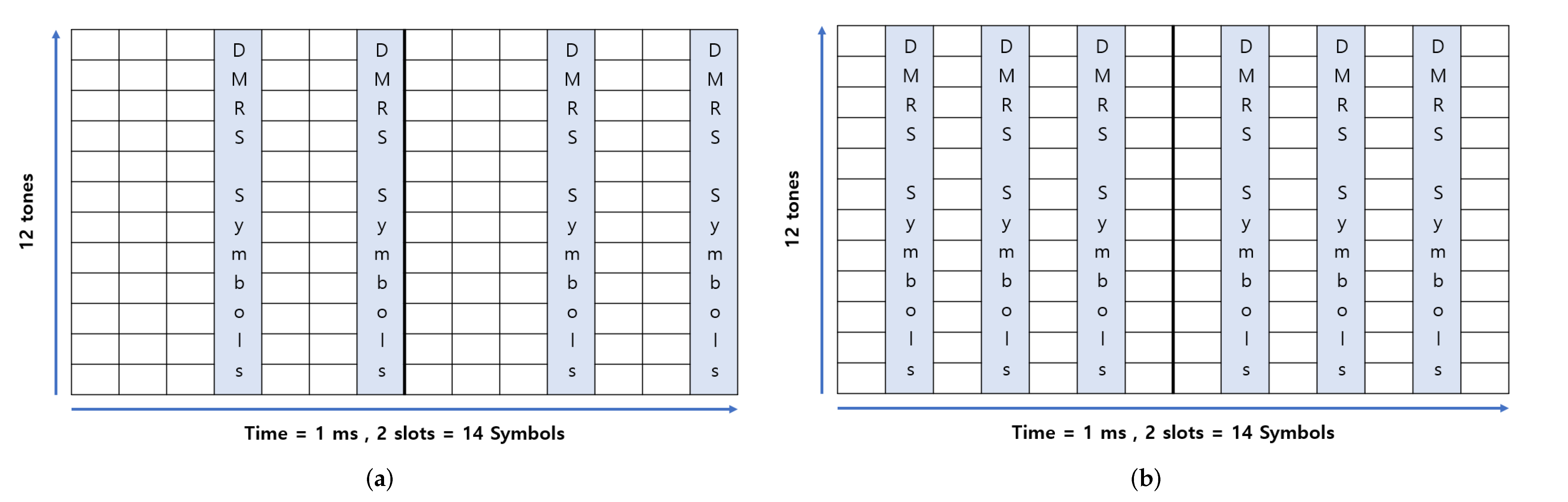
4.2. Addition of the DMRS Symbol
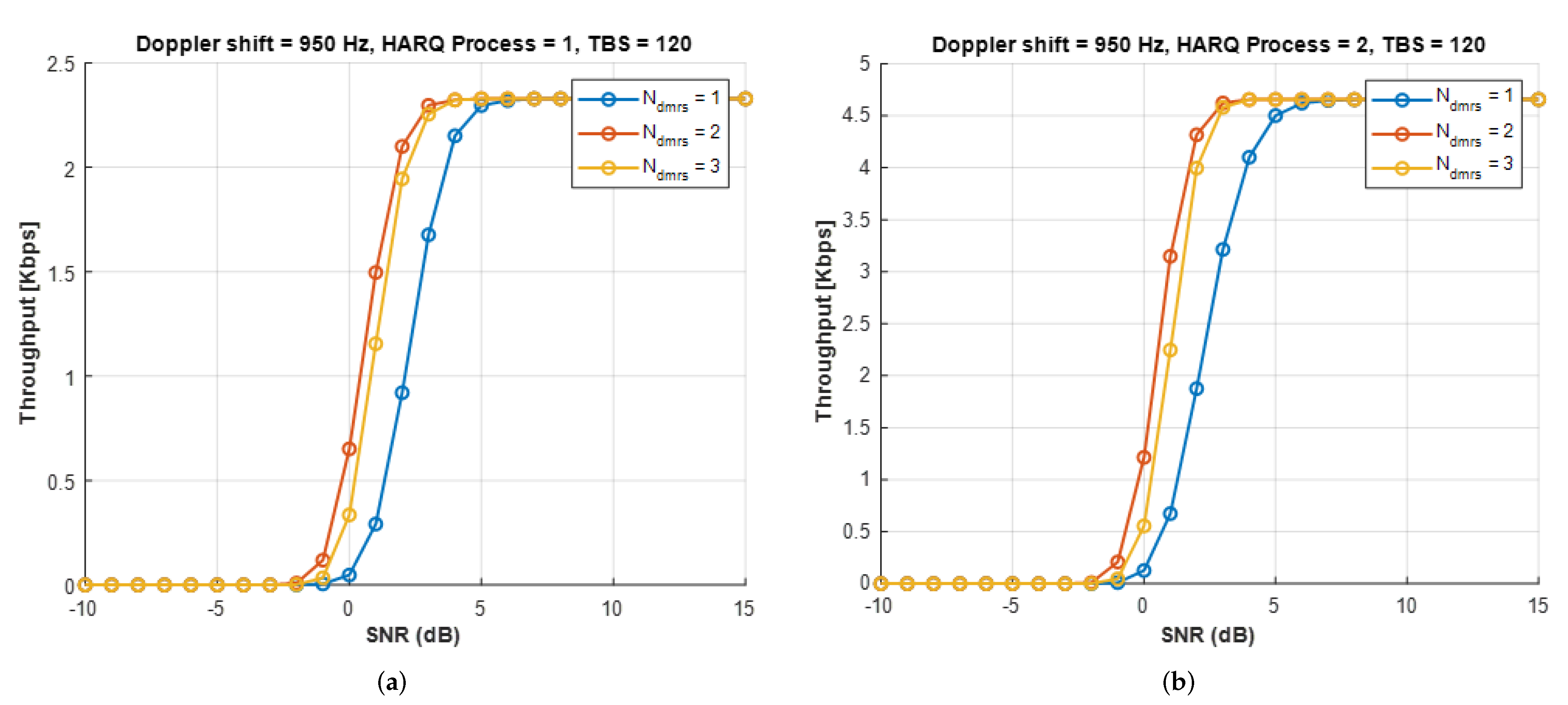
5. Performance Analysis
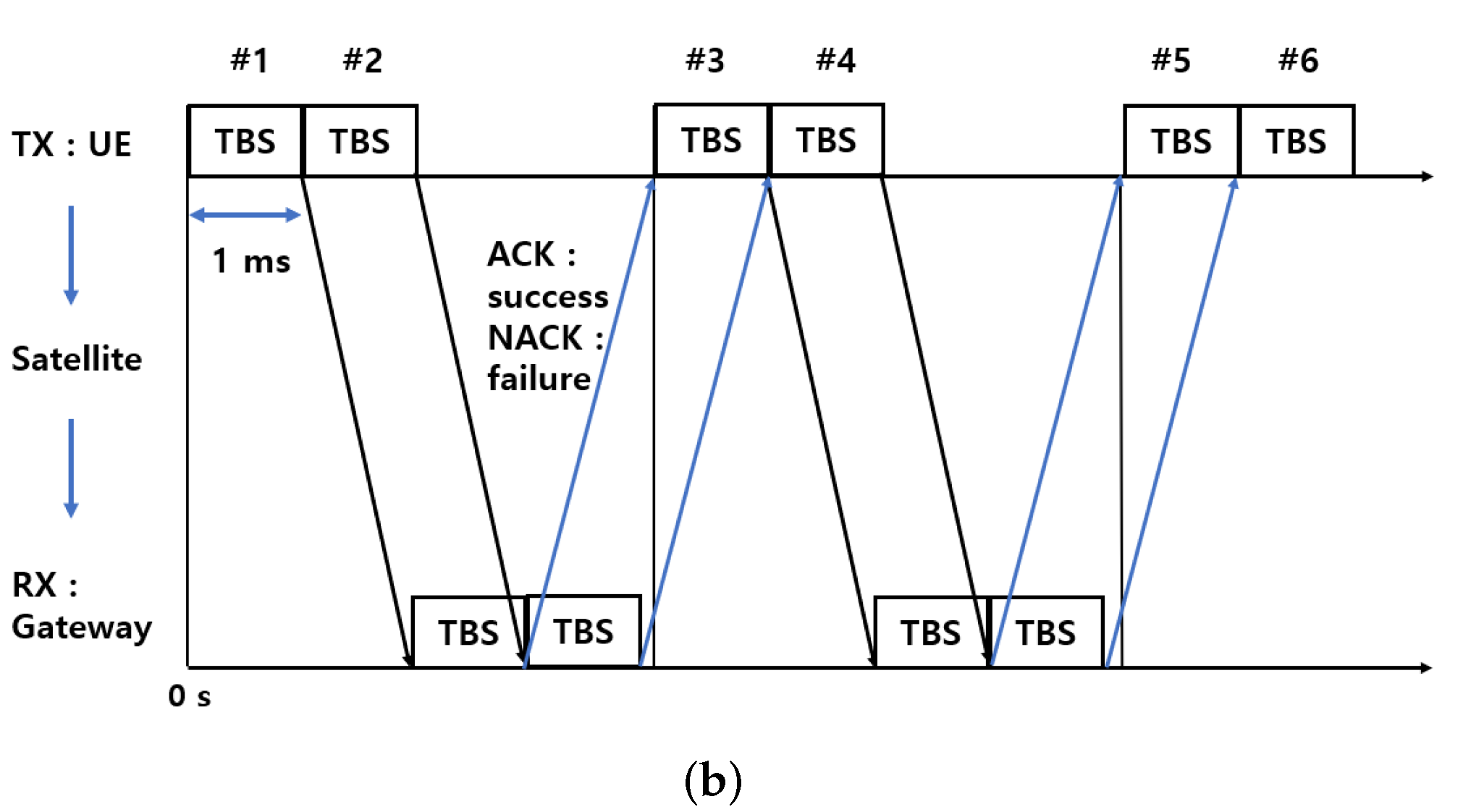
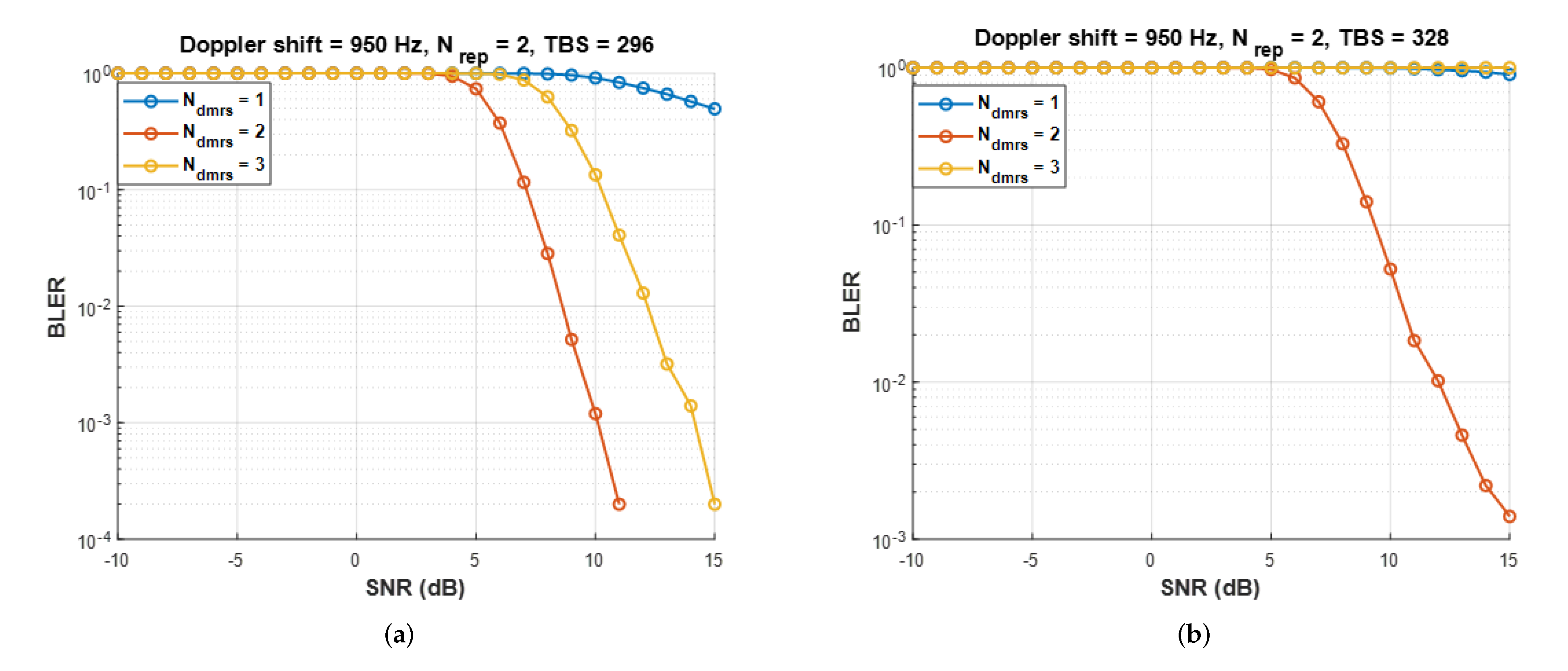
5.1. Block Error Rate (BLER)
5.2. Throughput
5.3. Link Margin
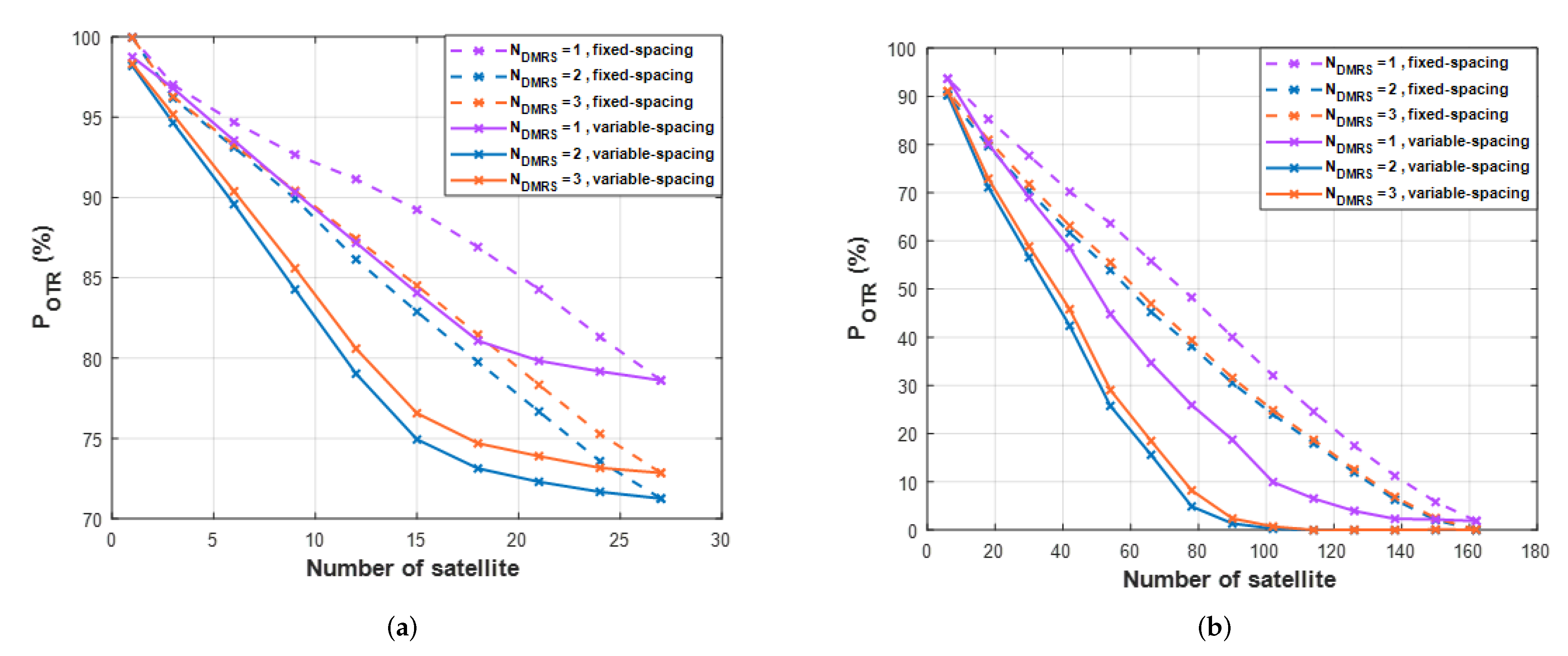
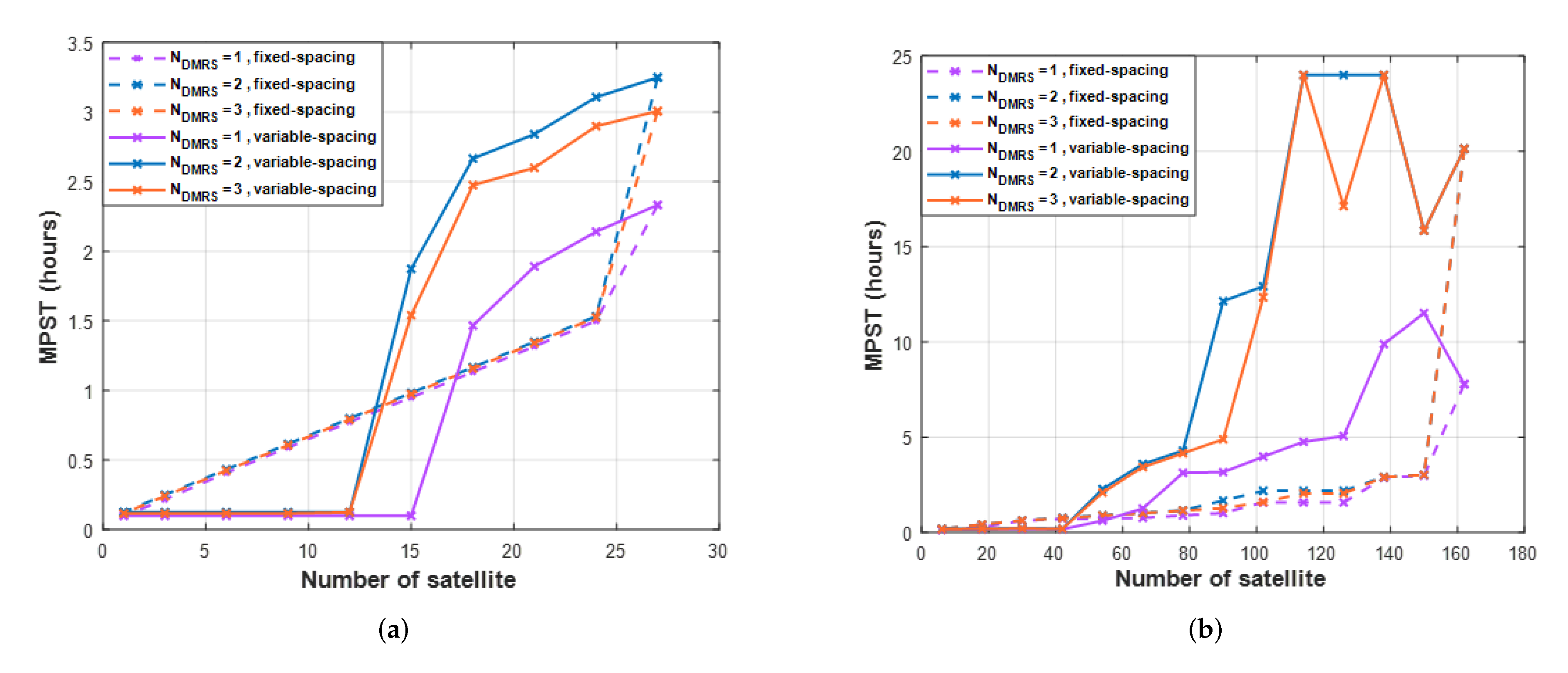
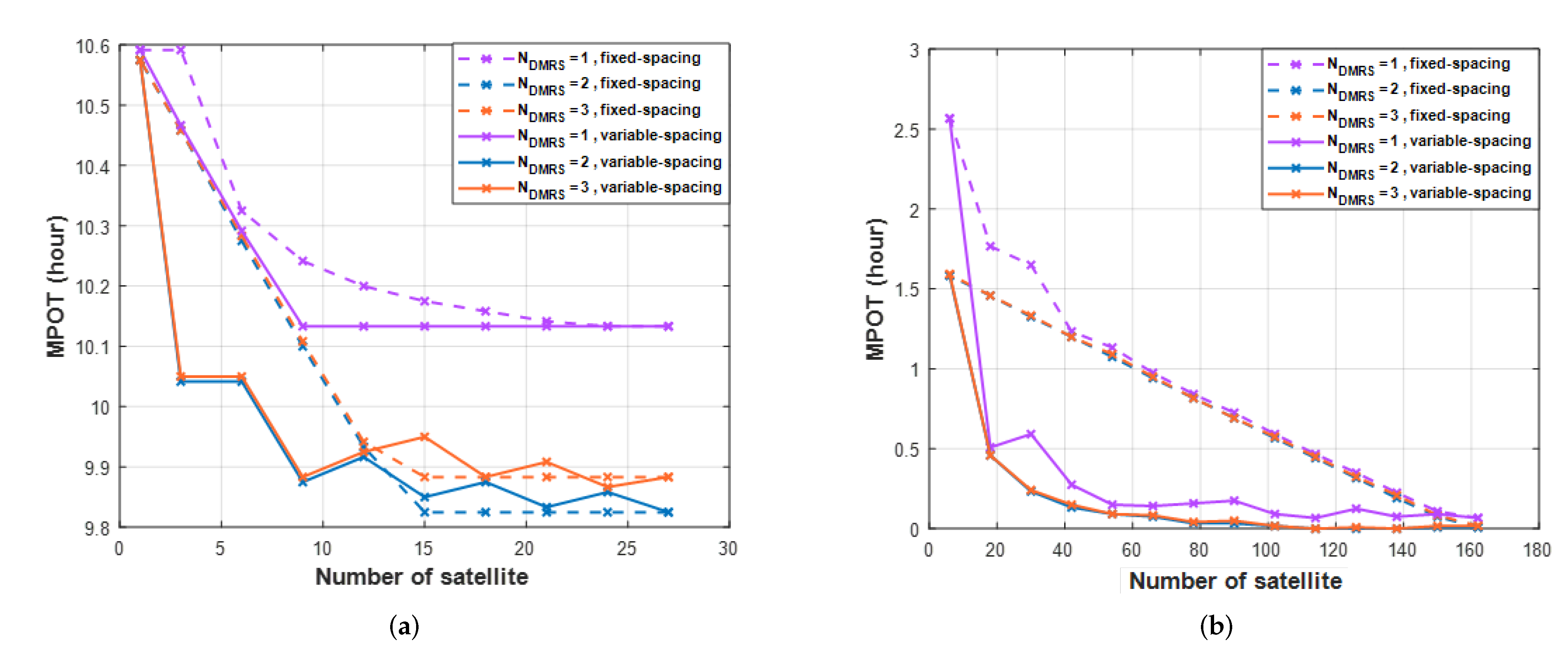
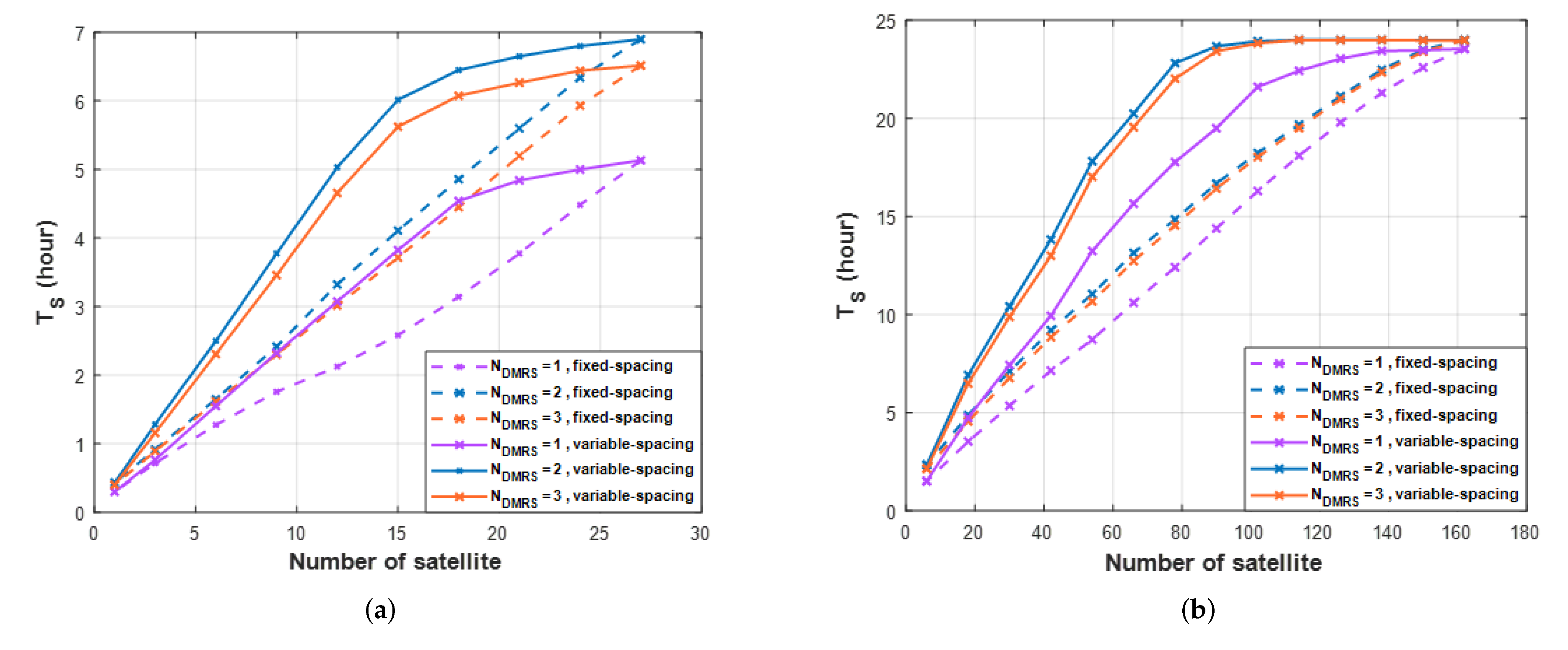
6. Numerical Results
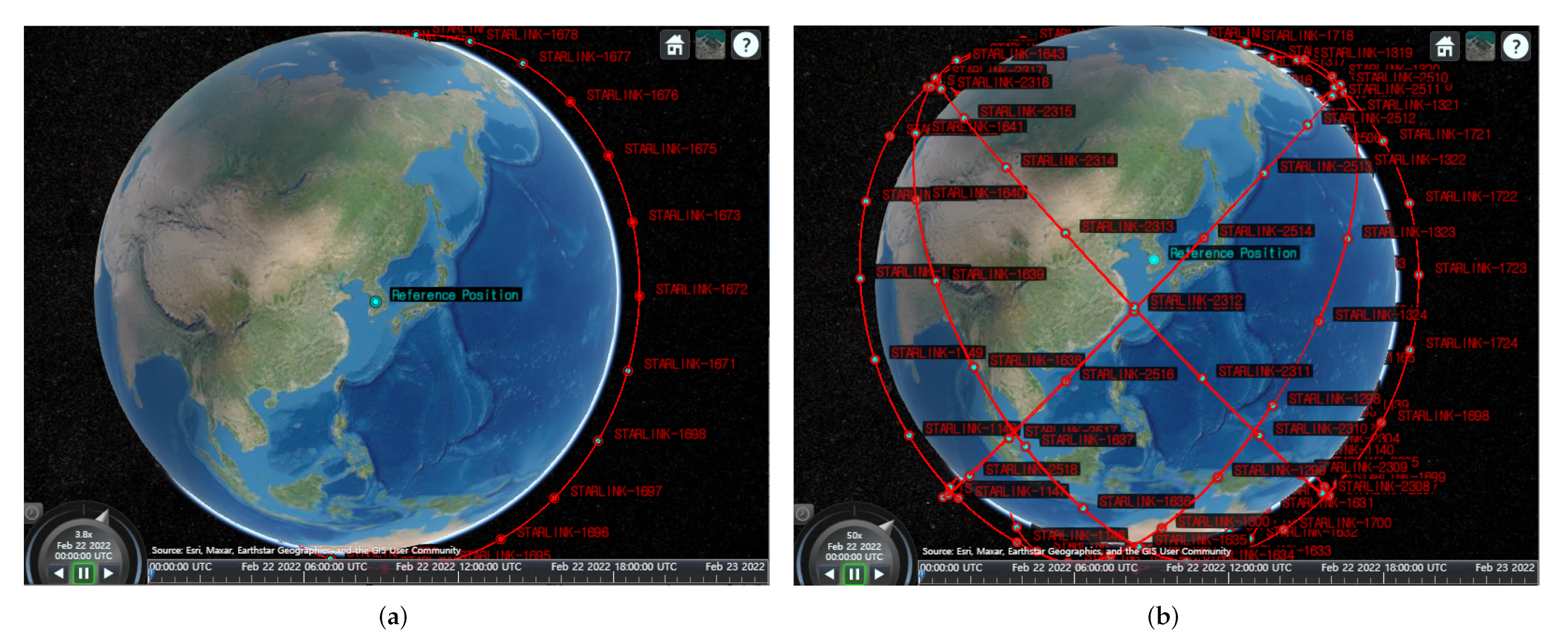
6.1. Link-Level Simulation
6.2. Link Budget Simulation
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cisco, U. Cisco Annual Internet Report (2018–2023) White Paper; Cisco: San Jose, CA, USA, 2020. [Google Scholar]
- ITU. Setting the Scene for 5G: Opportunities & Challenges; ITU: Geneva, Switzerland, 2018. [Google Scholar]
- Utochukwu, O.E.; Abu-Mahfouz, A.M.; Kurien, A.M. A Survey on 5G and LPWAN-IoT for Improved Smart Cities and Remote Area Applications: From the Aspect of Architecture and Security. Sensors 2022, 22, 6313. [Google Scholar]
- Guidotti, A.; Vanelli-Coralli, A.; Conti, M.; Andrenacci, S.; Chatzinotas, S.; Maturo, N.; Evans, B.; Awoseyila, A.; Ugolini, A.; Foggi, T.; et al. Architectures and Key Technical Challenges for 5g Systems Incorporating Satellites. IEEE Trans. Veh. Technol. 2019, 68, 2624–2639. [Google Scholar] [CrossRef]
- Study on New Radio (NR) to Support Non Terrestrial Networks. Document TR 38.811, Release 15, 3GPP, September 2020. Available online: https://www.3gpp.org/ (accessed on 30 June 2022).
- Study on NB-IoT/eMTC Support for Non-Terrestrial Network. Document RP-193235, 3GPP, TSG RAN Meeting, December 2019. Available online: https://www.3gpp.org/ (accessed on 30 June 2022).
- Study on NarrowBand Internet of Things (NB-IoT)/Enhanced Machine Type Communication (eMTC) Support for Non-Terrestrial Networks (NTN), Document TR 36.763, Release 17, 3GPP, May. 2021. Available online: https://www.3gpp.org/ (accessed on 30 June 2022).
- Cooper, P. Statement of Patricia Cooper Vice President, Satellite Government Affairs Space Exploration Technologies Corp (SpaceX); United States Senate: Washington, DC, USA, 2017. [Google Scholar]
- Latachi, I.; Karim, M.; Hanafi, A.; Rachidi, T.; Khalayoun, A.; Assem, N.; Dahbi, S.; Zouggar, S. Link budget analysis for a LEO cubesat communication subsystem. In Proceedings of the 2017 International Conference on Advanced Technologies for Signal and Image Processing (ATSIP), Fez, Morocco, 22–24 May 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Lin, Z.; Niu, H.; An, K.; Wang, Y.; Zheng, G.; Chatzinotas, S.; Hu, Y. Refracting RIS aided hybrid satellite-terrestrial relay networks: Joint beamforming design and optimization. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 3717–3724. [Google Scholar] [CrossRef]
- Lin, Z.; An, K.; Niu, H.; Hu, Y.; Chatzinotas, S.; Zheng, G.; Wang, J. SLNR-based Secure Energy Efficient Beamforming in Multibeam Satellite Systems. IEEE Trans. Aerosp. Electron. Syst. 2022. [Google Scholar] [CrossRef]
- An, K.; Liang, T.; Zheng, G.; Yan, X.; Li, Y.; Chatzinotas, S. Performance limits of cognitive-uplink FSS and terrestrial FS for Ka-band. IEEE Trans. Aerosp. Electron. Syst. 2018, 55, 2604–2611. [Google Scholar] [CrossRef]
- Choi, S.-W.; Kim, I.; Ahn, J.M. Uplink Frequency Offset Compensation Scheme for High-Speed moving terminals. J. Korean Inst. Commun. Inf. Sci. 2015, 40, 1699–1709. [Google Scholar]
- Lee, J.; Lou, H.; Toumpakaris, D.; Cioffi, J.M. Effect of carrier frequency offset on OFDM systems for multipath fading channels. In Proceedings of the IEEE Global Telecommunications Conference, GLOBECOM ’04, Dallas, TX, USA, 29 November–3 December 2004; Volume 6, pp. 3721–3725. [Google Scholar] [CrossRef]
- Cho, Y.S.; Kim, J.; Yang, W.Y.; Kang, C.G. MIMO-OFDM Wireless Communications with MATLAB; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Evans, B.G. Satellite Communication Systems; IET: London, UK, 1999; Volume 38. [Google Scholar]
- Kolawole, M.O. Satellite Communication Engineering; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Electronics and Telecommunications Research Institute. Compensation Method of the Doppler Shift Frequency in the Non-Geostationary Satellite Orbit Mobile Satellite Communication System. Korea Patent No. 1020000083264, 27 December 2000.
- Evolved Universal Terrestrial Radio Access (E-UTRA); Physical Channels and Modulation, Document TS 36.211, Release 16, 3GPP, June 2021. Available online: https://www.3gpp.org/ (accessed on 30 June 2022).
- Technical Specification Group Service and System Aspects; Service Requirements for the 5G System Document TS 22.261, Release 18, 3GPP, April 2021. Available online: https://www.3gpp.org/ (accessed on 30 June 2022).
- Solutions for NR to Support Non-Terrestrial Networks (NTN), Document TR 38.821, Release 16, 3GPP, January 2020. Available online: https://www.3gpp.org/ (accessed on 30 June 2022).
- Guidotti, A.; Vanelli-Coralli, A.; Caus, M.; Bas, J.; Colavolpe, G.; Foggi, T.; Cioni, S.; Modenini, A.; Tarchi, D. Satellite-enabled LTE systems in LEO constellations. In Proceedings of the 2017 IEEE International Conference on Communications Workshops (ICC Workshops), Paris, France, 21–25 May 2017; pp. 876–881. [Google Scholar]
- Evolved Universal Terrestrial Radio Access (E-UTRA) and Evolved UTRAN(E-UTRAN), Document TR 25.913. 3GPP, December 2009. Available online: https://www.3gpp.org/ (accessed on 30 June 2022).
- Kodheli, O.; Andrenacci, S.; Maturo, N.; Chatzinotas, S.; Zimmer, F. Resource Allocation Approach for Differential Doppler Reduction in NB-IoT over LEO Satellite. In Proceedings of the 2018 9th Advanced Satellite Multimedia Systems Conference and the 15th Signal Processing for Space Communications Workshop (ASMS/SPSC), Berlin, Germany, 10–12 September 2018; pp. 1–8. [Google Scholar]
- Conti, M.; Andrenacci, S.; Maturo, N.; Chatzinotas, S.; Vanelli-Coralli, A. Doppler Impact Analysis for NB-IoT and Satellite Systems Integration. In Proceedings of the ICC 2020-2020 IEEE International Conference on Communications (ICC), Dublin, Ireland, 7–11 June 2020; pp. 1–7. [Google Scholar]
- Sun, S.; Hu, J.; Peng, Y.; Pan, X.; Zhao, L.; Fang, J. Support for vehicle-to-everything services based on LTE. IEEE Wirel. Commun. 2016, 23, 4–8. [Google Scholar] [CrossRef]
- Kundu; Lopamudra; Xiong, G.; Cho, J. Physical uplink control channel design for 5G new radio. In Proceedings of the 2018 IEEE 5G World Forum (5GWF), Silicon Valley, CA, USA, 9–11 July 2018. [Google Scholar]
- Min-Gyu, K.; Jo, H. Problem and solution for NB-IoT uplink in Low Earth Orbit satellite communication. In Proceedings of the 2022 International Conference on Electronics, Information and Communication (ICEIC), Jeju, Korea, 6–9 February 2022. [Google Scholar]
- Kelso, T.S. NORAD General Perturbations (GP) Element Sets Current Data. 2022. Available online: http://www.celestrak.com/NORAD/elements/ (accessed on 22 February 2022).
- Evolved Universal Terrestrial Radio Access (EUTRA); LTE Coverage Enhancements, document TR 36.824, Release 11, 3GPP, June 2012. Available online: https://www.3gpp.org/ (accessed on 30 June 2022).
- Wang, Y.-P.E.; Lin, X.; Adhikary, A.; Grovlen, A.; Sui, Y.; Blankenship, Y.; Bergman, J.; Razaghi, H.S. A Primer on 3GPP Narrowband Internet of Things. IEEE Commun. Mag. 2017, 55, 117–123. [Google Scholar] [CrossRef]
- Chaitanya, T.V.K. HARQ Systems: Resource Allocation, Feedback Error Protection, and Bits-to-Symbol Mappings. Ph.D. Thesis, Linköping University Electronic Press, Linköping, Sweden, 2013. [Google Scholar]
- Evolved Universal Terrestrial Radio Access (EUTRA); Multiplexing and Channel Coding, Document TS 36.212, Release 16, 3GPP, October 2020. Available online: https://www.3gpp.org/ (accessed on 30 June 2022).
- Evolved Universal Terrestrial Radio Access (EUTRA); Physical Layer Procedures, Document TS 36.213, Release 16, 3GPP, October 2020. Available online: https://www.3gpp.org/ (accessed on 30 June 2022).
- Liberg, O.; Lowenmark, S.E.; Euler, S.; Hofstrom, B.; Khan, T.; Lin, X.; Sedin, J. Narrowband Internet of Things for Non-Terrestrial Networks. IEEE Commun. Stand. Mag. 2020, 4, 49–55. [Google Scholar] [CrossRef]
- Study on Channel Model for Frequencies from 0.5 to 100 GHz, Document TR 38.901, Release 16, 3GPP, October 2019. Available online: https://www.3gpp.org/ (accessed on 30 June 2022).
- Batariere, M.; Baum, K.; Krauss, T.P. Cyclic prefix length analysis for 4G OFDM systems. In Proceedings of the IEEE 60th Vehicular Technology Conference, VTC2004-Fall, Los Angeles, CA, USA, 26–29 September 2004; pp. 543–547. [Google Scholar]
- Ikpehai, A.; Adebisi, B.; Rabie, K.M.; Anoh, K.; Ande, R.E.; Hammoudeh, M.; Gacanin, H.; Mbanaso, U.M. Low-power wide area network technologies for Internet-of-Things: A comparative review. IEEE Internet Things J. 2018, 6, 2225–2240. [Google Scholar] [CrossRef] [Green Version]
- Ikpehai, A.; Adebisi, B.; Rabie, K.M.; Anoh, K.; Ande, R.E.; Hammoudeh, M.; Gacanin, H.; Mbanaso, U.M. An enhanced cooperative communication scheme for physical uplink shared channel in NB-IoT. Wirel. Pers. Commun. 2021, 120, 2367–2386. [Google Scholar]
- Xie, H.; Zhan, Y.; Zeng, G.; Pan, X. LEO mega-constellations for 6G global coverage: Challenges and opportunities. IEEE Access 2021, 9, 164223–164244. [Google Scholar] [CrossRef]
- Zhou; Haotian; Liu, L.; Ma, H. Coverage and capacity analysis of LEO satellite network supporting Internet of Things. In Proceedings of the ICC 2019-2019 IEEE International Conference on Communications (ICC), Shanghai, China, 20–24 May 2019. [Google Scholar]
- Huang, Y.; Boyle, K. Antennas: From Theory to Practice; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Chang, K. RF and Microwave Wireless Systems; John Wiley & Sons: Hoboken, NJ, USA, 2004; Volume 161. [Google Scholar]
- MATLAB Satellite Communication Toolbox. Model, Visualize, and Analyze Satellite Scenario. Available online: https://kr.mathworks.com/help/satcom/gs/model-and-visualize-satelliteScenario.html (accessed on 8 December 2021).





| Parameter | Value |
|---|---|
| Frequency band | S-band (2 GHz) |
| Satellite altitude | 600 [km] |
| Maximum Doppler shift | 24 [ppm] |
| Residual Doppler shift | 1.05 [ppm] for 50 km beam diameter |
| after | 1.88 [ppm] for 90 km beam diameter |
| pre-compensation | 15.82 [ppm] for 1000 km beam diameter |
| Parameter | Value |
|---|---|
| Satellite altitude | 552 [km] |
| Satellite effective isotropic radiated power (EIRP) | 34 [dBW/MHz] |
| Satellite antenna gain | 30 [dBi] |
| Equivalent satellite antenna aperture | 2 [m] |
| Antenna gain-to-noise-temperature (G/T) | 1.1 [dB/K] |
| Parameter | Value |
|---|---|
| Frequency band () | S-band (2 GHz) |
| Antenna type and configuration | (1,1,2) with omnidirectional antenna element |
| Polarization | Linear: |
| Antenna temperature | 290 [K] |
| Noise figure | 7 [dB] |
| Transmit power | 200 [mW] |
| Antenna gain | 0 [dBi] |
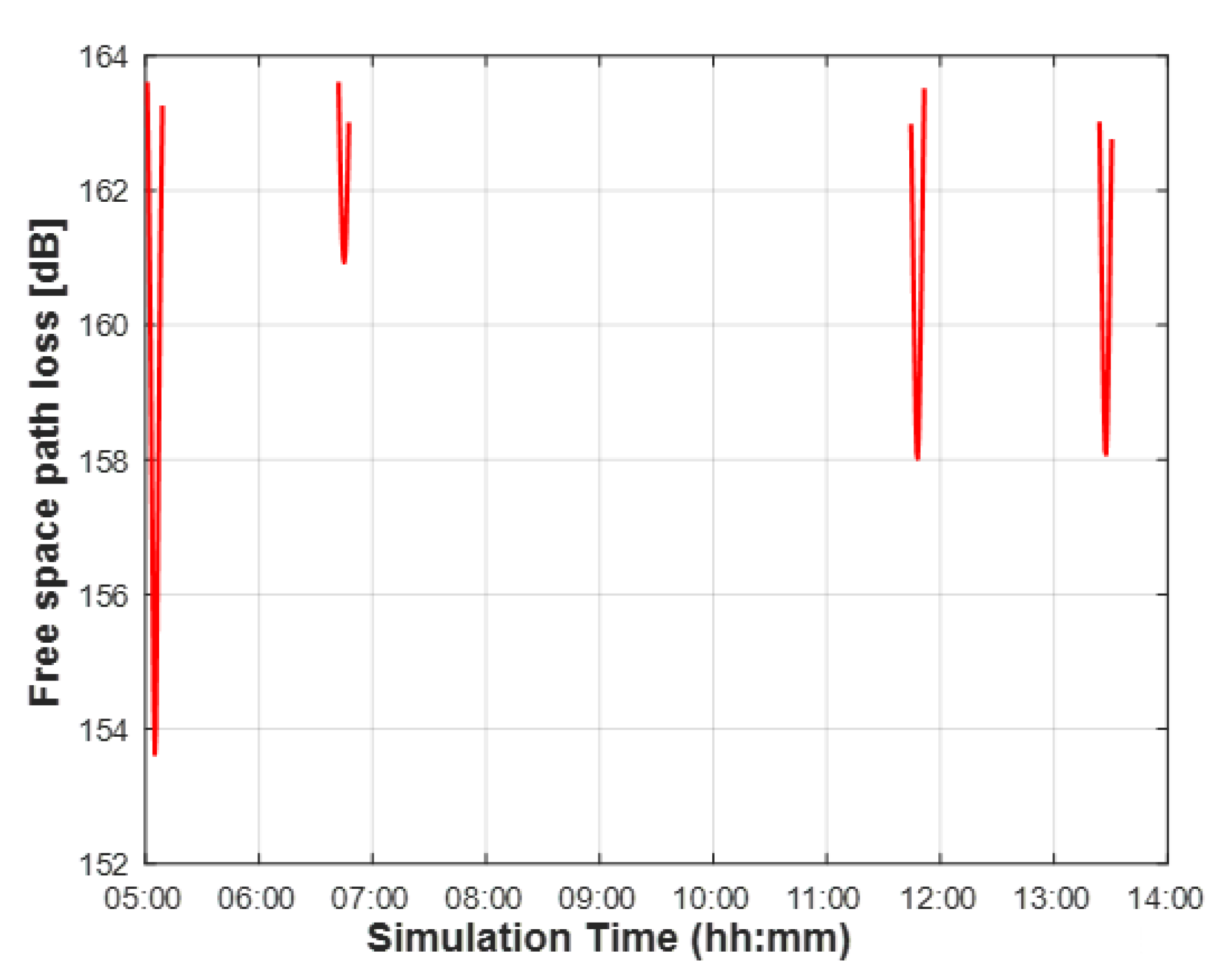
| Source | Target | Start Time | End Time | Duration [s] |
|---|---|---|---|---|
| Reference Position | STARLINK-1698 | 05:01:30 | 05:09:00 | 450 |
| Reference Position | STARLINK-1698 | 06:42:30 | 06:47:30 | 300 |
| Reference Position | STARLINK-1698 | 11:44:30 | 11:51:00 | 390 |
| Reference Position | STARLINK-1698 | 13:24:00 | 13:30:30 | 390 |
| Parameter | Value |
|---|---|
| FFT size | 128 |
| SCS | 15 [kHz] |
| Multiple access | SC-FDMA |
| Modulation | QPSK |
| Channel coding | 1/3 Turbo code |
| TBS | 120 bits |
| Fading channel model | 3GPP TDL-D |
| Residual Doppler shift | 0, 950 [Hz] |
| 2 | |
| Bandwidth | 180 [kHz] |
| Parameter | Value | |
|---|---|---|
| Transmit power | −6.99 dBW | 200 mW ->10log(0.2) |
| Transmit antenna gain | 0 dBi | Antenna gain |
| EIRP (effective isotropic radiated power) | −6.99 dBW | Transmit power + antenna gain |
| Atmospheric loss | 0.07 dB | [21] |
| Shadow fading margin | 3.00 dB | |
| Scintillation loss | 2.20 dB | |
| Polarization loss | 0.00 dB | |
| Additional losses | 0.00 dB | |
| Boltzmann’s constant [k] | −228.6 dBW/K/Hz | |
| Bandwidth [B] | 52.55 dBHz |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, M.-G.; Jo, H.-S. Performance Analysis of NB-IoT Uplink in Low Earth Orbit Non-Terrestrial Networks. Sensors 2022, 22, 7097. https://doi.org/10.3390/s22187097
Kim M-G, Jo H-S. Performance Analysis of NB-IoT Uplink in Low Earth Orbit Non-Terrestrial Networks. Sensors. 2022; 22(18):7097. https://doi.org/10.3390/s22187097
Chicago/Turabian StyleKim, Min-Gyu, and Han-Shin Jo. 2022. "Performance Analysis of NB-IoT Uplink in Low Earth Orbit Non-Terrestrial Networks" Sensors 22, no. 18: 7097. https://doi.org/10.3390/s22187097





