Accuracy of Inertial Measurement Units When Applied to the Countermovement Jump of Track and Field Athletes
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Overview
2.2. Participants
2.3. Experimental Procedures
2.4. Instruments
2.5. Data Processing
2.6. Statistical Analysis
3. Results
3.1. Descriptive Analysis
3.2. Force Data Signal
3.3. Accuracy Data
4. Discussion
4.1. Force Data Signal
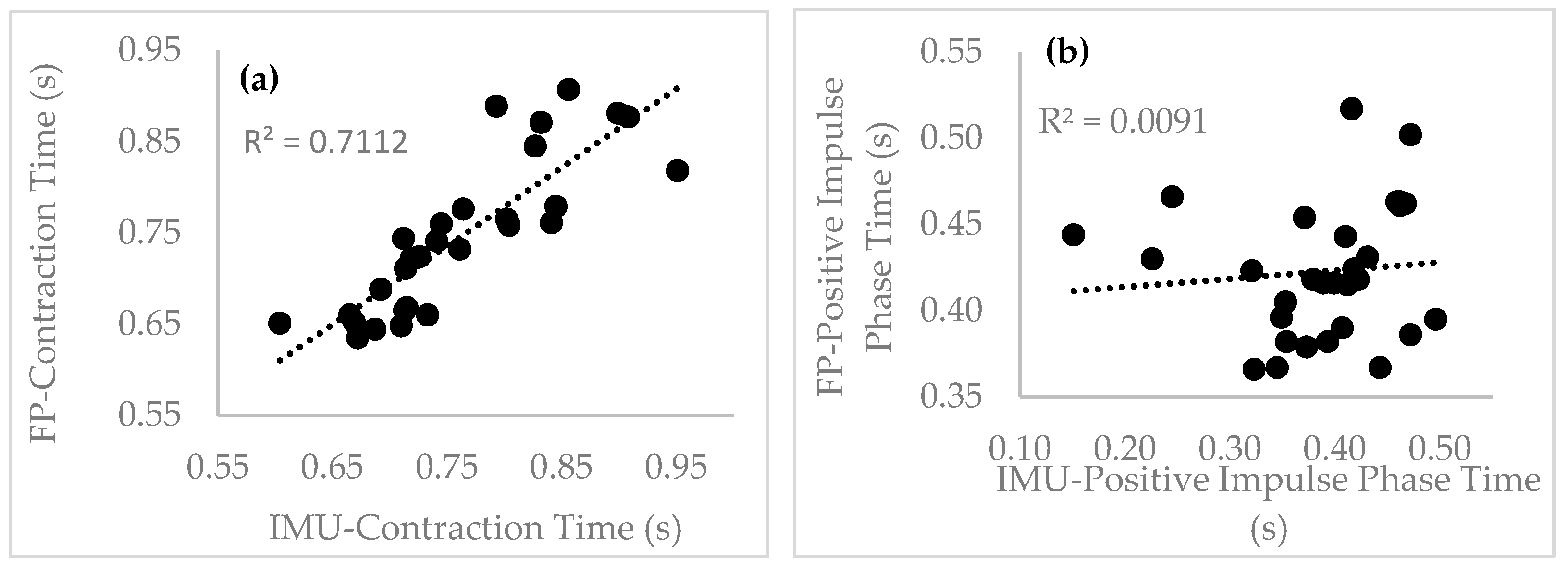
4.2. Accuracy of Temporal Parameters
4.3. Kinematic Parameter Accuracy
4.4. Kinetic Parameter Accuracy
4.5. Recommendations and Practical Applications
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Philpott, L.K.; Forrester, S.E.; van Lopik, K.A.; Hayward, S.; Conway, P.P.; West, A.A. Countermovement jump performance in elite male and female sprinters and high jumpers. J. Sports Eng. Technol. 2020, 135, 131–138. [Google Scholar] [CrossRef]
- González-Badillo, J.J.; Marques, M.C. Relationship Between Kinematic Factors and Countermovement Jump Height in Trained Track and Field Athletes. J. Strength Cond. Res. 2010, 24, 3443–3447. [Google Scholar] [CrossRef]
- Gathercole, R.; Sporer, B.; Stellingwerff, T. Countermovement Jump Performance with Increased Training Loads in Elite Female Rugby Athletes. Int. J. Sports Med. 2015, 36, 722–728. [Google Scholar] [CrossRef] [PubMed]
- Beattie, K.; Tawiah-Dodoo, J.; Graham-Smith, P. Counter-movement Jump Characteristics of World-Class Elite and Sub-Elite Male Sprinters. Sport Perform. Sci. Rep. 2020, 106, 1–4. [Google Scholar]
- Lake, J.; Mundy, P.; Comfort, P.; McMahon, J.J.; Suchomel, T.J.; Carden, P. Concurrent Validity of a Portable Force Plate Using Vertical Jump Force–Time Characteristics. J. Appl. Biomech. 2018, 34, 410–413. [Google Scholar] [CrossRef] [PubMed]
- Balsalobre-Fernández, C.; Glaister, M.; Lockey, R.A. The validity and reliability of an iPhone app for measuring vertical jump performance. J. Sports Sci. 2015, 33, 1574–1579. [Google Scholar] [CrossRef]
- Bosco, C.; Luhtanen, P.; Komi, P. A Simple Method for Measurement of Mechanical Power in Jumping. Eur. J. Appl. Physiol. 1983, 50, 273–282. [Google Scholar] [CrossRef]
- Buckthorpe, M.; Morris, J.; Folland, J.P. Validity of vertical jump measurement devices. J. Sports Sci. 2012, 30, 63–69. [Google Scholar] [CrossRef] [PubMed]
- Cruvinel-Cabral, R.M.; Oliveira-Silva, I.; Medeiros, A.R.; Claudino, J.G.; Jiménez-Reyes, P.; Boullosa, D.A. The validity and reliability of the “My Jump App” for measuring jump height of the elderly. PeerJ. 2018, 6, e5804. [Google Scholar] [CrossRef] [PubMed]
- Glatthorn, J.F.; Gouge, S.; Nussbaumer, S.; Stauffacher, S.; Impellizzeri, F.M.; Maffuletti, N.A. Validity and Reliability of Optojump Photoelectric Cells for Estimating Vertical Jump Height. J. Strength Cond. Res. 2011, 25, 556–560. [Google Scholar] [CrossRef] [PubMed]
- Grainger, M.; Weisberg, A.; Stergiou, P.; Katz, L. Comparison of two methods in the estimation of vertical jump height. J. Hum. Sport Exerc. 2020, 15, 623–632. [Google Scholar] [CrossRef] [Green Version]
- Heredia-Jimenez, J.; Orantes-Gonzalez, E. Comparison of three different measurement systems to assess the vertical jump height. Rev. Bras. Med. Esporte 2020, 20, 143–146. [Google Scholar] [CrossRef]
- Nielsen, E.T.; Jørgensen, P.B.; Mechlenburg, I.; Sørensen, H. Validation of an inertial measurement unit to determine countermovement jump height. Asia-Pac. J. Sports Med. Arthrosc. Rehabil. Technol. 2019, 16, 8–13. [Google Scholar] [CrossRef] [PubMed]
- Picerno, P.; Camomilla, V.; Capranica, L. Countermovement jump performance assessment using a wearable 3D inertial measurement unit. J. Sports Sci. 2011, 29, 139–146. [Google Scholar] [CrossRef] [PubMed]
- Leard, J.S.; Cirillo, M.A.; Katsnelson, E.; Kimiatek, D.A.; Miller, T.W.; Trebincevic, K.; Garbalosa, J.C. Validity of Two Alternative Systems for Measuring Vertical Jump Height. J. Strength Cond. Res. 2007, 21, 1296. [Google Scholar] [PubMed]
- Carlos-Vivas, J.; Martin-Martinez, J.P.; Hernandez-Mocholi, M.A.; Perez-Gomez, J. Validation of the iPhone app using the force platform to estimate vertical jump height. J. Sports Med. Phys. Fit. 2018, 58, 227–232. [Google Scholar] [CrossRef] [PubMed]
- Castagna, C.; Ganzetti, M.; Ditroilo, M.; Giovannelli, M.; Rocchetti, A.; Manzi, V. Concurrent Validity of Vertical Jump Performance Assessment Systems. J. Strength Cond. Res. 2013, 27, 761–768. [Google Scholar] [CrossRef]
- Fathian, R.; Khandan, A.; Chiu, L.; Rouhani, H. Assessment of countermovement jump with and without arm swing using a single inertial measurement unit. Sports Biomech. 2022, 1–18. [Google Scholar] [CrossRef]
- Marković, S.; Dopsaj, M.; Tomažič, S.; Kos, A.; Nedeljković, A.; Umek, A. Can IMU Provide an Accurate Vertical Jump Height Estimate? Appl. Sci. 2021, 11, 12025. [Google Scholar] [CrossRef]
- Mascia, G.; Camomilla, V. An automated method for the estimate of vertical jump power through inertial measurement units. In Proceedings of the 39th International Society of Biomechanics in Sports Conference (Online), Canberra, Australia, 3–6 September 2021. [Google Scholar]
- Camomilla, V.; Bergamini, E.; Fantozzi, S.; Vannozzi, G. Trends supporting the in-field use of wearable inertial sensors for sport performance evaluation: A systematic review. Sensors 2018, 18, 873. [Google Scholar] [CrossRef]
- Rantalainen, T.; Finni, T.; Walker, S. Jump height from inertial recordings: A tutorial for a sports scientist. Scand. J. Med. Sci. Sports 2020, 30, 38–45. [Google Scholar] [CrossRef]
- Chiang, Y.Y.; Shih, W.Y.; Chen, W.H.; Huang, J.L.; Shiang, T.Y. A Machine Learning-Based Countermovement Performance Measurement Method Using a Wearable IMU. In Proceedings of the 2020 International Conference on Pervasive Artificial Intelligence (ICPAI), Taipei, Taiwan, 3–5 December 2020; pp. 79–85. [Google Scholar] [CrossRef]
- Winter, A.D. Biomechanics and Motor Control of Human Movement, 3rd ed.; John Wiley & Sons, Inc: Hoboken, NJ, USA, 2005; pp. 34–53. [Google Scholar]
- McMahon, J.J.; Suchomel, T.J.; Lake, J.P.; Comfort, P. Understanding the Key Phases of the Countermovement Jump Force-Time Curve. Strength Cond. J. 2018, 40, 96–106. [Google Scholar] [CrossRef]
- Miranda-Oliveira, P.; Branco, M.; Fernandes, O.J.; Santos-Rocha, R. Comparison of the accuracy of a free 3D camera system with the Ariel performance system. Comput. Methods Biomech. Biomed. Eng. Imaging Vis. 2021, 9, 670–677. [Google Scholar] [CrossRef]
- Hopkins, W.G.; Marshall, S.W.; Batterham, A.M.; Hanin, J. Progressive statistics for studies in sports medicine and exercise science. Med. Sci. Sports Exerc. 2009, 41, 3–13. [Google Scholar] [CrossRef] [PubMed]
- Kenneally-Dabrowski, C.J.; Serpell, B.G.; Spratford, W. Are accelerometers a valid tool for measuring overground sprinting symmetry? Int. J. Sports Sci. Coach. 2018, 13, 270–277. [Google Scholar] [CrossRef]
- Setuain, I.; Lecumberri, P.; Ahtiainen, J.P.; Mero, A.A.; Häkkinen, K.; Izquierdo, M. Sprint mechanics evaluation using inertial sensor-based technology: A laboratory validation study. Scand. J. Med. Sci. Sports 2018, 28, 463–472. [Google Scholar] [CrossRef] [PubMed]
- Moorhouse, K.M.; Granata, K.P. Trunk stiffness and dynamics during active extension exertions. J. Biomech. 2005, 38, 2000–2007. [Google Scholar] [CrossRef] [PubMed]
- Ramayah, T.; Cheah, J.; Chuah, F.; Ting, H.; Memon, M.A. Assessment of Mediation Analysis. In Partial Least Squares Structural Equation Modeling (PLS-SEM) Using SmartPLS 3.0: An Updated Guide and Practical Guide to Statistical Analysis, 2nd ed.; Pearson: Kuala Lumpur, Malaysia, 2018. [Google Scholar]
- Rogers, S.A.; Hassmén, P.; Hunter, A.; Alcock, A.; Crewe, S.T.; Strauts, J.A.; Gilleard, W.L.; Weissensteiner, J.R. The Validity and Reliability of the MyJump2 Application to Assess Vertical Jumps in Trained Junior Athletes. Meas. Phys. Educ. Exerc. Sci. 2019, 23, 69–77. [Google Scholar] [CrossRef]
- Gallardo-Fuentes, F.; Gallardo-Fuentes, J.; Ramírez-Campillo, R.; Balsalobre-Fernández, C.; Martínez, C.; Caniuqueo, A.; Cañas, R.; Banzer, W.; Loturco, I.; Nakamura, F.Y.; et al. Intersession and Intrasession Reliability and Validity of the My Jump App for Measuring Different Jump Actions in Trained Male and Female Athletes. J. Strength Cond. Res. 2016, 30, 2049–2056. [Google Scholar] [CrossRef]
- McMahon, J.J.; Jones, P.A.; Suchomel, T.J.; Lake, J.; Comfort, P. Influence of the Reactive Strength Index Modified on Force–and Power–Time Curves. Int. J. Sports Physiol. Perform. 2018, 13, 220–227. [Google Scholar] [CrossRef]
- Ruddock, A.D.; Winter, E.M. Jumping depends on impulse not power. J. Sports Sci. 2016, 34, 584–585. [Google Scholar] [CrossRef] [Green Version]



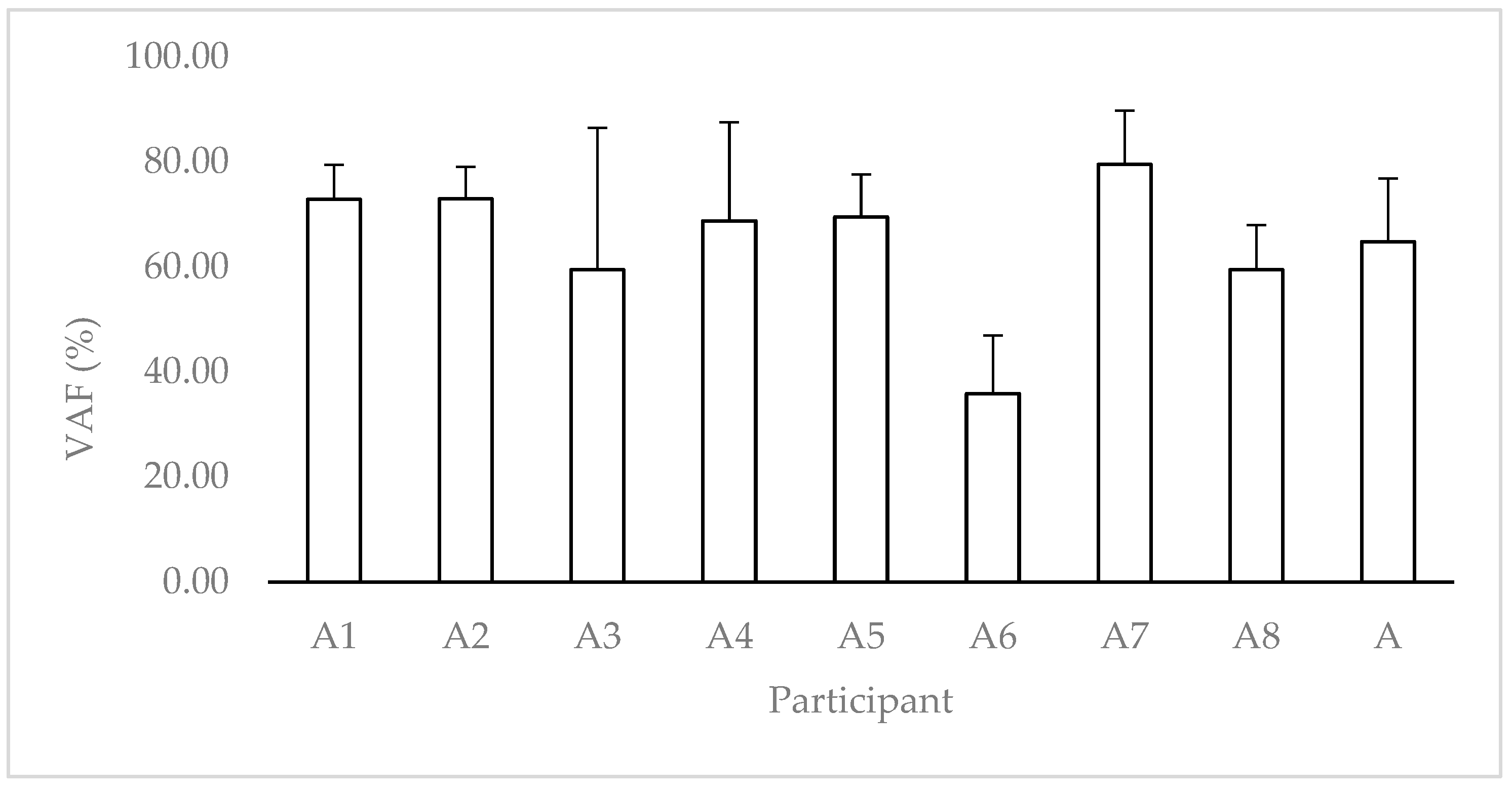

| Analyzed Parameter | Mean (SD) | Minimum | Maximum | |
|---|---|---|---|---|
| Contraction time IMU (s) | 0.761 (0.081) | 0.604 | 0.951 | |
| Contraction time FP (s) | 0.745 (0.083) | 0.635 | 0.907 | * |
| Positive impulse phase time IMU (s) | 0.387 (0.078) | 0.151 | 0.496 | * |
| Positive impulse phase time FP (s) | 0.423 (0.039) | 0.366 | 0.517 | |
| Negative impulse phase time IMU (s) | 0.373 (0.115) | 0.211 | 0.642 | * |
| Negative impulse phase time FP (s) | 0.322 (0.053) | 0.262 | 0.445 | * |
| Flight time IMU (s) | 0.660 (0.042) | 0.532 | 0,734 | |
| Flight time FP (s) | 0.665 (0.040) | 0.562 | 0.734 | |
| Jump height IMU (m) | 0.535 (0.067) | 0.347 | 0.660 | |
| Jump height FP (m) | 0.544 (0.065) | 0.387 | 0.660 | |
| RSI modified IMU (m/s) | 0.710 (0.113) | 0.505 | 1.090 | * |
| RSI modified FP (m/s) | 0.738 (0.119) | 0.567 | 1.020 | * |
| Maximum force IMU (N) | 1753 (270) | 1211 | 2291 | |
| Maximum force FP (N) | 2033 (262) | 1516 | 2485 | |
| Minimum force IMU (N) | 120 (121) | −179 | 386 | |
| Minimum force FP (N) | 108 (121) | −0.746 | 562 | * |
| Analyzed Parameter | Mean Error (SD) | Abs Mean Error | r | p | ¥ |
|---|---|---|---|---|---|
| Contraction time (s) | −0.016 (0.045) | 0.036 | 0.902 | 0.001 | 0.458 |
| Positive impulse Phase time (s) | 0.035 (0.082) | 0.055 | 0.230 | 0.221 | 0.088 |
| Negative impulse Phase time (s) | −0.051 (0.074) | 0.065 | 0.773 | 0.001 | 0.063 |
| Flight time (s) | 0.006 (0.030) | 0.024 | 0.737 | 0.001 | 0.599 |
| Jump height (m) | 0.009 (0.049) | 0.040 | 0.708 | 0.001 | 0.601 |
| RSI modified (m/s) | 0.028 (0.095) | 0.077 | 0.725 | 0.001 | 0.523 |
| Maximum force (N) | 280 (264) | 331 | 0.491 | 0.006 | <0.001 |
| Minimum force (N) | −13 (96) | 76 | 0.758 | 0.001 | 0.099 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miranda-Oliveira, P.; Branco, M.; Fernandes, O. Accuracy of Inertial Measurement Units When Applied to the Countermovement Jump of Track and Field Athletes. Sensors 2022, 22, 7186. https://doi.org/10.3390/s22197186
Miranda-Oliveira P, Branco M, Fernandes O. Accuracy of Inertial Measurement Units When Applied to the Countermovement Jump of Track and Field Athletes. Sensors. 2022; 22(19):7186. https://doi.org/10.3390/s22197186
Chicago/Turabian StyleMiranda-Oliveira, Paulo, Marco Branco, and Orlando Fernandes. 2022. "Accuracy of Inertial Measurement Units When Applied to the Countermovement Jump of Track and Field Athletes" Sensors 22, no. 19: 7186. https://doi.org/10.3390/s22197186






