Research on a Silicon Gyroscope Interface Circuit Based on Closed-Loop Controlled Drive Loop
Abstract
:1. Introduction
2. Drive Loop Modeling and Simulation
2.1. Mechanical Motion Principle of Silicon Gyroscope
2.2. The Establishment of the Closed-Loop Control Drive-Loop Model
2.3. Simulation Result of the Model
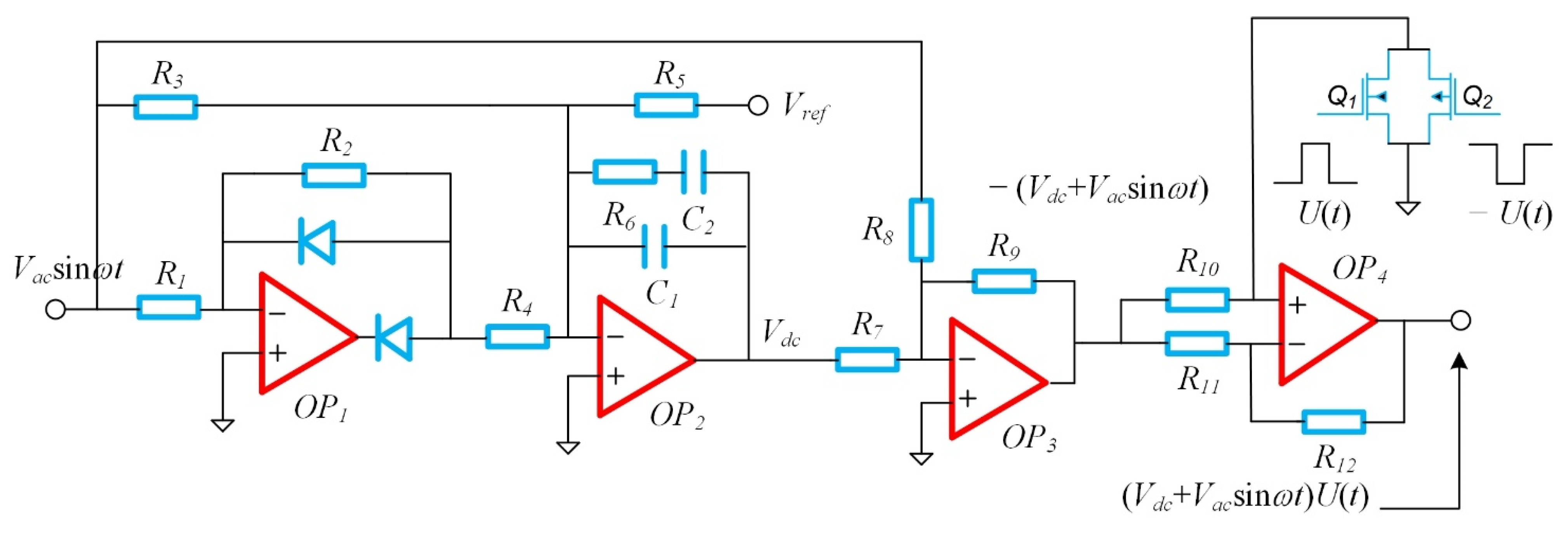
3. Circuit Design and Experiments
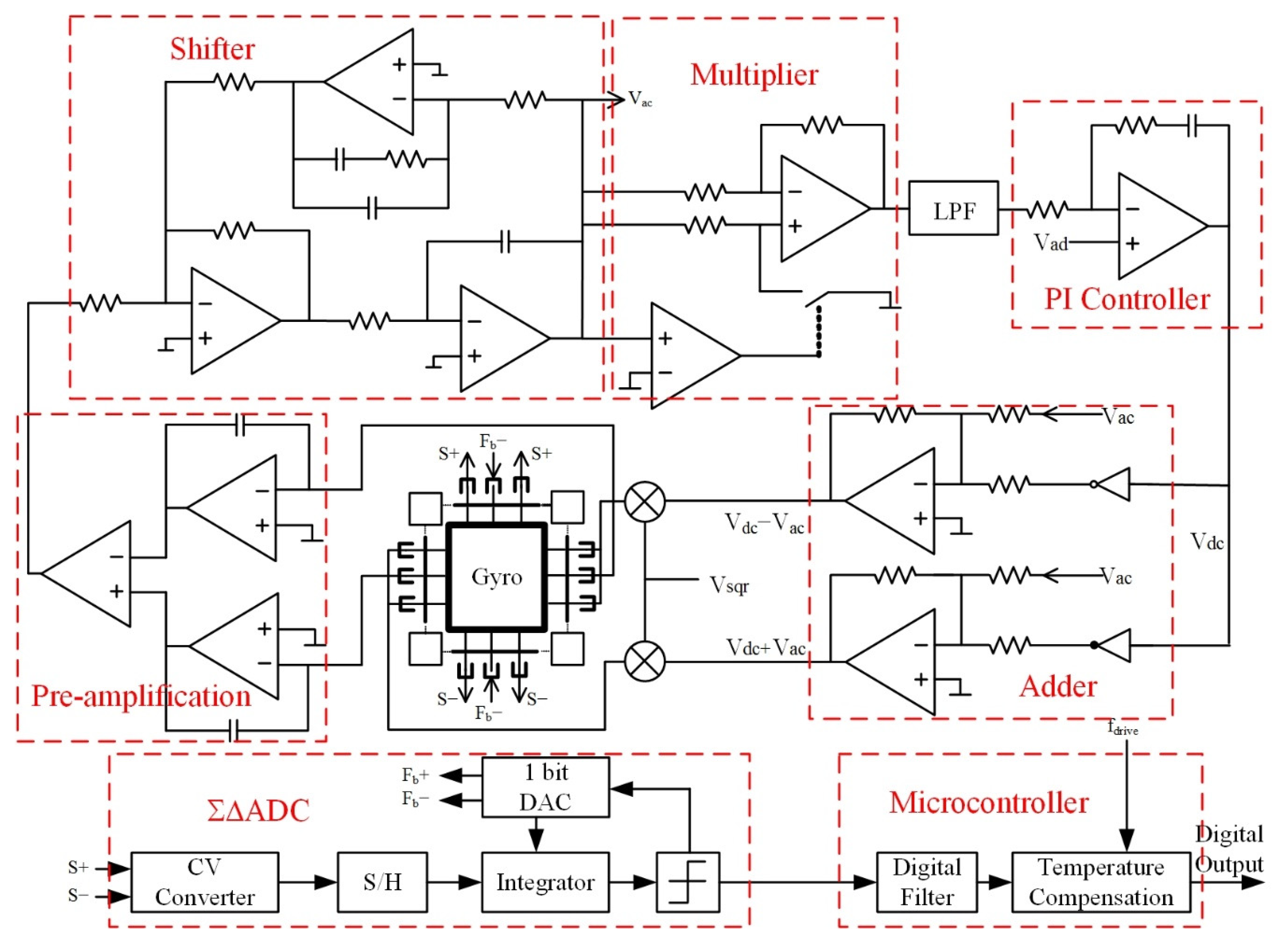
3.1. Overall Design of the Drive Loop
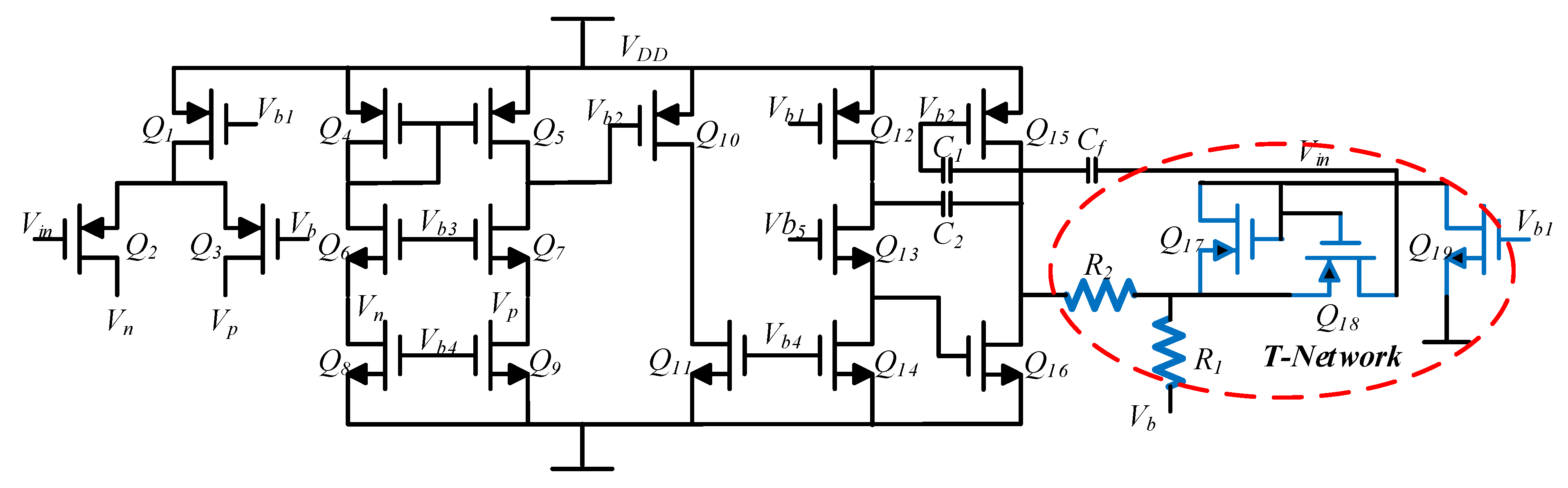
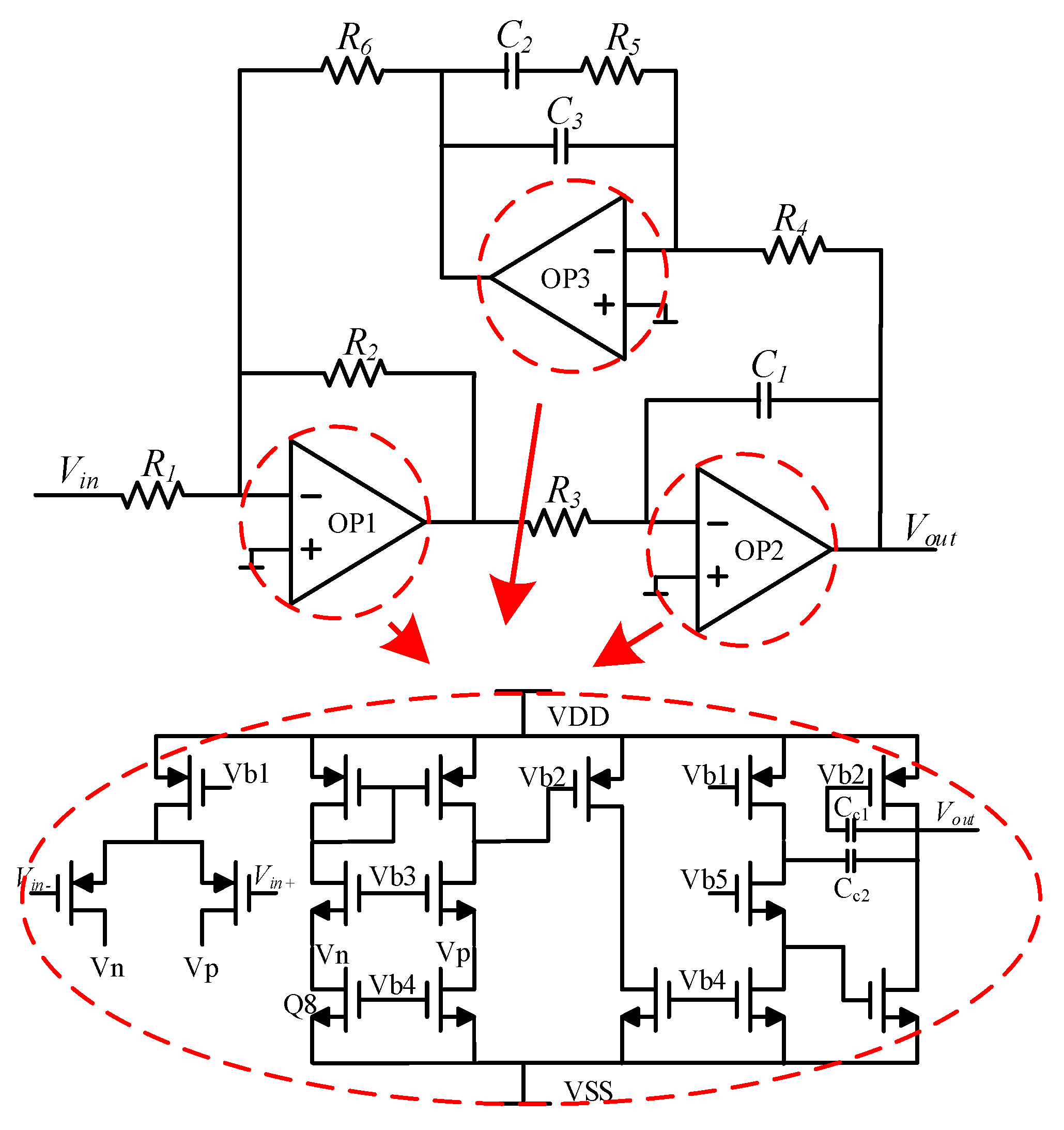
3.2. Circuit Implementation Details
3.2.1. Charge–Voltage (CV) Conversion Circuit
3.2.2. Phase-Compensation Circuit
3.2.3. Automatic Gain Control Circuit
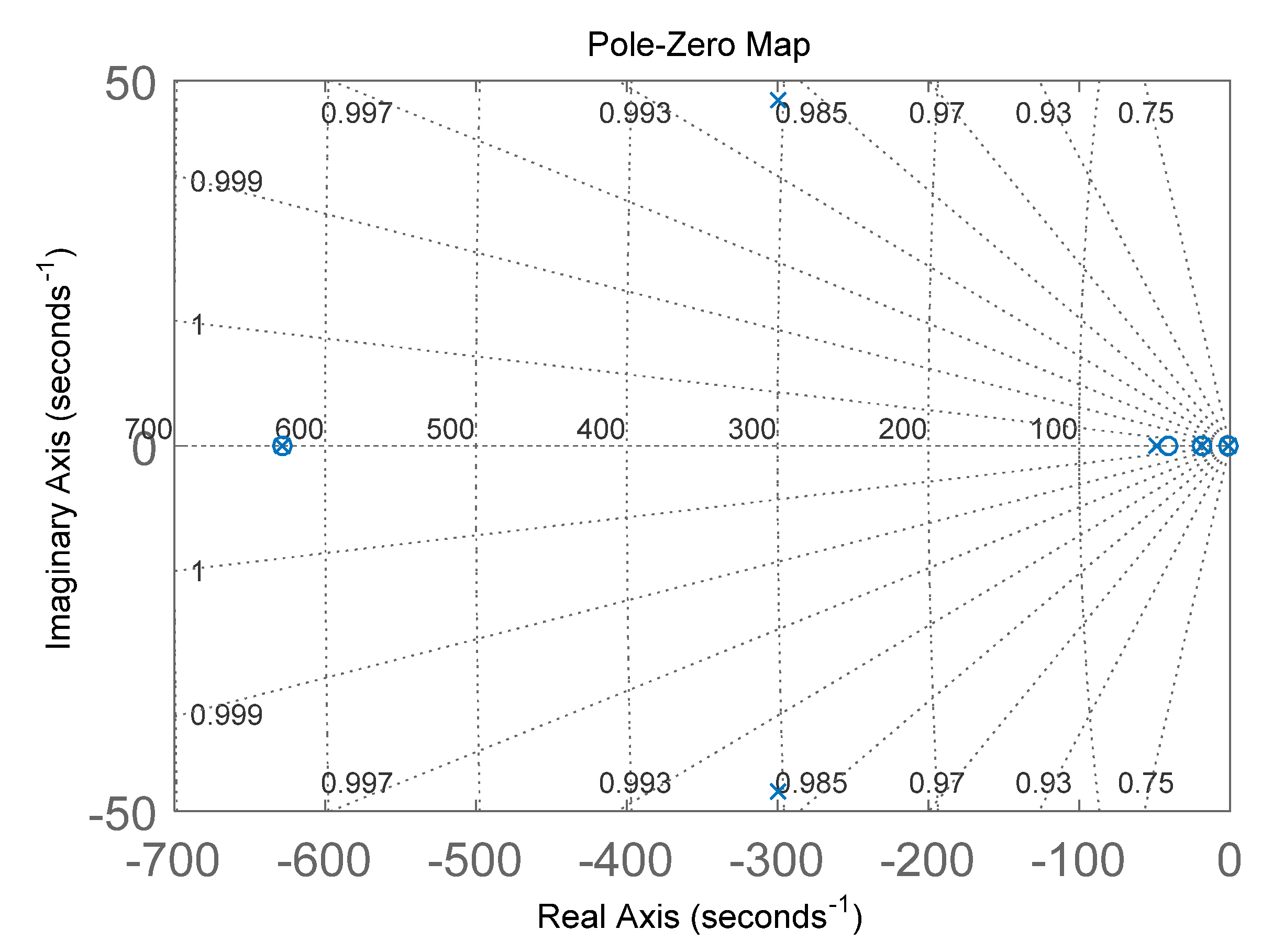
3.3. Verification of Closed-Loop Control Drive-Loop Model
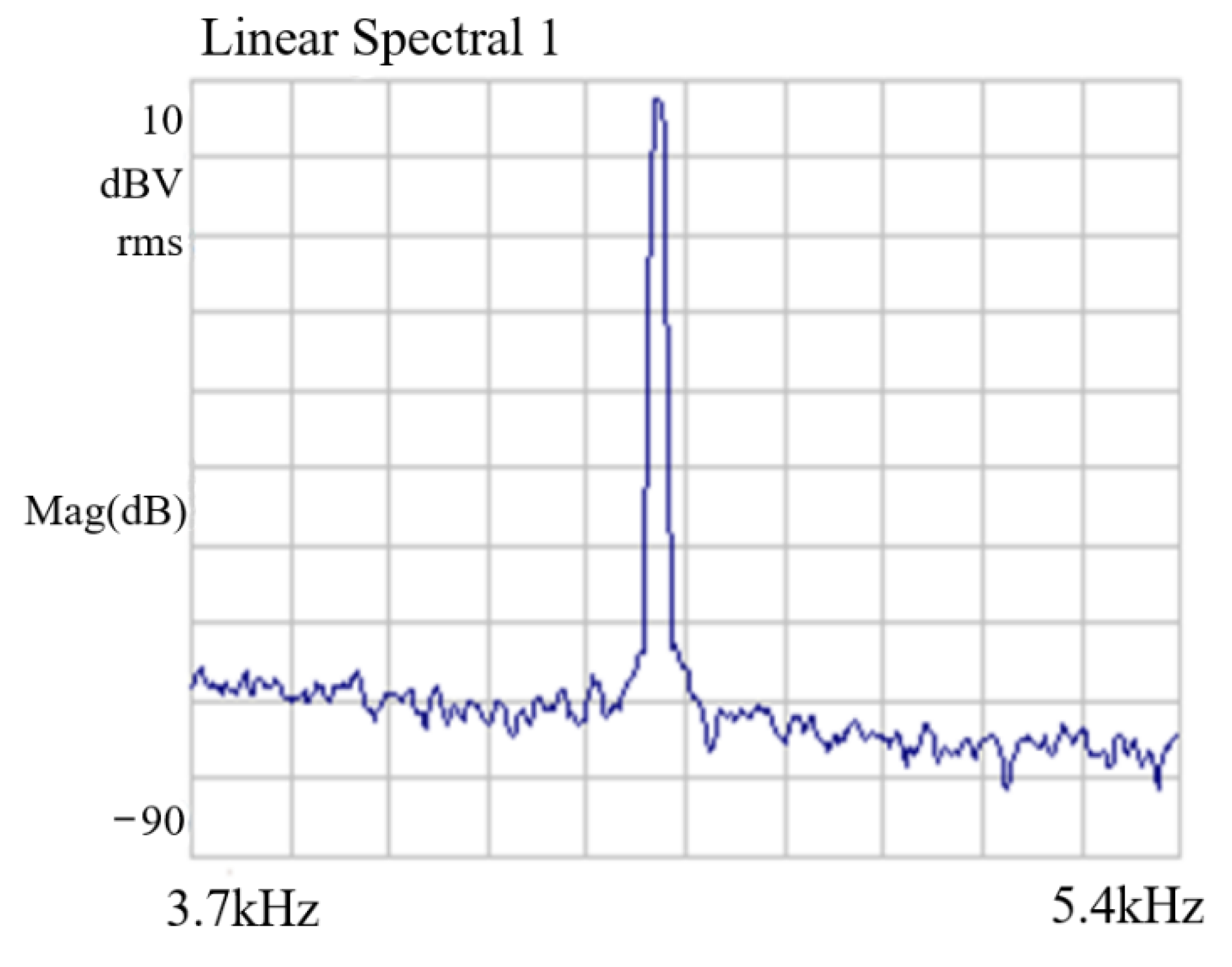
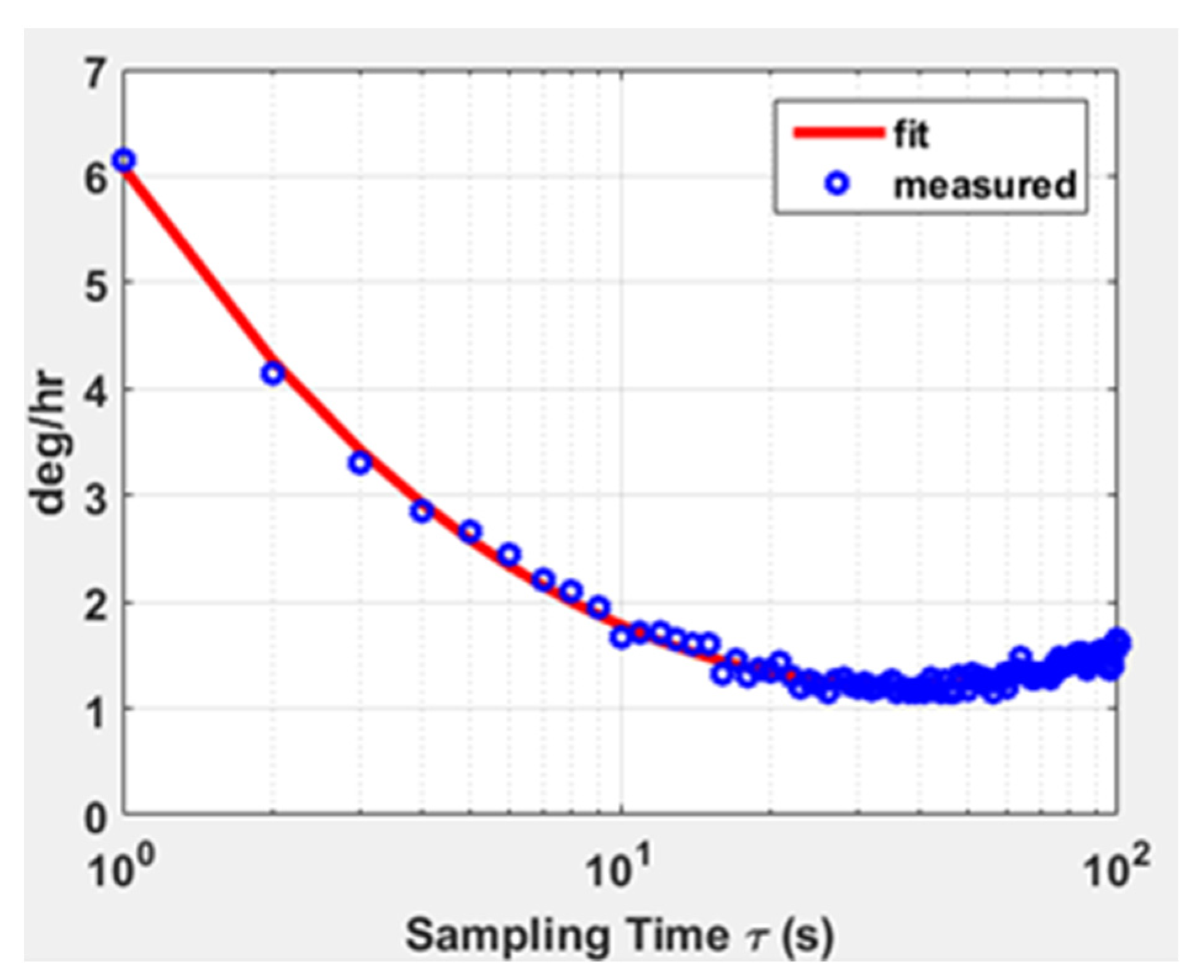
3.4. Experimental Results for the Whole System
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xia, D.Z.; Yu, C.; Kong, L. The Development of Micromachined Gyroscope Structure and Circuitry Technology. Sensors 2014, 14, 1394–1473. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Passaro, V.M.N.; Cuccovillo, A.; Vaiani, L.; Carlo, M.D.; Campanella, C.E. Gyroscope Technology and Applications: A Review in the Industrial Perspective. Sensors 2017, 17, 2284. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ren, X.J.; Zhou, X.; Yu, S.; Wu, X.Z.; Xiao, D.B. Frequency-Modulated MEMS Gyroscopes: A Review. IEEE Sens. J. 2021, 21, 26426–26446. [Google Scholar] [CrossRef]
- Huang, F.X.; Fu, Q.; Liu, X.L.; Zhang, Y.F.; Mao, Z.G. Research on digital silicon gyroscope interface circuit based on bandpass sigma-delta modulator. Int. J. Mod. Phys. B 2019, 33, 1950286. [Google Scholar] [CrossRef]
- Lv, R.S.; Fu, Q.; Yin, L.; Gao, Y.; Bai, W.; Zhang, W.B.; Zhang, Y.F.; Chen, W.P.; Liu, X.W. An Interface ASIC for MEMS Vibratory Gyroscopes with Nonlinear Driving Control. Micromachines 2019, 10, 270. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lv, R.S.; Fu, Q.; Chen, W.P.; Yin, L.; Liu, X.W.; Zhang, Y.F. A Digital Interface ASIC for Triple-Axis MEMS Vibratory Gyroscopes. Sensors 2020, 20, 5460. [Google Scholar] [CrossRef] [PubMed]
- Cao, H.L.; Li, H.S.; Shao, X.L.; Liu, Z.Y.; Kou, Z.W.; Shan, Y.H.; Shi, Y.B.; Shen, C.; Liu, J. Sensing mode coupling analysis for dual-mass MEMS gyroscope and bandwidth expansion within wide-temperature range. Mech. Syst. Signal Process. 2018, 98, 448–464. [Google Scholar] [CrossRef]
- Zhang, W.B.; Chen, W.P.; Yin, L.; Di, X.P.; Chen, D.L.; Fu, Q.; Zhang, Y.F.; Liu, X.W. Study of the Influence of Phase Noise on the MEMS Disk Resonator Gyroscope Interface Circuit. Sensors 2020, 20, 5470. [Google Scholar] [CrossRef] [PubMed]
- Zhu, H.J.; Jin, Z.H.; Hu, S.C.; Liu, Y.D. Constant-frequency oscillation control for vibratory micro-machined gyroscopes. Sens. Actuator A Phys. 2013, 193, 193–200. [Google Scholar] [CrossRef]
- Perl, T.; Maimon, R.; Krylov, S.; Shimkin, N. Control of Vibratory MEMS Gyroscope With the Drive Mode Excited Through Parametric Resonance. J. Vib. Acoust. 2021, 143, 051013. [Google Scholar] [CrossRef]
- Chen, F.; Li, X.X.; Kraft, M. Electromechanical Sigma-Delta Modulators (Sigma Delta M) Force Feedback Interfaces for Capacitive MEMS Inertial Sensors: A Review. IEEE Sens. J. 2016, 16, 6476–6495. [Google Scholar] [CrossRef]
- Baranov, P.; Nesterenko, T.; Tsimbalist, E.; Vtorushin, S. The stabilization system of primary oscillation for a micromechanical gyroscope. Meas. Sci. Technol. 2017, 28, 064004. [Google Scholar] [CrossRef]
- AL-Khazraji, H.; Cole, C.; Guo, W. Dynamics analysis of a production-inventory control system with two pipelines feedback. Kybernetes 2017, 46, 1632–1653. [Google Scholar] [CrossRef]
- Yin, T.; Lin, Y.S.; Yang, H.G.; Wu, H.M. A Phase Self-Correction Method for Bias Temperature Drift Suppression of MEMS Gyroscopes. J. Circuits Syst. Comput. 2020, 29, 2050198. [Google Scholar] [CrossRef]
- Xing, B.W.; Ding, X.K.; Li, H.S. MEMS vibration gyroscope AGC loop linearization model and controller design. Transducer Microsyst. Technol. 2019, 38, 65–68. [Google Scholar]
- Xiong, X.G.; Lu, D.R.; Wang, W.Y. A Bulk-micromachined Comb Vibratory Microgyroscope Design. In Proceedings of the 48th Midwest Symposium on Circuits and Systems, Covington, KY, USA, 7–10 August 2005; pp. 152–154. [Google Scholar]
- Mo, B.; Liu, X.W.; Ding, X.W.; Tan, X.Y. A Novel Closed-loop Drive Circuit for the Micromechined Gyroscope. In Proceedings of the 2007 IEEE International Conference on Mechatronics and Automation, Harbin, China, 5–8 August 2007; pp. 3384–3389. [Google Scholar]
- Maeda, D.; Ono, K.; Giner, J.; Matsumoto, M.; Kanamaru, M.; Sekiguchi, T.; Hayashi, M. MEMS Gyroscope With Less Than 1-deg/h Bias Instability Variation in Temperature Range From −40 °C to 125 °C. IEEE Sens. J. 2018, 18, 1006–1015. [Google Scholar] [CrossRef]
- Zhu, J.X.; Liu, X.M.; Shi, Q.F.; He, T.Y.; Sun, Z.D.; Guo, X.E.; Liu, W.X.; Sulaiman, O.B.; Dong, B.W.; Lee, C.K. Development Trends and Perspectives of Future Sensors and MEMS/NEMS. Micromachines 2020, 11, 7. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sung, W.T.; Sung, S.; Lee, J.Y.; Kang, T.; Lee, Y.J.; Lee, J.G. Development of a lateral velocity-controlled MEMS vibratory gyroscope and its performance test. J. Micromech. Microeng. 2008, 18, 055028. [Google Scholar] [CrossRef]
- Ajit, S.; Mohammad, F.Z.; Farrokh, A. A sub-0.2°/hr Bias Drift Micromechanical Silicon Gyroscope With Automatic CMOS Mode-Matching. IEEE J. Solid State Circuits 2009, 44, 1593–1608. [Google Scholar]






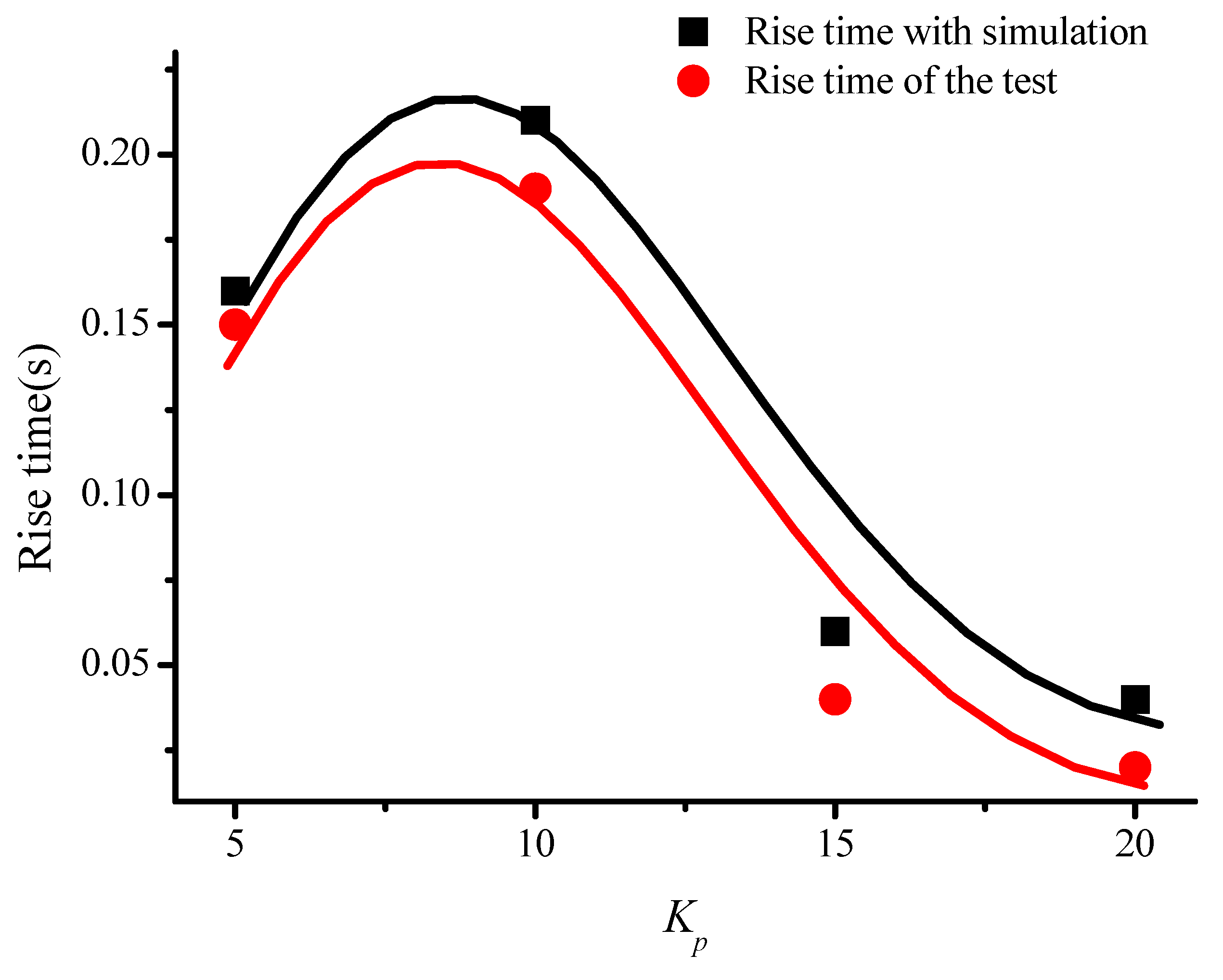

| Kp | 5 | 10 | 15 | 20 |
|---|---|---|---|---|
| Rise time with simulation (s) | 0.16 | 0.21 | 0.06 | 0.04 |
| Rise time of the test (s) | 0.15 | 0.19 | 0.04 | 0.02 |
| Equipment | Type | Manufacturer |
|---|---|---|
| High-precision current source | PW36-1.5ADP | KENWOOD |
| Current source | E3631A | Agilent |
| Dynamic signal analyzer | 35670A | HP |
| Oscilloscope | DSOX2002A | Agilent |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Q.; Ding, L.; Liu, X.; Zhang, Q. Research on a Silicon Gyroscope Interface Circuit Based on Closed-Loop Controlled Drive Loop. Sensors 2022, 22, 834. https://doi.org/10.3390/s22030834
Li Q, Ding L, Liu X, Zhang Q. Research on a Silicon Gyroscope Interface Circuit Based on Closed-Loop Controlled Drive Loop. Sensors. 2022; 22(3):834. https://doi.org/10.3390/s22030834
Chicago/Turabian StyleLi, Qiang, Lifeng Ding, Xiaowei Liu, and Qiang Zhang. 2022. "Research on a Silicon Gyroscope Interface Circuit Based on Closed-Loop Controlled Drive Loop" Sensors 22, no. 3: 834. https://doi.org/10.3390/s22030834






