Analytical and Experimental Investigation of a Curved Piezoelectric Energy Harvester
Abstract
:1. Introduction
2. Modelling by Dynamic Stiffness Method
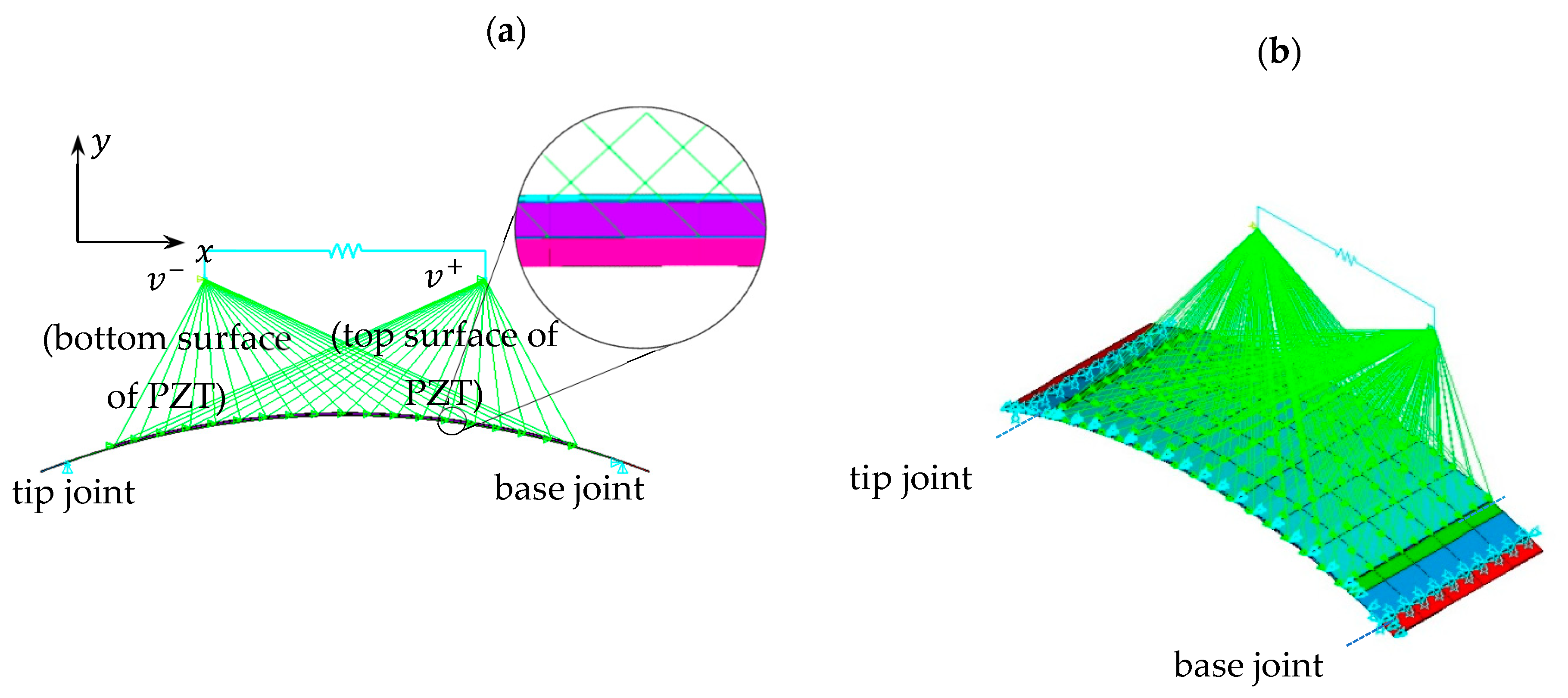
2.1. Equations of a Curved Piezoelectric Beam Segment
2.2. Dynamic Stiffness Matrix of Curved Beam
2.3. Matrix Assembly and Frequency Response Functions
- the rows relating to and , and columns relating to and are all padded with zeros due to the boundary conditions;
- the remainder of is where is obtained from by eliminating the columns relating to and , and the rows relating to and .
3. Finite Element Modelling Using Ansys
4. Experimental Testing
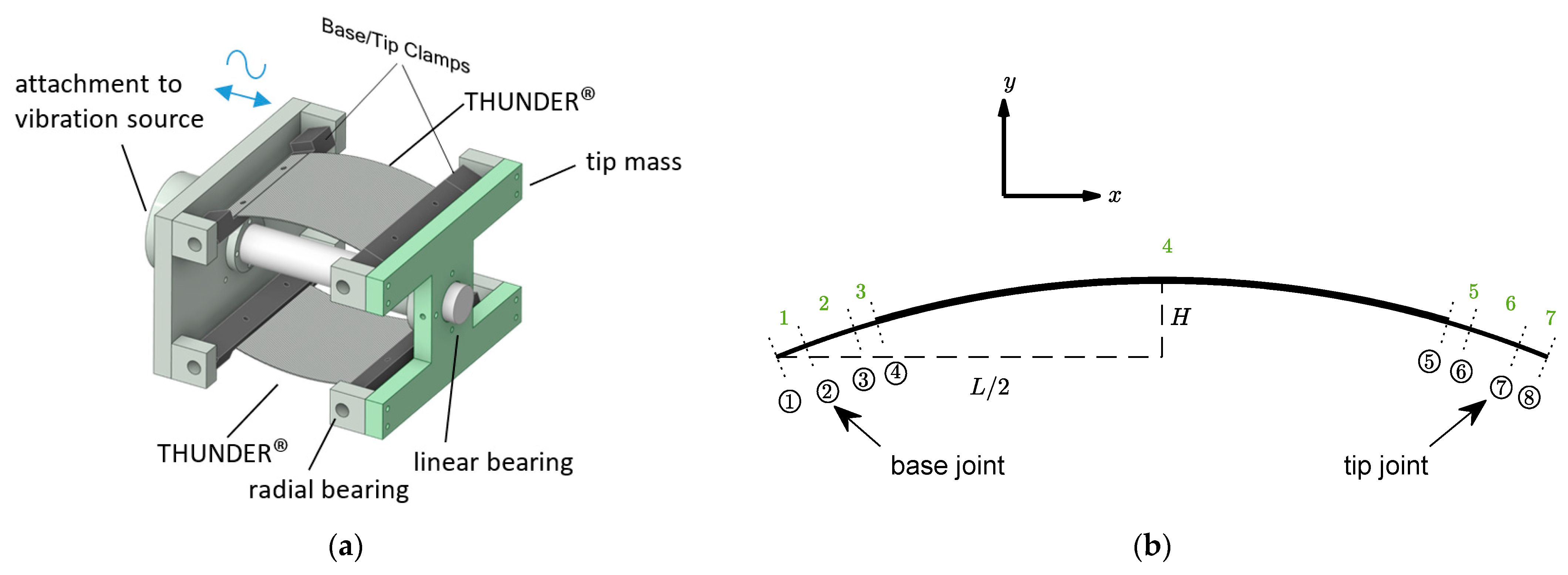
4.1. Experimental Setup
- A PC-controlled data acquisition (DAQ) system (not shown in Figure 6) consisting of hardware (LMS Scadas 5) and spectral analysis software (LMS Test.Lab).
- Two accelerometers (PCB 352C22), one attached to the base of the energy harvesting device and the other attached to its tip mass.
- A signal conditioner/amplifier, to remove the noise from signals received from accelerometers and amplify them before channeling to the DAQ system.
- An electromagnetic (EM) shaker on which the energy harvesting device was mounted.
- A power amplifier to control the gain of the random excitation signal output from the DAQ system, which was then fed to the EM shaker.
- A resistor box which was controlled manually to apply purely resistive electrical loads in the range 0.5–500 kΩ.


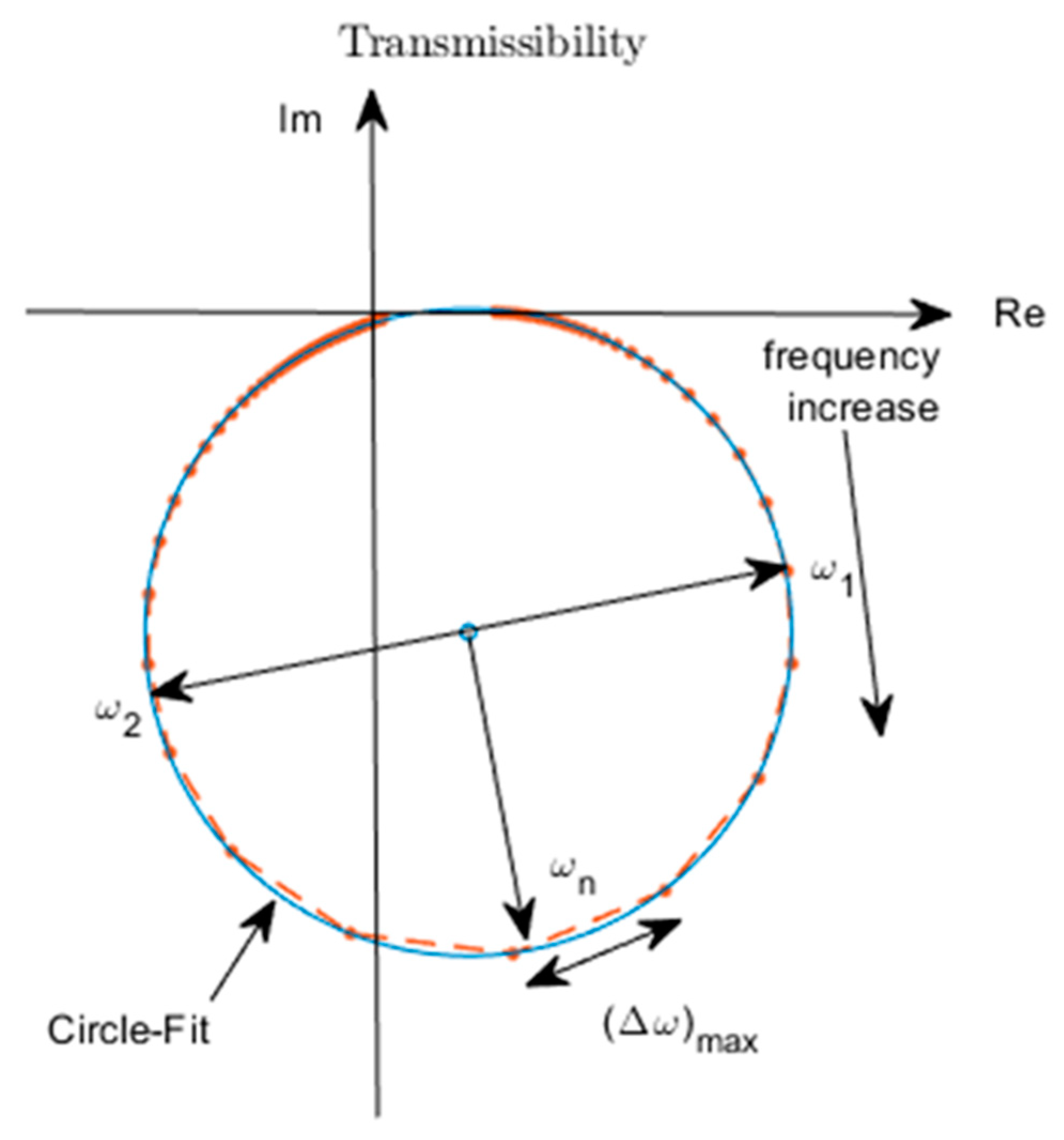
4.2. Estimation of Damping
- Transmissibility resonance peak frequency—frequency at which transmissibility FRF magnitude is maximum;
- Voltage FRF resonance peak frequency—frequency at which the voltage FRF magnitude is maximum.
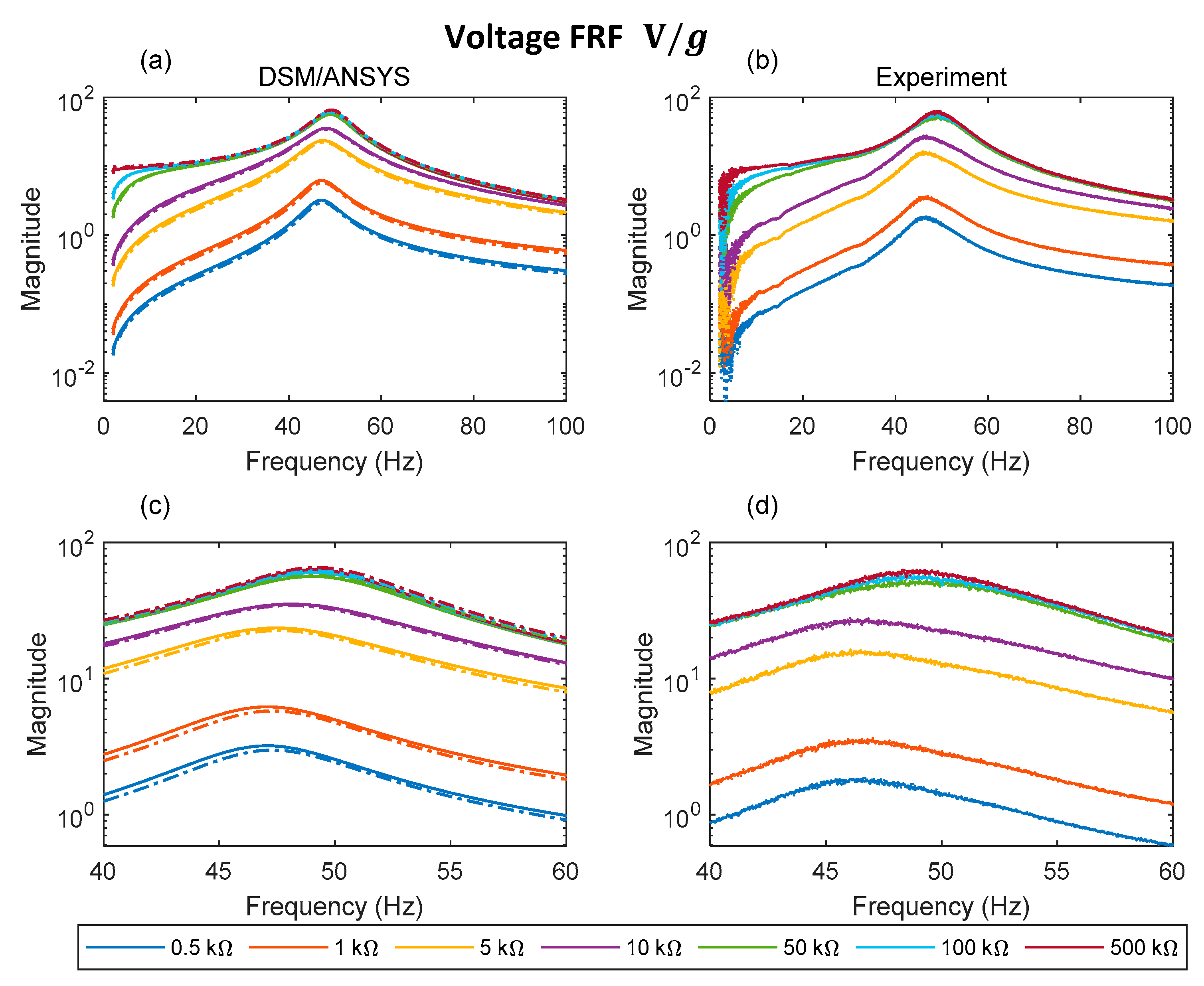
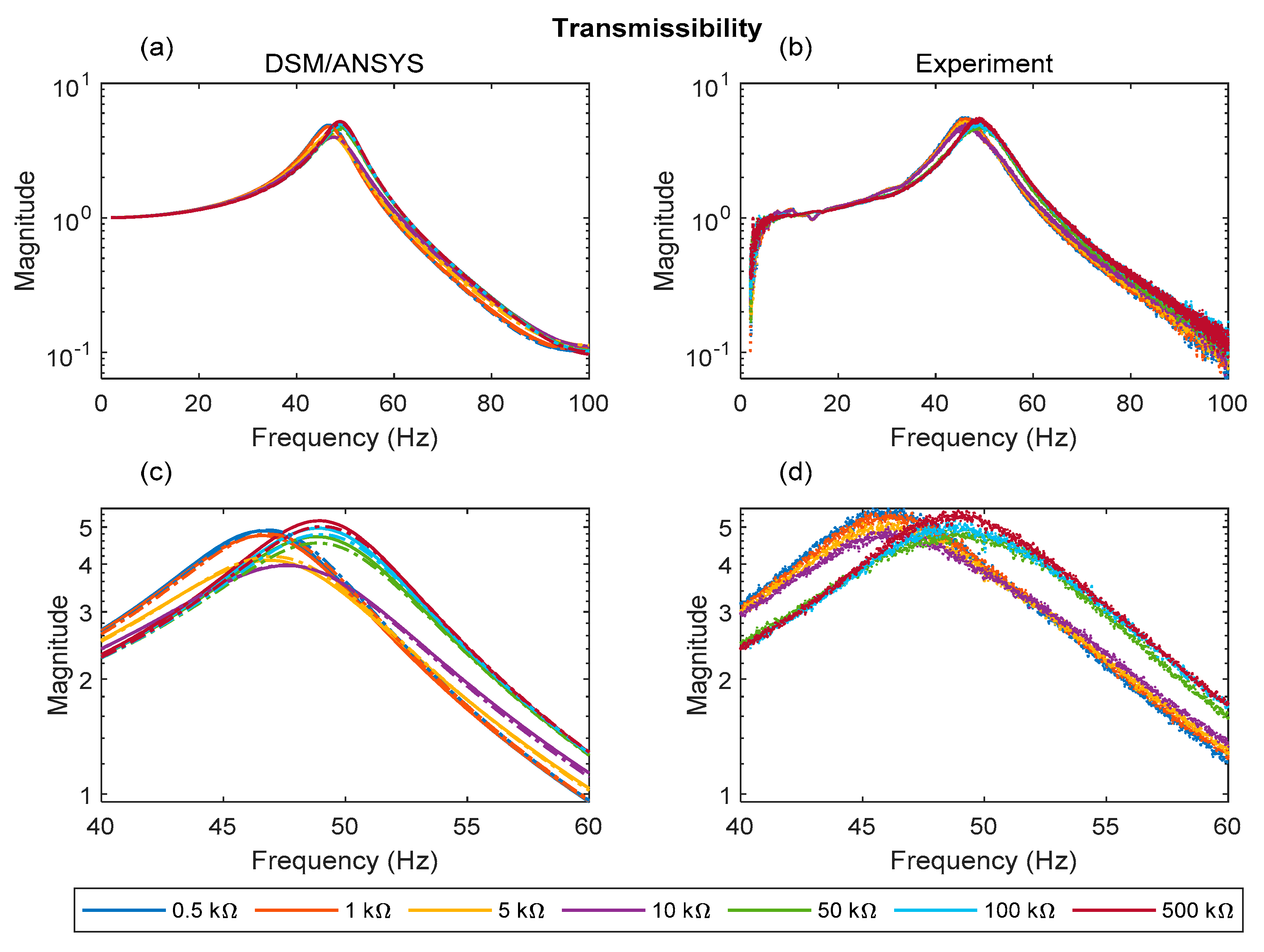
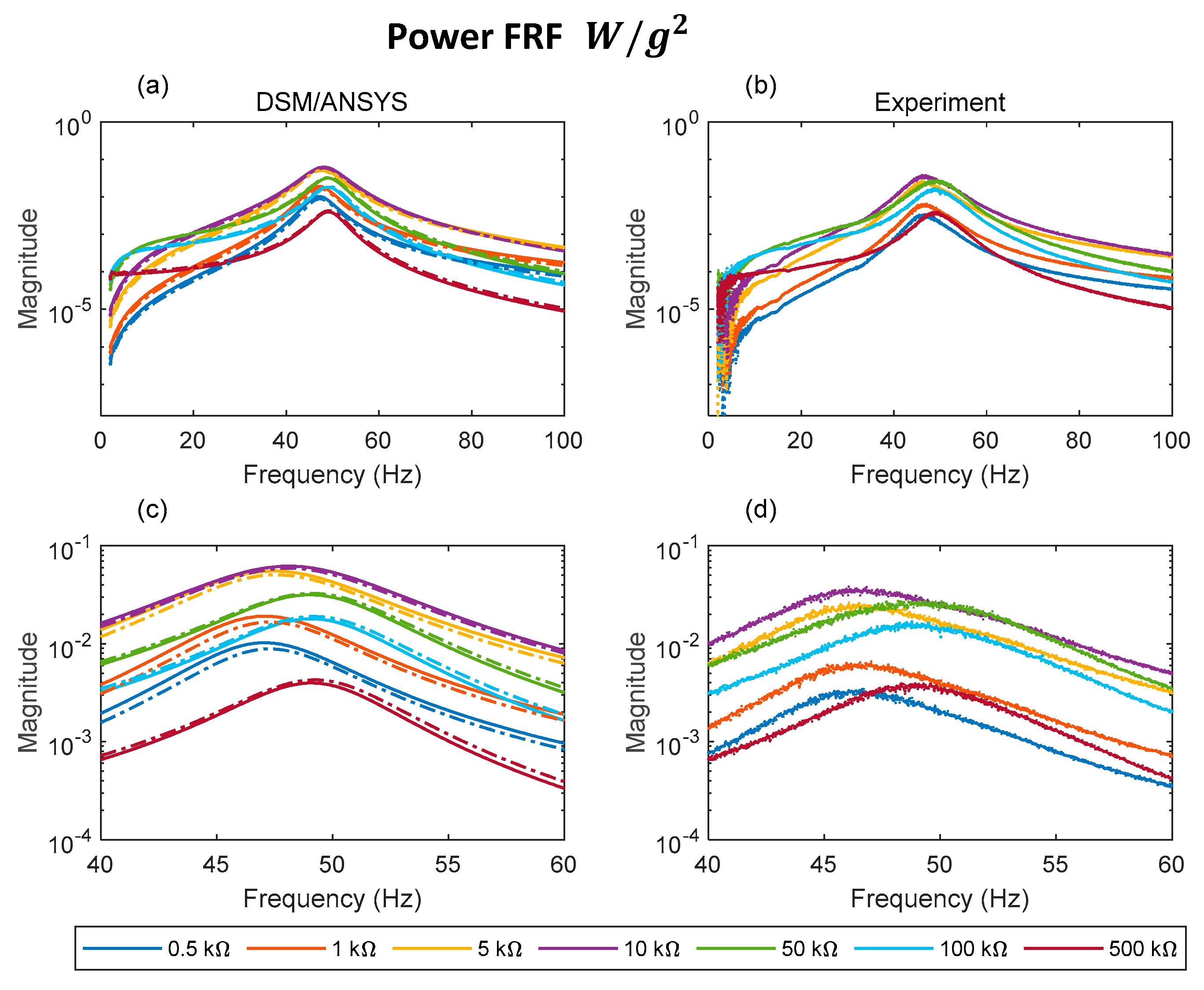
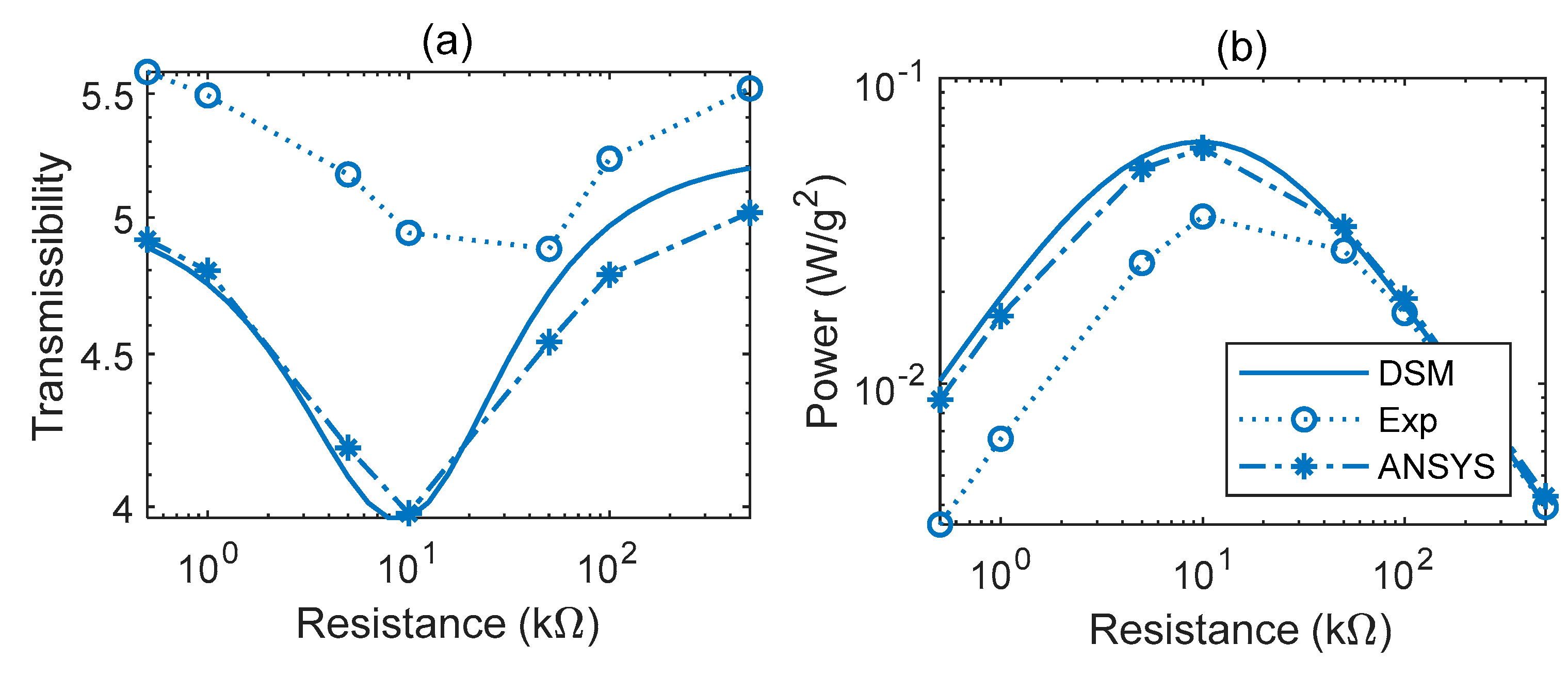
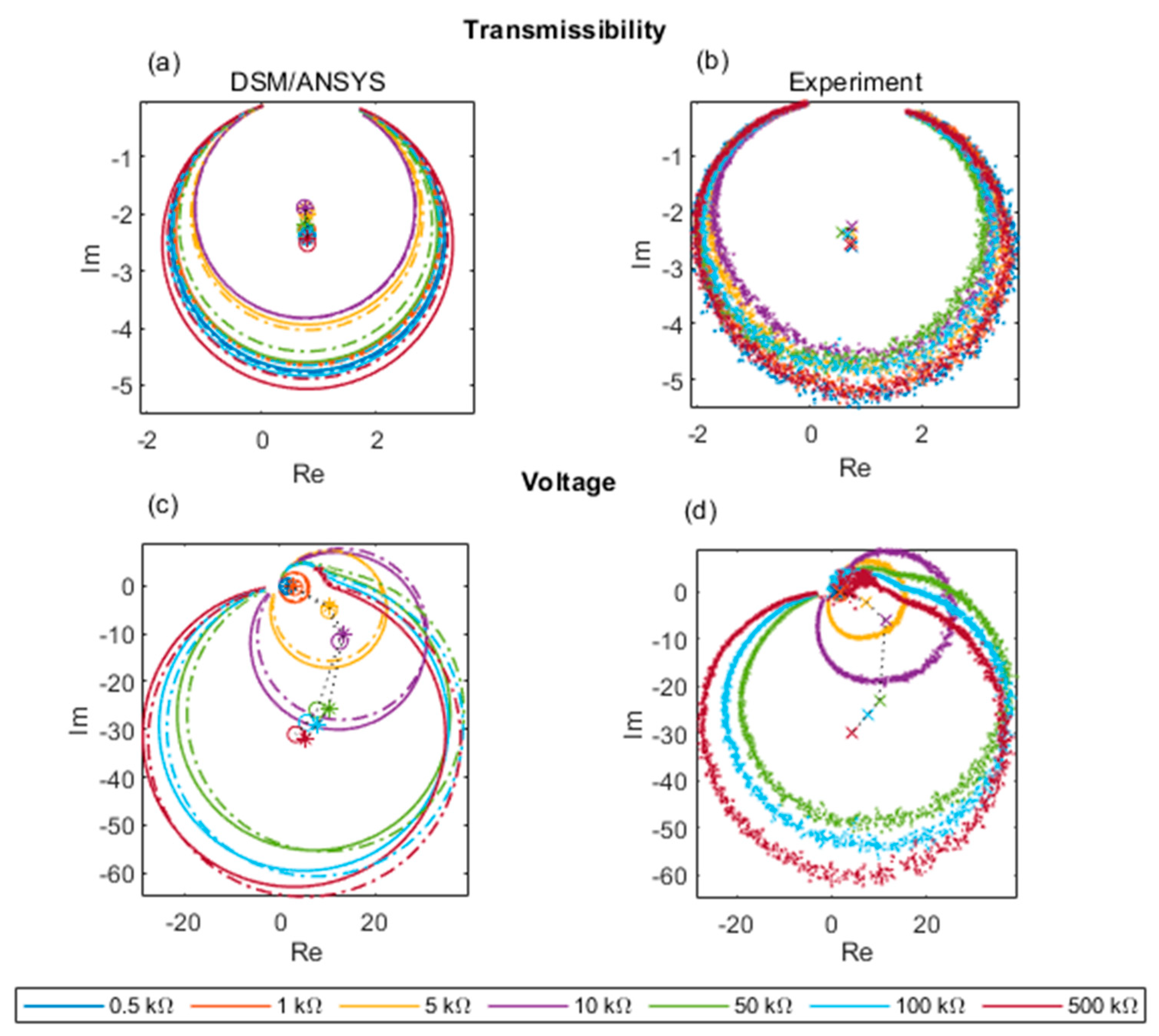
5. Presentation of FRF Results and Discussion
5.1. DSM vs. 2D/3D ANSYS vs. Experiment
5.2. DSM and 2D ANSYS vs. Experiment over a Range of Electrical Loads
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Amirtharajah, R.; Chandrakasan, A.P. Self-powered signal processing using vibration-based power generation. IEEE J. Solid-State Circuits 1998, 33, 687–695. [Google Scholar] [CrossRef] [Green Version]
- Ottman, G.K.; Hofmann, H.F.; Lesieutre, G.A. Optimized piezoelectric energy harvesting circuit using step-down converter in discontinuous conduction mode. IEEE Trans. Power Electron. 2003, 18, 696–703. [Google Scholar] [CrossRef]
- Roundy, S.; Wright, P.K. A piezoelectric vibration based generator for wireless electronics. Smart Mater. Struct. 2004, 13, 1131. [Google Scholar] [CrossRef] [Green Version]
- Staaf, L.G.H.; Smith, A.D.; Lundgren, P.; Folkow, P.D.; Enoksson, P. Effective piezoelectric energy harvesting with bandwidth enhancement by assymetry augmented self-tuning of conjoined cantilevers. Int. J. Mech. Sci. 2019, 150, 1–11. [Google Scholar] [CrossRef]
- Ramalingam, U.; Gandhi, U.; Mangalanathan, U.; Choi, S.B. A new piezoelectric energy harvester using two beams with tapered cavity for high power and wide broadband. Int. J. Mech. Sci. 2018, 142, 1224–1234. [Google Scholar] [CrossRef]
- Nechibvute, A.; Chawanda, A.; Luhanga, P. Piezoelectric energy harvesting devices: An alternative energy source for wireless sensors. Smart Mater. Res. 2012, 2012, 853481. [Google Scholar] [CrossRef] [Green Version]
- Robbins, D.H.; Reddy, J.N. Analysis of piezoelectrically actuated beams using a layer-wise displacement theory. Comput. Struct. 1991, 41, 265–279. [Google Scholar] [CrossRef]
- Benjeddou, A. Advances in piezoelectric finite element modeling of adaptive structural elements: A survey. Comput. Struct. 2000, 76, 347–363. [Google Scholar] [CrossRef]
- Erturk, A.; Inman, D.J. An experimentally validated bimorph cantilever model for piezoelectric energy harvesting from base excitations. Smart Mater. Struct. 2009, 18, 025009. [Google Scholar] [CrossRef]
- Kathpalia, B.; Tan, D.; Stern, I.; Valdes, F.; Kim, S.; Erturk, A. Modeling and characterization of a curved piezoelectric energy harvester for smart paver tiles. Procedia Comput. Sci. 2017, 109, 1060–1066. [Google Scholar] [CrossRef]
- Erturk, A.; Inman, D.J. Issues in mathematical modeling of piezoelectric energy harvesters. Smart Mater. Struct. 2008, 17, 065016. [Google Scholar] [CrossRef] [Green Version]
- Erturk, A. Piezoelectric energy harvesting for civil infrastructure system applications: Moving loads and surface strain fluctuations. J. Intell. Mater. Syst. Struct. 2011, 22, 1959–1973. [Google Scholar] [CrossRef]
- Sodano, H.A.; Lloyd, J.; Inman, D.J. An experimental comparison between several active composite actuators for power generation. Smart Mater. Struct. 2006, 15, 1211. [Google Scholar] [CrossRef]
- Ottman, G.K.; Hofmann, H.F.; Bhatt, A.C.; Lesieutre, G.A. Adaptive piezoelectric energy harvesting circuit for wireless remote power supply. IEEE Trans. Power Electron. 2002, 17, 669–676. [Google Scholar] [CrossRef] [Green Version]
- Adeodato, A.; Duarte, B.T.; Monteiro, L.L.S.; Pacheco, P.M.C.; Savi, M.A. Synergistic use of piezoelectric and shape memory alloy elements for vibration-based energy harvesting. Int. J. Mech. Sci. 2021, 194, 106206. [Google Scholar] [CrossRef]
- da Silveira, A.R.G.; Daniel, G.B. Piezoelectric harvester for smart tilting pad journal bearings. Energy Convers. Manag. 2020, 205, 112338. [Google Scholar] [CrossRef]
- Bonello, P.; Rafique, S.; Shuttleworth, R. A theoretical study of a smart electromechanical tuned mass damper beam device. Smart Mater. Struct. 2012, 21, 125004. [Google Scholar] [CrossRef]
- Rafique, S.; Bonello, P.; Shuttleworth, R. Experimental validation of a novel smart electromechanical tuned mass damper beam device. J. Sound Vib. 2013, 332, 4912–4926. [Google Scholar] [CrossRef]
- Elahi, H.; Eugeni, M.; Gaudenzi, P. A review on mechanisms for piezoelectric-based energy harvesters. Energies 2018, 11, 1850. [Google Scholar] [CrossRef] [Green Version]
- Karimi, M.; Karimi, A.H.; Tikani, R.; Ziaei-Rad, S. Experimental and theoretical investigations on piezoelectric-based energy harvesting from bridge vibrations under travelling vehicles. Int. J. Mech. Sci. 2016, 119, 1–11. [Google Scholar] [CrossRef]
- Ewere, F.; Wang, G.; Cain, B. Experimental investigation of galloping piezoelectric energy harvesters with square bluff bodies. Smart Mater. Struct. 2014, 23, 104012. [Google Scholar] [CrossRef]
- Erturk, A.; Inman, D.J. A distributed parameter electromechanical model for cantilevered piezoelectric energy harvesters. J. Vib. Acoust. 2008, 130, 041002. [Google Scholar] [CrossRef]
- Khazaee, M.; Rezania, A.; Rosendahl, L. An experimental study to determine damping of piezoelectric harvesters using transient analysis of unified electromechanical voltage equation. Energy Convers. Manag. 2021, 227, 113567. [Google Scholar] [CrossRef]
- Rafique, S.; Bonello, P. Experimental validation of a distributed parameter piezoelectric bimorph cantilever energy harvester. Smart Mater. Struct. 2010, 19, 094008. [Google Scholar] [CrossRef]
- Dalzell, P.; Bonello, P. Analysis of an energy harvesting piezoelectric beam with energy storage circuit. Smart Mater. Struct. 2012, 21, 105029. [Google Scholar] [CrossRef]
- Bonello, P.; Rafique, S. Modeling and analysis of piezoelectric energy harvesting beams using the dynamic stiffness and analytical modal analysis methods. J. Vib. Acoust. 2011, 133, 011009. [Google Scholar] [CrossRef]
- Bonello, P.; Brennan, M.J. Modelling the dynamic behaviour of a supercritical rotor on a flexible foundation using the mechanical impedance technique. J. Sound Vib. 2001, 239, 445–466. [Google Scholar] [CrossRef]
- Banerjee, J.R. Dynamic stiffness formulation for structural elements: A general approach. Comput. Struct. 1997, 63, 101–103. [Google Scholar] [CrossRef]
- Aimmanee, S.; Chutima, S.; Hyer, M.W. Nonlinear analysis of RAINBOW actuator characteristics. Smart Mater. Struct. 2009, 18, 045002. [Google Scholar] [CrossRef]
- Goo, N.S.; Yoon, K.J. Analysis of Lipca-C Actuators. Int. J. Mod. Phys. B 2003, 17, 1959–1964. [Google Scholar] [CrossRef]
- Wang, F.; Wang, Z.; Soroush, M.; Abedini, A. Energy harvesting efficiency optimization via varying the radius of curvature of a piezoelectric THUNDER. Smart Mater. Struct. 2016, 25, 095044. [Google Scholar] [CrossRef]
- Mossi, K.; Mouhli, M.; Smith, B.F.; Mane, P.P.; Bryant, R.G. Shape modeling and validation of stress-biased piezoelectric actuators. Smart Mater. Struct. 2006, 15, 1785. [Google Scholar] [CrossRef] [Green Version]
- Mossi, K.M.; Ounaies, Z.; Smith, R.C.; Ball, B. Prestressed curved actuators: Characterization and modeling of their piezoelectric behavior. In Smart Structures and Materials 2003: Active Materials: Behavior and Mechanics; International Society for Optics and Photonics: San Diego, CA, USA, 2003; Volume 5053, pp. 423–435. [Google Scholar] [CrossRef] [Green Version]
- Mossi, K.M.; Bishop, R.P. Characterization of different types of high-performance THUNDER actuators. In Smart Structures and Materials 1999: Smart Materials Technologies; SPIE: Newport Beach, CA, USA, 1999; Volume 3675, pp. 43–52. [Google Scholar] [CrossRef]
- Aimmanee, S.; Hyer, M.W. A comparison of the deformations of various piezoceramic actuators. J. Intell. Mater. Syst. Struct. 2006, 17, 167–186. [Google Scholar] [CrossRef]
- Hasan, M.N.; Wang, S.; Arab, A.; Wang, F. Optimum Study of Power Efficiency of a THUNDER Harvester. In Smart Materials, Adaptive Structures and Intelligent Systems; American Society of Mechanical Engineers: San Antonio, TX, USA, 2018; Volume 51951, p. V002T07A008. [Google Scholar] [CrossRef]
- Thonapalin, P.; Aimmanee, S.; Laoratanakul, P.; Das, R. Thermomechanical Effects on Electrical Energy Harvested from Laminated Piezoelectric Devices. Crystals 2021, 11, 141. [Google Scholar] [CrossRef]
- Bonello, P.; Brennan, M.J.; Elliott, S.J. Vibration control using an adaptive tuned vibration absorber with a variable curvature stiffness element. Smart Mater. Struct. 2005, 14, 1055. [Google Scholar] [CrossRef]
- Erturk, A.; Inman, D.J. Piezoelectric Energy Harvesting; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Petyt, M. Introduction to Finite Element Vibration Analysis; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Yang, Y.; Wei, X.; Zhang, L.; Yao, W. The effect of electrical impedance matching on the electromechanical characteristics of sandwiched piezoelectric ultrasonic transducers. Sensors 2017, 17, 2832. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Quattrocchi, A.; Montanini, R.; de Caro, S.; Panarello, S.; Scimone, T.; Foti, S.; Testa, A. A new approach for impedance tracking of piezoelectric vibration energy harvesters based on a zeta converter. Sensors 2020, 20, 5862. [Google Scholar] [CrossRef]
- Reddy, J.N. Mechanics of Laminated Composite Plates and Shells: Theory and Analysis; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Ewins, D.J. Modal Testing: Theory, Practice and Application; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Rao, S.S. Mechanical Vibrations; Addison-Wesley Publishing Company: Reading, MA, USA, 1995. [Google Scholar]
- Qatu, M.S. Vibration of Laminated Shells and Plates; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar]



| Layer No. (k) | Material | Poisson Ratio (For FE Models) | |||||
|---|---|---|---|---|---|---|---|
| 1 | Steel | 193 | 8000 | - | - | 203 | 0.25 |
| 3 | PZT | 67 | 7600 | −12.73 | 16.82 | 254 | 0.31 |
| 5 | Aluminum | 70 | 2700 | - | - | 25.4 | 0.33 |
| 2, 4 | Adhesive | 3.45 | 2200 | - | - | 25.4 | 0.40 |
| Property | Value |
|---|---|
| Dome height, H | 9.55 |
| Overall Length, L | 97.66 |
| Width, b | 73.41 |
| Active length | 72.3 |
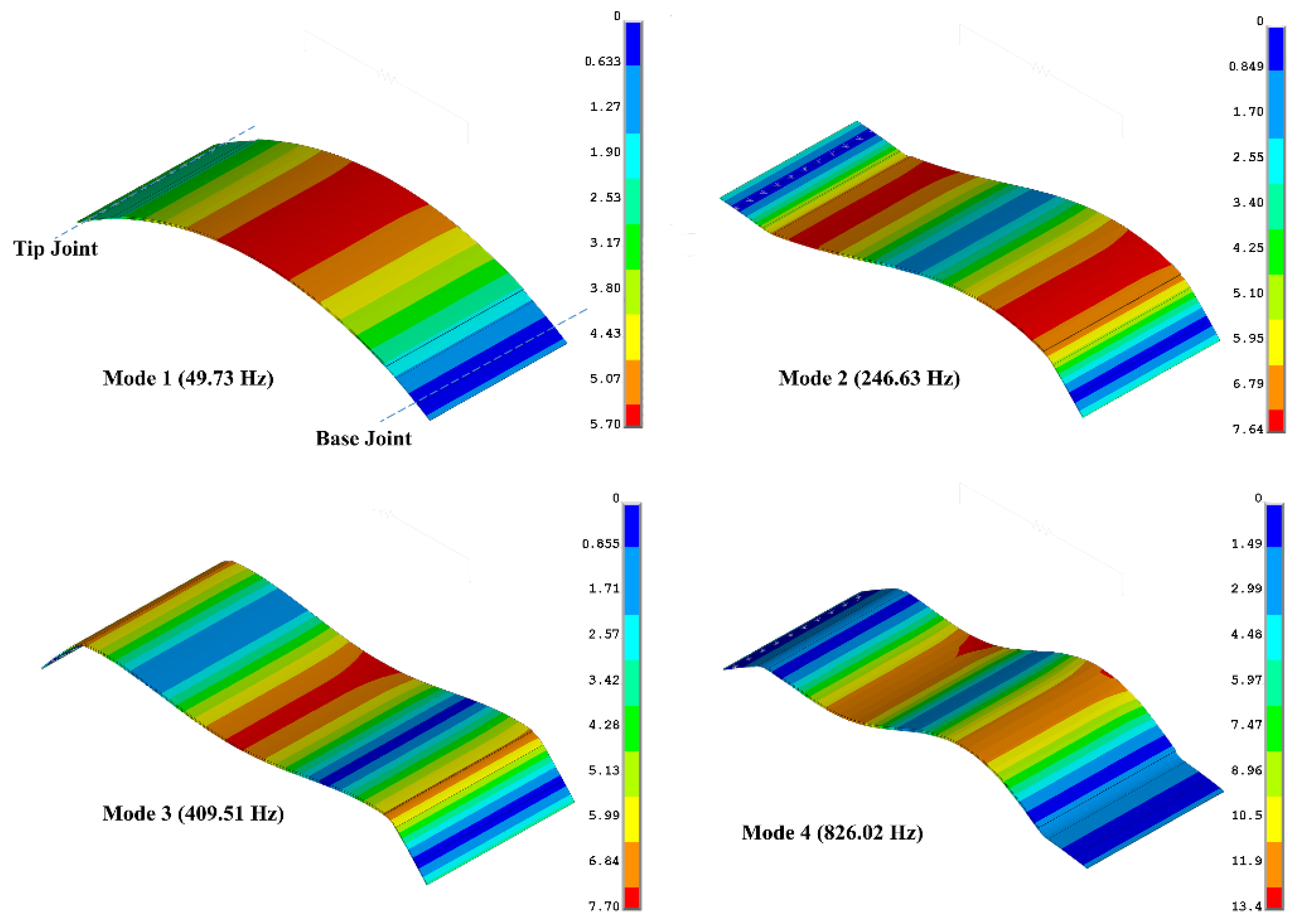
| Circumferential Mode Number | Natural Frequency: ANSYS Plane Elements (Hz) | Natural Frequency: ANSYS Shell Elements (Hz) | Natural Frequency: ANSYS Solid Elements (Hz) | % Difference (Plane vs. Shell) | % Difference (Plane vs. Solid) | Natural Frequency: DSM (Hz) | % Difference (Plane vs. DSM) |
|---|---|---|---|---|---|---|---|
| 1 | 47.28 | 48.80 | 49.73 | −3.1 | −4.9 | 47.0 | 0.6 |
| 2 | 233.74 | 246.15 | 246.63 | −5.0 | −5.2 | 237.0 | −1.4 |
| 3 | 388.32 | 408.56 | 409.51 | −5.0 | −5.2 | 395.2 | −1.8 |
| 4 | 785.68 | 811.63 | 826.02 | −3.2 | −4.9 | 783.4 | 0.3 |
| Damping Ratio (%) | |||
|---|---|---|---|
| Resonance Point Method, Equations (38a) and (38b) | Half-Power Point Method, Equations (39)–(41) | Circle-Fit Method, Equation (41) and Figure 7 | |
| 0.5 | 9.07 | 8.81 | 8.91 |
| 1 | 9.22 | 9.28 | 8.85 |
| 5 | 10.10 | 9.71 | 9.33 |
| 10 | 10.54 | 10.20 | 9.90 |
| 50 | 10.22 | 9.59 | 10.24 |
| 100 | 9.89 | 8.99 | 9.15 |
| 500 | 9.23 | 8.75 | 8.48 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pourashraf, T.; Bonello, P.; Truong, J. Analytical and Experimental Investigation of a Curved Piezoelectric Energy Harvester. Sensors 2022, 22, 2207. https://doi.org/10.3390/s22062207
Pourashraf T, Bonello P, Truong J. Analytical and Experimental Investigation of a Curved Piezoelectric Energy Harvester. Sensors. 2022; 22(6):2207. https://doi.org/10.3390/s22062207
Chicago/Turabian StylePourashraf, Talieh, Philip Bonello, and Jason Truong. 2022. "Analytical and Experimental Investigation of a Curved Piezoelectric Energy Harvester" Sensors 22, no. 6: 2207. https://doi.org/10.3390/s22062207






