Extraction of Human Limbs Based on Micro-Doppler-Range Trajectories Using Wideband Interferometric Radar
Abstract
:1. Introduction
2. Radar mDS and Interferometry
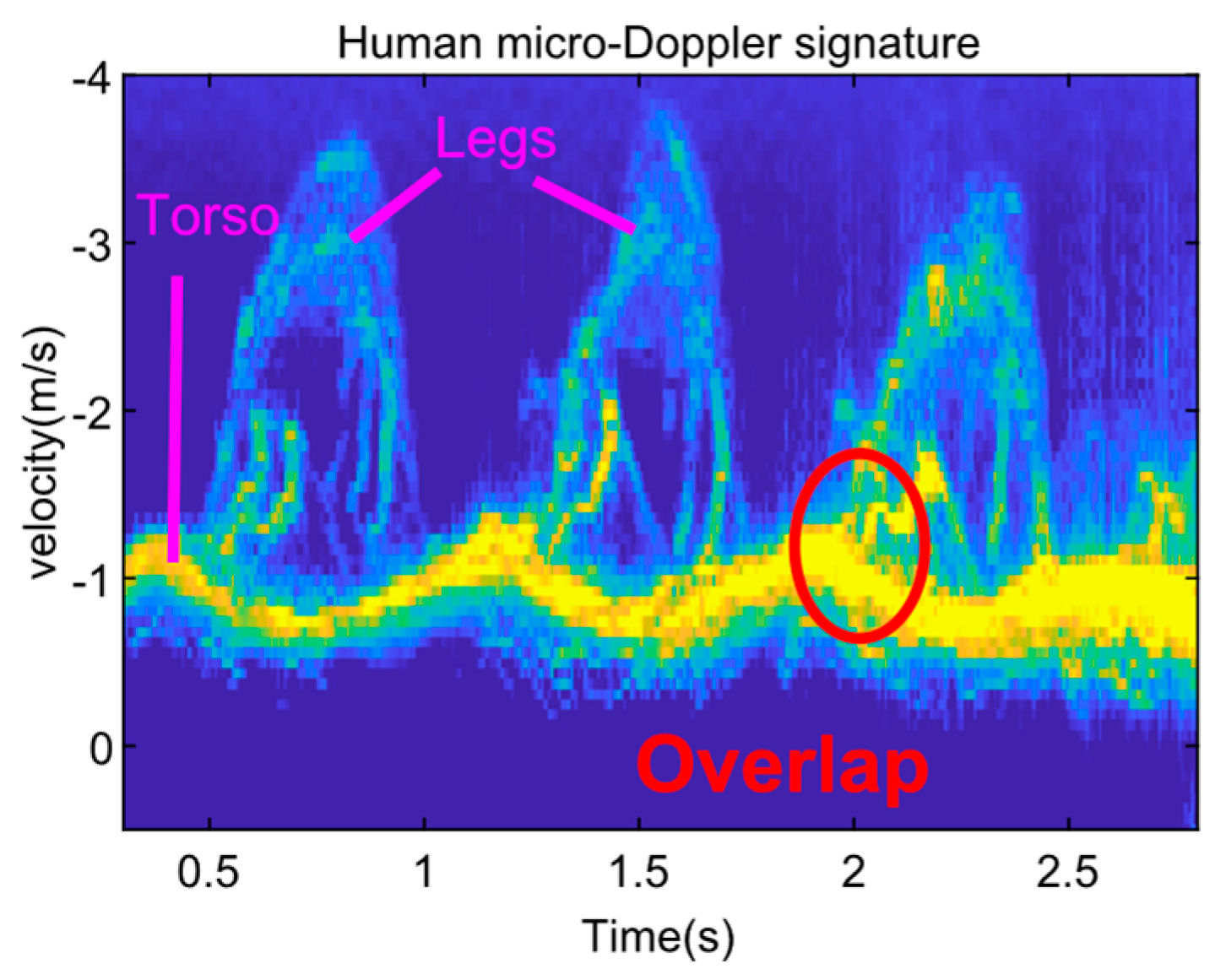
2.1. Human Micro-Doppler Signature
- The velocities of the torso, legs, and arms are hard to identify and interpret even by professionals without prior knowledge about human motions.
- The multiple m-D components including the torso, legs, and arms are overlapped with each other in the mDS. Thus, it is hard to extract human limbs accurately only based on mDS. As we will show in Section 3, the overlapping problem can be solved by incorporating the range information into mDS.
2.2. Radar Interferometry
3. Micro-Doppler-Range Trajectory Extraction
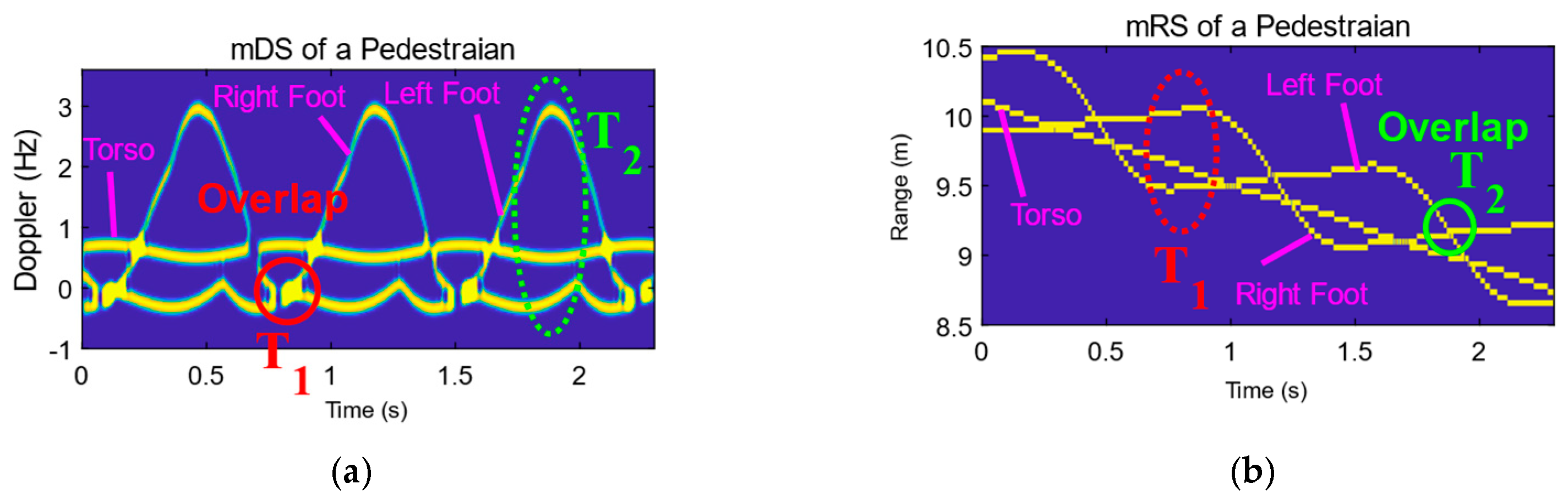
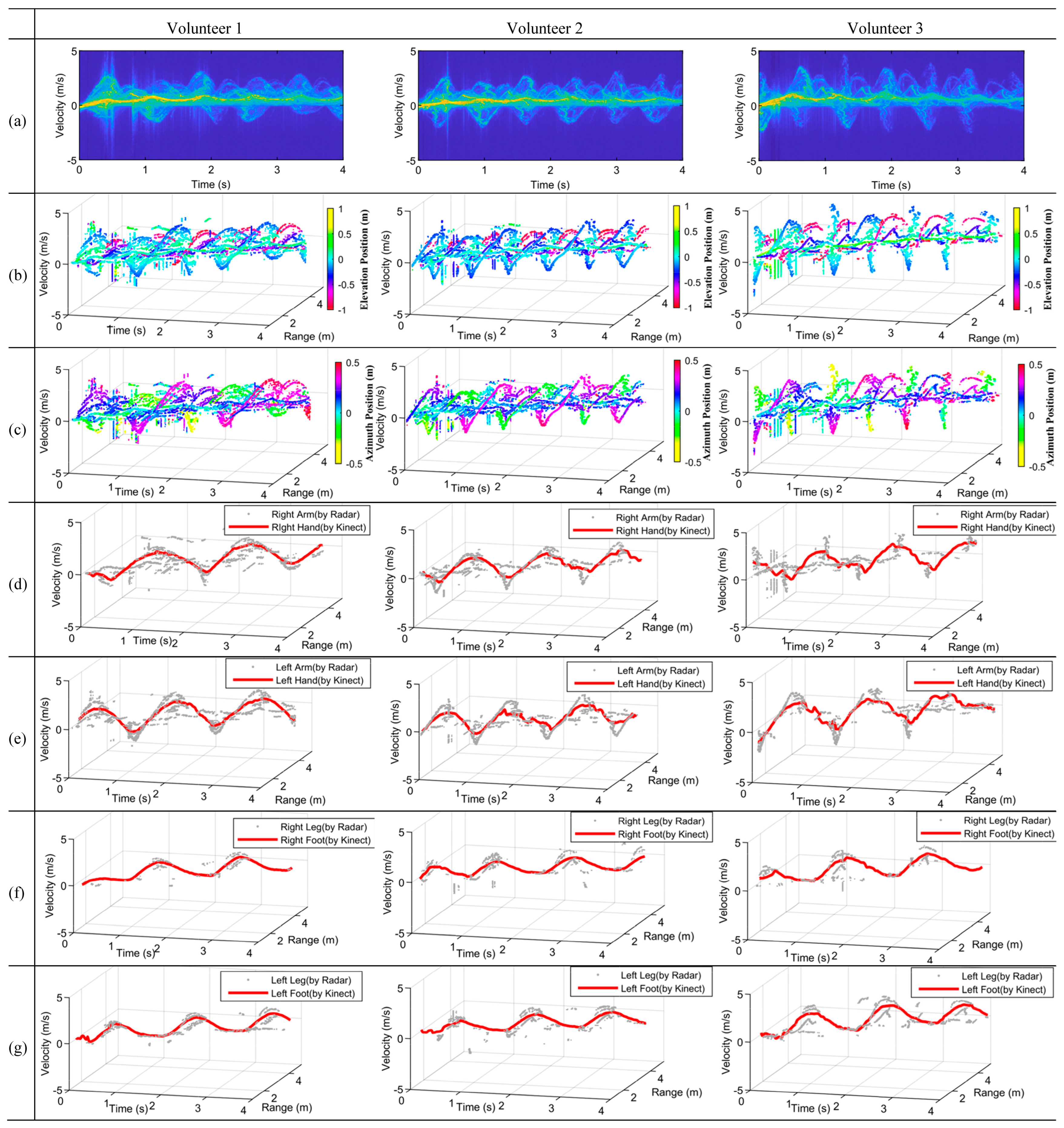
3.1. Human mDRS
- mDS overlap. In Figure 3a, the circled part in red denotes the mDS overlap, which is labeled by . They happen at the instants when both feet are on the ground. The red box in Figure 3c shows the corresponding diagram of the state.As the distances of the two feet from the radar are different in the state, there is no overlap for the mRS in Figure 3b, shown by the red dotted circle.
- mRS overlap. The green solid circle marked as in Figure 3b denotes the mRS overlap. In this situation, both feet have the same distance relative to the radar. The green box in Figure 3c shows the diagram of the state.Although the two feet have the same range, their velocities are different, i.e., the standing foot is at zero velocity, while the other foot is at the maximum radial velocity within a gait cycle. As shown in Figure 3a, the mDSs of the two feet do not overlap with each other.
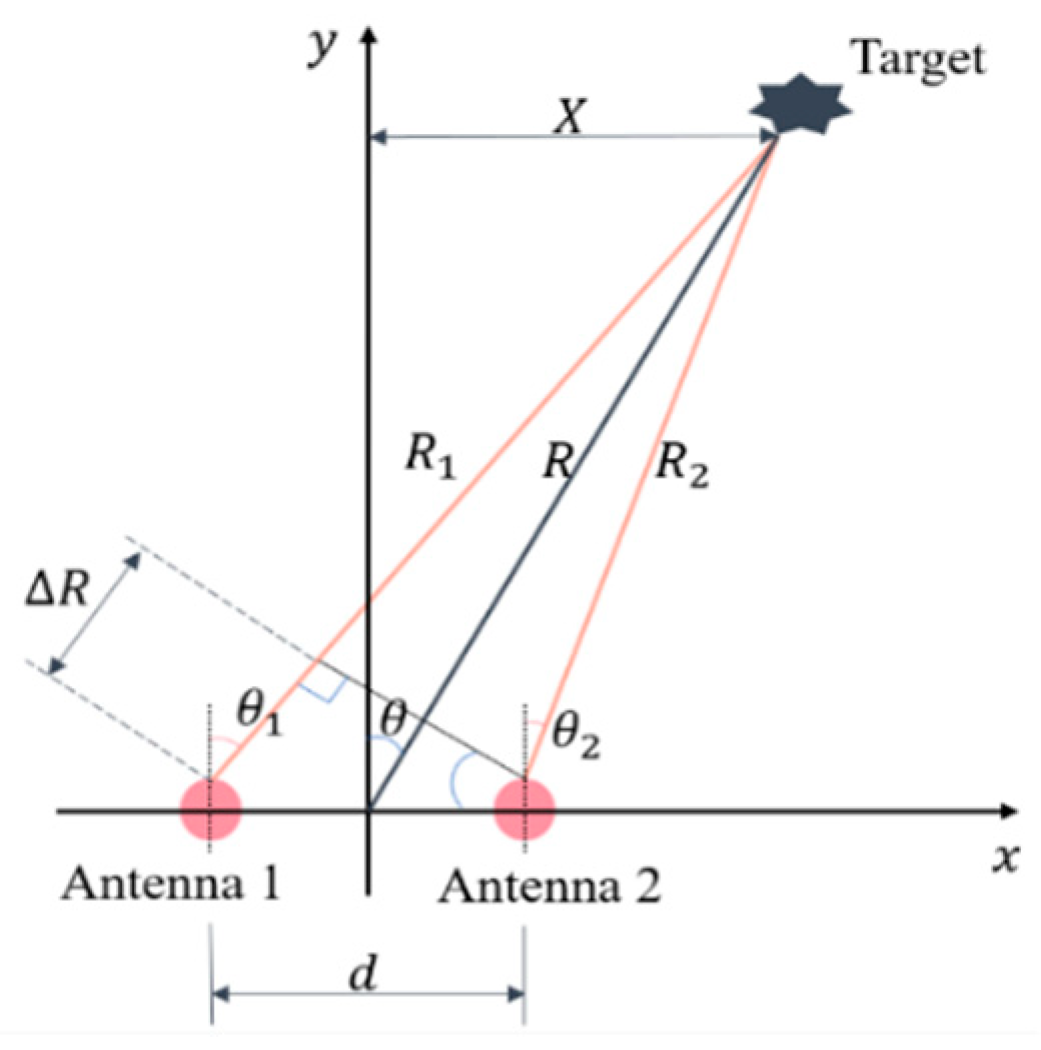
3.2. Interferometric Geometry and Retrieval of Positions
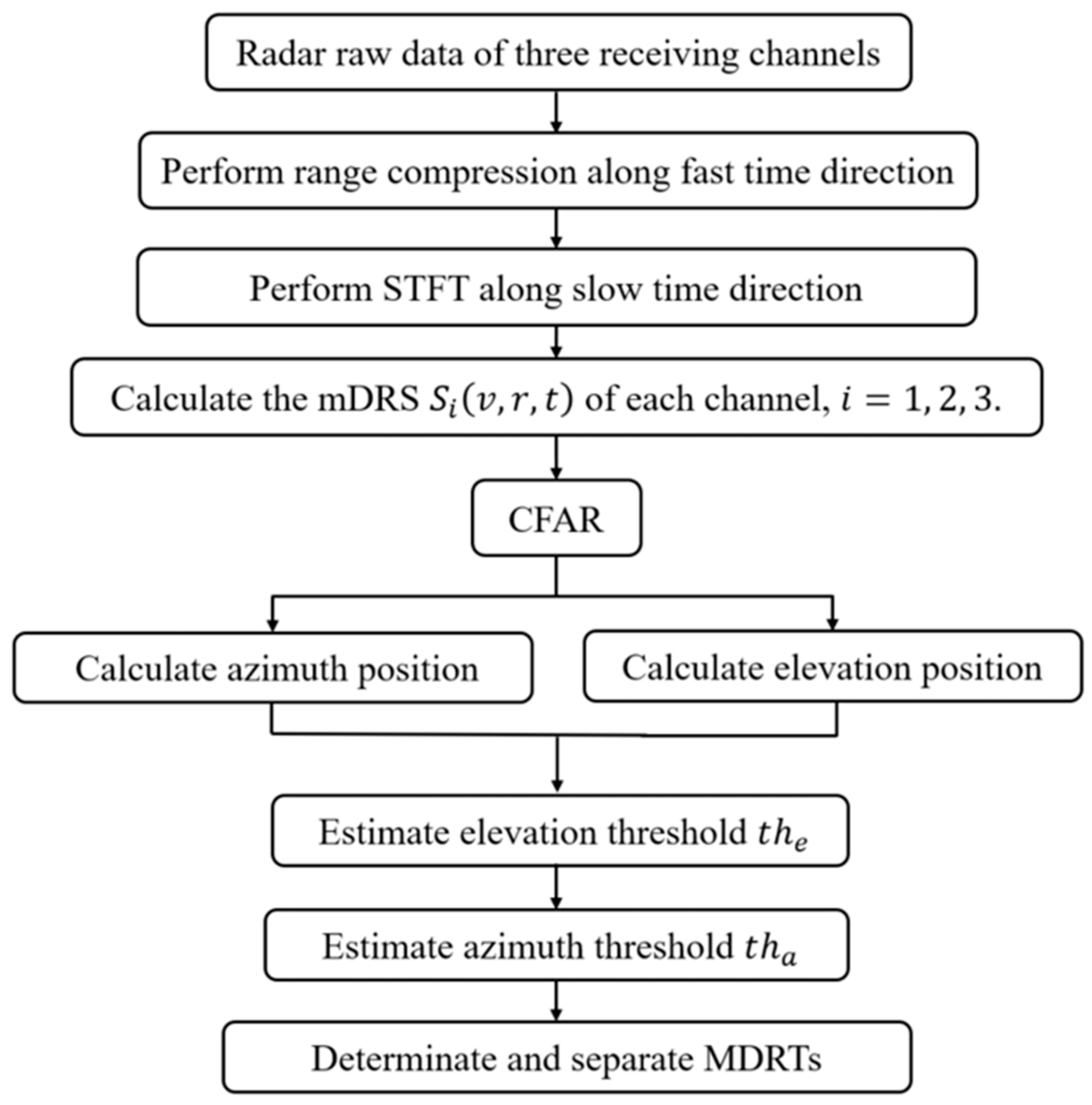
3.3. Extraction of the Micro-Doppler-Range Trajectory
- (1)
- Select the strongest scatter of the echo data at each moment and take the highest elevation position as the shoulder position.
- (2)
- Get the elevation threshold according to the relative elevation referring to the shoulder by (12).
- (3)
- Determine the indexes of echo data from the upper body.
- (4)
- Take the average of the corresponding azimuth positions as the azimuth threshold as conducted in (13).
4. Experimental Results
4.1. Experimental Setup
4.2. Experiment Swinging Arms
4.3. Experiment on Marking Time
4.4. Experiment on Walking
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Qiao, X.; Li, G.; Shan, T.; Tao, R. Human Activity Classification Based on Moving Orientation Determining Using Multistatic Micro-Doppler Radar Signals. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Hayashi, E.; Lien, J.; Gillian, N.; Giusti, L.; Weber, D.; Yamanaka, J.; Bedal, L.; Poupyrev, I. RadarNet: Efficient Gesture Recognition Technique Utilizing a Miniature Radar Sensor. In Proceedings of the 2021 CHI Conference on Human Factors in Computing Systems, Yokohama, Japan, 6 May 2021; pp. 1–14. [Google Scholar]
- Kang, W.; Zhang, Y.; Dong, X. Body Gesture Recognition Based on Polarimetric Micro-Doppler Signature and Using Deep Convolutional Neural Network. PIER M 2019, 79, 71–80. [Google Scholar] [CrossRef]
- Sengupta, A.; Jin, F.; Zhang, R.; Cao, S. Mm-Pose: Real-Time Human Skeletal Posture Estimation Using MmWave Radars and CNNs. IEEE Sens. J. 2020, 20, 10032–10044. [Google Scholar] [CrossRef]
- Lee, S.-P.; Kini, N.P.; Peng, W.-H.; Ma, C.-W.; Hwang, J.-N. HuPR: A Benchmark for Human Pose Estimation Using Millimeter Wave Radar. In Proceedings of the 2023 IEEE/CVF Winter Conference on Applications of Computer Vision (WACV), Waikoloa, HI, USA, 2–7 January 2023; pp. 5704–5713. [Google Scholar]
- Sengupta, A.; Cao, S. MmPose-NLP: A Natural Language Processing Approach to Precise Skeletal Pose Estimation Using MmWave Radars. IEEE Trans. Neural Netw. Learn. Syst. 2022, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Cao, D.; Liu, R.; Jiang, W.; Yao, T.; Lu, C.X. Human Parsing with Joint Learning for Dynamic MmWave Radar Point Cloud. Proc. ACM Interact. Mob. Wearable Ubiquitous Technol. 2022, 7, 1–22. [Google Scholar] [CrossRef]
- Xue, H.; Ju, Y.; Miao, C.; Wang, Y.; Wang, S.; Zhang, A.; Su, L. MmMesh: Towards 3D Real-Time Dynamic Human Mesh Construction Using Millimeter-Wave. In Proceedings of the 19th Annual International Conference on Mobile Systems, Applications, and Services, Virtual Event, WI, USA, 24 June 2021; pp. 269–282. [Google Scholar]
- Chen, A.; Wang, X.; Zhu, S.; Li, Y.; Chen, J.; Ye, Q. MmBody Benchmark: 3D Body Reconstruction Dataset and Analysis for Millimeter Wave Radar. In Proceedings of the 30th ACM International Conference on Multimedia, Lisboa, Portugal, 10 October 2022; pp. 3501–3510. [Google Scholar]
- Addabbo, P.; Bernardi, M.L.; Biondi, F.; Cimitile, M.; Clemente, C.; Orlando, D. Temporal Convolutional Neural Networks for Radar Micro-Doppler Based Gait Recognition. Sensors 2021, 21, 381. [Google Scholar] [CrossRef]
- Jiang, X.; Zhang, Y.; Yang, Q.; Deng, B.; Wang, H. Millimeter-Wave Array Radar-Based Human Gait Recognition Using Multi-Channel Three-Dimensional Convolutional Neural Network. Sensors 2020, 20, 5466. [Google Scholar] [CrossRef] [PubMed]
- Seifert, A.-K.; Amin, M.G.; Zoubir, A.M. Toward Unobtrusive In-Home Gait Analysis Based on Radar Micro-Doppler Signatures. IEEE Trans. Biomed. Eng. 2019, 66, 2629–2640. [Google Scholar] [CrossRef] [PubMed]
- Taylor, W.; Dashtipour, K.; Shah, S.A.; Hussain, A.; Abbasi, Q.H.; Imran, M.A. Radar Sensing for Activity Classification in Elderly People Exploiting Micro-Doppler Signatures Using Machine Learning. Sensors 2021, 21, 3881. [Google Scholar] [CrossRef]
- Chen, V.C. Advances in Applications of Radar Micro-Doppler Signatures. In Proceedings of the 2014 IEEE Conference on Antenna Measurements & Applications (CAMA), Antibes Juan-les-Pins, France, 16–19 November 2014; pp. 1–4. [Google Scholar]
- Qiao, X.; Amin, M.G.; Shan, T.; Zeng, Z.; Tao, R. Human Activity Classification Based on Micro-Doppler Signatures Separation. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Chen, V.C. Analysis of Radar Micro-Doppler with Time-Frequency Transform. In Proceedings of the Tenth IEEE Workshop on Statistical Signal and Array Processing (Cat. No.00TH8496), Pocono Manor, PA, USA, 16 August 2000; pp. 463–466. [Google Scholar]
- Raj, R.G.; Chen, V.C.; Lipps, R. Analysis of Radar Human Gait Signatures. IET Signal Process. 2010, 4, 234. [Google Scholar] [CrossRef]
- Shi, X.; Zhou, F.; Tao, M.; Zhang, Z. Human Movements Separation Based on Principle Component Analysis. IEEE Sens. J. 2016, 16, 2017–2027. [Google Scholar] [CrossRef]
- Qiao, X.; Shan, T.; Tao, R.; Bai, X.; Zhao, J. Separation of Human Micro-Doppler Signals Based on Short-Time Fractional Fourier Transform. IEEE Sens. J. 2019, 19, 12205–12216. [Google Scholar] [CrossRef]
- Li, G.; Zhang, R.; Rao, W.; Wang, X. Separation of Multiple Micro-Doppler Components via Parametric Sparse Recovery. In Proceedings of the 2013 IEEE International Geoscience and Remote Sensing Symposium-IGARSS, Melbourne, Australia, 21–26 July 2013; pp. 2978–2981. [Google Scholar]
- Abdulatif, S.; Aziz, F.; Kleiner, B.; Schneider, U. Real-Time Capable Micro-Doppler Signature Decomposition of Walking Human Limbs. In Proceedings of the 2017 IEEE Radar Conference (RadarConf), Seattle, WA, USA, 8–12 May 2017; pp. 1093–1098. [Google Scholar]
- Fogle, O.R.; Rigling, B.D. Micro-Range/Micro-Doppler Decomposition of Human Radar Signatures. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 3058–3072. [Google Scholar] [CrossRef]
- Lin, A.; Ling, H. Doppler and Direction-of-Arrival (DDOA) Radar for Multiple-Mover Sensing. IEEE Trans. Aerosp. Electron. Syst. 2007, 43, 1496–1509. [Google Scholar] [CrossRef]
- Lin, A.; Ling, H. Frontal Imaging of Human Using Three- Element Doppler and Direction-of-Arrival Radar. Electron. Lett. 2006, 42, 660. [Google Scholar] [CrossRef]
- Lin, A.; Ling, H. Three-Dimensional Tracking of Humans Using Very Low-Complexity Radar. Electron. Lett. 2006, 42, 1062. [Google Scholar] [CrossRef]
- Ram, S.S.; Li, Y.; Lin, A.; Ling, H. Human Tracking Using Doppler Processing and Spatial Beamforming. In Proceedings of the 2007 IEEE Radar Conference, Waltham, MA, USA, 17–20 April 2007; pp. 546–551. [Google Scholar]
- Ram, S.S.; Ling, H. Through-Wall Tracking of Human Movers Using Joint Doppler and Array Processing. IEEE Geosci. Remote Sens. Lett. 2008, 5, 537–541. [Google Scholar] [CrossRef]
- Saho, K.; Homma, H.; Sakamoto, T.; Sato, T.; Inoue, K.; Fukuda, T. Accurate Image Separation Method for Two Closely Spaced Pedestrians Using UWB Doppler Imaging Radar and Supervised Learning. IEICE Trans. Commun. 2014, E97.B, 1223–1233. [Google Scholar] [CrossRef]
- Saho, K.; Sakamoto, T.; Sato, T.; Inoue, K.; Fukuda, T. Accurate and Real-Time Pedestrian Classification Based on UWB Doppler Radar Images and Their Radial Velocity Features. IEICE Trans. Commun. 2013, E96.B, 2563–2572. [Google Scholar] [CrossRef]
- Sakamoto, T.; Matsuki, Y.; Sato, T. Method for the Three-Dimensional Imaging of a Moving Target Using an Ultra-Wideband Radar with a Small Number of Antennas. IEICE Trans. Commun. 2012, E95-B, 972–979. [Google Scholar] [CrossRef]
- Steinhauser, D.; HeId, P.; Kamann, A.; Koch, A.; Brandmeier, T. Micro-Doppler Extraction of Pedestrian Limbs for High Resolution Automotive Radar. In Proceedings of the 2019 IEEE Intelligent Vehicles Symposium (IV), Paris, France, 9–12 June 2019; pp. 764–769. [Google Scholar]
- Held, P.; Steinhauser, D.; Koch, A.; Brandmeier, T.; Schwarz, U.T. A Novel Approach for Model-Based Pedestrian Tracking Using Automotive Radar. IEEE Trans. Intell. Transport. Syst. 2022, 23, 7082–7095. [Google Scholar] [CrossRef]
- Kang, W.; Zhang, Y.; Dong, X.; Yang, J. Three-Dimensional Micromotion Trajectory Reconstruction of Rotating Targets by Interferometric Radar. J. Appl. Remote Sens. 2020, 14, 046506. [Google Scholar] [CrossRef]
- Chen, V.C. The Micro-Doppler Effect in Radar, 2nd ed.; Artech: Morristown, NJ, USA, 2019; ISBN 978-1-63081-548-6. [Google Scholar]
- Wang, G.; Xia, X.; Chen, V.C. Three-Dimensional ISAR Imaging of Maneuvering Targets Using Three Receivers. IEEE Trans. Image Process. 2001, 10, 436–447. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Y.; Dong, X. Squint Model InISAR Imaging Method Based on Reference Interferometric Phase Construction and Coordinate Transformation. Remote Sens. 2021, 13, 2224. [Google Scholar] [CrossRef]
- Richards, M.A. Fundamentals of Radar Signal Processing, 3rd ed.; McGraw Hill: New York, NY, USA, 2022; ISBN 978-1-260-46871-7. [Google Scholar]
- Patole, S.M.; Torlak, M.; Wang, D.; Ali, M. Automotive Radars: A Review of Signal Processing Techniques. IEEE Signal Process. Mag. 2017, 34, 22–35. [Google Scholar] [CrossRef]
- Shafiq, M.A. Real Time Implementation and Profiling of Different CFAR Algorithms over DSP Kit. In Proceedings of the 2014 11th International Bhurban Conference on Applied Sciences & Technology (IBCAST), Islamabad, Pakistan, 14–18 January 2014; pp. 466–470. [Google Scholar]
- Tölgyessy, M.; Dekan, M.; Chovanec, Ľ. Skeleton Tracking Accuracy and Precision Evaluation of Kinect V1, Kinect V2, and the Azure Kinect. Appl. Sci. 2021, 11, 5756. [Google Scholar] [CrossRef]
- Romeo, L.; Marani, R.; Malosio, M.; Perri, A.G.; D’Orazio, T. Performance Analysis of Body Tracking with the Microsoft Azure Kinect. In Proceedings of the 2021 29th Mediterranean Conference on Control and Automation (MED), Puglia, Italy, 22 June 2021; pp. 572–577. [Google Scholar]
- He, X.; Zhang, Y.; Dong, X.; Yang, J.; Li, D.; Shi, X. Discrimination of Single-Channel Radar Micro-Doppler of Human Joints Based on Kinect Sensor. In Proceedings of the 2022 Photonics & Electromagnetics Research Symposium (PIERS), Hangzhou, China, 25 April 2022; pp. 640–646. [Google Scholar]





| Ref. | Tx/Rx Channels | Angle Information | Object | Aim | Data Represented Domain | Operating Freq. | Year |
|---|---|---|---|---|---|---|---|
| [25] | 1 × 3 | Azimuth and Elevation | Moving humans | Multiple humans tracking | Azimuth elevation range domain | = 2.4 GHz = 2.39 GHz | 2006 |
| [28] | 1 × 3 | Azimuth and Elevation | Two pedestrians | Image separation | Azimuth elevation range domain | = 26.4 GHz = 500 MHz | 2014 |
| [31] | 1 × 10 | Azimuth | Human limbs | Extraction of limbs | Time-Doppler domain | = 77 GHz, = 2 GHz | 2019 |
| [2] | 1 × 3 | Azimuth and Elevation | Human hands | Gesture recognition | Range-Doppler map interferometry map | = 60.75 GHz = 4.5 GHz | 2021 |
| [32] | 16 (Rx) | Azimuth and Elevation | Pedestrian | Feet tracking | Time-Doppler range domain | = 76.5 = 1 GHz | 2022 |
| [this work] | 1 × 3 | Azimuth and Elevation | Human limbs | Extraction of limbs | Time-Doppler range domain | = 79 GHz, = 4 GHz | 2023 |
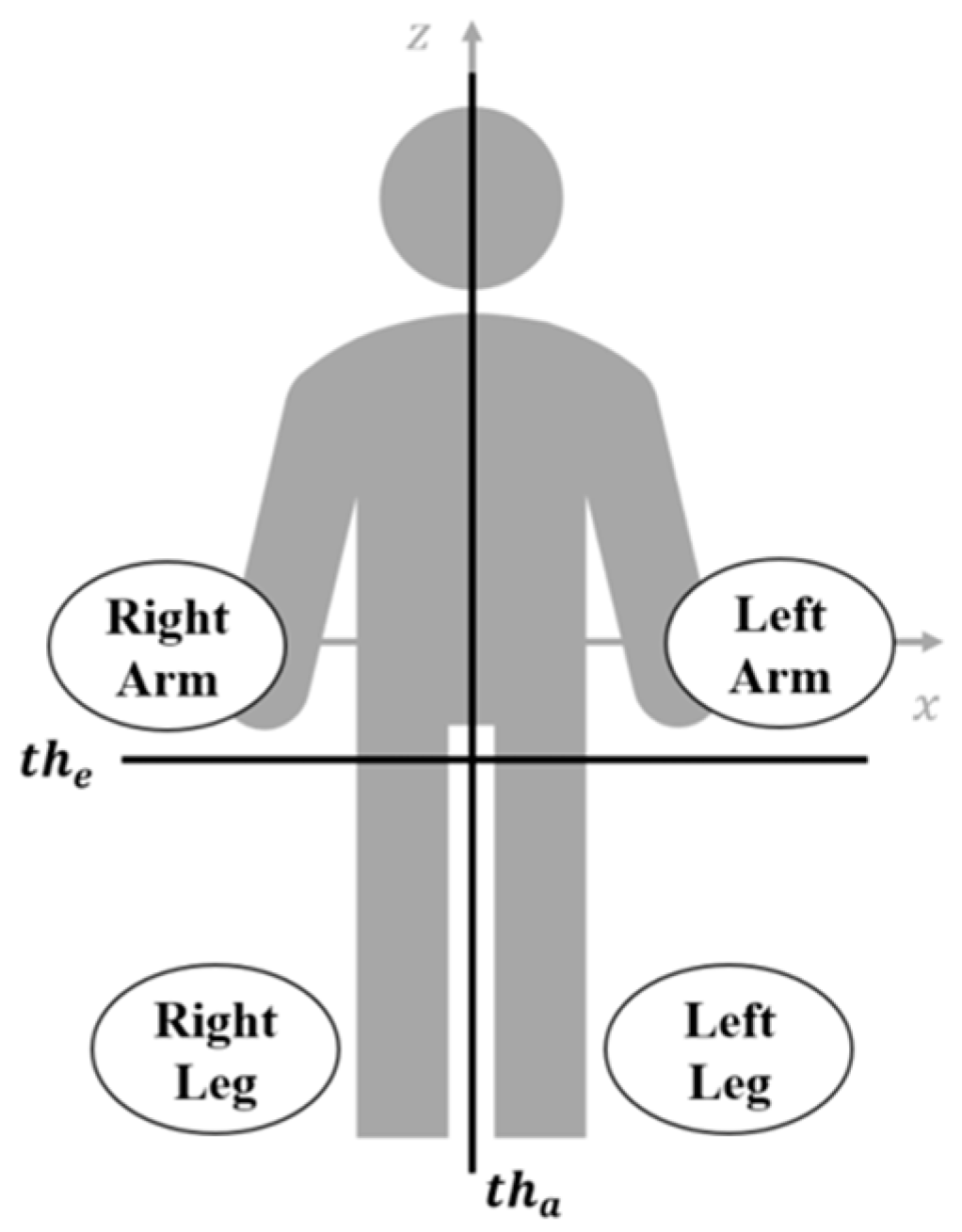
| Right Arm | ||
| Left Arm | ||
| Right Leg | ||
| Left Leg |
| Volunteer 1 | Volunteer 2 | Volunteer 3 | |
|---|---|---|---|
| Height | 176 cm | 166 cm | 170 cm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, X.; Zhang, Y.; Dong, X. Extraction of Human Limbs Based on Micro-Doppler-Range Trajectories Using Wideband Interferometric Radar. Sensors 2023, 23, 7544. https://doi.org/10.3390/s23177544
He X, Zhang Y, Dong X. Extraction of Human Limbs Based on Micro-Doppler-Range Trajectories Using Wideband Interferometric Radar. Sensors. 2023; 23(17):7544. https://doi.org/10.3390/s23177544
Chicago/Turabian StyleHe, Xianxian, Yunhua Zhang, and Xiao Dong. 2023. "Extraction of Human Limbs Based on Micro-Doppler-Range Trajectories Using Wideband Interferometric Radar" Sensors 23, no. 17: 7544. https://doi.org/10.3390/s23177544





