Reconstruction of Water-Filled Pipe Ultrasonic Guided Wave Signals in the Distance Domain by Orthogonal Matching Pursuit Based on Dispersion and Multi-Mode
Abstract
:1. Introduction
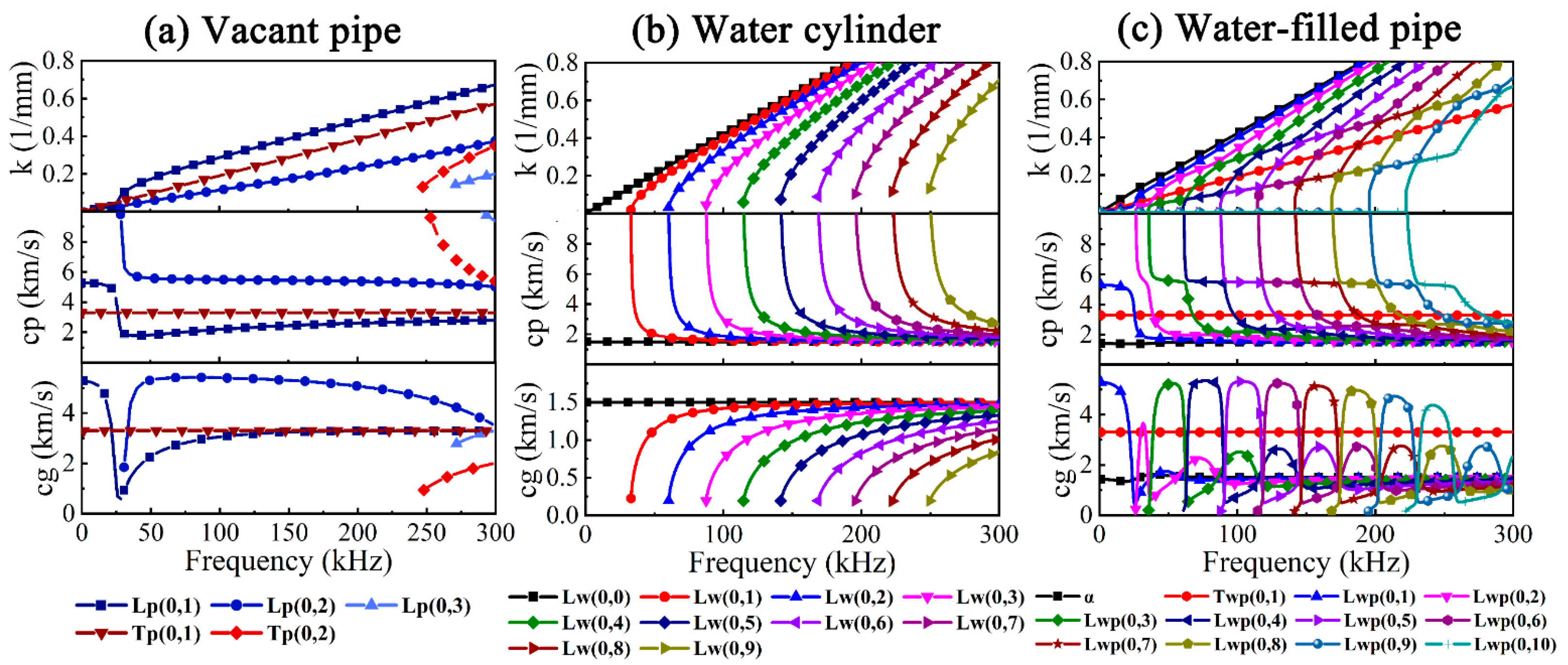
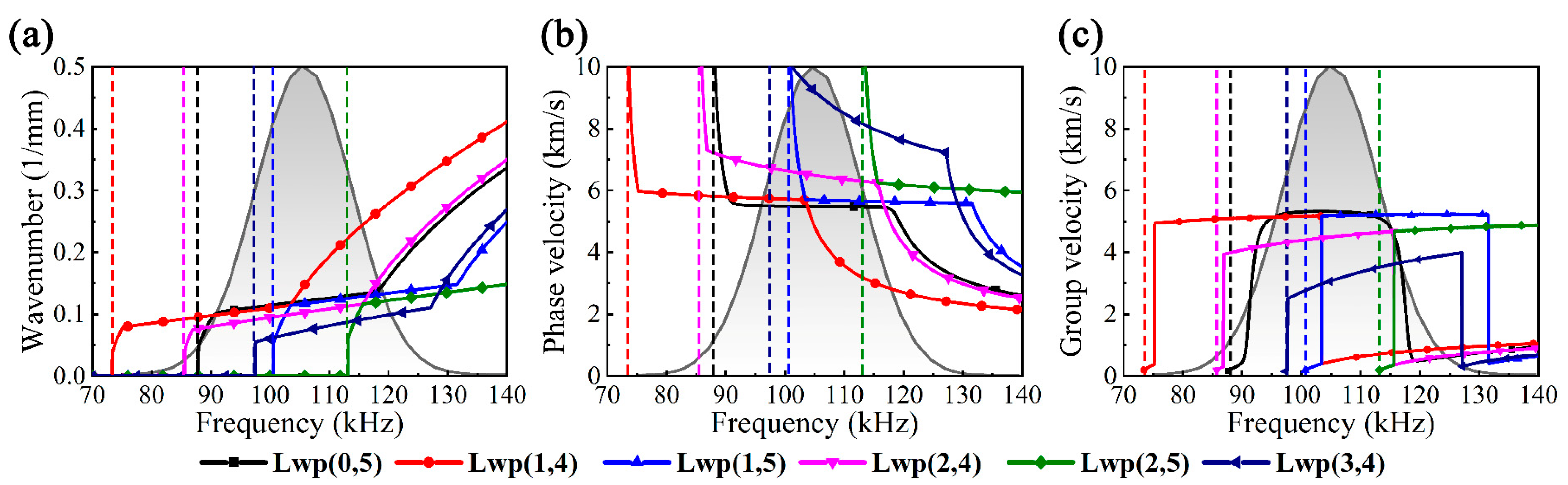
2. UGW Characteristics of Water-Filled Pipe
2.1. Dispersion
2.2. Multi-Mode
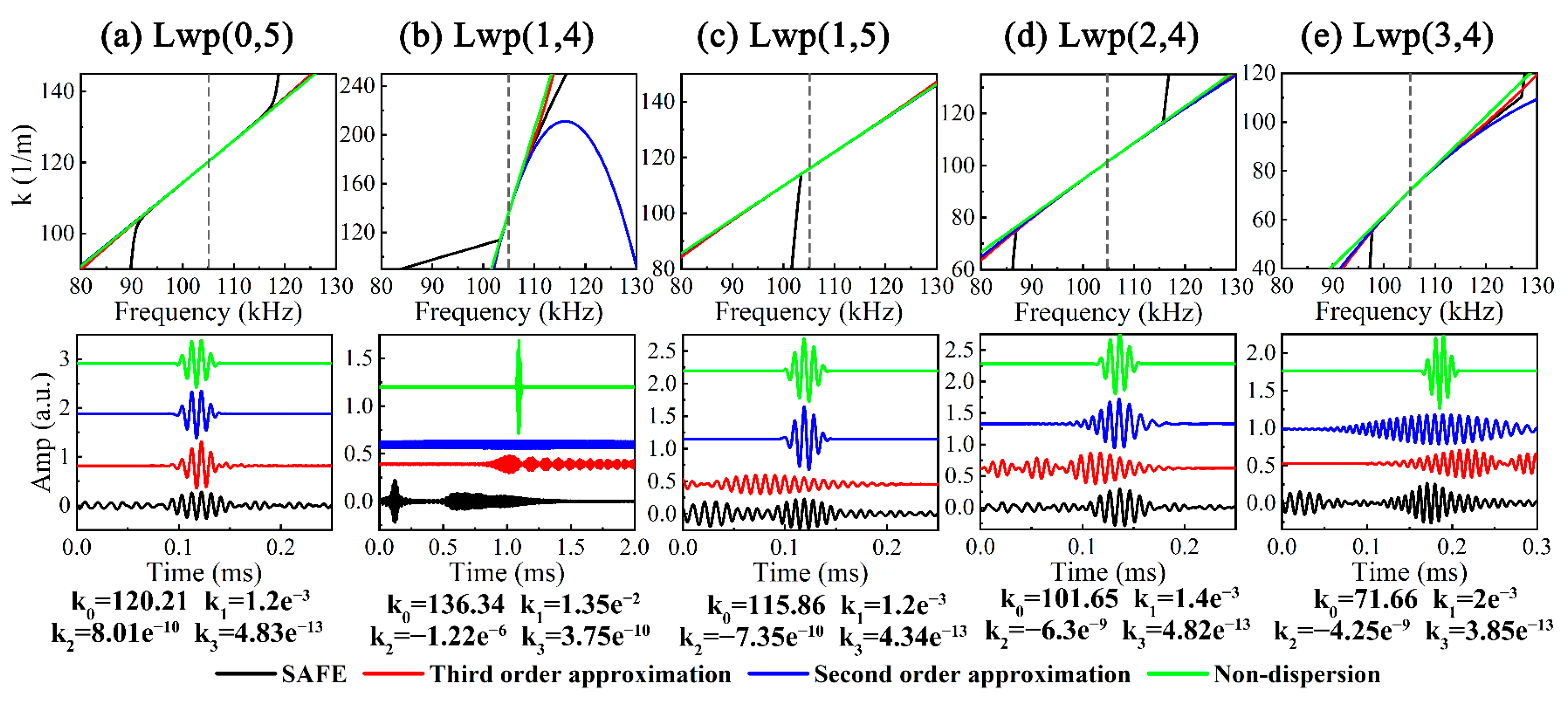
3. Dispersion-Compensated Time-Distance Mapping
3.1. Dispersion Compensation
3.2. Time-Distance Mapping
3.3. Analysis of Synthesized UGW Signals
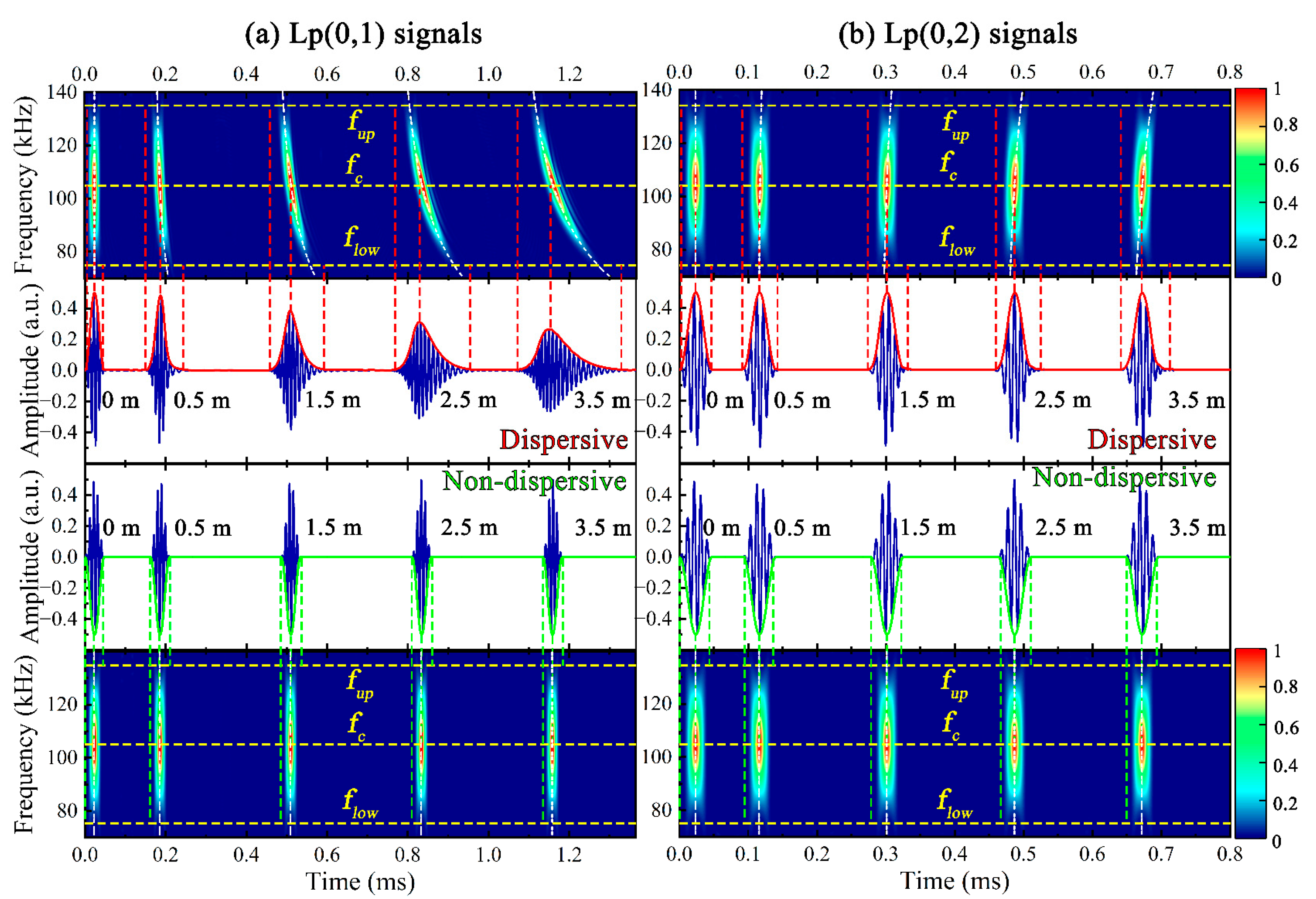
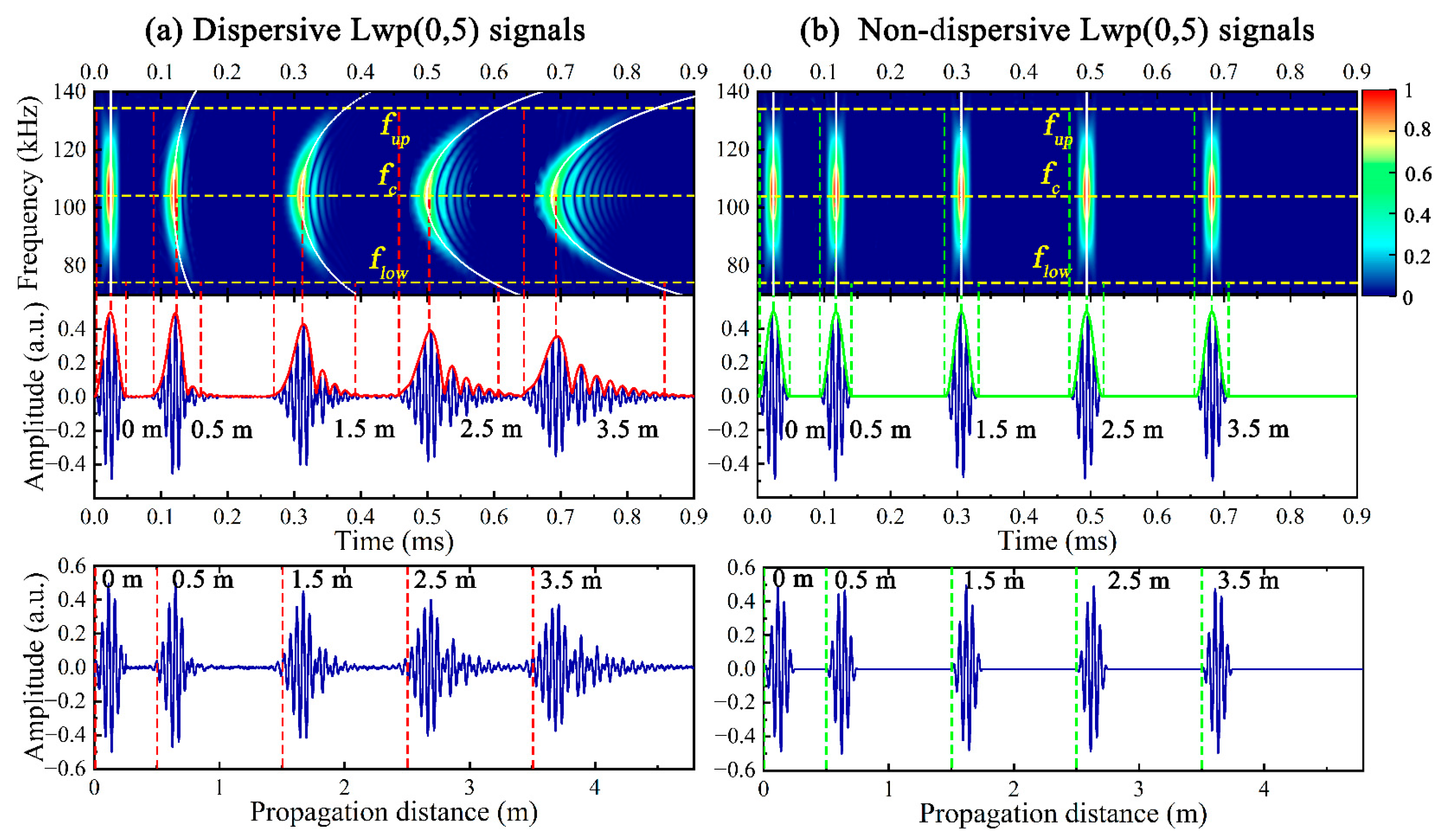
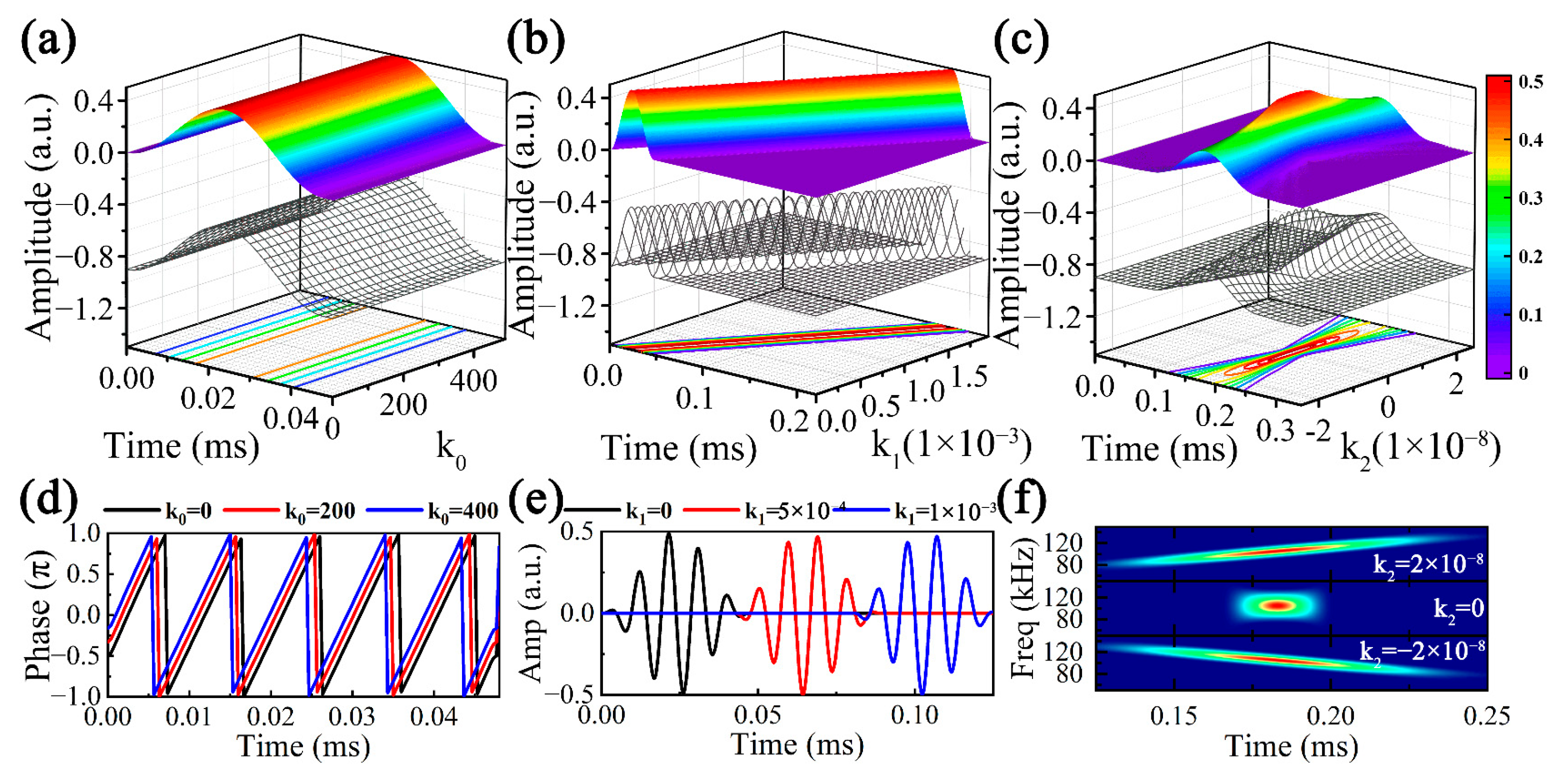
4. Dispersive and Non-Dispersive Atoms
4.1. Analysis of UGW Dispersive and Non-Dispersive Atoms
4.2. Effects of Atom Parameters
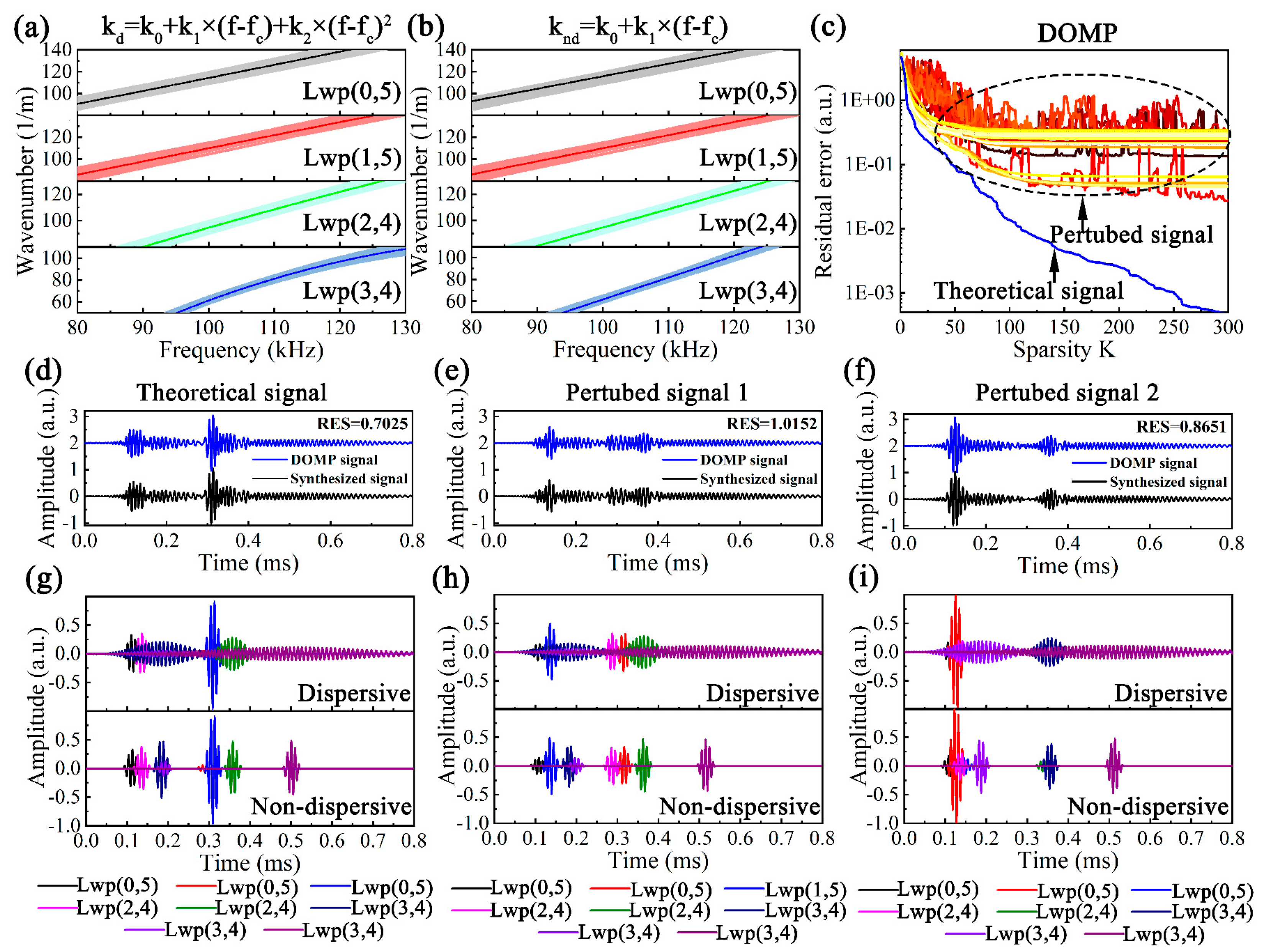
5. Orthogonal Matching Pursuit Based on Dispersion (DOMP)
5.1. Methodology
| Algorithm 1: DOMP. |
for k = 1:K do end for |
5.2. Simulation Results
6. Orthogonal Matching Pursuit Based on Dispersion and Multi-Mode (DMOMP)
6.1. Methodology
| Algorithm 2: DMOMP. |
while i <= K1 do for j = 1:L do end for end while |
- (1)
- The target mode UGW is dominant in fr, for which the dictionary D1d and propagation distance set x1 can be constructed and can be obtained by applying DOMP on fr with the sparsity K1. Determine the set of possible propagation distances for each target mode guide wave based on the coarsely selected , and the range can be expressed by upper ub and lower lb bounds;
- (2)
- For the i-th target mode UGW, traverse according to lb(i) and ub(i) (j refers to the j-th iteration and ), and construct the dictionary , which is consistent with the dictionaries of K2 mode at the given . The residual error can be obtained by DOMP, taking the index k to correspond to the smallest RES (), and the decomposed results of i-th target mode and its flexural modes are determined, namely and ;
- (3)
- Repeat step (2) K1 times to obtain the reconstructed signals corresponding to i-th target mode and its flexural modes, the time-domain reconstructed results can be obtained by summing. The final distance-domain non-dispersive signal can be obtained by the dispersion-compensated time-distance mapping.
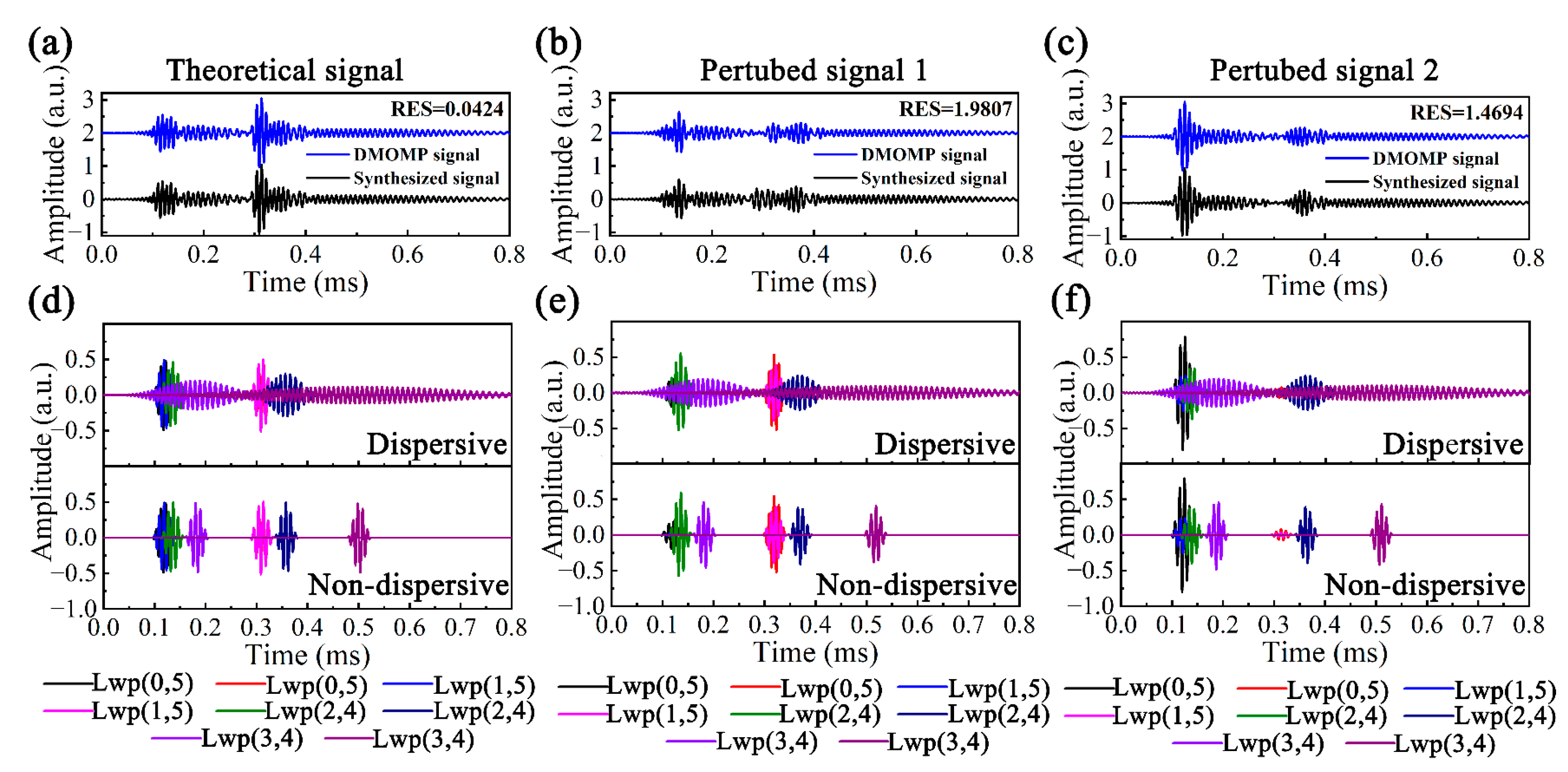
6.2. Sensitivity of Perturbation
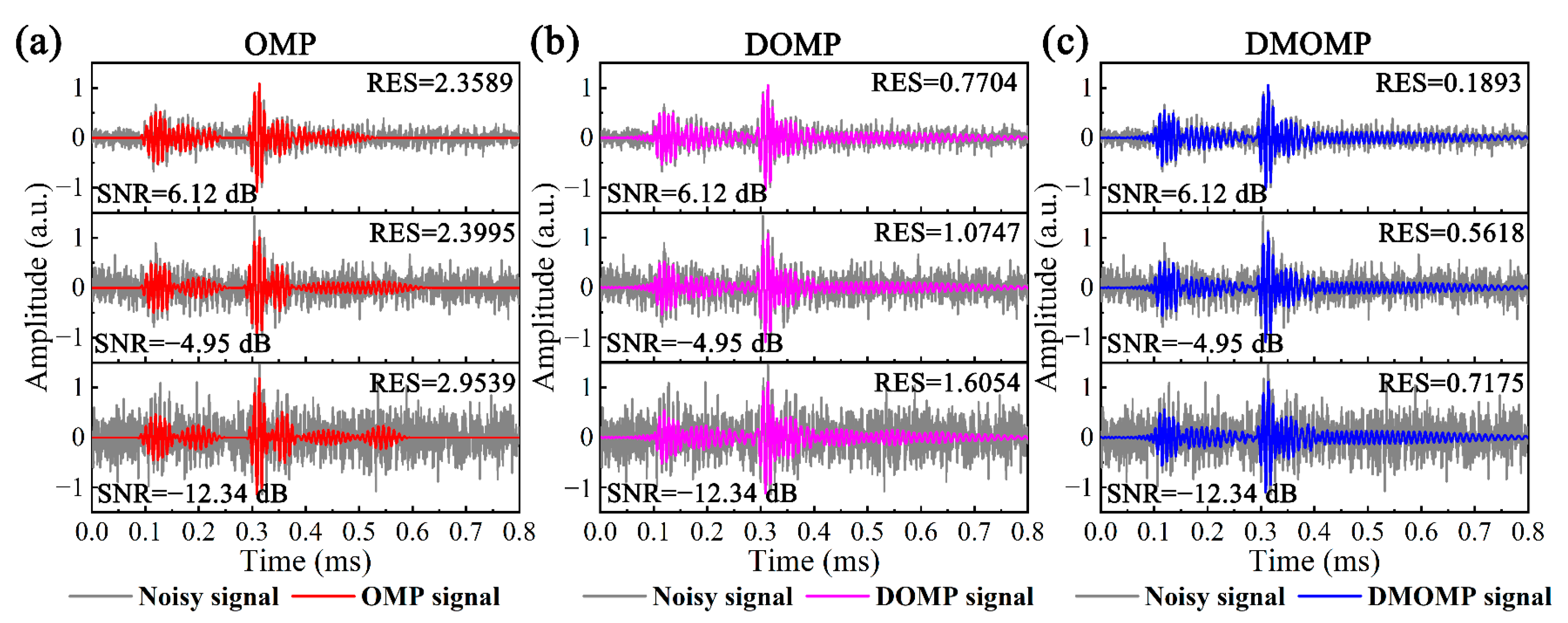
6.3. Sensitivity to Noise
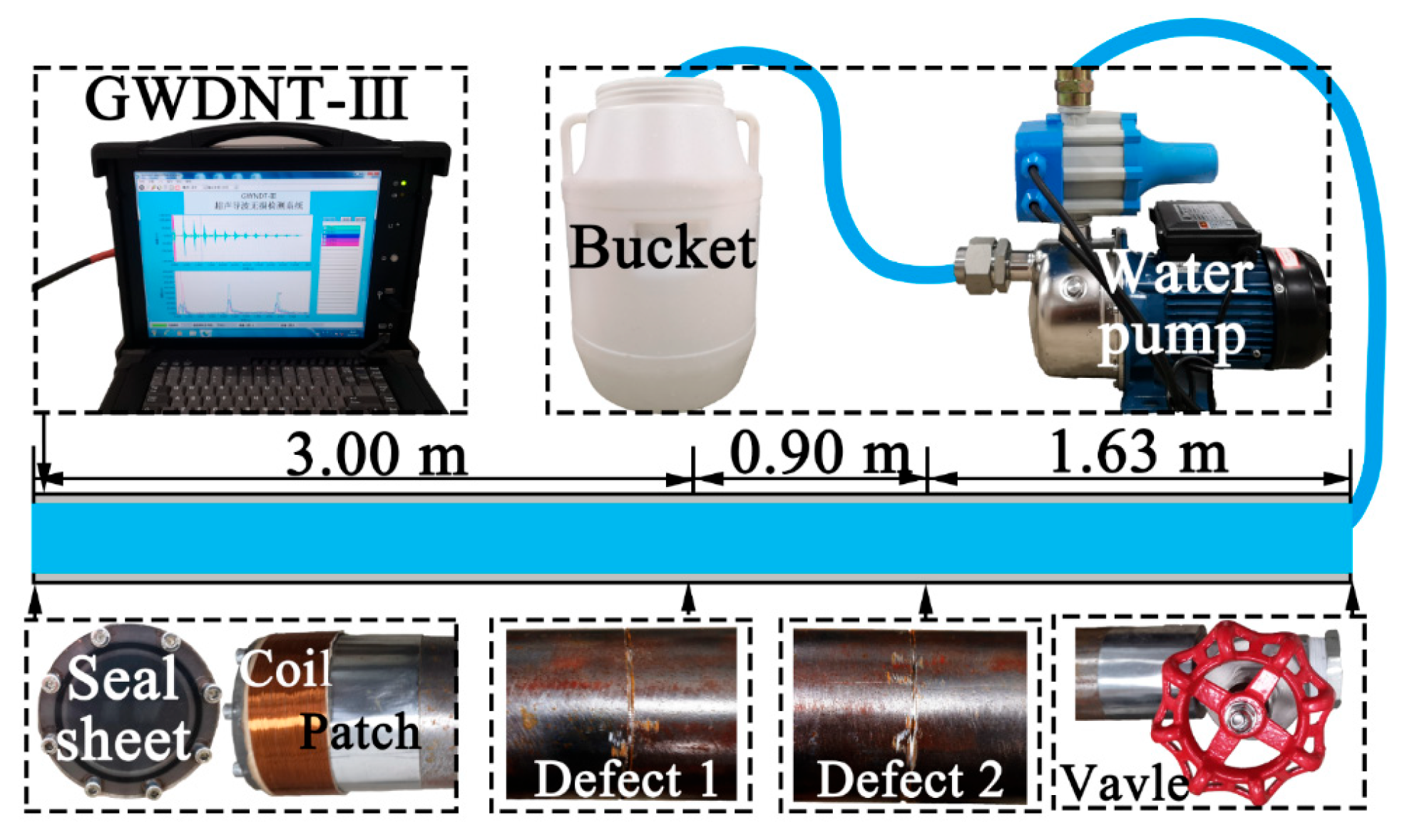
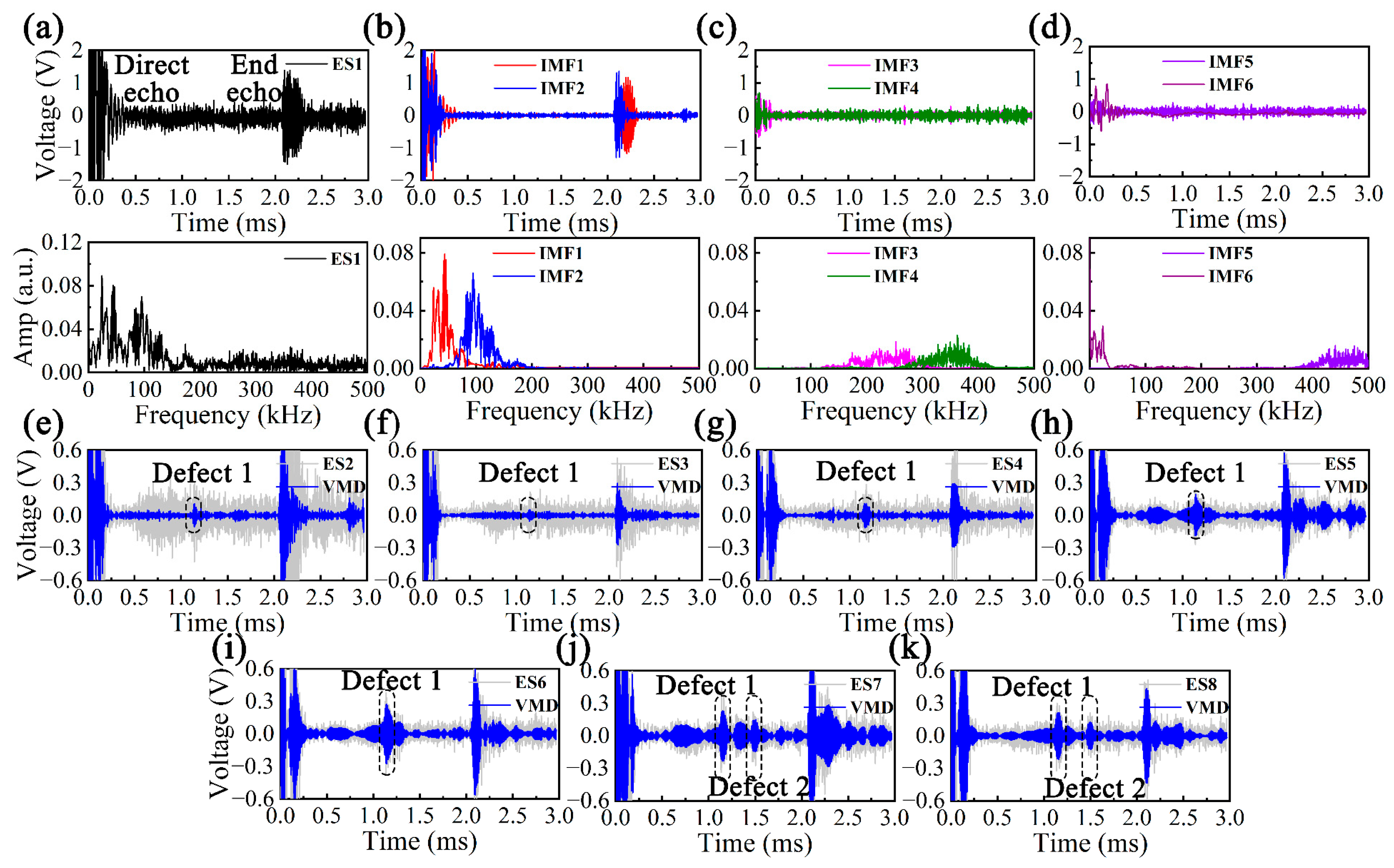
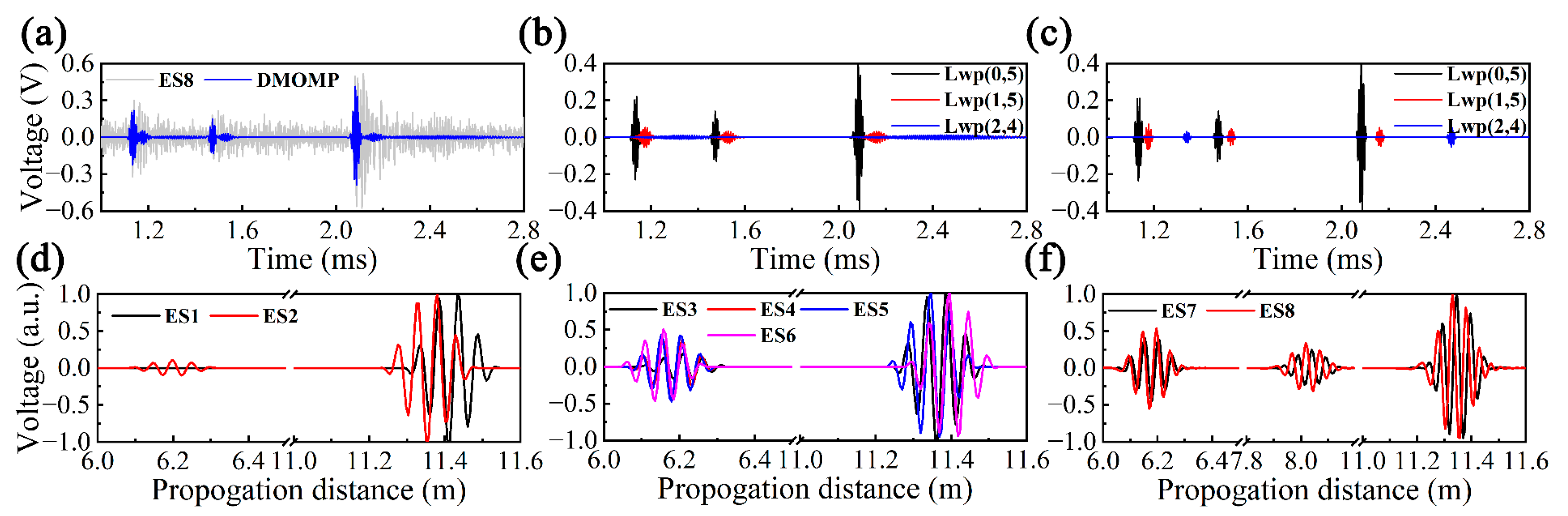
7. Experimental UGW Testing Results
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, H.L.; Ling, F.Y.; Zhu, W.J.; Sun, D.; Liu, X.Y.; Li, Y.; Li, D.; Xu, K.L.; Liu, Z.H.; Ta, D. Waveform inversion for wavenumber extraction and waveguide characterization using ultrasonic Lamb waves. Measurement 2023, 207, 112360. [Google Scholar] [CrossRef]
- Diogo, A.R.; Moreira, B.; Gouveia CA, J.; Tavares, J.M.R.S. A review of signal processing techniques for ultrasonic guided wave testing. Metals 2022, 12, 936. [Google Scholar] [CrossRef]
- Abbassi, A.; Römgens, N.; Tritschel, F.F.; Penner, N.; Rolfes, R. Evaluation of machine learning techniques for structural health monitoring using ultrasonic guided waves under varying temperature conditions. Struct. Health Monit. 2023, 22, 1308–1325. [Google Scholar] [CrossRef]
- Liao, W.L.; Sun, H.; Wang, Y.S.; Qing, X.L. A novel damage index integrating piezoelectric impedance and ultrasonic guided wave for damage monitoring of bolted joints. Struct. Health Monit. 2023, 22, 3514–3533. [Google Scholar] [CrossRef]
- Olisa, S.C.; Khan, M.A.; Starr, A. Review of current guided wave ultrasonic testing (GWUT) limitations and future directions. Sensors 2021, 21, 811. [Google Scholar] [CrossRef] [PubMed]
- Huang, M.K.; Han, C.; An, Y.; Qu, Z.G.; Chen, C.X.; Yin, W.L. Influence of temperature on fouling removal for pipeline based on eco-friendly ultrasonic guided wave technology. Clean Technol. Environ. Policy 2023, 25, 1211–1221. [Google Scholar] [CrossRef]
- Qu, Z.G.; Fu, Y.K.; Zhang, Q.P.; An, Y.; Shan, X.; Sun, Y.; Zhao, J.Y.; Chen, C.X. Structural health monitoring for multi-strand aircraft wire insulation layer based on ultrasonic guided waves. Appl. Acoust. 2022, 201, 109109. [Google Scholar] [CrossRef]
- Chen, Z.H.; Xu, G.C.; Wei, L.; Li, C.G.; Chao, L. Nonlinear lamb wave imaging method for testing Barely Visible Impact Damage of CFRP laminates. Appl. Acoust. 2022, 192, 108699. [Google Scholar] [CrossRef]
- Masmoudi, M.; Yaacoubi, S.; Koabaz, M.; Akrout, M.; Skaiky, A. On the use of ultrasonic guided waves for the health monitoring of rails. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2022, 236, 469–489. [Google Scholar] [CrossRef]
- Li, Z.; Jing, L.W.; Wang. W., J.; Lee, P.; Murch, R. The influence of pipeline thickness and radius on guided wave attenuation in water-filled steel pipelines: Theoretical analysis and experimental measurement. J. Acoust. Soc. Am. 2019, 145, 361–371. [Google Scholar] [CrossRef]
- Ma, Q.; Du, G.F.; Yu, Z.Y.; Yuan, H.Q.; Wei, X.L. Classification of damage types in liquid-filled buried pipes based on deep learning. Meas. Sci. Technol. 2022, 34, 025010. [Google Scholar] [CrossRef]
- Zhang, J.N.; Cho, Y.H.; Kim, J.; Malikov AK, U.; Kim, Y.H.; Yi, J.H. Nondestructive inspection of underwater coating layers using ultrasonic lamb waves. Coatings 2023, 13, 728. [Google Scholar] [CrossRef]
- Mehrabi, M.; Soorgee, M.H.; Habibi, H.; Kappatos, V. An experimental technique for evaluating viscoelastic damping using ultrasonic guided waves. Ultrasonics 2022, 123, 106707. [Google Scholar] [CrossRef] [PubMed]
- Narayanan, M.M.; Arjun, V.; Kumar, A.; Mukhopadhyay, C.K. Development of in-bore magnetostrictive transducer for ultrasonic guided wave based-inspection of steam generator tubes of PFBR. Ultrasonics 2020, 106, 106148. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.M.; Yang, B. Theory and Method of Magnetostrictive Guided Wave Nondestructive Testing; Science Press: Beijing, China, 2015. [Google Scholar]
- Tang, B.H.; Wang, Y.M.; Chen, A.; Zhao, Y.W.; Xu, J.J. Split-spectrum processing with raised cosine filters of constant frequency-to-bandwidth ratio for L (0, 2) ultrasonic guided wave testing in a pipeline. Appl. Sci. 2022, 12, 7611. [Google Scholar] [CrossRef]
- Pedram, S.K.; Fateri, S.; Gan, L.; Haig, A.; Thornicroft, K. Split-spectrum processing technique for SNR enhancement of ultrasonic guided wave. Ultrasonics 2018, 83, 48–59. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.C.; Li, J.; Wang, D.P.; Huang, X.J.; Liang, L.; Tang, Z.F.; Fan, Z.; Liu, Y. Sparse ultrasonic guided wave imaging with compressive sensing and deep learning. Mech. Syst. Signal Process. 2022, 178, 109346. [Google Scholar] [CrossRef]
- Gao, Y.; Mu, W.; Yuan, F.G.; Liu, G. A defect localization method based on self-sensing and orthogonal matching pursuit. Ultrasonics 2023, 128, 106889. [Google Scholar] [CrossRef]
- Wang, Y.S.; Wang, G.; Wu, D.; Wang, Y.; Miao, B.R.; Sun, H.; Qing, X.L. An improved matching pursuit-based temperature and load compensation method for ultrasonic guided wave signals. IEEE Access 2020, 8, 67530–67541. [Google Scholar] [CrossRef]
- Zheng, S.H.; Chen, H.L.; Ling, F.Y.; Minonzio, J.G.; Ta, D.; Xu, K.L. Orthogonal Matching Pursuit based Sparse Dispersive Radon Transform for Ultrasonic Guided Mode Extraction. In Proceedings of the 2022 IEEE International Ultrasonics Symposium (IUS), Venice, Italy, 10–13 October 2022; pp. 1–4. [Google Scholar]
- Fan, W.; Wan, D.Y.; Xu, Z.Y.; Wang, Y.; Du, H. Feature extraction of echo signal of weld defect guided waves based on sparse representation. IEEE Sens. J. 2019, 20, 2692–2700. [Google Scholar] [CrossRef]
- Zhang, H.; Hua, J.D.; Gao, F.; Lin, J. Efficient Lamb-wave based damage imaging using multiple sparse Bayesian learning in composite laminates. NDT E Int. 2020, 116, 102277. [Google Scholar] [CrossRef]
- Ladpli, P.; Liu, C.; Kopsaftopoulos, F.; Chang, F.K. Estimating lithium-ion battery state of charge and health with ultrasonic guided waves using an efficient matching pursuit technique. In Proceedings of the 2018 IEEE Transportation Electrification Conference and Expo, Asia-Pacific (ITEC Asia-Pacific), Bangkok, Thailand, 6–9 June 2018; pp. 1–5. [Google Scholar]
- Chen, H.L.; Liu, Z.H.; Wu, B.; He, C.F. A technique based on nonlinear Hanning-windowed chirplet model and genetic algorithm for parameter estimation of Lamb wave signals. Ultrasonics 2021, 111, 106333. [Google Scholar] [CrossRef] [PubMed]
- Mu, W.L.; Gao, Y.Q.; Liu, G.J. Ultrasound defect localization in shell structures with Lamb waves using spare sensor array and orthogonal matching pursuit decomposition. Sensors 2021, 21, 8127. [Google Scholar] [CrossRef]
- Cai, J.; Yuan, S.F.; Qing XL, P.; Chang, F.K.; Shi, L.H.; Qiu, L. Linearly dispersive signal construction of Lamb waves with measured relative wavenumber curves. Sens. Actuators A Phys. 2015, 221, 41–52. [Google Scholar] [CrossRef]
- Lian, M.; Liu, H.B.; Bo, Q.L.; Zhang, T.Y.; Li, T.; Wang, Y.Q. An improved matching pursuit method for overlapping echo separation in ultrasonic thickness measurement. Meas. Sci. Technol. 2019, 30, 065001. [Google Scholar] [CrossRef]
- Chen, H.L.; Liu, Z.H.; Wu, B.; He, C.F. A Nonlinear Hanning-Windowed Chirplet Model for Ultrasonic Guided Waves Signal Parameter Representation. J. Nondestruct. Eval. 2020, 39, 65. [Google Scholar] [CrossRef]
- Xu, C.B.; Yang, Z.B.; Chen, X.F.; Tian, S.H.; Xie, Y. A guided wave dispersion compensation method based on compressed sensing. Mech. Syst. Signal Process. 2018, 103, 89–104. [Google Scholar] [CrossRef]
- Kim, H.; Yuan, F.G. Adaptive signal decomposition and dispersion removal based on the matching pursuit algorithm using dispersion-based dictionary for enhancing damage imaging. Ultrasonics 2020, 103, 106087. [Google Scholar] [CrossRef]
- Rostami, J.; Tse PW, T.; Fang, Z. Sparse and dispersion-based matching pursuit for minimizing the dispersion effect occurring when using guided wave for pipe inspection. Materials 2017, 10, 622. [Google Scholar] [CrossRef]
- Gao, Y.; Sui, F.S.; Muggleton, J.M.; Yang, J. Simplified dispersion relationships for fluid-dominated axisymmetric wave motion in buried fluid-filled pipes. J. Sound Vib. 2016, 375, 386–402. [Google Scholar] [CrossRef]
- Bathe, K.J. Finite Element Procedures, 2nd ed.; Klaus-Jurgen Bathe: Watertown, MA, USA, 2006. [Google Scholar]
- Pierce, A.D. Acoustics: An Introduction to Its Physical Principles and Applications; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Kalkowski, M.K.; Muggleton, J.M.; Rustighi, E. Axisymmetric semi-analytical finite elements for modelling waves in buried/submerged fluid-filled waveguides. Comput. Struct. 2018, 196, 327–340. [Google Scholar] [CrossRef]
- Bartoli, I.; Marzani, A.; Di Scalea, F.L.; Viola, E. Modeling wave propagation in damped waveguides of arbitrary cross-section. J. Sound Vib. 2006, 295, 685–707. [Google Scholar] [CrossRef]
- Song, Z.H.; Qi, X.S.; Liu, Z.H.; Ma, H.W. Experimental study of guided wave propagation and damage detection in large diameter pipe filled by different fluids. NDT E Int. 2018, 93, 78–85. [Google Scholar] [CrossRef]
- Aristegui, C.; Lowe, M.J.S.; Cawley, P. Guided waves in fluid-filled pipes surrounded by different fluids. Ultrasonics 2001, 39, 367–375. [Google Scholar] [CrossRef]
- Meitzler, A.H. Mode coupling occurring in the propagation of elastic pulses in wires. J. Acoust. Soc. Am. 1961, 33, 435–445. [Google Scholar] [CrossRef]
- Wu, W.J.; Wang, Y.M. A simplified dispersion compensation algorithm for the interpretation of guided wave signals. J. Press. Vessel Technol. 2019, 141, 021204. [Google Scholar] [CrossRef]
- Si, D.; Gao, B.; Guo, W.; Yan, Y.; Tian, G.Y.; Yin, Y. Variational mode decomposition linked wavelet method for EMAT denoise with large lift-off effect. NDT E Int. 2019, 107, 102149. [Google Scholar] [CrossRef]
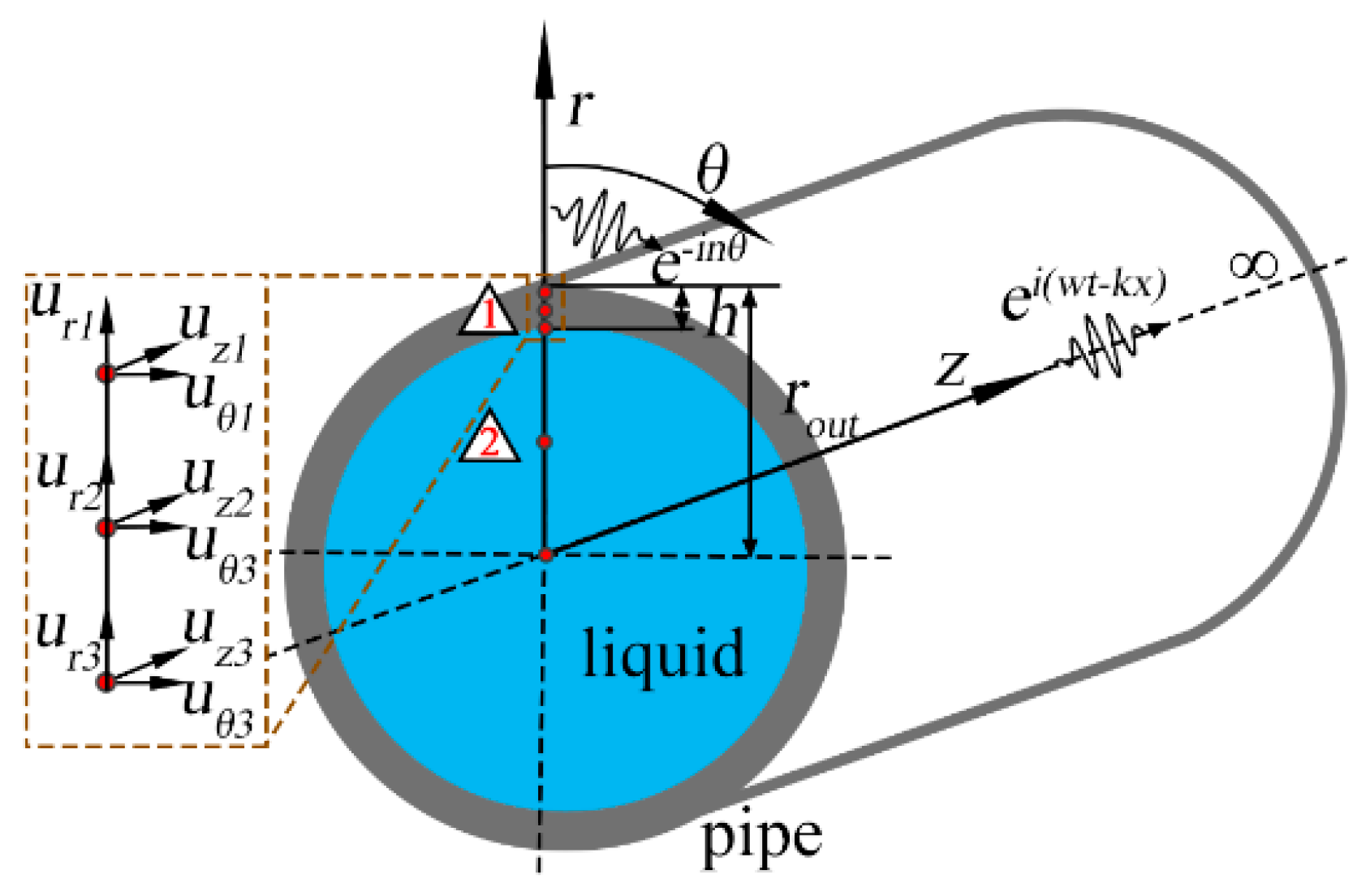



| Material | ρ (kg/m3) | E (Pa) | μ | K (Pa) | rin (mm) | h (mm) |
|---|---|---|---|---|---|---|
| Pipe | 7800 | 2.17 × 1011 | 0.28 | - | 28 | 7 |
| Water | 1000 | - | - | 2.25 × 109 | 0 | 28 |
| TS | DOMP (TS) | DOMP (PS1) | DOMP (PS2) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mode (Lwp) | x (m) | Amp (a.u.) | Mode (Lwp) | x (m) | Amp (a.u.) | Mode (Lwp) | x (m) | Mode (Lwp) | x (m) | |
| 1 | (0,5) | 0.50 | 0.48 | (0,5) | 0.4627 | 0.33 | (0,5) | 0.4381 | (0,5) | 0.4575 |
| 2 | (0,5) | 1.50 | 0.47 | (0,5) | 1.3808 | 0.06 | (0,5) | 1.5301 | (0,5) | 0.5360 |
| 3 | (1,5) | 0.50 | 0.49 | (0,5) | 1.4986 | 0.91 | (1,5) | 0.5952 | (0,5) | 0.6509 |
| 4 | (1,5) | 1.50 | 0.47 | (2,4) | 0.5043 | 0.35 | (2,4) | 1.3819 | (2,4) | 0.5061 |
| 5 | (2,4) | 0.50 | 0.46 | (2,4) | 1.4998 | 0.28 | (2,4) | 1.5238 | (2,4) | 1.4189 |
| 6 | (2,4) | 1.50 | 0.30 | (3,4) | 0.5043 | 0.21 | (3,4) | 0.4997 | (3,4) | 1.4898 |
| 7 | (3,4) | 0.50 | 0.21 | (3,4) | 0.5260 | 0.05 | (3,4) | 0.5518 | (3,4) | 0.5119 |
| 8 | (3,4) | 1.50 | 0.12 | (3,4) | 1.5015 | 0.11 | (3,4) | 1.5467 | (3,4) | 1.5331 |
| SNR = Inf dB | SNR = 6.12 dB | SNR = −4.95 dB | SNR = −12.34 dB | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Value (a.u.) | Error (%) | Value (a.u.) | Error (%) | Value (a.u.) | Error (%) | Value (a.u.) | Error (%) | ||
| OMP | x1 | 0.4834 | 3.3200 | 0.4877 | 2.4661 | 0.4663 | 6.7299 | 0.4577 | 8.4600 |
| x2 | 1.5092 | 0.6133 | 1.51897 | 1.2653 | 1.5322 | 2.1543 | 1.5430 | 2.8636 | |
| DOMP | x1 | 0.4627 | 7.4600 | 0.4621 | 7.5800 | 1.3755 | 175.1000 | 0.4873 | 2.5400 |
| x2 | 1.4986 | 0.0933 | 1.4986 | 0.0933 | 1.4986 | 0.0933 | 1.4986 | 0.0933 | |
| DMOMP | x1 | 0.5000 | 0.0000 | 0.5001 | 0.0200 | 0.5001 | 0.0200 | 0.5011 | 0.2200 |
| x2 | 1.5001 | 0.0067 | 1.5001 | 0.0067 | 1.5001 | 0.0067 | 1.5001 | 0.0067 | |
| ES1 | ES2 | ES3 | ES4 | ES5 | ES6 | ES7 | ES8 | Actual Value | Accuracy | |
|---|---|---|---|---|---|---|---|---|---|---|
| x1 (m) | - | 3.0348 | 3.0409 | 3.0146 | 3.0267 | 3.0247 | 3.0247 | 3.0227 | 3.0000 | 99.10% |
| x2 (m) | - | - | - | - | - | 3.9530 | 3.9469 | 3.9000 | 98.72% | |
| x3 (m) | 5.6436 | 5.6146 | 5.6188 | 5.6354 | 5.6105 | 5.6105 | 5.6105 | 5.6064 | 5.5300 | 98.36% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Tang, B.; Gong, R.; Zhou, F.; Chen, A. Reconstruction of Water-Filled Pipe Ultrasonic Guided Wave Signals in the Distance Domain by Orthogonal Matching Pursuit Based on Dispersion and Multi-Mode. Sensors 2023, 23, 8683. https://doi.org/10.3390/s23218683
Wang Y, Tang B, Gong R, Zhou F, Chen A. Reconstruction of Water-Filled Pipe Ultrasonic Guided Wave Signals in the Distance Domain by Orthogonal Matching Pursuit Based on Dispersion and Multi-Mode. Sensors. 2023; 23(21):8683. https://doi.org/10.3390/s23218683
Chicago/Turabian StyleWang, Yuemin, Binghui Tang, Ruqing Gong, Fan Zhou, and Ang Chen. 2023. "Reconstruction of Water-Filled Pipe Ultrasonic Guided Wave Signals in the Distance Domain by Orthogonal Matching Pursuit Based on Dispersion and Multi-Mode" Sensors 23, no. 21: 8683. https://doi.org/10.3390/s23218683





