A Novel Four-Step Algorithm for Detecting a Single Circle in Complex Images
Abstract
:1. Introduction
1.1. Background
1.2. Literature Review
1.3. Organization
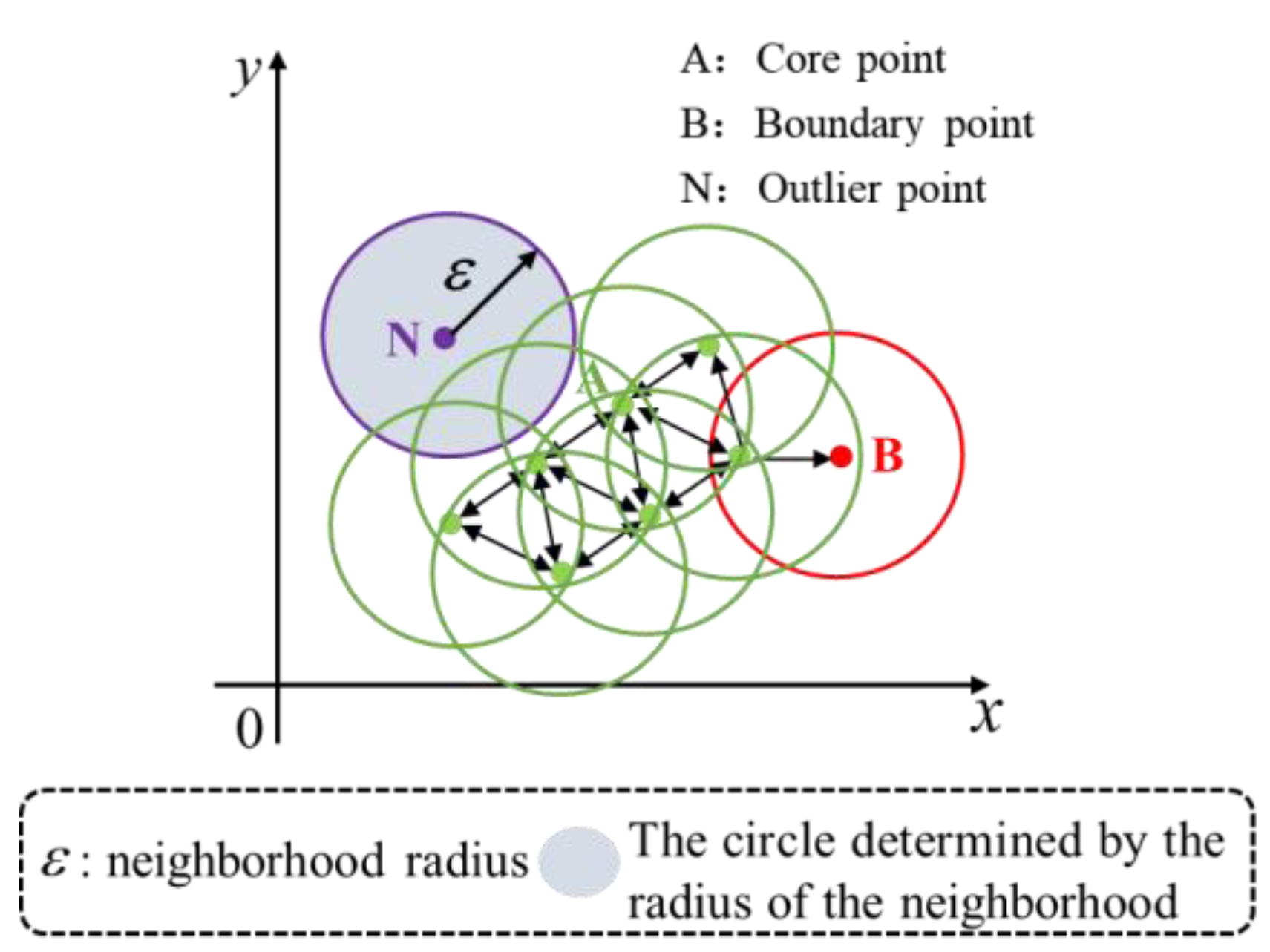
2. Problem Statement
- The removal of mass noise in the image edge preprocessing stage. Interfering points are an adverse factor affecting the accuracy and efficiency of single-circle detection. Mass noise increases the difficulty of de-noising and main contour detection; therefore, the noise needs to be removed accurately when detecting single circle with a complex background.
- The selection of sample points for fitting circles. After image edge processing, interfering points affect the fitting results. These interfering points are scattered in a low-density region. In contrast, the sample points of the main contour are connected in an arc and are more tightly connected in a high-density area. Considering the characteristics of the interfering points and sample points, establishing a sample point selection method for fitting candidate circles is another challenge.
- The iteration of candidate circles and determination of ideal circles. Overfitting and underfitting are prevented via suitable methods during the exact fitting of circles. We need to find an effective and fast iterative solution for the candidate circle, which in turn ensures the quality of the ideal circle.
- The improvement of output circle detection accuracy. Despite reducing the frequency of overfitting and underfitting occurrences, there may still be an error between the ideal circle and the real-world circle due to the influence of various interfering points. To improve the accuracy of output circle detection, the effect of interfering points on output circle parameters needs to be further reduced.
3. Methods
- Step 1. Image edge preprocessing.
- Step 2. Selection of sample points for fitting curves.
- Step 3. Iteration of candidate circles and determination of the ideal circles.
- Step 4. Accuracy improvement of the output circle detection.
3.1. Image Edge Preprocessing
3.1.1. Canny Edge Detection
3.1.2. Main Contour Screening
| Algorithm 1: Image Edge Preprocessing |
| Input: The image with a circle outline, the Gaussian kernel size , the number of retained edges , threshold value 1 is and threshold value 2 is in Canny edge detection algorithm. |
| Output: Edge pixels under retention. |
| 1: Initialize = 9, = 6, = 200, = 255. 2: Calculate the by Canny edge detection algorithm and Formula (1). 3: Calculate the with (2). 4: Calculate the with (3). |
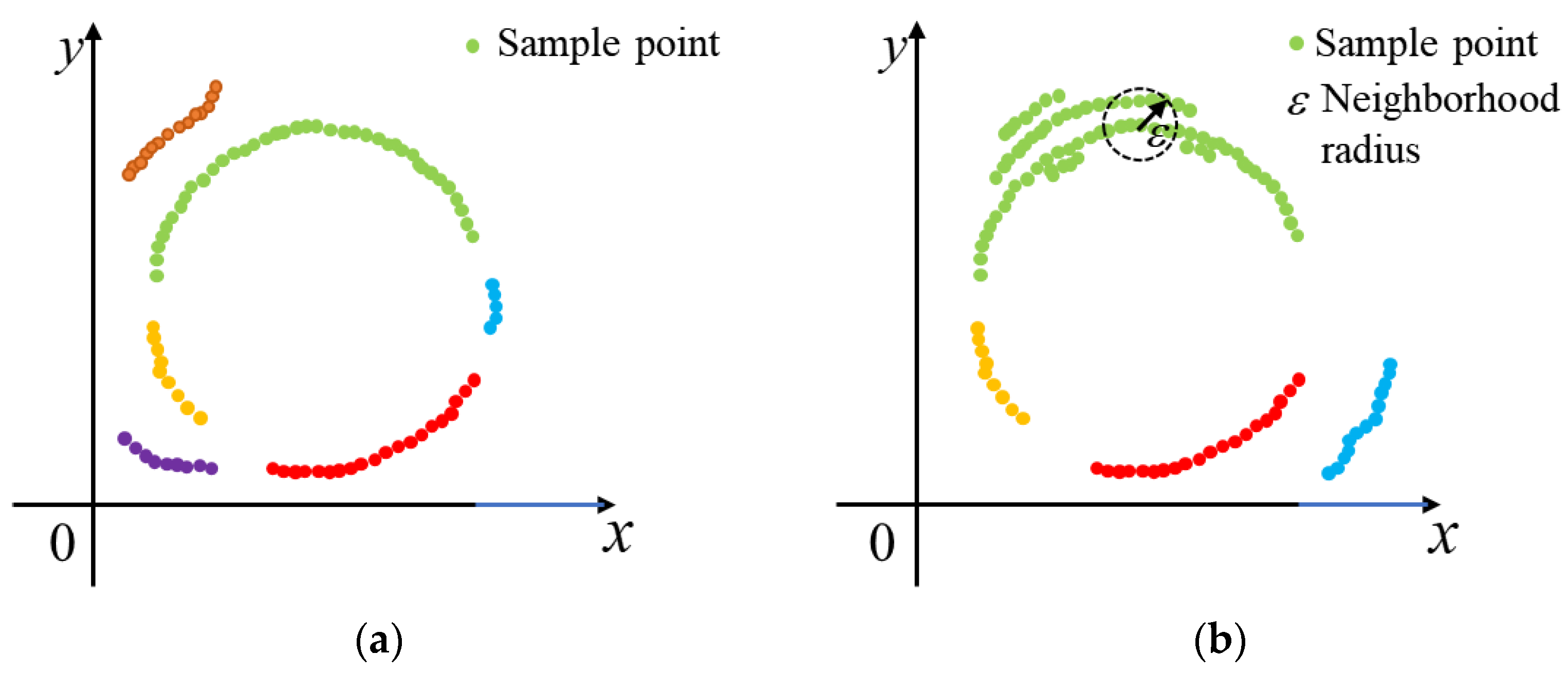
3.2. Selection of Fitting Sample Points
| Algorithm 2: Select the Fitting Sample Points |
| Input: The in Algorithm 1, the radius of the neighborhood and the minimum number of points in the neighborhood in the DBSCAN algorithm. |
| Output: The edge set with the most sample points. |
| 1: Initialize = 5, = 3. |
| 2: According to Section 3.2, clustering the sample points in . 3: Calculate the number of sample points in each cluster and retain the class with the most sample points. |
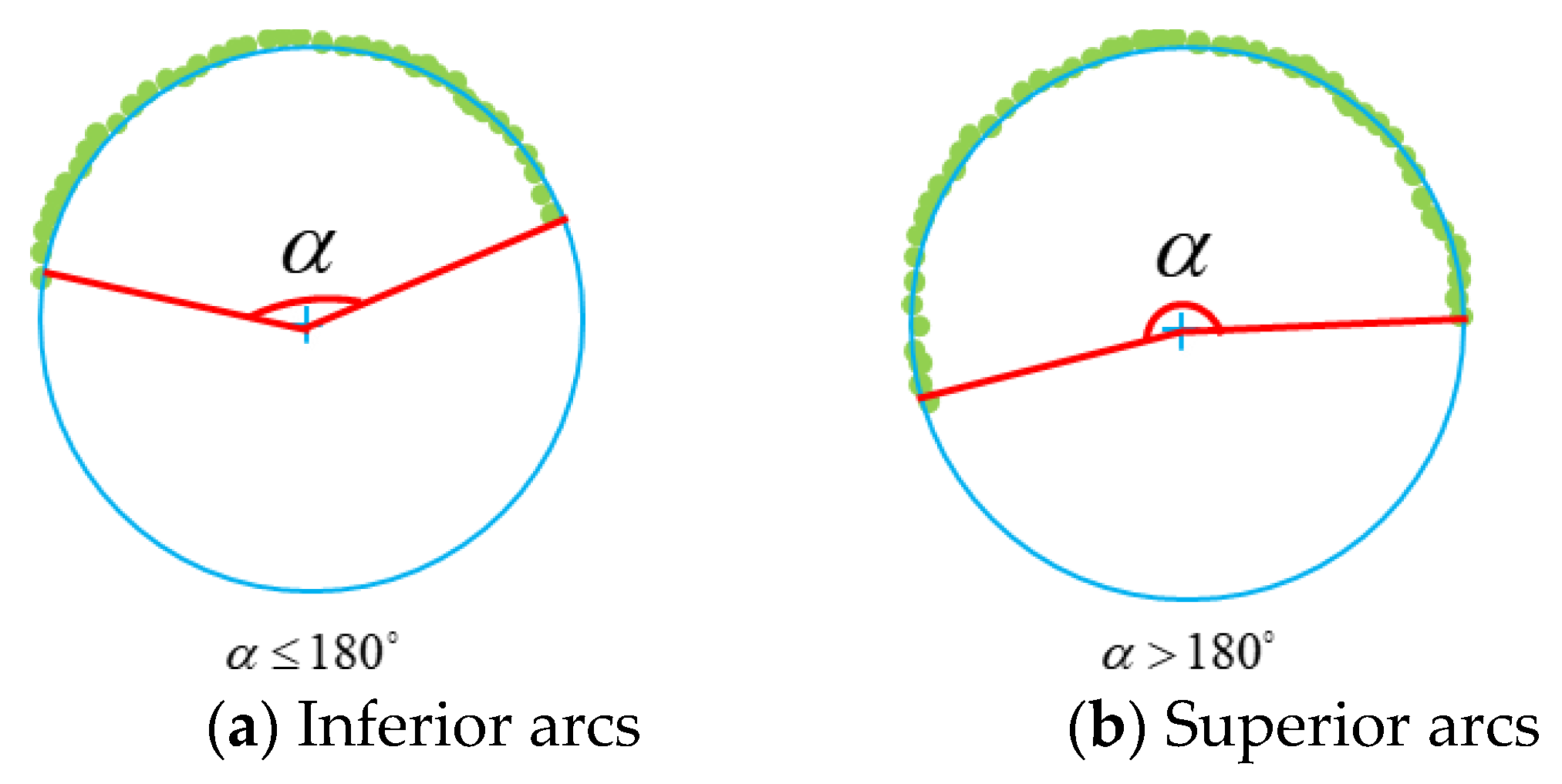
3.3. Candidate Circle Iteration and Ideal Circle Determination
- (1).
- (2).
- Besides the sample points of the main contour, a few interfering points are distributed on the outer side of the main contour. Fitting candidate and ideal circles in such cases is studied in this section.
| Algorithm 3: Fit Candidate Circles and Determine Ideal Circles |
| Input: The edge set in Algorithm 2, the maximum number of iterations allowed , the critical residual sum of squares , the iteration number . |
| Output: Center (,) and radius of the candidate circle. |
| 1: Initialize = 6, = 0.003, k = 1. |
| 2: Calculate the , (,) and with (7) and (8). 3: while or do 4: Calculate the with (9). 5: if then 6: Save (,) 7: else 8: Delete (,) 9: end if 10: Update 11: end while |
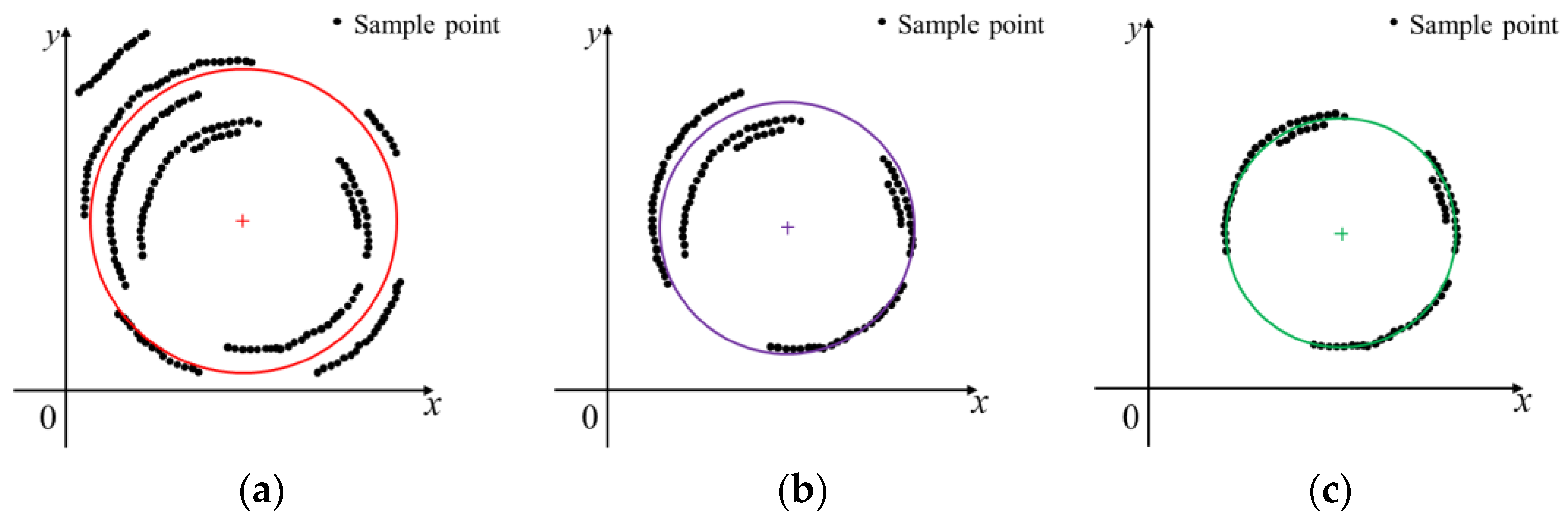
3.4. Improvement of Output Circle Detection Accuracy
- (1)
- Different numbers of data points in the two clustering results.
- (2)
- Same number of data points in two clustering results.
| Algorithm 4: Improve the Output Circle’s Detection Accuracy |
| Input: The k-means algorithm clustering number , center (,) and radius of the candidate circle in Algorithm 3. |
| Output: Center coordinates and radius of the output circle. |
| 1: Initialize = 2. |
| 2: According to the method in Section 3.4, the center coordinates are clustered into and, respectively. 3: if num() is not equal to num() then 4: Calculate with (13). 5: Calculate and with (14). 6: else 7: Calculate , and with (15), (16) and (17), respectively. 8: if < then 9: , = mean((,),) ( ) 10: if < then 11: , = mean((,),) ( ) 12: end if 13: end if |
4. Experiments and Results
- (1).
- All experiments are carried out using the same computer. The computer parameters are shown in Table 2.
- (2).
- To comparatively validate the detection speed, the four algorithms are terminated as soon as a circle was detected in the image.
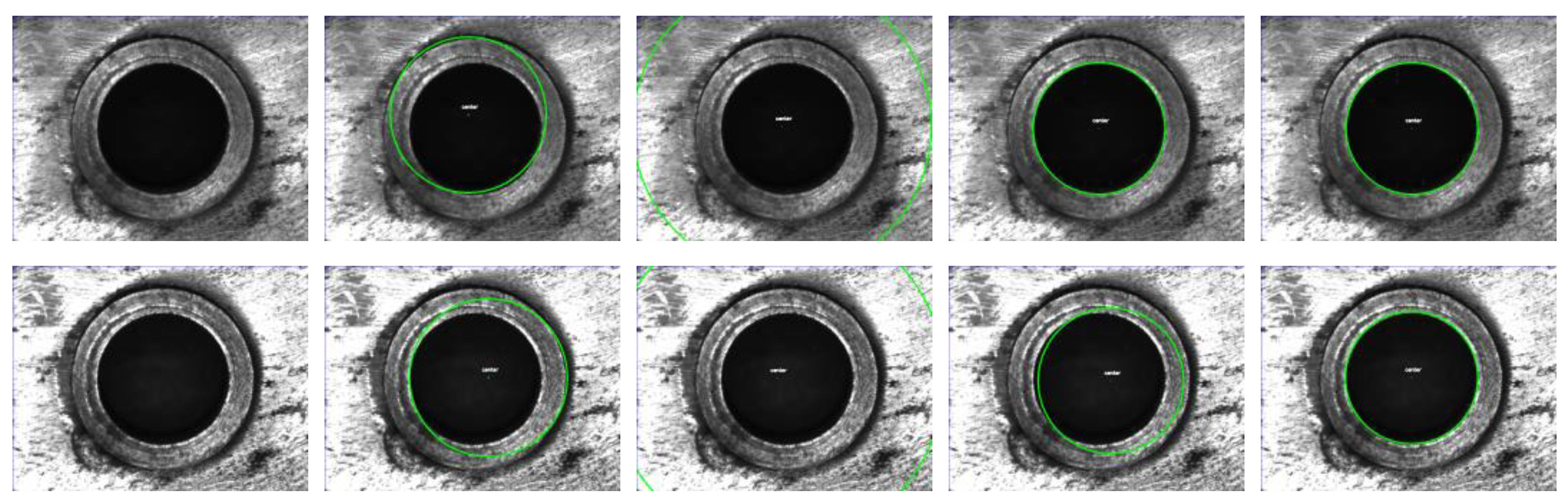
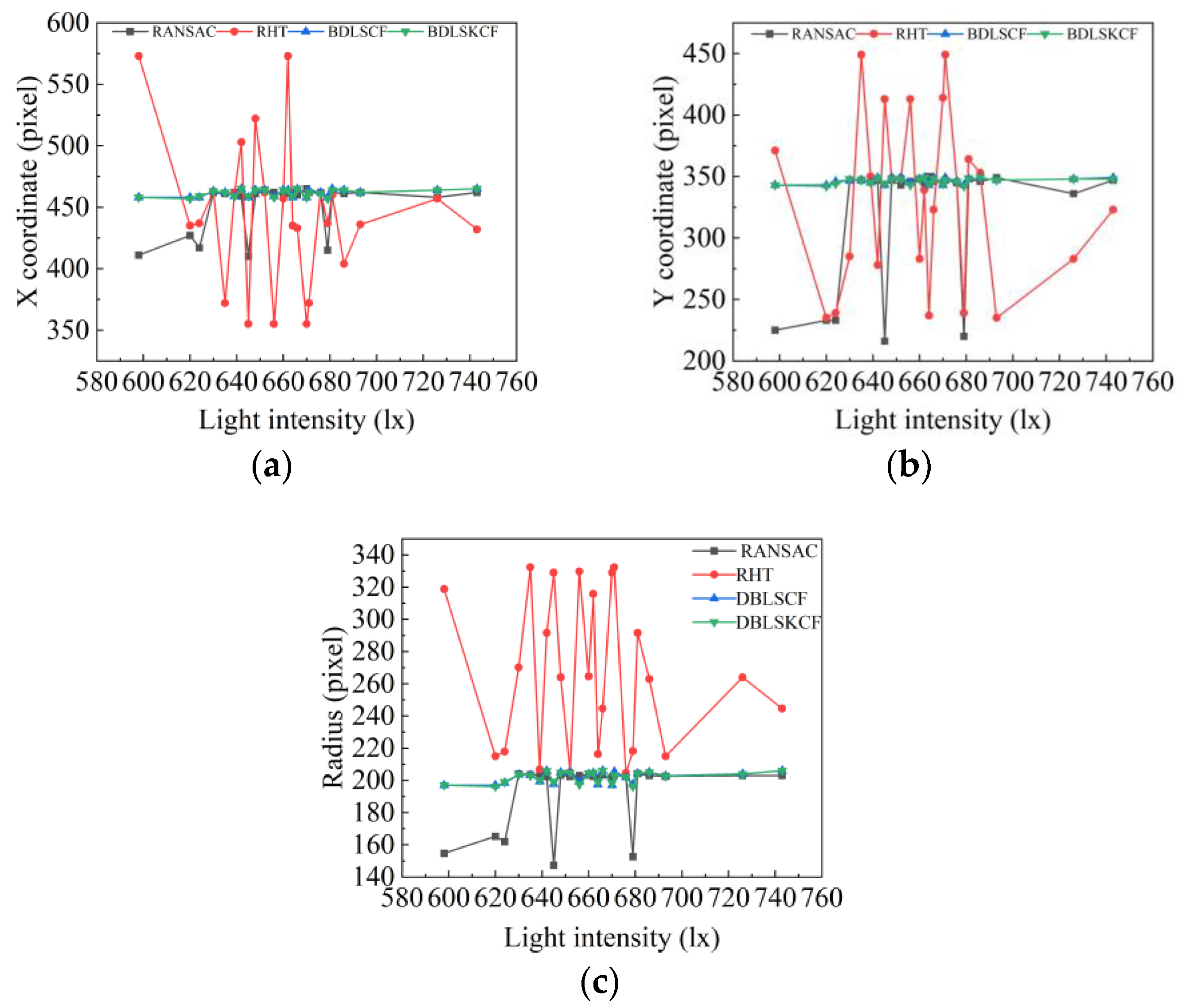
4.1. Comparison of Stability of Circle Detection
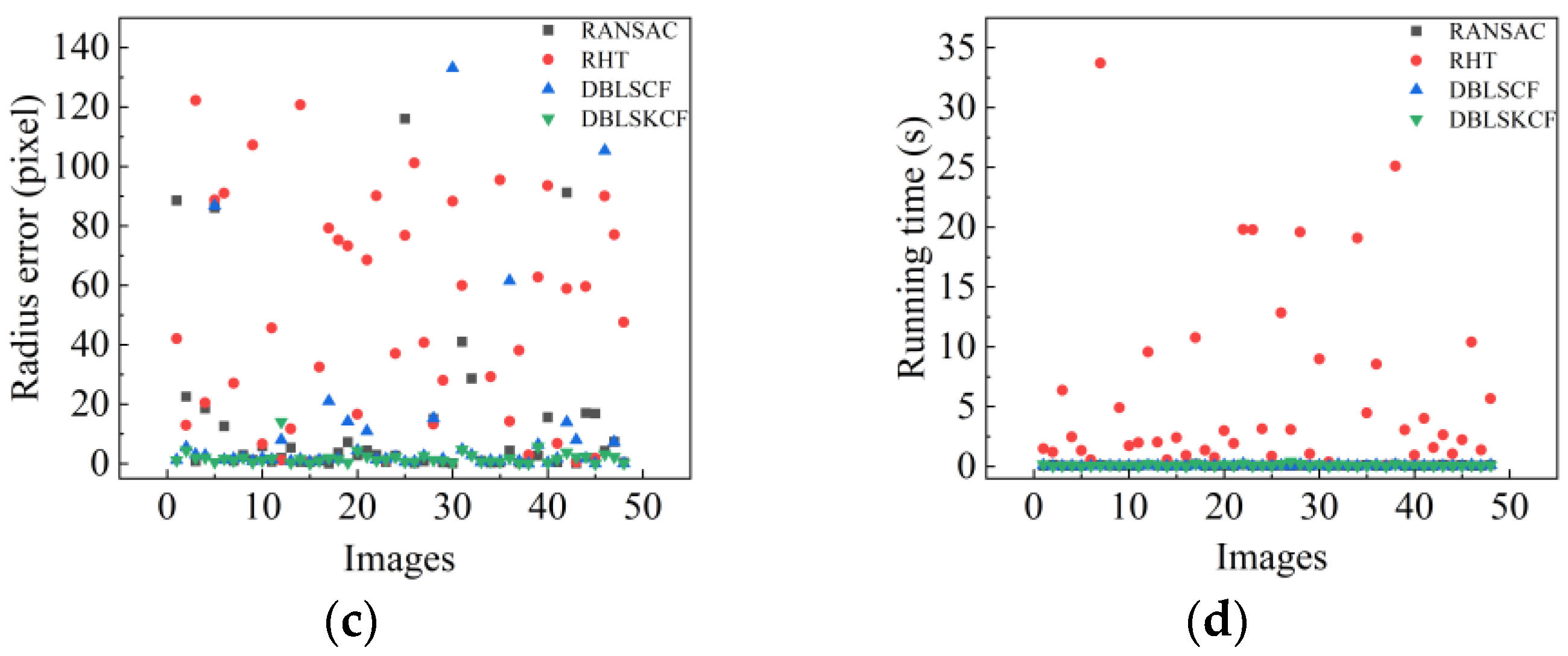
4.2. Validation of Algorithm Detection Accuracy and Efficiency
5. Conclusions
- Image edge preprocessing removes as many interfering points as possible while retaining the main contour edge information.
- The DBSCAN algorithm is utilized to cluster the main contours and interfering points into different clusters, from which the cluster with more sample points is extracted as the fitting samples of the candidate circles.
- An improved least square fitting of the circle with the residual sum of squares is raised. Removing the fitting failure points one by one makes the circle fitting result gradually closer to the real-world circle.
- The K-means clustering algorithm is implemented to cluster the center coordinates and radius of all candidate circles to improve the accuracy of output circle detection.
- (1).
- Stability: The standard deviation of the X-coordinate, Y-coordinate, and radius detection results are 2.7 pixels, 2.3 pixels, and 3.27 pixels, respectively.
- (2).
- Detection accuracy: The average errors of X-coordinate, Y-coordinate, and radius detection are 1.8 pixels, 1.4 pixels, and 1.9 pixels, respectively.
- (3).
- Running time: The average running time is 0.1 s.
- (1).
- Adaptively determining the neighborhood radius and the minimum number of sample points within the neighborhood radius in the DBSCAN clustering algorithm.
- (2).
- An improvement of the proposed algorithm to enable multi-circle detection.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Comparison Result of the DBLSKCF Algorithm with the Other Three Algorithms
| Image Number | RANSAC | RHT | DBLSCF | DBLSKCF |
|---|---|---|---|---|
| 1 | 1.43 | 0.5 | 0.51 | 2.38 |
| 2 | 20.5 | 18 | 3.74 | 3.73 |
| 3 | 2.26 | 4.5 | 0.32 | 0.41 |
| 4 | 19.71 | 16.5 | 2.32 | 1.09 |
| 5 | 8 | 7.5 | 7.15 | 7.41 |
| 6 | 2.5 | 123 | 1.31 | 0.08 |
| 7 | 0.46 | 0 | 0.05 | 0.18 |
| 8 | 1.67 | - | 1.49 | 1.49 |
| 9 | 2.5 | 129.5 | 0.36 | 0.65 |
| 10 | 4.26 | 52.5 | 2.19 | 0.38 |
| 11 | 1.5 | 100 | 0.71 | 0.38 |
| 12 | 1.24 | 0.88 | 0.89 | 0.9 |
| 13 | 2.81 | 0.49 | 1.55 | 1.75 |
| 14 | 2 | 156.5 | 1.14 | 1.15 |
| 15 | 3 | 32 | 0.39 | 1.43 |
| 16 | 5 | 6 | 0.3 | 0.37 |
| 17 | 0.39 | 0.5 | 2.19 | 2.04 |
| 18 | 2.02 | 9 | 0.21 | 1.85 |
| 19 | 4.5 | 130 | 0.07 | 1.14 |
| 20 | 7.48 | 15.5 | 7.384 | 0.7 |
| 21 | 6.83 | 77 | 6.7 | 5.31 |
| 22 | 1.87 | 29 | 0.48 | 0.59 |
| 23 | 9.65 | 1 | 0.35 | 0.35 |
| 24 | 0.5 | 5 | 1.92 | 2.04 |
| 25 | 10 | 80.29 | 0.75 | 0.84 |
| 26 | 0.36 | 0.5 | 0.57 | 0.57 |
| 27 | 0.27 | 0 | 1.09 | 1.09 |
| 28 | 1.37 | 2.06 | 1.34 | 3.5 |
| 29 | 1.01 | 0.5 | 0.55 | 0.17 |
| 30 | 200.5 | 1.5 | 145.34 | 0.92 |
| 31 | 25 | 4 | 2.55 | 2.53 |
| 32 | 0.48 | - | 0.72 | 0.68 |
| 33 | 0.79 | - | 0.87 | 1 |
| 34 | 1.1 | 1 | 1.04 | 1.03 |
| 35 | 1.21 | 2 | 1.21 | 1.1 |
| 36 | 5.2 | 0 | 24.09 | 0.83 |
| 37 | 9.5 | 70.5 | 1.9 | 0.25 |
| 38 | 0.8 | 0.18 | 0.48 | 0.45 |
| 39 | 1.25 | 0.5 | 1.52 | 6.44 |
| 40 | 5 | 1 | 1.55 | 1.76 |
| 41 | 1.73 | 2 | 1.58 | 1.69 |
| 42 | 4 | 70.75 | 10.25 | 10.23 |
| 43 | 2.14 | 0.7 | 3.43 | 3.58 |
| 44 | 17.94 | 16 | 1.88 | 3.21 |
| 45 | 19.08 | 0.46 | 0.8 | 0.8 |
| 46 | 1.81 | 2 | 2.54 | 0.39 |
| 47 | 2.021 | 2.5 | 2.72 | 2.71 |
| 48 | 0.37 | 105 | 0.48 | 0.69 |
| Image Number | RANSAC | RHT | DBLSCF | DBLSKCF |
|---|---|---|---|---|
| 1 | 6.27 | 120.5 | 0.61 | 1.48 |
| 2 | 97 | 80.5 | 2.66 | 2.68 |
| 3 | 3.13 | 157.5 | 1.25 | 1.28 |
| 4 | 11.87 | 93 | 2.15 | 1.05 |
| 5 | 0 | 19.5 | 0.2 | 0.12 |
| 6 | 29 | 123.5 | 3.18 | 0.35 |
| 7 | 0.46 | 112 | 1.86 | 1.88 |
| 8 | 0.1 | - | 0.09 | 0.11 |
| 9 | 0 | 155 | 0.53 | 0.53 |
| 10 | 12.5 | 8 | 0.2 | 0.23 |
| 11 | 0.5 | 95 | 0.12 | 0.1 |
| 12 | 4.09 | 0.46 | 1.82 | 1.84 |
| 13 | 3.4 | 3.26 | 0.21 | 0.12 |
| 14 | 5 | 141 | 1.53 | 1.55 |
| 15 | 5 | 1.5 | 1.74 | 1.47 |
| 16 | 6 | 48 | 1.03 | 1 |
| 17 | 0.48 | 158 | 21.46 | 0.85 |
| 18 | 2.17 | 81.5 | 0.245 | 0.03 |
| 19 | 0.5 | 89 | 0.38 | 0.29 |
| 20 | 4.45 | 4 | 1.925 | 4.6 |
| 21 | 2.05 | 93 | 2.241 | 1.7 |
| 22 | 1.69 | 22.5 | 1.36 | 1.24 |
| 23 | 0.95 | 0.65 | 0.42 | 0.39 |
| 24 | 1.8 | 96.5 | 0.44 | 0.34 |
| 25 | 89.5 | 68.75 | 0.66 | 0.75 |
| 26 | 0.02 | 20 | 0.41 | 0.38 |
| 27 | 0.14 | 81 | 0.33 | 0.33 |
| 28 | 0.29 | 0.05 | 0.09 | 1.5 |
| 29 | 0.69 | 55.5 | 0.94 | 0.32 |
| 30 | 401.5 | 268 | 53 | 2.02 |
| 31 | 4 | 163 | 3.3 | 3.28 |
| 32 | 0.11 | - | 0.29 | 0.26 |
| 33 | 0.39 | - | 0.92 | 0.88 |
| 34 | 0.32 | 145.5 | 0.54 | 0.51 |
| 35 | 0.59 | 136.5 | 1.07 | 1.1 |
| 36 | 0.44 | 63.5 | 2.05 | 1.4 |
| 37 | 6 | 13.5 | 1.56 | 2.04 |
| 38 | 1.35 | 1.79 | 1.28 | 1.25 |
| 39 | 99.6 | 108.5 | 7.29 | 4.65 |
| 40 | 25 | 188.5 | 8.71 | 0.5 |
| 41 | 0.75 | 50.5 | 0.95 | 0.35 |
| 42 | 5 | 29.61 | 10.26 | 10.25 |
| 43 | 1.19 | 0.24 | 5.42 | 5.47 |
| 44 | 12.17 | 5.5 | 0.03 | 0.07 |
| 45 | 3.66 | 0.05 | 0.03 | 0.02 |
| 46 | 3.3 | 140.5 | 99.14 | 0.03 |
| 47 | 2.75 | 102.5 | 2.22 | 2.19 |
| 48 | 0.28 | 128.5 | 0.52 | 0.72 |
| Image Number | RANSAC | RHT | DBLSCF | DBLSKCF |
|---|---|---|---|---|
| 1 | 88.55 | 42 | 1.2 | 1.13 |
| 2 | 22.55 | 12.96 | 5.53 | 4.45 |
| 3 | 0.82 | 122.25 | 3.08 | 1.96 |
| 4 | 18.52 | 20.5 | 2.81 | 2 |
| 5 | 86.09 | 88.75 | 86.73 | 0.49 |
| 6 | 12.59 | 91 | 1.28 | 1.66 |
| 7 | 0.91 | 27 | 1.63 | 1 |
| 8 | 2.99 | - | 1.97 | 1.98 |
| 9 | 1.19 | 107.25 | 0.95 | 0.38 |
| 10 | 5.81 | 6.59 | 1.8 | 1 |
| 11 | 0.61 | 45.62 | 1.39 | 1.69 |
| 12 | 1.87 | 1.14 | 7.94 | 13.99 |
| 13 | 5.36 | 11.73 | 0.84 | 0.36 |
| 14 | 0.53 | 120.75 | 1.51 | 1.53 |
| 15 | 0.49 | 0.62 | 0.7 | 0.07 |
| 16 | 1 | 32.45 | 1.22 | 0.93 |
| 17 | 0.02 | 79.25 | 20.99 | 1.91 |
| 18 | 3.62 | 75.25 | 1.56 | 1.49 |
| 19 | 7.25 | 73.25 | 14.19 | 0.32 |
| 20 | 2.73 | 16.59 | 4.48 | 4.4 |
| 21 | 4.48 | 68.54 | 10.94 | 2.46 |
| 22 | 2.97 | 90.09 | 1.35 | 1.09 |
| 23 | 0.55 | 1.18 | 1.52 | 1.34 |
| 24 | 2.71 | 37 | 2.27 | 2.26 |
| 25 | 116.04 | 76.78 | 0.58 | 0.61 |
| 26 | 0.22 | 101.19 | 0.72 | 0.65 |
| 27 | 0.82 | 40.75 | 2.64 | 2.63 |
| 28 | 15.06 | 13.27 | 15.26 | 1.2 |
| 29 | 0.4 | 28 | 1.57 | 1 |
| 30 | 0.13 | 88.25 | 133.16 | 0.35 |
| 31 | 41 | 59.94 | 4.69 | 4.69 |
| 32 | 28.66 | - | 2.84 | 2.8 |
| 33 | 0.95 | - | 0.51 | 0.67 |
| 34 | 0.29 | 29.25 | 1 | 0.83 |
| 35 | 0.37 | 95.5 | 0.84 | 0.67 |
| 36 | 4.38 | 14.24 | 61.55 | 1.85 |
| 37 | 0.25 | 38.07 | 0.89 | 0.28 |
| 38 | 1.76 | 2.89 | 0 | 0.06 |
| 39 | 2.69 | 62.75 | 6.4 | 5.65 |
| 40 | 15.59 | 93.5 | 0.36 | 0.29 |
| 41 | 0.47 | 6.75 | 1.72 | 1.54 |
| 42 | 91.18 | 58.9 | 13.93 | 3.78 |
| 43 | 0.09 | 0.46 | 7.97 | 2.15 |
| 44 | 17.03 | 59.62 | 1.75 | 2.36 |
| 45 | 16.83 | 1.74 | 0.09 | 0.01 |
| 46 | 4.27 | 90.05 | 105.35 | 3.1 |
| 47 | 7.31 | 77 | 7.29 | 2.24 |
| 48 | 0.42 | 47.53 | 0.04 | 0.15 |
| Image Number | RANSAC | RHT | DBLSCF | DBLSKCF |
|---|---|---|---|---|
| 1 | 0.06 | 1.49 | 0.099 | 0.177 |
| 2 | 0.139 | 1.196 | 0.026 | 0.033 |
| 3 | 0.059 | 6.37 | 0.05 | 0.059 |
| 4 | 0.061 | 2.48 | 0.058 | 0.104 |
| 5 | 0.051 | 1.34 | 0.024 | 0.025 |
| 6 | 0.164 | 0.55 | 0.033 | 0.061 |
| 7 | 0.123 | 33.72 | 0.067 | 0.079 |
| 8 | 0.079 | - | 0.063 | 0.122 |
| 9 | 0.062 | 4.91 | 0.067 | 0.099 |
| 10 | 0.058 | 1.73 | 0.057 | 0.09 |
| 11 | 0.056 | 1.99 | 0.035 | 0.038 |
| 12 | 0.129 | 9.58 | 0.113 | 0.233 |
| 13 | 0.067 | 2.03 | 0.07 | 0.122 |
| 14 | 0.053 | 0.559 | 0.028 | 0.036 |
| 15 | 0.068 | 2.407 | 0.066 | 0.096 |
| 16 | 0.057 | 0.92 | 0.026 | 0.029 |
| 17 | 0.223 | 10.77 | 0.1 | 0.234 |
| 18 | 0.059 | 1.35 | 0.071 | 0.109 |
| 19 | 0.06 | 0.739 | 0.055 | 0.066 |
| 20 | 0.069 | 2.99 | 0.134 | 0.177 |
| 21 | 0.062 | 1.931 | 0.068 | 0.076 |
| 22 | 0.143 | 19.81 | 0.206 | 0.263 |
| 23 | 0.053 | 19.8 | 0.046 | 0.062 |
| 24 | 0.065 | 3.14 | 0.069 | 0.121 |
| 25 | 0.057 | 0.85 | 0.038 | 0.083 |
| 26 | 0.067 | 12.84 | 0.083 | 0.208 |
| 27 | 0.05 | 3.078 | 0.031 | 0.419 |
| 28 | 0.063 | 19.59 | 0.177 | 0.243 |
| 29 | 0.053 | 1.05 | 0.028 | 0.033 |
| 30 | 0.101 | 8.98 | 0.082 | 0.161 |
| 31 | 0.054 | 0.387 | 0.02 | 0.029 |
| 32 | 0.076 | - | 0.164 | 0.168 |
| 33 | 0.059 | - | 0.059 | 0.114 |
| 34 | 0.052 | 19.086 | 0.033 | 0.041 |
| 35 | 0.119 | 4.48 | 0.042 | 0.054 |
| 36 | 0.059 | 8.55 | 0.13 | 0.174 |
| 37 | 0.043 | 0.123 | 0.017 | 0.024 |
| 38 | 0.17 | 25.1 | 0.146 | 0.198 |
| 39 | 0.06 | 3.054 | 0.066 | 0.096 |
| 40 | 0.06 | 0.94 | 0.047 | 0.064 |
| 41 | 0.052 | 4.02 | 0.066 | 0.08 |
| 42 | 0.058 | 1.57 | 0.046 | 0.063 |
| 43 | 0.155 | 2.65 | 0.051 | 0.062 |
| 44 | 0.057 | 1.05 | 0.043 | 0.059 |
| 45 | 0.133 | 2.24 | 0.035 | 0.041 |
| 46 | 0.061 | 10.4 | 0.124 | 0.114 |
| 47 | 0.055 | 1.37 | 0.037 | 0.046 |
| 48 | 0.129 | 5.68 | 0.122 | 0.102 |
References
- Mohammadi, S.; Mohammadi, M.; Dehlaghi, V.; Ahmadi, A. Automatic Segmentation, Detection, and Diagnosis of Abdominal Aortic Aneurysm (AAA) Using Convolutional Neural Networks and Hough Circles Algorithm. Cardiovasc. Eng. Technol. 2019, 10, 490–499. [Google Scholar] [CrossRef] [PubMed]
- Liang, Q.; Long, J.; Nan, Y.; Coppola, G.; Zou, K.; Zhang, D.; Sun, W. Angle Aided Circle Detection Based on Randomized Hough Transform and Its Application in Welding Spots Detection. Math. Biosci. Eng. 2019, 16, 1244–1257. [Google Scholar] [CrossRef] [PubMed]
- Liu, T.; Zheng, P.; Bao, J. Deep Learning-Based Welding Image Recognition: A Comprehensive Review. J. Manuf. Syst. 2023, 68, 601–625. [Google Scholar] [CrossRef]
- Cheng, L.; Zhu, Y.; Kersemans, M. DMD-T: Thermographic Inspection of Composites Using Dynamic Mode Decomposition. In Proceedings of the 5th International Conference on Industrial Artificial Intelligence, Shenyang, China, 21–24 August 2023. [Google Scholar]
- Zhu, W.; Gu, H.; Su, W. A Fast PCB Hole Detection Method Based on Geometric Features. Meas. Sci. Technol. 2020, 31, 095402. [Google Scholar] [CrossRef]
- Shakarji, C.M.; Srinivasan, V. On Algorithms and Heuristics for Constrained Least-Squares Fitting of Circles and Spheres to Support Standards. J. Comput. Inf. Sci. Eng. 2019, 19, 031012. [Google Scholar] [CrossRef]
- Jing, Z.; Hongtao, C.; Fan, L. Remote Sensing Image Fusion Based on Multivariate Empirical Mode Decomposition and Weighted Least Squares Filter. Acta Photonica Sin. 2019, 48, 510003. [Google Scholar] [CrossRef]
- Xu, L.; Oja, E.; Kultanen, P. A New Curve Detection Method: Randomized Hough Transform (RHT). Pattern Recognit. Lett. 1990, 11, 331–338. [Google Scholar] [CrossRef]
- Li, D.; Nan, F.; Xue, T.; Yu, X. Circle Detection of Short Arc Based on Randomized Hough Transform. In Proceedings of the 2017 IEEE International Conference on Mechatronics and Automation (ICMA), Takamatsu, Japan, 6–9 August 2017; pp. 258–263. [Google Scholar]
- Mukhopadhyay, P.; Chaudhuri, B.B. A Survey of Hough Transform. Pattern Recognit. 2015, 48, 993–1010. [Google Scholar] [CrossRef]
- Wang, G. A Sub-Pixel Circle Detection Algorithm Combined with Improved RHT and Fitting. Multimed. Tools Appl. 2020, 79, 29825–29843. [Google Scholar] [CrossRef]
- Jiang, L. Efficient Randomized Hough Transform for Circle Detection Using Novel Probability Sampling and Feature Points. Optik 2012, 123, 1834–1840. [Google Scholar] [CrossRef]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Kiddee, P.; Fang, Z.; Tan, M. A Real-Time and Robust Feature Detection Method Using Hierarchical Strategy and Modified Kalman Filter for Thick Plate Seam Tracking. Int. J. Autom. Control. 2017, 11, 428–446. [Google Scholar] [CrossRef]
- Ma, Y.; Fan, J.; Yang, H.; Yang, L.; Ji, Z.; Jing, F.; Tan, M. A Fast and Robust Seam Tracking Method for Spatial Circular Weld Based on Laser Visual Sensor. IEEE Trans. Instrum. Meas. 2021, 70, 1–11. [Google Scholar] [CrossRef]
- Chaudhuri, D. A Simple Least Squares Method for Fitting of Ellipses and Circles Depends on Border Points of a Two-Tone Image and Their 3-D Extensions. Pattern Recognit. Lett. 2010, 31, 818–829. [Google Scholar] [CrossRef]
- Ahn, S.J.; Rauh, W. Least-Squares Orthogonal Distances fitting of Circle, Sphere, Ellipse, Hyperbola, and Parabola. Pattern Recognit. 2001, 34, 2283–2303. [Google Scholar] [CrossRef]
- Umbach, D.; Jones, K.N. A Few Methods for Fitting Circles to Data. IEEE Trans. Instrum. Meas. 2003, 52, 1881–1885. [Google Scholar] [CrossRef]
- Zhou, X.; Wang, Y.; Zhu, Q.; Zhang, H.; Chen, Q. Circle Detection with Model Fitting in Polar Coordinates for Glass Bottle Mouth Localization. Int. J. Adv. Manuf. Technol. 2022, 120, 1041–1051. [Google Scholar] [CrossRef]
- Cao, B.; Li, J.; Liang, Y.; Sun, X.; Li, W. Real-Time Detection of Nickel Plated Punched Steel Strip Parameters Based on Improved Circle Fitting Algorithm. Electronics 2023, 12, 1865. [Google Scholar] [CrossRef]
- Park, M.-J.; Kim, H.-J. A Real-Time Edge-Detection CMOS Image Sensor for Machine Vision Applications. IEEE Sens. J. 2023, 23, 9254–9261. [Google Scholar] [CrossRef]
- Agrawal, S.; Dean, B.K. Edge Detection Algorithm for $Musca-Domestica$ Inspired Vision System. IEEE Sens. J. 2019, 19, 10591–10599. [Google Scholar] [CrossRef]
- Circle Detection. Available online: https://Github.Com/Zikai1/CircleDetection (accessed on 10 April 2022).










| K | Q* | Ideal Circle |
|---|---|---|
| Large | Large | underfitting |
| Large | Small | overfitting |
| Small | Large | underfitting |
| Small | Small | overfitting |
| Development Environment | Internal Storage | Executive System | Development Tool |
|---|---|---|---|
| CPU:AMD Ryzen 7 6800HS Creator Edition 3.20 GHz | 16 G | Windows 11 | Python 3.6 |
| Algorithm | RANSAC | RHT | DBLSCF | DBLSKCF |
|---|---|---|---|---|
| X coordinate (pixel) | 18.7 | 58.1 | 2.8 | 2.7 |
| Y coordinate (pixel) | 49.2 | 66.6 | 2.4 | 2.3 |
| Radius (pixel) | 19.2 | 46.3 | 3.37 | 3.27 |
| Algorithm | RANSAC | RHT | DBLSCF | DBLSKCF |
|---|---|---|---|---|
| X-coordinate error (pixel) | 8.9 | 28.4 | 5.3 | 1.8 |
| Y-coordinate error (pixel) | 36.5 | 77.2 | 5.2 | 1.4 |
| Radius error (pixel) | 13.3 | 51 | 11.4 | 1.9 |
| Running time (s) | 0.08 | 6 | 0.07 | 0.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, J.; Gao, Y.; Wang, C. A Novel Four-Step Algorithm for Detecting a Single Circle in Complex Images. Sensors 2023, 23, 9030. https://doi.org/10.3390/s23229030
Cao J, Gao Y, Wang C. A Novel Four-Step Algorithm for Detecting a Single Circle in Complex Images. Sensors. 2023; 23(22):9030. https://doi.org/10.3390/s23229030
Chicago/Turabian StyleCao, Jianan, Yue Gao, and Chuanyang Wang. 2023. "A Novel Four-Step Algorithm for Detecting a Single Circle in Complex Images" Sensors 23, no. 22: 9030. https://doi.org/10.3390/s23229030







