Vibration and Slope Conditions during Harvesting Affect Radish Mass Measurements for Yield Monitoring: An Experimental Study Using a Laboratory Test Bench
Abstract
:1. Introduction
2. Materials and Methods
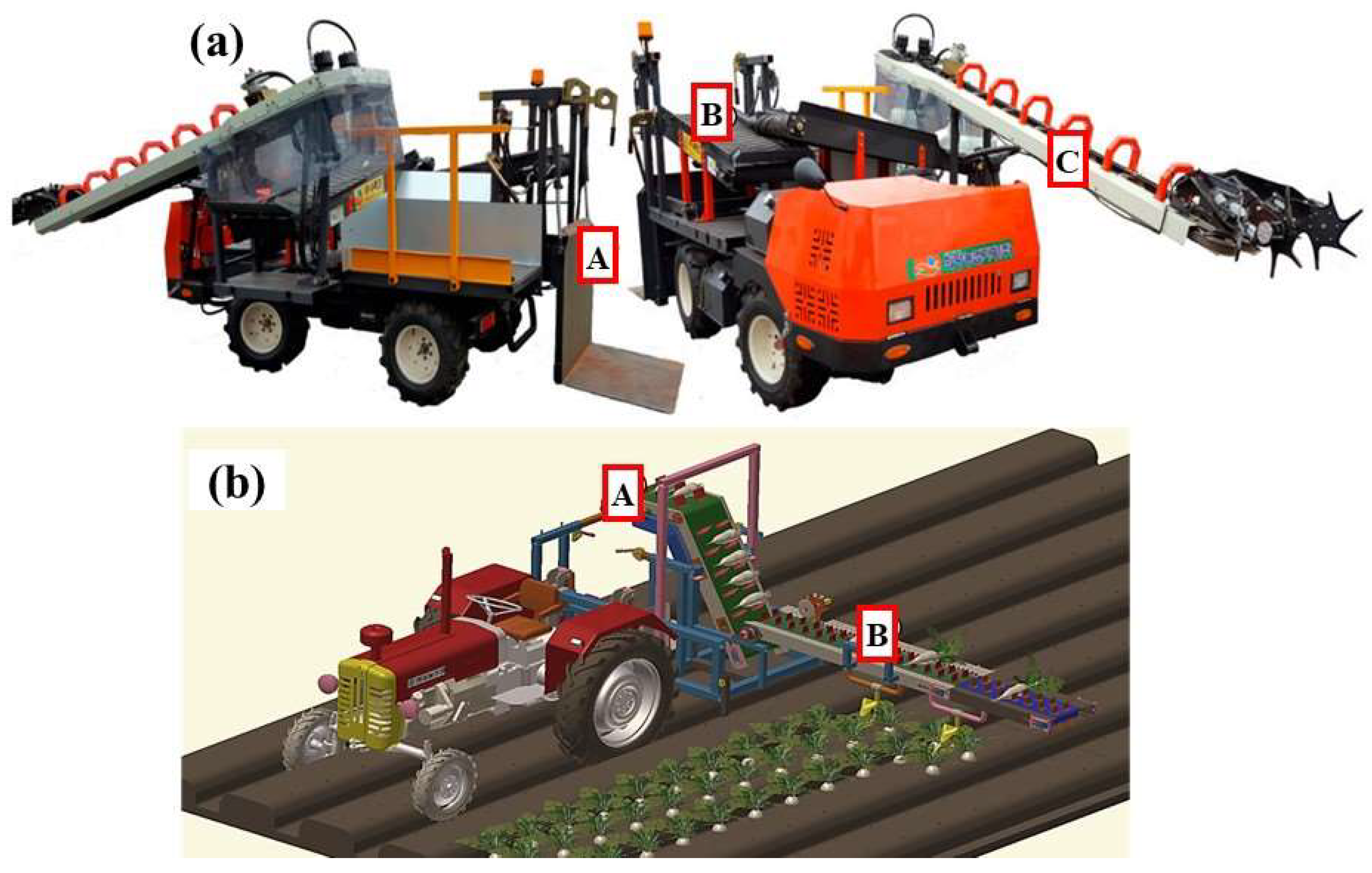
2.1. Radish Harvesting Using Radish Collectors and Harvesters
2.2. Design and Fabrication of the Experimental Laboratory Test Bench
2.3. Experimental Setup and Calibration Procedures for the Load Cells and Vibration Table
2.3.1. Data Acquisition
2.3.2. Calibration of Load Cells
2.3.3. Calibration of the Vibration Table
2.4. Experimental Variables and Levels for Radish Mass Measurements
2.4.1. Mass Measurement Tests without Slope and Vibration
2.4.2. Mass Measurement Tests with Slope and Vibration
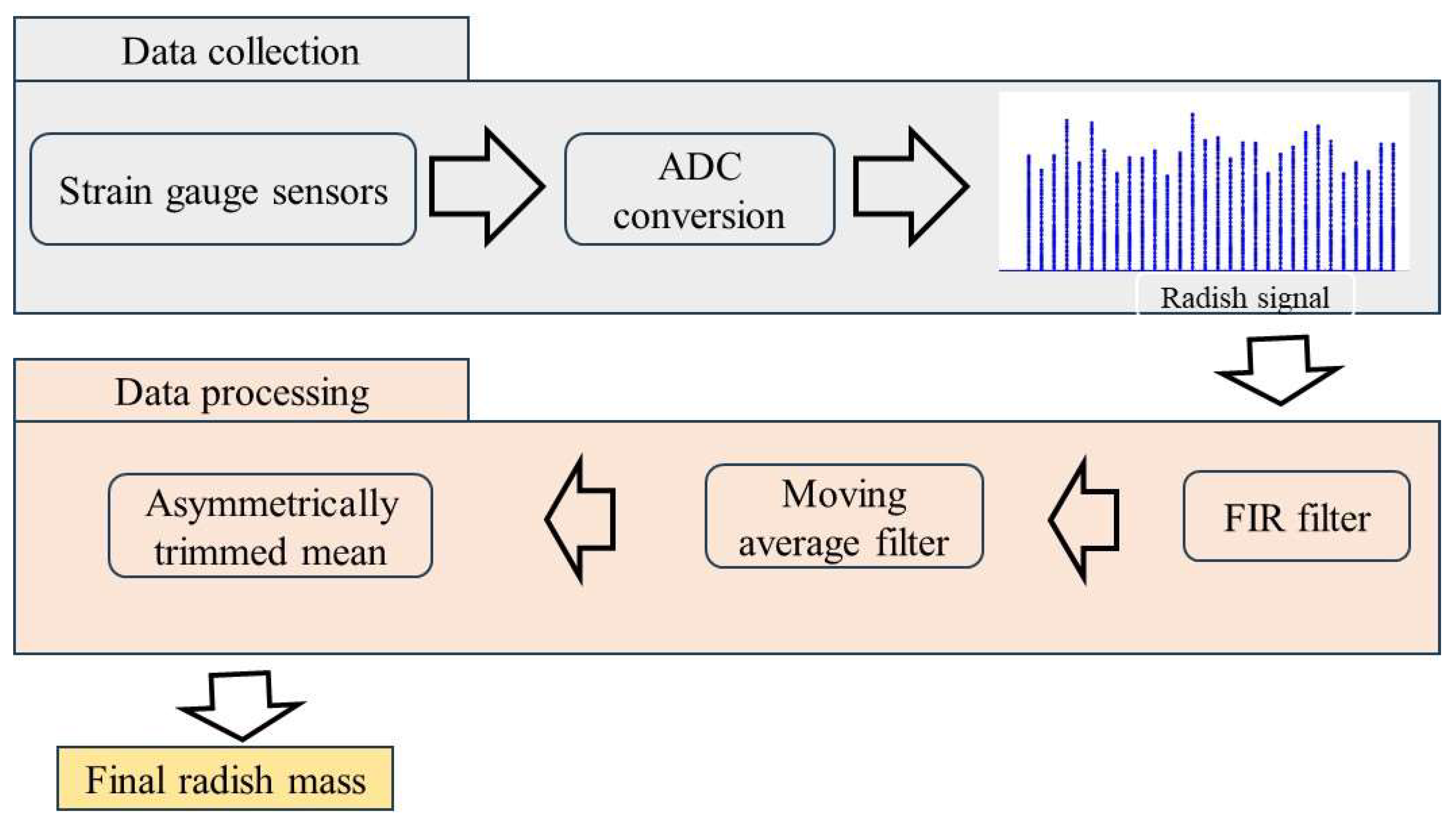
2.4.3. Radish Signal Processing and Mass Estimation
2.5. Analytical Procedures
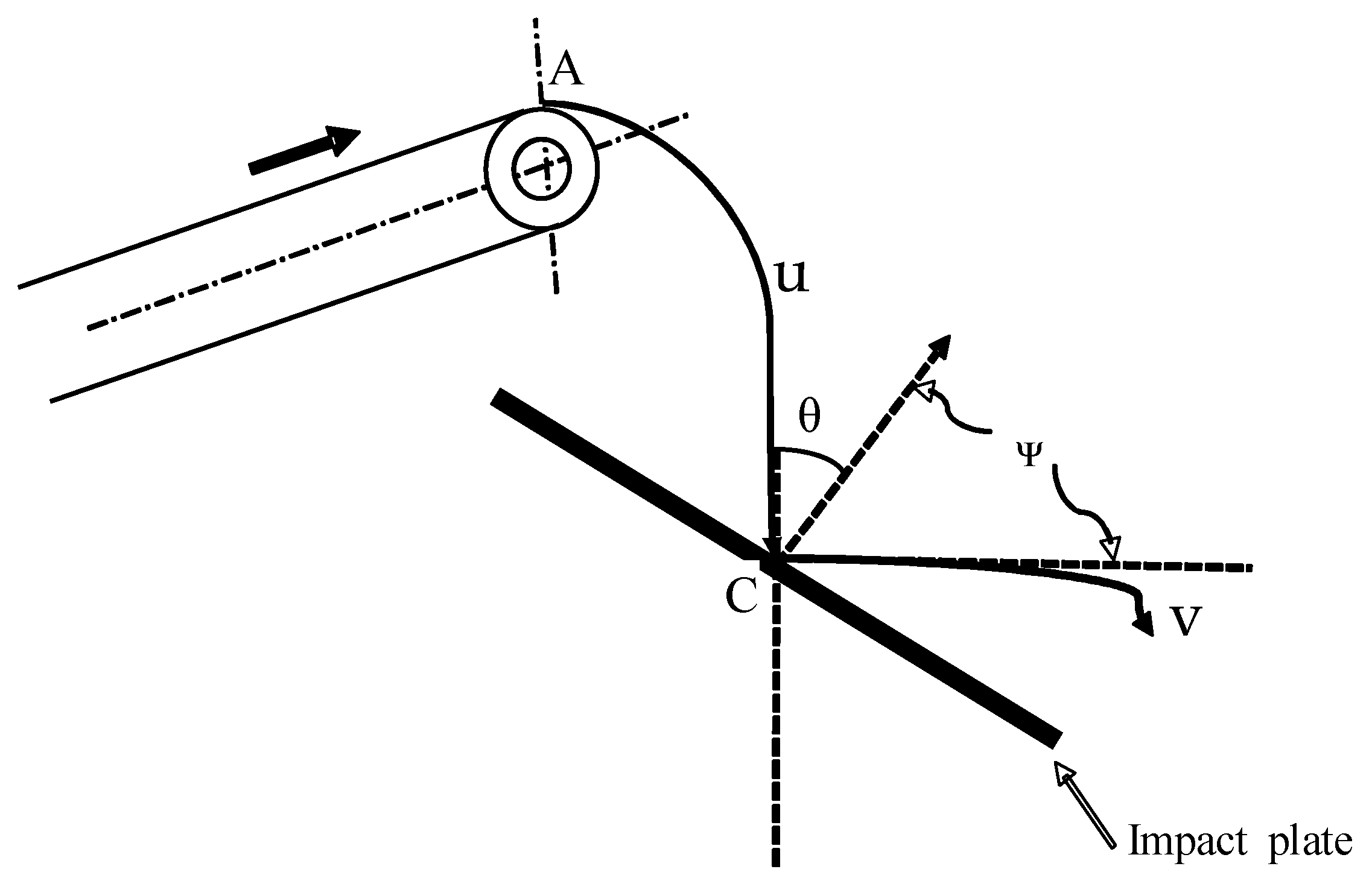
2.5.1. Mathematical Modeling of the Radish Trajectory onto the Impact Plate
2.5.2. Statistical Analysis of Load Cell Mass Measurements
3. Results
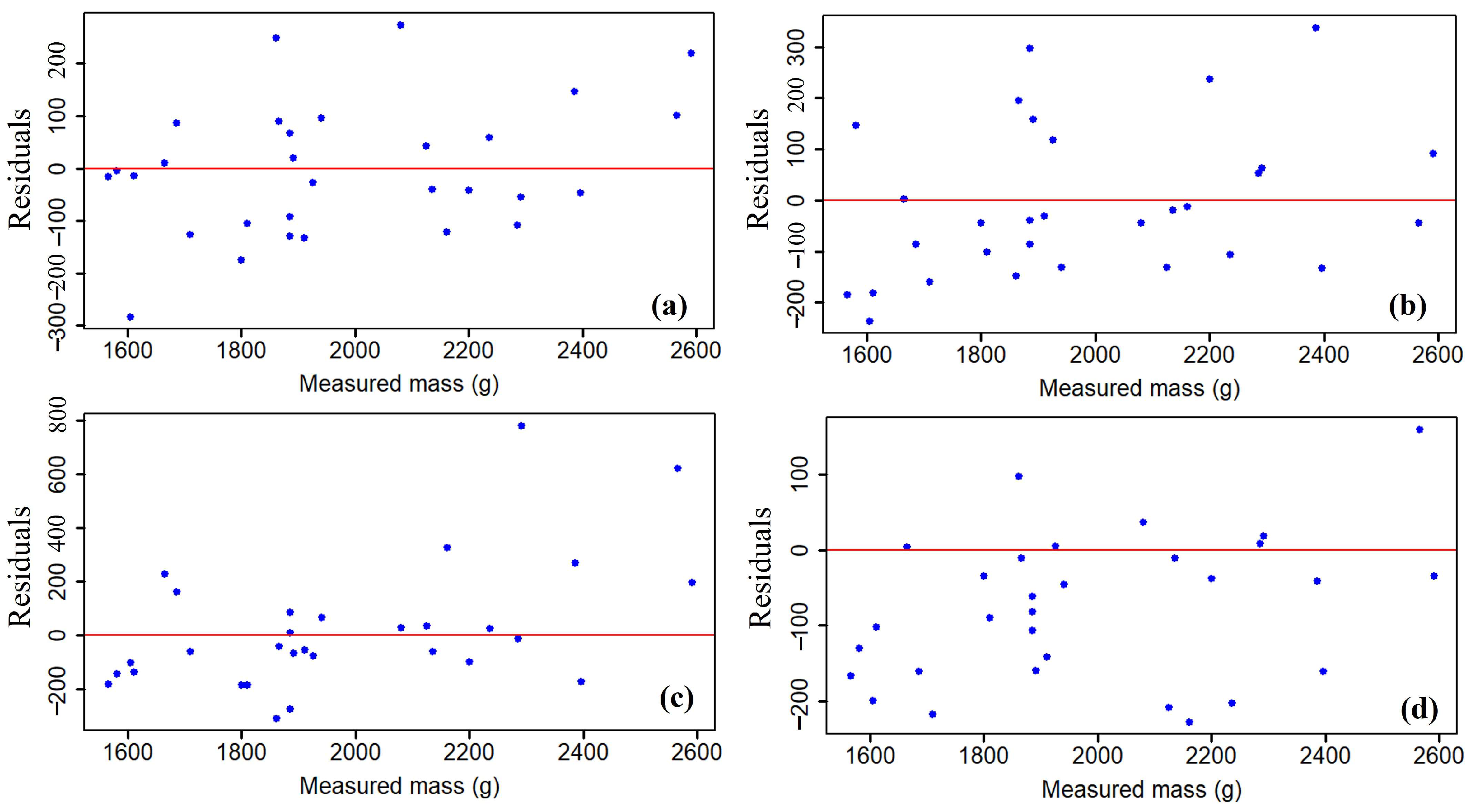
3.1. Mass Measurements under Static Conditions
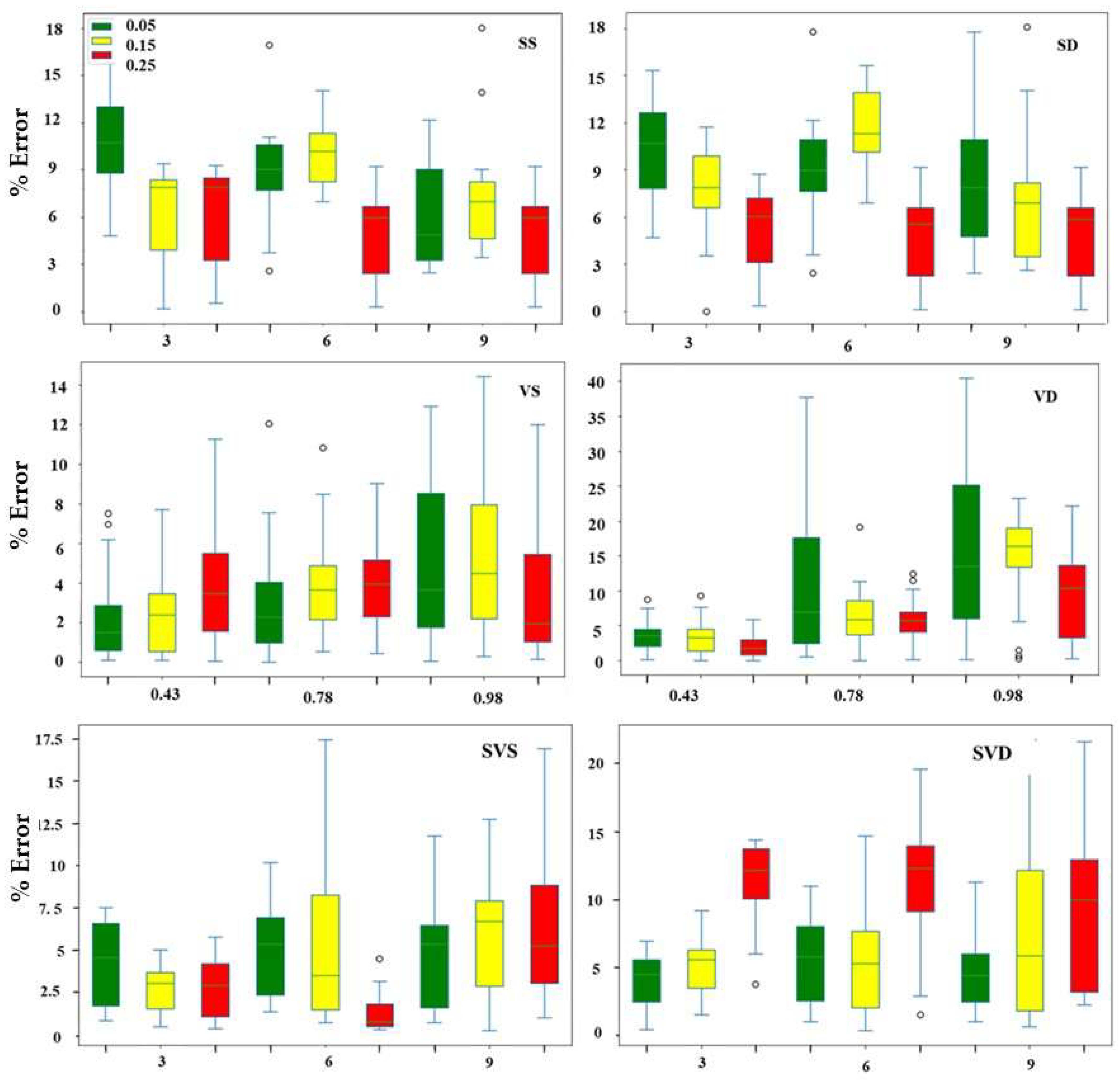
3.2. Radish Mass Estimation under Different Slope and Vibration Conditions
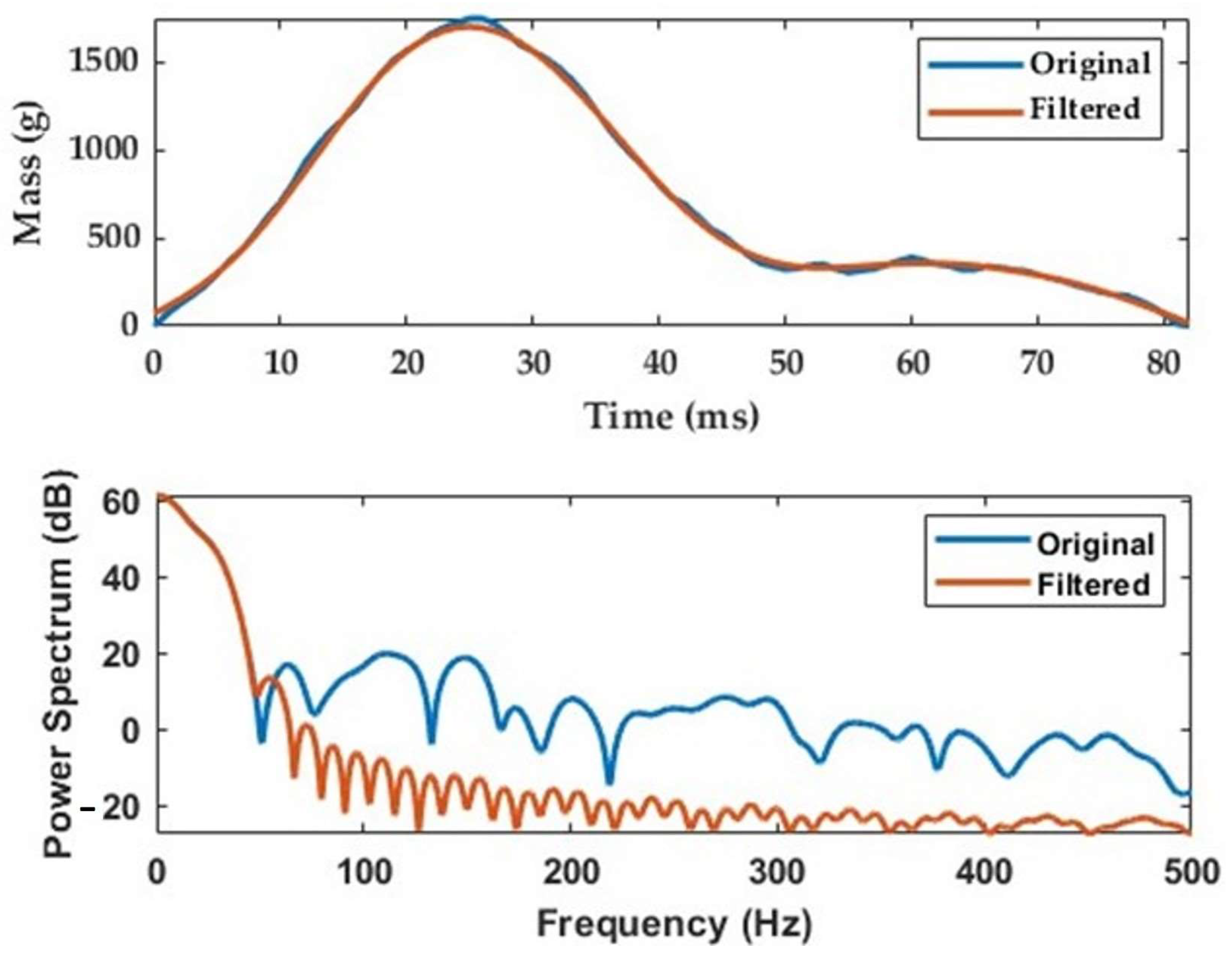
Results of Radish Signal Filtering
4. Discussion
4.1. Mass Measurement Tests without Slope and Vibration
4.2. Mass Measurement Tests with Slope and Vibration
5. Summary and Conclusions
- Standard errors (<4 g) can be achieved for impact-based radish mass estimations for tests conducted without slope or vibration effects on a laboratory test bench.
- The machine structure and orientation of the impact plate, as well as its layout, had a significant effect on radish mass measurements. In contrast, the harvesting method, represented by the falling height of the radish to the impact plate, had no significant effect on the measurements.
- Uneven field conditions represented by the various slope and vibration levels significantly influenced radish mass estimates. For each slope level, maximum errors were observed at the highest speed tested (0.25 m/s). These were 13.74, 12.31, and 13.34% at 3°, 6°, and 9°, respectively. Tests under vibration produced a mean relative error of 9.89%, lower than that under various slope conditions (13.92%). Tests combining both slope and vibration induced a relative error of 9.13%. This was reduced to 5.42% via subsequent signal filtering.
- Based on the harvesting conditions tested in this study, a single impact plate placed at an angle of −10° and a radish falling height of 40 cm are recommended as suitable for radish measurements under conveyor speeds of less than 0.1 m/s.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, J.; He, P.; Ding, W.; Xu, X.; Ullah, S.; Abbas, T.; Ai, C.; Li, M.; Cui, R.; Jin, C.; et al. Estimating nutrient uptake requirements for radish in China based on QUEFTS model. Sci. Rep. 2019, 9, 11663. [Google Scholar] [CrossRef]
- Mitsui, Y.; Shimomura, M.; Komatsu, K.; Namiki, N.; Shibata-Hatta, M.; Imai, M.; Katayose, Y.; Mukai, Y.; Kanamori, H.; Kurita, K.; et al. The radish genome and comprehensive gene expression profile of tuberous root formation and development. Sci. Rep. 2015, 5, 10835. [Google Scholar] [CrossRef]
- Zhang, J.; Ding, W.; Cui, R.; Li, M.; Ullah, S.; He, P. The Nutrient Expert decision support system improves nutrient use efficiency and environmental performance of radish in North China. J. Integr. Agric. 2022, 21, 1501–1512. [Google Scholar] [CrossRef]
- Kim, T.J.; Lee, L.J.; Jung, H.J. Study on the Overturning Angle of a Self-Propelled Pulling-Type Radish Harvester. Precis. Agric. 2019, 1, 30. [Google Scholar]
- LLC, A. Daikon Radish-Japanese Agriculture|Japan CROPS. 2022. Available online: https://japancrops.com/en/crops/daikon-radish/ (accessed on 4 June 2022).
- Shin, S.Y.; Kang, C.H.; Yu, S.C.; Kim, Y.Y.; Noh, J.S. Criteria for Determining Working Area and Operating Cost for Long-Term Lease of Agricultural Machinery. J. Biosyst. Eng. 2015, 40, 178–185. [Google Scholar] [CrossRef]
- Hong, S.; Lee, K.; Kang, D.; Park, W. Analysis of Static Lateral Stability Using Mathematical Simulations for 3-Axis Tractor-Baler System. J. Biosyst. Eng. 2017, 42, 86–97. [Google Scholar]
- Liu, R.; Sun, Y.; Li, M.; Zhang, M.; Zhang, Z.; Li, H.; Yang, W. Development and application experiments of a grain yield monitoring system. Comput. Electron. Agric. 2022, 195, 106851. [Google Scholar] [CrossRef]
- Chung, S.O.; Choi, M.C.; Lee, K.H.; Kim, Y.J.; Hong, S.J.; Li, M. Sensing technologies for grain crop yield monitoring systems: A review. J. Biosyst. Eng. 2016, 41, 408–417. [Google Scholar] [CrossRef]
- Zamani, D.M.; Ghoşamiparashkohi, M.; Faghavi, A.; Ghezavati, J.E. Design, implementation and evaluation of potato yield monitoring system. Int. J. Tech. Res. Appl. 2014, 2, 36–39. [Google Scholar]
- Maja, J.M.; Ehsani, R. Development of a yield monitoring system for citrus mechanical harvesting machines. Precis. Agric. 2010, 11, 475–487. [Google Scholar] [CrossRef]
- Upadhyaya, S.K.; Shafii, M.S.; Garciano, L.O. Development of an impact type electronic weighing system for processing tomatoes. In Proceedings of the 2006 ASAE Annual Meeting. American Society of Agricultural and Biological Engineers, Boston, MA, USA, 19–22 August 2006; p. 1. [Google Scholar]
- Ehsani, R.; Karimi, D. Yield Monitors for Specialty Crops. Landbauforsch. Völkenrode 2010, 340, 31–44. [Google Scholar]
- Kharel, T.P.; Swink, S.N.; Maresma, A.; Youngerman, C.; Kharel, D.; Czymmek, K.J.; Ketterings, Q.M. Yield Monitor Data Cleaning is Essential for Accurate Corn Grain and Silage Yield Determination. Agron. J. 2019, 111, 509–516. [Google Scholar] [CrossRef]
- Richiedei, D.; Trevisani, A. Shaper-Based Filters for the compensation of the load cell response in dynamic mass measurement. Mech. Syst. Signal Process. 2018, 98, 281–291. [Google Scholar] [CrossRef]
- Boschetti, G.; Caracciolo, R.; Richiedei, D.; Trevisani, A. Model-based dynamic compensation of load cell response in weighing machines affected by environmental vibrations. Mech. Syst. Signal Process. 2013, 34, 116–130. [Google Scholar] [CrossRef]
- Zhou, J.; Cong, B.; Liu, C. Elimination of vibration noise from an impact-type grain mass flow sensor. Precis. Agric. 2014, 15, 627–638. [Google Scholar] [CrossRef]
- Chowdhury, M.; Islam, M.N.; Iqbal, M.Z.; Islam, S.; Lee, D.-H.; Kim, D.-G.; Jun, H.-J.; Chung, S.-O. Analysis of Overturning and Vibration during Field Operation of a Tractor-Mounted 4-Row Radish Collector toward Ensuring User Safety. Machines 2020, 8, 77. [Google Scholar] [CrossRef]
- El-Desuki, M.; Salman, S.R.; El-Nemr, M.A.; Abdel-Mawgoud, A.M.R. Effect of plant density and nitrogen application on the growth, yield and quality of radish (Raphanus sativus L.). J. Agron. 2005, 4, 225–229. [Google Scholar] [CrossRef]
- Kim, W.-S.; Siddique, M.A.A.; Kim, Y.-J.; Jung, Y.-J.; Baek, S.-M.; Baek, S.-Y.; Kim, Y.-S.; Lim, R.-G. Simulation of the Rollover Angle of a Self-Propelled Radish Harvester for Different Load Conditions. Appl. Sci. 2022, 12, 10733. [Google Scholar] [CrossRef]
- Chung, S.-O.; Sudduth, K.A.; Hummel, J.W. Design and validation of an on-the-go soil strength profile sensor. Trans. ASABE 2006, 49, 5–14. [Google Scholar] [CrossRef]
- Boo, C.G.; Hong, S.J.; Lee, Y.; Park, S.-S.; Shin, E.-C. Quality Characteristics of Wintering Radishes Produced in Jeju Island Using E-Nose, E-Tongue, and GC-MSD Approach. J. Korean Soc. Food Sci. Nutr. 2020, 49, 1407–1415. [Google Scholar] [CrossRef]
- Glancey, J.L.; Hofstetter, D.; Kee, W.E. Impact characteristics of pickling cucumber and their potential effect on mass flow rate measurement. Acta Hortic. 2009, 824, 223–230. [Google Scholar] [CrossRef]
- Zhang, J.; Ying, Y.; Jiang, H.; Wang, H.; Yang, C.; Yu, Y.; Wang, J. Application of Optimized Digital Filters and Asymmetrically Trimmed Mean to Improve the Accuracy of Dynamic Egg Weighing. Trans. ASABE 2017, 60, 1099–1111. [Google Scholar] [CrossRef]
- Ehlert, D. Measuring mass flow by bounce plate for yield mapping of potatoes. Precis. Agric. 2000, 2, 119–130. [Google Scholar] [CrossRef]
- Liu, R.; Zhang, Z.; Zhang, M.; Yang, W.; Li, M. Performance Analysis and Modelling of Impact-based Sensor in Yield Monitor System. IFAC-Pap. 2018, 51, 613–618. [Google Scholar] [CrossRef]
- Qarallah, B.; Shoji, K.; Kawamura, T. Development of a yield sensor for measuring individual weights of onion bulbs. Biosyst. Eng. 2008, 100, 511–515. [Google Scholar] [CrossRef]
- Porter, W.M.; Ward, J.; Taylor, R.K.; Godsey, C.B. A Note on the Application of an AgLeader® Cotton Yield Monitor for Measuring Peanut Yield: An Investigation in Two US states. Peanut Sci. 2020, 47, 115–122. [Google Scholar] [CrossRef]
- Fravel, J.B.; Kirk, K.R.; Mornfort, W.S.; Thomas, J.S.; Henderson, W.G.; Massey, H.F.; Chastain, J.P. Development and Testing of an Impact Plate Yield Monitor for Peanuts; American Society of Agricultural and Biological Engineers: Kansas City, MI, USA, 21–24 July 2013; p. 1. [Google Scholar]
- Piskorowski, J.; Barcinski, T. Dynamic compensation of load cell response: A time-varying approach. Mech. Syst. Signal Process. 2008, 22, 1694–1704. [Google Scholar] [CrossRef]
- Shoji, K.; Kawamura, T.; Horio, H. Impact-based Grain Yield Sensor with Compensation for Vibration and Drift. J. JSAM 2002, 64, 108–115. [Google Scholar]
- Hessling, J.P. Models of dynamic measurement error variations of material testing machines. Mech. Syst. Signal Process. 2009, 23, 2510–2518. [Google Scholar] [CrossRef]
- Fulton, J.P.; Sobolik, C.J.; Shearer, S.A.; Higgins, S.F.; Burks, T.F. Grain Yield Monitor Flow Sensor Accuracy for Simulated Varying Field Slopes. Appl. Eng. Agric. 2009, 25, 15–21. [Google Scholar] [CrossRef]




| Item | Specification | |||
|---|---|---|---|---|
| Vibration table | Weight (kg) (kg) | Power rating (kW) | RPM | Dimensions (L × W × H) (mm) |
| 560 | 1.1 | 200 ~ 3600 | 2000 × 1000 × 900 | |
| Slope platform | Slope types | Measuring range (°) | Dimensions (L × W × H) (mm) | |
| Pitch; roll | 0~15 | 2200 × 1100 × 2000 | ||
| Conveyor system | Conveyor speed (m/s) | Angle of incline (°) | Dimensions (L × W × H) (mm) | |
| 0~0.25 | 27 | 1700 × 500 | ||
| Experimental Variable | Levels | ||||
|---|---|---|---|---|---|
| Mass measurement without slope and vibration | |||||
| Conveyor speed (ms–1) | 0.05 | 0.15 | 0.25 | ||
| Falling height (cm) | 20 | 30 | 40 | ||
| Impact plate angle (°) | −10 | −30 | −50 | ||
| Impact plate layout (no. of load cells) | Single | Double | |||
| Mass measurement with slope and vibration | |||||
| Measurement with vibration | Conveyor speed (m s−1) | 0.05 | 0.15 | 0.25 | |
| Falling height (cm) | 40 | ||||
| Impact plate angle (°) | −10 | ||||
| No. of load cells | Single | ||||
| Vibration (m s−2) | 0.43 | 0.78 | 0.98 | ||
| Measurement with slope | Conveyor speed (m s−1) | 0.05 | 0.15 | 0.25 | |
| Falling height (cm) | 40 | ||||
| No. of load cells | Single | ||||
| Impact plate angle (°) | −10 | ||||
| Slope(°) | 3 | 6 | 9 | ||
| Measurement with slope and vibration conditions | Conveyor speed (m s−1) | 0.05 | 0.15 | 0.25 | |
| Falling height (cm) | 40 | ||||
| Impact plate angle (°) | −10 | ||||
| No. of load cells | Single | ||||
| Vibration (m s−2) | 0.43 | ||||
| Slope (°) | 3 | 6 | 9 | ||
| Source | Sum of Squares | df | Mean Square | F-Value | Pr > F |
|---|---|---|---|---|---|
| Model | 0.0224 | 6 | 0.0112 | 6.31 | 0.0029 |
| Error | 0.0238 | 20 | 0.001 | ||
| Total | 0.0461 | 26 |
| Single-Load-Cell Impact Plate | |||||
|---|---|---|---|---|---|
| Calibration (n = 5) | Validation (n = 30) | ||||
| Level | R2 | RE (%) | SE (g) | R2 | |
| Conveyor speed | 0.05 | 0.97 | 8.6 a | 2.76 a | 0.89 |
| 0.15 | 0.98 | 9.1 a | 2.64 a | 0.77 | |
| 0.25 | 0.96 | 13.6 b | 2.45 b | 0.75 | |
| Falling height | 20 | 0.99 | 10.7 a | 2.51 a | 0.78 |
| 30 | 0.95 | 8.7 a | 2.62 a | 0.85 | |
| 40 | 0.96 | 11.9 a | 2.72 a | 0.58 | |
| Plate angle | −10 | 0.97 | 7.5 a | 2.29 a | 0.84 |
| −30 | 0.94 | 8.2 a | 2.48 a | 0.82 | |
| −50 | 0.96 | 15.7 b | 2.91 b | 0.69 | |
| Double-Load-Cell Impact Plate | |||||
| Calibration (n = 5) | Validation (n = 30) | ||||
| Level | R2 | RE (%) | SDE (g) | R2 | |
| Conveyor speed | 0.05 | 0.98 | 8.4 a | 2.7 a | 0.81 |
| 0.15 | 0.97 | 9.5 a | 2.7 a | 0.77 | |
| 0.25 | 0.95 | 10.9 a | 2.7 a | 0.74 | |
| Falling height | 20 | 0.96 | 10.5 a | 2.3 a | 0.75 |
| 30 | 0.97 | 8.8 a | 2.9 a | 0.80 | |
| 40 | 0.99 | 9.6 a | 2.6 a | 0.76 | |
| Plate angle | −10 | 0.96 | 8.3 b | 2.3 b | 0.80 |
| −30 | 0.98 | 7.9 b | 2.5 b | 0.82 | |
| −50 | 0.94 | 13.7 a | 3.4 a | 0.69 | |
| Experimental Factor | Static Tests | Experimental Factor | Dynamic Tests | Moving Average | |||
|---|---|---|---|---|---|---|---|
| Vibration Level (m/s2) | Conveyor Speed (m/s) | RE (%) | Slope (°) | RE (%) | N | ||
| 5 | 10 | 15 | |||||
| 0.43 | 0.05 | 6.61 | 3 | 4.52 | 3.6 | 3.4 | 6.2 |
| 0.15 | 4.89 | 6.78 | 3.3 | 4.2 | 6.8 | ||
| 0.25 | 5.10 | 13.74 | 4.8 | 5.8 | 4.7 | ||
| 0.05 | 7.02 | 6 | 8.05 | 6.6 | 6.2 | 7.6 | |
| 0.15 | 9.29 | 7.68 | 7.4 | 5.7 | 6.1 | ||
| 0.25 | 2.39 | 12.31 | 7.8 | 8.1 | 9.2 | ||
| 0.05 | 6.46 | 9 | 7.2 | 4.7 | 7.4 | 3.8 | |
| 0.15 | 9.09 | 8.59 | 4.8 | 4.9 | 3.8 | ||
| 0.25 | 6.49 | 13.34 | 5.7 | 5.5 | 6.2 | ||
| Mean error, % | 6.37 | 9.13 | 5.42 | 5.69 | 6.04 | ||
| Source | Sum of Squares | df | Mean Square | F-Value | Pr > F |
|---|---|---|---|---|---|
| Model | 4616.667 | 2 | 2308.333 | 0.07 | 0.930 |
| Error | 2,594,188.889 | 78 | 33,258.832 | ||
| Total | 2,598,805.556 | 80 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kiraga, S.; Reza, M.N.; Chowdhury, M.; Gulandaz, M.A.; Ali, M.; Kabir, M.S.; Habineza, E.; Kabir, M.S.N.; Chung, S.-O. Vibration and Slope Conditions during Harvesting Affect Radish Mass Measurements for Yield Monitoring: An Experimental Study Using a Laboratory Test Bench. Sensors 2023, 23, 9744. https://doi.org/10.3390/s23249744
Kiraga S, Reza MN, Chowdhury M, Gulandaz MA, Ali M, Kabir MS, Habineza E, Kabir MSN, Chung S-O. Vibration and Slope Conditions during Harvesting Affect Radish Mass Measurements for Yield Monitoring: An Experimental Study Using a Laboratory Test Bench. Sensors. 2023; 23(24):9744. https://doi.org/10.3390/s23249744
Chicago/Turabian StyleKiraga, Shafik, Md Nasim Reza, Milon Chowdhury, Md Ashraffuzzaman Gulandaz, Mohammod Ali, Md Sazzadul Kabir, Eliezel Habineza, Md Shaha Nur Kabir, and Sun-Ok Chung. 2023. "Vibration and Slope Conditions during Harvesting Affect Radish Mass Measurements for Yield Monitoring: An Experimental Study Using a Laboratory Test Bench" Sensors 23, no. 24: 9744. https://doi.org/10.3390/s23249744









