Designing of an Enhanced Fuzzy Logic Controller of an Interior Permanent Magnet Synchronous Generator under Variable Wind Speed
Abstract
:1. Introduction
2. Related Work
3. Proposed EFLC-Based Torque Ripple Reduction in IPMSG
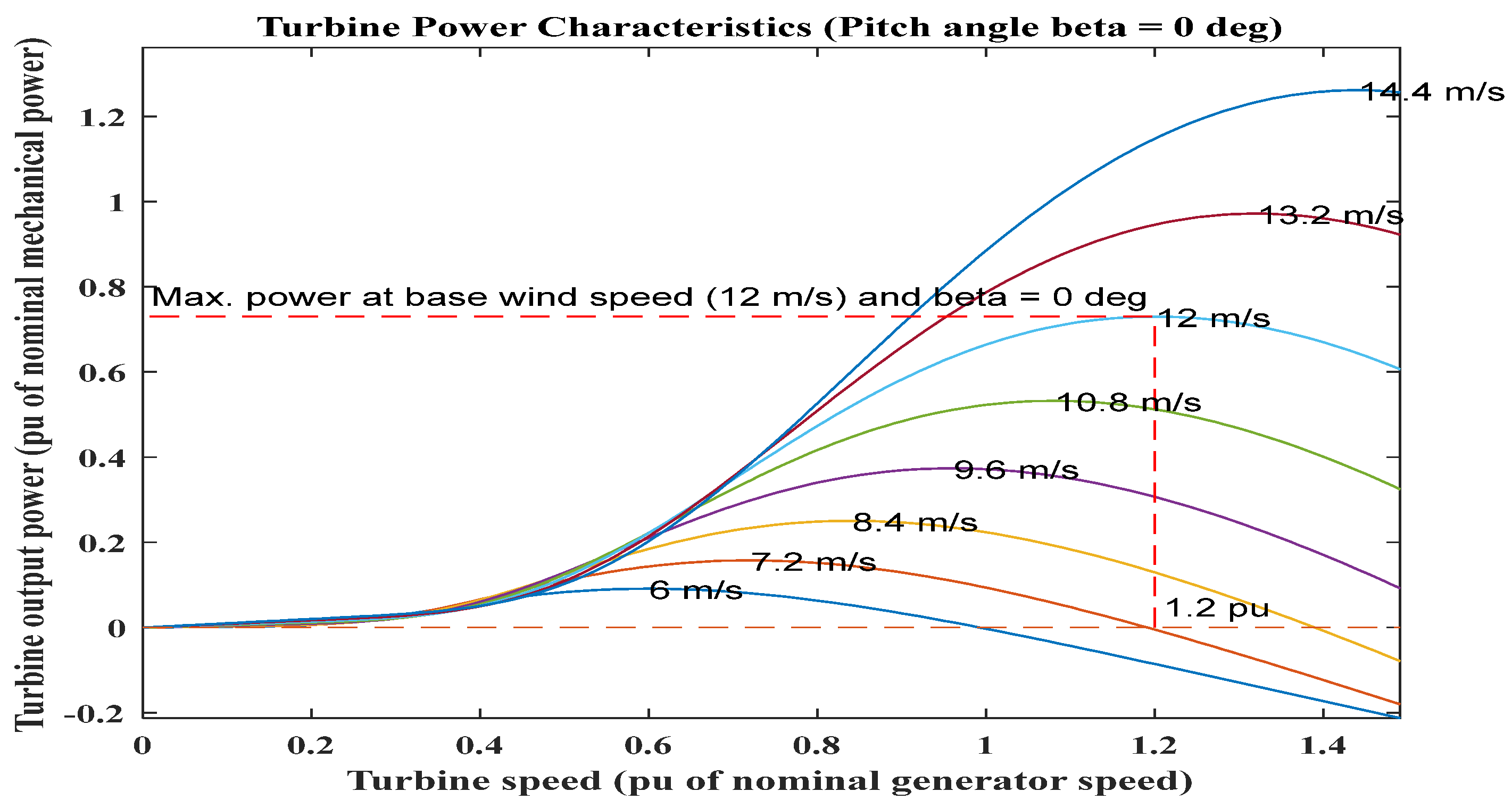
3.1. Modeling of Wind Turbine
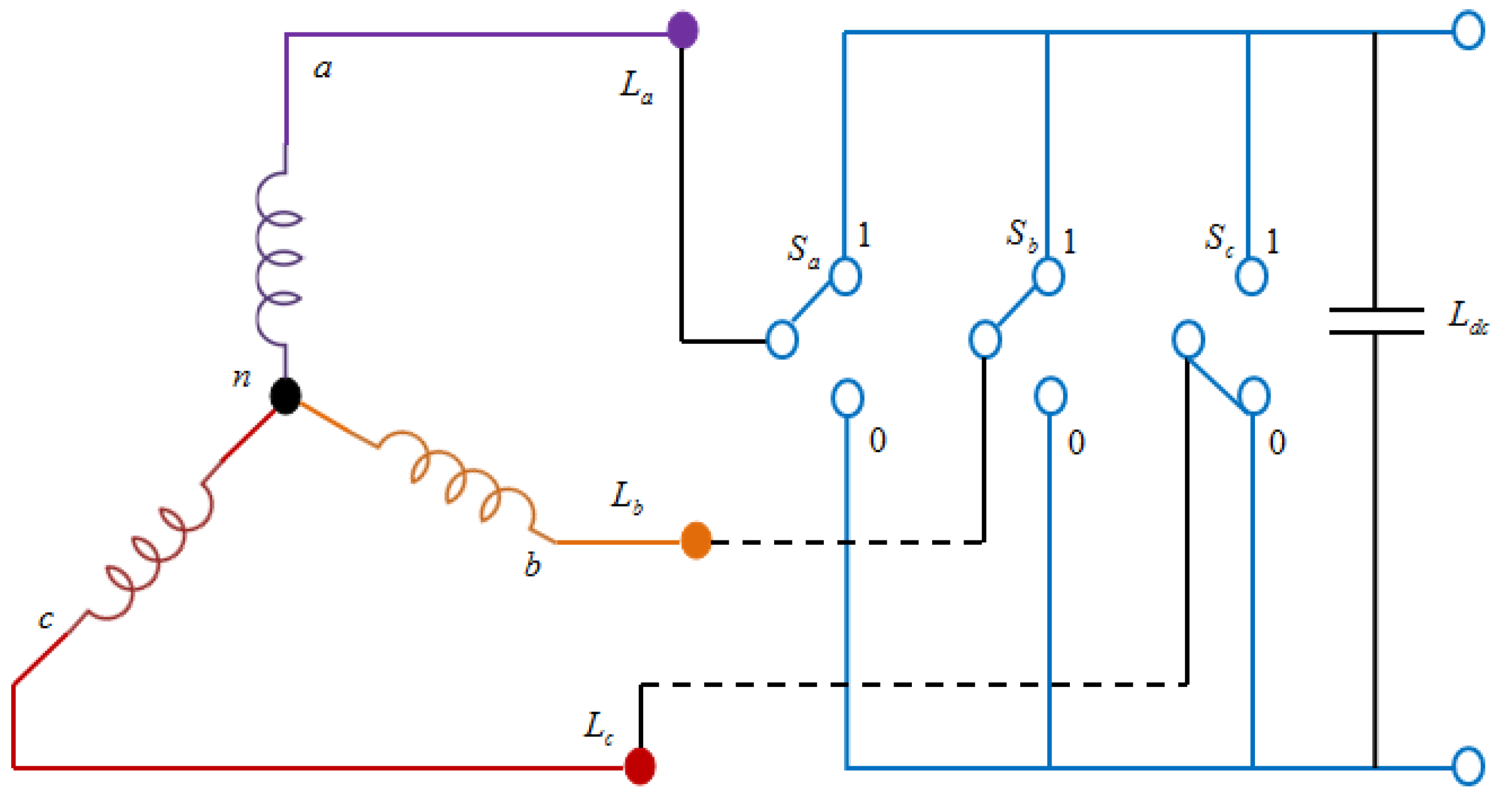
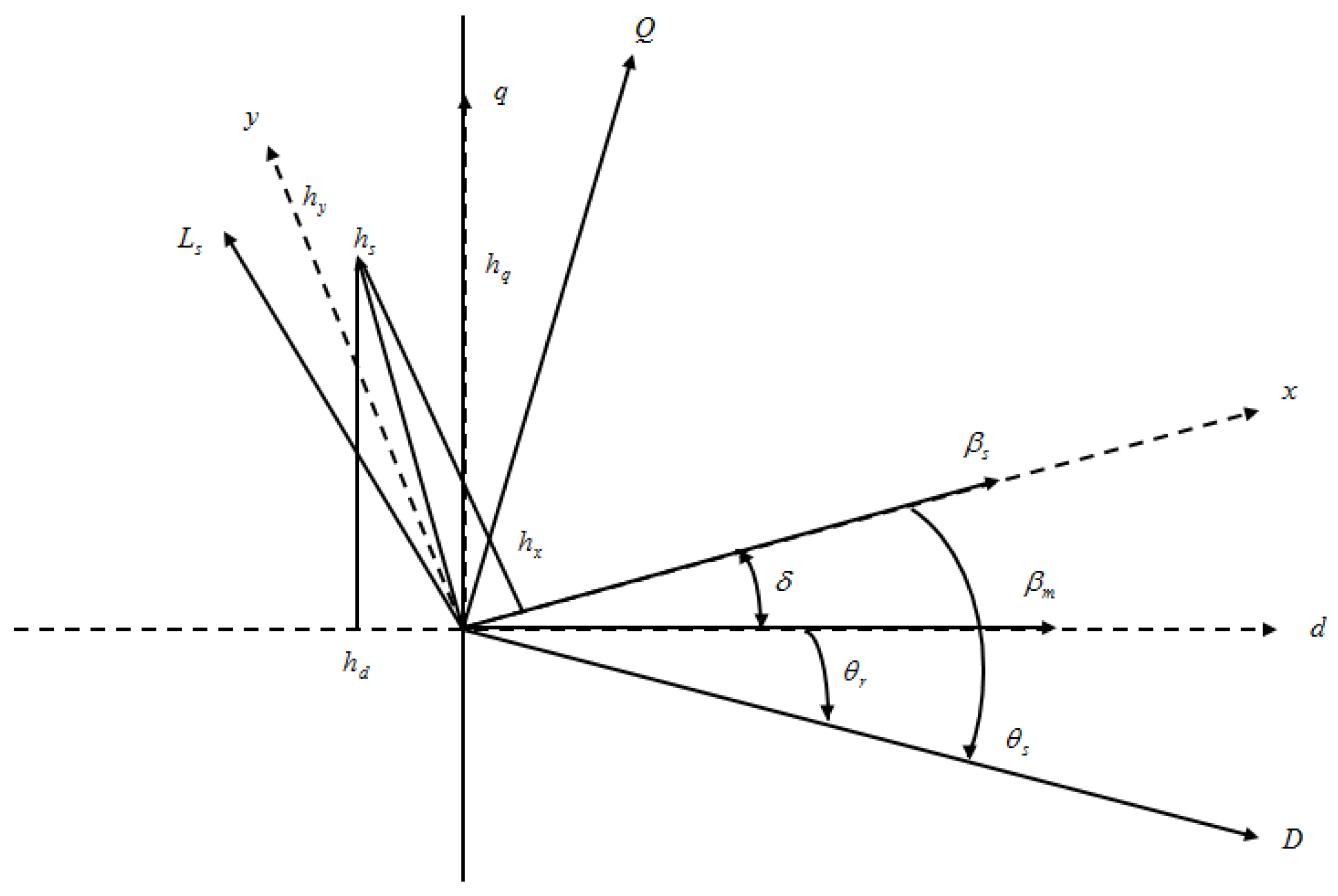
3.2. Modeling of IPMSG
- (a)
- Neglect of saturation.
- (b)
- The induced EMF is sinusoidal.
- (c)
- Negligible losses in Eddy current and hysteresis.
- (d)
- No field current dynamics.
3.3. Controllers
3.3.1. Hysteresis Controller
3.3.2. Fuzzy Controller
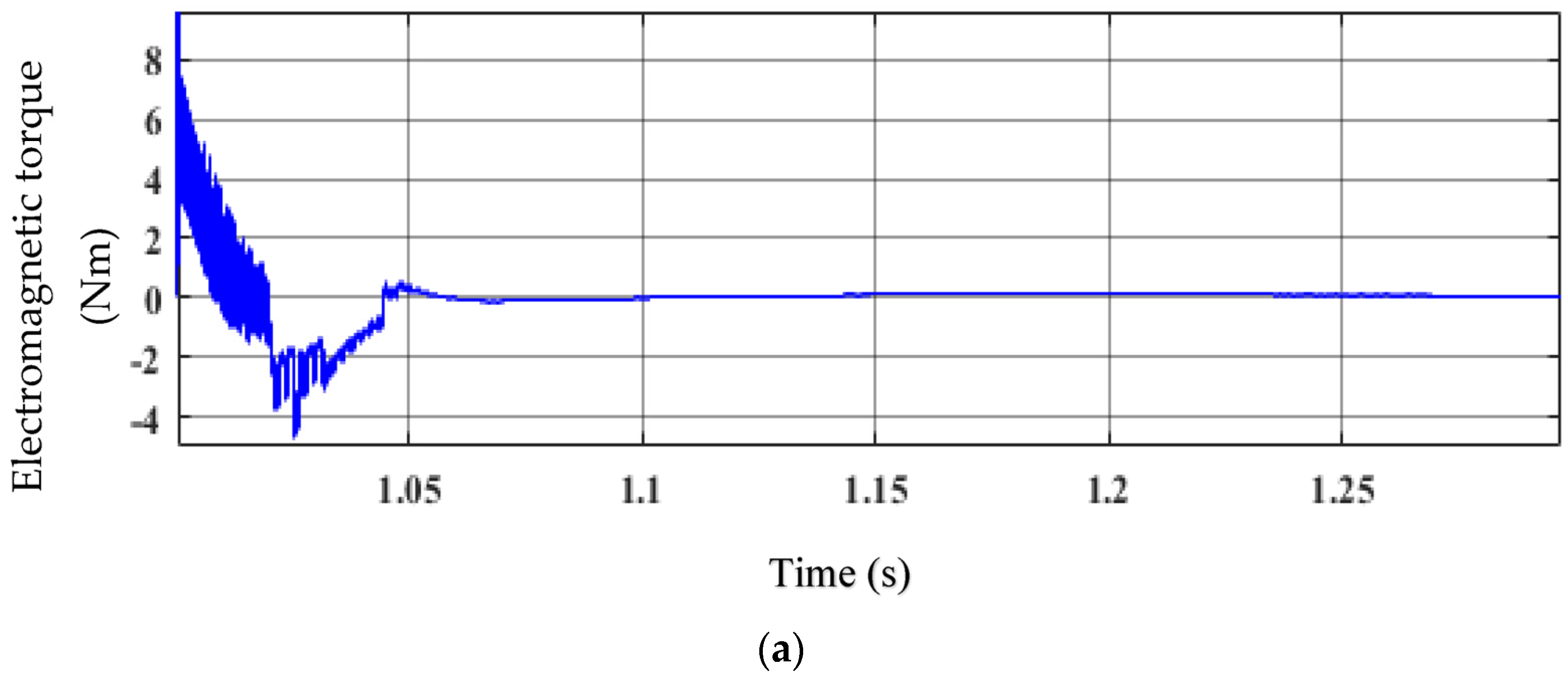
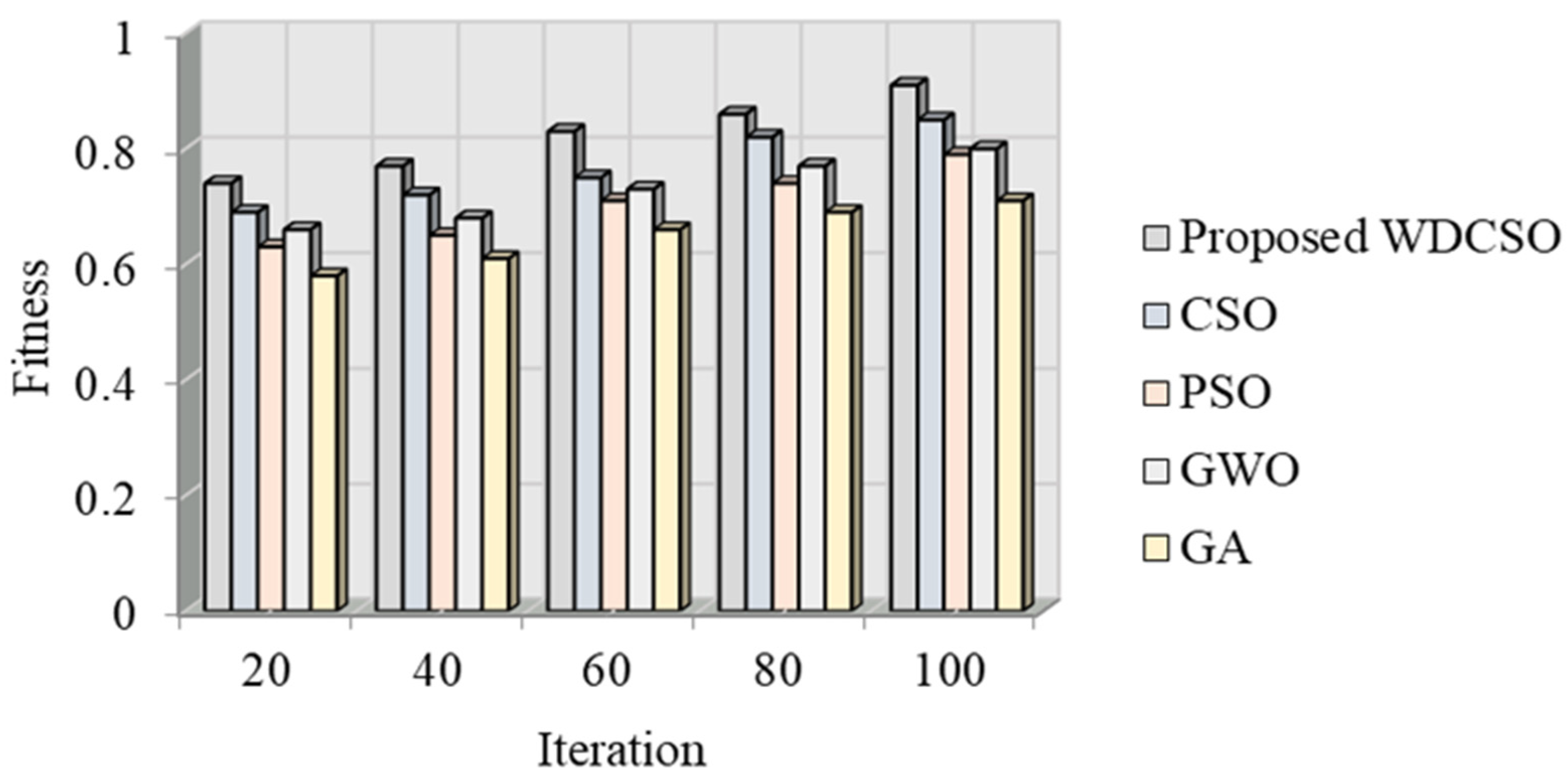
4. Result and Discussion
Performance Analysis
5. Conclusions
6. Limitations of Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hassan, M.; Ge, X.; Woldegiorgis, A.T.; Mastoi, M.S.; Shahid, M.B.; Atif, R.; Shaikh, M.S.; Kumar, S. A look-up table-based model predictive torque control of IPMSM drives with duty cycle optimization. ISA Trans. 2023, in press.
- Bıçak, A.; Gelen, A. Sensorless direct torque control based on seven-level torque hysteresis controller for five-phase IPMSM using a sliding-mode observer. Eng. Sci. Technol. Int. J. 2021, 24, 1134–1143. [Google Scholar] [CrossRef]
- Huang, M.; Deng, Y.; Li, H.; Wang, J. Torque ripple suppression of PMSM using fractional-order vector resonant and robust internal model control. IEEE Trans. Transp. Electrif. 2021, 7, 1437–1453. [Google Scholar] [CrossRef]
- Huang, J.; Fu, W.; Niu, S.; Zhao, X.; Bi, Y.; Qiao, Z. A General Pattern-Based Design Optimization for Asymmetric Spoke-Type Interior PM Machines. Energies 2022, 15, 9385. [Google Scholar] [CrossRef]
- Bounasla, N.; Barkat, S. Optimum design of fractional order PIᵅ speed controller for predictive direct torque control of a sensorless five-phase Permanent Magnet Synchronous Machine (PMSM). J. Eur. Des Systèmes Autom. 2020, 53, 437–449. [Google Scholar] [CrossRef]
- Qu, B.; Yang, Q.; Li, Y.; Sotelo, M.A.; Ma, S.; Li, Z. A novel surface inset permanent magnet synchronous motor for electric vehicles. Symmetry 2020, 12, 179. [Google Scholar] [CrossRef] [Green Version]
- Beltran-Carbajal, F.; Tapia-Olvera, R.; Lopez-Garcia, I.; Valderrabano-Gonzalez, A.; Rosas-Caro, J.C.; Hernandez-Avila, J.L. Extended PI feedback tracking control for synchronous motors. Int. J. Control. Autom. Syst. 2019, 17, 1346–1358. [Google Scholar] [CrossRef]
- Suriano-Sánchez, S.I.; Ponce-Silva, M.; Olivares-Peregrino, V.H.; De León-Aldaco, S.E. A Review of Torque Ripple Reduction Design Methods for Radial Flux PM Motors. Eng 2022, 3, 646–661. [Google Scholar] [CrossRef]
- Le, X.C.; Duong, M.Q.; Le, K.H. Review of the Modern Maximum Power Tracking Algorithms for Permanent Magnet Synchronous Generator of Wind Power Conversion Systems. Energies 2023, 16, 402. [Google Scholar] [CrossRef]
- Kumar, R.; Zhu, Z.Q.; Duke, A.; Thomas, A.; Clark, R.; Azar, Z.; Wu, Z.Y. A review on transverse flux permanent magnet machines for wind power applications. IEEE Access 2020, 8, 216543–216565. [Google Scholar] [CrossRef]
- Chen, W.; Ma, J.; Wu, G.; Fang, Y. Torque ripple reduction of a salient pole permanent magnet synchronous machine with an advanced step skewed rotor design. IEEE Access 2017, 8, 118989–118999. [Google Scholar] [CrossRef]
- Kano, Y. Torque ripple reduction of saliency-based sensorless drive concentrated winding IPMSM using novel flux barrier. IEEE Trans. Ind. Appl. 2015, 51, 2905–2916. [Google Scholar] [CrossRef]
- Saha, S.; Haque, M.E.; Mahmud, M.A. Diagnosis and mitigation of sensor malfunctioning in a permanent magnet synchronous generator based wind energy conversion system. IEEE Trans. Energy Convers. 2018, 33, 938–948. [Google Scholar] [CrossRef]
- Qu, G.; Fan, Y.; Chen, Q. Suppression of Torque Ripple in a New Consequent-Pole Permanent Magnet Machine by Segmented Structure. IEEE Trans. Magn. 2022, 58, 1–6. [Google Scholar] [CrossRef]
- Bianchi, N.; Degano, M.; Fornasiero, E. Sensitivity analysis of torque ripple reduction of synchronous reluctance and interior PM motors. IEEE Transactions on Industry Applications. In Proceedings of the IEEE Energy Conversion Congress and Exposition, Denver, CO, USA, 15–19 September 2013. [Google Scholar] [CrossRef]
- Alnami, H.; Pang, C.; Papineni, A.; Wang, X. Maximum torque per ampere and maximum power per ampere sliding mode control for interior permanent magnet synchronous motors. Syst. Sci. Control. Eng. 2021, 9, 704–713. [Google Scholar] [CrossRef]
- Muteba, M. Influence of mixed stator winding configurations and number of rotor flux-barriers on torque and torque ripple of five phase synchronous reluctance motors. In Proceedings of the IEEE Transportation Electrification Conference and Exposition, Detroit, MI, USA, 19–21 June 2019. [Google Scholar] [CrossRef]
- Uberti, F.; Frosini, L.; Szabó, L. A new design procedure for rotor laminations of synchronous reluctance machines with fluid shaped barriers. Electronics 2022, 11, 134. [Google Scholar] [CrossRef]
- Lai, C.; Feng, G.; Iyer, K.L.V.; Mukherjee, K.; Kar, N.C. Genetic algorithm based current optimization for torque ripple reduction of interior PMSMs. IEEE Trans. Ind. Appl. 2017, 53, 4493–4503. [Google Scholar] [CrossRef]
- Wu, H.; Depernet, D.; Lanfranchi, V.; Benkara, K.E.K.; Rasid, M.A.H. A novel and simple torque ripple minimization method of synchronous reluctance machine based on torque function method. IEEE Trans. Ind. Electron. 2020, 68, 92–102. [Google Scholar] [CrossRef]
- El Ouanjli, N.; Derouich, A.; El Ghzizal, A.; Motahhir, S.; Chebabhi, A.; El Mourabit, Y.; Taoussi, M. Modern improvement techniques of direct torque control for induction motor drives-a review. Prot. Control. Mod. Power Syst. 2019, 4, 11. [Google Scholar] [CrossRef] [Green Version]
- Ge, H.; Qiu, X.; Guo, B.; Yang, J.; Bai, C.; Jin, Z. Optimized rotor shape for reducing torque ripple and electromagnetic noise. IEEE Trans. Magn. 2021, 58, 8102905. [Google Scholar] [CrossRef]
- Liu, Q.; Hameyer, K. Torque ripple minimization for direct torque control of PMSM with modified FCSMPC. IEEE Trans. Ind. Appl. 2016, 52, 4855–4864. [Google Scholar] [CrossRef]
- Mohan, D.; Zhang, X.; Foo, G.H.B. Three level inverter fed direct torque control of IPMSM with constant switching frequency and torque ripple reduction. IEEE Trans. Ind. Electron. 2016, 63, 7908–7918. [Google Scholar] [CrossRef]
- Bahri, E.; Pusca, R.; Romary, R.; Belkhayat, D. A new approach for torque ripple reduction in a faulty surface permanent magnet synchronous motor by inverse current injection. Electr. Eng. 2018, 100, 565–579. [Google Scholar] [CrossRef]




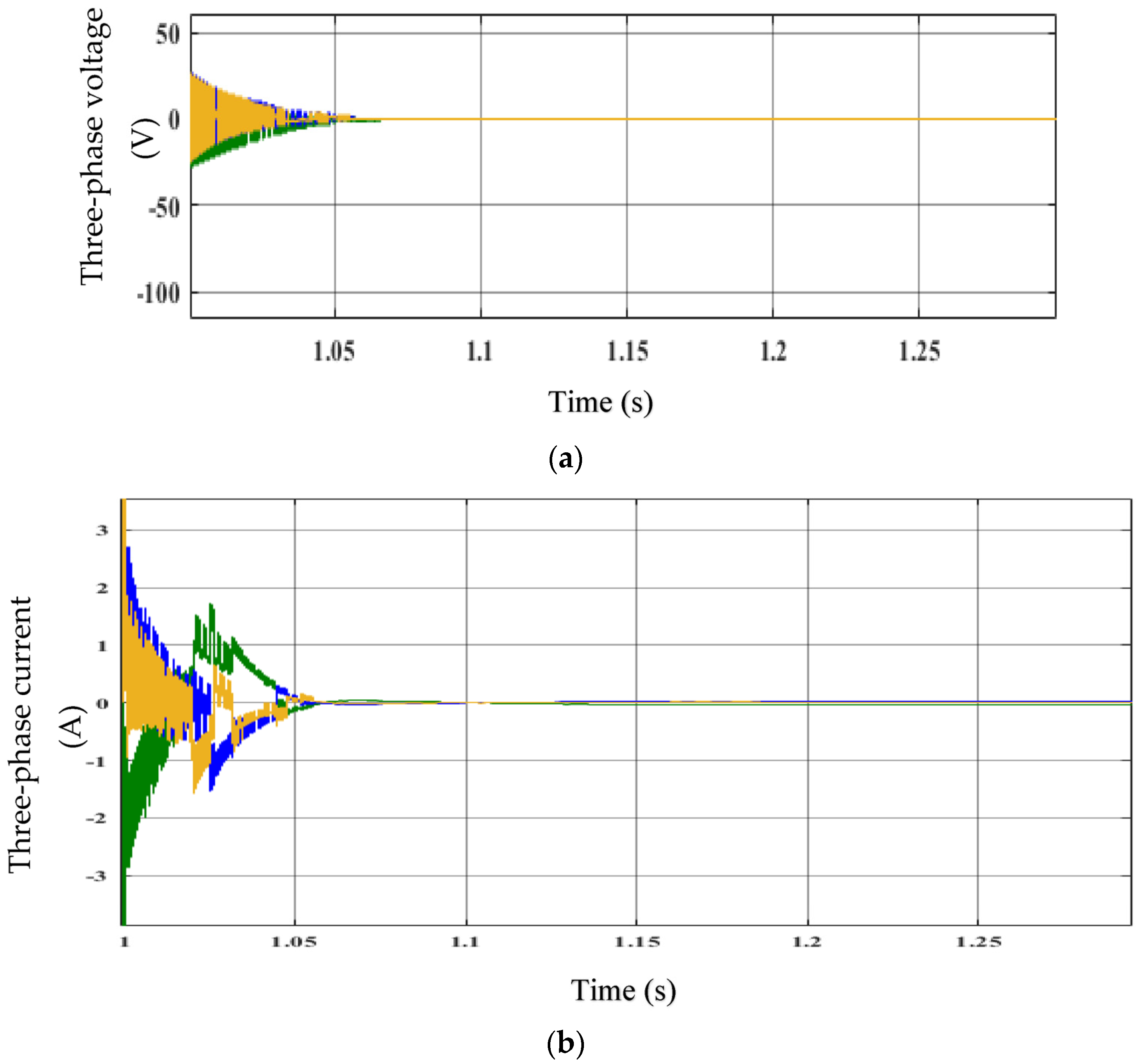

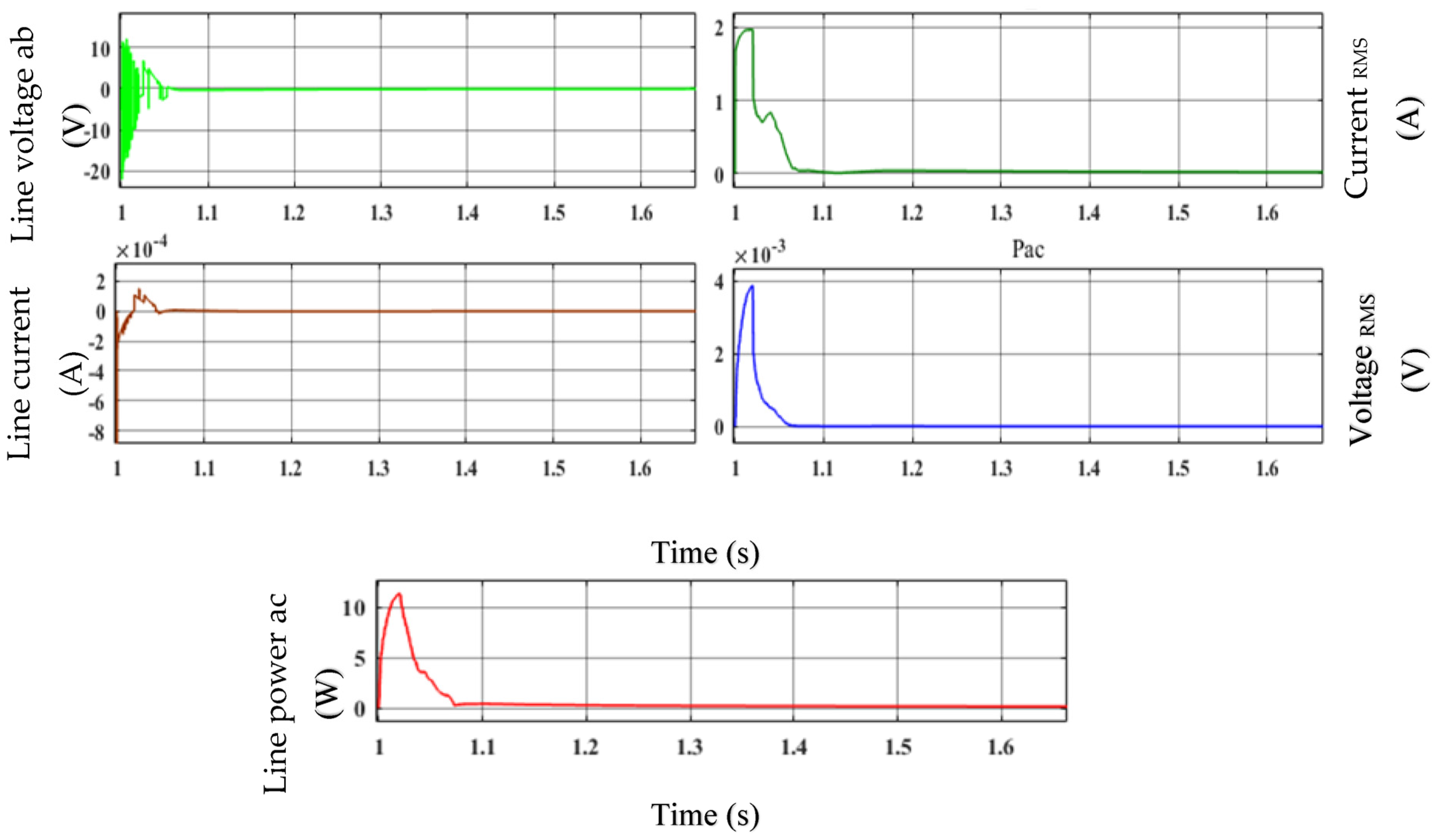
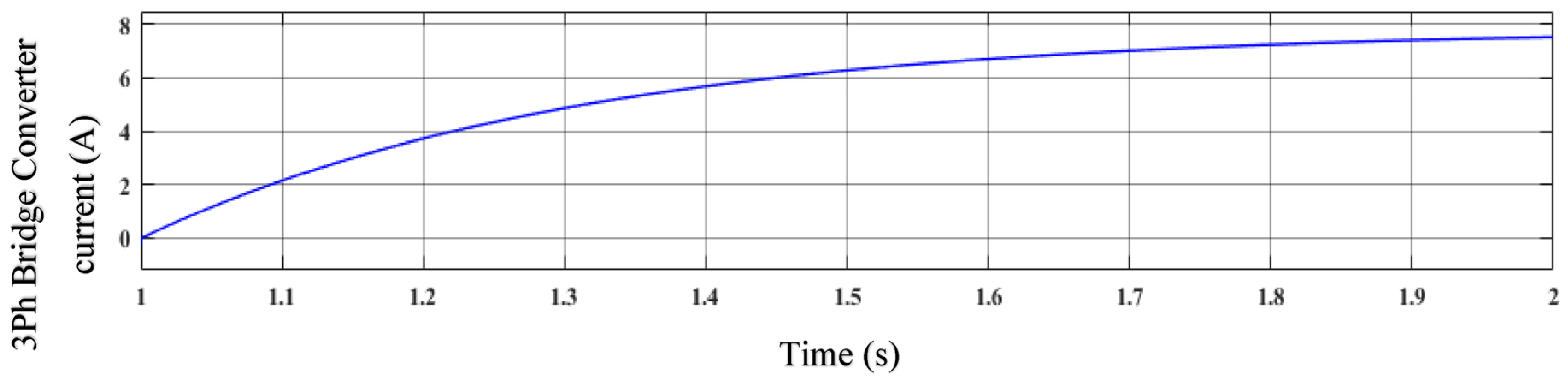

| S. No | Parameters | Values |
|---|---|---|
| (a) | ||
| 1 | Nominal mechanical output power (W) | 1.50 × 106 |
| 2 | Electrical generator’s base power (VA) | 1.5 × 106/0.9 |
| 3 | Base WS (m/s) | 12 |
| 4 | Maximum power at base WS (p.u. of nominal mechanical power) | 0.73 |
| 5 | Base rotational speed (p.u. of base generator speed) | 1.2 |
| 6 | Pitch angle beta to exhibit WT power characteristics (beta ≥ 0) (deg) | 0 |
| (b) | ||
| 1 | Ldc | 288 Vdc |
| 2 | Rated power | 100 kw |
| 3 | Rated speed | 12,500 rpm |
| 4 | Number of phases | 3 |
| 5 | Back EMF waveform | sinusoidal |
| 6 | Rotor type | salient-pole |
| 7 | Mechanical input | speed w |
| 8 | Preset model | No |
| 9 | Stator phase resistance Rs (ohm) | 0.425 |
| 10 | Inductances | [0.017415845761, 0.029268882377] H |
| 11 | Flux linkage | 0.433 Wb |
| 12 | Pole pairs p | 4 |
| 13 | Initial conditions | [0,0,0,0] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Masoud, U.M.M.; Tiwari, P.; Gupta, N. Designing of an Enhanced Fuzzy Logic Controller of an Interior Permanent Magnet Synchronous Generator under Variable Wind Speed. Sensors 2023, 23, 3628. https://doi.org/10.3390/s23073628
Masoud UMM, Tiwari P, Gupta N. Designing of an Enhanced Fuzzy Logic Controller of an Interior Permanent Magnet Synchronous Generator under Variable Wind Speed. Sensors. 2023; 23(7):3628. https://doi.org/10.3390/s23073628
Chicago/Turabian StyleMasoud, Uossif Mohamed Matoug, Pratibha Tiwari, and Nishu Gupta. 2023. "Designing of an Enhanced Fuzzy Logic Controller of an Interior Permanent Magnet Synchronous Generator under Variable Wind Speed" Sensors 23, no. 7: 3628. https://doi.org/10.3390/s23073628







