Buck Converter with Cubic Static Conversion Ratio †
Abstract
:1. Introduction
- The dc analysis for the ideal converter, together with the semiconductor stresses and ripples calculation;
- The expression of the duty cycle for which a conversion from a given input voltage Vg to a desired output voltage Vo is achieved;
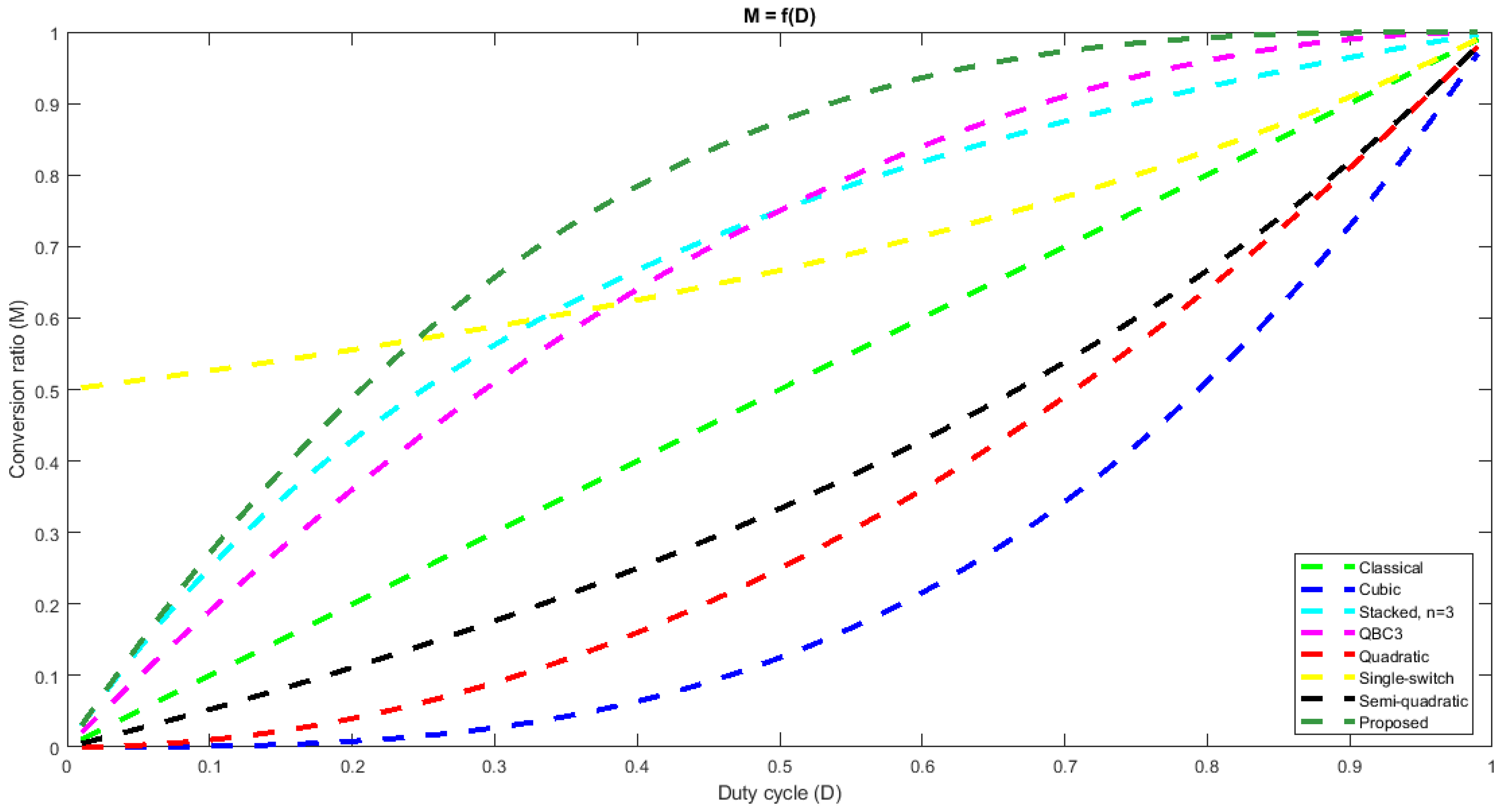
- A comprehensive comparison of the proposed converter with other buck-type topologies, revealing superior features, at least compared to the cubic topologies;
- The continuous conduction mode (CCM) operation conditions for a proper design of the inductors;
- The analysis of the non-ideal converter in the presence of conduction losses with the help of the state-space matrices. The abovementioned, together with the design equations, can be found in Section 2;
- A simulation for validating the theoretical operation of the ideal converter, as well as the experimental results on a 12 V–10 W prototype all confirm the feasibility of the proposed topology. These aspects are presented in Section 3;
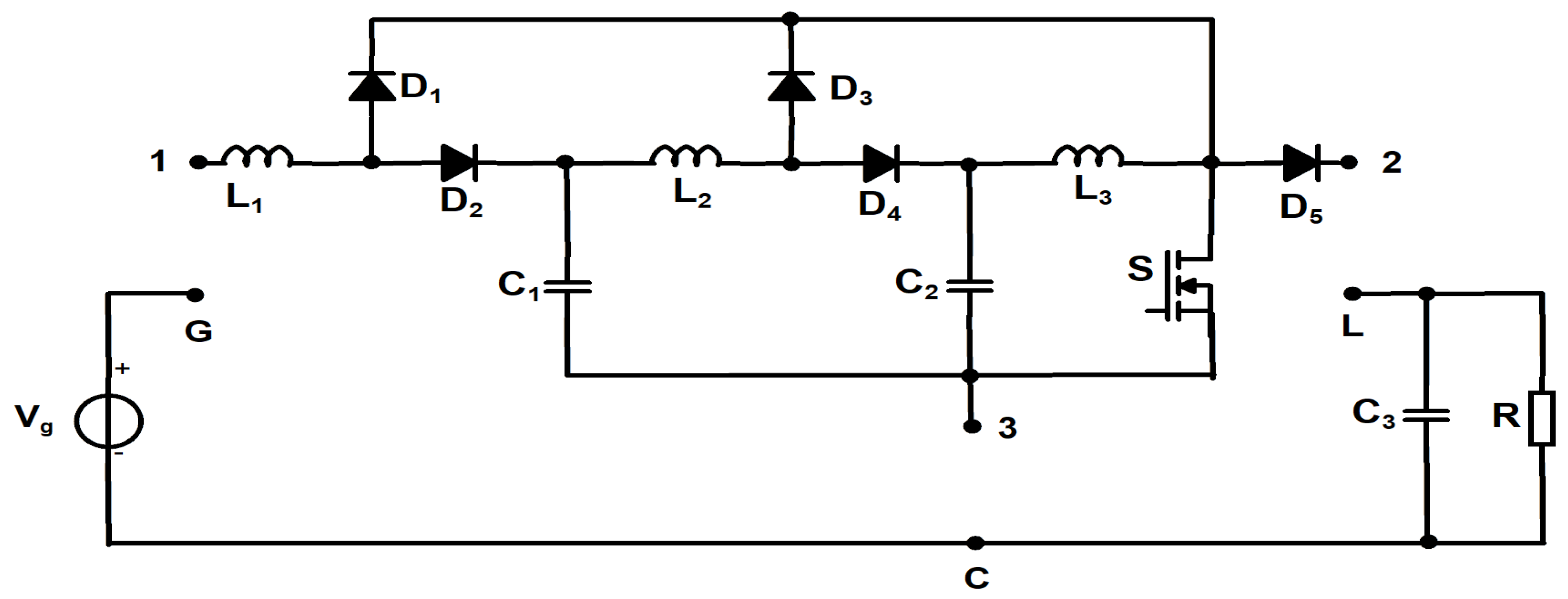
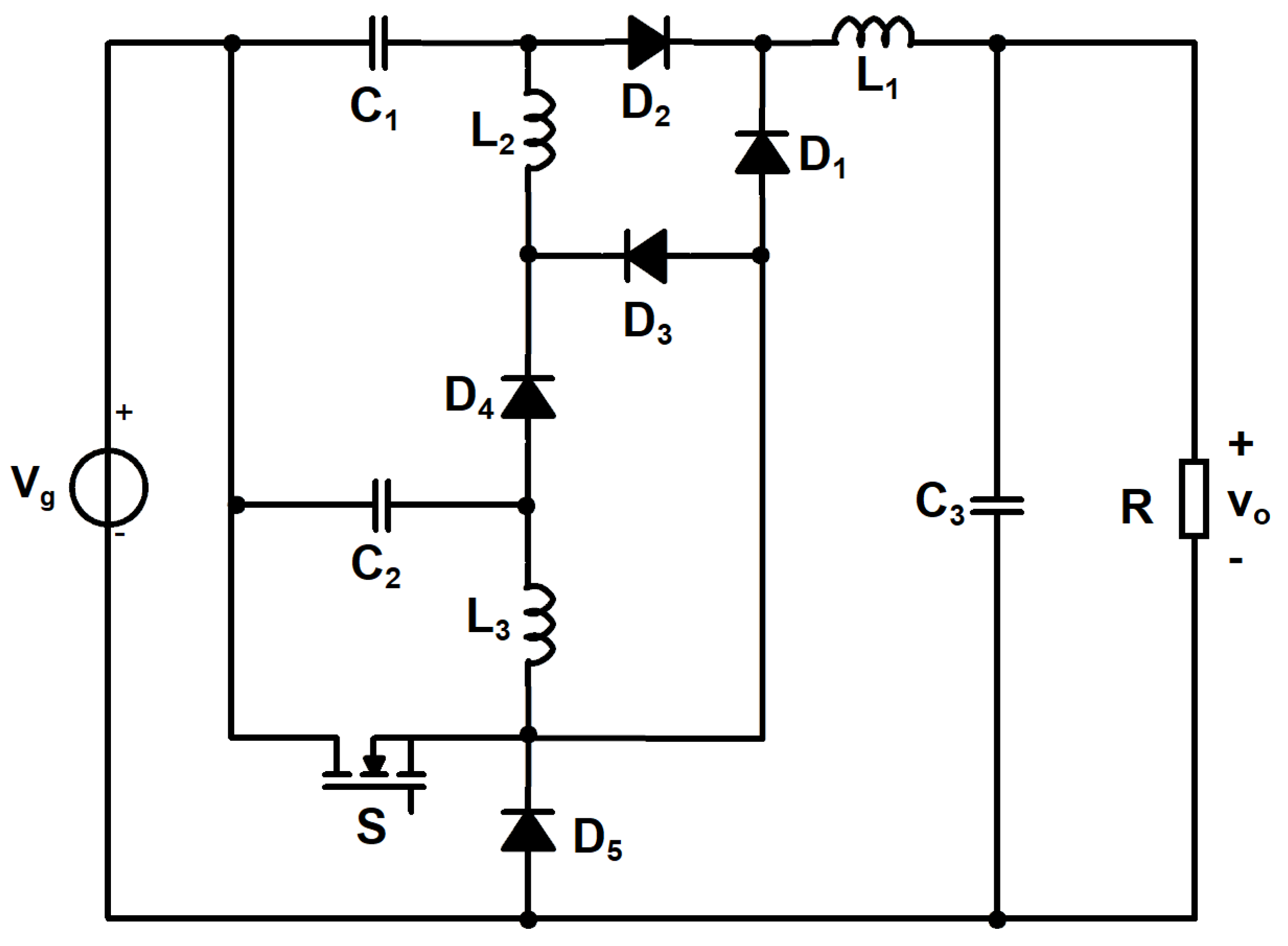
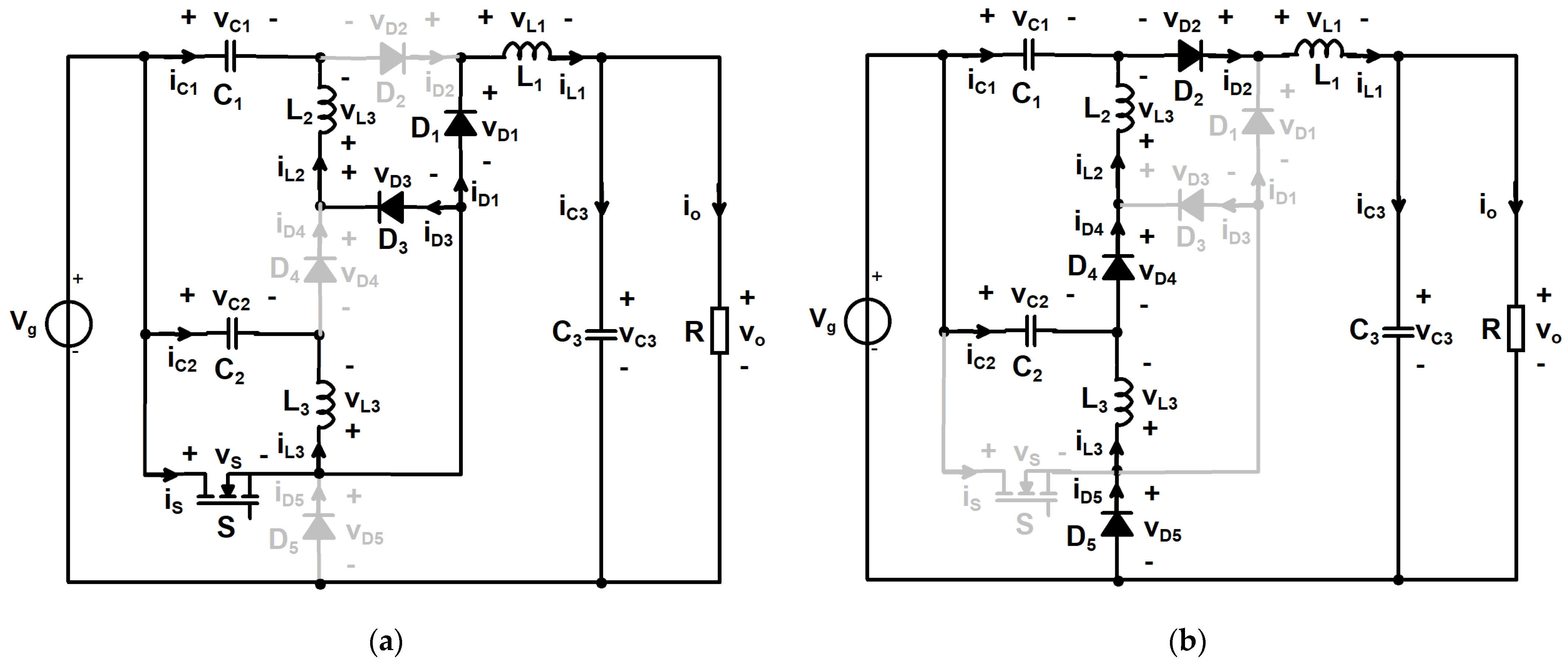
2. Materials and Methods
- Input voltage: Vg = 15 V;
- Output voltage: Vo = 12 V;
- Output power: Po = 10 W;
- Switching frequency: fs = 100 kHz.
3. Results
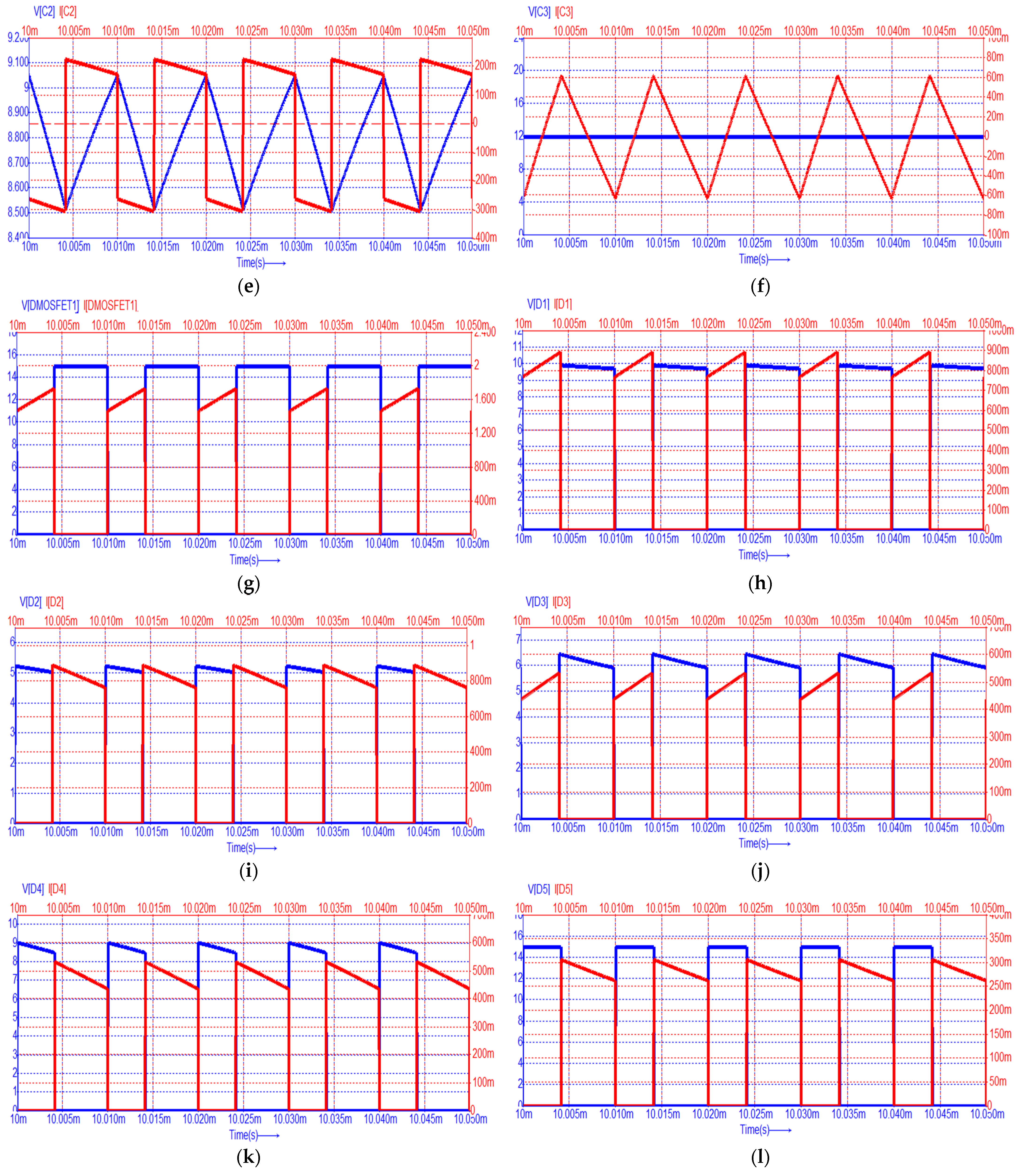
3.1. Simulation Results
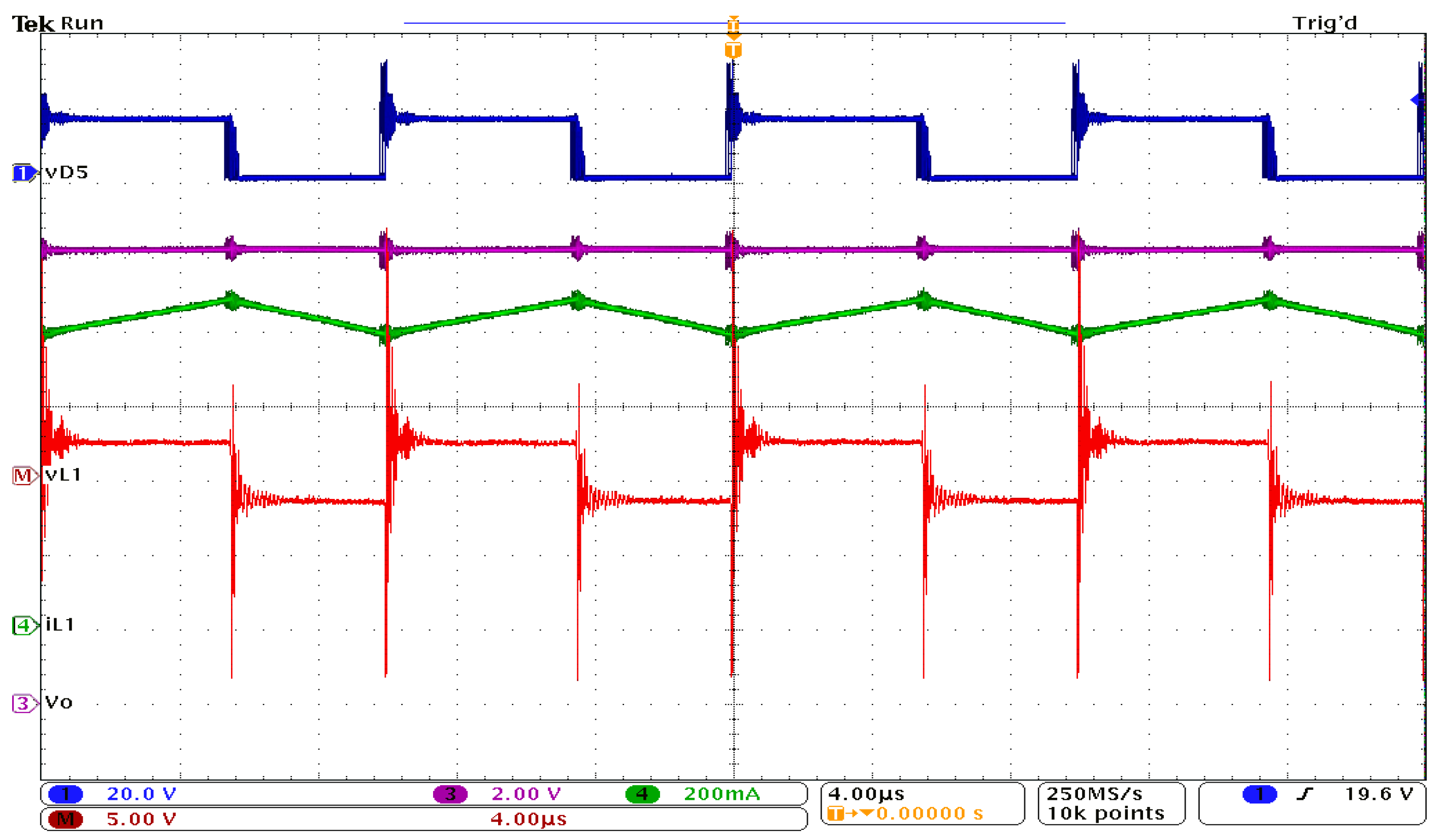
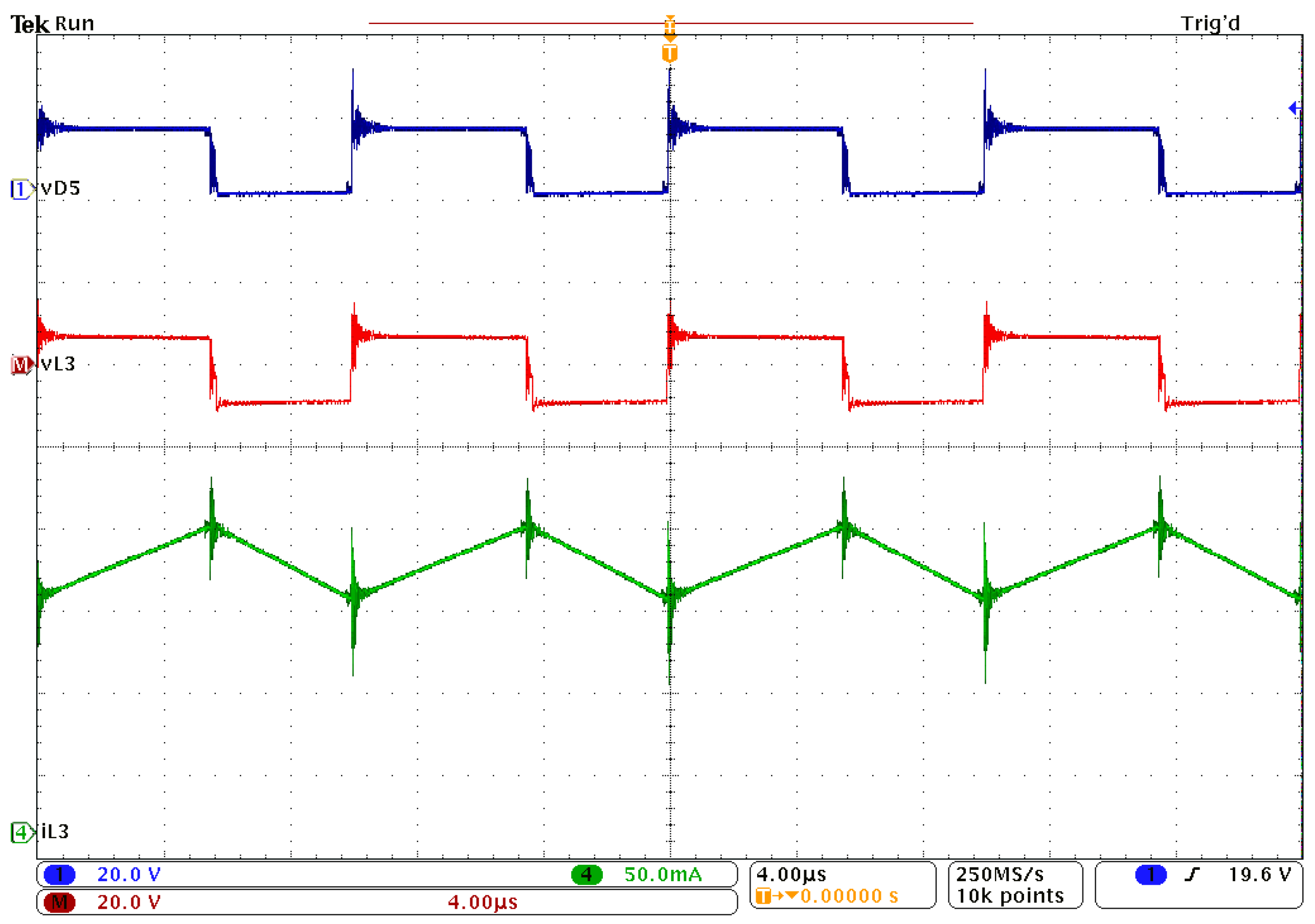
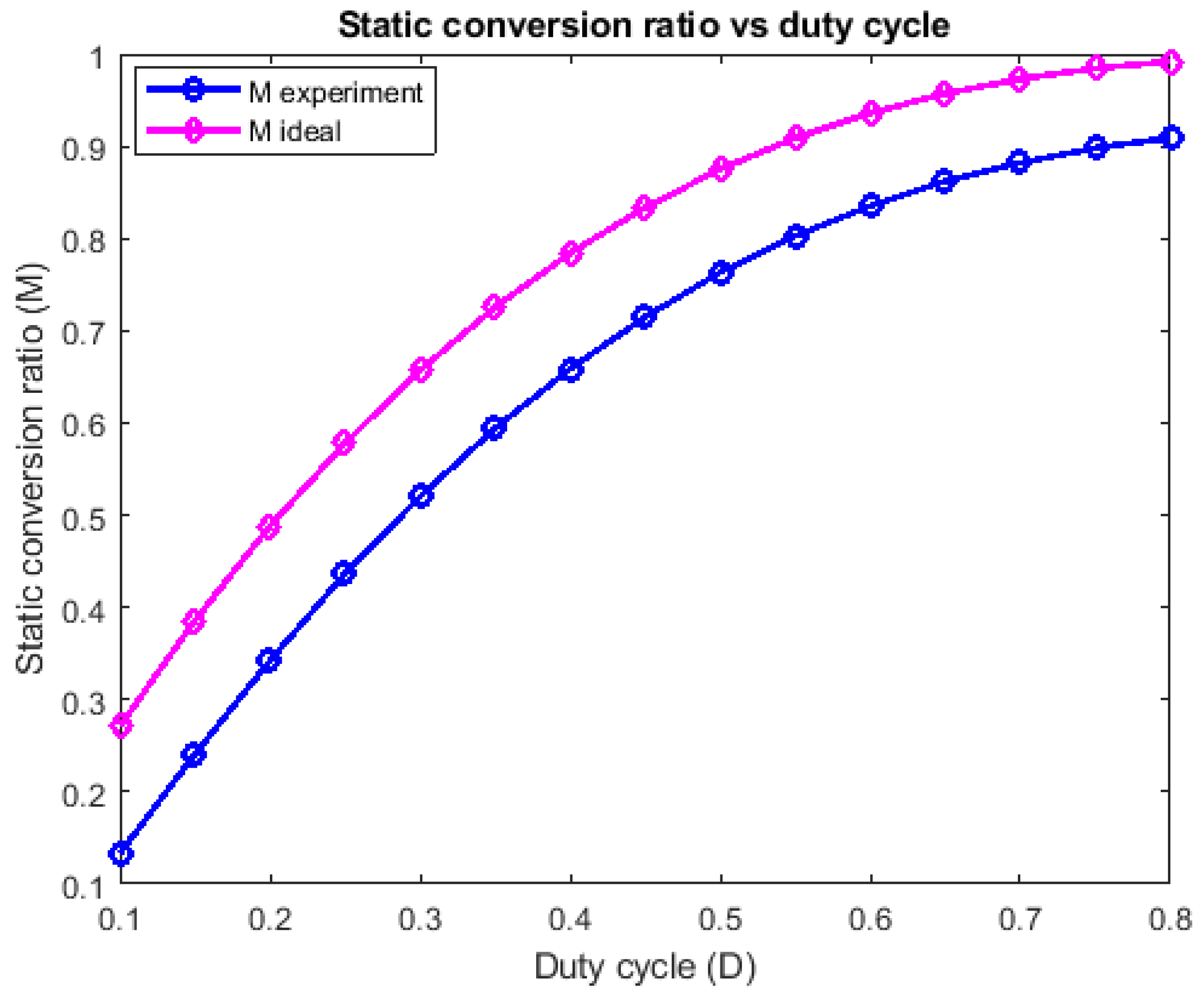
3.2. Experimental Results
- Case 1: different values of the duty cycle and constant output resistor value;
- Case 2: different resistor values while keeping a constant output voltage.
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Erickson, R.W.; Maksimovic, D. Fundamentals of Power Electronics, 2nd ed.; Springer: New York, NY, USA, 2012. [Google Scholar]
- Nayak, G.; Nath, S. Voltage Mode Control of Magnetically Coupled SIDO Buck Converter. In Proceedings of the 2018 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Chennai, India, 18–21 December 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Rehman, H.U. Modified Switched-Inductor Based DC-DC Buck-Boost Converter for Low-Power Applications. In Proceedings of the IECON 2021—47th Annual Conference of the IEEE Industrial Electronics Society, Toronto, ON, Canada, 13–16 October 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Serra, F.M.; Magaldi, G.L.; Gil-González, W.; Montoya, O. Passivity–Based PI Controller of a Buck Converter for Output Voltage Regulation. In Proceedings of the 2020 IEEE ANDESCON, Quito, Ecuador, 13–16 October 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Zhou, X.; Su, D.; Ma, Y.; Pan, J. Research on Auto Disturbance Rejection Control Strategy of Battery Energy Storage Staggered Parallel Buck Converter. In Proceedings of the 2021 IEEE International Conference on Mechatronics and Automation (ICMA), Takamatsu, Japan, 8–11 August 2021; pp. 414–419. [Google Scholar] [CrossRef]
- Li, Z.; Xue, Z.; Liang, C.; Zhang, Y.; Duan, M.; Zhao, S.; Liu, X.; Guo, Z.; Geng, L. A Single-input Dual-output Three-level Buck Converter for SoC Applications. In Proceedings of the 2022 IEEE International Conference on Integrated Circuits, Technologies and Applications (ICTA), Xi’an, China, 28–30 October 2022; pp. 127–128. [Google Scholar] [CrossRef]
- Tsang, H.K.T.; Fong, Y.C.; Kan, K.L.J.; Raman, S.R.; Cheng, K.W.E. A Study of LLC Converter with Buck Converter for CC-CV Charging. In Proceedings of the 2020 8th International Conference on Power Electronics Systems and Applications (PESA), Hong Kong, China, 7–10 December 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Liu, Y.; Kumar, A.; Maksimovic, D.; Afridi, K.K. A High-Power-Density High-Efficiency Three-Level Buck Converter for Cellphone Battery Charging Applications. In Proceedings of the 2018 IEEE Energy Conversion Congress and Exposition (ECCE), Portland, OR, USA, 23–27 September 2018; pp. 5265–5270. [Google Scholar] [CrossRef]
- El Kattel, M.B.; Mayer, R.; Possamai, M.D.; Oliveira, S.V.G. A Simplified Analysis of Buck-Type Interleaved DC-DC Converter for Battery Chargers Application. In Proceedings of the 2019 IEEE 15th Brazilian Power Electronics Conference and 5th IEEE Southern Power Electronics Conference (COBEP/SPEC), Santos, Brazil, 1–4 December 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Zanatta, N.; Caldognetto, T.; Biadene, D.; Spiazzi, G.; Mattavelli, P. A Two-Stage Twin-Bus Buck Converter for Battery Charging Applications. In Proceedings of the 2023 IEEE Applied Power Electronics Conference and Exposition (APEC), Orlando, FL, USA, 19–23 March 2023; pp. 1908–1914. [Google Scholar] [CrossRef]
- Hossain, M.K.; Islam, M.R. Power Stage Design of a Synchronous Buck Converter for Battery Charger Application. In Proceedings of the 2018 International Conference on Advancement in Electrical and Electronic Engineering (ICAEEE), Gazipur, Bangladesh, 22–24 November 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Sharma, H.; Sharma, M.; Sharma, C.; Haque, A.; Jaffery, Z.A. Performance Analysis of Solar Powered DC-DC Buck Converter for Energy Harvesting IoT Nodes. In Proceedings of the 2018 3rd International Innovative Applications of Computational Intelligence on Power, Energy and Controls with their Impact on Humanity (CIPECH), Ghaziabad, India, 1–2 November 2018; pp. 26–29. [Google Scholar] [CrossRef]
- Talukder, R.; Sridharan, S.; Kapat, S. Performance and Stability Analysis of a Multiphase Buck Converter under Mixed-Signal Current Mode Control for Mobile and Automotive Applications. In Proceedings of the 2022 IEEE 1st Industrial Electronics Society Annual On-Line Conference (ONCON), Kharagpur, India, 9–11 December 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Deekshitha, C.; Shenoy, K.L. Design and simulation of synchronous buck converter for LED application. In Proceedings of the 2017 2nd IEEE International Conference on Recent Trends in Electronics, Information & Communication Technology (RTEICT), Bangalore, India, 19–20 May 2017; pp. 142–146. [Google Scholar] [CrossRef]
- Widjonarko; Rahardi, G.A.; Avian, C.; Hadi, W.; Herdiyanto, D.W.; Satrio, P.L. Driver for LED Lamp with Buck Converter Controlled by PID. In Proceedings of the 2021 International Seminar on Intelligent Technology and Its Applications (ISITIA), Surabaya, Indonesia, 21–22 July 2021; pp. 216–219. [Google Scholar] [CrossRef]
- Raj, A.; Arulgandhi, N.; Patha, L.; Bhaskar, D.V. Fuzzy logic based master-slave controller for paralleling DC-DC converters in LED applications. In Proceedings of the 2018 International Conference on Power Energy, Environment and Intelligent Control (PEEIC), Greater Noida, India, 13–14 April 2018; pp. 676–682. [Google Scholar] [CrossRef]
- MMalik, S.; Khan, H.A.; Zaffar, N.A. Evaluation of a Single Inductor based Single-Input Dual-Output Buck Converter for DC Microgrid Applications. In Proceedings of the 2018 IEEE 7th World Conference on Photovoltaic Energy Conversion (WCPEC) (A Joint Conference of 45th IEEE PVSC, 28th PVSEC & 34th EU PVSEC), Waikoloa, HI, USA, 10–15 June 2018; pp. 0613–0617. [Google Scholar] [CrossRef]
- Altuğ, B.A.; Kababiyik, A.; Dincol, E.; Batunlu, C. Buck Converter with Optocoupler Based Switching. In Proceedings of the 2021 8th International Conference on Electrical and Electronics Engineering (ICEEE), Antalya, Turkey, 9–11 April 2021; pp. 184–190. [Google Scholar] [CrossRef]
- Veerachary, M.; Misal, S. Single-switch Semi-Quadratic Buck Converter. In Proceedings of the 2020 IEEE International Conference on Power Electronics, Smart Grid and Renewable Energy (PESGRE2020), Cochin, India, 2–4 January 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Trakuldit, S.; Tattiwong, K.; Bunlaksananusorn, C. Design and evaluation of a Quadratic Buck Converter. In Proceedings of the 2021 8th International Conference on Power and Energy Systems Engineering (CPESE 2021), Fukuoka, Japan, 10–12 September 2021. [Google Scholar]
- Li, G.; Amirabadi, M.; Chen, X.; Lehman, B. The Methodology of Constructing the Quadratic Converters. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 6586–6606. [Google Scholar] [CrossRef]
- Esam, H. Ismail. Large step-down DC–DC converters with reduced current stress. Energy Convers. Manag. 2009, 50, 232–239. [Google Scholar]
- Uno, M.; Kukita, A. PWM Switched Capacitor Converter with Switched-Capacitor-Inductor Cell for Adjustable High Step-Down Voltage Conversion. IEEE Trans. Power Electron. 2019, 34, 425–437. [Google Scholar] [CrossRef]
- Lica, S.; Lie, I.; Wegner, A.N.; Pop-Călimanu, I.M. A Generalized Model for Single-Switch Stacked Step-Down Converters. In Proceedings of the 2020 International Symposium on Electronics and Telecommunications (ISETC), Timisoara, Romania, 5–6 November 2020; pp. 1–4. [Google Scholar] [CrossRef]
- Palomo, R.L.; Morales-Saldana, J.A.; Hernandez, E.P. Quadratic Step-Down dc-dc Converters Based on Reduced Redundant Power Processing Approach. IET Power Electron. 2013, 6, 136–145. [Google Scholar] [CrossRef]
- Botila, D.-A.; Pop-Calimanu, I.-M.; Lascu, D. A Novel Single Switch Step Down Converter. In Proceedings of the 2021 IEEE 19th International Power Electronics and Motion Control Conference (PEMC), Gliwice, Poland, 25–29 April 2021; pp. 31–38. [Google Scholar] [CrossRef]
- Santos, E.C.D. Dual-output dc–dc buck converters with bidirectional and unidirectional characteristics. IET Power Electron. 2013, 6, 999–1009. [Google Scholar] [CrossRef]
- Chen, G.; Deng, Y.; Dong, J.; Hu, Y.; Jiang, L.; He, X. Integrated Multiple-Output Synchronous Buck Converter for Electric Vehicle Power Supply. IEEE Trans. Veh. Technol. 2017, 66, 5752–5761. [Google Scholar] [CrossRef]
- Yau, Y.T. A Non-Isolated Dual-Output High-Step-Down Converter. In Proceedings of the 2022 IEEE Applied Power Electronics Conference and Exposition (APEC), Houston, TX, USA, 20–24 March 2022; pp. 2029–2033. [Google Scholar] [CrossRef]
- Roh, Y.-S.; Moon, Y.-J.; Park, J.; Jeong, M.-G.; Yoo, C. A Multiphase Synchronous Buck Converter with a Fully Integrated Current Balancing Scheme. IEEE Trans. Power Electron. 2015, 30, 5159–5169. [Google Scholar] [CrossRef]
- Martinez, W.; Imaoka, J.; Itoh, Y.; Yamamoto, M.; Umetani, K. A novel high step-down interleaved converter with coupled inductor. In Proceedings of the 2015 IEEE International Telecommunications Energy Conference (INTELEC), Osaka, Japan, 18–22 October 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Montazerolghaem, R.; Adib, E.; Semiromizadeh, J.; Wheeler, P. Zero-Voltage-Switching High-Step-Down Buck Converter with Continuous Output Current. IEEE Trans. Power Electron. 2023, 38, 12886–12894. [Google Scholar] [CrossRef]
- Hafez, A.A.A. Multi-level cascaded DC/DC converters for PV applications. Alex. Eng. J. 2015, 54, 1135–1146. [Google Scholar] [CrossRef]
- Nejad, M.L.; Esteki, M.; Heidari, R.; Adib, E. An Improved Cascade Buck Converter for High Step-Down DC-DC Applications. IEEE J. Emerg. Sel. Top. Ind. Electron. 2022, 3, 626–634. [Google Scholar] [CrossRef]
- Nayanasiri, D.; Li, Y. Step-Down DC–DC Converters: An Overview and Outlook. Electronics 2022, 11, 1693. [Google Scholar] [CrossRef]
- Demian, A.E.; Treviso, C.H.G.; Gallo, C.A.; Tofoli, F.L. Non-isolated DC-DC converters with wide conversion range used to drive high-brightness LEDs. In Proceedings of the 2009 Brazilian Power Electronics Conference, Bonito-Mato Grosso do Sul, Brazil, 27 September–1 October 2009; pp. 598–605. [Google Scholar] [CrossRef]
- Botila, D.-A.; Pop-Calimanu, I.-M.; Lascu, D. Cubic Buck-Boost Converter with High Step-Up Capability. In Proceedings of the 2022 International Symposium on Electronics and Telecommunications (ISETC), Timisoara, Romania, 10–11 November 2022; pp. 1–4. [Google Scholar] [CrossRef]
- Ahmad, J.; Pervez, I.; Sarwar, A.; Tariq, M.; Fahad, M.; Chakrabortty, R.K.; Ryan, M.J. Performance Analysis and Hardware-in-the-Loop (HIL) Validation of Single Switch High Voltage Gain DC-DC Converters for MPP Tracking in Solar PV System. IEEE Access 2021, 9, 48811–48830. [Google Scholar] [CrossRef]
- Lascu, D. Controlled Energy Transfer Using PWM and Resonant Converter. Ph.D. Thesis, Politehnica University Timisoara, Timisoara, Romania, 1998. [Google Scholar]
- Simulation Research, Caspoc, User Manual. Available online: https://www.simulationresearch.com (accessed on 1 October 2023).
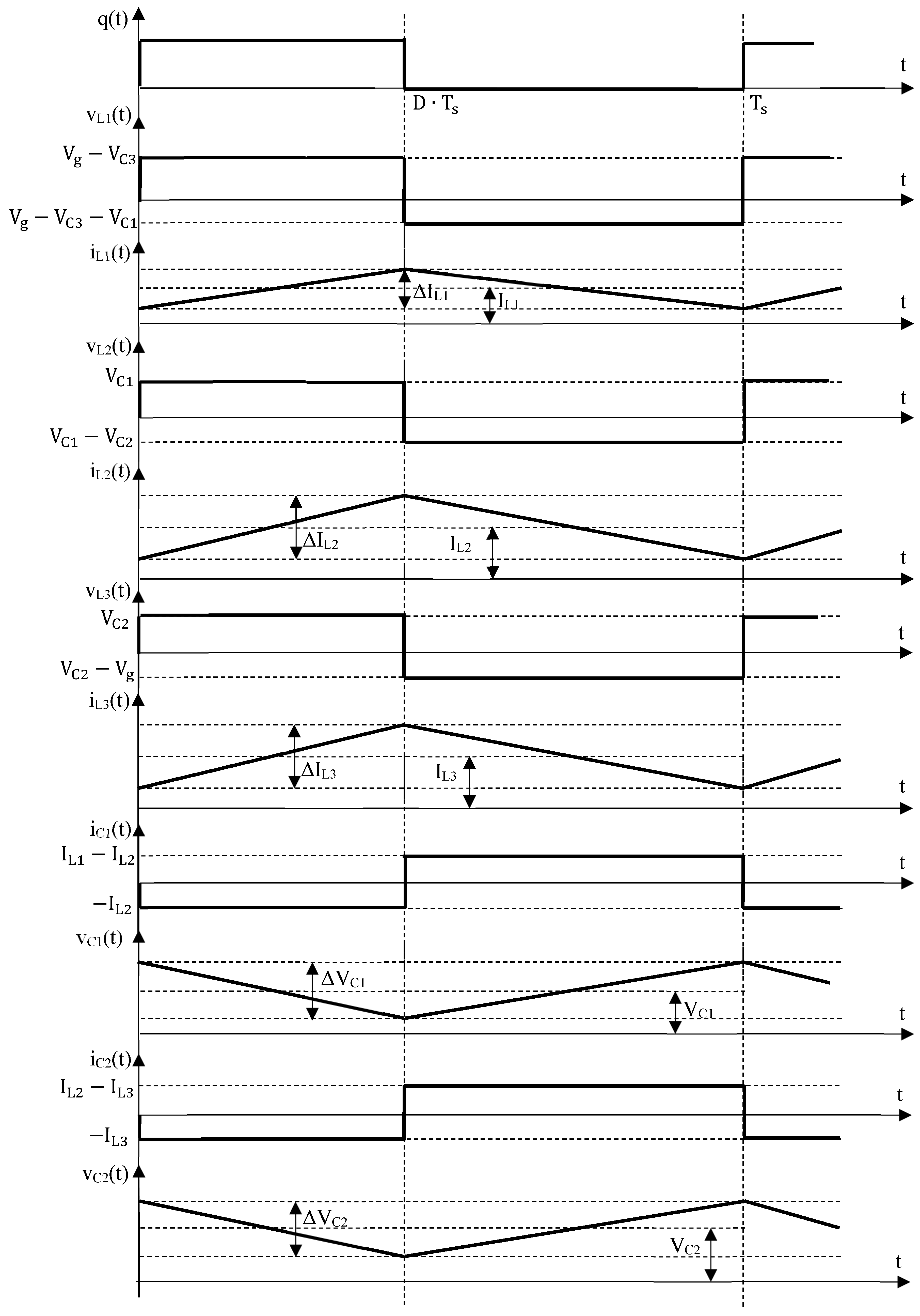
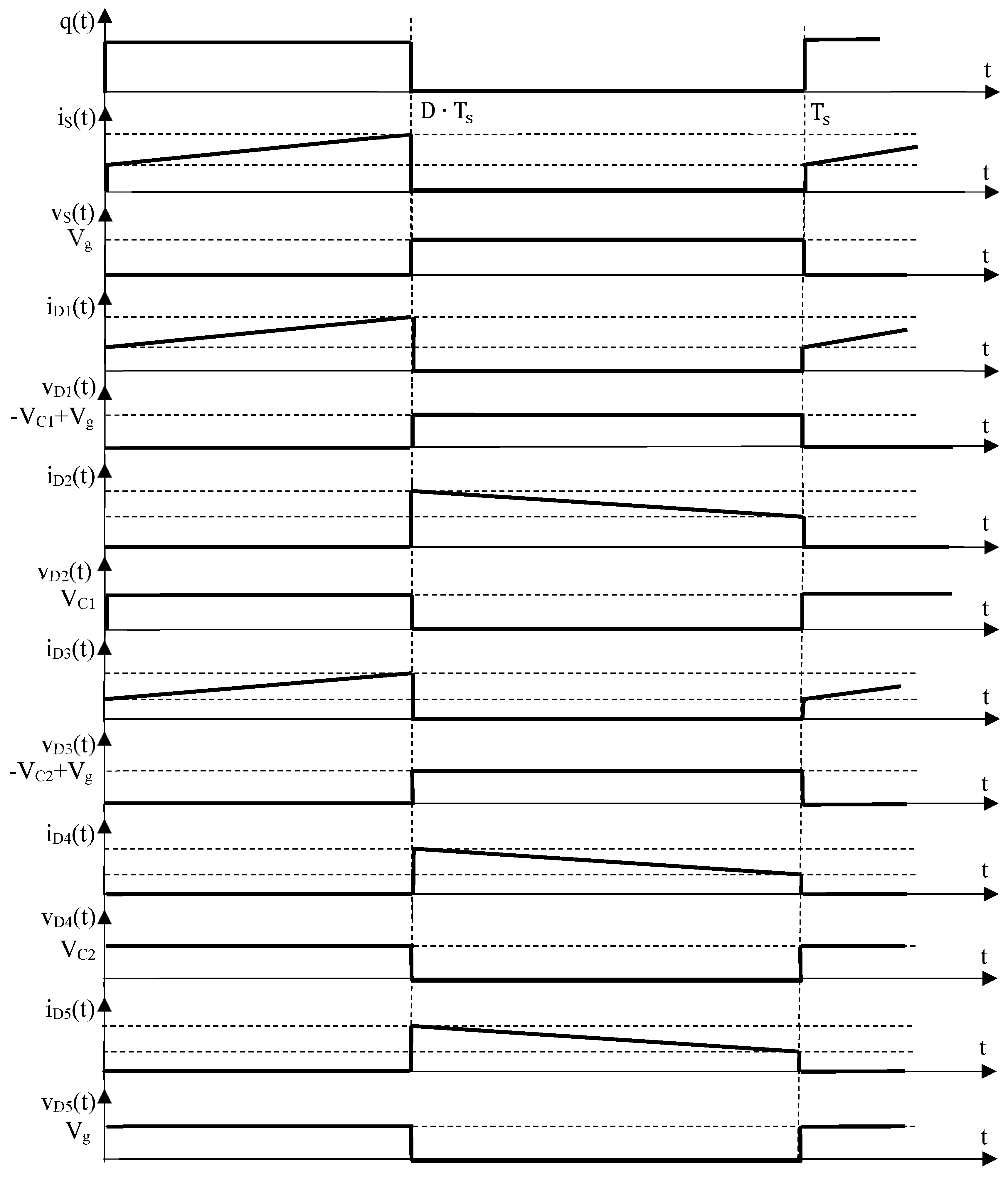
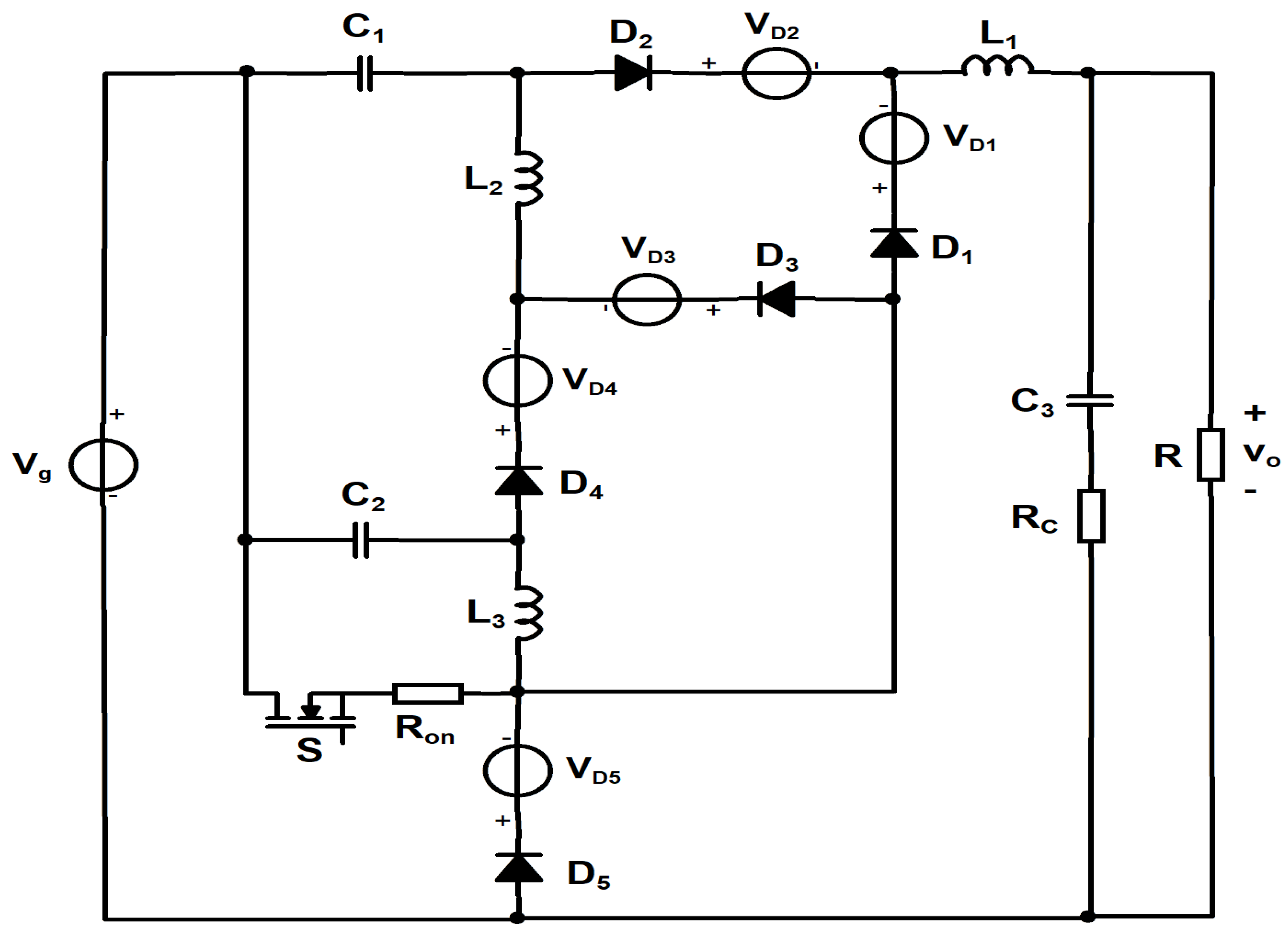
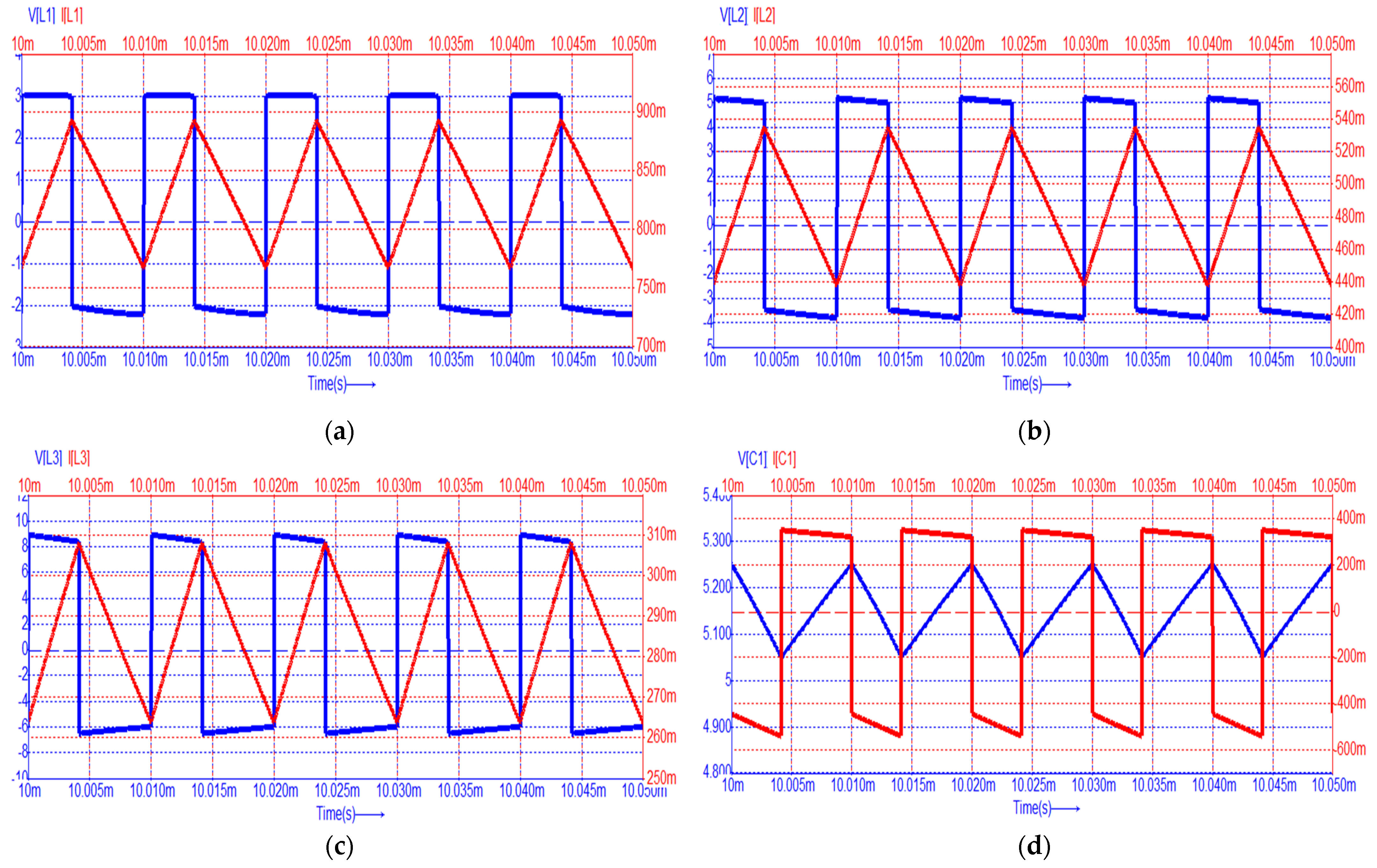


| Parameter | Classical [1] | Cubic [36] | Stacked [24] | QBC3 [25] | Quadratic [20] | Single Switch [26] | Semi-Quadratic [19] | Proposed |
|---|---|---|---|---|---|---|---|---|
| Total no. of components | 4 | 13 | 12 | 8 | 9 | 8 | 11 | 13 |
| No. of transistors | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| No. of diodes | 1 | 5 | 3 | 3 | 3 | 2 | 4 | 5 |
| System order | 2 | 6 | 8 | 4 | 4 | 5 | 5 | 6 |
| Static Conversion Ratio (M) | ||||||||
| Transistor dc current stress | ||||||||
| Transistor voltage stress | ||||||||
| Maximum diode dc current stress | ||||||||
| Maximum diode voltage stress |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Botila, D.-A.; Pop-Calimanu, I.-M.; Lascu, D. Buck Converter with Cubic Static Conversion Ratio. Sensors 2024, 24, 696. https://doi.org/10.3390/s24020696
Botila D-A, Pop-Calimanu I-M, Lascu D. Buck Converter with Cubic Static Conversion Ratio. Sensors. 2024; 24(2):696. https://doi.org/10.3390/s24020696
Chicago/Turabian StyleBotila, Delia-Anca, Ioana-Monica Pop-Calimanu, and Dan Lascu. 2024. "Buck Converter with Cubic Static Conversion Ratio" Sensors 24, no. 2: 696. https://doi.org/10.3390/s24020696
APA StyleBotila, D.-A., Pop-Calimanu, I.-M., & Lascu, D. (2024). Buck Converter with Cubic Static Conversion Ratio. Sensors, 24(2), 696. https://doi.org/10.3390/s24020696







