Experimental Investigation of Pore Pressure on Sandy Seabed around Submarine Pipeline under Irregular Wave Loading
Abstract
:1. Introduction
2. Laboratory Experiment
2.1. Experimental Facility
2.2. Experimental Soil Property Parameter
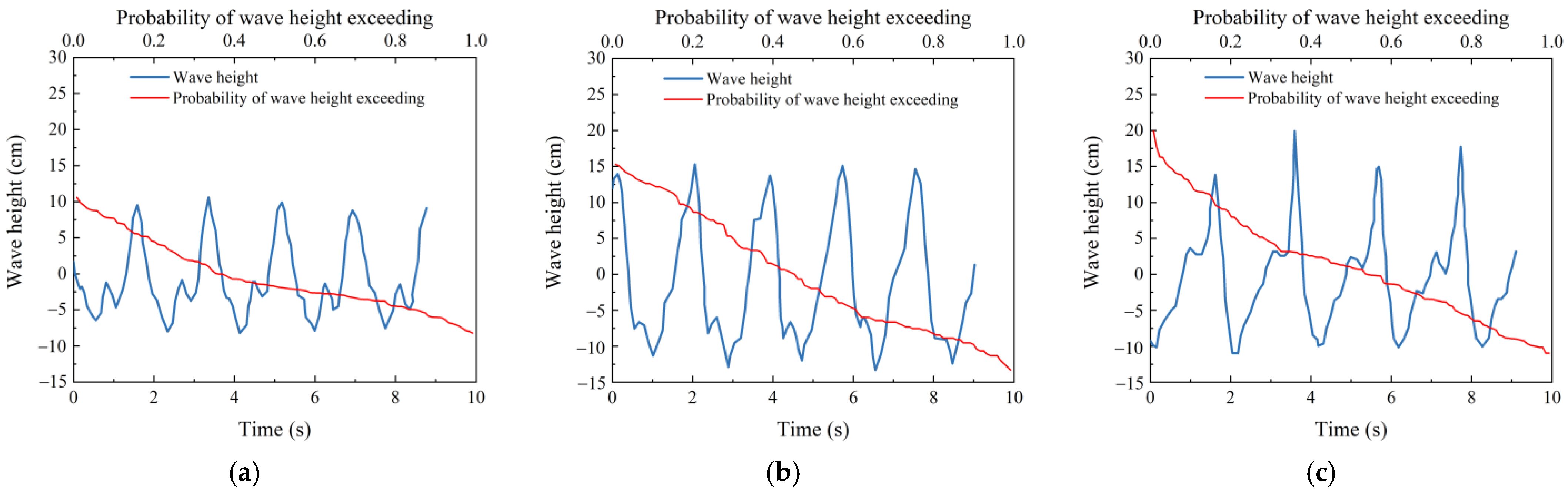
2.3. Experimental Wave Parameter
2.4. Experimental Process
- Before conducting the wave tests, corresponding spectrum tests were performed to obtain the anticipated control signals for the wave generator. Based on the collected wave spectrum, the wave maker was calibrated. According to statistical data and spectral shape, the wave series was determined.
- To ensure accurate results, it was crucial to control the saturation of soil samples when studying the seabed. Since the seabed was already assumed to be saturated, proper sample preparation was necessary. We used the underwater sand loading method to prepare the samples, which guaranteed full saturation.
- To install soil samples in the seabed area of the test section, we followed the steps given below. First, we opened the inlet valve and adjusted it until the water level was slightly below the surface of the model seabed. Next, we installed the pre-soaked soil samples. After that, we placed the pipeline on top of the sand samples at a predefined distance of approximately 10 cm from the seabed surface. We filled the samples continuously until the height was slightly above the top surface of the model seabed, and then, smoothed the bed surface. We let the samples consolidate for 24 h under the influence of self-weight, and added water continuously to the predetermined depth.
- Before measurement, all air within the pressure sensors was purged to ensure test accuracy. The pressure sensors were then connected to a computer to verify proper functioning. Before starting the wave-making process, the pore pressure sensor data was reset to zero under still water conditions after it stabilized.
- During the spectrum collection process, control signals were obtained for the wave generator, which were then used to conduct wave tests.
- The values of excess pore-water pressure were collected every 0.02 s, with a total acquisition time of 200 s.
- The test conditions (as shown in Table 3) were restored to their original settings, and the next set of tests was performed.
3. Experimental Results and Discussions
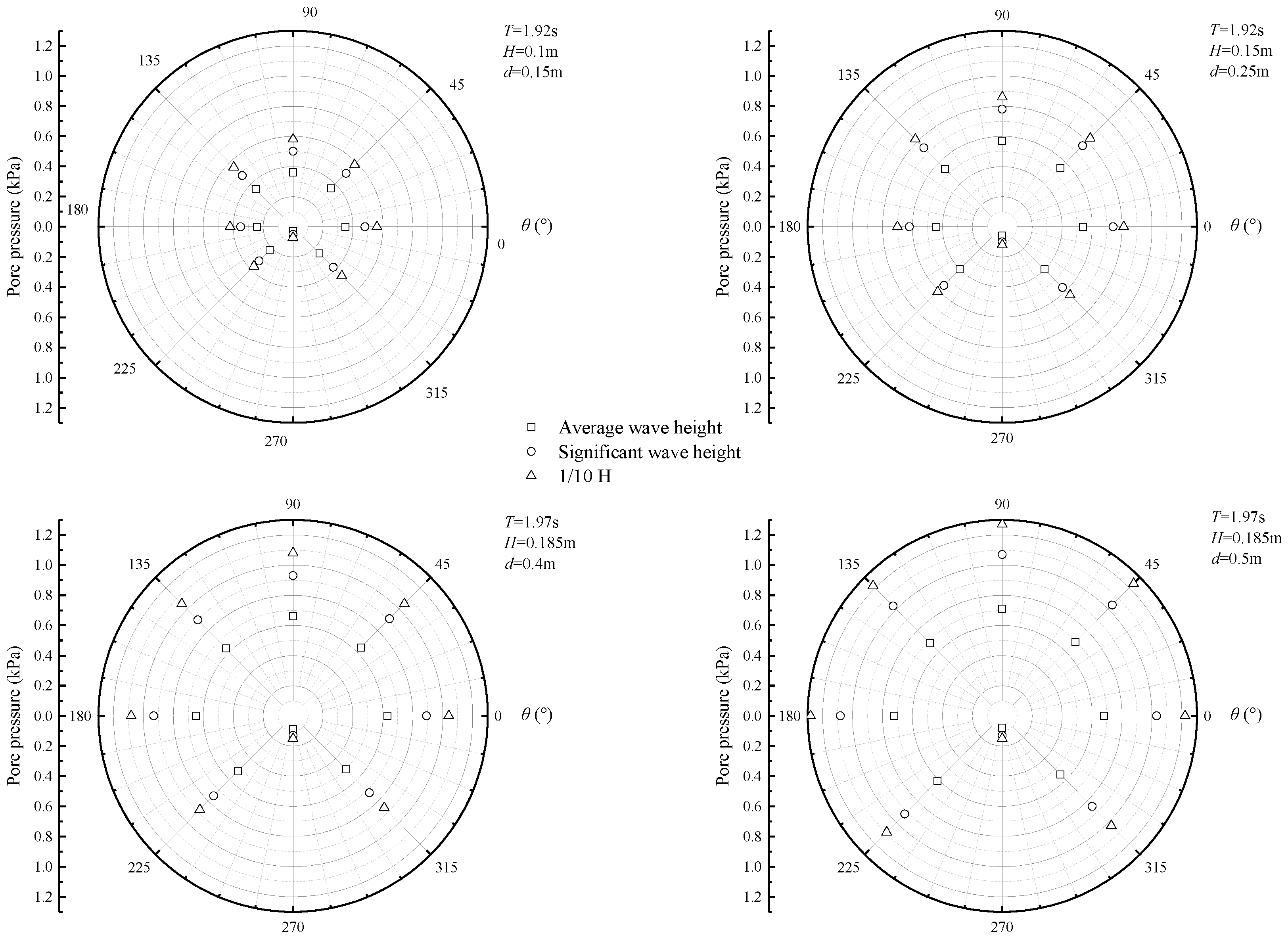
3.1. Excess Pore Pressure Distribution around Pipeline
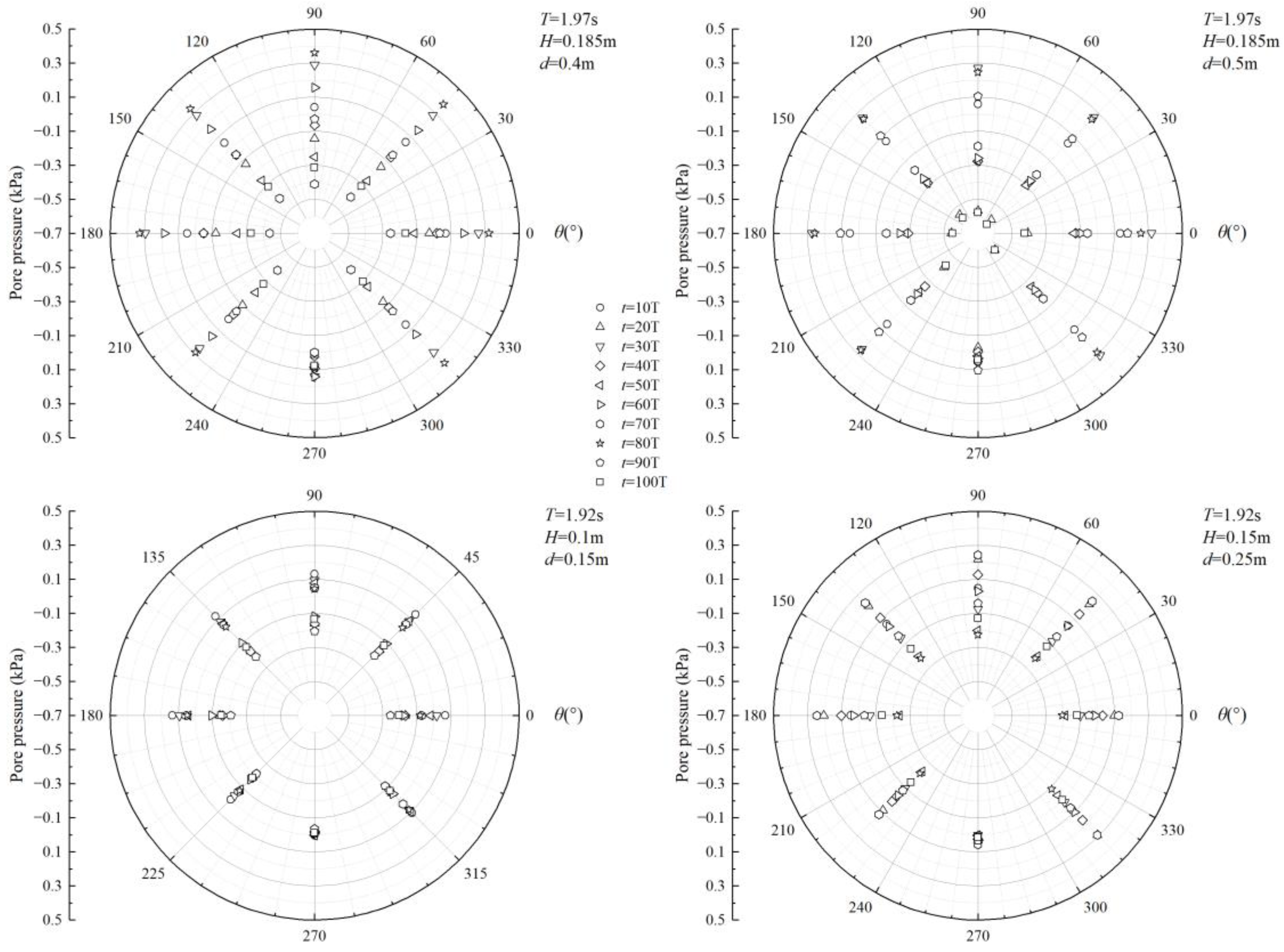
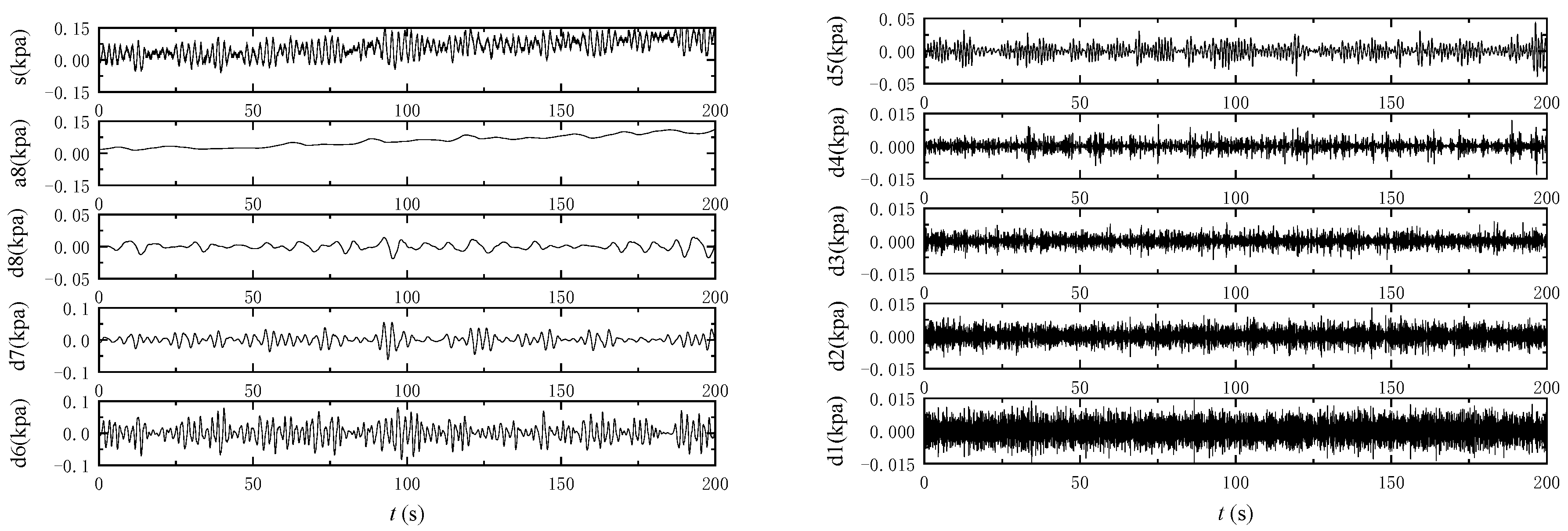
3.2. Type Analysis of Excess Pore Pressure Response around the Pipeline
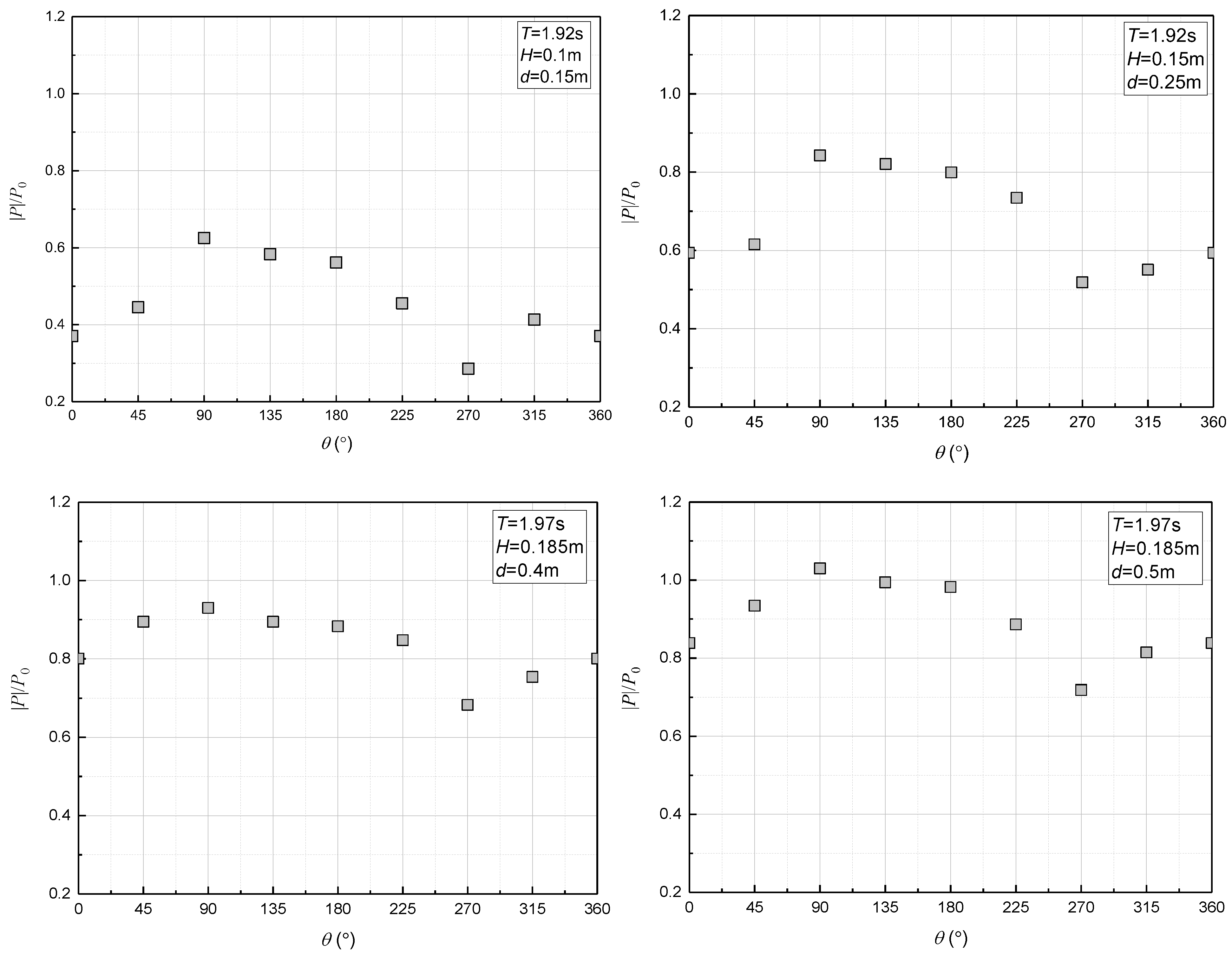
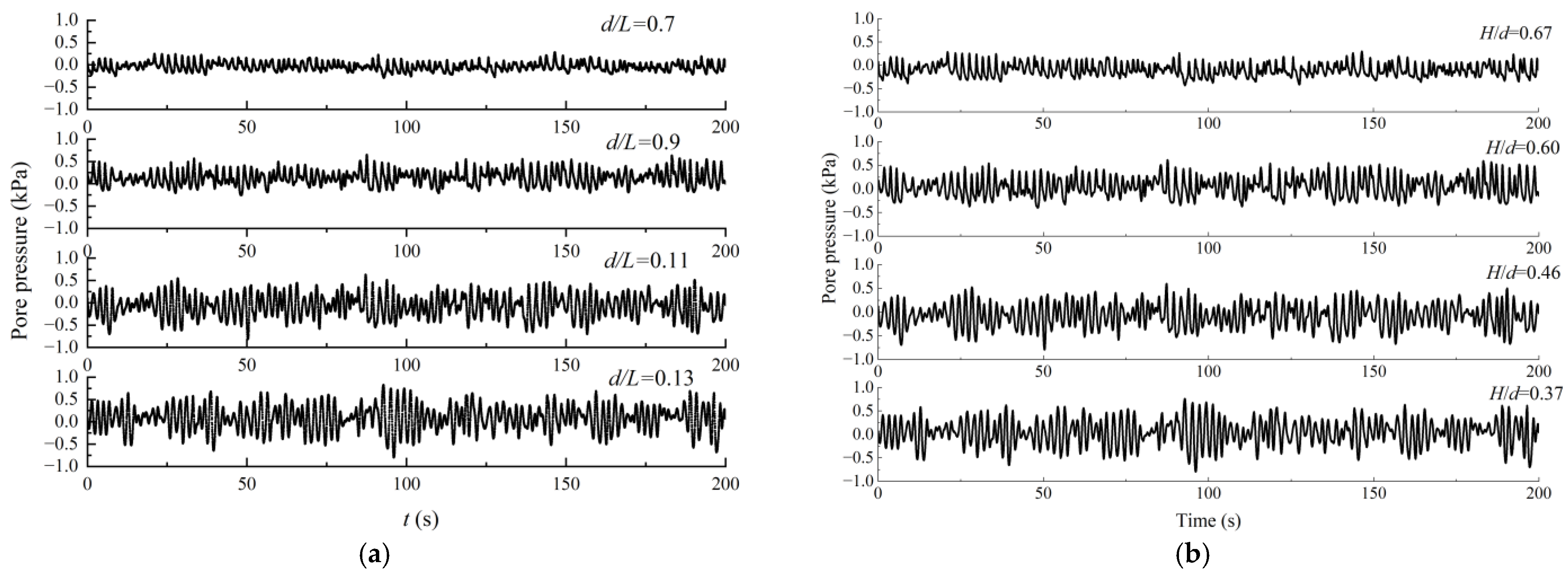
3.3. Effect of Relative Water Depth and Relative Wave Height
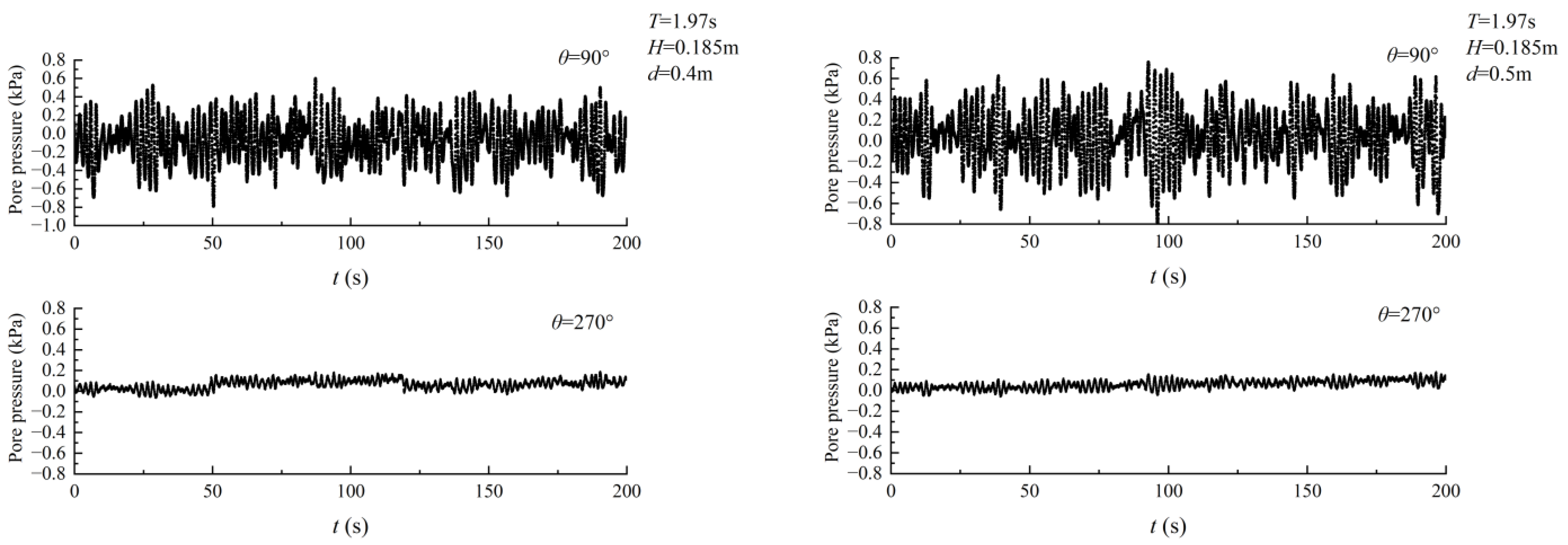
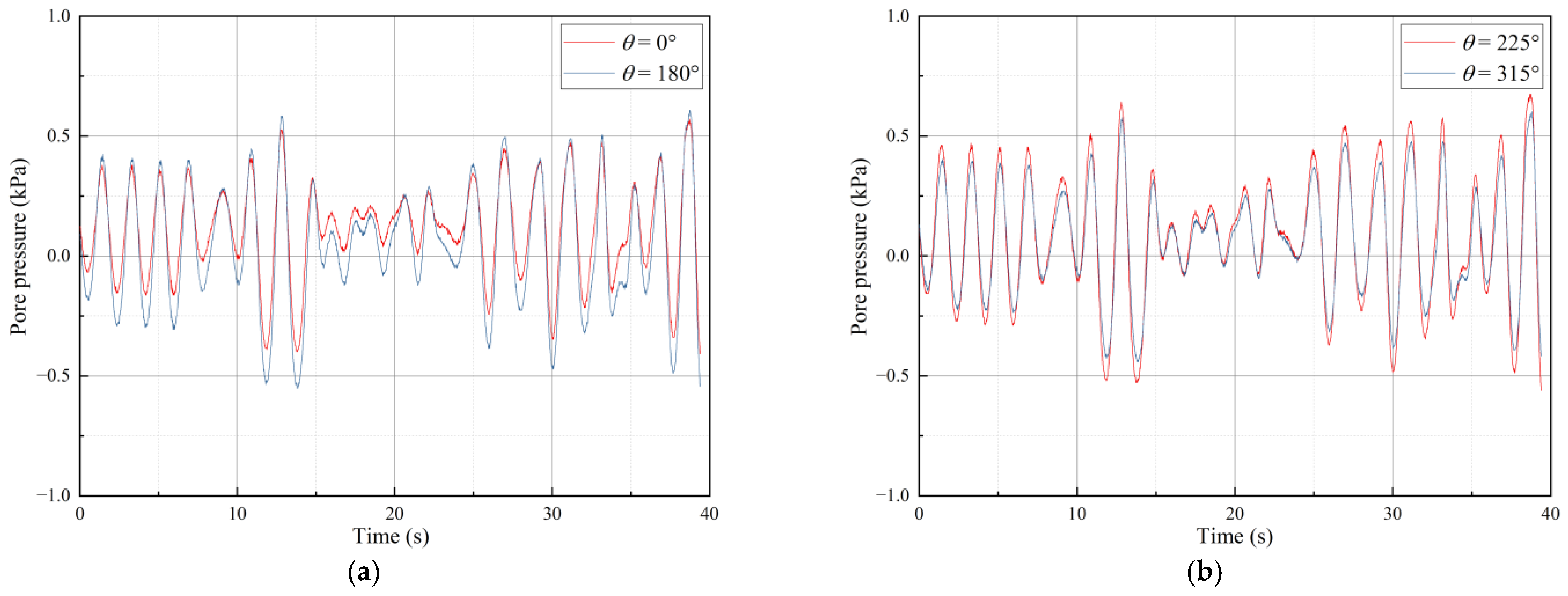
3.4. Effect of Vertical Depths and Horizontal Distances
4. Conclusions
- The excess pore pressure induced by irregular waves exhibited significant fluctuations, with noticeable irregularity in its amplitude. This variation was markedly distinct from the changes in excess pore pressure observed under the influence of regular waves on the sandy seabed.
- The response of excess pore-water pressure induced by irregular waves around the pipeline was primarily oscillatory. Nonetheless, in addition to the oscillatory response, there was also a phenomenon of excess pore pressure accumulation at the bottom of the pipeline.
- The excess pore pressure generated by irregular waves surrounding the pipeline exhibited a sinusoidal distribution. After analyzing the excess pore pressure data measured at eight measuring points, it was found that the greatest dynamic excess pore pressure was recorded at the cylinder’s apex, with the lowest pressure detected at the base.
- The excess pore pressure was significantly affected by the relative water depth (d/L) and the relative wave height (H/d). As the relative water depth (d/L) increased, the excess pore pressure increased noticeably. Similarly, as the relative wave height (H/d) decreased, the excess pore pressure also increased considerably.
- The excess pore-water pressure gradually increased with the increase in water depth under the same wave height (H) and period (T). In addition, this effect was the result of wave–seabed–structure coupling. The fluctuation of the excess pore pressure around the pipeline was significantly influenced by the permeability of the seabed soil, but it was also influenced by its own location. On the upper half of the seabed, the pressure fluctuations caused by waves were significant, while on the lower half, the amplitude remained relatively stable.
- Previous studies have generally assumed that a sandy seabed is less prone to the accumulation of excess pore pressure. However, in this experiment, it was found that the accumulation of excess pore pressure around the pipeline, especially at the bottom, may result in the instability of the pipeline. Therefore, in practical engineering, the potential instability of pipelines caused by the accumulation of excess pore pressure in seabed soil needs to be taken into consideration.
- As a limitation of this study, the authors overlooked the influence of reflected waves on the experimental results. In the experiments, the efficiency of the absorbing slope had a significant impact on the test results. In future research, the author will further slow down the slope ratio of the absorbing slope at the end of the flume to further reduce the impact of reflected waves and their accumulation on the experimental results to improve their accuracy.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Leng, J.; Ye, G.; Liao, C.; Jeng, D. On the soil response of a coastal sandy slope subjected to tsunami-like solitary wave. Bull. Eng. Geol. Environ. 2018, 77, 999–1014. [Google Scholar] [CrossRef]
- Biot, M.A. General theory of three-dimensional consolidation. J. Appl. Phys. 1941, 12, 155–164. [Google Scholar] [CrossRef]
- Zhou, X.L.; Xu, B.; Wang, J.H.; Li, Y.L. An analytical solution for wave-induced seabed response in a multi-layered poroelastic seabed. Ocean Eng. 2011, 38, 119–129. [Google Scholar] [CrossRef]
- Jeng, D.S.; Wang, X.; Tsai, C.C. Meshless model for wave-induced oscillatory seabed response around a submerged breakwater due to regular and irregular wave loading. J. Mar. Sci. Eng. 2020, 9, 15. [Google Scholar] [CrossRef]
- Zhou, X.L.; Jeng, D.S.; Yan, Y.G.; Wang, J.H. wave-induced multi-layered seabed response around a buried pipeline. Ocean Eng. 2013, 72, 195–208. [Google Scholar] [CrossRef]
- Zhao, H.Y.; Jeng, D.S.; Liao, C.C.; Zhang, J.S.; Guo, Z.; Chen, W.Y. Numerical modelling of liquefaction in loose sand deposits subjected to ocean waves. Appl. Ocean Res. 2018, 73, 27–41. [Google Scholar] [CrossRef]
- Jeng, D.S. Numerical modelling for wave-seabed-pipe interaction in a non-homogeneous porous seabed. Soil Dyn. Earthq. Eng. 2001, 21, 669–712. [Google Scholar] [CrossRef]
- Chen, W.Y.; Chen, G.X.; Chen, W.; Chen, C.L.; Hong, M.G. Numerical simulation of the nonlinear wave-induced dynamic response of anisotropic poro-elastoplastic seabed. Mar. Georesour. Geotechnol. 2019, 37, 924–935. [Google Scholar] [CrossRef]
- Yang, G.; Ye, J. Wave & current-induced progressive liquefaction in loosely deposited seabed. Ocean Eng. 2017, 142, 303–314. [Google Scholar] [CrossRef]
- Peng, X.Y.; Zhang, L.L.; Jeng, D.S.; Chen, L.H.; Liao, C.C.; Yang, H.Q. Effects of cross-correlated multiple spatially random soil properties on wave-induced oscillatory seabed response. Appl. Ocean Res. 2017, 62, 57–69. [Google Scholar] [CrossRef]
- Zen, K.; Yamazaki, H. Oscillatory pore pressure and liquefaction in seabed induced by ocean waves. Soils Found. 1990, 30, 147–161. [Google Scholar] [CrossRef]
- Liu, B.; Jeng, D.S.; Ye, G.L.; Yang, B. Laboratory study for pore pressure in sandy deposit under wave loading. Ocean Eng. 2015, 106, 207–219. [Google Scholar] [CrossRef]
- Zhu, J.F.; Zhao, H.Y.; Jeng, D.S. Effects of principal stress rotation on wave-induced soil response in a poro-elastoplastic sandy seabed. Acta Geotech. 2019, 14, 1717–1739. [Google Scholar] [CrossRef]
- Sudhan, C.M.; Sundar, V.; Rao, S.N. Wave induced forces around buried pipeline. Ocean Eng. 2002, 29, 533–544. [Google Scholar] [CrossRef]
- Teh, T.C.; Palmer, A.C.; Damgaard, J.S. Experimental study of marine pipelines on unstable and liquefied seabed. Coast. Eng. 2003, 50, 1–17. [Google Scholar] [CrossRef]
- Zhai, Y.Y.; He, R.; Zhao, J.L.; Zhang, J.S.; Jeng, D.S. Physical model of wave-induced response around trenched pipeline in sandy seabed. Appl. Ocean Res. 2018, 74, 37–52. [Google Scholar] [CrossRef]
- Miyamoto, J.; Sassa, S.; Sekiguchi, H. Progressive solidification of a liquefied sand layer during continued wave loading. Geotechnique 2004, 54, 617–629. [Google Scholar] [CrossRef]
- Qi, H.; Chen, Z.; Li, Y.; Feng, S.; Chen, H. Wave and current-induced dynamic response in a multilayered poroelastic seabed. Bull. Eng. Geol. Environ. 2020, 79, 11–26. [Google Scholar] [CrossRef]
- Sumer, B.M.; Fredsoe, J.; Christensen, S.; Lind, M.T. Sinking/floatation of pipelines and other objects in liquefied soil under waves. Coast. Eng. 1999, 38, 53–90. [Google Scholar] [CrossRef]
- Hsu, C.; Tsai, C.; Chen, Y. Wave-induced seabed momentary liquefaction in shallow water. Appl. Ocean Res. 2021, 115, 102819. [Google Scholar] [CrossRef]
- Tzang, S.Y. Water Wave-Induced Soil Fluidization in a Cohesionless Fine-Grained Seabed. Ph.D. Dissertation, University of California, Berkeley, CA, USA, 1992. [Google Scholar]
- Quiuqui JP, C.; Tamayo, J.P.; Maghous, S. Closed-form solutions for wave-induced poroelastic response in seabed under dynamic and quasi-static regimes. J. Braz. Soc. Mech. Sci. Eng. 2021, 44, 16. [Google Scholar] [CrossRef]
- Shan, Z.; Zhu, Z.; Wang, D.; Ye, G. Numerical Modeling of the Dynamic Response of an Elastoplastic Seabed under Wave-Current Interactions. J. Ocean Univ. China 2023, 22, 43–52. [Google Scholar] [CrossRef]
- Cheng, Y.Z.; Li, Q.F.; Pan, Y. Experimental study of different breaking waves impact on sandy seabed. Acta Oceanol. Sin. 2014, 5, 130–135. [Google Scholar] [CrossRef]
- Yang, Z.; Jia, Y.; Zhang, L.; Liu, X.; Shan, H. An Experimental Study on Wave-Induced Failure Process in Silty Bottom Bed. Period. Ocean Univ. China 2015, 45, 75–81. [Google Scholar] [CrossRef]
- Jeng, D.S.; Qu, J. 3-D models for wave-induced pore pressure near breakwater heads. Acta Mech. 2010, 215, 85–104. [Google Scholar] [CrossRef]
- Wang, L.Z.; Pan, D.Z.; Pan, C.H.; Hu, J.C. Experimental investigation on wave-induced response of seabed. China Civ. Eng. J. 2007, 40, 101–109. [Google Scholar] [CrossRef]









| Index | Length | Wave Height | Velocity | Time | Pressure |
|---|---|---|---|---|---|
| Similarity ratio | 1/20 | 1/20 | 1/4.47 | 1/4.47 | 1/20 |
| Properties | Shear Modulus Gs | Poisson’s Ratio υs | Porosity ns | Permeability ks | Saturation Sr |
|---|---|---|---|---|---|
| Values | 4 × 106 Pa | 0.3 | 0.40 | 7.5 × 10−4 m/s | 1 |
| Conditions | H1/3 (cm) | d (cm) | T1/3 (s) | Test Duration |
|---|---|---|---|---|
| 1 | 10 | 15 | 1.92 | 100 T1/3 |
| 2 | 15 | 25 | 1.92 | 100 T1/3 |
| 3 | 18 | 40 | 1.96 | 100 T1/3 |
| 4 | 18 | 50 | 1.96 | 100 T1/3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, C.; Wang, J.; Zhao, T. Experimental Investigation of Pore Pressure on Sandy Seabed around Submarine Pipeline under Irregular Wave Loading. Sensors 2024, 24, 704. https://doi.org/10.3390/s24020704
Fu C, Wang J, Zhao T. Experimental Investigation of Pore Pressure on Sandy Seabed around Submarine Pipeline under Irregular Wave Loading. Sensors. 2024; 24(2):704. https://doi.org/10.3390/s24020704
Chicago/Turabian StyleFu, Changjing, Jinguo Wang, and Tianlong Zhao. 2024. "Experimental Investigation of Pore Pressure on Sandy Seabed around Submarine Pipeline under Irregular Wave Loading" Sensors 24, no. 2: 704. https://doi.org/10.3390/s24020704
APA StyleFu, C., Wang, J., & Zhao, T. (2024). Experimental Investigation of Pore Pressure on Sandy Seabed around Submarine Pipeline under Irregular Wave Loading. Sensors, 24(2), 704. https://doi.org/10.3390/s24020704






