Integrating Map Algebra and Statistical Modeling for Spatio- Temporal Analysis of Monthly Mean Daily Incident Photosynthetically Active Radiation (PAR) over a Complex Terrain
Abstract
:1. Introduction
2. Materials and Methods
2.1. Primary Motivation
2.2. Study Region
2.3. Climate Data
2.4. Mapping Geographical and Climate Variables
2.5. Spatio-temporal Modeling of Monthly Mean Daily Incident PAR
2.5. Statistical Analyses
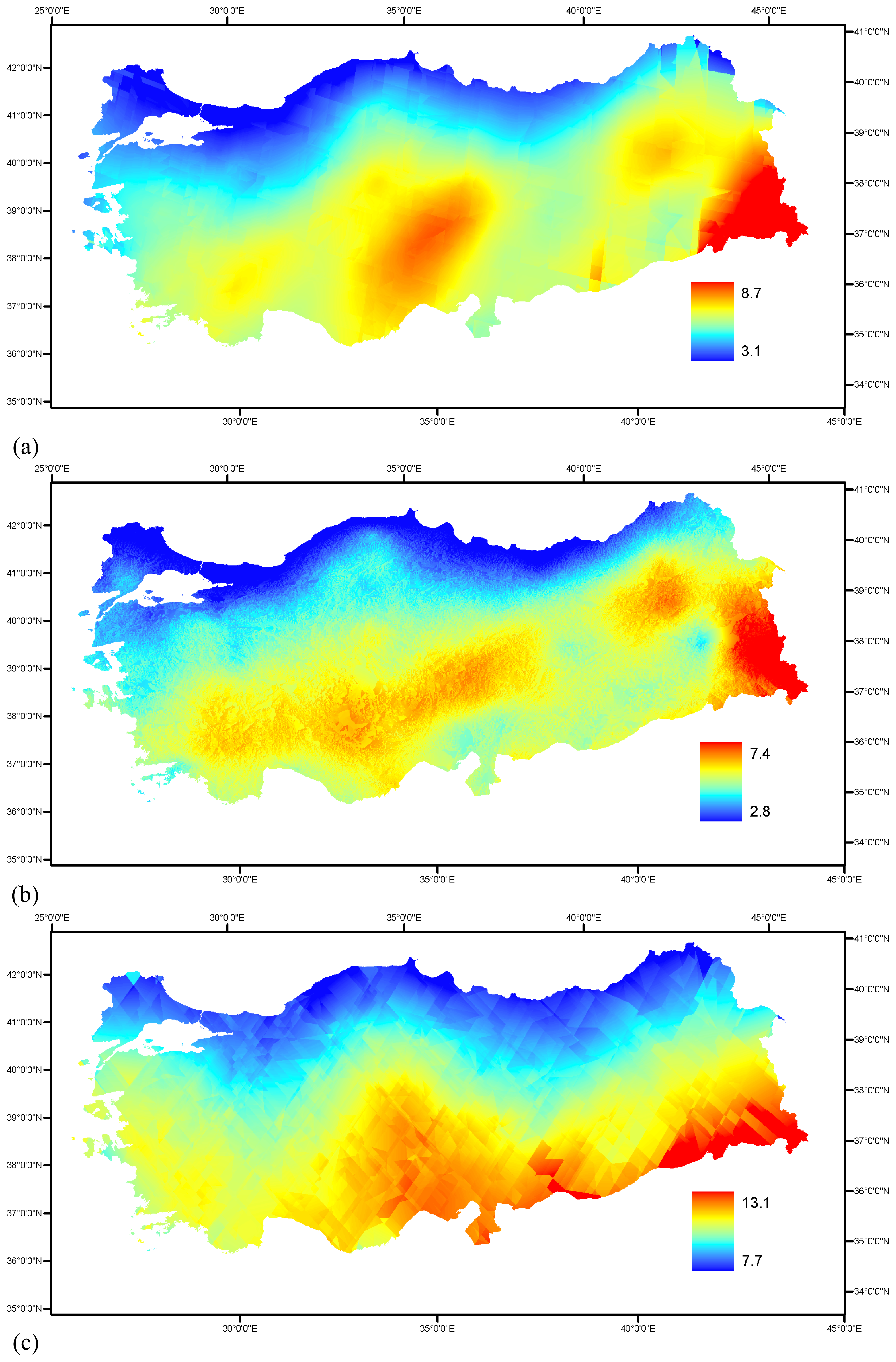
3. Results and Discussion
4. Conclusions
Acknowledgments
References
- Pinker, R.T.; Laszlo, I. Global distribution of photosynthetically active radiation as observed from satellites. Journal of Climate 1992, 5, 56–65. [Google Scholar]
- Landsberg, J.J.; Waring, R.H. A generalised model of forest productivity using simplified concepts of radiation-use efficiency, carbon balance and partitioning. Forest Ecology and Management 1997, 95, 209–228. [Google Scholar]
- Field, C.B.; Randerson, J.T.; Malmström, C.M. Global net primary production: combining ecology and remote sensing. Remote Sensing of Environment 1995, 51, 74–88. [Google Scholar]
- Goetz, S.J.; Prince, S.D. Modeling terrestrial carbon exchange and storage: evidence and implications of functional convergence in light use efficiency. Advances in Ecological Research 1999, 28, 57–92. [Google Scholar]
- Evrendilek, F.; Wali, M.K. Changing global climate: historical carbon and nitrogen budgets and projected responses of Ohio's Cropland Ecosystems. Ecosystems 2004, 7, 381–392. [Google Scholar]
- Kobayashi, H.; Matsunaga, T.; Hoyano, A.; Aoki, M.; Komori, D.; Boonyawat, S. Satellite estimation of photosynthetically active radiation in Southeast Asia: Impacts of smoke and cloud cover. Journal of Geophysical Research 2004, 109, D04102. [Google Scholar] [CrossRef]
- Diao, Y.; Wang, A.; Guan, D.; Jin, C.; Pei, T. Modeling CO2 source-sink and flux over broadleaved Koreanpine forest in Changbai Mountain using inverse Lagrangian dispersion analysis. Journal of Geophysical Research 2006, 111, D15S90. [Google Scholar] [CrossRef]
- Spitters, C.J.T.; Toussaint, H.A.J.M.; Goudriaan, J. Separating the diffuse and direct component of global radiation and its implications for modeling canopy photosynthesis. Part I. Components of incoming radiation. Agricultural and Forest Meteorology 1986, 38, 217–229. [Google Scholar]
- Tsubo, M.; Walker, S. Relationships between photosynthetically active radiation and clearness index at Bloemfontein, South Africa. Theoretical and Applied Climatology 2005, 80, 17–25. [Google Scholar]
- Hatfield, J.L.; Asrar, G.; Kanemasu, E.T. Intercepted photosynthetically active radiation estimated by spectral reflectance. Remote Sensing of Environment 1984, 14, 65–75. [Google Scholar]
- Asrar, G.; Myneni, R.B.; Choudhury, B.J. Spatial heterogeneity in vegetation canopies and remote sensing of absorbed photosynthetically active radiation: a modelling study. Remote Sensing of Environment 1992, 41, 85–103. [Google Scholar]
- Paruelo, J.M.; Epstein, H.E.; Lauenroth, W.K.; Burke, I.C. ANPP estimates from NDVI for the central grassland region of the U.S. Ecology 1997, 78, 953–958. [Google Scholar]
- Monteith, J.L. Solar radiation and productivity in tropical ecosystems. Journal of Applied Ecology 1972, 9, 747–766. [Google Scholar]
- Monteith, J.L. Climate and the efficiency of crop production in Britain. Philosophical Transactions of the Royal Society of London. Series B, Biological Sciences 1977, 281, 277–294. [Google Scholar]
- Kumar, M.; Monteith, J.L. Remote sensing of crop growth. In Plants and the Daylight Spectrum; Smith, H., Ed.; Academic Press: London, 1981; pp. 133–144. [Google Scholar]
- McCree, K.J. Test of current definitions of photosynthetic active radiation against leaf photosynthesis data. Agricultural Meteorology 1972, 10, 443–453. [Google Scholar]
- Bégué, A. Leaf Area Index, intercepted photosynthetically active radiation, and spectral vegetation indices: a sensitivity analysis for regular-clumped canopies. Remote Sensing of Environment 1993, 46, 45–59. [Google Scholar]
- Frouin, R.; Pinker, R.T. Estimating photosynthetically active radiation (PAR) of the Earth's surface from satellite observations. Remote Sensing of Environment 1995, 51, 98–107. [Google Scholar]
- Duffie, J.A.; Beckman, W.A. Solar Engineering of Thermal Process; Wiley: New York, 2006; p. 908. [Google Scholar]
- ESRI Inc. ArcGIS 8.2; ESRI Inc.: Redlands, 2002. [Google Scholar]
- Deutsch, C.V.; Journel, A.G. GSLIB. In Geostatistical Software Library and User's Guide; Oxford University Press: Oxford, 1998; p. 369. [Google Scholar]
- Goovaerts, P. Geostatistics for Natural Resources Evaluation; Oxford University Press: Oxford, 1997; p. 483. [Google Scholar]
- Webster, R.; Oliver, M.A. Geostatistics for Environmental Scientists; Wiley: New York, 2001; pp. 225–271. [Google Scholar]
- Baigorria, G.A.; Villegas, E.B.; Trebejo, I.; Carlos, J.F.; Quiroz, R. Atmospheric transmissivity: distribution and empirical estimation around the central Andes. International Journal of Climatology 2004, 24, 1121–1136. [Google Scholar]
- Castrignano, A.; Buttafuoco, G. Geostatistical stochastic simulation of soil water content in a forested area of south Italy. Biosystems Engineering 2004, 87, 257–266. [Google Scholar]
- Ertekin, C.; Evrendilek, F. Spatio-temporal modeling of global solar radiation dynamics as a function of sunshine duration for Turkey. Agricultural and Forest Meteorology 2007, 145, 36–47. [Google Scholar]
- Evrendilek, F.; Berberoglu, S.; Gulbeyaz, O.; Ertekin, C. Modeling potential distribution and carbon dynamics of natural terrestrial ecosystems: a case study of Turkey. Sensors 2007, 7(10), 2273–2296. [Google Scholar]
- Evrendilek, F.; Ertekin, C. Assessing solar radiation models using multiple variables over Turkey. Climate Dynamics 2008. [Google Scholar] [CrossRef]
- Evrendilek, F.; Berberoglu, S. Quantifying spatial patterns of bioclimatic zones and controls in Turkey. Theoretical and Applied Climatology 2007. [Google Scholar] [CrossRef]
- Ruimy, A.; Saugier, B.; Dedieu, G. Methodology for the estimation of terrestrial primary production from remotely sensed data. Journal of Geophysical Research 99 1994, 5263–5283. [Google Scholar]
- TSMS (Turkish State Meteorological Service). Monthly climate data between 1968 and 2004; Turkish State Meteorological Service: Ankara, 2005. [Google Scholar]
- Mallows, C.L. Some comments on Cp. Technometrics 1973, 15, 661–675. [Google Scholar]
- Bishop, T.F.A.; McBratney, A.B. A comparison of prediction methods for the creation of field-extent soil property maps. Geoderma 2001, 103, 149–160. [Google Scholar]
- Tomlin, C.D. Geographic information systems and cartographic modeling; Prentice Hall: New Jersey, 1990. [Google Scholar]


| Month | PAR (MJ m-2 day-1) | S (h) | So (h) | Ho (MJ m-2 day-1) | T (°C) | Tmin (°C) | Tmax (°C) | RH (%) | RHmin (%) | RHmax (%) | CLD (%) | ET (mm) | PPT (mm) | ST5 (°C) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n | 160 | 160 | 160 | 160 | 160 | 160 | 160 | 160 | 160 | 160 | 160 | 159 | 160 | 160 |
| January | 3.3 ± 0.6 | 3.4 ± 0.8 | 9.5 ± 0.13 | 15.8 ± 0.9 | 2 ± 5 | -9 ± 7 | 13 ± 5 | 73 ± 5 | 36 ± 7 | 96 ± 1 | 0.59 ± 0.09 | 13 ± 25 | 79 ± 48 | 3 ± 4 |
| February | 4.7 ± 0.8 | 4.3 ± 0.8 | 10.5 ± 0.07 | 21.0 ± 0.8 | 3 ± 5 | -9 ± 7 | 15 ± 4 | 71 ± 5 | 33 ± 7 | 96 ± 1 | 0.57 ± 0.08 | 14 ± 27 | 67 ± 36 | 4 ± 4 |
| March | 6.5 ± 0.9 | 5.5 ± 0.8 | 11.7 ± 0.02 | 27.8 ± 0.6 | 7 ± 4 | -5 ± 5 | 20 ± 4 | 68 ± 5 | 26 ± 7 | 96 ± 1 | 0.53 ± 0.07 | 25 ± 36 | 64 ± 27 | 8 ± 3 |
| April | 8.0 ± 0.9 | 6.6 ± 0.8 | 13.0 ± 0.05 | 34.8 ± 0.3 | 12 ± 3 | 0.3 ± 4 | 26 ± 3 | 65 ± 6 | 24 ± 6 | 96 ± 1 | 0.52 ± 0.07 | 70 ± 44 | 60 ± 19 | 14 ± 3 |
| May | 9.6 ± 1.0 | 8.4 ± 0.9 | 14.1 ± 0.11 | 39.7 ± 0.1 | 16 ± 3 | 5 ± 4 | 29 ± 3 | 63 ± 8 | 24 ± 7 | 94 ± 2 | 0.42 ± 0.08 | 119 ± 61 | 48 ± 17 | 20 ± 3 |
| June | 10.8 ± 1.1 | 10.3 ± 1.1 | 14.7 ± 0.14 | 41.7 ± 0.04 | 21 ± 3 | 9 ± 4 | 33 ± 3 | 57 ± 10 | 23 ± 9 | 91 ± 4 | 0.27 ± 0.09 | 162 ± 84 | 30 ± 18 | 26 ± 3 |
| July | 10.8 ± 1.2 | 10.9 ± 1.3 | 14.4 ± 0.13 | 40.6 ± 0.03 | 24 ± 3 | 13 ± 4 | 36 ± 3 | 54 ± 12 | 22 ± 10 | 87 ± 8 | 0.19 ± 0.11 | 203 ± 106 | 176 ± 17 | 29 ± 3 |
| August | 9.7 ± 1.1 | 10.4 ± 1.2 | 13.4 ± 0.08 | 36.7 ± 0.2 | 24 ± 3 | 12 ± 4 | 35 ± 3 | 55 ± 12 | 23 ± 10 | 88 ± 8 | 0.19 ± 0.11 | 188 ± 99 | 18 ± 23 | 29 ± 3 |
| September | 8.1 ± 1.0 | 8.9 ± 1.1 | 12.2 ± 0.02 | 30.3 ± 0.5 | 20 ± 3 | 8 ± 5 | 33 ± 3 | 57 ± 11 | 22 ± 9 | 92 ± 5 | 0.22 ± 0.10 | 134 ± 71 | 24 ± 27 | 24 ± 3 |
| October | 5.6 ± 0.8 | 6.5 ± 1.0 | 10.9 ± 0.05 | 23.0 ± 0.7 | 14 ± 3 | 2 ± 5 | 28 ± 3 | 64 ± 7 | 24 ± 8 | 96 ± 1 | 0.38 ± 0.09 | 78 ± 43 | 53 ± 33 | 16 ± 3 |
| November | 3.7 ± 0.6 | 4.6 ± 0.8 | 9.8 ± 0.11 | 17.0 ± 0.8 | 8 ± 4 | -3 ± 5 | 21 ± 3 | 70 ± 5 | 29 ± 6 | 96 ± 1 | 0.48 ± 0.08 | 29 ± 25 | 73 ± 29 | 9 ± 3 |
| December | 2.8 ± 0.5 | 3.0 ± 0.8 | 9.3 ± 0.14 | 14.3 ± 0.9 | 4 ± 5 | -7 ± 6 | 15 ± 4 | 74 ± 5 | 36 ± 6 | 96 ± 1 | 0.59 ± 0.08 | 14 ± 21 | 91 ± 53 | 4 ± 4 |
| Lat | Lon | Elev | DtS | Asp | S | T | Tmin | Tmax | RH | RHmin | RHmax | CLD | ET | PPT | ST5 | So | Ho | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Lon | -0.03 | |||||||||||||||||
| Elev | -0.05* | 0.63*** | ||||||||||||||||
| DtS | -0.16*** | 0.67*** | 0.79*** | |||||||||||||||
| Asp | 0.13*** | -0.01 | -0.09** | -0.06** | ||||||||||||||
| S | -0.25*** | -0.03 | 0.03 | 0.07** | -0.02 | |||||||||||||
| T | -0.18*** | -0.17*** | -0.33*** | -0.21*** | 0.02 | 0.88*** | ||||||||||||
| Tmin | -0.16*** | -0.19*** | -0.44*** | -0.29*** | 0.06* | 0.79*** | 0.98*** | |||||||||||
| Tmax | -0.12*** | -0.17*** | -0.27*** | -0.18*** | 0.004 | 0.88*** | 0.97*** | 0.92*** | ||||||||||
| RH | 0.33*** | -0.21*** | -0.26*** | -0.37*** | 0.03 | -0.75*** | -0.63*** | -0.53*** | -0.66*** | |||||||||
| RHmin | 0.37*** | -0.10*** | -0.23*** | -0.25*** | 0.10*** | -0.59*** | -0.49*** | -0.38*** | -0.59*** | 0.80*** | ||||||||
| RHmax | 0.19*** | -0.20*** | -0.11*** | -0.26*** | -0.01 | -0.59*** | -0.55*** | -0.49*** | -0.51*** | 0.75*** | 0.39*** | |||||||
| CLD | 0.40*** | 0.01 | -0.02 | -0.07*** | 0.02 | -0.89*** | -0.82*** | -0.74*** | -0.80*** | 0.73*** | 0.56*** | 0.60*** | ||||||
| ET | -0.24*** | -0.02 | -0.09*** | 0.02 | 0.002 | 0.79*** | 0.77*** | 0.73*** | 0.75*** | -0.65*** | -0.47*** | -0.63*** | -0.75*** | |||||
| PPT | 0.001 | -0.05* | -0.27*** | -0.22*** | 0.01 | -0.59*** | -0.39*** | -0.28*** | -0.46*** | 0.49*** | 0.35*** | 0.42*** | 0.55*** | -0.43*** | ||||
| ST5 | -0.17*** | -0.12*** | -0.25*** | -0.15*** | 0.02 | 0.92*** | 0.99*** | 0.95*** | 0.97*** | -0.65*** | -0.49*** | -0.57*** | -0.85*** | 0.79*** | -0.47*** | |||
| So | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 | 0.86*** | 0.76*** | 0.69*** | 0.78*** | -0.55*** | -0.44*** | -0.43*** | -0.61*** | 0.64*** | -0.48*** | 0.81*** | ||
| Ho | -0.05* | 0.002 | 0.003 | 0.009 | -0.007 | 0.87*** | 0.76*** | 0.69*** | 0.78*** | -0.57*** | -0.47*** | -0.43*** | -0.63*** | 0.65*** | -0.48*** | 0.81*** | 0.99*** | |
| PAR | -0.17*** | 0.05* | 0.11*** | 0.12*** | 0.01 | 0.92*** | 0.75*** | 0.67*** | 0.77*** | -0.67*** | -0.54*** | -0.51*** | -0.72*** | 0.68*** | -0.56*** | 0.81*** | 0.94*** | 0.94*** |
| Daily PAR | Intercept | Coefficients of monthly explanatory variables | R2adj (%) | R2 (%) for validation | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Lat | Lon | Elev | Month | DtS | Asp | T | PPT | CLD | RH | Ho | Ho.(S/So) | Ho.PPT | Ho.RH | ST5 | (1) | (2) | |||
| (1) Generic MLR model | |||||||||||||||||||
| 3.53 | -0.095 | 0.0005 | -0.021 | 0.155 | 0.147 | 94.3 | |||||||||||||
| (2) Month-specific MLR model | |||||||||||||||||||
| January | -1.63 | -0.066 | 0.234 | 0.292 | -0.0001 | 76.5 | 71.8 | 72.5 | |||||||||||
| February | -3.67 | 0.0008 | 0.307 | 0.293 | -0.0001 | -0.125 | 73.2 | 58.9 | 68.7 | ||||||||||
| March | -19.7 | 0.045 | -0.091 | 0.292 | 0.749 | 0.348 | -0.0105 | 66.9 | 55.4 | 55.2 | |||||||||
| April | -24.9 | 0.0003 | 0.0012 | 6.14 | 0.680 | 0.312 | 53.0 | 39.4 | 43.8 | ||||||||||
| May | -246 | 0.0015 | 5.72 | 6.260 | 0.154 | 35.5 | 30.0 | 26.6 | |||||||||||
| June | 25.3 | -0.393 | 0.000003 | 0.0015 | 3.84 | -0.0005 | 35.6 | 27.8 | 12.5 | ||||||||||
| July | -520 | 0.0004 | 13.0 | 0.085 | 33.1 | 36.9 | 32.3 | ||||||||||||
| August | -39.4 | 0.0005 | 0.682 | 1.26 | 0.094 | -0.018 | 42.4 | 40.3 | 41.5 | ||||||||||
| September | 3.2 | 0.0003 | 0.208 | 49.7 | 45.1 | 45.3 | |||||||||||||
| October | 6.19 | 0.0008 | 0.120 | -0.24 | 0.142 | -0.005 | 0.009 | -0.037 | 67.6 | 61.3 | 61.1 | ||||||||
| November | 4.31 | -0.055 | -0.03 | 0.283 | 72.1 | 73.2 | 71.7 | ||||||||||||
| December | 1.03 | 0.0004 | -0.001 | 0.330 | 74.3 | 74.0 | 77.4 | ||||||||||||
| Variable | Anisotropy | Moran's Index | Lag size | Nugget | Partial sill | Range | MPE | RMSPE | ASE | MSPE | RMSSPE | R2 (%) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| January | Yes | 0.15 | 0.42 | 0.148 | 0.122 | 4.978 | -0.003 | 0.443 | 0.486 | -0.030 | 0.922 | 58.5 |
| February | Yes | 0.15 | 0.41 | 0.234 | 0.204 | 4.859 | -0.028 | 0.558 | 0.594 | -0.053 | 0.949 | 56.3 |
| March | Yes | 0.13 | 0.35 | 0.365 | 0.283 | 4.148 | -0.063 | 0.690 | 0.756 | -0.083 | 0.948 | 53.3 |
| April | Yes | 0.11 | 0.84 | 0.544 | 0.126 | 9.956 | -0.064 | 0.770 | 0.819 | -0.078 | 0.945 | 42.5 |
| May | No | 0.07 | 2.5 | 0.883 | 0 | 18.34 | -0.061 | 0.950 | 1.002 | -0.065 | 0.953 | 27.5 |
| June | No | 0.07 | 1.5 | 1.015 | 0 | 16.90 | -0.096 | 0.990 | 1.074 | -0.091 | 0.934 | 28.6 |
| July | Yes | 0.06 | 0.33 | 0.812 | 0.556 | 3.911 | -0.069 | 1.048 | 1.079 | -0.066 | 0.987 | 29.2 |
| August | Yes | 0.07 | 0.22 | 0.648 | 0.353 | 2.607 | -0.070 | 0.915 | 0.994 | -0.073 | 0.939 | 36.4 |
| September | Yes | 0.09 | 0.22 | 0.485 | 0.237 | 2.607 | -0.058 | 0.792 | 0.852 | -0.072 | 0.943 | 43.4 |
| October | Yes | 0.13 | 0.50 | 0.279 | 0.164 | 5.656 | -0.041 | 0.584 | 0.630 | -0.066 | 0.949 | 55.6 |
| November | Yes | 0.15 | 1.4 | 0.173 | 0.052 | 16.47 | -0.056 | 0.431 | 0.460 | -0.122 | 0.938 | 62.2 |
| December | Yes | 0.15 | 0.52 | 0.106 | 0.059 | 6.163 | -0.031 | 0.364 | 0.377 | -0.084 | 0.959 | 61.9 |
© 2007 by MDPI ( http://www.mdpi.org). Reproduction is permitted for noncommercial purposes.
Share and Cite
Evrendilek, F. Integrating Map Algebra and Statistical Modeling for Spatio- Temporal Analysis of Monthly Mean Daily Incident Photosynthetically Active Radiation (PAR) over a Complex Terrain. Sensors 2007, 7, 3242-3257. https://doi.org/10.3390/s7123242
Evrendilek F. Integrating Map Algebra and Statistical Modeling for Spatio- Temporal Analysis of Monthly Mean Daily Incident Photosynthetically Active Radiation (PAR) over a Complex Terrain. Sensors. 2007; 7(12):3242-3257. https://doi.org/10.3390/s7123242
Chicago/Turabian StyleEvrendilek, Fatih. 2007. "Integrating Map Algebra and Statistical Modeling for Spatio- Temporal Analysis of Monthly Mean Daily Incident Photosynthetically Active Radiation (PAR) over a Complex Terrain" Sensors 7, no. 12: 3242-3257. https://doi.org/10.3390/s7123242
APA StyleEvrendilek, F. (2007). Integrating Map Algebra and Statistical Modeling for Spatio- Temporal Analysis of Monthly Mean Daily Incident Photosynthetically Active Radiation (PAR) over a Complex Terrain. Sensors, 7(12), 3242-3257. https://doi.org/10.3390/s7123242




