Metaheuristic Based Scheduling Meta-Tasks in Distributed Heterogeneous Computing Systems
Abstract
:1. Introduction
2. Problem Definition
3. Particle Swarm Optimization
4. PSO for Task Scheduling in HC Systems
4.1. Particles Encoding
4.2. Updating Particles
4.3. Fitness Evaluation
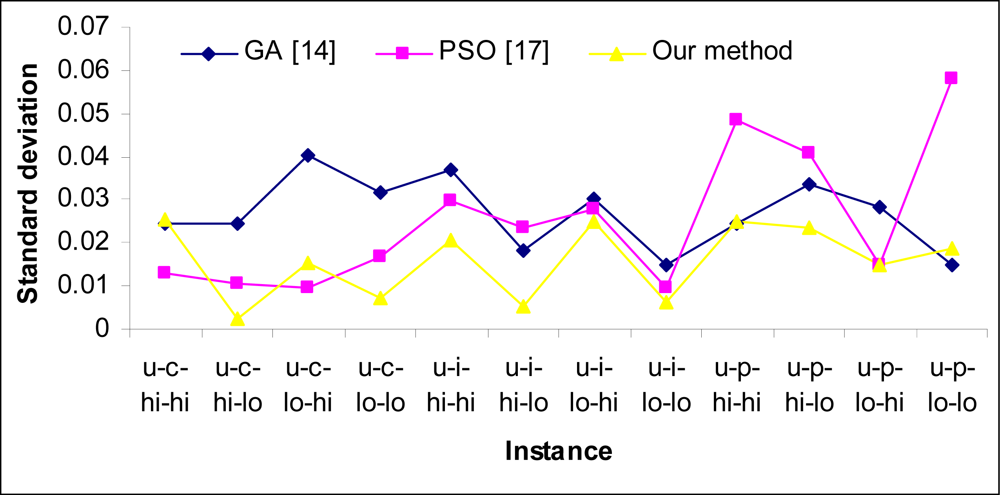
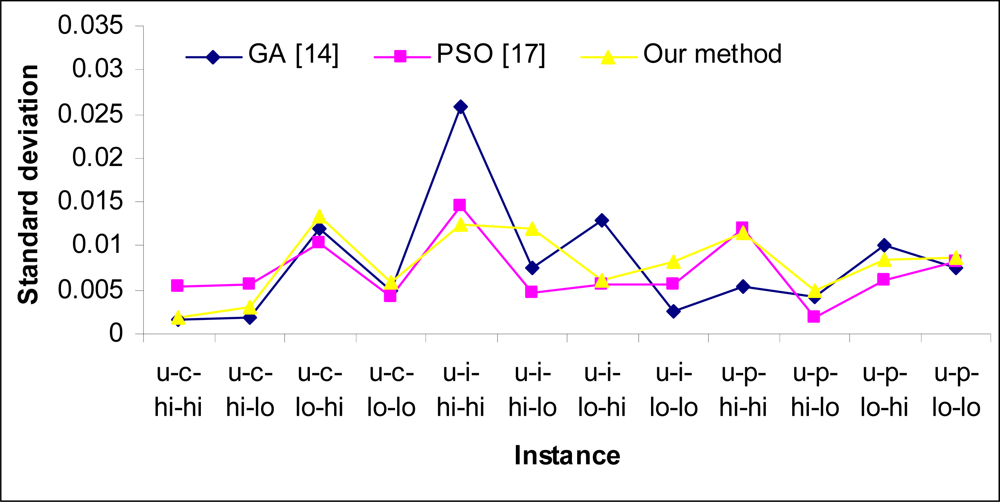
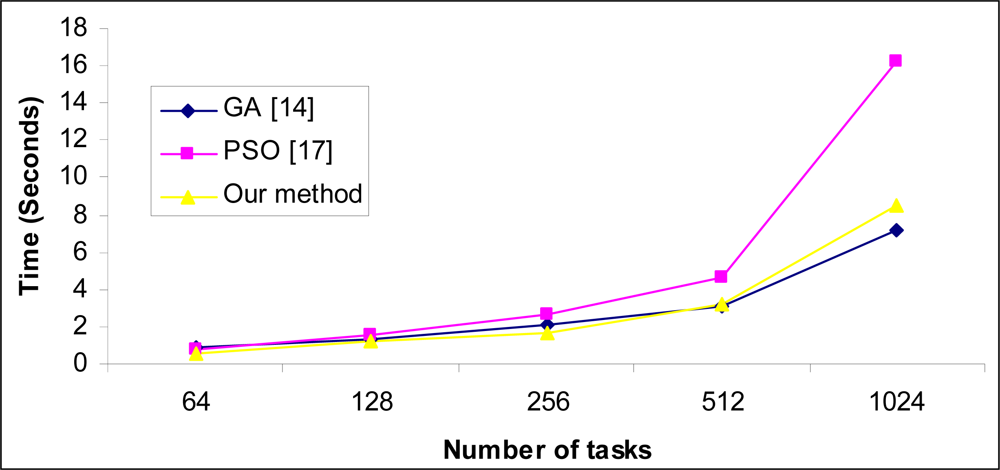
5. Experimental Results
- u means uniform distribution used in generating the matrices.
- x shows the type of inconsistency; c means consistent, i means inconsistent, and p means partially-consistent.
- yy indicates the heterogeneity of the tasks; hi means high and lo means low.
- zz represents the heterogeneity of the machines; hi means high and lo means low.
6. Conclusions
References and Notes
- Foster, I.; Kesselman, C.; Tuecke, S. The anatomy of the grid: enabling scalable virtual organizations. Int. J. Supercomput. Appl 2001, 15, 3–23. [Google Scholar]
- Fernandez-Baca, D. Allocating modules to processors in a distributed system. IEEE Trans. Software Engg 1989, 15, 1427–1436. [Google Scholar]
- Macheswaran, M.; Ali, S.; Siegel, H.J.; Hensgen, D.; Freund, R.F. Dynamic mapping of a class of independent tasks onto heterogeneous computing systems. J. Parallel Distribut. Comput 1999, 59, 107–131. [Google Scholar]
- Freund, R.F.; Gherrity, M.; Ambrosius, S.; Campbell, M.; Halderman, M.; Hensgen, D.; Keith, E.; Kidd, T.; Kussow, M.; Lima, J.D.; Mirabile, F.; Moore, L.; Rust, B.; Siegel, H.J. Scheduling resources in multi-user, heterogeneous, computing environments with SmartNet. Proceedings of the 7th IEEE Heterogeneous Computing Workshop (HCW 98’), Orlando, FL, USA, 1998; pp. 184–199.
- Abraham, A.; Buyya, R.; Nath, B. Nature’s heuristics for scheduling jobs on computational grids. 8th IEEE International Conference on Advanced Computing and Communications, Pune, India, 2000; pp. 45–52.
- Izakian, H.; Abraham, A.; Snášel, V. Comparison of heuristics for scheduling independent tasks on heterogeneous distributed environments. Proceedings of the IEEE International Workshop on HPC and Grid Applications, Sanya, P.R. China, April 24–26, 2009; pp. 8–12.
- Goldberg, D.E. Genetic Algorithms in Search, Optimization, and Machine Learning; Addison Wesley: Reading, MA, USA, 1997. [Google Scholar]
- Kirkpatrick, S.; Gelatt, C.; Vecchi, M. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar]
- Dorigo, M. Optimization, learning, and natural algorithms, Ph.D. Thesis,. Dip. Elettronica e Informazione, Politecnico di Milano, Milan, Italy, 1992.
- Kennedy, J.; Eberhart, R.C. Particle swarm optimization. Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia, 1995; pp. 1942–1948.
- Ritchie, G.; Levine, J. A hybrid ant algorithm for scheduling independent jobs in heterogeneous computing environments. Proceedings of the 23rd Workshop of the UK Planning and Scheduling Special Interest Group, Cork, Ireland, 2004; pp. 1–7.
- Yarkhan, A.; Dongarra, J. Experiments with scheduling using simulated annealing in a grid environment. Proceedings of the 3rd International Workshop on Grid Computing (GRID2002), Baltimore, MD, USA, November 18, 2002; pp. 232–242.
- Page, J.; Naughton, J. Framework for task scheduling in heterogeneous distributed computing using genetic algorithms. Artif. Intell. Rev 2005, 24, 415–429. [Google Scholar]
- Braun, T.D.; Siege, H.J.; Beck, N.; Boloni, L.L.; Maheswaran, M.; Reuther, A.I.; Robertson, J.P.; Theys, M.D.; Yao, B. A comparison of eleven static heuristics for mapping a class of independent tasks onto heterogeneous distributed computing systems. J. Parall. Distrib. Comp 2001, 61, 810–837. [Google Scholar]
- Xhafa, F.; Carretero, J.; Abraham, A. Genetic algorithm based schedulers for grid computing systems. Int. J. Innov. Comput. Inf. Control 2007, 3, 1053–1071. [Google Scholar]
- Xhafa, F.; Duran, B.; Abraham, A.; Dahal, K. Tuning struggle strategy in genetic algorithms for scheduling in computational grids. Neural Network World 2008, 209–225. [Google Scholar]
- Abraham, A.; Liu, H.; Zhang, W.; Chang, T.G. Scheduling jobs on computational grids using fuzzy particle swarm algorithm. Proceedings of the 10th International Conference on Knowledge-Based & Intelligent Information & Engineering Systems; Springer: Heidelberg, Germany, 2006; pp. 500–507. [Google Scholar]
- Izakian, H.; Tork Ladani, B.; Zamanifar, K.; Abraham, A. A novel particle swarm optimization approach for grid job scheduling. Proceedings of the Third International Conference on Information Systems, Technology and Management; Springer: Heidelberg, Germany, 2009; pp. 100–110. [Google Scholar]
- Xhafa, F.; Alba, E.; Dorronsoro, B.; Duran, B.; Abraham, A. Efficient batch job scheduling in grids using cellular memetic algorithms. In Studies in Computational Intelligence; Springer Verlag: Heidelberg, Germany, 2008; pp. 273–299. [Google Scholar]
- Abraham, A.; Liu, H.; Grosan, C.; Xhafa, F. Nature inspired meta-heuristics for grid scheduling: single and multi-objective optimization approaches. In Studies in Computational Intelligence; Springer Verlag: Heidelberg, Germany, 2008; pp. 247–272. [Google Scholar]
- Xhafa, F.; Abraham, A. Meta-heuristics for grid scheduling problems. In Studies in Computational Intelligence; Springer Verlag: Heidelberg, Germany, 2008; pp. 1–37. [Google Scholar]
- Angeline, P.J. Evolutionary optimization versus particle swarm optimization: philosophy and performance differences. Proceedings of the Seventh Annual Conference on Evolutionary Programming, San Diego, 1998; pp. 601–610.
- Salerno, J. Using the particle swarm optimization technique to train a recurrent neural model. Proceedings of the IEEE International Conference on Tools with Artificial Intelligence, Newport Beach, CA, USA, November 3–8, 1997; pp. 45–49.
- Eberhart, R.C.; Shi, Y. Evolving artificial neural networks. Proceedings of the International Conference on Neural Networks and Brain, Beijing, P.R. China, October 27–30, 1998; pp. 5–13.
- Salman, A.; Ahmad, I.; Al-Madani, S. Particle swarm optimization for task assignment problem. Microproc. Microsyst 2002, 26, 363–371. [Google Scholar]



| Instance | GA[14] | PSO[25] | Proposed method |
|---|---|---|---|
| u-c-hi-hi | 21508486 | 13559696 | 10173411 |
| u-c-hi-lo | 236653 | 223008 | 191878 |
| u-c-lo-hi | 695320 | 463241 | 371355 |
| u-c-lo-lo | 8021 | 7684 | 6379 |
| u-i-hi-hi | 21032954 | 23114941 | 6642987 |
| u-i-hi-lo | 245107 | 286339 | 149997 |
| u-i-lo-hi | 693461 | 849702 | 228971 |
| u-i-lo-lo | 8281 | 9597 | 4496 |
| u-p-hi-hi | 21249982 | 22073358 | 8325090 |
| u-p-hi-lo | 242258 | 266825 | 162601 |
| u-p-lo-hi | 712203 | 772882 | 293335 |
| u-p-lo-lo | 8233 | 8647 | 5213 |
| Instance | Min-min | GA[14] | PSO[25] | Proposed method |
|---|---|---|---|---|
| u-c-hi-hi | 8145395 | 7892199 | 7867899 | 7796844 |
| u-c-hi-lo | 164490 | 161634 | 161437 | 160639 |
| u-c-lo-hi | 279651 | 276489 | 274636 | 266747 |
| u-c-lo-lo | 5468 | 5292 | 5322 | 5309 |
| u-i-hi-hi | 3573987 | 3496209 | 3560537 | 3220459 |
| u-i-hi-lo | 82936 | 81715 | 81915 | 80754 |
| u-i-lo-hi | 113944 | 112703 | 113171 | 108597 |
| u-i-lo-lo | 2734 | 2636 | 2680 | 2644 |
| u-p-hi-hi | 4701249 | 4571336 | 4580666 | 4462357 |
| u-p-hi-lo | 106322 | 104854 | 104987 | 103794 |
| u-p-lo-hi | 157307 | 153970 | 154933 | 150375 |
| u-p-lo-lo | 3599 | 3449 | 3473 | 3461 |
© 2009 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Izakian, H.; Abraham, A.; Snášel, V. Metaheuristic Based Scheduling Meta-Tasks in Distributed Heterogeneous Computing Systems. Sensors 2009, 9, 5339-5350. https://doi.org/10.3390/s90705339
Izakian H, Abraham A, Snášel V. Metaheuristic Based Scheduling Meta-Tasks in Distributed Heterogeneous Computing Systems. Sensors. 2009; 9(7):5339-5350. https://doi.org/10.3390/s90705339
Chicago/Turabian StyleIzakian, Hesam, Ajith Abraham, and Václav Snášel. 2009. "Metaheuristic Based Scheduling Meta-Tasks in Distributed Heterogeneous Computing Systems" Sensors 9, no. 7: 5339-5350. https://doi.org/10.3390/s90705339





