Hazard Assessment of Debris-Flow along the Baicha River in Heshigten Banner, Inner Mongolia, China
Abstract
:1. Introduction
2. Study Area
3. Methodology
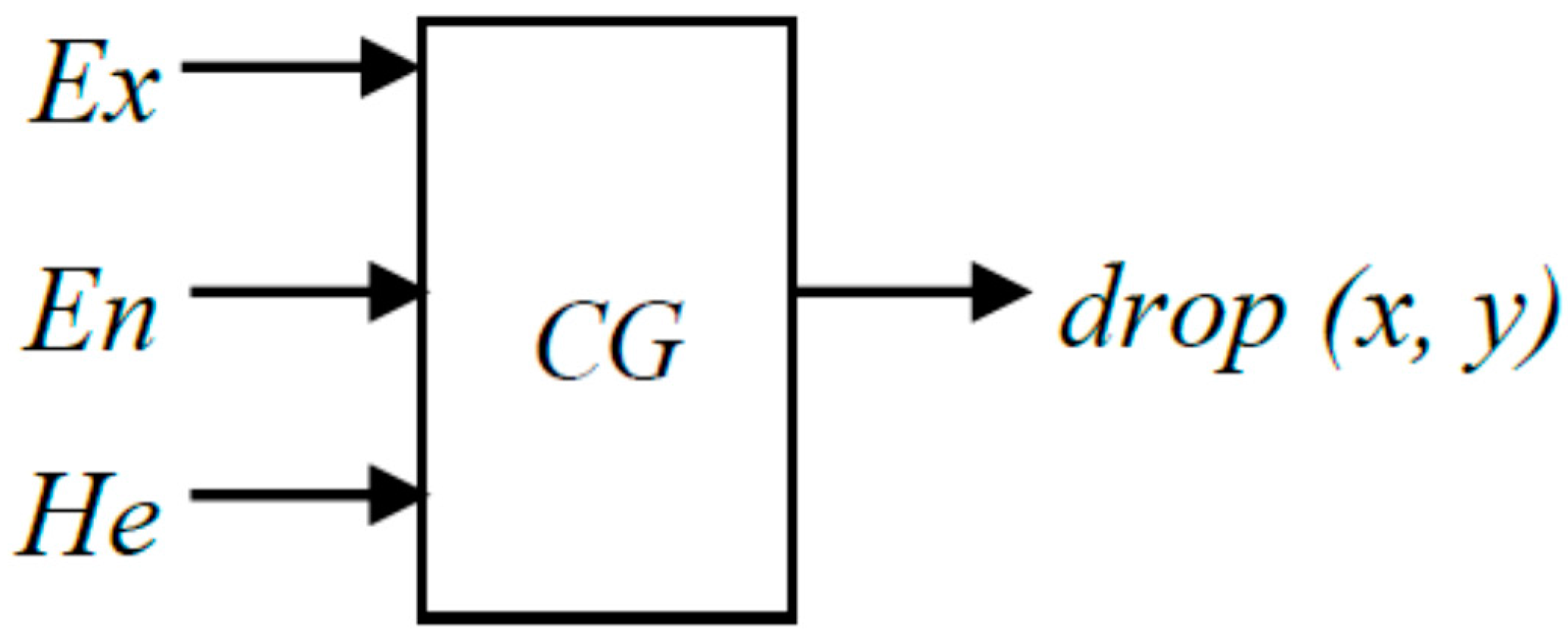
3.1. Cloud Model
- Generate a normally distributed random number yi, whose mean value is En and standard deviation is He.
- Generate a normally distributed random number xi, whose mean value is Ex and standard deviation is yi.
- Let xi be a specific quantitative value of qualitative characteristics, named a cloud drop.
- Calculate the certainty degree of the random number: .
- Output a cloud drop (xi, μi).
- Repeat steps 1–5 until N cloud drops are generated and all the cloud drops comprise the cloud and realize a qualitative presentation.
3.2. Weighting Methods
- The first step is to build the hierarchical structure of the target problem.
- Saaty [24] proposed a scaling method to score the parameters in each layer. By comparing the importance of the parameters in each level, aij is used to present the ratio of xi and xj, which builds the judgment matrix A = (aij):
- The judgment matrix needs to satisfy the following equation: 𝐴𝜔 = 𝜆max𝜔, where ω is the maximum characteristic vector matching the feature vector of judgment matrix A. The weight value can be obtained after normalizing the feature vector.
- In order to analyze whether the weighting distribution is reasonable, a consistency check is needed. The consistency parameter (CI) can be obtained using the following equation:
- Standardize the data. After standardizing the original data matrix X = (xij)m×n, obtain the normalized matrix R = (rij)m×n. The normalizing equations are:The greater the better:The smaller the better:
- Calculate the i-th catchment j-th factor proportion:
- Calculate the information entropy of the factor:where k > 0, ln is the natural logarithm, ej ≥ 0, k is relative to the DF catchment number m, k = 1/lnm, and 0 ≤ e ≤ 1.
- Calculate the information entropy redundancy:As for the j-th factor, the greater the difference of the factor value Xij, the greater the role that factor plays and the smaller the entropy value ej.
- Calculate the factor weights:
4. Debris-Flow Hazard Assessment
4.1. Evaluation Parameters
1. Catchment area (x1/km2)
2. Main channel length (x2/km)
3. Maximum elevation difference (x3/km)
4. Ravine density (x4/km·km−2)
5. Curvature of the main channel (x5)
6. Loose material length supply ratio (x6)
7. Twenty-four-hour maximum rainfall (x7/mm)
8. Population density (x8/per·km−2)
9. Loose material volume (x9/104 m3)
10. Outbreak frequency (x10/%)
11. Main channel gradient (x11)
4.2. Establishment of the Cloud Model
4.3. Calculation of Weights Using the EAHP Method
4.4. Hazard Assessment of Debris-Flow
5. Results and Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Jakob, M.; Hungr, O.; Jakob, D.M. Debris-Flow Hazards and Related Phenomena; Springer: Berlin, Germany, 2005. [Google Scholar]
- Giannecchini, R.; Naldini, D.; Avanzi, G.D.A.; Puccinelli, A. Modelling of the initiation of rainfall-induced debris flows in the Cardoso basin (Apuan Alps, Italy). Quat. Int. 2007, 171, 108–117. [Google Scholar] [CrossRef]
- De Scally, F.; Owens, I.; Louis, J. Controls on fan depositional processes in the schist ranges of the Southern Alps, New Zealand, and implications for debris-flow hazard assessment. Geomorphology 2010, 122, 99–116. [Google Scholar] [CrossRef]
- Zhang, W.; Chen, J.; Wang, Q.; An, Y.; Qian, X.; Xiang, L.; He, L. Susceptibility analysis of large-scale debris flows based on combination weighting and extension methods. Nat. Hazards 2013, 66, 1073–1100. [Google Scholar] [CrossRef]
- Niu, C.-C.; Wang, Q.; Chen, J.-P.; Wang, K.; Zhang, W.; Zhou, F.-J. Debris-flow hazard assessment based on stepwise discriminant analysis and extension theory. Q. J. Eng. Geol. Hydrogeol. 2014, 47, 211–222. [Google Scholar] [CrossRef]
- Ni, H.; Zheng, W.; Li, Z.; Ba, R. Recent catastrophic debris flows in Luding county, SW China: Geological hazards, rainfall analysis and dynamic characteristics. Nat. Hazards 2010, 55, 523–542. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, J.-P.; Wang, Q.; Zhang, W. Study on debris flow based on fractal theory and characteristics of water system. Shuili Xuebao (J. Hydraul. Eng.) 2011, 42, 351–356. [Google Scholar]
- Zhang, W.; Li, H.; Chen, J.; Zhang, C.; Xu, L.; Sang, W. Comprehensive hazard assessment and protection of debris flows along Jinsha river close to the Wudongde dam site in China. Nat. Hazards 2011, 58, 459–477. [Google Scholar] [CrossRef]
- Eldeen, M.T. Predisaster physical planning: Integration of disaster risk analysis into physical planning–A case study in Tunisia. Disasters 1980, 4, 211–222. [Google Scholar] [CrossRef] [PubMed]
- Hollingsworth, R.; Kovacs, G. Soil slumps and debris flows: Prediction and protection. Bull. Assoc. Eng. Geol. 1981, 18, 17–28. [Google Scholar] [CrossRef]
- Özdemir, A.; Delikanli, M. A geotechnical investigation of the retrogressive Yaka landslide and the debris flow threatening the town of Yaka (Isparta, sw Turkey). Nat. Hazards 2009, 49, 113–136. [Google Scholar] [CrossRef]
- Chiou, I.J.; Chen, C.H.; Liu, W.L.; Huang, S.M.; Chang, Y.M. Methodology of disaster risk assessment for debris flows in a river basin. Stoch. Environ. Res. Risk A 2015, 29, 775–792. [Google Scholar] [CrossRef]
- Liu, H.; Tang, C. Development of digital disaster reduction system for debris flow in urban district of Dongchuan. J. Nat. Disasters 2007, 16, 7. [Google Scholar]
- Carrara, A.; Crosta, G.; Frattini, P. Comparing models of debris-flow susceptibility in the Alpine environment. Geomorphology 2008, 94, 353–378. [Google Scholar] [CrossRef]
- Liang, W.; Zhuang, D.; Jiang, D.; Pan, J.; Ren, H. Assessment of debris flow hazards using a bayesian network. Geomorphology 2012, 171, 94–100. [Google Scholar] [CrossRef]
- Chang, T.-C. Risk degree of debris flow applying neural networks. Nat. Hazards 2007, 42, 209–224. [Google Scholar] [CrossRef]
- Han, G.; Wang, D. Numerical modeling of Anhui debris flow. J. Hydraul. Eng. 1996, 122, 262–265. [Google Scholar] [CrossRef]
- Gomez, H.; Kavzoglu, T. Assessment of shallow landslide susceptibility using artificial neural networks in Jabonosa river basin, Venezuela. Eng. Geol. 2005, 78, 11–27. [Google Scholar] [CrossRef]
- Lin, G.-F.; Chen, L.-H.; Lai, J.-N. Assessment of risk due to debris flow events: A case study in central Taiwan. Nat. Hazards 2006, 39, 1–14. [Google Scholar] [CrossRef]
- Chang, T.-C.; Chien, Y.-H. The application of genetic algorithm in debris flows prediction. Environ. Geol. 2007, 53, 339–347. [Google Scholar] [CrossRef]
- Deyi, L.; Haijun, M.; Xuemei, S. Membership clouds and membership cloud generators. J. Comput. Res. Dev. 1995, 6, 15–20. [Google Scholar]
- Li, D.; Liu, C.; Gan, W. A new cognitive model: Cloud model. Int. J. Intell. Syst. 2009, 24, 357–375. [Google Scholar] [CrossRef]
- Chen, J.-F.; Zhao, S.-F.; Shao, Q.-X.; Wang, H.-M. Risk assessment on drought disaster in China based on integrative cloud model. Res. J. Appl. Sci. Eng. Technol. 2012, 4, 1137–1146. [Google Scholar]
- Saaty, T.L. How to make a decision: The analytic hierarchy process. Eur. J. Oper. Res. 1990, 48, 9–26. [Google Scholar] [CrossRef]
- Zeleny, M.; Cochrane, J.L. Multiple Criteria Decision Making; University of South Carolina Press: Columbia, SC, USA, 1973. [Google Scholar]
- Kuang, L.; Xu, L.; Liu, B. Debris flow hazard assessment based on extension method. China Railw. Sci. 2006, 5, 1–6. [Google Scholar]
- Niu, C.; Wang, Q.; Chen, J.; Zhang, W.; Xu, L.; Wang, K. Hazard assessment of debris flows in the reservoir region of wudongde hydropower station in China. Sustainability 2015, 7, 15099–15118. [Google Scholar] [CrossRef]
- Tiranti, D.; Cremonini, R.; Asprea, I.; Marco, F. Driving factors for torrential mass-movements occurrence in the Western Alps. Front. Earth Sci. 2016, 4, 16. [Google Scholar] [CrossRef]
- Nikolopoulos, E.; Borga, M.; Creutin, J.; Marra, F. Estimation of debris flow triggering rainfall: Influence of rain gauge density and interpolation methods. Geomorphology 2015, 243, 40–50. [Google Scholar] [CrossRef]
- Stoffel, M.; Tiranti, D.; Huggel, C. Climate change impacts on mass movements—Case studies from the European Alps. Sci. Total Environ. 2014, 493, 1255–1266. [Google Scholar] [CrossRef] [PubMed]
- Kean, J.W.; McCoy, S.W.; Tucker, G.E.; Staley, D.M.; Coe, J.A. Runoff-generated debris flows: Observations and modeling of surge initiation, magnitude, and frequency. J. Geophys. Res. Earth Surf. 2013, 118, 2190–2207. [Google Scholar] [CrossRef]
- Tiranti, D.; Deangeli, C. Modeling of debris flow depositional patterns according to the catchment and sediment source area characteristics. Front. Earth Sci. 2015, 3, 8. [Google Scholar] [CrossRef]
- Surian, N.; Righini, M.; Lucía, A.; Nardi, L.; Amponsah, W.; Benvenuti, M.; Borga, M.; Cavalli, M.; Comiti, F.; Marchi, L. Channel response to extreme floods: Insights on controlling factors from six mountain rivers in Northern Apennines, Italy. Geomorphology 2016, 272, 78–91. [Google Scholar] [CrossRef]
- Cavalli, M.; Trevisani, S.; Comiti, F.; Marchi, L. Geomorphometric assessment of spatial sediment connectivity in small alpine catchments. Geomorphology 2013, 188, 31–41. [Google Scholar] [CrossRef]
- Theule, J.; Liébault, F.; Loye, A.; Laigle, D.; Jaboyedoff, M. Sediment budget monitoring of debris-flow and bedload transport in the Manival Torrent, SE France. Nat. Hazards Earth Syst. Sci. 2012, 12, 731–749. [Google Scholar] [CrossRef]
- Guzzetti, F.; Ardizzone, F.; Cardinali, M.; Rossi, M.; Valigi, D. Landslide volumes and landslide mobilization rates in Umbria, central Italy. Earth Planet. Sci. Lett. 2009, 279, 222–229. [Google Scholar] [CrossRef]
- Tiranti, D.; Cavalli, M.; Crema, S.; Zerbato, M.; Graziadei, M.; Barbero, S.; Cremonini, R.; Silvestro, C.; Bodrato, G.; Tresso, F. Semi-quantitative method for the assessment of debris supply from slopes to river in ungauged catchments. Sci. Total Environ. 2016, 554, 337–348. [Google Scholar] [CrossRef] [PubMed]
- Tiranti, D.; Cremonini, R.; Marco, F.; Gaeta, A.R.; Barbero, S. The defense (debris flows triggered by storms–nowcasting system): An early warning system for torrential processes by radar storm tracking using a geographic information system (GIS). Comput. Geosci. 2014, 70, 96–109. [Google Scholar] [CrossRef]
- Chang, T.-C.; Chao, R.-J. Application of back-propagation networks in debris flow prediction. Eng. Geol. 2006, 85, 270–280. [Google Scholar] [CrossRef]
- Liu, X.; Tang, C. Debris Flow Hazardous Assessment; Science Press: Beijing, China, 1995. [Google Scholar]
- Catani, F.; Casagli, N.; Ermini, L.; Righini, G.; Menduni, G. Landslide hazard and risk mapping at catchment scale in the Arno river basin. Landslides 2005, 2, 329–342. [Google Scholar] [CrossRef]
- Lee, S.; Pradhan, B. Landslide hazard mapping at Selangor, Malaysia using frequency ratio and logistic regression models. Landslides 2007, 4, 33–41. [Google Scholar] [CrossRef]
- Tunusluoglu, M.; Gokceoglu, C.; Nefeslioglu, H.; Sonmez, H. Extraction of potential debris source areas by logistic regression technique: A case study from Barla, Besparmak and Kapi mountains (NW Taurids, Turkey). Environ. Geol. 2008, 54, 9–22. [Google Scholar] [CrossRef]
- Duo, T.; Wang, Y.; Huang, Z.; Duo, T. A fuzzy math evaluation on debris-flow occurrence in the three main gullies in Chayuangou Alley. J. Geol. Hazards Environ. Preserv. 2011, 22, 31–35. [Google Scholar]
- Tiranti, D.; Bonetto, S.; Mandrone, G. Quantitative basin characterisation to refine debris-flow triggering criteria and processes: An example from the Italian Western Alps. Landslides 2008, 5, 45–57. [Google Scholar] [CrossRef]
- Lin, P.-S.; Lin, J.Y.; Hung, J.-C.; Yang, M.-D. Assessing debris-flow hazard in a watershed in Taiwan. Eng. Geol. 2002, 66, 295–313. [Google Scholar] [CrossRef]
- Ohlmacher, G.C.; Davis, J.C. Using multiple logistic regression and GIS technology to predict landslide hazard in Northeast Kansas, USA. Eng. Geol. 2003, 69, 331–343. [Google Scholar] [CrossRef]
- Lan, H.; Zhou, C.; Wang, L.; Zhang, H.; Li, R. Landslide hazard spatial analysis and prediction using GIS in the Xiaojiang watershed, Yunnan, China. Eng. Geol. 2004, 76, 109–128. [Google Scholar] [CrossRef]
- Lu, G.Y.; Chiu, L.S.; Wong, D.W. Vulnerability assessment of rainfall-induced debris flows in Taiwan. Nat. Hazards 2007, 43, 223–244. [Google Scholar] [CrossRef]
- Liu, C.-N.; Dong, J.J.; Peng, Y.F.; Huang, H.-F. Effects of strong ground motion on the susceptibility of gully type debris flows. Eng. Geol. 2009, 104, 241–253. [Google Scholar] [CrossRef]
- Yu, B.; Zhu, Y.; Wang, T.; Chen, Y.; Zhu, Y.; Tie, Y.; Lu, K. A prediction model for debris flows triggered by a runoff-induced mechanism. Nat. Hazards 2014, 74, 1141–1161. [Google Scholar] [CrossRef]
- Cai, W. The extension set and incompatibility problem. J. Sci. Explor. 1983, 1, 81–93. [Google Scholar]
- Zheng, G.; Jing, Y.; Huang, H.; Zhang, X.; Gao, Y. Application of life cycle assessment (LCA) and extenics theory for building energy conservation assessment. Energy 2009, 34, 1870–1879. [Google Scholar] [CrossRef]
- Li, X.; Zhang, H.; Zhu, Z.; Xiang, Z.; Chen, Z.; Shi, Y. An intelligent transformation knowledge mining method based on extenics. J. Internet Technol. 2013, 14, 315–325. [Google Scholar]
- Wang, M.H.; Huang, M.L.; Liou, K.J. Application of extension theory with chaotic signal synchronization on detecting islanding effect of photovoltaic power system. Int. J. Photoenergy 2015, 2015, 1–10. [Google Scholar] [CrossRef]
- Zhao, B.; Xu, W.; Liang, G.; Meng, Y. Stability evaluation model for high rock slope based on element extension theory. Bull. Eng. Geol. Environ. 2015, 74, 301–314. [Google Scholar] [CrossRef]
- Wang, M.H.; Tseng, Y.F.; Chen, H.C.; Chao, K.H. A novel clustering algorithm based on the extension theory and genetic algorithm. Expert Syst. Appl. 2009, 36, 8269–8276. [Google Scholar] [CrossRef]
- Ye, J. Application of extension theory in misfire fault diagnosis of gasoline engines. Expert Syst. Appl. 2009, 36, 1217–1221. [Google Scholar] [CrossRef]
- Zhang, L.; Wu, X.; Chen, Q.; Skibniewski, M.J.; Zhong, J. Developing a cloud model based risk assessment methodology for tunnel-induced damage to existing pipelines. Stoch. Environ. Res. Risk A 2015, 29, 513–526. [Google Scholar] [CrossRef]
- Li, L.; Liu, L.; Yang, C.; Li, Z. The comprehensive evaluation of smart distribution grid based on cloud model. Energy Procedia 2012, 17, 96–102. [Google Scholar] [CrossRef]
- Sun, X.; Cai, C.; Yang, J.; Shen, X. Route assessment for unmanned aerial vehicle based on cloud model. Math. Probl. Eng. 2014, 2014, 1–13. [Google Scholar] [CrossRef]
- Wan, S.; Lei, T.; Huang, P.; Chou, T. The knowledge rules of debris flow event: A case study for investigation Chen Yu Lan River, Taiwan. Eng. Geol. 2008, 98, 102–114. [Google Scholar] [CrossRef]
- Liu, H.C.; Gu, X.Z. Hazard assessment of debris flow along highway based on extension ahp. Chin. J. Geol. Hazard Control 2010, 21, 61–66. [Google Scholar]
- Zhang, L.; Zhou, W.D. Sparse ensembles using weighted combination methods based on linear programming. Pattern Recognit. 2011, 44, 97–106. [Google Scholar] [CrossRef]
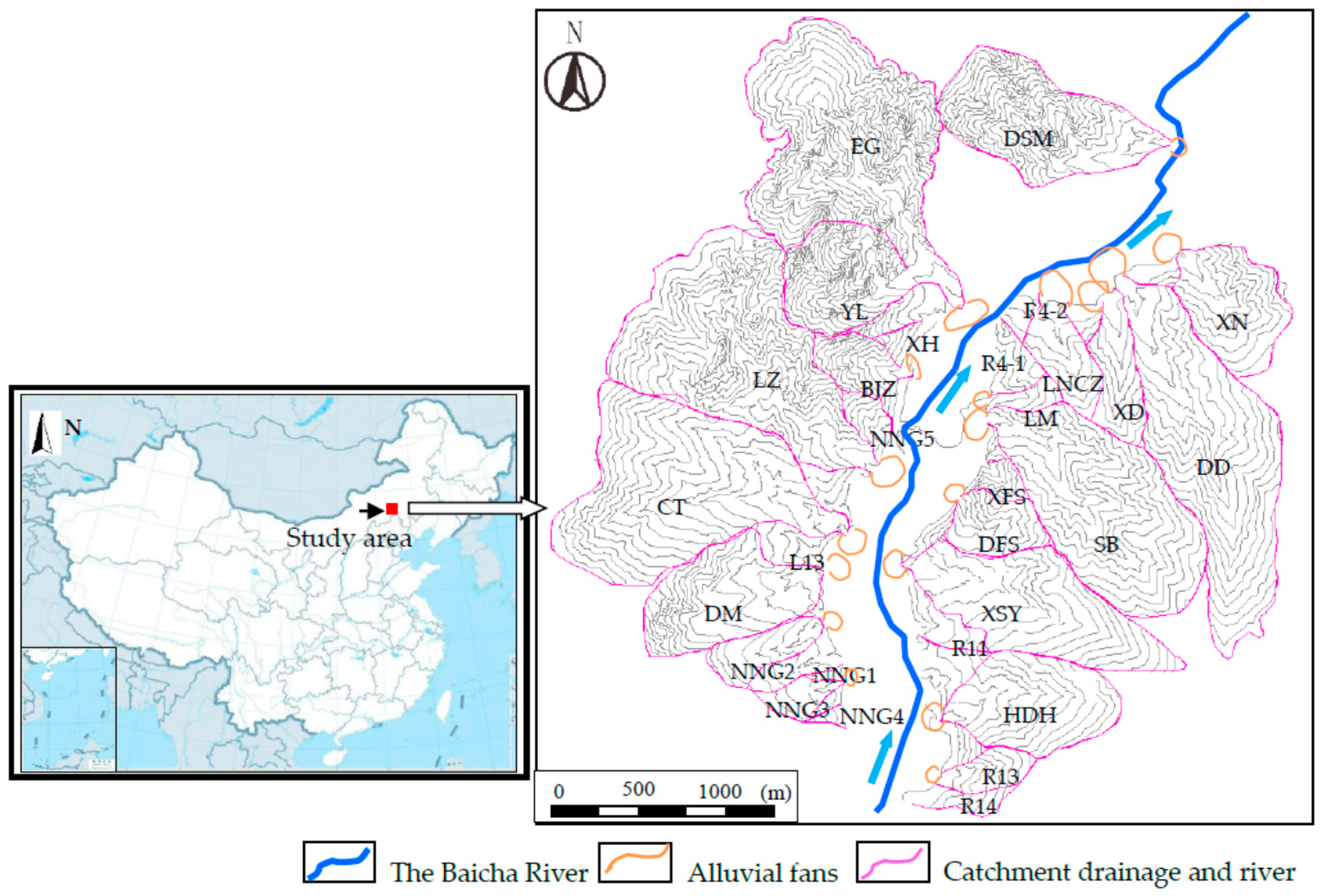
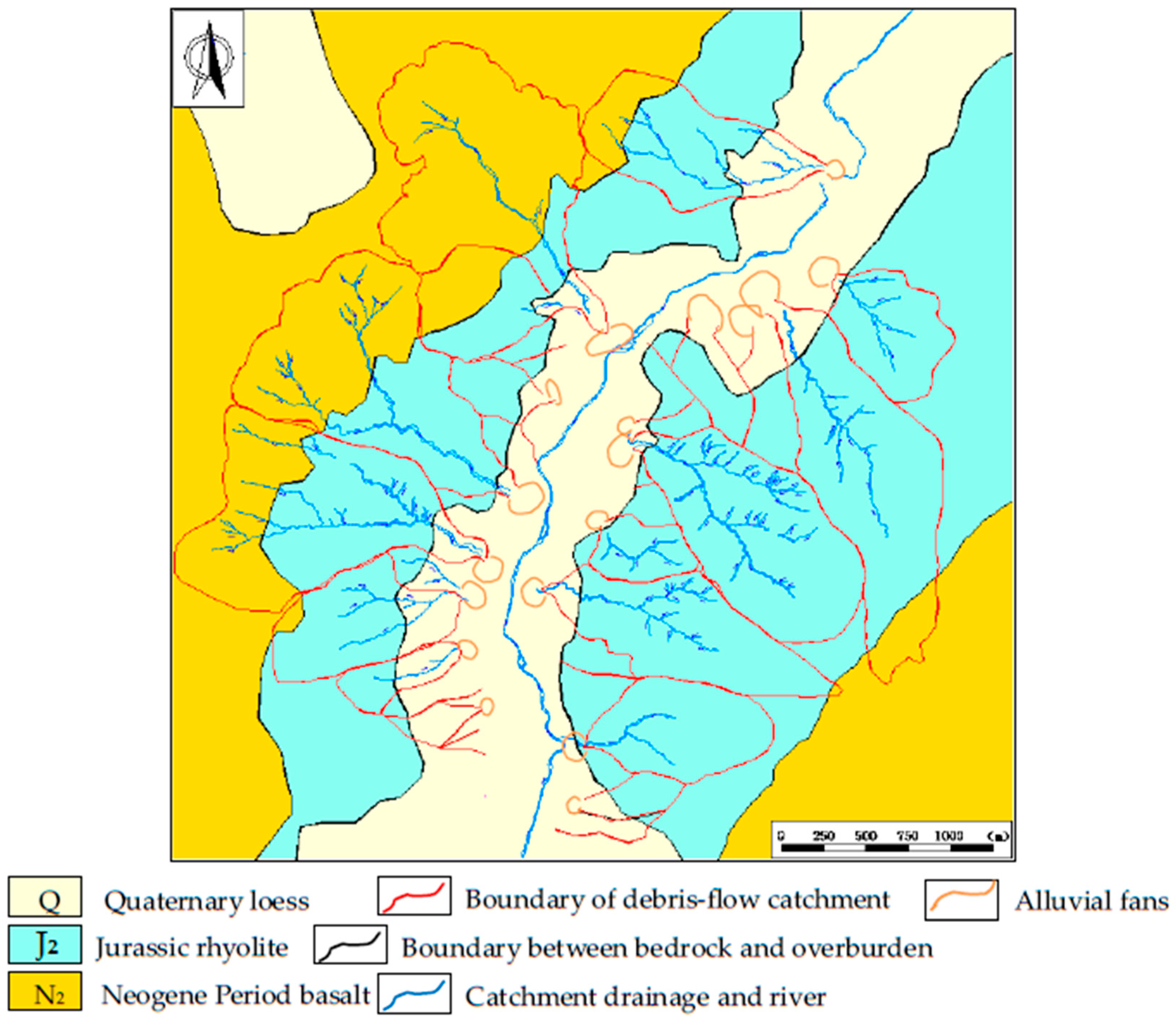


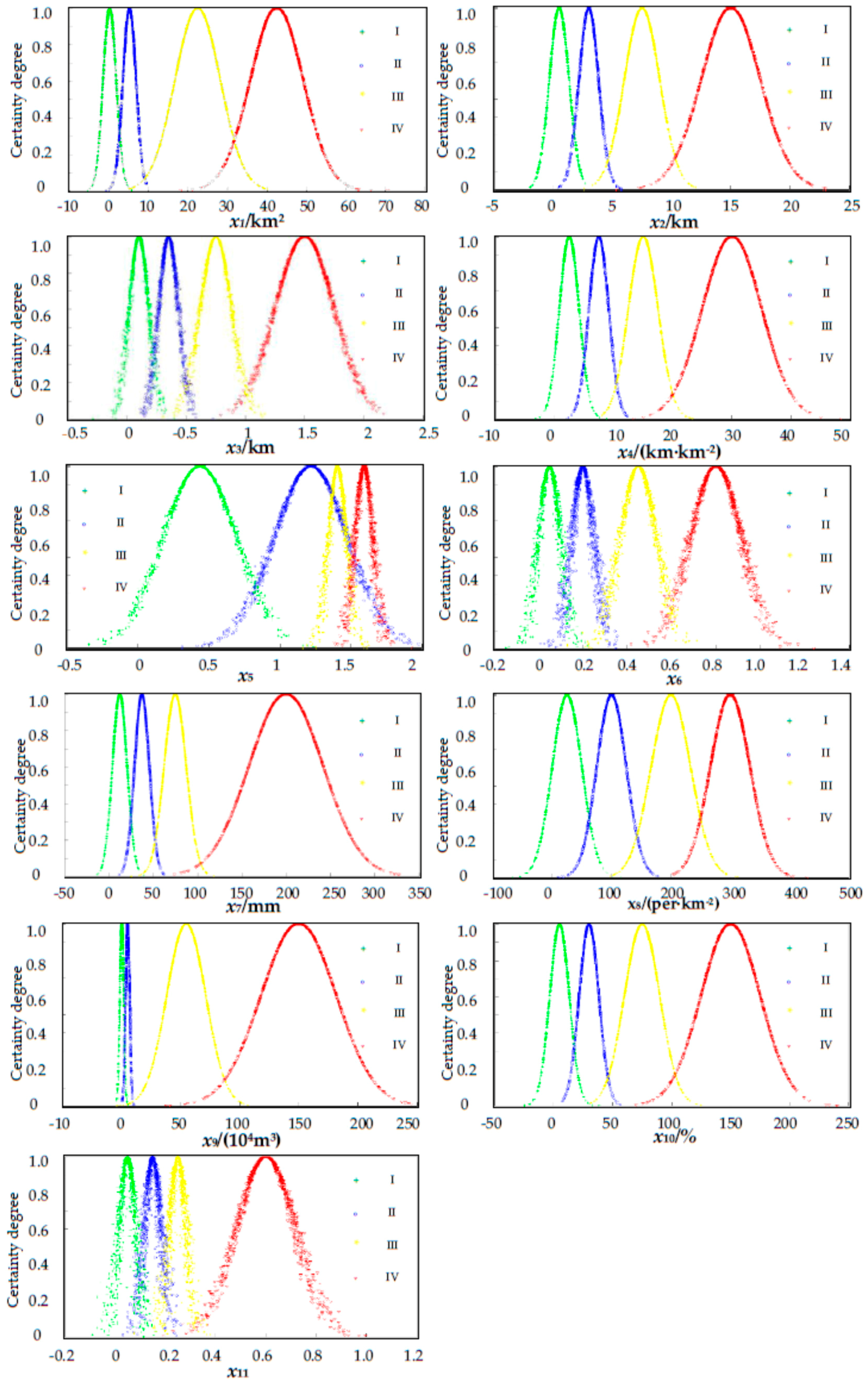



| Parameters | I | II | III | IV |
|---|---|---|---|---|
| x1 (km2) | 0–0.5 | 0.5–10 | 10–35 | 35–50 |
| x2 (km) | 0–1 | 1–5 | 5–10 | 10–20 |
| x3 (km) | 0–0.2 | 0.2–0.5 | 0.5–1.0 | 1.0–2.0 |
| x4 (km·km−2) | 0–5 | 5–10 | 10–20 | 20–40 |
| x5 | 0–1.10 | 1.10–1.25 | 1.25–1.40 | 1.40–1.55 |
| x6 | 0–0.1 | 0.1–0.3 | 0.3–0.6 | 0.6–1.0 |
| x7 (mm) | 0–25 | 25–50 | 50–100 | 100–300 |
| x8 (per·km−2) | 0–50 | 50–150 | 150–250 | 250–350 |
| x9 (104 m3) | 0–1 | 1–10 | 10–100 | 100–200 |
| x10 (%) | 0–10 | 10–50 | 50–100 | 100–200 |
| x11 | 0–0.1 | 0.1–0.2 | 0.2–0.35 | 0.35–0.85 |
| Catchment | x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 | x11 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| DSM | 0.667 | 1.276 | 0.445 | 1.927 | 1.226 | 0.55 | 251.8 | 0.1 | 0.608 | 1.06 | 0.35 |
| EG | 1.803 | 2.119 | 0.423 | 3.566 | 1.072 | 0.15 | 251.8 | 0.1 | 3.276 | 0.93 | 0.26 |
| XH | 0.034 | 0.249 | 0.159 | 12.44 | 1.073 | 0.38 | 251.8 | 0.1 | 0.044 | 0.97 | 0.36 |
| BJZ | 0.143 | 0.326 | 0.092 | 2.28 | 1.02 | 0.4 | 251.8 | 0.1 | 0.092 | 1.06 | 0.27 |
| NN5 | 0.069 | 0.281 | 0.088 | 6.493 | 1.156 | 0.56 | 251.8 | 0.1 | 0.104 | 0.95 | 0.32 |
| LZ | 1.313 | 2.051 | 0.391 | 4.726 | 1.222 | 0.6 | 251.8 | 0.1 | 0.77 | 1.11 | 0.24 |
| CT | 1.302 | 2.051 | 0.4 | 4.51 | 1.145 | 0.6 | 251.8 | 0.1 | 3.995 | 2.90 | 0.27 |
| DM | 0.5525 | 0.856 | 0.098 | 2.77 | 1.07 | 0.3 | 251.8 | 0.1 | 0.7 | 1.07 | 0.32 |
| NNG2 | 0.161 | 0.67 | 0.139 | 7.66 | 1.098 | 0.2 | 251.8 | 0.1 | 0.193 | 1.12 | 0.19 |
| NNG1 | 0.06 | 0.334 | 0.057 | 11.75 | 1.034 | 0.2 | 251.8 | 0.1 | 0.055 | 1.05 | 0.19 |
| NNG3 | 0.052 | 0.331 | 0.061 | 13.423 | 1.078 | 0.08 | 251.8 | 0.1 | 0.058 | 1.09 | 0.23 |
| NNG4 | 0.021 | 0.187 | 0.057 | 10.667 | 1.022 | 0.08 | 251.8 | 0.1 | 0.0001 | 1.00 | 0.34 |
| L13 | 0.099 | 0.387 | 0.064 | 5.21 | 1.06 | 0.3 | 251.8 | 0.1 | 0.006 | 1.00 | 0.19 |
| XN | 0.408 | 0.858 | 0.215 | 6.3 | 1.007 | 0.4 | 251.8 | 0.1 | 0.393 | 0.89 | 0.21 |
| DD | 1.598 | 2.591 | 0.463 | 3.992 | 1.328 | 0.4 | 251.8 | 0.1 | 6.513 | 3.56 | 0.19 |
| XD | 0.211 | 0.977 | 0.233 | 6.93 | 1.132 | 0.61 | 251.8 | 0.1 | 1.452 | 0.64 | 0.21 |
| LNCZ | 0.154 | 0.697 | 0.129 | 7.08 | 1.057 | 0.2 | 251.8 | 0.1 | 0.217 | 0.81 | 0.16 |
| R4-1 | 0.028 | 0.196 | 0.097 | 16.1 | 1.021 | 1.0 | 251.8 | 0.1 | 0.0001 | 1.00 | 0.14 |
| R4-2 | 0.013 | 0.26 | 0.1 | 20 | 1.066 | 1.0 | 251.8 | 0.1 | 0.0001 | 1.00 | 0.18 |
| R5 | 0.038 | 0.226 | 0.087 | 11.63 | 1.092 | 0.45 | 251.8 | 0.1 | 0.085 | 0.45 | 0.27 |
| LM | 0.069 | 0.393 | 0.131 | 9.975 | 1.251 | 0.35 | 251.8 | 0.1 | 0.19 | 0.76 | 0.42 |
| SB | 1.082 | 1.664 | 0.355 | 5.21 | 1.074 | 0.4 | 251.8 | 0.1 | 3.38 | 0.46 | 0.18 |
| XFS | 0.064 | 0.247 | 0.16 | 7.78 | 1.025 | 0.25 | 251.8 | 0.1 | 0.307 | 0.62 | 0.37 |
| DFS | 0.197 | 0.633 | 0.203 | 7.761 | 1.347 | 0.31 | 251.8 | 0.1 | 0.605 | 0.50 | 0.18 |
| XSY | 0.755 | 1.565 | 0.258 | 3.91 | 1.059 | 0.53 | 251.8 | 0.1 | 3.244 | 0.53 | 0.18 |
| R11 | 0.1142 | 0.37 | 0.161 | 3.616 | 1.09 | 0.25 | 251.8 | 0.1 | 0.154 | 0.83 | 0.31 |
| HDH | 0.516 | 1.25 | 0.245 | 4.73 | 1.136 | 0.35 | 251.8 | 0.1 | 1.732 | 0.61 | 0.14 |
| R13 | 0.078 | 0.472 | 0.16 | 11.22 | 1.103 | 0.006 | 251.8 | 0.1 | 0.424 | 0.83 | 0.32 |
| R14 | 0.058 | 0.291 | 0.155 | 17.5 | 1.111 | 0.35 | 251.8 | 0.1 | 0.146 | 0.66 | 0.31 |
| Method | x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 | x11 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| AHP | 0.132 | 0.053 | 0.085 | 0.037 | 0.017 | 0.062 | 0.105 | 0.017 | 0.18 | 0.18 | 0.132 |
| Entropy | 0.287 | 0.132 | 0.078 | 0.069 | 0.001 | 0.076 | 0 | 0 | 0.323 | 0.015 | 0.019 |
| Combined | 0.178 | 0.076 | 0.083 | 0.046 | 0.012 | 0.066 | 0.073 | 0.012 | 0.223 | 0.13 | 0.098 |
| CCD | k1 | k2 | k3 | k4 | Cloud Model | Extenics |
|---|---|---|---|---|---|---|
| DSM | 0.573 | 0.074 | 0.067 | 0.110 | Low | Low |
| EG | 0.277 | 0.384 | 0.079 | 0.074 | Moderate | Low |
| XH | 0.624 | 0.111 | 0.053 | 0.080 | Low | Low |
| BJZ | 0.504 | 0.152 | 0.115 | 0.048 | Low | Low |
| L5 | 0.652 | 0.156 | 0.032 | 0.083 | Low | Low |
| LZ | 0.478 | 0.168 | 0.106 | 0.093 | Low | Low |
| CT | 0.306 | 0.363 | 0.120 | 0.093 | Moderate | Moderate |
| DM | 0.443 | 0.146 | 0.057 | 0.103 | Low | Low |
| NNG2 | 0.346 | 0.172 | 0.072 | 0.072 | Low | Low |
| NNG1 | 0.468 | 0.116 | 0.035 | 0.013 | Low | Low |
| NNG3 | 0.504 | 0.164 | 0.011 | 0.085 | Low | Low |
| NNG4 | 0.382 | 0.090 | 0.031 | 0.017 | Low | Low |
| L13 | 0.425 | 0.110 | 0.077 | 0.082 | Low | Low |
| XN | 0.463 | 0.117 | 0.130 | 0.073 | Low | Low |
| DD | 0.153 | 0.179 | 0.218 | 0.089 | High | High |
| XD | 0.461 | 0.136 | 0.042 | 0.076 | Low | Low |
| LNCZ | 0.329 | 0.101 | 0.036 | 0.076 | Low | Low |
| R4-1 | 0.442 | 0.037 | 0.053 | 0.015 | Low | Low |
| R4-2 | 0.503 | 0.102 | 0.098 | 0.073 | Low | Low |
| R5 | 0.333 | 0.086 | 0.074 | 0.014 | Low | Low |
| LM | 0.533 | 0.099 | 0.085 | 0.027 | Low | Low |
| SB | 0.292 | 0.396 | 0.075 | 0.072 | Moderate | Moderate |
| XFS | 0.304 | 0.186 | 0.096 | 0.077 | Low | Moderate |
| DFS | 0.427 | 0.096 | 0.113 | 0.030 | Low | Low |
| XSY | 0.306 | 0.113 | 0.077 | 0.071 | Low | Low |
| R11 | 0.395 | 0.104 | 0.142 | 0.070 | Low | Low |
| HDH | 0.452 | 0.218 | 0.099 | 0.063 | Low | Low |
| R13 | 0.425 | 0.046 | 0.030 | 0.041 | Low | Low |
| R14 | 0.393 | 0.086 | 0.056 | 0.020 | Low | Low |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, C.; Xu, P.; Chen, J.; Zheng, L.; Niu, C. Hazard Assessment of Debris-Flow along the Baicha River in Heshigten Banner, Inner Mongolia, China. Int. J. Environ. Res. Public Health 2017, 14, 30. https://doi.org/10.3390/ijerph14010030
Cao C, Xu P, Chen J, Zheng L, Niu C. Hazard Assessment of Debris-Flow along the Baicha River in Heshigten Banner, Inner Mongolia, China. International Journal of Environmental Research and Public Health. 2017; 14(1):30. https://doi.org/10.3390/ijerph14010030
Chicago/Turabian StyleCao, Chen, Peihua Xu, Jianping Chen, Lianjing Zheng, and Cencen Niu. 2017. "Hazard Assessment of Debris-Flow along the Baicha River in Heshigten Banner, Inner Mongolia, China" International Journal of Environmental Research and Public Health 14, no. 1: 30. https://doi.org/10.3390/ijerph14010030
APA StyleCao, C., Xu, P., Chen, J., Zheng, L., & Niu, C. (2017). Hazard Assessment of Debris-Flow along the Baicha River in Heshigten Banner, Inner Mongolia, China. International Journal of Environmental Research and Public Health, 14(1), 30. https://doi.org/10.3390/ijerph14010030







