Estimation of the Fe and Cu Contents of the Surface Water in the Ebinur Lake Basin Based on LIBS and a Machine Learning Algorithm
Abstract
:1. Introduction
2. Materials and Methods
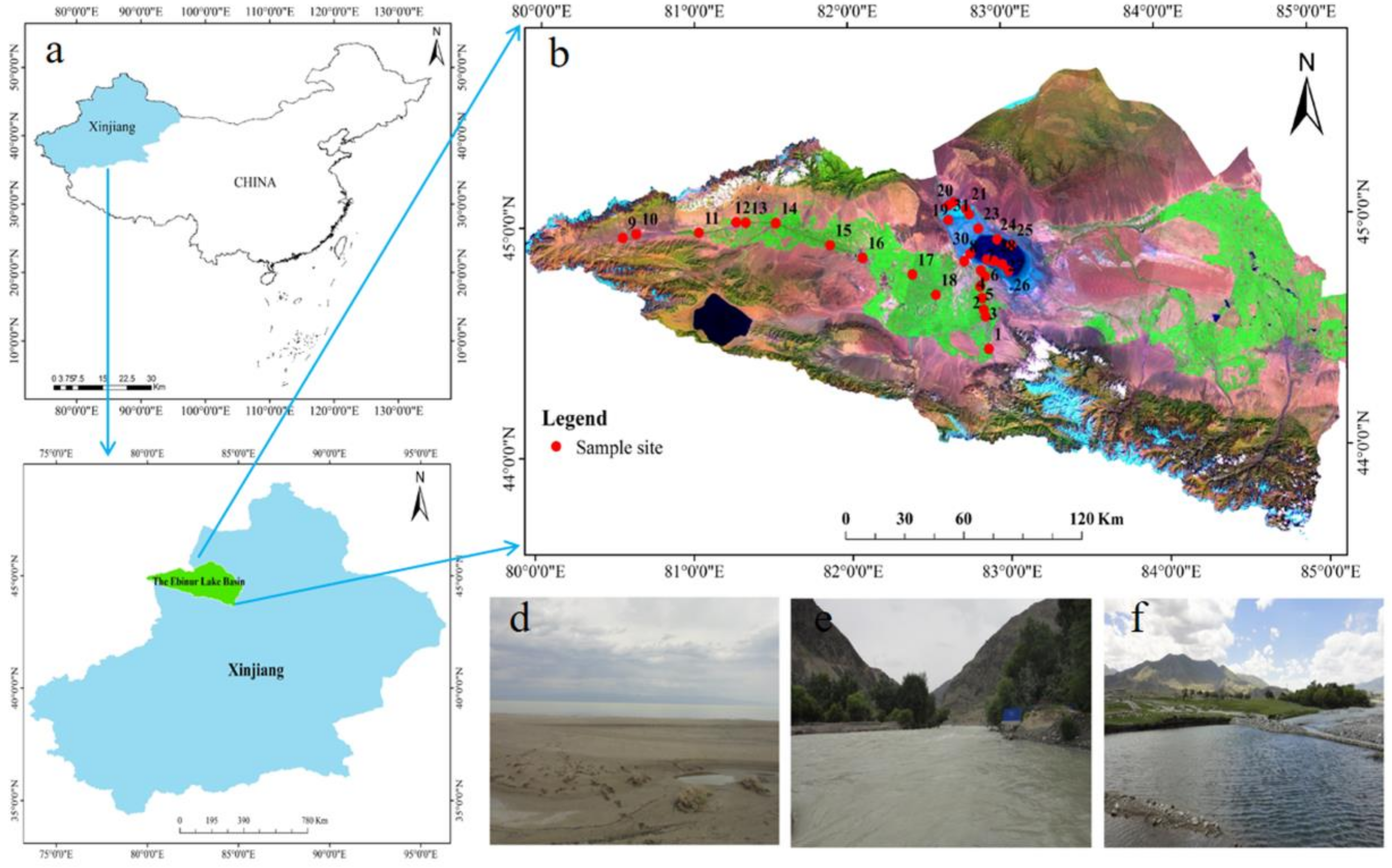
2.1. Study Area
2.2. Sample Collection and Laboratory Analysis
2.3. LIBS Experiment Device and Data Acquisition
2.4. LIBS Data Preprocessing
2.4.1. Baseline Correction Principle and Method
2.4.2. Wavelet Transform Principle and Method
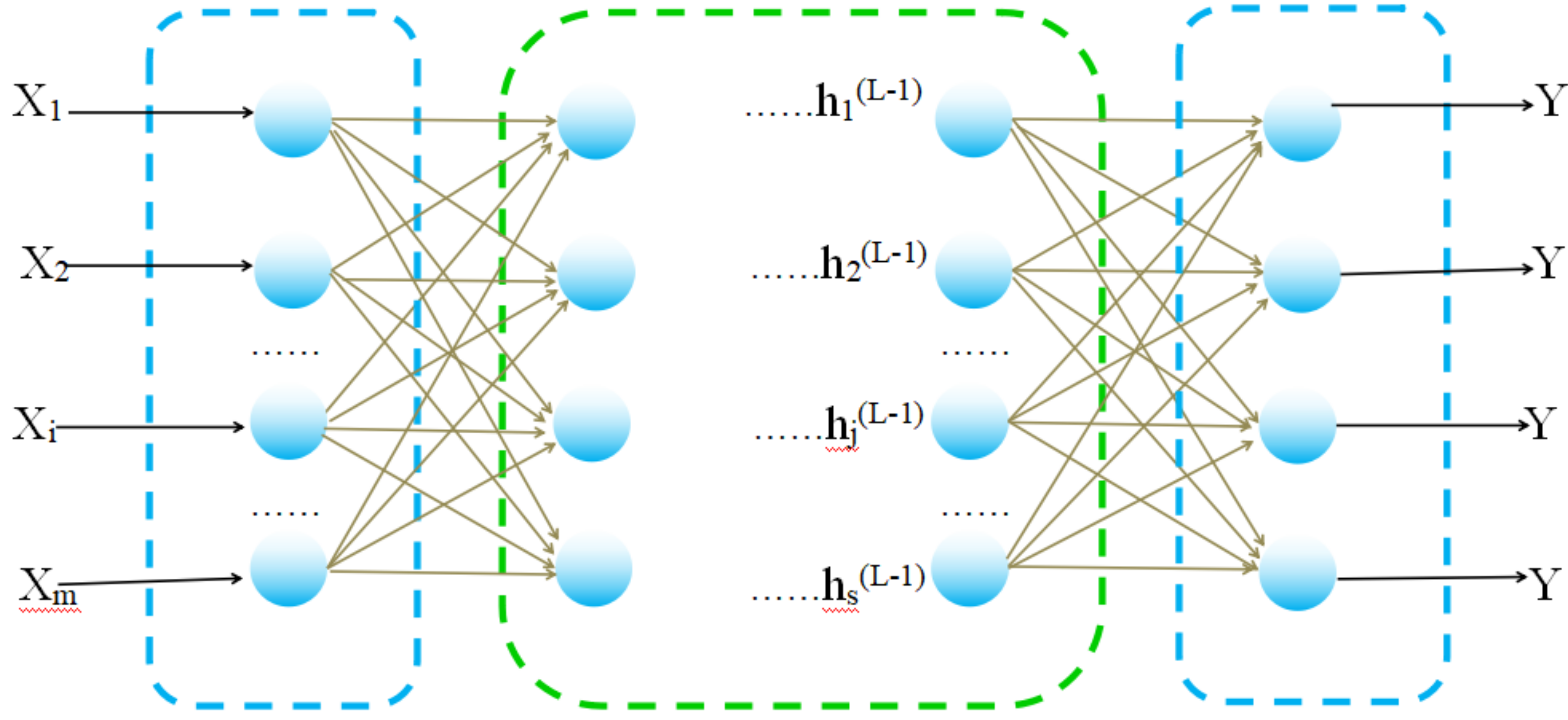
2.5. BP Neural Network Model
2.6. K-Means Clustering Method
2.7. Model Accuracy Test Method
3. Results and Analysis
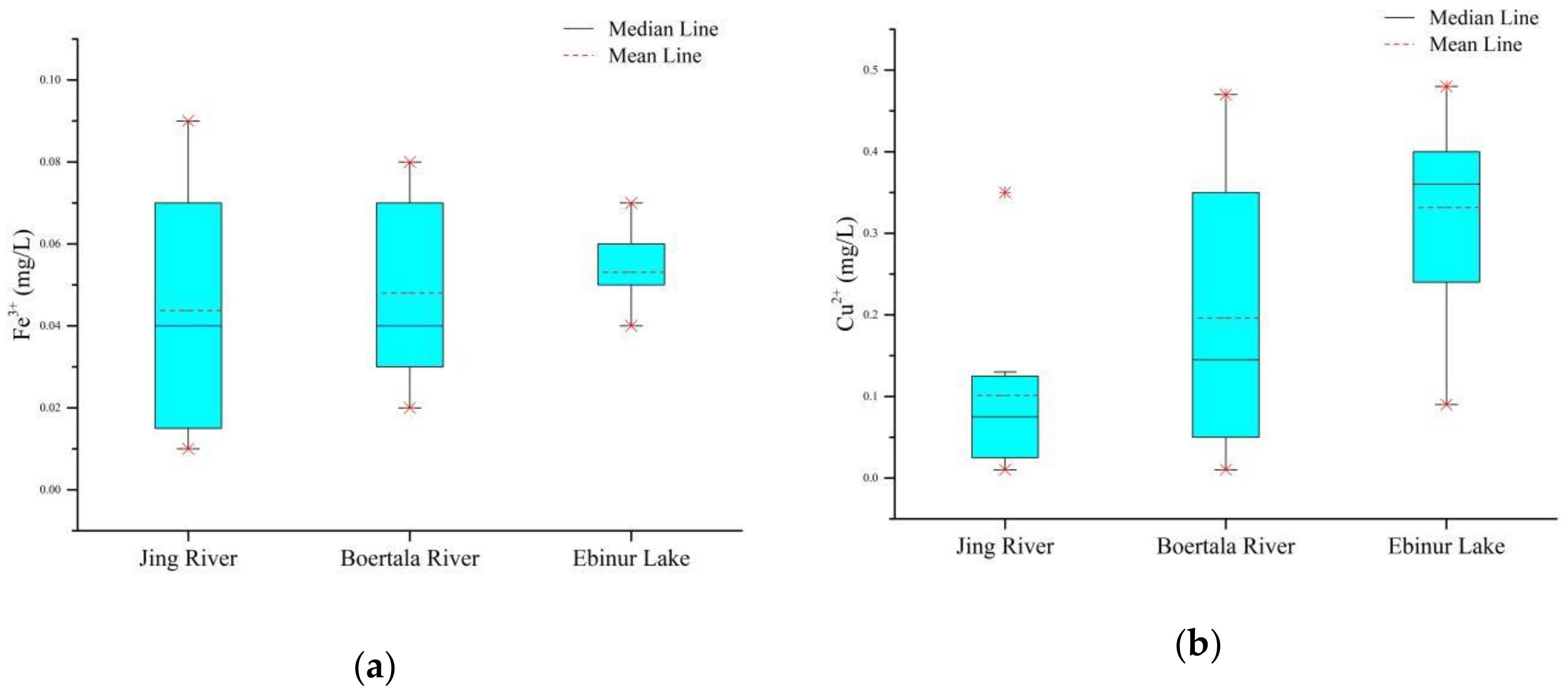
3.1. Statistical Analysis of Fe and Cu Contents
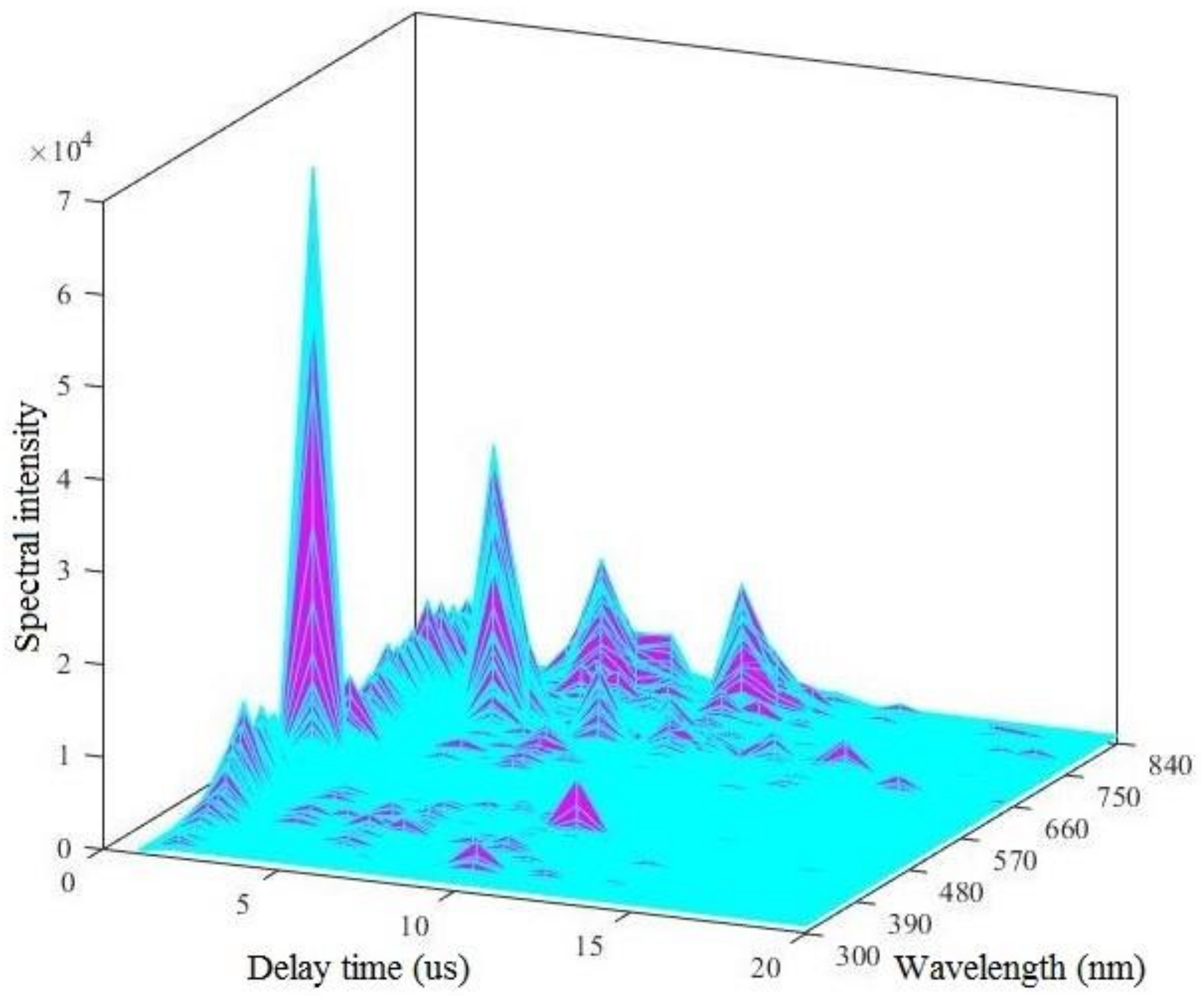
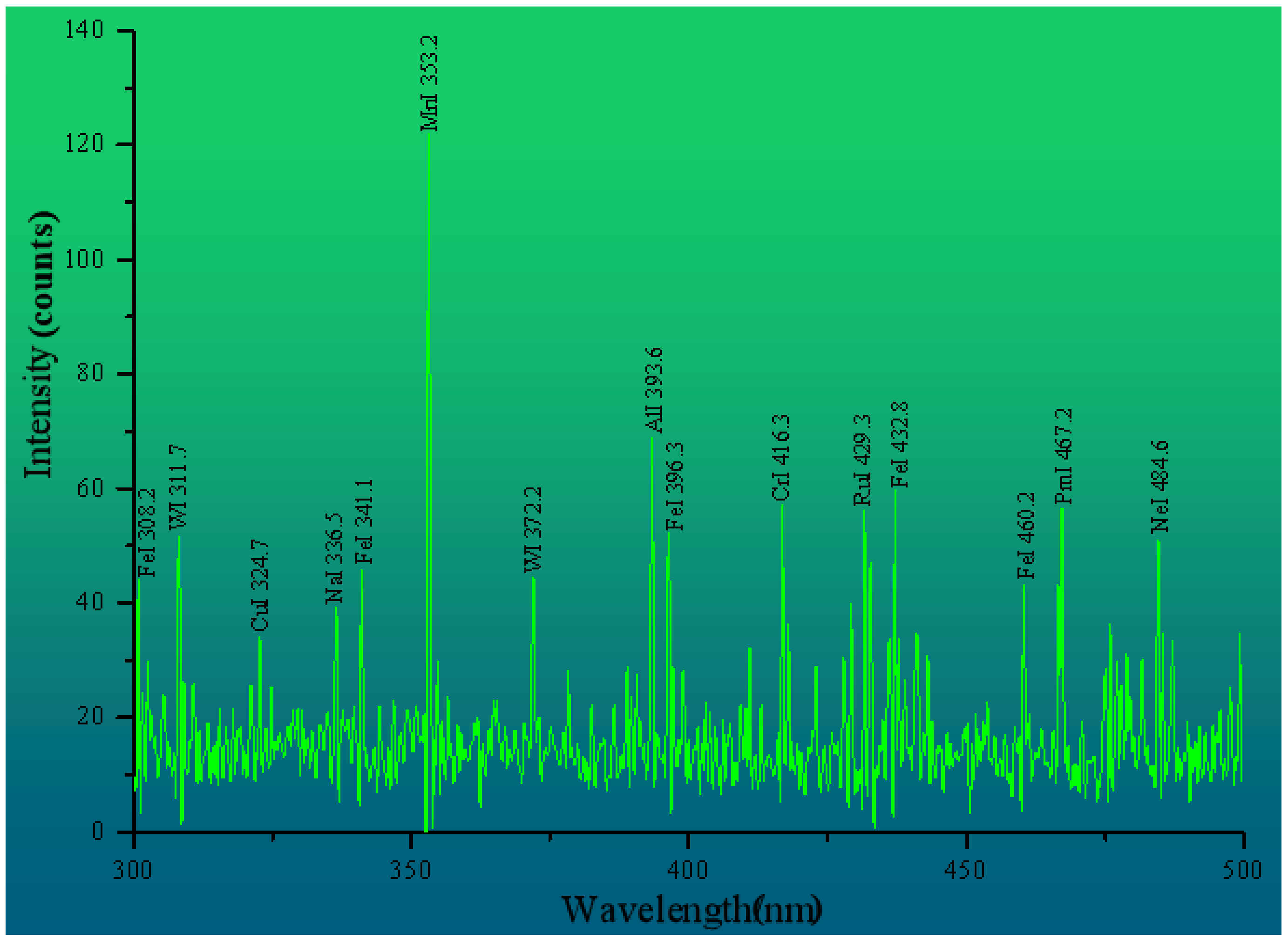
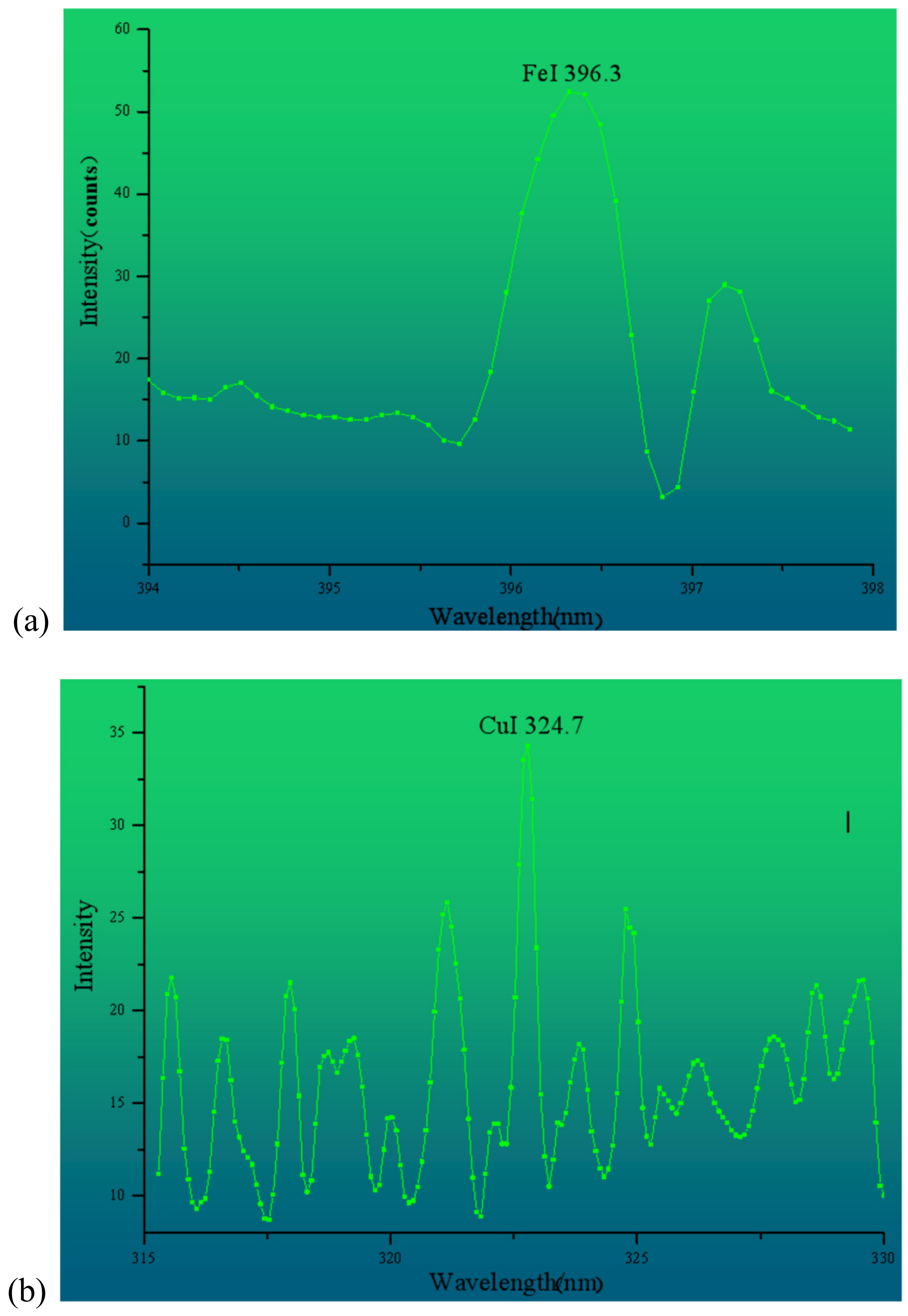
3.2. LIBS Spectral Characteristics of Water Samples
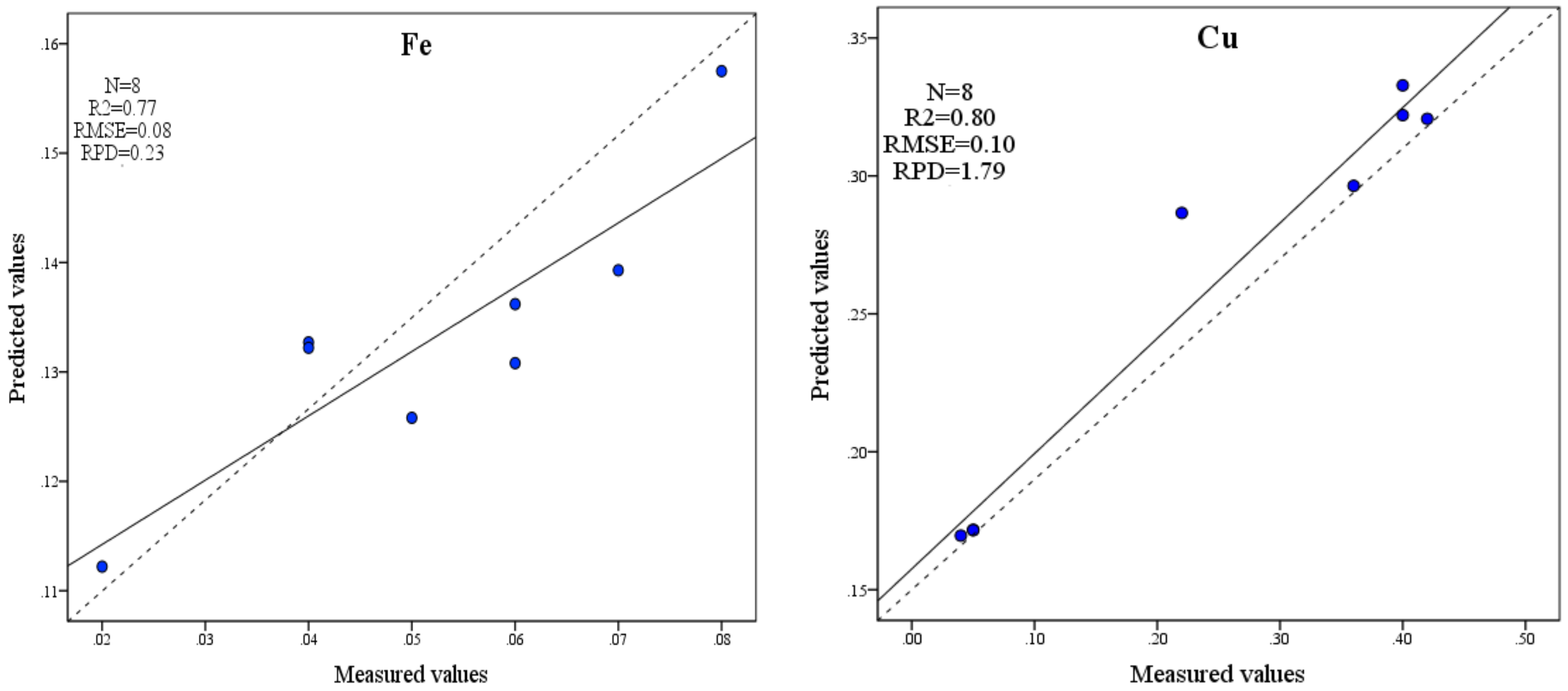
3.3. Establishment and Accuracy Test of the Estimation Model
4. Discussion
4.1. The Innovation of Fe and Cu Content Estimation
4.2. The Shortages of LIBS Data Acquisition and Processing
4.3. The Applicability of the Estimation Model
5. Conclusions
- (1)
- The content of Cu in the Ebinur Lake Basin is higher than that of Fe in general. The average contents of Fe and Cu were highest in Ebinur Lake, and the contents of Fe and Cu were lowest in the Jing River.
- (2)
- A number of peaks were found from the LIBS curve. The characteristic analysis lines of Fe and Cu were finally determined according to factors such as intensities of the characteristic lines for Fe and Cu, transition probability and high S/B. Their wavelengths were 396.3 and 324.7 nm, respectively.
- (3)
- The RPD of the Fe content BP neural network estimation model is 0.23, and the prediction ability is poor; thus, it is impossible to accurately predict the Fe contents of a sample. In the BP neural network estimation model of Cu content, the R2 is 0.8, the RMSE is 0.1 and the RPD is 1.79. This result indicates that the BP neural network estimation model of Cu content has good accuracy and strong predictive ability and can accurately predict the Cu content in the sample.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Guo, M.; Wu, W.; Zhou, X.; Chen, Y.; Li, J. Investigation of the dramatic changes in lake level of the Bosten lake in Northwestern China. Theor. Appl. Climatol. 2015, 119, 341–351. [Google Scholar] [CrossRef]
- Xiao, J.; Jin, Z.; Wang, J.; Zhang, F. Major ion chemistry, weathering process and water quality of natural waters in the Bosten Lake catchment in an extreme arid region, NW China. Environ. Earth Sci. 2015, 73, 3697–3708. [Google Scholar] [CrossRef]
- Zhang, Q.; Xu, H.; Li, Y.; Fan, Z.; Zhang, P.; Yu, P.; Ling, H. Oasis evolution and water resource utilization of a typical area in the inland river basin of an arid area: A case study of the Manas River valley. Environ. Earth Sci. 2012, 66, 683–692. [Google Scholar] [CrossRef]
- Cui, B.; Zhang, Q.; Zhang, K.; Liu, X.; Zhang, H. Analyzing trophic transfer of heavy metals for food webs in the newly-formed wetlands of the Yellow River Delta, China. Environ. Pollut. 2011, 159, 1297–1306. [Google Scholar] [CrossRef] [PubMed]
- Duodu, G.O.; Goonetilleke, A.; Ayoko, G.A. Comparison of pollution indices for the assessment of heavy metal in Brisbane River sediment. Environ. Pollut. 2016, 219, 1077–1091. [Google Scholar] [CrossRef] [PubMed]
- Koelmel, J.; Amarasiriwardena, D. Imaging of metal bioaccumulation in Hay-scented fern (Dennstaedtia punctilobula) rhizomes growing on contaminated soils by laser ablation ICP-MS. Environ. Pollut. 2012, 168, 62–70. [Google Scholar] [CrossRef] [PubMed]
- Massadeh, A.M.; Alomary, A.A.; Mir, S.; Momani, F.A.; Haddad, H.I.; Hadad, Y.A. Analysis of Zn, Cd, As, Cu, Pb, and Fe in snails as bioindicators and soil samples near traffic road by ICP-OES. Environ. Sci. Pollut. Res. 2016, 23, 13424–13431. [Google Scholar] [CrossRef] [PubMed]
- Rao, K.S.; Balaji, T.; Rao, T.P.; Babu, Y.; Naidu, G.R.K. Determination of iron, cobalt, nickel, manganese, zinc, copper, cadmium and lead in human hair by inductively coupled plasma-atomic emission spectrometry. Spectroc. Acta Pt. B-Atom. Spectr. 2002, 57, 1333–1338. [Google Scholar]
- Daşbaşı, T.; Saçmacı, Ş.; Çankaya, N.; Soykan, C. A new synthesis, characterization and application chelating resin for determination of some trace metals in honey samples by FAAS. Food Chem. 2016, 203, 283–291. [Google Scholar] [CrossRef] [PubMed]
- Siraj, K.; Kitte, S.A. Analysis of copper, zinc and lead using atomic absorption spectrophotometer in ground water of Jimma town of Southwestern Ethiopia. Int. J. Chem. Anal. Sci. 2013, 4, 201–204. [Google Scholar] [CrossRef]
- Turdi, M.; Abuduwaili, J.; Jiang, F.Q. Distribution characteristics of soil heavy metal content in northern slope of Tianshan Mountains and its source explanation. Chin. J. Eco-Agric. 2013, 21, 883–890. [Google Scholar]
- O’Neil, M.; Niemiec, N.A.; Demko, A.R.; Petersen, E.L.; Kulatilaka, W.D. Laser induced breakdown spectroscopy based detection of metal particles released into the air during combustion of solid propellants. Appl. Optics 2018, 57, 1910–1917. [Google Scholar] [CrossRef] [PubMed]
- Ji, G.; Ye, P.; Shi, Y.; Yuan, L.; Chen, X.; Yuan, M.; Zhu, D.; Chen, X.; Hu, X. Laser-Induced Breakdown Spectroscopy for Rapid Discrimination of Heavy-Metal-Contaminated Seafood Tegillarca granosa. Sensors 2017, 17, 2655. [Google Scholar] [CrossRef] [PubMed]
- Noda, M.; Deguchi, Y.; Iwasaki, S.; Yoshikawa, N. Detection of carbon content in a high-temperature and high-pressure environment using laser-induced breakdown spectroscopy. Spectroc. Acta Pt. B-Atom. Spectr. 2002, 57, 701–709. [Google Scholar] [CrossRef]
- Barbini, R.; Colao, F.; Lazic, V.; Fantoni, R.; Palucci, A.; Angelone, M. On board LIBS analysis of marine sediments collected during the XVI Italian campaign in Antarctica. Spectroc. Acta Pt. B-Atom. Spectr. 2002, 57, 1203–1218. [Google Scholar] [CrossRef]
- Noll, R.; Bette, H.; Brysch, A.; Kraushaar, M.; Mönch, I.; Peter, L.; Sturm, V. Laser-induced breakdown spectrometry—applications for production control and quality assurance in the steel industry. Spectroc. Acta Pt. B-Atom. Spectr. 2001, 56, 637–649. [Google Scholar] [CrossRef]
- Schmidt, N.E.; Goode, S.R. Analysis of aqueous solutions by laser-induced breakdown spectroscopy of ion exchange membranes. Appl. Spectrosc. 2002, 56, 370–374. [Google Scholar] [CrossRef]
- Gondal, M.A.; Hussain, T. Determination of poisonous metals in wastewater collected from paint manufacturing plant using laser-induced breakdown spectroscopy. Talanta 2007, 71, 73–80. [Google Scholar] [CrossRef] [PubMed]
- Hussain, T.; Gondal, M.A. Detection of toxic metals in waste water from dairy products plant using laser induced breakdown spectroscopy. Bull. Environ. Contam. Toxicol. 2008, 80, 561. [Google Scholar] [CrossRef] [PubMed]
- Järvinen, S.T.; Saari, S.; Keskinen, J.; Toivonen, J. Detection of Ni, Pb and Zn in water using electrodynamic single-particle levitation and laser-induced breakdown spectroscopy. Spectroc. Acta Pt. B-Atom. Spectr. 2014, 99, 9–14. [Google Scholar]
- Bhatt, C.R.; Jain, J.C.; Goueguel, C.L.; McIntyre, D.L.; Singh, J.P. Measurement of Eu and Yb in aqueous solutions by underwater laser induced breakdown spectroscopy. Spectroc. Acta Pt. B-Atom. Spectr. 2017, 137, 8–12. [Google Scholar] [CrossRef]
- Jia, R.; Zhou, J.; Zhou, Y.; Li, Q.; Gao, Y. A Vulnerability Evaluation of the Phreatic Water in the Plain Area of the Junggar Basin, Xinjiang Based on the VDEAL Model. Sustainability 2014, 6, 8604–8617. [Google Scholar] [CrossRef] [Green Version]
- Zhang, F.; Kung, H.T.; Johnson, V.C. Assessment of land-cover/land-use change and landscape patterns in the two national nature reserves of Ebinur Lake Watershed, Xinjiang, China. Sustainability 2017, 9, 724. [Google Scholar] [CrossRef]
- Liu, X.L.; Li, J.G.; Li, X.; Wang, Q.L.; Zhang, L.F.; Liao, W.L. Digital drainage network model of ebinur lake basin of bortala mongol autonomous prefecture based on DEM data. Appl. Mech. Mater. 2014, 522, 1161–1165. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, F.; Ghulam, A.; Trumbo, A.L.; Yang, J.; Ren, Y.; Jing, Y. Evaluation and estimation of surface water quality in an arid region based on EEM-PARAFAC and 3D fluorescence spectral index: A case study of the Ebinur Lake Watershed, China. Catena 2017, 155, 62–74. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, F.; Ding, J. Evaluation of water quality based on a machine learning algorithm and water quality index for the Ebinur Lake watershed, China. Sci. Rep. 2017, 7, 12858. [Google Scholar] [CrossRef] [PubMed]
- Peng, X.L.; Li, Z.H.; Qiang, D.Z. Determination of cadmium content in the food paper and plastic packaging materials with wet digestion-flame atomic absorption spectrometry. In Proceedings of the 2012 International Conference on Biobase Material Science and Engineering, Changsha, China, 21–23 October 2012. [Google Scholar]
- Sallé, B.; Lacour, J.L.; Mauchien, P.; Fichet, P.; Maurice, S.; Manhes, G. Comparative study of different methodologies for quantitative rock analysis by laser-induced breakdown spectroscopy in a simulated Martian atmosphere. Spectroc. Acta Pt. B-Atom. Spectr. 2006, 61, 301–313. [Google Scholar]
- Hwang, S.J.; Moon, S.K.; Kim, S.E.; Kim, J.H.; Choi, S.W. Production of uniform emulsion droplets using a simple fluidic device with a peristaltic pump. Macromol. Res. 2014, 22, 557–561. [Google Scholar] [CrossRef]
- Nge, P.N.; Rogers, C.I.; Woolley, A.T. Advances in microfluidic materials, functions, integration, and applications. Chem. Rev. 2013, 113, 2550–2583. [Google Scholar] [CrossRef] [PubMed]
- Martin, M.Z.; Mayes, M.A.; Heal, K.R.; Brice, D.J.; Wullschleger, S.D. Investigation of laser-induced breakdown spectroscopy and multivariate analysis for differentiating inorganic and organic C in a variety of soils. Spectroc. Acta Pt. B-Atom. Spectr. 2013, 87, 100–107. [Google Scholar] [CrossRef]
- Radziemski, L.; Cremers, D. A brief history of laser-induced breakdown spectroscopy: From the concept of atoms to LIBS 2012. Acta Pt. B-Atom. Spectr. 2013, 87, 3–10. [Google Scholar] [CrossRef]
- Caridi, F. Laser-induced breakdown spectroscopy: Theory and applications, edited by Sergio Musazzi and Umberto Perini. Contemp. Phys. 2017, 58, 273. [Google Scholar] [CrossRef]
- Mccammon, D.; Almy, R.; Apodaca, E.; Bergmanntiest, W.; Cui, W.; Deiker, S.; Morgenthaler, J.P. A high spectral resolution observation of the soft x-ray diffuse background with thermal detectors. Astrophys. J. 2002, 576, 188. [Google Scholar] [CrossRef]
- Sobron, P.; Wang, A.; Sobron, F. Extraction of compositional and hydration information of sulfates from laser-induced plasma spectra recorded under Mars atmospheric conditions—Implications for ChemCam investigations on Curiosity rover. Spectroc. Acta Pt. B-Atom. Spectr. 2012, 68, 1–16. [Google Scholar] [CrossRef]
- Ke, K.E.; Yong, L.; Can-Can, Y.I. Improvement of convex optimization baseline correction in laser-induced breakdown spectral quantitative analysis. Spectrosc. Spectr. Anal. 2018, 38, 2256–2261. [Google Scholar]
- Zhang, B.; Sun, L.X.; Yu, H.B. An improving method for background correction in laser induced breakdown spectroscopy. Appl. Mech. Mater. 2015, 751, 86–91. [Google Scholar] [CrossRef]
- Mallat, S.G. A theory for multiresolution signal decomposition: The wavelet representation. IEEE Trans. Pattern Anal. Mach. Intell. 1989, 11, 674–693. [Google Scholar] [CrossRef]
- Gilles, J. Empirical wavelet transform. IEEE Trans. Signal Process. 2013, 61, 3999–4010. [Google Scholar] [CrossRef]
- Aballe, A.; Bethencourt, M.; Botana, F.J.; Marcos, M. Using wavelets transform in the analysis of electrochemical noise data. Electrochim. Acta 1999, 44, 4805–4816. [Google Scholar] [CrossRef]
- Lu, C.; Shi, B.; Chen, L. Hybrid BP-GA for multilayer feedforward neural networks. IEEE Int. Conference Electron. Circuit Syst. 2000, 2, 958–961. [Google Scholar]
- Cheng, C.G.; Yu, P. Recognition of MIR data of semen armeniacae amarum and semen persicae using discrete wavelet transformation and bp-artificial neural network. Spectroscopy 2012, 27, 253–264. [Google Scholar] [CrossRef]
- Taormina, R.; Chau, K.W.; Sivakumar, B. Neural network river forecasting through baseflow separation and binary-coded swarm optimization. J. Hydrol. 2015, 529, 1788–1797. [Google Scholar] [CrossRef]
- Wu, C.; Chau, K.W. Rainfall–runoff modeling using artificial neural network coupled with singular spectrum analysis. J. Hydrol. 2011, 399, 394–409. [Google Scholar] [CrossRef] [Green Version]
- Pan, H.; Wang, X.Y.; Chen, Q.; Huang, S.L. Application of BP neural network based on genetic algorithm. Comput. Appl. 2005, 25, 2777–2779. [Google Scholar]
- Li, Z.; Zhang, J. Application of the combination of genetic algorithm and artificial neural network on crop yield estimation in Jilin Province. Acta Ecologica Sinica 2001, 21, 716–720. [Google Scholar]
- Verma, M.; Srivastava, M.; Chack, N.; Diswar, A.K.; Gupta, N. A comparative study of various clustering algorithms in data mining. Int. J. Comput. Sci. Mob. Comput. 2014, 3, 1379–1384. [Google Scholar]
- Jain, A.K.; Maheswari, S. Survey of recent clustering techniques in data mining. Int. J. Comput. Sci. Manag. Res. 2012, 3, 72–78. [Google Scholar]
- Berkhin, P. A Survey of Clustering Data Mining Techniques. Grouping Multidimensional Data; Springer: Berlin/Heidelberg, Germany, 2006; pp. 43–71. ISBN 978-3-540-28349-2. [Google Scholar]
- Razakamanarivo, R.H.; Grinand, C. Mapping organic carbon stocks in eucalyptus plantations of the central highlands of madagascar: A multiple regression approach. Geoderma 2011, 162, 335–346. [Google Scholar] [CrossRef]
- Dernoncourt, D.; Hanczar, B.; Zucker, J.D. Stability of ensemble feature selection on high-dimension and low-sample size data: Influence of the aggregation method. In Proceedings of the International Conference on Pattern Recognition Applications and Methods, Angers, France, 6–8 March 2014. [Google Scholar]
- Agranat, M.B.; Andreev, N.E.; Ashitkov, S.I.; Veĭsman, M.E.; Levashov, P.R.; Ovchinnikov, A.V.; Sitnikov, D.S.; Fortov, V.E.; Khishchenko, K.V. Determination of the transport and optical properties of a nonideal solid-density plasma produced by femtosecond laser pulses. JETP Lett. 2007, 85, 271–276. [Google Scholar] [CrossRef]
- Durgesh, K.T.; Rohit, K.; Devendra, K.C.; Awadhesh, K.R.; Dane, B. Laser-induced breakdown spectroscopy for the study of the pattern of silicon deposition in leaves of saccharum species. Instrum. Sci. Tech. 2011, 39, 510–521. [Google Scholar]
- Senesi, G.S.; Dell’Aglio, M.; Gaudiuso, R.; Giacomo, A.D.; Zaccone, C.; Pascale, O.D. Heavy metal concentrations in soils as determined by laser-induced breakdown spectroscopy (libs), with special emphasis on chromium. Environ. Res. 2009, 109, 413–420. [Google Scholar] [CrossRef] [PubMed]
- Guan, Q.; Wang, L.; Wang, L.; Pan, B.; Zhao, S.; Zheng, Y. Analysis of trace elements (heavy metal based) in the surface soils of a desert–loess transitional zone in the south of the tengger desert. Environ. Earth Sci. 2014, 72, 3015–3023. [Google Scholar] [CrossRef]
- Kurniawan, K.H.; Lie, T.J.; Suliyanti, M.M.; Hedwig, R.; Pardede, M.; Kurniawan, D.P.; Kagawa, K. Quantitative analysis of deuterium using laser-induced plasma at low pressure of helium. Anal. Chem. 2014, 78, 5768–5773. [Google Scholar] [CrossRef] [PubMed]
- Bassiotis, I.; Diamantopoulou, A.; Giannoudakos, A.; Roubani-Kalantzopoulou, F.; Kompitsas, M. Effects of experimental parameters in quantitative analysis of steel alloy by laser-induced breakdown spectroscopy. Spectroc. Acta Pt. B-Atom. Spectr. 2001, 56, 671–683. [Google Scholar] [CrossRef]
- Geertsen, C.; Lacour, J.L.; Mauchien, P.; Pierrard, L. Evaluation of laser ablation optical emission spectrometry for microanalysis in aluminium samples. Spectroc. Acta Pt. B-Atom. Spectr. 1996, 51, 1403–1416. [Google Scholar]
- Aguilera, J.A.; Aragón, C. Temperature and electron density distributions of laser-induced plasmas generated with an iron sample at different ambient gas pressures. Appl. Surf. Sci. 2002, 197, 273–280. [Google Scholar] [CrossRef]
- Aguilera, J.A.; Aragón, C.; Peñalba, F. Plasma shielding effect in laser ablation of metallic samples and its influence on libs analysis. Appl. Surf. Sci. 1998, 127, 309–314. [Google Scholar] [CrossRef]
- Paliwal, M.; Kumar, U.A. Neural networks and statistical techniques: A review of applications. Expert Syst. Appl. 2009, 36, 2–17. [Google Scholar] [CrossRef]
- Sirven, J.B.; Bousquet, B.; Canioni, L.; Sarger, L. Laser-induced breakdown spectroscopy of composite samples: Comparison of advanced chemometrics methods. Anal. Chem. 2006, 78, 1462–1469. [Google Scholar] [CrossRef] [PubMed]

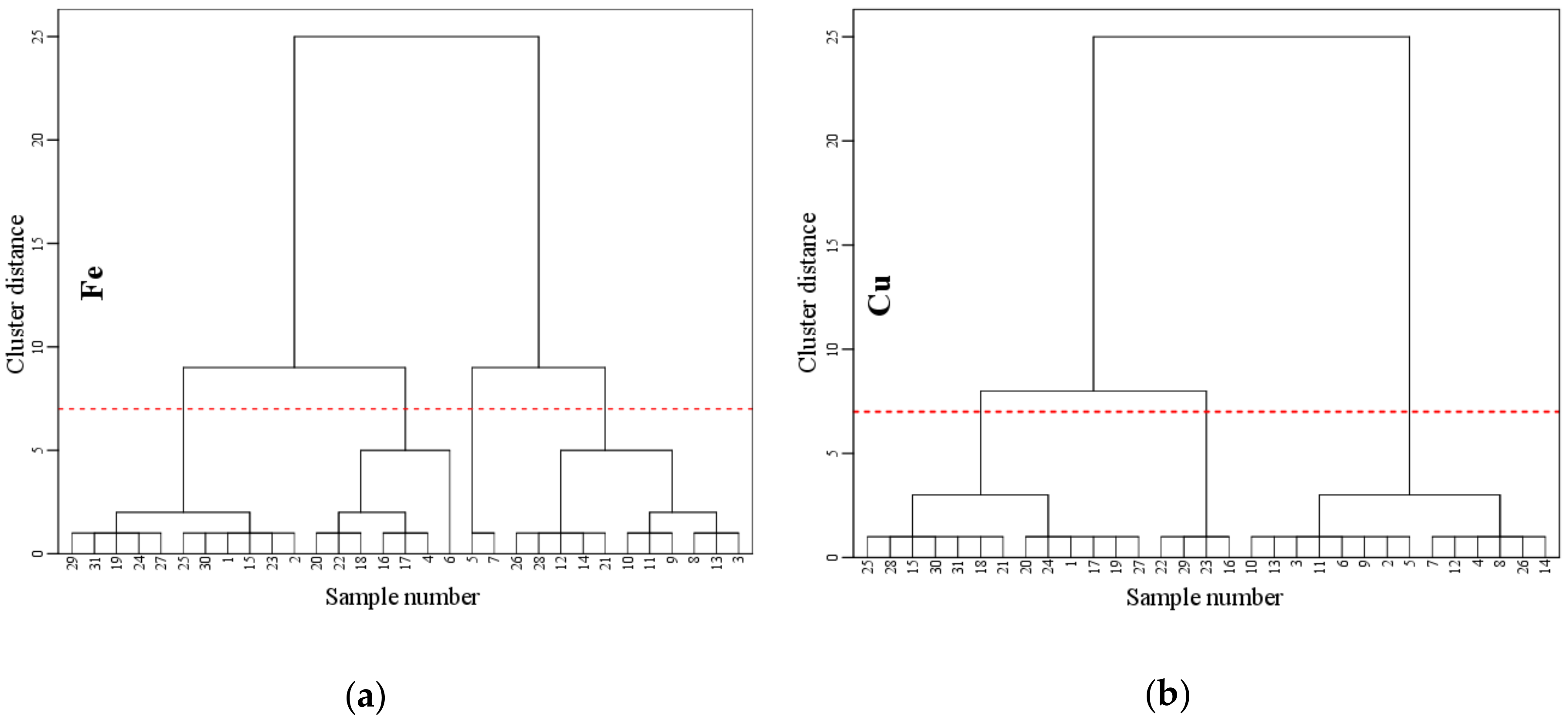
| Ion Species | Sample No. | Clustering Category | Cluster Distance | Sample No. | Clustering Category | Cluster Distance | Sample No. | Clustering Category | Cluster Distance |
|---|---|---|---|---|---|---|---|---|---|
| Fe | #1 | 1 | 0.00143 | #29 | 1 | 0.00857 | #11 | 3 | 0.00625 |
| #2 | 1 | 0.00143 | #30 | 1 | 0.00143 | #12 | 3 | 0.00375 | |
| #15 | 1 | 0.00143 | #31 | 1 | 0.00857 | #14 | 3 | 0.00375 | |
| #18 | 1 | 0.01143 | #3 | 2 | 0.004 | #21 | 3 | 0.00375 | |
| #19 | 1 | 0.00857 | #5 | 2 | 0.006 | #26 | 3 | 0.00375 | |
| #20 | 1 | 0.01143 | #7 | 2 | 0.006 | #28 | 3 | 0.00375 | |
| #22 | 1 | 0.01143 | #8 | 2 | 0.004 | #4 | 4 | 0.0025 | |
| #23 | 1 | 0.00143 | #13 | 2 | 0.004 | #6 | 4 | 0.0075 | |
| #24 | 1 | 0.00857 | #9 | 3 | 0.00625 | #16 | 4 | 0.0025 | |
| #25 | 1 | 0.00143 | #10 | 3 | 0.00625 | #17 | 4 | 0.0025 | |
| #27 | 1 | 0.00857 | |||||||
| Cu | #1 | 1 | 0.04538 | #30 | 1 | 0.04462 | #10 | 2 | 0.01385 |
| #15 | 1 | 0.02462 | #31 | 1 | 0.05462 | #11 | 2 | 0.02385 | |
| #17 | 1 | 0.04538 | #2 | 2 | 0.03385 | #12 | 2 | 0.06615 | |
| #18 | 1 | 0.07462 | #3 | 2 | 0.02385 | #13 | 2 | 0.01385 | |
| #19 | 1 | 0.03538 | #4 | 2 | 0.05615 | #26 | 2 | 0.02615 | |
| #20 | 1 | 0.07538 | #5 | 2 | 0.04385 | #14 | 3 | 0.062 | |
| #21 | 1 | 0.08462 | #6 | 2 | 0.05385 | #16 | 3 | 0.058 | |
| #24 | 1 | 0.06538 | #7 | 2 | 0.06615 | #22 | 3 | 0.002 | |
| #25 | 1 | 0.00462 | #8 | 2 | 0.04615 | #23 | 3 | 0.018 | |
| #27 | 1 | 0.02538 | #9 | 2 | 0.05385 | #29 | 3 | 0.012 | |
| #28 | 1 | 0.00462 |
| Ion Species | Model | Sample Size | Minimum (mg/L) | Maximum (mg/L) | Mean (mg/L) | Standard Deviation | Variance/% |
|---|---|---|---|---|---|---|---|
| Fe | Estimation | 23 | 0.01 | 0.09 | 0.05 | 0.02 | 47.16 |
| Verification | 8 | 0.02 | 0.08 | 0.05 | 0.02 | 34.9 | |
| Cu | Estimation | 23 | 0.01 | 0.48 | 0.22 | 0.16 | 71.97 |
| Verification | 8 | 0.04 | 0.42 | 0.24 | 0.17 | 71.52 |
| Elements | Wavelength (nm) | Transition | Rel. Int. | |
|---|---|---|---|---|
| Upper Level | Lower Level | |||
| OΙ | 777.2 | 2s22p3(4s°)3p | 2s22p3(4s°)3s | 870 |
| H | 656.3 | 3p 2P° 1/2 | 2s 2S 1/2 | 500000 |
| FeΙ | 308.2 | 3d6(3F2)4s4p(3P°) | 3d7(4F)4s | 1 |
| FeΙ | 341.1 | 3d6(3G)4s4p(3P°) | 3d7(2G)4s | 1550 |
| FeΙ | 396.3 | 3d6(5D)4s(6D)4d | 3d6(5D)4s4p(3P°) | 5500 |
| FeΙ | 460.2 | 3d7(4F)4p | 3d7(4F)4s | 760 |
| CuΙ | 324.7 | 3d104p | 3d104s | 10000r |
| CuΙ | 327.4 | 3d104p | 3d104s | 10000r |
| Estimation Model of Elements | R2 | RMSE | SD | RPD |
|---|---|---|---|---|
| Fe | 0.89 | 0.82 | 6.51 | 7.93 |
| Cu | 0.82 | 0.40 | 8.28 | 20.48 |
© 2018 by the authors. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Zhang, F.; Kung, H.-t.; Shi, P.; Yushanjiang, A.; Zhu, S. Estimation of the Fe and Cu Contents of the Surface Water in the Ebinur Lake Basin Based on LIBS and a Machine Learning Algorithm. Int. J. Environ. Res. Public Health 2018, 15, 2390. https://doi.org/10.3390/ijerph15112390
Zhang X, Zhang F, Kung H-t, Shi P, Yushanjiang A, Zhu S. Estimation of the Fe and Cu Contents of the Surface Water in the Ebinur Lake Basin Based on LIBS and a Machine Learning Algorithm. International Journal of Environmental Research and Public Health. 2018; 15(11):2390. https://doi.org/10.3390/ijerph15112390
Chicago/Turabian StyleZhang, Xianlong, Fei Zhang, Hsiang-te Kung, Ping Shi, Ayinuer Yushanjiang, and Shidan Zhu. 2018. "Estimation of the Fe and Cu Contents of the Surface Water in the Ebinur Lake Basin Based on LIBS and a Machine Learning Algorithm" International Journal of Environmental Research and Public Health 15, no. 11: 2390. https://doi.org/10.3390/ijerph15112390
APA StyleZhang, X., Zhang, F., Kung, H.-t., Shi, P., Yushanjiang, A., & Zhu, S. (2018). Estimation of the Fe and Cu Contents of the Surface Water in the Ebinur Lake Basin Based on LIBS and a Machine Learning Algorithm. International Journal of Environmental Research and Public Health, 15(11), 2390. https://doi.org/10.3390/ijerph15112390







