In practical water quality monitoring applications, the number of monitoring stations is mainly restricted by several factors such as the total costs of building and operating the infrastructure, the requirement of monitoring performance, etc. In order to gain a deeper understanding about how the dynamic characteristics of a river system affect the optimum design of water quality monitoring network, we carry out four groups of simulations in the following section. We also assume that only 3 monitoring devices will be deployed within the 12 potential monitoring locations.
3.1. Simulation for River Network A with a Pollution Detection Threshold of 0.01 mg/L
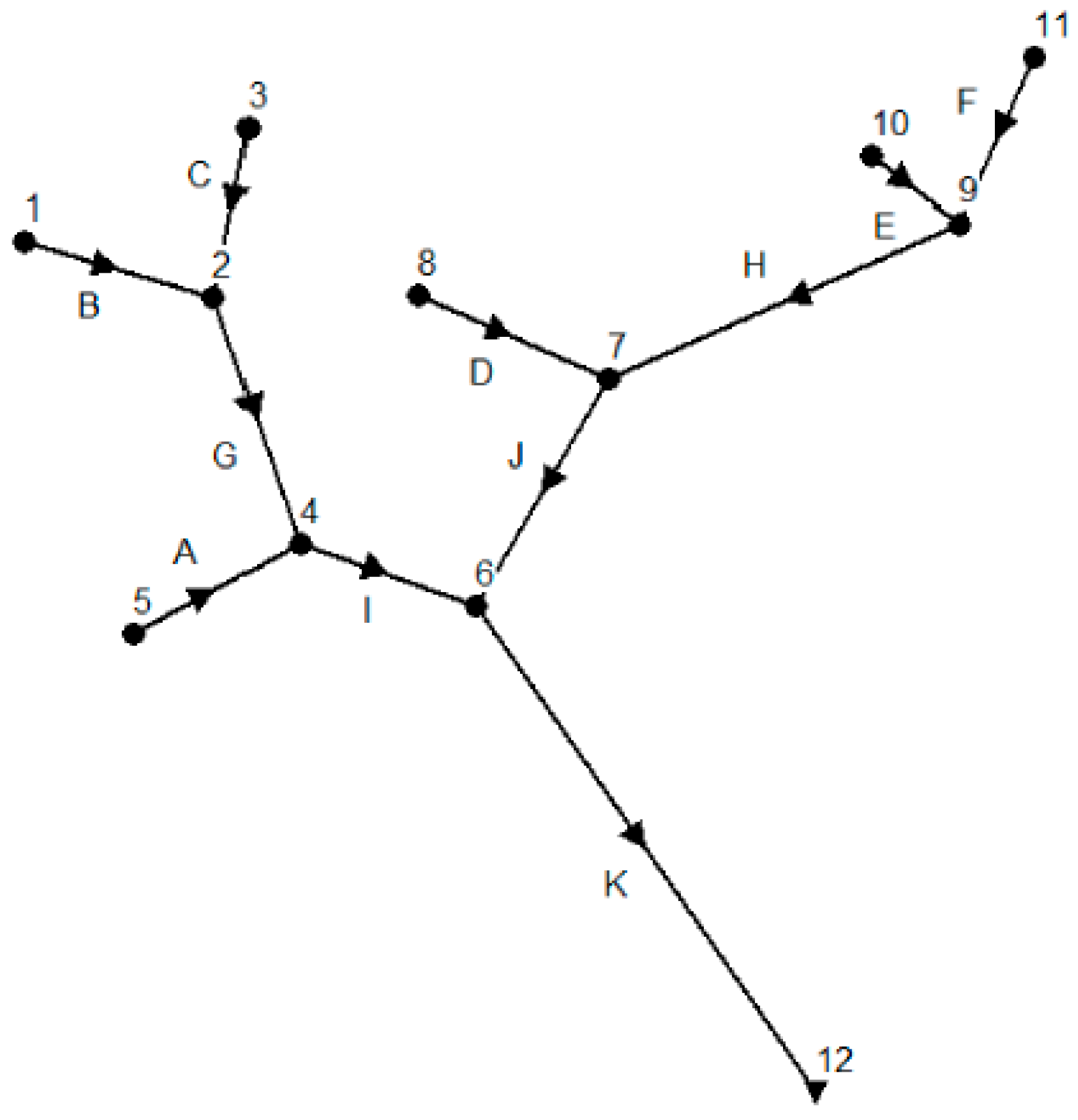
Before simulation, we set the simulation options for the hypothetical river network A shown in
Figure 1. We use the Kinematic Wave routing model and the Horton infiltration model in the simulation. We let the reporting time step and routing time step be 60 s and 30 s separately. Simulation results show that the continuity error for flow routing and quality routing are only −0.77% and 0.00% respectively. We simulate pollution events at each potential monitoring location and get pollution time and pollutant concentration from the report generated by SWMM. A simple program is also developed to automatically calculate the pollution detection time for each potential monitoring location according to the pollutant detection threshold.
Table 2 shows the simulation results of pollution detection time for each potential monitoring location when we set the pollution detection threshold to 0.01 mg/L. The value of ‘-’ in
Table 2 represents an infinite value, which means the pollution event cannot be successfully detected at a monitoring location. For example, the first row in
Table 2 demonstrates a scenario that a pollution event occurs at location 1 and can be detected at locations 1, 2, 4, 6, and 12. The pollution detection time for these locations are 0 (detected immediately), 27, 81, 118, and 198 min respectively. However, this pollution event cannot be detected at locations 3, 5, 7, 8, 9, 10, or 11 because the polluted water flow cannot reach these locations.
We run the MOPSO algorithm based on data in
Table 2. For the validation of MOPSO to confirm whether the simulation results are steady or not, we run the simulation several times. The simulation results show that though the main particles are quite different from each other, their Pareto frontiers are almost the same.
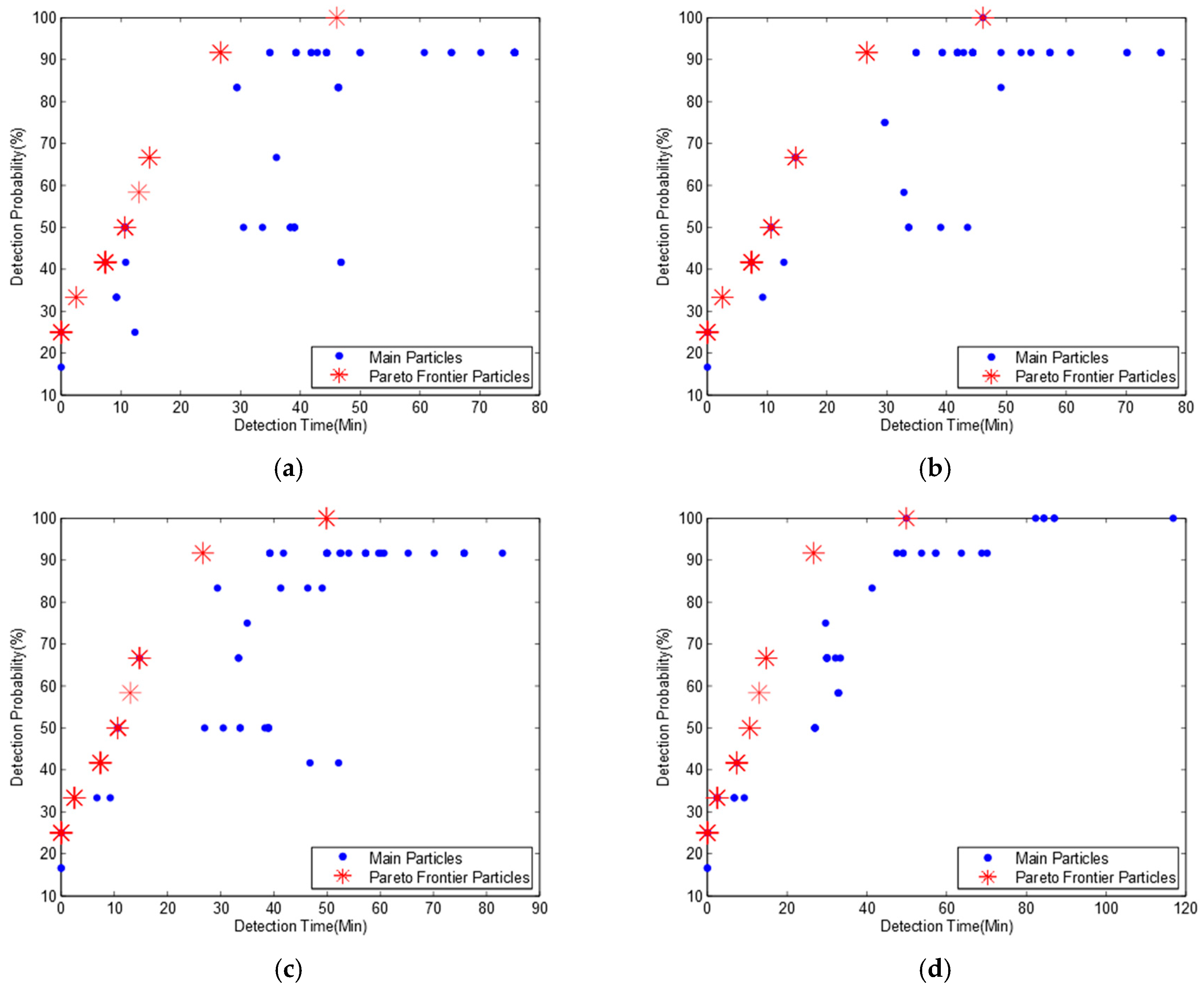
Figure 2 shows four Pareto frontiers in four different sub-diagrams with eight non-dominated particles. The mean pollution detection time, pollution detection probability and optimum monitoring locations for each non-dominated particle are shown in
Table 3.
Table 3 indicates that if we deploy three monitoring devices at locations 6, 9, and 12 respectively, all the pollution events can be detected, which is the same as the result in Telci’s paper. If monitoring devices are deployed at locations 2, 6, and 9, the pollution detection probability will be slightly decreased to 91.7% while the mean pollution detection time is also reduced from 45.8 min to 26.6 min. It is also the second maximum pollution detection probability on the Pareto frontier. However, the second maximum pollution detection probability in Telci’s paper is 83%, and the monitoring locations are 4, 7, and 9, which can also be found in our main particles in
Figure 2, but it is not a non-dominated particle. Based on this observation, we confirm that our algorithm can get a better Pareto frontier and more detailed optimal deployment solutions. It should be noted that some deployment solutions in
Table 3 have much lower pollution detection time and pollution detection probability than others. Though these deployment solutions are also from non-dominated particles, they have little chance to be selected from an engineering point of view.
Telci et al. (2008) used a penalty for non-detected pollution scenarios resulting in a much higher pollution detection time for non-100% detected pollution scenarios. We argue that it is not reasonable, because the mean detection time represents how long the pollution event will be detected if it can be detected by current monitoring network. On the contrary, if a pollution event cannot be detected, the detection probability will be decreased to reflect this non-detected scenario. So, we ignore these non-detected pollution events when we calculate the mean pollution detection time, which results in a shorter mean pollution detection time than in Telci’s paper.
Comparing
Table 3 to
Figure 2, we find that there are 13 different monitoring deployment solutions mapping to eight non-dominated particles. This is because some deployment solutions with different monitoring locations have the same mean detection time and detection probability, and they map to a same non-dominated particle.
To further confirm whether our algorithm can obtain a full Pareto frontier or not, we developed an enumeration search algorithm. It can exhaustively search all the combinations of potential deployment solutions and obtain all non-dominated deployment solutions.
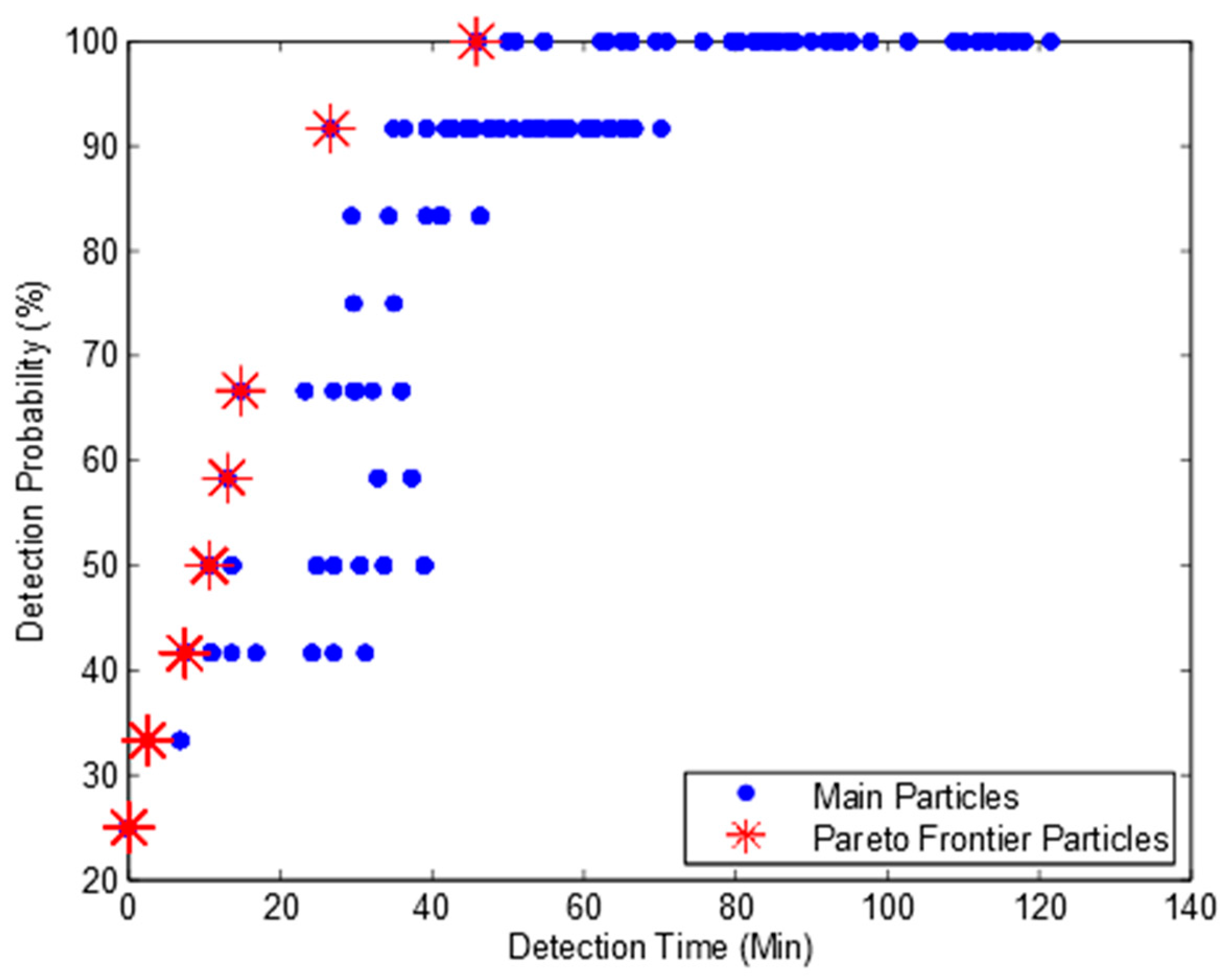
Figure 3 shows the Pareto frontier. We can find from
Figure 2 and
Figure 3 that the enumeration search algorithm obtains much more particles than our algorithm. This is because the enumeration search algorithm lists all the possible combinations. However, both our algorithm and enumeration search algorithm obtain the same Pareto frontier with eight Pareto particles. Based on this observation, we can confirm that our algorithm can obtain the full Pareto frontier and is suitable to be used for the optimum design of water quality monitoring network.
3.2. Simulation for a Reversed River Network B with Pollution Detection Threshold of 0.01 mg/L
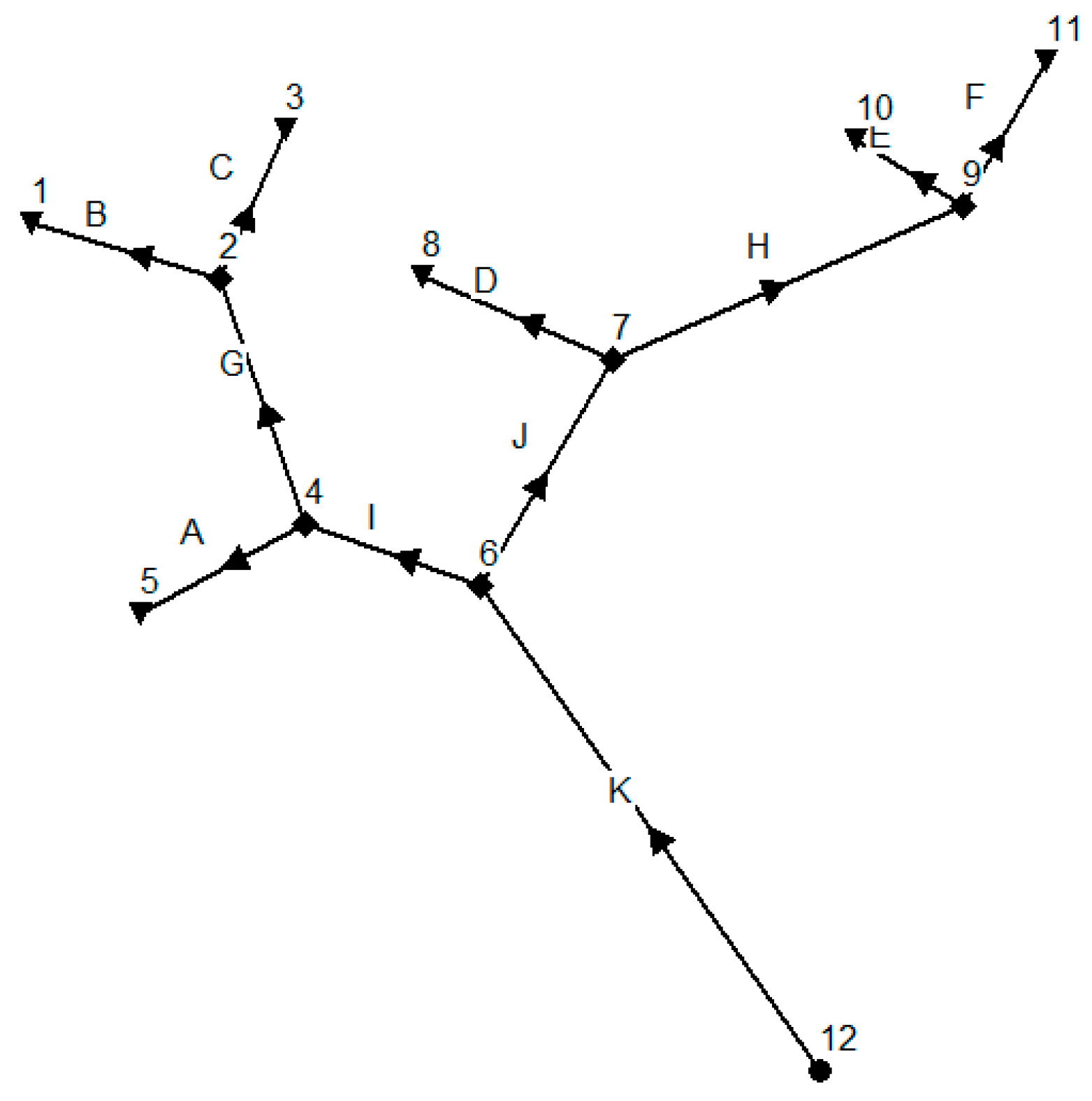
Most of the literature only considers the unidirectional water flow. However, influenced by tides, some river systems have bidirectional water flows. In order to observe how far the bidirectional water flows can affect the monitoring network optimization, we create river network B shown in
Figure 4 with the same parameters and settings as river network A in
Figure 1 but having a reversed water flow direction, resulting in a new river network with six outlet nodes, five intermediate nodes, and only one inlet node. We set the water flow rate of inlet node 12 to 60 ft
3/s, which is as same as the water flow rate at outlet node 12 in
Figure 1. We run the hydraulic simulation in SWMM again and obtain pollution detection time shown in
Table 4. We can find from
Table 2 and
Table 4 that when we reverse the water flow, we get a transposed pollution detection time matrix.
Due to the page limit, only one MOPSO Pareto frontier is shown here in
Figure 5. The optimum deployment solutions are shown in
Table 5.
We find that when we reverse the water flow direction, there are seven non-dominated particles in Pareto frontier and there is no 100% detection probability solution for river network B. The maximum pollution detection probability is decreased to 75% with a mean pollution detection time of 38.2 min and the optimization monitoring locations are 3, 5, and 10. This is because there are six outlet locations in river network B, and only three monitoring devices cannot detect all the pollution scenarios occurred randomly in 12 potential locations.
Comparing
Table 5 to
Table 3, we find that the optimization results for both water flow directions are quite different. Based on this observation, we argue that the water flow direction has a significant effect on optimization results of monitoring network design even for the same river system and we should consider the bidirectional water flows when we design an optimization monitoring network for a river system affected by tides regularly.
3.3. Simulation with Bidirectional Water Flows
For having a deep insight of the influence of bidirectional water flows for an optimum monitoring network design, we calculate the mean pollution detection time for both the original river network A (
Figure 1) and the reversed river network B (
Figure 4) at the same time based on the data of pollution detection time in
Table 2 and
Table 4. As water flow directions can be changed regularly due to tides and the duration for each flow direction may not be equal in a river system. So, we consider two scenarios here when a pollution event occurs:
We slightly modify the previous fitness function in Algorithm 2 and add two extra parameters of probA and probB in the procedure to denote the probability of the two water flows in a river system. We calculate the pollution detection time and pollution detection probability for bidirectional water flows respectively and get the final mean pollution detection time and probability for two water flows at last. The new fitness function is shown in Algorithm 3.
3.3.1. Bidirectional Water Flows with the Same Probability
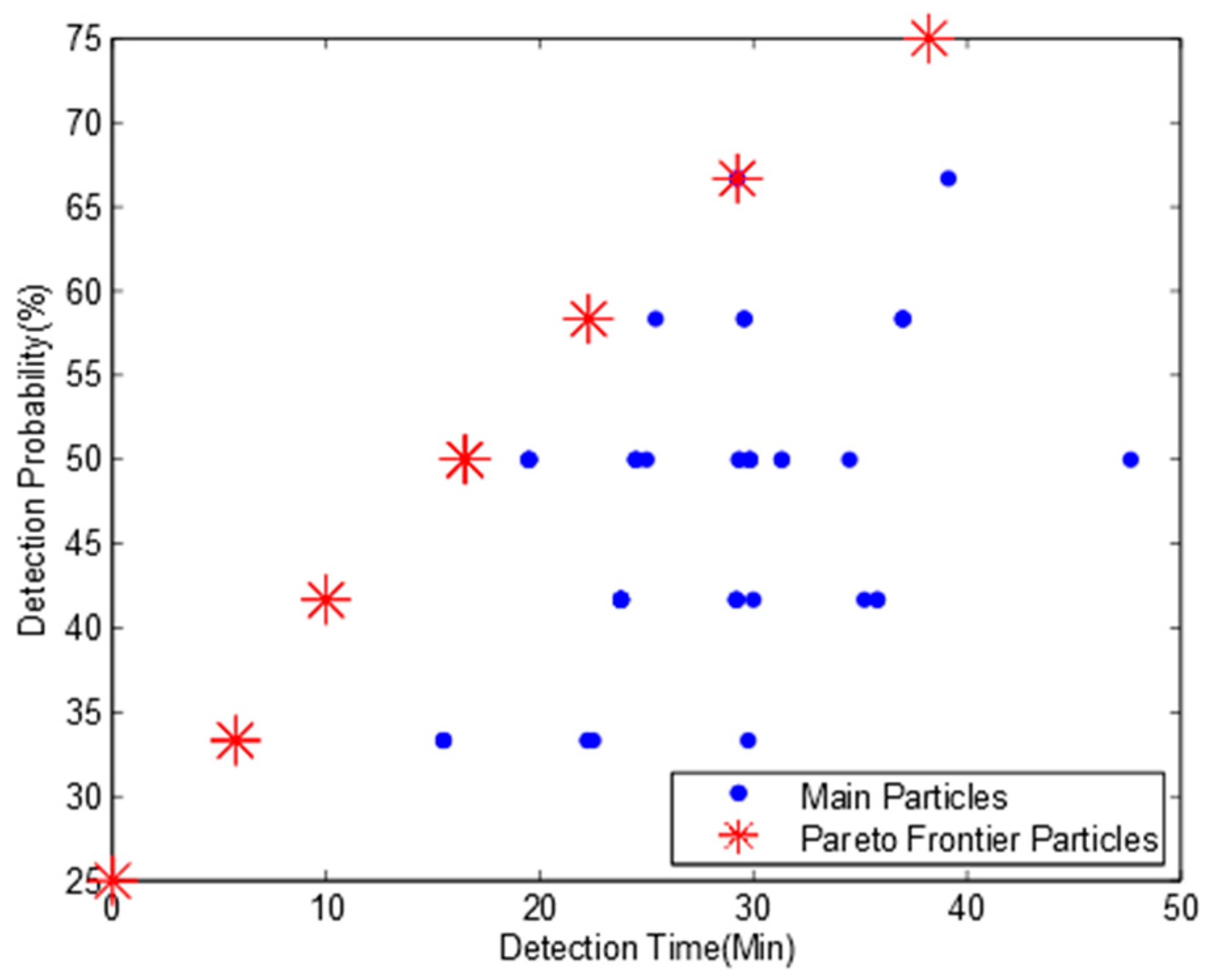
We let
probA and
probB in Algorithm 3 be 0.5 separately to assume that each water flow with a different direction has the same probability. The simulation results of Pareto frontier and optimization monitoring locations are shown in
Figure 6 and
Table 6.
Comparing
Table 6 to
Table 3 and
Table 5, we observe that when we consider the bidirectional water flows, the maximum detection probability is decreased from 100% (in
Table 3) and 75% (in
Table 5) to 66.7%, respectively, while the mean pollution detection time is increased from 45.8 and 38.2 min to 57.9 min. This is because we consider the pollution detection time and detection probability for each water flow respectively and combine them together to obtain the mean pollution detection time and probability based on the time ratio of two reversed water flows, which will significantly increase the pollution detection time and decrease the detection probability. We also find that the optimum deployment solutions are quite different from the previous results in
Table 3 and
Table 5 and the deployment solution of monitoring locations 3, 10, 12 has the highest pollution detection probability of 66.7% with a mean pollution detection time of 57.9 min.
| Algorithm 3 Pseudocode of Bidirectional Fitness Function
|
| Procedure BidirectionalFitnessCost (Particle p, probA, probB) |
| Array pos = n position values in particle p |
| Array loc =[] |
| For each element in pos |
| node = round(element) |
| loc = node |
| EndFor |
| meanTime = 0 |
| count = 0 |
| probability = 0 |
| For each row 1 in Table 2 and row 2 in Table 4 |
| detectTimeA = MAX |
| detectTimeB = MAX |
| For each l in loc |
| detectTimeA = min (detectTimeA, row 1(l)) |
| detectTimeB = min (detectTimeB, row 2(l)) |
| EndFor |
| If detectTimeA ≠ MAX & detectTimeB ≠ MAX then |
| avgTime = detectTimeA * porbA + detectTimeB * probB |
| meanTime = meanTime + avgTime |
| count = count + 1 |
| EndIf |
| EndFor |
| meanTime = meanTime/count |
| probability = row.length/count |
| Return (meanTime, probability) |
| End Procedure |
3.3.2. Bidirectional Water Flows with Different Probabilities
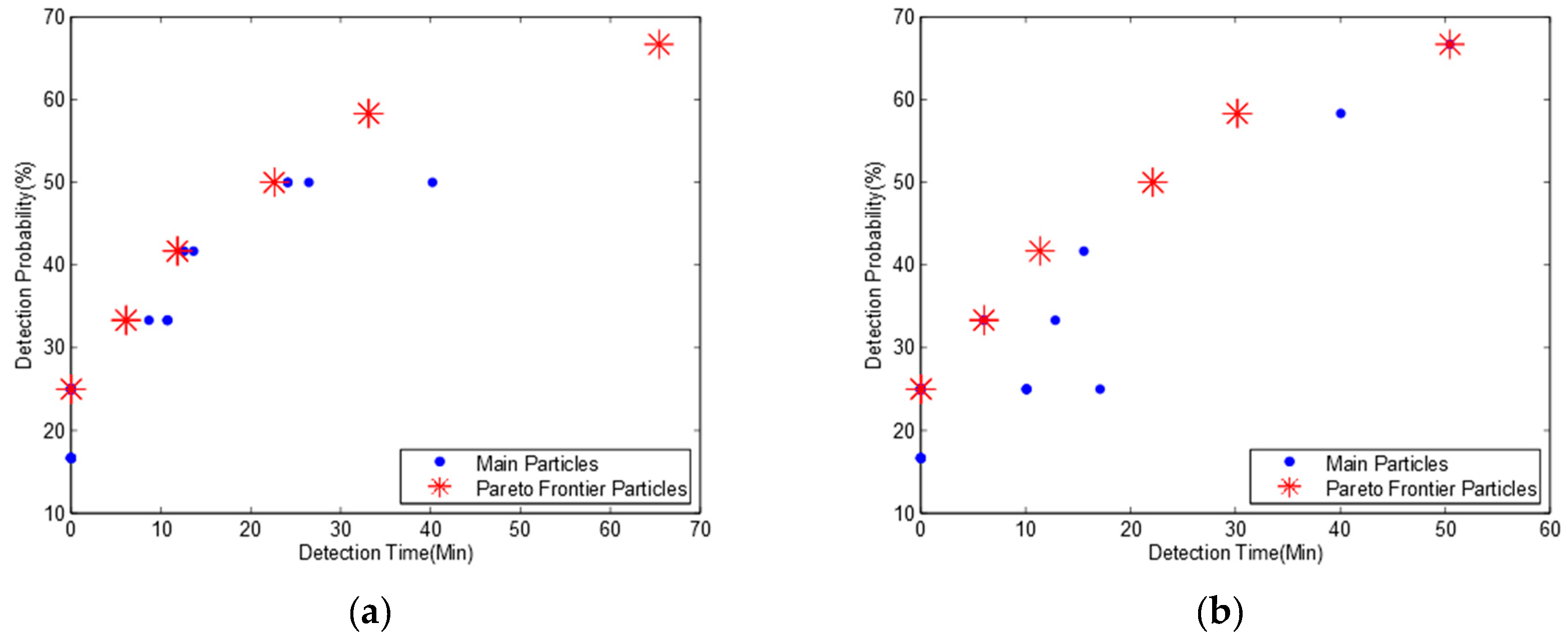
Here we assume that two water flows in a river system have different probabilities. We consider two scenarios: (1) the probability of the water flow as river network A is 70% and the reversed water flow as river network B is 30%. (2) the probability of the water flow as river network A is 30% and the reversed water flow as river network B is 70%. We set the parameter of
probA to 0.7 and
probB to 0.3 for the first scenario and exchange the value with each other for the second scenario. We obtain two Pareto frontiers in
Figure 7 and two pollution detection time and probabilities in
Table 7.
We find from
Table 6 and
Table 7a, that though we set 70% probability for river network A and 30% probability for river network B, we get the same optimization monitoring locations and detection probabilities while the pollution detection time is slightly increased. This is because the pollution detection time for river network A (
Table 3) is slightly higher than for river network B (
Table 5) resulting in a higher mean pollution detection time. When we reverse the probability of the two water flows, we get similar results but with a lower mean pollution detection time in
Table 7b.
Comparing
Table 7a to
Table 7b, we observe that though we exchange the probabilities of two water flows, we obtain the same optimal monitoring locations and the same detection probability while the pollution detection time is slightly increased.
Based on the observation above, we draw a conclusion that the bidirectional water flows have a significant effect on an optimal monitoring network design. However, the different probabilities of bidirectional water flows have no effect on the optimization results of monitoring location selection or the pollution detection probability but slightly affect the pollution detection time.
3.4. Higher Pollution Detection Threshold for Bidirectional Water Flows
To observe how far the pollution detection threshold can affect the optimum deployment solution for a bidirectional water flow river system, we assume two bidirectional water flows have the same probability and set the pollution detection threshold to 1 mg/L and 2 mg/L respectively. We run the hydraulic simulation in SWMM again based on river networks A and B.
Table 8 and
Table 9 show four pollution detection time tables for both detection thresholds.
We find that all the pollution detection time in
Table 8a are much higher than in
Table 2 except for non-detected scenarios. This is because when we increase the pollution detection threshold from 0.01 mg/L to 1 mg/L for river network A, it will take more time to reach a certain pollutant concentration at each potential monitoring location before pollutants can be detected, which will significantly increase the pollution detection time.
Comparing
Table 8a to
Table 8b, we find that all the pollution events can be successfully detected at location 12 when the pollution detection threshold is 1 mg/L. However, no pollution event can be detected at location 12 when the pollution detection threshold is 2 mg/L, even if the pollution event occurs at location 12 itself. This is because the pollution detection threshold is so high that it is even higher than the maximum pollutant concentration at location 12 when any pollution event occurs.
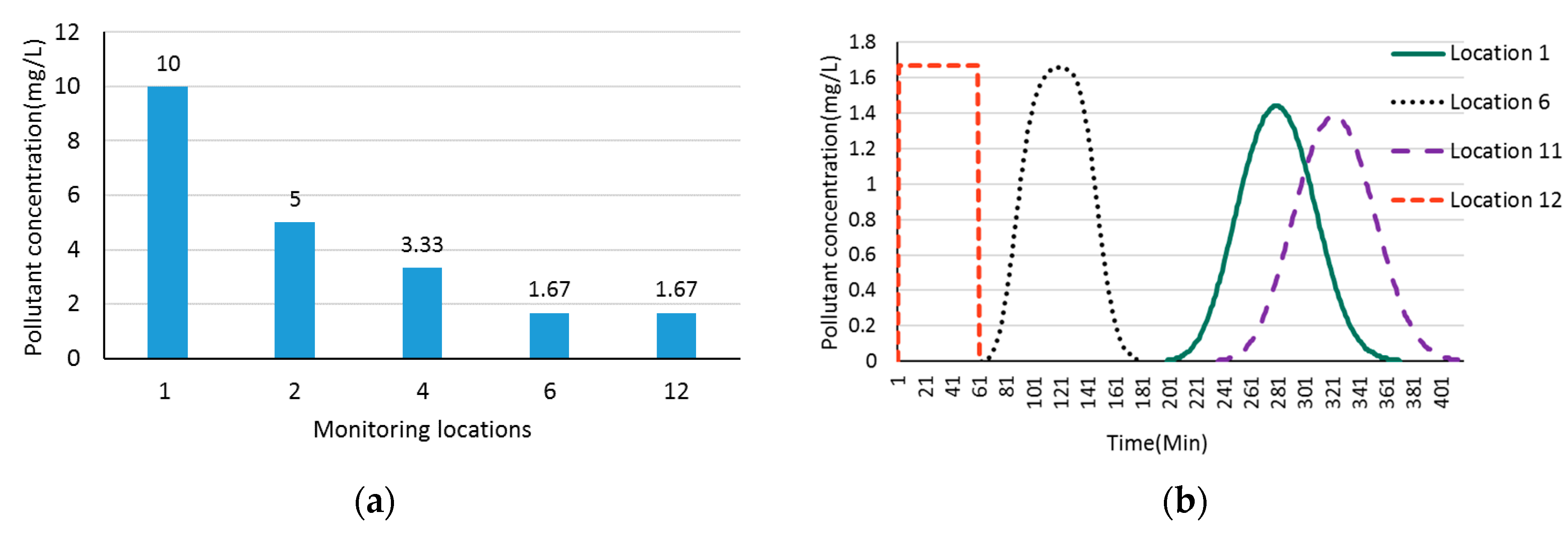
Figure 8a shows the pollutant dilution along downstream locations when a pollution event occurs at the upstream location 1 in the hypothetical river network A (
Figure 1). We can find that the pollutant concentration is decreased from maximal value of 10 mg/L at location 1 to minimal value of 1.67 mg/L at outlet location 12 along the downstream.
Figure 8b demonstrates the changing process of pollutant concentration at location 12 when a pollution event occurs at monitoring locations 1, 6, 11, and 12, respectively. We can see from
Figure 8b that when a pollution event occurs at location 1, the pollutant will arrive at location 12 in 198 min and will be completely discharged in 368 min with a maximum pollutant concentration of 1.44 mg/L in the pollution event duration. When the pollution occurs at location 12 itself, the pollutant will be diluted by upstream water flows and the maximum pollutant concentration is only 1.67 mg/L. That is why none of the pollution events can be detected when we set pollution detection threshold to 2 mg/L. We get similar results in
Table 9 when we increase the pollution detection threshold to 1 mg/L and 2 mg/L, respectively, for river network B.
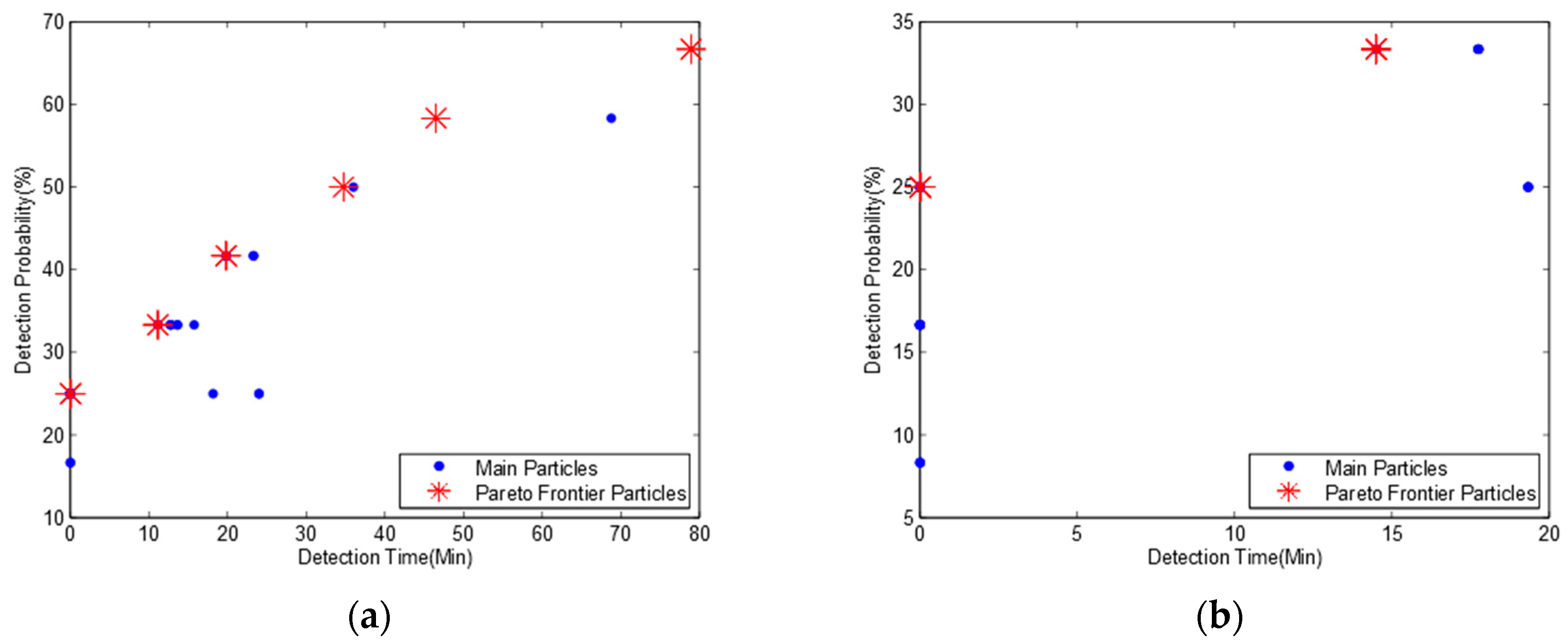
Figure 9 shows the Pareto frontier for bidirectional water flows based on the pollution time data in
Table 8 and
Table 9. We can find that
Figure 9a is quite different from
Figure 9b, and there are five Pareto frontier particles in
Figure 9a but only two Pareto frontier particles in
Figure 9b.
Table 10 shows the detailed pollution detection time and probability.
Comparing the monitoring location distribution in
Table 6 and
Table 10a, we observe that though we increase the pollution detection threshold from 0.01 mg/L to 1 mg/L, the two optimum deployment solutions are the same while the detection time is slightly increased. However, from
Table 10b, we know that when we continue to increase the pollution detection threshold to 2 mg/L, which is higher than the maximum pollutant concentration in pollution events, the pollution detection probability is significantly decreased, and we get quite different optimum solutions. Based on the observation above, we make a conclusion that a slight change of monitoring device’s pollution detection threshold may not affect the design of optimum monitoring network when the threshold is smaller than the maximal pollutant concentration in the pollution events.
In addition, we consider pollution events with different flow rates to simulate different flow regimes in different seasons. Results indicate that the change of flow rate can affect the optimal deployment solutions. This is because different flow rates result in different pollution detection time at monitoring locations. As we know, the transport processes such as hydrodynamic dispersion and advection can affect the flow rate. So, it also changes the pollution detection time at monitoring locations and ultimately affects the optimal deployment solutions.