What to Do When Accumulated Exposure Affects Health but Only Its Duration Was Measured? A Case of Linear Regression
Abstract
1. Introduction
2. Theoretical Analysis of Impact on Estimate of Effect of Cumulative Exposure
3. Naïve Analysis
4. Adjusted Analysis: The Limit of What We can Learn when Only D is Available, but ρ and k are Known
5. Bayesian Analysis when Information of Exposure Duration and Intensity is Disjointed
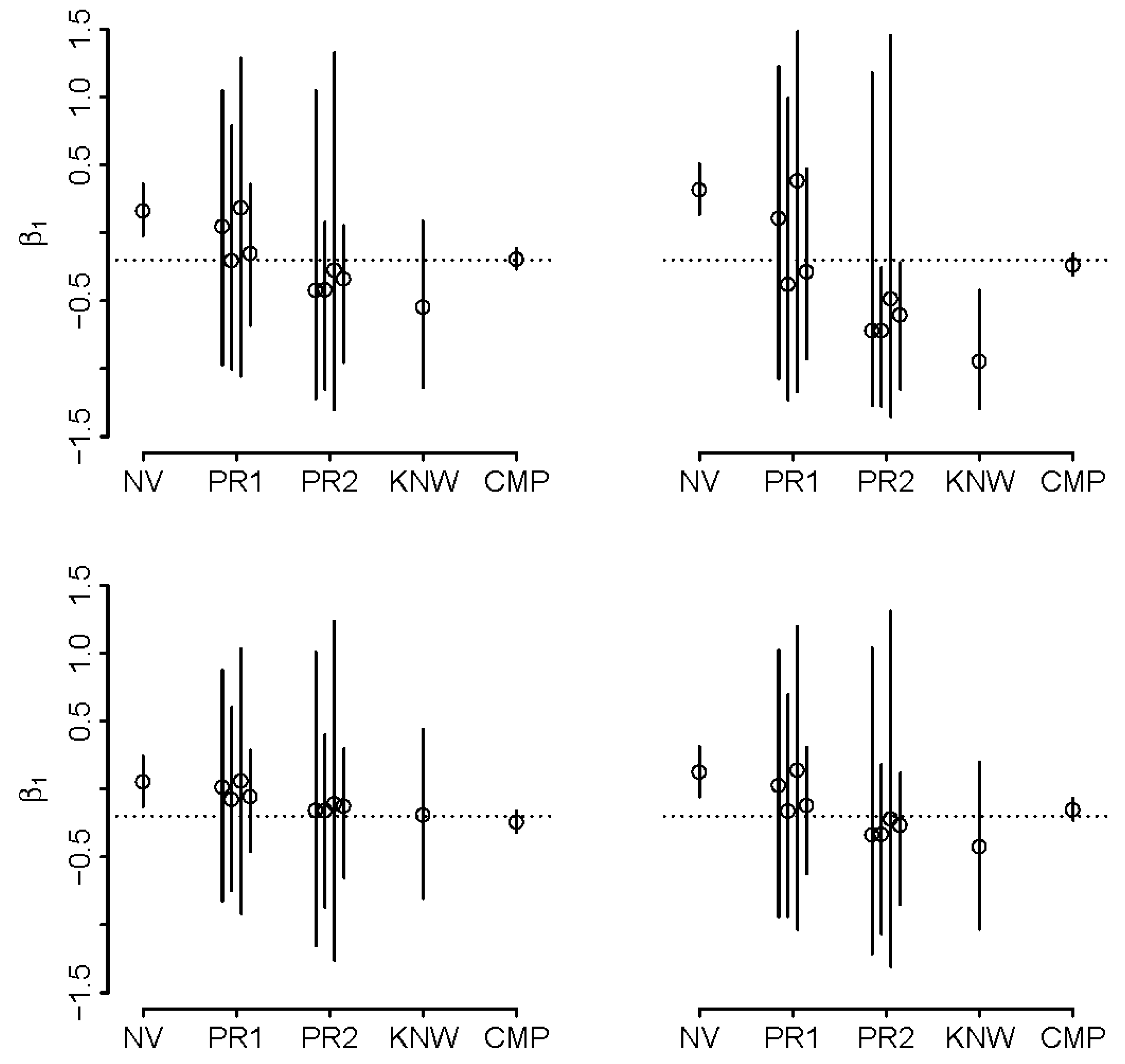
5.1. Models
5.2. Synthetic Example
- the naïve approach (duration only);
- four wide priors on ρ (two of which admit uncertainty about the sign of the correlation, when the prior mean is one standard deviation below) and k (Priors 1);
- four narrow priors on ρ and k (Priors 2);
- assuming known ρ and k; and
- complete data.
5.3. Real-World Application
6. Discussion
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Theory
References
- Johnson, E.S. Duration of exposure as a surrogate for dose in the examination of dose response relations. Br. J. Ind. Med. 1986, 43, 427–429. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Blair, A.; Thomas, K.; Coble, J.; Sandler, D.P.; Hines, C.J.; Lynch, C.F.; Knott, C.; Purdue, M.P.; Zahm, S.H.; Alavanja, M.C.; et al. Impact of pesticide exposure misclassification on estimates of relative risks in the Agricultural Health Study. Occup. Environ. Med. 2011, 68, 537–541. [Google Scholar] [CrossRef]
- Westberg, H.B.; Hardell, L.O.; Malmqvist, N.; Ohlson, C.G.; Axelson, O. On the use of different measures of exposure-experiences from a case-control study on testicular cancer and PVC exposure. J. Occup. Environ. Hyg. 2005, 2, 351–356. [Google Scholar] [CrossRef]
- de Vocht, F.; Burstyn, I.; Sanguanchaiyakrit, N. Rethinking cumulative exposure in epidemiology, again. J. Expo. Sci. Environ. Epidemiol. 2015, 25, 467. [Google Scholar] [CrossRef]
- Preller, L.; Burstyn, I.; De, P.N.; Kromhout, H. Characteristics of peaks of inhalation exposure to organic solvents. Ann. Occup. Hyg. 2004, 48, 643–652. [Google Scholar]
- Nieuwenhuijsen, M.J.; Lowson, D.; Venables, K.M.; Newman-Taylor, A.J. Correlation between different measures of exposure in a cohort of bakery workers and flour millers. Ann. Occup. Hyg. 1995, 39, 291–298. [Google Scholar] [CrossRef]
- McDonald, J.C.; McDonald, A.D.; Hughes, J.M.; Rando, R.J.; Weill, H. Mortality from lung and kidney disease in a cohort of North American industrial sand workers: An update. Ann. Occup. Hyg. 2005, 49, 367–373. [Google Scholar] [PubMed]
- Lipworth, L.; Sonderman, J.S.; Mumma, M.T.; Tarone, R.E.; Marano, D.E.; Boice, J.D., Jr.; McLaughlin, J.K. Cancer mortality among aircraft manufacturing workers: An extended follow-up. J. Occup. Environ. Med. 2011, 53, 992–1007. [Google Scholar] [CrossRef] [PubMed]
- Purdue, M.P.; Bakke, B.; Stewart, P.; De Roos, A.J.; Schenk, M.; Lynch, C.F.; Bernstein, L.; Morton, L.M.; Cerhan, J.R.; Severson, R.K. A case-control study of occupational exposure to trichloroethylene and non-Hodgkin lymphoma. Environ. Health Perspect. 2011, 119, 232–238. [Google Scholar] [CrossRef]
- Burstyn, I.; Yang, Y.; Schnatter, A.R. Effects of non-differential exposure misclassification on false conclusions in hypothesis-generating studies. Int. J. Environ. Res. Public Health 2014, 11, 10951–10966. [Google Scholar] [CrossRef]
- Loken, E.; Gelman, A. Measurement error and the replication crisis. Science 2017, 355, 584–585. [Google Scholar] [CrossRef]
- Hoar, S. Job exposure matrix methodology. J. Toxicol. Clin. Toxicol. 1983, 21, 9–26. [Google Scholar] [CrossRef]
- Peters, S.; Vermeulen, R.; Portengen, L.; Olsson, A.; Kendzia, B.; Vincent, R.; Savary, B.; Lavoue, J.; Cavallo, D.; Cattaneo, A.; et al. SYN-JEM: A Quantitative Job-Exposure Matrix for Five Lung Carcinogens. Ann. Occup. Hyg. 2016, 60, 795–811. [Google Scholar] [CrossRef]
- Kim, H.M.; Richardson, D.; Loomis, D.; Van Tongeren, M.; Burstyn, I. Bias in the estimation of exposure effects with individual-or group-based exposure assessment. J. Expo. Sci. Environ. Epidemiol. 2011, 21, 212–221. [Google Scholar] [CrossRef]
- Tielemans, E.; Kupper, L.L.; Kromhout, H.; Heederik, D.; Houba, R. Individual-based and group-based occupational exposure assessment: Some equations to evaluate different strategies. Ann. Occup. Hyg. 1998, 42, 115–119. [Google Scholar] [CrossRef]
- Xing, L.; Burstyn, I.; Richardson, D.B.; Gustafson, P. A comparison of Bayesian hierarchical modeling with group-based exposure assessment in occupational epidemiology. Stat. Med. 2013, 32, 3686–3699. [Google Scholar] [CrossRef]
- Poole, C. Low P-values or narrow confidence intervals: Which are more durable? Epidemiology 2001, 12, 291–294. [Google Scholar] [CrossRef]
- Lash, T.L. The Harm Done to Reproducibility by the Culture of Null Hypothesis Significance Testing. Am. J. Epidemiol. 2017, 186, 627–635. [Google Scholar] [CrossRef]
- Lash, T.L.; Fox, M.P.; Fink, A.K. Applying Quantitative Bias Analysis to Epidemiologic Data; Springer Science+Business Media: Berlin, Germany, 2009. [Google Scholar]
- Talbott, E.O.; Gibson, L.B.; Burks, A.; Engberg, R.; McHugh, K.P. Evidence for a dose-response relationship between occupational noise and blood pressure. Arch. Environ. Health 1999, 54, 71–78. [Google Scholar] [CrossRef]
- Seixas, N.S.; Neitzel, R.; Stover, B.; Sheppard, L.; Feeney, P.; Mills, D.; Kujawa, S. 10-Year prospective study of noise exposure and hearing damage among construction workers. Occup. Environ. Med. 2012, 69, 643–650. [Google Scholar] [CrossRef]
- Kennedy, S.M.; Chan-Yeung, M.; Marion, S.; Lea, J.; Teschke, K. Maintenance of stellite and tungsten carbide saw tips: Respiratory health and exposure-response evaluations. Occup. Environ. Med. 1995, 52, 185–191. [Google Scholar] [CrossRef]
- Gustafson, P.; Burstyn, I. Bayesian inference of gene-environment interaction from incomplete data: What happens when information on environment is disjoint from data on gene and disease? Stat. Med. 2011, 30, 877–889. [Google Scholar] [CrossRef]
- Koch, A.L. The logarithm in biology 1. Mechanisms generating the log-normal distribution exactly. J. Theor. Biol. 1966, 12, 276–290. [Google Scholar] [CrossRef]
- Limpert, E.; Stahel, W.A.; Abbt, M. Log-normal distributions across the sciences: Keys and clues. BioScience 2001, 51, 341–352. [Google Scholar] [CrossRef]
- Gualandi, S.; Toscani, G. Human Behavior And Lognormal Distribution. A Kinetic Description. arXiv 2018, arXiv:1809.01365. [Google Scholar] [CrossRef]
- The R Development Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2006; ISBN 3-900051-07-0. [Google Scholar]
- Berkson, J. Are there two regressions? Am. Stat. Assoc. J. 1950, 45, 164–180. [Google Scholar] [CrossRef]
- Zellner, A. On assessing prior distributions and Bayesian regression analysis with g-prior distributions. Bayesian Inference Decis. Techn. 1986, 28, 253–305. [Google Scholar]
- Hoff, P.D. Linear regression. In A First Course in Bayesian Statistical Methods, 1st ed.; Springer: New York, NY, USA, 2009; pp. 149–170. [Google Scholar]
- Reeves, G.K.; Cox, D.R.; Darby, S.C.; Whitley, E. Some aspects of measurement error in explanatory variables for continuous and binary regression models. Stat. Med. 1998, 17, 2157–2177. [Google Scholar] [CrossRef]
- Prentice, R. Covariate measurement errors and parametric estimation in a failure time regression model. Biometrika 1982, 69, 331–341. [Google Scholar] [CrossRef]
- Kim, H.M.; Yasui, Y.; Burstyn, I. Attenuation in risk estimates in logistic and Cox proportional-hazards models due to group-based exposure assessment strategy. Ann. Occup. Hyg. 2006, 50, 623–635. [Google Scholar]
- Gustafson, P. Measurement Error and Misclassification in Statistics and Epidemiology; Chapman & Hall/CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Carrol, R.J.; Ruppert, D.; Stefanski, L.A.; Crainiceanu, C.M. Measurement error in Nonlinear Models, 2nd ed.; Chapman & Hall/CRC: Boca Raton, FL, USA, 2006. [Google Scholar]
- Lin, N.X.; Logan, S.; Henley, W.E. Bias and sensitivity analysis when estimating treatment effects from the cox model with omitted covariates. Biometrics 2013, 69, 850–860. [Google Scholar] [CrossRef]
- Gail, M.H.; Wieand, S.; Piantadosi, S. Biased estimates of treatment effect in randomized experiments with nonlinear regressions and omitted covariates. Biometrika 1984, 71, 431–444. [Google Scholar] [CrossRef]
- Lin, D.Y.; Psaty, B.M.; Kronmal, R.A. Assessing the sensitivity of regression results to unmeasured confounders in observational studies. Biometrics 1998, 54, 948–963. [Google Scholar] [CrossRef]
- McCandless, L.C.; Gustafson, P.; Levy, A. Bayesian sensitivity analysis for unmeasured confounding in observational studies. Stat. Med. 2007, 26, 2331–2347. [Google Scholar] [CrossRef]
- Seixas, N.S.; Robins, T.G.; Becker, M. A novel approach to the characterization of cumulative exposure for the study of chronic occupational disease. Am. J. Epidemiol. 1993, 137, 463–471. [Google Scholar] [CrossRef]
- Lubin, J.H.; Caporaso, N.E. Cigarette smoking and lung cancer: Modeling total exposure and intensity. Cancer Epidemiol. Biomarkers Prev. 2006, 15, 517–523. [Google Scholar] [CrossRef]
- Smith, T.J.; Kriebel, D. A Biologic Approach to Environmental Assessment and Epidemiology; Oxford University Press: New York, NY, USA, 2010. [Google Scholar]
- Wang, D.; Shen, T.; Gustafson, P. Partial Identification arising from Nondifferential Exposure Misclassification: How Informative are Data on the Unlikely, Maybe, and Likely Exposed? Int. J. Biostat. 2012, 8, 1557–4679. [Google Scholar] [CrossRef]
- Gustafson, P.; Le, N.D. Comparing the effects of continuous and discrete covariate mismeasurement, with emphasis on the dichotomization of mismeasured predictors. Biometrics 2002, 58, 878–887. [Google Scholar] [CrossRef]
- Heavner, K.K.; Phillips, C.V.; Burstyn, I.; Hare, W. Dichotomization: 2 × 2 (×2 × 2 × 2...) categories: Infinite possibilities. BMC Med. Res. Methodol. 2010, 10, 59. [Google Scholar] [CrossRef]





© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Burstyn, I.; Barone-Adesi, F.; de Vocht, F.; Gustafson, P. What to Do When Accumulated Exposure Affects Health but Only Its Duration Was Measured? A Case of Linear Regression. Int. J. Environ. Res. Public Health 2019, 16, 1896. https://doi.org/10.3390/ijerph16111896
Burstyn I, Barone-Adesi F, de Vocht F, Gustafson P. What to Do When Accumulated Exposure Affects Health but Only Its Duration Was Measured? A Case of Linear Regression. International Journal of Environmental Research and Public Health. 2019; 16(11):1896. https://doi.org/10.3390/ijerph16111896
Chicago/Turabian StyleBurstyn, Igor, Francesco Barone-Adesi, Frank de Vocht, and Paul Gustafson. 2019. "What to Do When Accumulated Exposure Affects Health but Only Its Duration Was Measured? A Case of Linear Regression" International Journal of Environmental Research and Public Health 16, no. 11: 1896. https://doi.org/10.3390/ijerph16111896
APA StyleBurstyn, I., Barone-Adesi, F., de Vocht, F., & Gustafson, P. (2019). What to Do When Accumulated Exposure Affects Health but Only Its Duration Was Measured? A Case of Linear Regression. International Journal of Environmental Research and Public Health, 16(11), 1896. https://doi.org/10.3390/ijerph16111896





