Numerical Simulation of Corneal Fibril Reorientation in Response to External Loading
Abstract
:1. Introduction
2. Methods
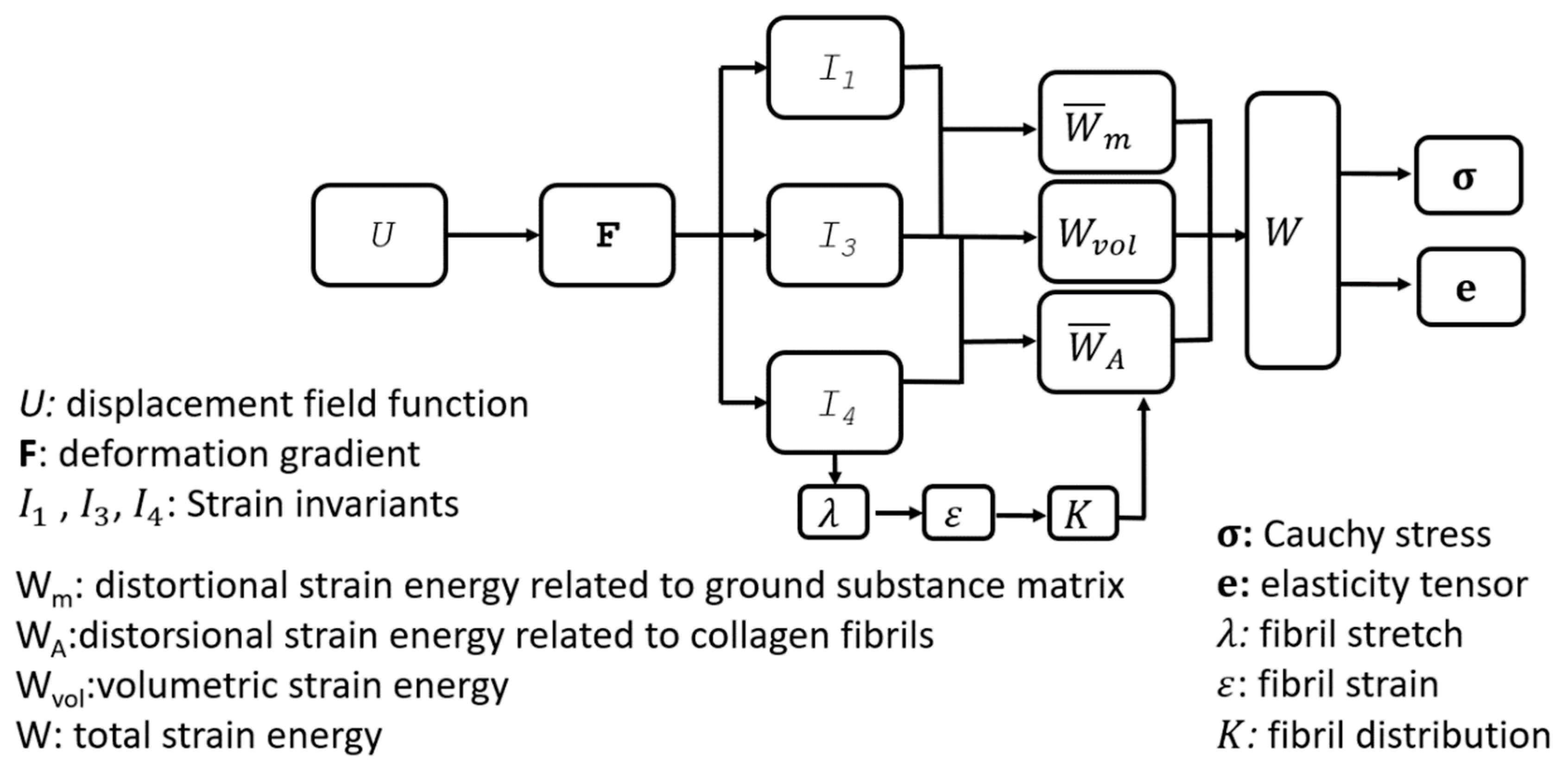
2.1. Material Constitutive Model
2.2. Data Analysis
Microstructure Measurements
2.3. Normalisation
2.4. Number of Measurements of Fibril Density at Each Point
2.5. Fibril Reorientation
2.6. Assumptions
2.7. Development of Reorientation Algorithm
2.7.1. Implementation of Fibril Reorientation in Numerical Models
2.7.2. Validation of Reorientation Algorithm
2.8. Further Numerical Assessments
2.8.1. Single Element Model
2.8.2. Full Eye Model
3. Results
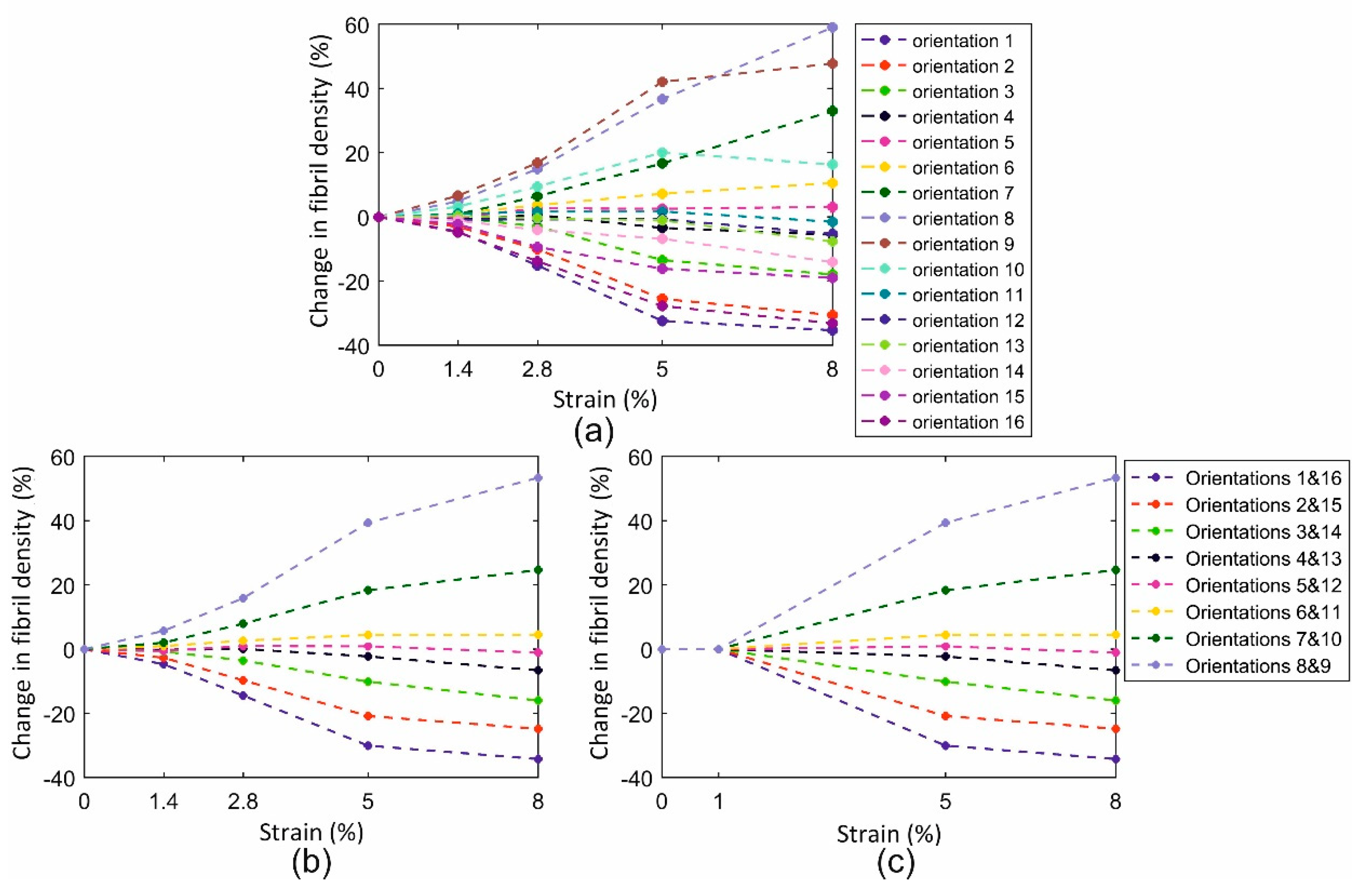
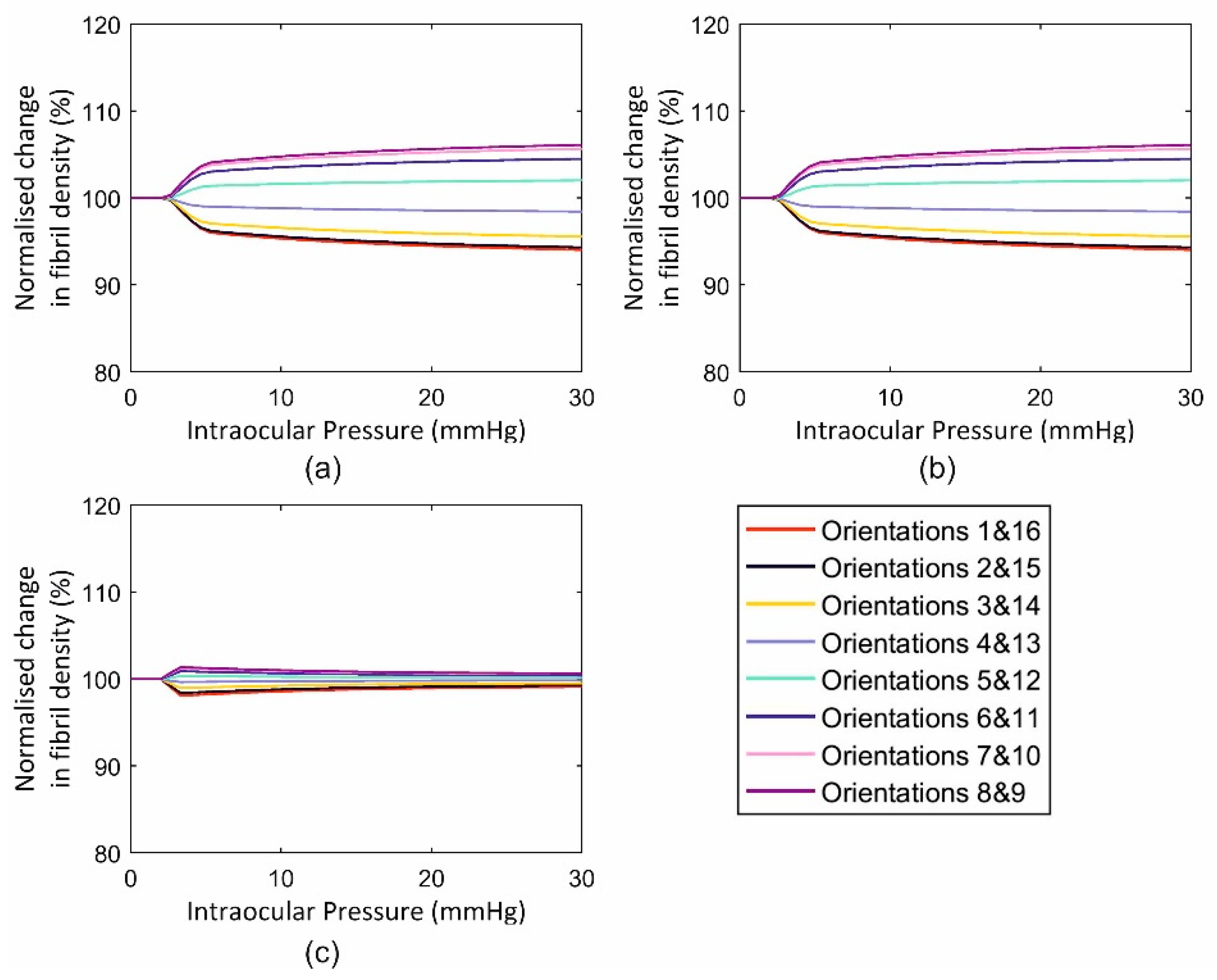
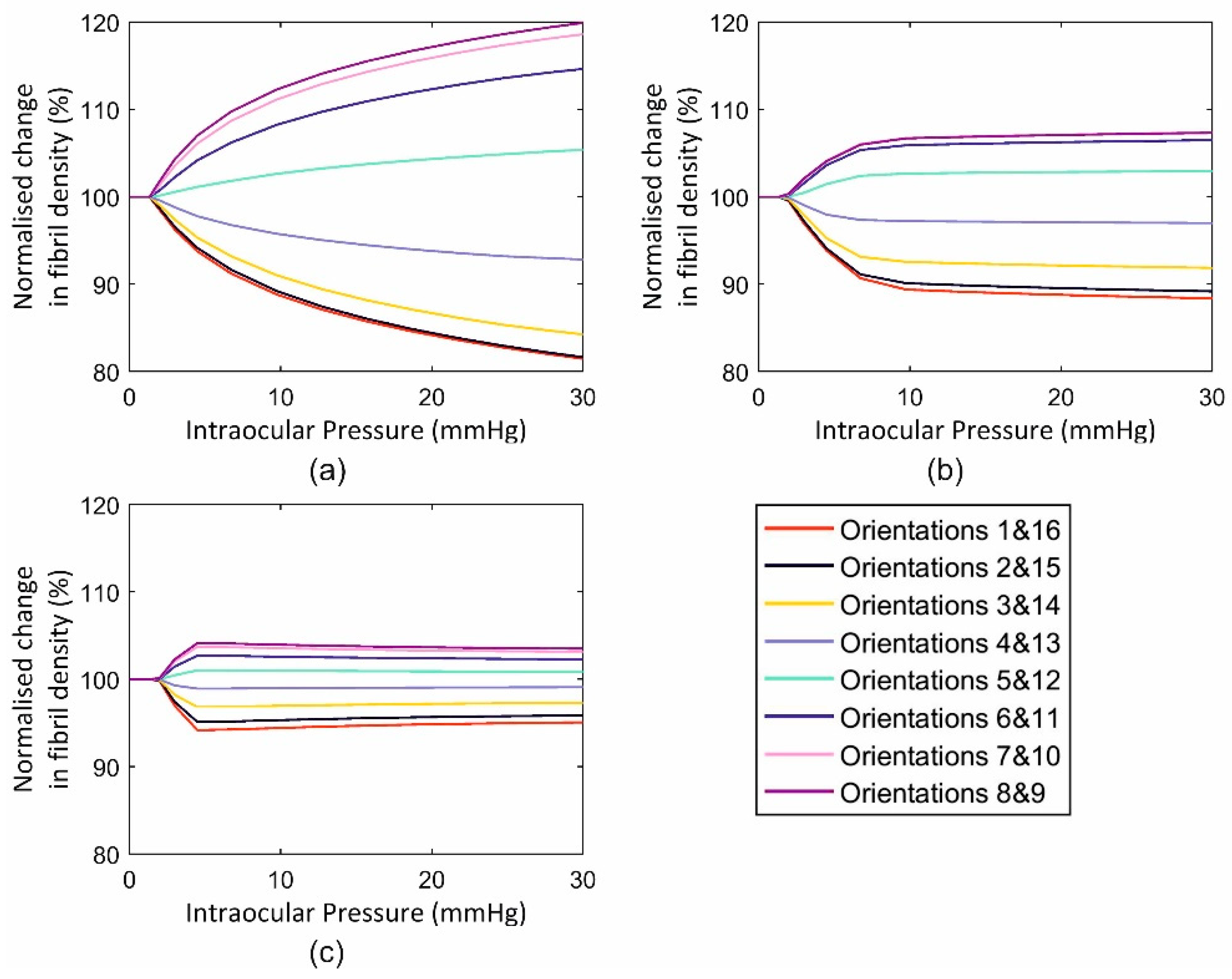
3.1. Fibril Reorientation Trends
3.2. Validation of Reorientation Trends against Experimental Measurements
3.3. Finite Element Assessment
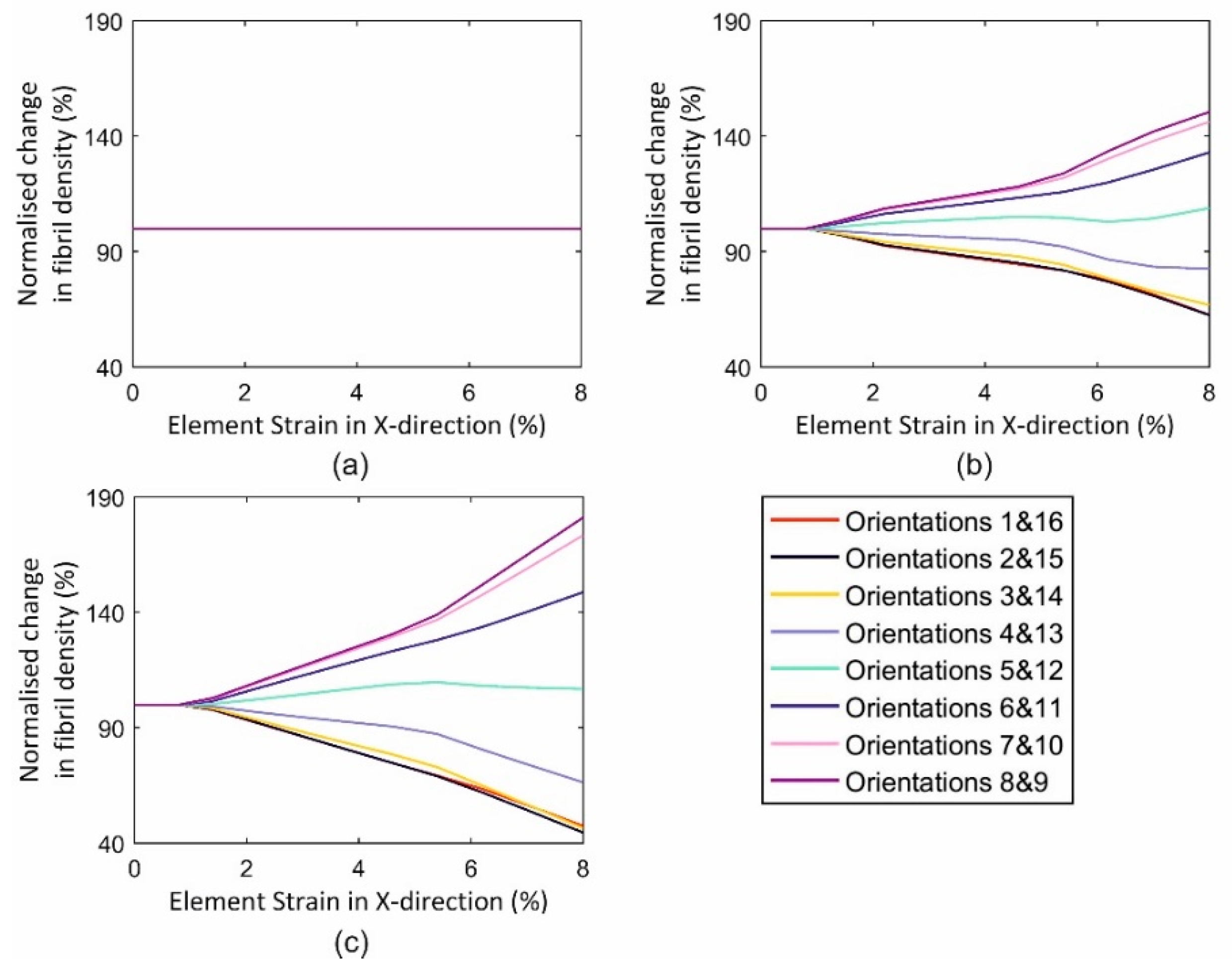
3.3.1. Single Element Model
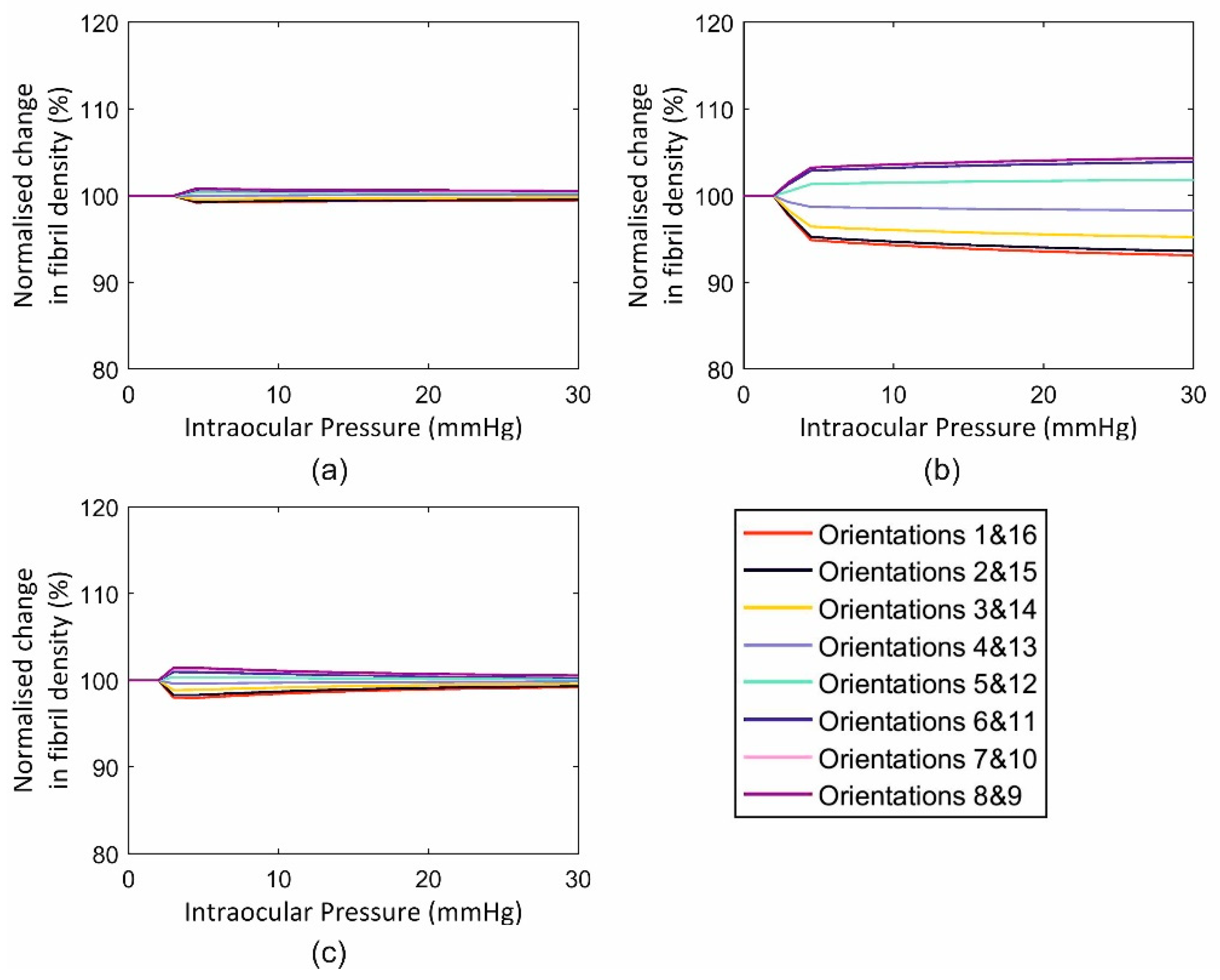
3.3.2. Full Eye Model Application
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Humphrey, J.D. Review Paper: Continuum biomechanics of soft biological tissues. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 2003, 459, 3–46. [Google Scholar] [CrossRef] [Green Version]
- Pandolfi, A.; Holzapfel, G.A. Three-dimensional modeling and computational analysis of the human cornea considering distributed collagen fibril orientations. J. Biomech. Eng. 2008, 130, 061006. [Google Scholar] [CrossRef]
- Pandolfi, A.; Manganiello, F. A model for the human cornea: Constitutive formulation and numerical analysis. Biomech. Model. Mechanobiol. 2006, 5, 237–246. [Google Scholar] [CrossRef]
- Whitford, C.; Studer, H.; Boote, C.; Meek, K.M.; Elsheikh, A. Biomechanical model of the human cornea: Considering shear stiffness and regional variation of collagen anisotropy and density. J. Mech. Behav. Biomed. Mater. 2015, 42, 76–87. [Google Scholar] [CrossRef]
- Grytz, R.; Meschke, G. Constitutive modeling of crimped collagen fibrils in soft tissues. J. Mech. Behav. Biomed. Mater. 2009, 2, 522–533. [Google Scholar] [CrossRef]
- McDonnell, P.J. Constitutive Laws for Biomechanical IVIodeling of Refractive Surgery. J. Biomech. Eng. 1996, 118, 473–481. [Google Scholar]
- Girard, M.J.A.; Downs, J.C.; Burgoyne, C.F.; Suh, J.K.F. Peripapillary and Posterior Scleral Mechanics—Part I: Development of an Anisotropic Hyperelastic Constitutive Model. J. Biomech. Eng. 2009, 131, 051011. [Google Scholar] [CrossRef]
- Coudrillier, B.; Pijanka, J.; Jefferys, J.; Sorensen, T.; Quigley, H.A.; Boote, C.; Nguyen, T.D. Collagen structure and mechanical properties of the human sclera: Analysis for the effects of age. J. Biomech. Eng. 2015, 137, 041006. [Google Scholar] [CrossRef]
- Studer, H.; Larrea, X.; Riedwyl, H.; Buchler, P. Biomechanical model of human cornea based on stromal microstructure. J. Biomech. 2010, 43, 836–842. [Google Scholar] [CrossRef]
- Zhou, D.; Abass, A.; Eliasy, A.; Studer, H.P.; Movchan, A.; Movchan, N.; Elsheikh, A. Microstructure-based numerical simulation of the mechanical behaviour of ocular tissue. J. R. Soc. Interface 2019, 16, 20180685. [Google Scholar] [CrossRef] [Green Version]
- Boote, C.; Dooley, E.P.; Gardner, S.J.; Kamma-Lorger, C.S.; Hayes, S.; Nielsen, K.; Hjortdal, J.; Sorensen, T.; Terrill, N.J.; Meek, K.M. Quantification of collagen ultrastructure after penetrating keratoplasty–implications for corneal biomechanics. PLoS ONE 2013, 8, e68166. [Google Scholar] [CrossRef]
- Hayes, S.; Boote, C.; Tuft, S.J.; Quantock, A.J.; Meek, K.M. A study of corneal thickness, shape and collagen organisation in keratoconus using videokeratography and X-ray scattering techniques. Exp. Eye Res. 2007, 84, 423–434. [Google Scholar] [CrossRef]
- Sawaguchi, S.; Fukuchi, T.; Abe, H.; Kaiya, T.; Sugar, J.; Yue, B.T. Three-dimensional scanning electron microscopic study of keratoconus corneas. Arch. Ophthalmol. 1998, 116, 62–68. [Google Scholar] [CrossRef]
- Lu, P.; Takai, K.; Weaver, V.M.; Werb, Z. Extracellular matrix degradation and remodeling in development and disease. Cold Spring Harb. Perspect. Biol. 2011, 3, a005058. [Google Scholar] [CrossRef]
- Hayashi, K. Biomechanical studies of the remodeling of knee joint tendons and ligaments. J. Biomech. 1996, 29, 707–716. [Google Scholar] [CrossRef]
- Mann, B.K.; Schmedlen, R.H.; West, J.L. Tethered-TGF-β increases extracellular matrix production of vascular smooth muscle cells. Biomaterials 2001, 22, 439–444. [Google Scholar] [CrossRef]
- Humphrey, J.D. Remodeling of a Collagenous Tissue at Fixed Lengths. J. Biomech. Eng. 1999, 121, 591–597. [Google Scholar] [CrossRef]
- Grytz, R.; Meschke, G. A computational remodeling approach to predict the physiological architecture of the collagen fibril network in corneo-scleral shells. Biomech. Model. Mechanobiol. 2010, 9, 225–235. [Google Scholar] [CrossRef]
- Hernandez, M.R.; Andrzejewska, W.M.; Neufeld, A.H. Changes in the Extracellular Matrix of the Human Optic Nerve Head in Primary Open-Angle Glaucoma. Am. J. Ophthalmol. 1990, 109, 180–188. [Google Scholar] [CrossRef]
- Kenney, M.; Nesburn, A.; Burgeson, R.; Butkowski, R.; Ljubimov, A. Abnormalities of the extracellular matrix in keratoconus corneas. Cornea 1997, 16, 345–351. [Google Scholar] [CrossRef]
- MacKenna, D.; Summerour, S.R.; Villarreal, F.J. Role of mechanical factors in modulating cardiac fibroblast function and extracellular matrix synthesis. Cardiovasc. Res. 2000, 46, 257–263. [Google Scholar] [CrossRef] [Green Version]
- Bell, J.S.; Hayes, S.; Whitford, C.; Sanchez-Weatherby, J.; Shebanova, O.; Vergari, C.; Winlove, C.P.; Terrill, N.; Sorensen, T.; Elsheikh, A.; et al. The hierarchical response of human corneal collagen to load. Acta Biomater. 2018, 65, 216–225. [Google Scholar] [CrossRef]
- Sawhney, R.K.; Howard, J. Slow local movements of collagen fibers by fibroblasts drive the rapid global self-organization of collagen gels. J. Cell Biol. 2002, 157, 1083–1092. [Google Scholar] [CrossRef]
- Taber, L.A.; Humphrey, J.D. Stress-modulated growth, residual stress, and vascular heterogeneity. J. Biomech. Eng. 2001, 123, 528–535. [Google Scholar] [CrossRef]
- Gleason, R.; Humphrey, J. A mixture model of arterial growth and remodeling in hypertension: Altered muscle tone and tissue turnover. J. Vasc. Res. 2004, 41, 352–363. [Google Scholar] [CrossRef]
- Driessen, N.J.; Boerboom, R.A.; Huyghe, J.M.; Bouten, C.V.; Baaijens, F.P. Computational analyses of mechanically induced collagen fiber remodeling in the aortic heart valve. J. Biomech. Eng. 2003, 125, 549–557. [Google Scholar] [CrossRef]
- Driessen, N.; Wilson, W.; Bouten, C.; Baaijens, F. A computational model for collagen fibre remodelling in the arterial wall. J. Theor. Biol. 2004, 226, 53–64. [Google Scholar] [CrossRef]
- Hariton, I.; Gasser, T.; Holzapfel, G. Stress-driven collagen fiber remodeling in arterial walls. Biomech. Model. Mechanobiol. 2007, 6, 163–175. [Google Scholar] [CrossRef]
- Driessen, N.J.; Cox, M.A.; Bouten, C.V.; Baaijens, F.P. Remodelling of the angular collagen fiber distribution in cardiovascular tissues. Biomech. Model. Mechanobiol. 2008, 7, 93–103. [Google Scholar] [CrossRef]
- Markert, B.; Ehlers, W.; Karajan, N. A general polyconvex strain-energy function for fiber-reinforced materials. PAMM 2005, 5, 245–246. [Google Scholar] [CrossRef]
- Zhou, D.; Eliasy, A.; Abass, A.; Markov, P.; Whitford, C.; Boote, C.; Movchan, A.; Movchan, N.; Elsheikh, A. Analysis of X-ray scattering microstructure data for implementation in numerical simulations of ocular biomechanical behaviour. PLoS ONE 2019, 14, e0214770. [Google Scholar] [CrossRef]
- Dubbelman, M.; Weeber, H.A.; Van Der Heijde, R.G.L.; Völker-Dieben, H.J. Radius and asphericity of the posterior corneal surface determined by corrected Scheimpflug photography. Acta Ophthalmol. Scand. 2002, 80, 379–383. [Google Scholar] [CrossRef]
- Dubbelman, M.; Sicam, V.A.D.P.; Van der Heijde, G.L. The shape of the anterior and posterior surface of the aging human cornea. Vis. Res. 2006, 46, 993–1001. [Google Scholar] [CrossRef] [Green Version]
- Avitabile, T.; Marano, F.; Uva, M.G.; Reibaldi, A. Evaluation of central and peripheral corneal thickness with ultrasound biomicroscopy in normal and keratoconic eyes. Cornea 1997, 16, 639–644. [Google Scholar] [CrossRef]
- Piñero, D.P.; Puche, A.B.P.; Alió, J.L. Corneal diameter measurements by corneal topography and angle-to-angle measurements by optical coherence tomography: Evaluation of equivalence. J. Cataract Refract. Surg. 2008, 34, 126–131. [Google Scholar] [CrossRef]
- Hashemi, H.; Khabazkhoob, M.; Emamian, M.H.; Shariati, M.; Yekta, A.; Fotouhi, A. White-to-white corneal diameter distribution in an adult population. J. Curr. Ophthalmol. 2015, 27, 21–24. [Google Scholar] [CrossRef] [Green Version]
- Jesus, D.A.; Kedzia, R.; Iskander, D.R. Precise measurement of scleral radius using anterior eye profilometry. Contact Lens Anterior Eye 2017, 40, 47–52. [Google Scholar] [CrossRef]
- Elsheikh, A.; Geraghty, B.; Alhasso, D.; Knappett, J.; Campanelli, M.; Rama, P. Regional variation in the biomechanical properties of the human sclera. Exp. Eye Res. 2010, 90, 624–633. [Google Scholar] [CrossRef]
- Kuhl, E.; Holzapfel, G.A. A continuum model for remodeling in living structures. J. Mater. Sci. 2007, 42, 8811–8823. [Google Scholar] [CrossRef]
- Baaijens, F.; Bouten, C.; Driessen, N. Modeling collagen remodeling. J. Biomech. 2010, 43, 166–175. [Google Scholar] [CrossRef]
- Meek, K. The cornea and sclera. In Collagen: Structure and Mechanics; Springer: Berlin, Germany, 2008; pp. 359–396. [Google Scholar]






© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, D.; Abass, A.; Eliasy, A.; Movchan, A.; Movchan, N.; Elsheikh, A. Numerical Simulation of Corneal Fibril Reorientation in Response to External Loading. Int. J. Environ. Res. Public Health 2019, 16, 3278. https://doi.org/10.3390/ijerph16183278
Zhou D, Abass A, Eliasy A, Movchan A, Movchan N, Elsheikh A. Numerical Simulation of Corneal Fibril Reorientation in Response to External Loading. International Journal of Environmental Research and Public Health. 2019; 16(18):3278. https://doi.org/10.3390/ijerph16183278
Chicago/Turabian StyleZhou, Dong, Ahmed Abass, Ashkan Eliasy, Alexander Movchan, Natalia Movchan, and Ahmed Elsheikh. 2019. "Numerical Simulation of Corneal Fibril Reorientation in Response to External Loading" International Journal of Environmental Research and Public Health 16, no. 18: 3278. https://doi.org/10.3390/ijerph16183278
APA StyleZhou, D., Abass, A., Eliasy, A., Movchan, A., Movchan, N., & Elsheikh, A. (2019). Numerical Simulation of Corneal Fibril Reorientation in Response to External Loading. International Journal of Environmental Research and Public Health, 16(18), 3278. https://doi.org/10.3390/ijerph16183278






