Credit Scoring by Fuzzy Support Vector Machines with a Novel Membership Function
Abstract
:1. Introduction
2. SVM and Fuzzy SVM
2.1. Standard Support Vector Machines
2.2. Fuzzy Support Vector Machines
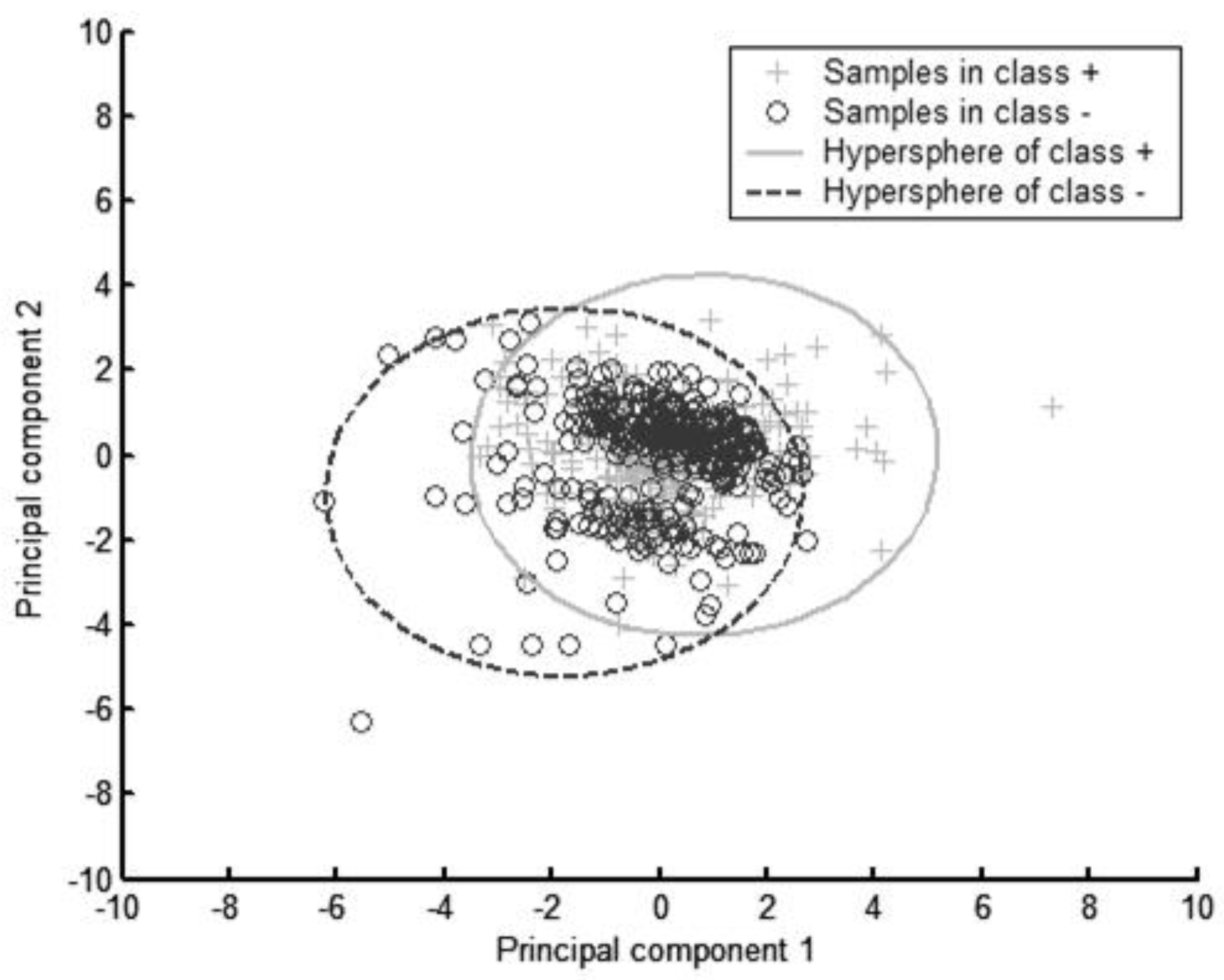
3. Fuzzy SVM with SVDD Membership Function
4. Experimental Results and Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- L.C. Thomas, D.B. Edelman, and J.N. Crook. Credit Scoring and Its Applications. Philadelphia, PA, USA: Siam, 2002. [Google Scholar]
- A. Blöchlinger, and M. Leippold. “Economic benefit of powerful credit scoring.” J. Bank. Financ. 30 (2006): 851–873. [Google Scholar] [CrossRef]
- L. Einav, M. Jenkins, and J. Levin. “The impact of credit scoring on consumer lending.” RAND J. Econ. 44 (2013): 249–274. [Google Scholar] [CrossRef]
- D. West. “Neural network credit scoring models.” Comput. Oper. Res. 27 (2000): 1131–1152. [Google Scholar] [CrossRef]
- C.L. Chuang, and S.T. Huang. “A hybrid neural network approach for credit scoring.” Expert Syst. 28 (2011): 185–196. [Google Scholar] [CrossRef]
- V.N. Vapnik. The Nature of Statistical Learning Theory. New York, NY, USA: Springer, 1995. [Google Scholar]
- V.N. Vapnik. Statistical Learning Theory. New York, NY, USA: John Wiley & Sons, 1998. [Google Scholar]
- A. Christmann, and R. Hable. “Consistency of support vector machines using additive kernels for additive models.” Comput. Stat. Data Anal. 56 (2012): 854–873. [Google Scholar] [CrossRef]
- H. Jiang, Z. Yan, and X. Liu. “Melt index prediction using optimized least squares support vector machines based on hybrid particle swarm optimization algorithm.” Neurocomputing 119 (2013): 469–477. [Google Scholar] [CrossRef]
- A.E. Ruano, G. Madureira, O. Barros, H.R. Khosravani, M.G. Ruano, and P.M. Ferreira. “Seismic detection using support vector machines.” Neurocomputing 135 (2014): 273–283. [Google Scholar] [CrossRef]
- S. Maldonado, and J. López. “Imbalanced data classification using second-order cone programming support vector machines.” Pattern Recognit. 47 (2014): 2070–2079. [Google Scholar] [CrossRef]
- B. Baesens, T. van Gestel, S. Viaene, M. Stepanova, J. Suykens, and J. Vanthienen. “Benchmarking state-of-the-art classification algorithms for credit scoring.” J. Oper. Res. Soc. 54 (2003): 627–635. [Google Scholar] [CrossRef]
- L.C. Thomas, R.W. Oliver, and D.J. Hand. “A survey of the issues in consumer credit modelling research.” J. Oper. Res. Soc. 56 (2005): 1006–1015. [Google Scholar] [CrossRef]
- C.-L. Huang, M.-C. Chen, and C.-J. Wang. “Credit scoring with a data mining approach based on support vector machines.” Expert Syst. Appl. 33 (2007): 847–856. [Google Scholar] [CrossRef]
- D. Martens, B. Baesens, T. van Gestel, and J. Vanthienen. “Comprehensible credit scoring models using rule extraction from support vector machines.” Eur. J. Oper. Res. 183 (2007): 1466–1476. [Google Scholar] [CrossRef]
- D. Niklis, M. Doumpos, and C. Zopounidis. “Combining market and accounting-based models for credit scoring using a classification scheme based on support vector machines.” Appl. Math. Comput. 234 (2014): 69–81. [Google Scholar] [CrossRef]
- T. Harris. “Credit scoring using the clustered support vector machine.” Expert Syst. Appl. 42 (2015): 741–750. [Google Scholar] [CrossRef] [Green Version]
- C.-C. Chen, and S.-T. Li. “Credit rating with a monotonicity-constrained support vector machine model.” Expert Syst. Appl. 41 (2014): 7235–7247. [Google Scholar] [CrossRef]
- C.-F. Lin, and S.-D. Wang. “Fuzzy support vector machines.” IEEE. Trans. Neural Netw. 13 (2002): 464–471. [Google Scholar]
- W. An, and M. Liang. “Fuzzy support vector machine based on within-class scatter for classification problems with outliers or noises.” Neurocomputing 110 (2013): 101–110. [Google Scholar] [CrossRef]
- A. Chaudhuri. “Modified fuzzy support vector machine for credit approval classification.” AI Commun. 27 (2014): 189–211. [Google Scholar]
- Z. Wu, H. Zhang, and J. Liu. “A fuzzy support vector machine algorithm for classification based on a novel PIM fuzzy clustering method.” Neurocomputing 125 (2014): 119–124. [Google Scholar] [CrossRef]
- M.-D. Shieh, and C.-C. Yang. “Classification model for product form design using fuzzy support vector machines.” Comput. Ind. Eng. 55 (2008): 150–164. [Google Scholar] [CrossRef]
- T. Van Gestel, J.A. Suykens, B. Baesens, S. Viaene, J. Vanthienen, G. Dedene, B. De Moor, and J. Vandewalle. “Benchmarking least squares support vector machine classifiers.” Mach. Learn. 54 (2004): 5–32. [Google Scholar] [CrossRef]
- W.M. Tang. “Fuzzy SVM with a new fuzzy membership function to solve the two-class problems.” Neural Process. Lett. 34 (2011): 209–219. [Google Scholar] [CrossRef]
- S. Lessmann, and S. Voß. “A reference model for customer-centric data mining with support vector machines.” Eur. J. Oper. Res. 199 (2009): 520–530. [Google Scholar] [CrossRef]
- D.M. Tax, and R.P. Duin. “Support vector data description.” Mach. Learn. 54 (2004): 45–66. [Google Scholar] [CrossRef]
- R. Strack, V. Kecman, B. Strack, and Q. Li. “Sphere Support Vector Machines for large classification tasks.” Neurocomputing 101 (2013): 59–67. [Google Scholar] [CrossRef]
- I. Jolliffe. Principal Component Analysis. New York, NY, USA: John Wiley & Sons, 2005. [Google Scholar]
- L. Zhou, K.-K. Lai, and L. Yu. “Least squares support vector machines ensemble models for credit scoring.” Expert Syst. Appl. 37 (2010): 127–133. [Google Scholar] [CrossRef]

| Original Attributes | Input Variables | Variable Type | Attribute Description |
|---|---|---|---|
| A1 | V1 | qualitative | Status of existing checking account |
| A2 | V2 | numerical | Duration in month |
| A3 | V3 | qualitative | Credit history |
| A4 | V4,V5 | dummy | Purpose (V4: new car, V5: used car) |
| A5 | V6 | numerical | Credit amount |
| A6 | V7 | qualitative | Savings account/bonds |
| A7 | V8 | qualitative | Present employment since |
| A8 | V9 | qualitative | Personal status and sex |
| A9 | V10,V11 | dummy | Other debtors/guarantors (V10: none, V11: co-applicant) |
| A10 | V12 | numerical | Present residence since |
| A11 | V13 | qualitative | Property |
| A12 | V14 | numerical | Age in years |
| A13 | V15 | qualitative | Other installment plans |
| A14 | V16,V17 | dummy | Housing (V16: rent, V17: own) |
| A15 | V18 | numerical | Number of existing credits at this bank |
| A16 | V19,V20,V21 | dummy | Job (V19: unemployed/unskilled (non-resident), V20: unskilled (resident), V21: skilled employee/official) |
| A17 | V22 | numerical | Number of people being liable to provide maintenance for |
| A18 | V23 | qualitative | Telephone |
| A19 | V24 | qualitative | foreign worker |
| Methods | Sensitivity (%) | Specificity (%) | Accuracy (%) |
|---|---|---|---|
| SVDD-FSVM | 87.53 | 86.84 | 87.25 |
| Nonlinear FSVM | 89.87 | 85.13 | 87.10 |
| Linear FSVM | 86.95 | 86.48 | 86.67 |
| Methods | Sensitivity (%) | Specificity (%) | Accuracy (%) |
|---|---|---|---|
| SVDD-FSVM | 89.59 | 48.60 | 77.30 |
| Nonlinear FSVM | 92.15 | 41.75 | 77.00 |
| Linear FSVM | 95.18 | 23.42 | 73.60 |
© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, J.; Xu, B. Credit Scoring by Fuzzy Support Vector Machines with a Novel Membership Function. J. Risk Financial Manag. 2016, 9, 13. https://doi.org/10.3390/jrfm9040013
Shi J, Xu B. Credit Scoring by Fuzzy Support Vector Machines with a Novel Membership Function. Journal of Risk and Financial Management. 2016; 9(4):13. https://doi.org/10.3390/jrfm9040013
Chicago/Turabian StyleShi, Jian, and Benlian Xu. 2016. "Credit Scoring by Fuzzy Support Vector Machines with a Novel Membership Function" Journal of Risk and Financial Management 9, no. 4: 13. https://doi.org/10.3390/jrfm9040013





