Ion Migration in the Process of Water Freezing under Alternating Electric Field and Its Impact on Insulator Flashover

Abstract

Ice flashover threatens the security and reliability of power transmission. However, the ice flashover mechanism of insulators remains poorly understood. This study analyses water droplet freezing and ion distribution in ice layer under alternating electric field. It also investigates ion migration during icing process of insulator string under alternating electric field and its effects on insulator flashover. Results showed that the average freezing time of water droplets was related to electric field strength. The extent of ion migration during freezing decreased with increasing electric field strength. The maximal melting water conductivity of the ice layer and icicle of the insulator formed under energized condition was higher than the corresponding freezing water conductivity but lower than that under non-energized condition. Furthermore, the hanging location of each insulator significantly affected the melting water conductivity of the ice layer. The surface conductivity of the ice layer increased because of the conductive ion migration in freezing water during freezing, which was an important factor that decreased the flashover voltage of the ice-covered insulator. The existence of alternating electric field would impact the extent of ion migration. This study may serve as a reference for updating prediction flashover model of ice-covered insulators during the melting period.

1. Introduction

Many countries have suffered from serious icing disasters, which exert a strong impact on power grid [1]. The number of accidents has been estimated to exceed 1000 times since the first record of ice accidents on transmission lines [2,3]. Flashover accidents constantly occur, resulting in masses of extra high voltage line outages during ice disaster [4,5].

To date, several local and international researchers have investigated the ice flashover mechanism of insulators. Experimental investigations and field observations indicated that the flashover of ice-covered insulator string typically occurs during the ice-melting period [6,7,8]. Reasons are as follows. An ice layer forms on an insulator during the icing period. Although ice bulk is considered to be non-conductive, water film will be formed on the surface of accumulated ice due to the increase of ambient temperature, which tends to be conductive. The presence of a highly conductive water film on the ice surface makes the body resistance decrease and causes a voltage drop along the air gaps. Under a certain electrical stress, the flashover of ice-covered insulator string is very likely to happen [9,10]. The high surface conductivity of ice layer due to ion migration is closely related to freezing. The freezing of water droplets on a cold surface are divided into three states, namely, liquid, liquid-solid, and entirely solid. Previous works have established many models based on the theory of energy and mass balance [11,12,13]. The surface current increases with increasing water film conductivity, indicating that a high conductivity of water film plays an important role in flashover incidents [14]. In a previous experiment, triangular plane ice samples were used for flashover tests, and the water dripping from the ice samples during flashover was collected. Experimental results showed that the conductivity of melting water during flashover is 5–11 times higher than that of freezing water. Flashover normally occurs when the surface conductivity of an ice sample is at its maximum value [15]. A conductivity measurement system was designed for measurement, and results showed that the conductivity of melting water increases quickly to reach a maximum value; this value is higher than that of freezing water and gradually decreases to a low level [16]. Deng [17] observed the salt migration in cooling water by adding KMnO₄ solution and found that salt migration affects the flashover voltage and leakage current. Most of the abovementioned research focused on the conductivity of ice layers formed under non-energized conditions. However, alternating electric field can cause the polarization of water molecules and impact the movement of conductive ions during freezing. Consequently, the ion distribution in ice layer and flashover voltage of ice-covered insulators are affected. Nevertheless, insufficient research has been conducted on this area.

To understand ion migration during freezing under alternating electric field and its impact on insulator flashover, this study investigated the freezing of water droplets under alternating electric field, the ion distribution in ice layer formed by NaCl aqueous solution under alternating electric field, and the extent of ion migration during the icing of insulator string. This study also analyzed the influence of ion migration on the flashover voltage of an ice-covered insulator.

2. Freezing of Water Droplets under Alternating Electric Field

Ion migration in water droplets on insulator surface is closely bound with its freezing process. This section discusses the freezing process of water droplets under alternating electric field. The test platform is described in Figure 1.

Experiments were performed in a climate chamber, in which the temperature and humidity were controlled at −10 °C and above 50%, respectively. A digital microscope (Supereyes A005, Supereyes technology, Shenzhen, China) was used to observe the freezing process of water droplets. The dynamic changes during freezing were recorded using CCD cameras. The interval between two electrodes was 5 mm, and the copper electrode dimension was 30 mm × 30 mm × 3 mm. The applied power source was a withstanding voltage tester (DBNY-S, Electric Power Automation, Wuhan, China) that can generate 0–5 kV sine AC. The output voltage error was ±5%. The alarm current was set at 200 mA, and the source frequency was 50 Hz. Seven types of applied voltage were employed on the electrodes. It is important to note that the peak value of electric field (E₀) without considering the edge effect of parallel electrodes and electric field distortion effects caused by water droplet was only used to characterize the size of electric field between the two electrodes. The NaCl aqueous solution and glass slide samples were placed into the climate chamber for cooling. When the temperature of the solution was near 1 °C, water droplets were obtained. The water droplet volume was 10 μL controlled by a microsyringe. The conductivity of the solution was 200 μS/cm.

As shown in Figure 2a, the freezing process of water droplets with E₀ ($200\sqrt{2}$ kV/m) can be described as follows. Freezing of water droplets begins with the contact surface between the solid and the liquid. The frontal surface of freezing gradually transfers from the bottom to the top. The movement gradually slows down when the frontal surface is distanced from a cold surface. At the end of freezing, a small obvious raised crystalline lens is formed on the top of the water droplets. The morphological changes in the water droplets during the freezing process show no significant differences with those in the droplets under no electric field condition (Figure 2b).

When time starts at contact between the water droplets and the glass pane, the moment at which a small raised crystalline lens forms can be regarded as the end time [18]. To reduce the errors, the tests were repeated at least five times, and the average value was obtained. The relationship between the average freezing time of water droplets and the peak value of electric field (E₀) is shown in

Table 1. Influence of the peak value of electric field (E₀) on average freezing time.

E0 (kV/m)	0	$25\sqrt{2}$	$50\sqrt{2}$	$80\sqrt{2}$	$90\sqrt{2}$	$100\sqrt{2}$	$150\sqrt{2}$	$200\sqrt{2}$
Average Freezing Time (s)	73.9	74.1	74.1	74.4	75.3	76.4	79.1	80.5
Variance of Measuring Values	0.00895	0.0064	0.0128	0.028878	0.0395	0.0253	0.01346	0.0338

. Results showed that the average freezing time of the water droplets with consideration of the error was almost unaffected when E₀ was lower than $80\sqrt{2}$ kV/m. However, certain inhibitive effects on the freezing of water droplets tended to become strong with increasing of electric field strength.

This phenomenon may be attributed to the following reason. Water molecule is strongly polar, resulting in existing natural dipole moment. When applied to uniform electric field, the dipole moment would be forced and has a tendency to turn in the direction of external electric field to reach a stable state [19]. The stronger the strength of electric field is, the better the consistency between dipole moment and electric field direction is. The dipole orientation polarization produces polarization charges which also can generate additional electric field. However, the direction of additional electric field is contrast to the applied external electric field, which weakens the external electric field. The alternating electric field, which was used in this experiment, is the function of time. The direction and strength of electric field changed over time. Equation (1) shows that the intensity of polarization also varies with the electric field, which leaded to the fact that the electric force which polarization charges suffered from constantly changed. According to References [20,21,22], during the freezing process, water molecules need to overcome the kinetic energy of thermal motion, constraint of potential energy and interfacial energy between solid and liquid, then they can cluster into an ice crystal structures and finish the phrase transition from liquid to solid. However, at the growth stage of ice crystals, water molecules rotated continuously at equilibrium position, which makes it more difficult for water molecules to overcome the resistance to cluster into an ice crystal structure. The inhibiting effect on the growth of ice crystals becomes obvious, and the freezing time increases. As the change in dielectric constant of water was small, ranging from 1 to −10 °C [23], this part did not take the impact of temperature into account and mainly focused on the effect of electric field strength on intensity of polarization.

$$P={\mathsf{\epsilon }}_0\left({\mathsf{\epsilon }}_r-1\right)E_0\sin \mathsf{\omega }t$$

(1)

where P is the polarization intensity, ${\mathsf{\epsilon }}_0$ is the vacuum permittivity, ${\mathsf{\epsilon }}_r$ is the relative dielectric constant, $E_0$ is the field amplitude, and $\mathsf{\omega }$ is the circular frequency of the electric field.

3. Ion Distribution in Ice Layer under Alternating Electric Field

Understanding the effects of the electric field strength on ion distribution in ice layer on insulator string is difficult because of its complex geometries. Therefore, a regular cuboid glass container was used in this part. The conductivity of freezing water in this part was also 200 μS/cm. The test container and freezing water were placed in the climate chamber until their temperature cooled down to −12 °C and near 1 °C, respectively. This cooling ensured that the contact surface between the freezing water and the container was first frozen. The glass container size was 130 mm × 40 mm × 35 mm (length × width × height), and its wall thickness was 5 mm. The copper electrode dimension was 30 mm × 30 mm × 0.5 mm; this electrode was located on the inner sides of the container. Three types of alternating voltage were applied on the electrodes, and the power source was the same as that in Section 2.

Specific operation was as follows. Condensation method was on the basis of the layer. As shown in Figure 3, by controlling the water flow by valve, the fact that the water is freezing layer by layer, resulting in the identically growing pattern of ice layer, is reasonably confirmed. The water flow needed to be controlled well and cannot be too much or less. Too much water flow may lead to change of frozen surface [24]. Too little may not be able to ensure that the ions in the cooling water have sufficient time to transfer before complete freezing [17]. Therefore, the velocity adopt in the experiment is about 2–4 min/mm. When the ice thickness was 15 mm, the valve was closed. By using a cutter knife, an ice cube was divided equally into three blocks on the basis of the ice cube height. The cutter knife should be washed with deionized water before cutting. Three small ice cubes were placed in three clean beakers for melting. The melting process was completed in room temperature which was less than 20 °C, at the same time, the relative humidity of environment exceeded 70%. In addition, by the observation the melting process, the melting period is short and the ice cube totally often melt in 30 min. The evaporation capacity during the melting process is very slight. Therefore, this part ignored the effect of evaporation on the melting water conductivity. When the melting process was completed, the temperature and melting water conductivity were measured simultaneously, and conductivity was converted into a value at 20 °C. The measurement result is shown in Figure 4.

Results showed that the melting water conductivity of ice layer decreased with position from top to bottom, which indicates that ion migration occurred during the freezing process of NaCl aqueous solution. In addition, the maximal melting water conductivity of the ice layer formed under the energized condition was lower than that under the non-energized condition.

This result may be explained as follows. (1) During the phase transition under the non-energized condition, the natrium and chloride ions in water are squeezed out under the crowding-out effect of dendritic crystals and move toward the direction of unfrozen liquid water. However, ions move along the direction of the electric field line under the energized condition. The applied electric field is sine alternating, thus the ion movement changes with sine alternating electric field. In other words, the direction and strength of the ion movement will change accordingly when the strength and direction of the electric field changes. The result may lead to the fact that the direction and magnitude of velocity changes, so the ions may display a reciprocal motion, which significantly impacts the migration movement and migration quantity of ions; (2) Dipole polarization of water molecules is produced by electric field. Furthermore, NaCl is a strong electrolyte that can be ionized completely in week solution. The size and direction of the electric field force applied on electric dipoles constantly change, which results in polarization and conduction losses that lead to the decrease in energy absorbed by conductive ions in water.

As shown in Figure 4, the maximal melting water conductivity of the ice layer decreases with increasing external voltage. The reason for such observation might be as follows. The electric field strength increases with increasing of external voltage. Combining the analysis above, the movement of ions along the electric field line and polarization and conduction losses would be affected by the increasing strength of electric field, which might be a key factor influencing the extent of ion migration weakening.

4. Ion Migration of Freezing Water during the Icing of Insulator under Alternating Electric Field

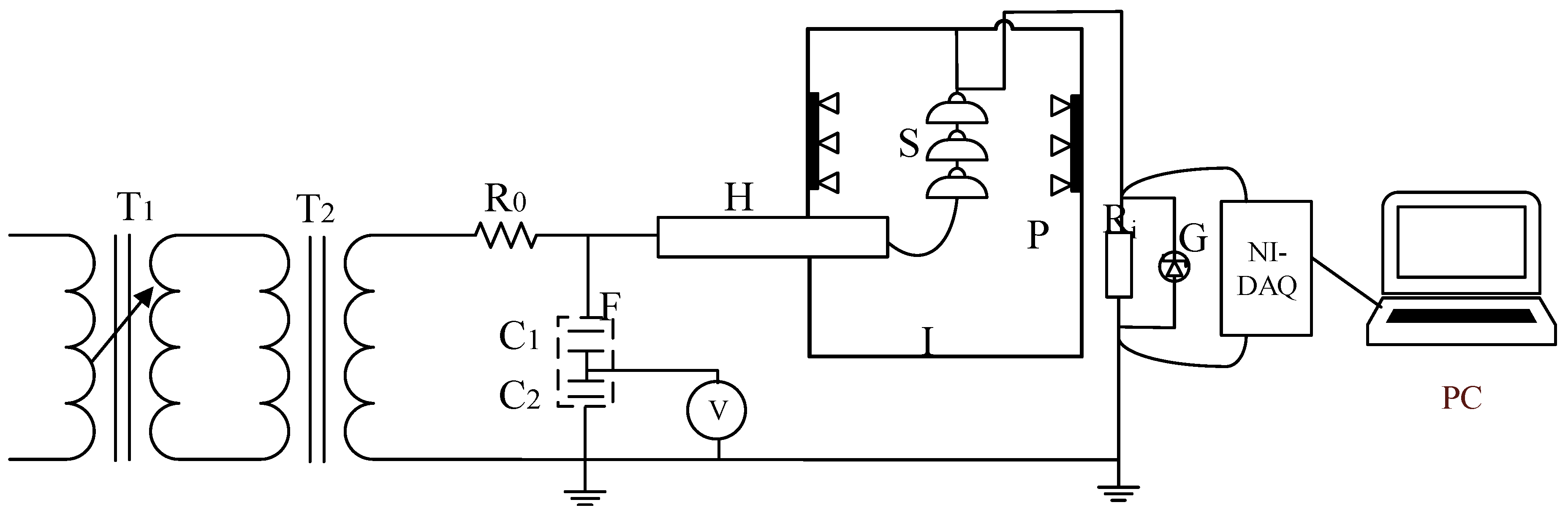
4.1. Experimental Equipment and Sample

This experiment was implemented in a multifunctional artificial climate chamber, which meets the requirement of artificial wet-growth ice accumulation [25]. The AC icing test circuit is shown in Figure 5. Leakage current measuring instrument is composed of R_i and G. The former is non-inductive resistance (RX24-50W, Aviation Industry, Beijing, China) and its resistance is 1 Ω. The latter is the TVS protecting tube. NI-DAQ is data acquisition instrument (USB-6215) produced by NI company, Austen, TX, USA. The maximum of sampling rate is 250 kS/s. The waveform of leakage current can be displayed by software LABVIEW (2012) on the PC. The samples used in the experiment were glass insulator. The technical parameters and profiles are shown in

Table 2. Parameters and Profile of LXY4-160.

Parameters						Profile
D (mm)	H (mm)	L (mm)	I (kV)	F (kV)	M (kV)
280	146	450	110	45	130

, in which D is the diameter, H is the connection length, L is the leakage distance, I is impulse withstand voltage, F is frequency withstand voltage under the condition of rain, and M is minimum break-down voltage.

4.2. Test Procedures

(1) Pollution simulation method

To date, two main methods are used to simulate the contamination of an ice-covered insulator [26]. The freezing water conductivity method, which had small dispersion of test results and can easily control the uniformity of the contaminants, was used in this study [27]. Various pollution levels were simulated by adding NaCl into deionized water. The conductivity water ${\mathsf{\gamma }}_{20}$ values elected for the experiments, which were corrected at 20 °C, were 50, 200, 500, and 800 μS/cm.

(2) Ice accretion method

The insulator were cleaned first and hung on the shelf for drying before the tests. At the earlier stage of test, the samples were hung on the desired position in the climate chamber, in which the temperature was adjusted to −6 °C. Freezing water was placed in the climate chamber until the water temperature neared 1 °C. Additionally, spray nozzle was adjusted such that the water droplet diameter was within 80–100 μm. Two groups of spay nozzles were established from the relative position in consideration of icing uniformity. The spaying system was terminated once the ice deposit had finished. To clarify, energized condition in Section 4 means the 3-unit insulator string with applied 22 kV AC during the whole icing process. On the contrary, the non-energized condition means 3-unit insulator string without applied alternating voltage during the same icing process.

(3) Measurement of melting water conductivity

Measurement for the melting water conductivity of the insulator includes ice layer and icicles. They have similar measuring methods; hence, the ice layer was used as an example. The measuring steps are described as follows. (1) After icing, the ice-covered insulator string was continued to be frozen for 15 min. Subsequently, the insulator string was placed in a normal temperature environment, and the serial numbers 1–3 denoted these three insulators from near-ground end to near-high voltage end; (2) The ice layer began to melt as the heat absorbed by the ice layer on the insulator was increased. Water droplets slid along a funnel with a large diameter and were conveyed into the graduated cylinder in the end. The conductivity of melting water was measured every 1 min; (3) The ice accreted on the insulator surface was assumed to be uniform, and the melting velocity was assumed to be consistent. The thickness of melting was also equal.

The termination criterion for collecting melting ice water was when ice shedding occurred or the melting water conductivity slightly changed.

(4) Measuring method for flashover voltage

To obtain the minimum AC flashover voltage (U_mf) during the melting period, the U-shaped method was adopted and U_mf can be expressed using Equation (2). The test procedure was referred to References [7,8,10].

U_mf = Minimum(U_f1, U_f2, …, U_fn)

(2)

4.3. Test Results and Analysis

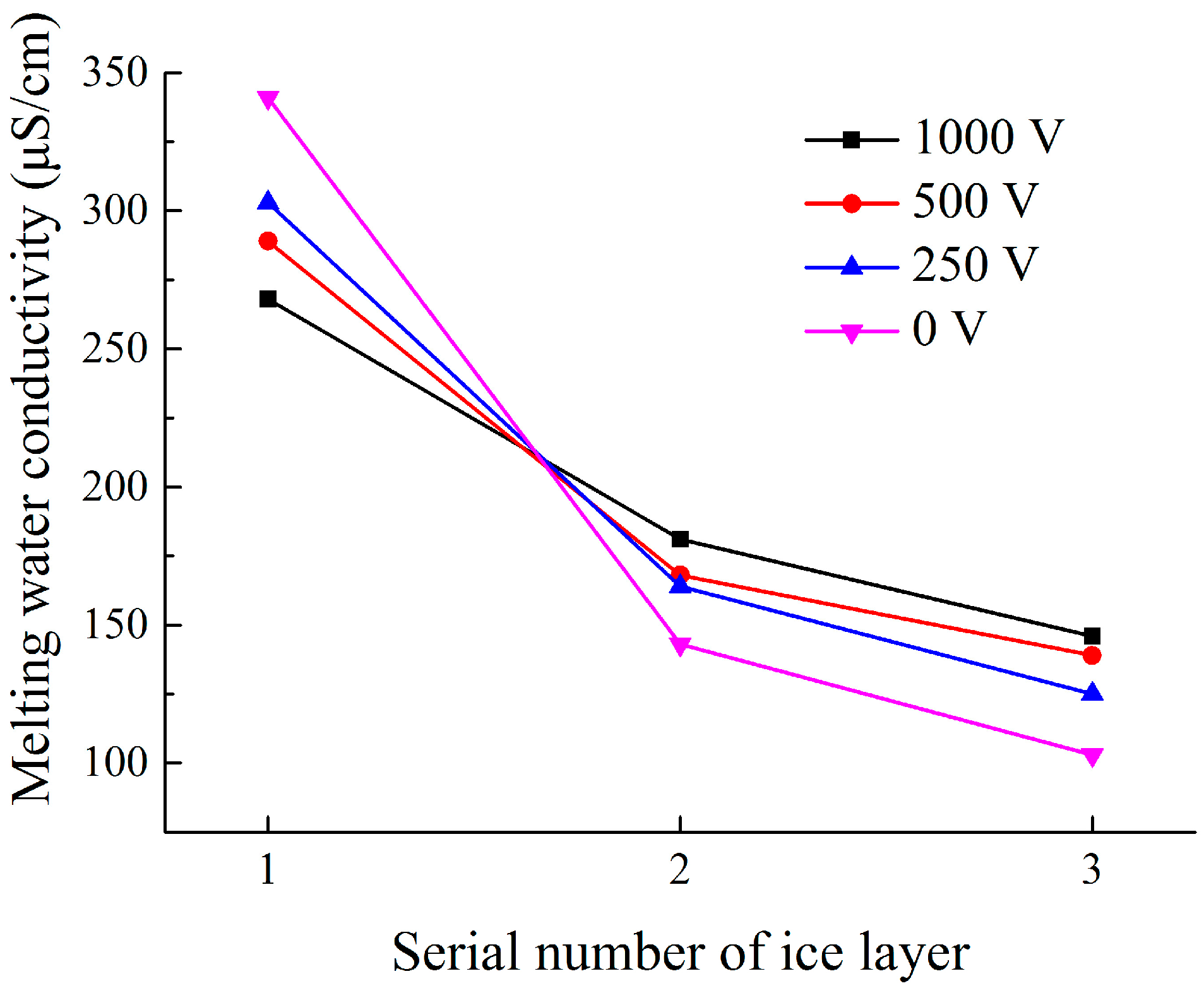
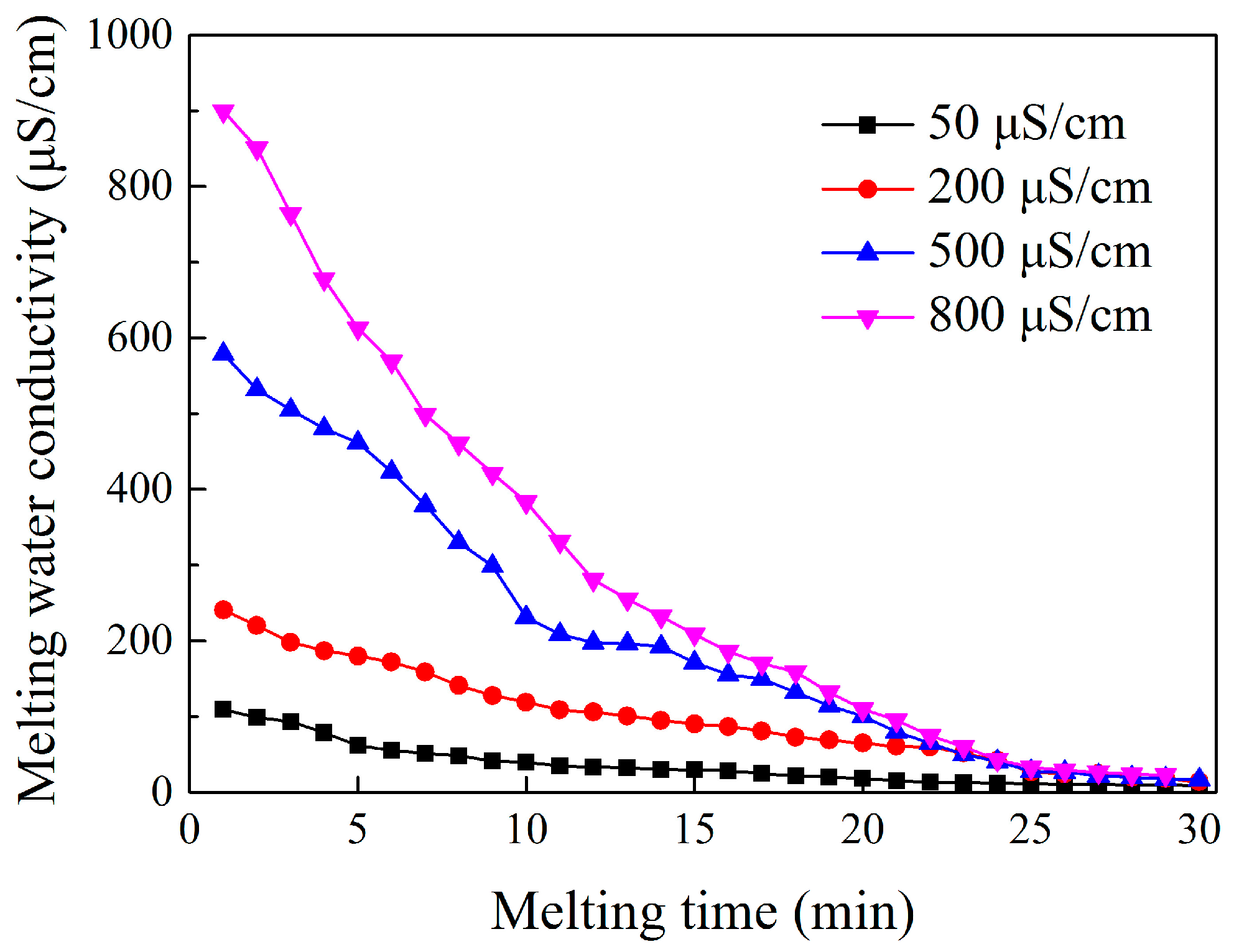
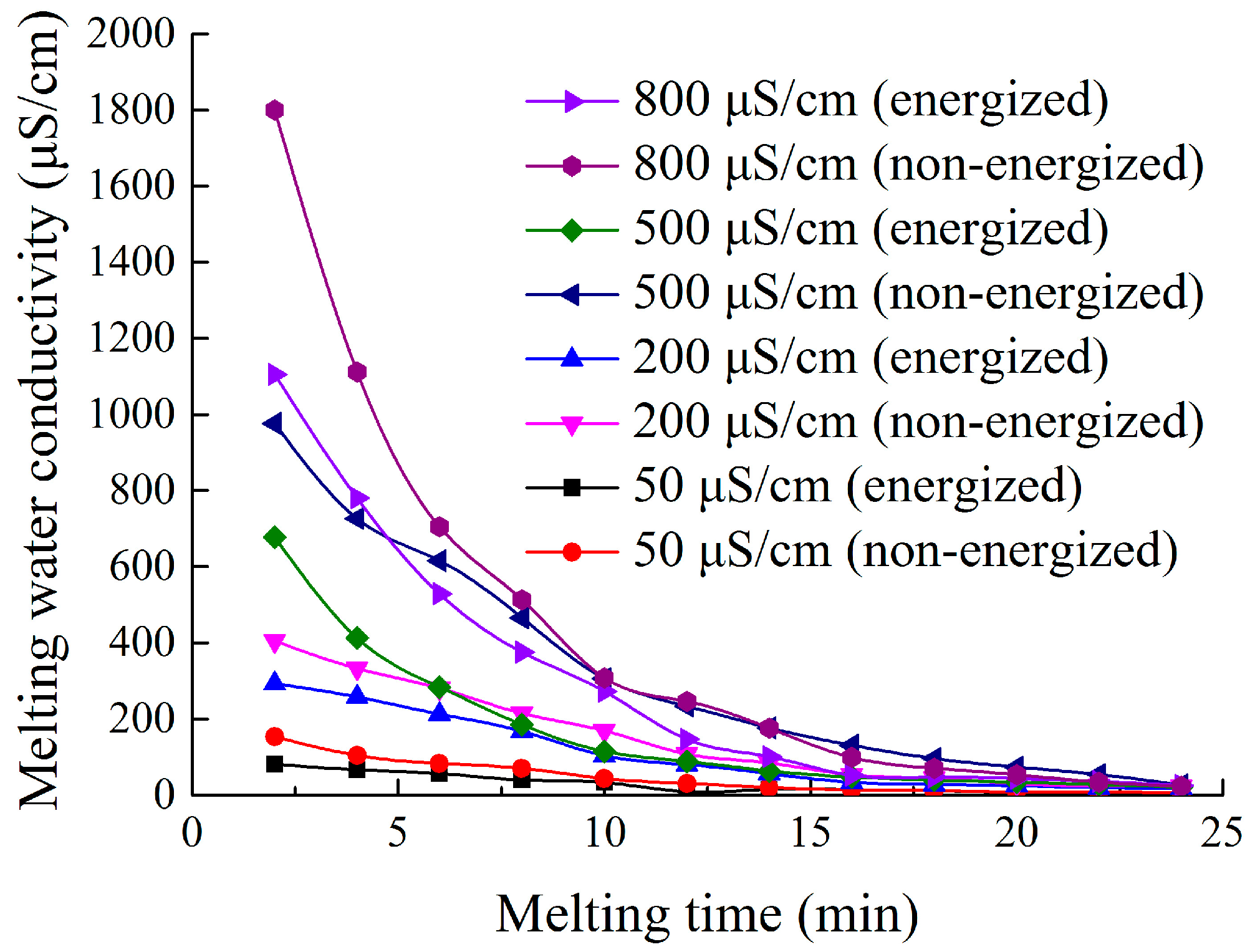
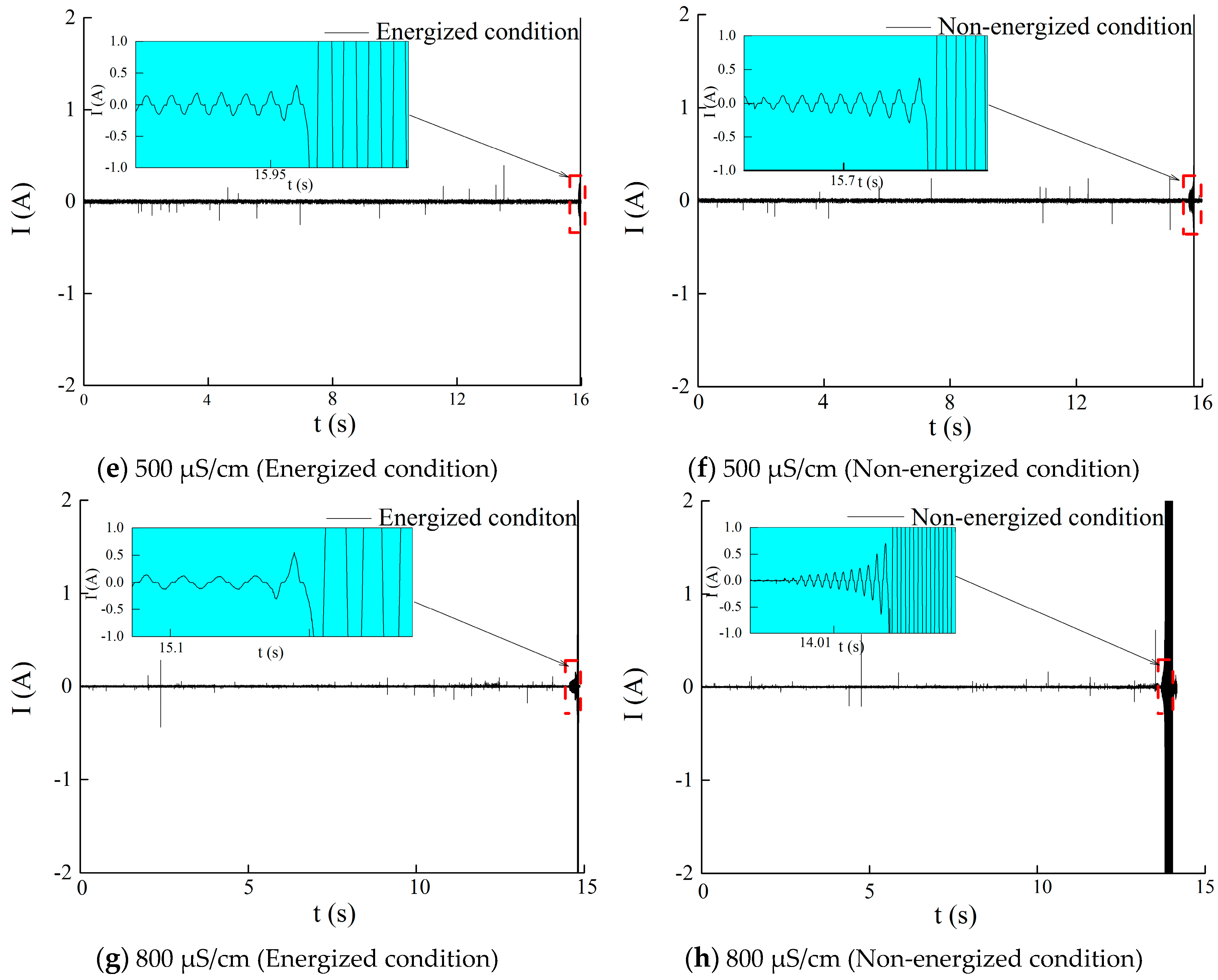
4.3.1. Effect of Freezing Water Conductivity on the Ion Distribution in the Ice Layer and Icicle of the Insulator

Three units of glass insulator string were used for the icing under the energized condition. The melting water conductivity of the ice layer on No. 1 insulator surface changed depending on melting time (Figure 6). Melting water conductivity continuously declined with prolonged melting time and showed a non-linear relationship with melting time. Melting water conductivity reached its maximum value at the beginning of melting. These values were 100, 241, 579, and 901 μS/cm, which were higher than their freezing water conductivity. Meanwhile, it could be also found that the higher the conductivity of freezing water was, the higher the melting water conductivity of ice layer surface was. The number of conductive ions per unit volume water increased with the increasing of freezing water conductivity, thus leading to the number of ion migration becoming greater. The inner surface of ice layer near the insulator surface had lower melting water conductivity. The minimum values were only 12.3, 17, 18, and 24.5 μS/cm, which were significantly lower than their freezing water conductivity. This result indicates that ion migration occurred during the freezing of water droplets on the insulator surface.

The reasons for this phenomenon might be as follows. (1) Water molecules are tightly lined on the basis of the crystal structure during freezing. The solubility of solute decreases with decreasing temperature. The ions and air in supercooled water droplets are squeezed out under the crowding-out effect of dendritic crystals. A mass of conductive ions in water droplets begin to move toward the direction of unfrozen supercooled water droplets; (2) Ice nucleus spontaneously forms, and ice crystal branches grow rapidly during the transition from liquid to solid, thereby accelerating the freezing of water droplets. Latent heat released from the phase transition process provides energy for conductive ions to migrate, which accelerates the extent of ion migration.

Icicle growth involves longitudinal and diameter growths. Longitudinal growth is caused by the fact that liquid water freezes during sliding under the action of gravity so that the icicles are elongated along the longitudinal direction. Diameter growth is caused by the fact that a part of liquid water that is sticking to the icicle surface during sliding occurs to freeze so that the icicles become coarse.

According to the measuring method mentioned above, icicles under the circumstance of non-bridging, which is located between the No. 2 and 3 insulators, are selected. This selection was based on the fact that bridging adjacent sheds under the energized condition is difficult. The relationship between melting water conductivity and melting time is described in Figure 7. With prolonged melting time, melting water conductivity gradually decreased from the outer layer to the inner layer of the icicles. The maximum and minimum values of melting water conductivity were higher and lower than those of freezing water, respectively.

The possible reason for this observation may be as follows. (1) Ion migration first occurred on the insulator surface. A part of supercooled water has a mass of conductive ions, and its conductivity is higher than the corresponding freezing water conductivity, which will slide along the umbrella skirt and be used for icicle growth. The freezing process is continuous, more and more conductive ions migrate into outside surface of ice layer, resulting in higher conductivity near outside surface of icicles; (2) Icicle growth is also the freezing process of water droplets; hence, it is accompanied by ion migration. Combining that with Reference [17], ion migration occurs in both cross and longitudinal directions, which is aligned with the direction of freezing.

As shown in Figure 7, the melting water conductivity of the icicles under the energized condition was lower than that under the non-energized condition, and the differences increased with increasing of freezing water conductivity.

The reason might be as follows. (1) The freezing rate of water droplets on the icicle surfaces decreases because of the heat effect of leakage and partial arcs. Specific analyses are as follows. Freezing water conductivity (800 μS/cm) is taken for an example. The leakage current in the process of icing is monitored, which is shown in Figure 8. The leakage current in most icing process is less than 15 mA. At some certain moments, the peak value of leakage current can suddenly increase near 90 mA. Combing the References [8,28], when local arc discharge appears, some air gaps are short connected, resulting in body resistance decreasing and higher current. Based on the principle of Joule’s law, heating effect will be produced, which may affect the temperature of ice surface and slow down the icing rate; (2) According to the simulation and experimental measuring in References [7,17,29], the icicle tips make the electric field deform because of the large curvature of the icicles. The electric field strength around the icicle tips increases so that point corona discharge may occur and its heat effect may melt ice. In addition, combining the conclusion in Section 2, the strong electric field strength around the icicle tips might slow down the freezing rate of the icicles accordingly, which further leads to the drainage of highly conductive water. The reasons mentioned above can hinder icicle growth and thus weaken the extent of ion migration.

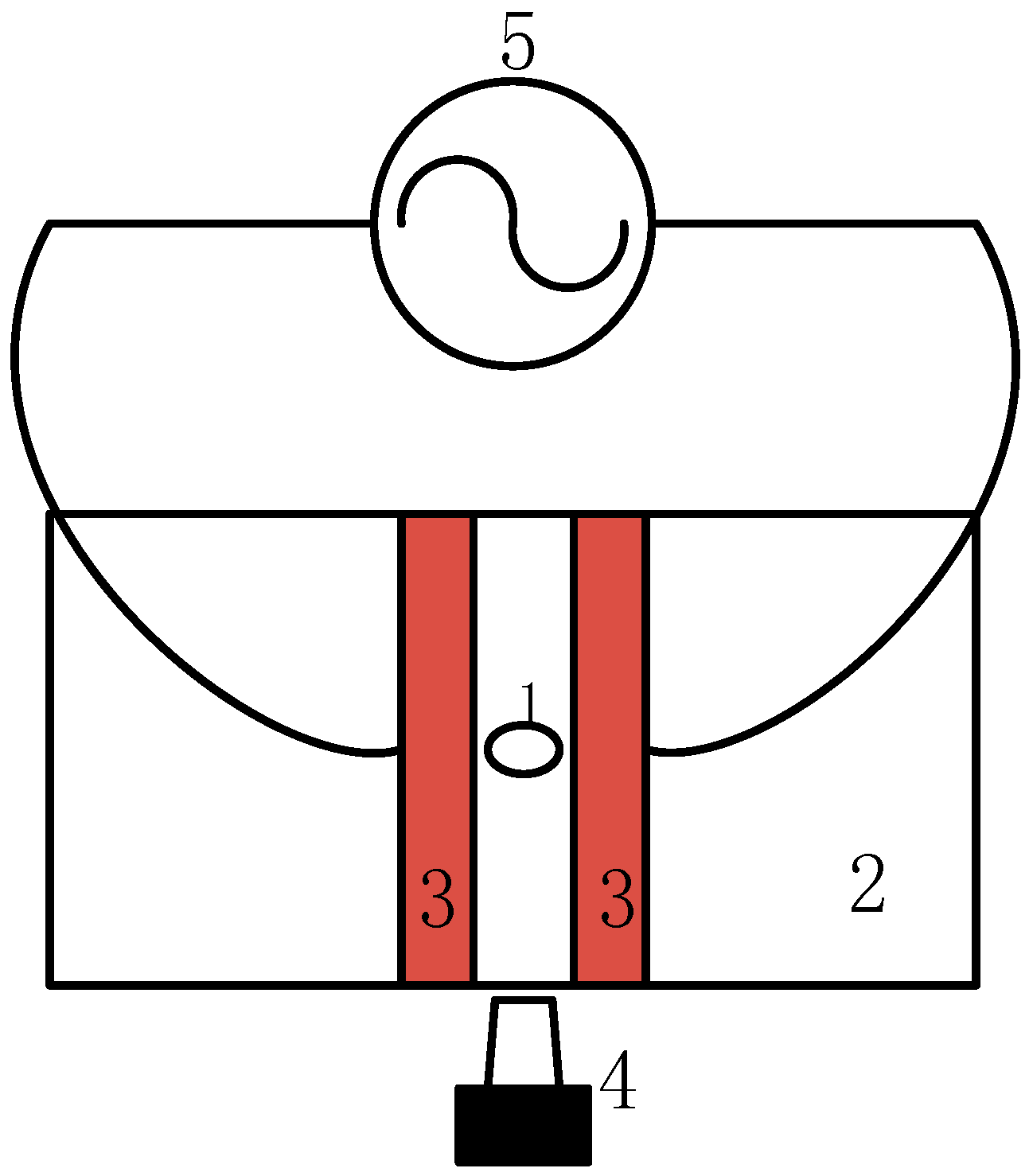
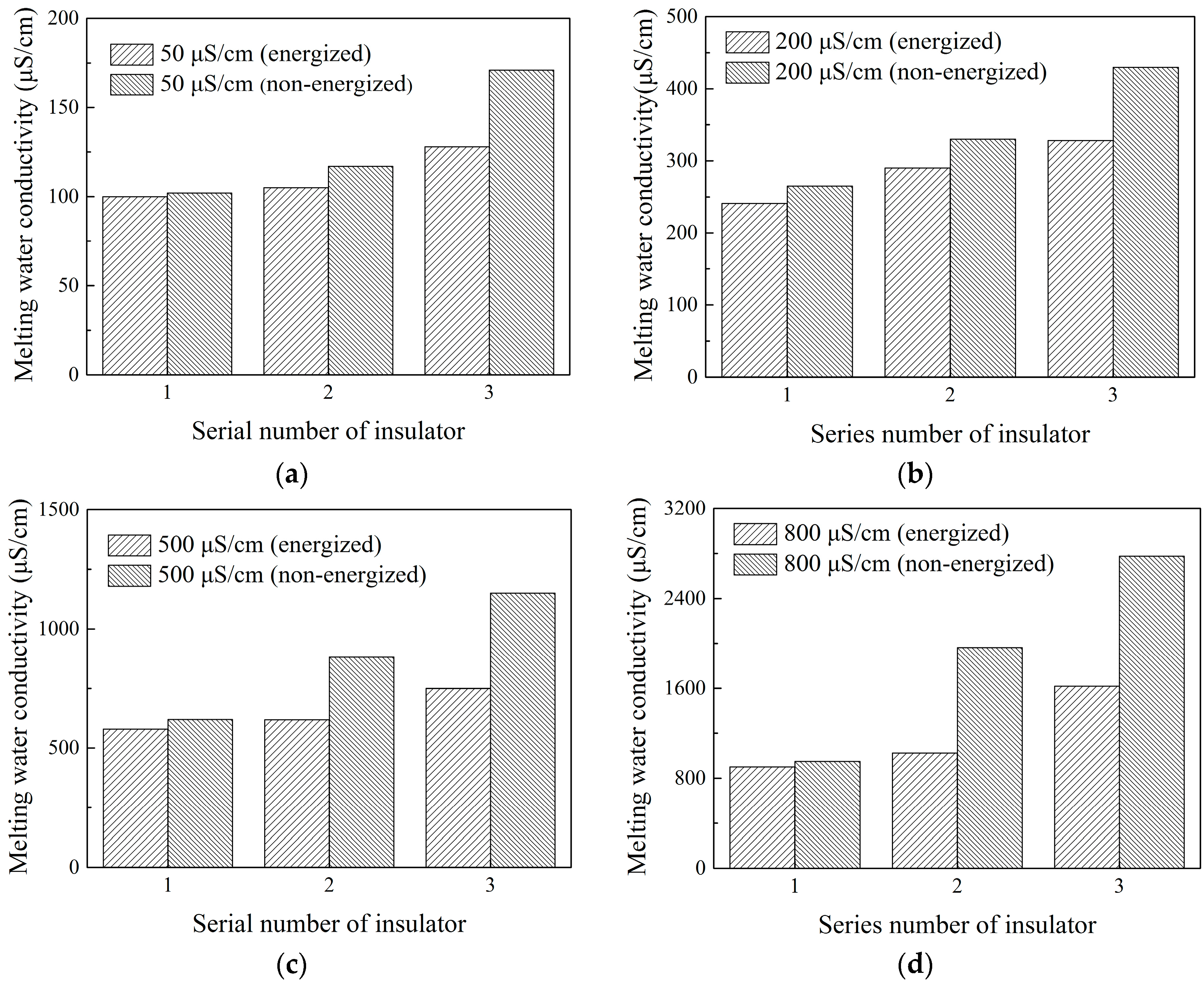
4.3.2. Effect of Insulator Suspension Position on the Ion Distribution in the Ice Layer

The maximal melting water conductivity of the ice layer on each insulator of insulator strings under different freezing water conductivities is shown in Figure 9. The hanging location of each insulator significantly affected the melting water conductivity. The maximal melting water conductivity of ice layer formed under the energized condition gradually increased from No. 1 insulator to No. 3 insulator (top to bottom), and its maximum value could be 2.02 times as the freezing water conductivity.

The reason might be explained as follows. The freezing rate in glaze icing cannot freeze all water droplets immediately. The unfrozen water containing massive conductive ions caused by ion migration slides along the umbrella skirt and icicles and reaches the bottom insulator. Under the combined effects of ion migration on the insulator surface, the ice layer conductivity on the bottom insulator (No. 3) surface increases most.

The ice layer formed under non-energized condition had similar characteristics. However, there still existed differences under the energized and non-energized conditions. The maximal melting water conductivity of ice layer on each insulator formed under the energized condition was obviously lower than that under the non-energized condition, particularly the ice layer on No. 3 insulator surface.

The reason for this observation might be as follows. (1) The direction of ion movement constantly changes with the effect of alternating electric field; the ion movement, polarization and conduction losses would be affected, which might weaken the extent of ion migration under the energized condition. Part 3 has illustrated this point in detail; (2) Water droplet freezes at a low velocity arising from the heat effect of the leakage current and corona discharge, which drains the water droplets along the insulator surface.

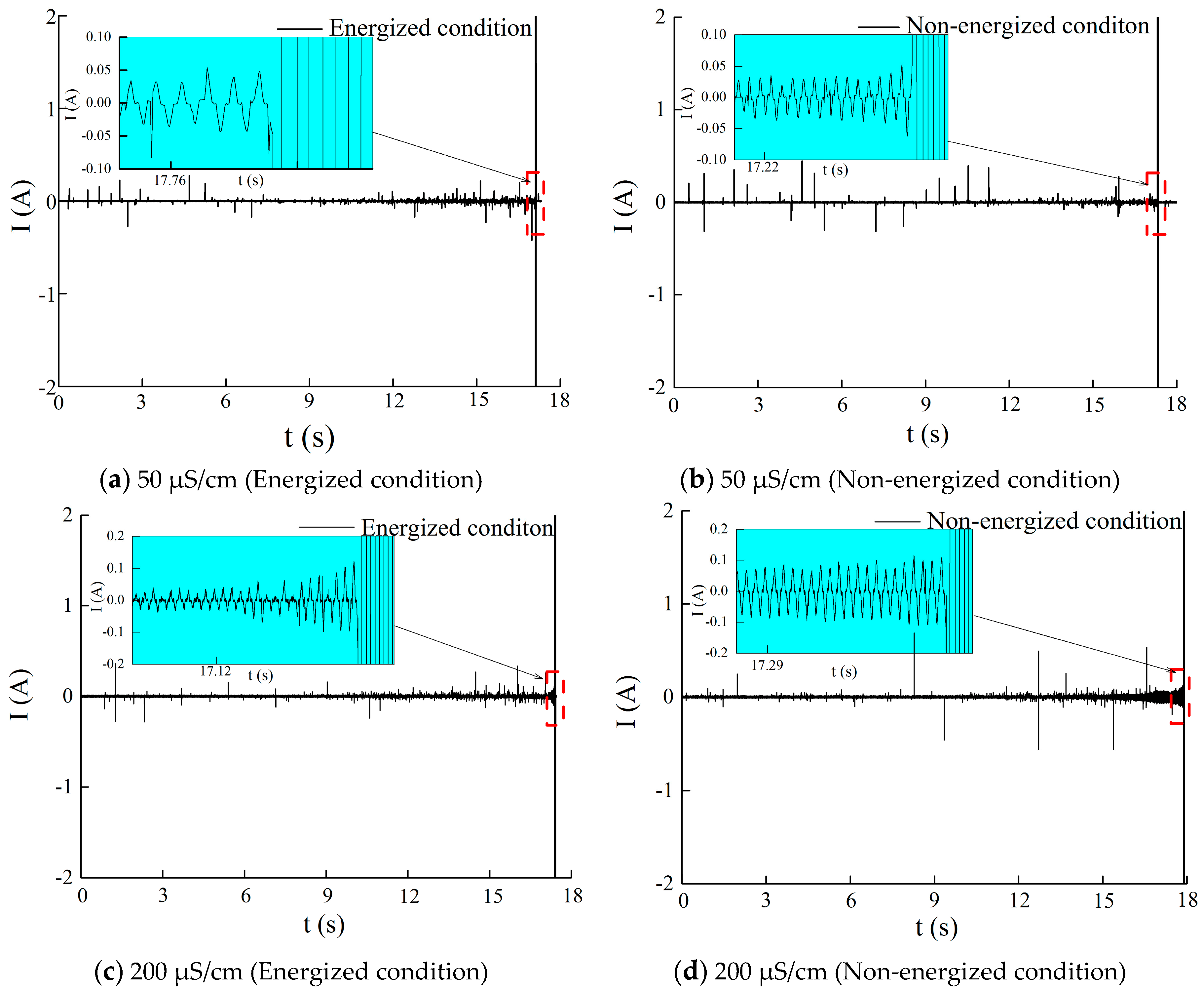
5. Effect of Ion Migration during Phase Transition under Alternating Electric Field on Insulator Flashover

Ice flashover tests were carried out to explore the effect of ion migration on ice flashover voltage. Melting water during flashover was collected using a salver which had been cleaned by deionized water before tests. When the flashover was over, the value of melting water conductivity should be measured immediately and corrected to the values at 20 °C.

According to existing research results, iced insulators have two discharge paths, namely, the outer surface of ice and the interface between the ice layer and the insulator [30]. Compared with the interface between ice and insulator, the outer surface is more likely to melt with increasing ambient temperature. Subsequently, a water film is formed, which can dissolve conductive ions quickly and considerably increase conductivity. The high-definition camera (Sony FDR-AX30, Sony, Tokyo, Japan) with fifty frames per second is used to record the flashover process. Other technical parameter of camera is shown in the

Table 3. Key technical parameter of camera.

Product Models	Sony FDR-AX30
Sensor pixel	About 18.90 mega pixels
Type of sensor	Exmor R CMOS
Image resolution	AVCHD model: 1920 × 1080/50p

. The flashover process lasted for about 14.3 s. t₀ means 0.02 s.

As shown in Figure 10, corona discharge and partial arc first appeared around the pin of the ice-covered insulator string (T = 210t₀) and gradually developed and intensified. With the increase of applied voltage, partial discharges were especially obvious and the melting phenomenon also gradually increased (T = 287t₀–356t₀). Bluish violet partial discharge turned pink first and then suddenly became intermittent white. The energy supplied by power was used for maintaining the arc burning and melting the ice layer .When the ice layer further melted, the thickness of water film increased, which accelerated the re-ignition of arc (T = 400t₀–489t₀). As applied voltage was further increased, more new partial arcs were produced and developed gradually from single arc to multi-arcs and the frequency of arc re-ignition also increased (T = 541t₀–643t₀). These arcs can keep steadily burning and propagate along the surface of conductive water film and air in the mid to late period. When the arcs became longer and wider, combination among adjacent arcs commonly occurred (T = 658t₀–690t₀). When the length of the partial arc reached the critical flashover distance of the insulator string, the flashover along with the insulator string occurred (T = 713t₀).

According to the experimental observations, highly conductive water film is essential to the flashover of ice-covered insulator string, which is in accordance with studies by Farzaneh et al. [16,31]. The wave forms of leakage current during the flashover process of an ice-covered insulator are shown in Figure 11. The peak value of leakage current at half a cycle before flashover can also be recorded [32]. From the Figure 11, it can be also found that the average critical leakage current increased with the increasing of freezing water as a whole. Surface resistance of ice layer decreased with the increasing conductivity of water film, which is a key factor leading to the frequent activity of arc and critical leakage current increasing. Melting water could be obtained because of the effects of Joule heating produced by the arc on the surface of the ice-covered insulator string. Thus, the melting water conductivity can be used to characterize the surface conductivity of the ice layer indirectly, namely, water film conductivity mentioned above.

The conductivity of melting water, obtained during the flashover process, is linearly fitted with the conductivity of freezing water. As shown in Figure 12 and

Table 4. Value of A, B and R² under different electric field condition.

Linear Fitting Expression: γmelting = Aσfreezing + B A,B: the Fitting Coefficients; R2: the Square of Correlation Coefficient
Condition	A	B	R2
Energized	1.28	22.8	0.973
Non-energized	1.69	0.97	0.988

, fitting result indicated that the melting water conductivity during flashover has a good linear relationship with freezing water conductivity, no matter whether both sides of insulator string is energized or not in the icing process. However, the fitting coefficients have significant differences under energized and non-energized conditions.

On the basis of the arc discharge modeling [33], critical flashover voltage peak could be described in Equations (3)–(5).

$$V_m=Ax{I}_m^{-n}+I_{m}R\left(x\right)$$

(3)

where $V_m$ (V) and $I_m$ (A) are the peak values of the applied voltage and leakage current; A and n are arc constants with values of 204.7 and 0.5607, respectively; $x$ (cm) is the length of arc; and $R\left(x\right)$ (Ω) is the residual resistance, which is directly related to the conductivity of the iced insulator surface.

$$I_m={\left(\frac{kx}{V_m}\right)}^{\frac{1}{b}}$$

(4)

where k and b are arc re-ignition constants with values of 1118 for the arc propagating upward (or 1300 for the arc propagating downward) and 0.5277, respectively.

$$R\left(x\right)=\frac{1}{2{\mathsf{\pi }\mathsf{\gamma }}_e}\left[\frac{4\left(L-x\right)}{D+2d}+\ln \left(\frac{D+2d}{4r}\right)\right]$$

(5)

where ${\mathsf{\gamma }}_e$ (μS/cm) is the surface conductivity of the ice layer; L and D are the length and diameter of the insulator string, respectively; d is the thickness of the ice layer; and $r$ is the arc root radius.

Based on Figure 12 and Equations (3)–(5), the melting water conductivity of ice-covered insulator string obtained during flashover process increased with the increasing of freezing water conductivity. Therefore, the residual resistance decreased, which may lead to lower flashover voltage. The above analysis is consistent with the data in

Table 5. Influence of freezing water conductivity on flashover voltage.

Freezing Water Conductivity (μS/cm)		50	200	500	800
Umf (kV)	Energized condition	97.4	74.0	59.2	49.4
	Non-energized condition	96.9	69.5	52.7	39.1

. By comparison, it also can be found that the melting water conductivity of ice layer formed under energized condition is obviously lower than that under non-energized condition. Based on the Equation (5), the residual resistance under energized condition is larger than that under non-energized condition, which is an important reason why it leads to higher flashover voltage.

According to Equations (3)–(5) and analysis above, accurately calculating the surface conductivity of ice layer formed in energized condition is very important for accurately predicting flashover voltage of ice-covered insulator. References [33,34] provided a linear fitting equation which was often used to calculate the equivalent surface conductivity of ice layer. The ice sample in References [33,34] formed in the triangular glass mould was not under electric field, that is, it ignored the effect of alternating electric field during the icing process. However, the experimental data in Section 3 and Section 4 of this paper showed that electric field did have an effect on the conductive ion distribution of ice layer. For this reason, it is necessary to update the calculation of surface conductivity of ice layer in order to obtain a more accurate value. Therefore, this paper proposes that the effect of alternating electric field on conductive ion distribution in ice layer should be taken into consideration in further predicting flashover model of ice-covered insulator. In addition, the future work is to do masses of field tests to derive the quantitative relationship between the electric field intensity and conductivity of ice surface. In addition, the range of freezing water conductivity should be extended in order to satisfy the needs of practical engineering.

6. Conclusions

According to the above experimental results, the following conclusions can be obtained:

(1)

The morphological change of water droplets during freezing had no obvious differences between having the amplitude of electric field (E₀ = $200\sqrt{2}$ kV/m) and without electric field. The average freezing time of the water droplets with consideration of the error was almost unaffected when E₀ was lower than $80\sqrt{2}$ kV/m. However, the inhibitive effects on drop freezing intensified with increasing electric field strength.

(2)

After freezing the NaCl aqueous solution in a glass container with applied alternating voltage, the maximal melting water conductivity of the ice layer formed under the energized condition was lower than that under the non-energized condition. The extent of conductive ion migration decreased with the increasing of applied electric field strength, resulting in decreasing of the maximal melting water conductivity of ice layer.

(3)

The melting water conductivity of the ice layer formed under energized condition showed a non-linear decreasing relation with melting time. The maximal and minimal melting water conductivity of ice layer was higher and lower than freezing water conductivity, respectively. Icicles also had similar features. Besides, the melting water conductivity of the ice layer and icicles formed under the energized condition was lower than that under the non-energized condition.

(4)

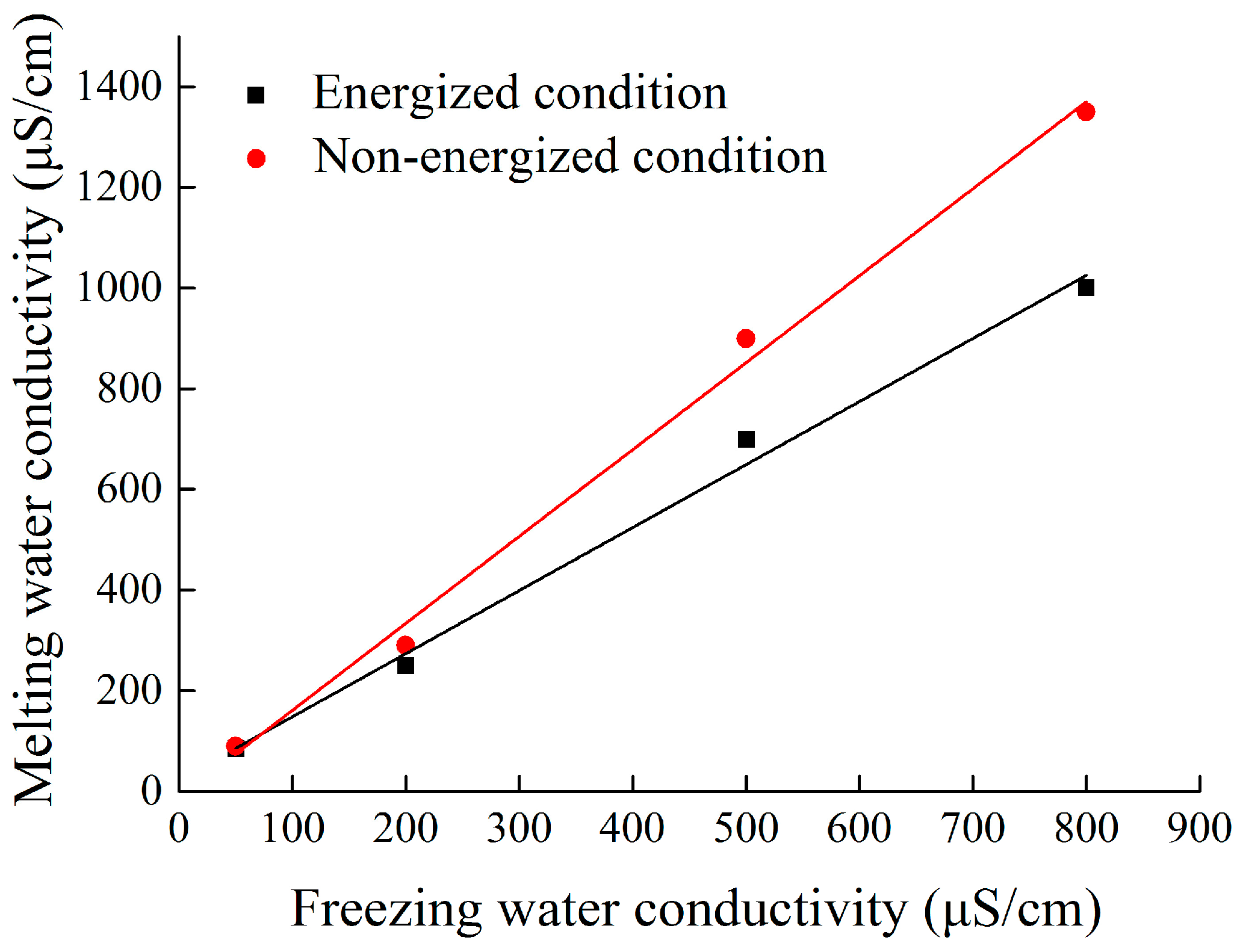
The hanging location of each insulator obviously affected melting water conductivity. The maximal melting water conductivity of the ice layer on insulator surface gradually increased from No. 1 to No. 3 insulator (top to bottom). The melting water conductivity of ice-covered insulator string obtained during flashover had a good linear relation with freezing water conductivity, but the fitting coefficients have significant differences under energized and non-energized condition.

(5)

Accurately calculating the surface conductivity of ice layer formed in energized condition is an important factor to improve the predicting flashover model of ice-covered insulator. The alternating electric field affects the conductivity distribution in ice layer, which should be taken into consideration when calculating the surface conductivity of ice layer during the melting period.