Analysis of Power Loss and Improved Simulation Method of a High Frequency Dual-Buck Full-Bridge Inverter

Abstract

A high frequency dual-buck full-bridge inverter for small power renewable energy application is proposed in this paper. A switching frequency of 400 kHz is achieved with the adoption of the SiC power device. A two-pole two-zero (2P2Z) compensator is employed in the outer voltage loop to generate the current reference for inner current loop. A 3P3Z compensator is adopted in the inner current loop to track the current reference. A systematic way for calculating the losses of high frequency inverter is presented, and the losses of the components are thoroughly analyzed. The turn-on and turn-off procedures of the inverter are discussed in detail. The losses caused by high frequency are calculated accurately, and the loss distribution is established as well. The procedure of the loss analysis gives a practical example for calculating the loss of similar type inverters. Moreover, deviation between pulse width modulation (PWM) control signal and switching response in high frequency switching is thoroughly analyzed. The influence of deviation is verified by designed experiment. Hence, a compensation method is proposed in order to minimize the influence. The compensation effect is validated by experiment and simulation. Finally, a 1-kW prototype is built to verify the feasibility of the theoretical analyses. The grid-connected maximum output power experiment is completed at 1 kW with the efficiency of 96.1% and the total harmonic distortion (THD) of 1.8%. The comparison experiments of power loss between Si and SiC power devices are carried out. The experiment results confirm the loss calculation method to be valid.

1. Introduction

In order to make the social development less fossil fuel-dependent and more environment-friendly, renewable energy becomes an important alternative energy source [1,2]. With the development of distributed renewable energy generation, small-scale inverter becomes a focus of research. Being able to convert all kinds of distributed energy into a unified AC power, the grid-connected inverter extensively broadens the application range of renewable energies, and thus acts as an indispensable role in the renewable energy generation system [3,4].

For the rapid development of the new power devices, the wide band gap power devices, such as SiC and GaN, begin to replace the traditional Si power devices. Its outstanding performance, including high switching speed, low switching loss, high stability in high temperature operating and so on, makes the high frequency inverter a new research hot spot. A three-level SiC inverter is proposed in [5]. By employing the SiC MOSFET and FPGA control platform, a 100 kHz switching frequency is achieved. GaN high-electron mobility transistors (HEMT) power devices are adopted in a single-phase T-Type inverter in [6]. Switching performance and efficiency performance are analyzed among Si, SiC and GaN HEMT. The results demonstrate the advantage of the wide band gap power devices in high frequency inverting. It can be seen that all these inverters adopt the wide band gap power devices and have a working frequency, which is much higher than the traditional ones. As a result, the THD of the inverters is significantly reduced and the output power quality is improved obviously. Meanwhile, smaller components can be used and the volume of the inverter is significantly decreased, which broaden the application range of the inverter. On the other hand, as frequency increases, the losses of the inverter under high frequency circumstances become a major problem, which is not discussed in detail in this paper.

With the application of high frequency switching, loss analysis is even more important, because it can offer a guideline for the system efficiency improvement [7,8,9,10,11,12,13,14]. In [7], a detailed investigation into loss distribution for diverse components is conducted, which includes losses of switches, diodes, inductors and capacitors. In [8,9], the switch and diode losses of several inverter topologies are studied and compared, which gives an evident insight into the loss distribution for each low-frequency topology. Nevertheless, this comparison may show less accuracy when it comes to high frequency case, because more details of the switching procedure must be taken into account in the high frequency operation, which will affect the losses and are not included in this literature. In [10], the mechanism reflecting the relation between transition characteristics and power losses is discussed. Diode losses based on traditional Si semi-conductor are analyzed as well. In [11], comparative experiments of losses between Si and SiC power devices are carried out, which proves that the SiC devices are superior in switching speed, operating temperature and switching losses than the traditional Si. Although the loss analyses previously mentioned are very comprehensive and detailed, all these works are also based on traditional low frequency simplified method, which show less accuracy for the high frequency loss analysis. This is because some losses, overlooked in low frequency condition, may become an indispensable part of the total losses in high frequency implementation. Hence, deviations will be introduced if low frequency loss calculation method is implanted directly into the high frequency operation.

Moreover, the influence of the high frequency switching is not confined to losses analysis. The impact of high frequency on the simulation model is also noteworthy. Model of the wide band gap power devices are established in [15,16,17,18,19]. A compact model of the SiC metal-oxide-semiconductor field-effect transistor (MOSFET) is built including the carrier-trap influences in [15], the simulation results is verified by the experiments. Jun Wang et al. [16] discusses a 10-kV 4H-SiC MOSFET and key characteristics are extensively investigated. A simple behavioral SPICE model for the SiC MOSFETs is proposed to predict their realistic application prospect. The impact of nonlinear junction capacitance on switching transient is studied in [17], and a simulation circuit for switching transient analysis is built. A dynamic model of GaN cascaded current aperture vertical electron transistor (CAVET) is established in ATLAS-SPICE-integrated simulator. The simulation model successfully models and projects the switching performance of the GaN CAVET. These simulation models are very thorough. However, most of the researches concentrate on the component level influence. The impact of high frequency switching on the output of the converter is not detailed discussed. On the other hand, the component level model is too complicated and time-consuming for converter analysis. The influence of high frequency switching on the inverter simulation model is rarely studied.

In this paper, a high frequency single phase dual-buck full-bridge grid-connect inverter for small power renewable energy is proposed. The SiC components, as the power devices, are employed to achieve high switching frequency and to limit the conversion loss simultaneously. For the controller, the proposed inverter adopts a current voltage dual-loop. The 3P3Z compensator is adopted in the inner current loop in order to track the current reference which is generated by the 2P2Z compensator. The 2P2Z compensator is employed in the outer voltage loop in order to regulate the DC bus voltage by balancing the input and output power. A systematic way for calculating the losses of high switching frequency inverter is presented. The losses of each component in the inverter are thoroughly analyzed. The switching procedure and the corresponding losses are discussed in detail. The high frequency losses are also taken into account during the analysis. The distribution of the losses is established based on the presented method. Moreover, the deviation between PWM control signal and switching response, which emerges in high frequency switching, is thoroughly analyzed. A designed experiment verifies the influence of deviation. Thus, a compensation method is proposed in order to minimize the influence of deviation. Experiment and simulation confirm the compensation effect. Finally, a 1-kW prototype is made and a 400 kHz switching frequency is achieved. The comparison experiments of the power losses are carried out between Si and SiC power devices to verify the loss calculation method. The results proved the loss analysis is valid.

2. Circuit Configuration and Control Method

2.1. Operation Principles

The topology of the dual-buck full-bridge inverter is presented in Figure 1a. The inverter can be regarded as two individual buck converters. Buck 1 consists of S₁, S₃, D₁ and L_i1, connecting to the DC bus positively. Buck 2 consists of S₂, S₄, D₂ and L_i2, connecting to the bus negatively. The output inductors of the buck converters L_i1 and L_i2 constitute a LCL filter with C_f, L_g1 and L_g2.

To drive the inverter, the unipolar modulation has been adopted and the waveforms of the driving signal are shown in Figure 1b. In one AC cycle, both bucks work in their own half cycles separately. When Buck 1 works, S₃ keeps turn-on in the half AC cycle and S₁ switches at high frequency to follow a sinusoidal reference in order to generate the positive half of the grid current i_g. D₁ offers the free-wheeling path when S₁ turns off. Unlike the H-bridge inverter, no switches are at the same leg. Accordingly, the dead time is no longer needed. Moreover, the free-wheeling current is running through D₁ instead of the body diode. Because the independent diodes have a better performance, the total losses of the inverter can be reduced. The operation principle of Buck 2 is similar to Buck 1 and will not be discussed further.

2.2. Control Theory

The control system structure of the inverter is shown in Figure 2. For the renewable energy distributed generation application, two-stage system structure is often adopted. The gird-connected inverter as the post-stage is responsible for transferring the energy into power grid. The inverter can stabilize the DC bus voltage by balancing the input and output power. A voltage-current dual loop is employed to fulfill the function which is mentioned above.

A notch filter is used to filter out the ripple in the bus voltage V_bus. By comparing with the bus voltage reference V_{bus_ref}, the bus voltage error is acquired and compensated by a 2P2Z compensator. Then, the current reference amplitude i_ref is generated by the 2P2Z compensator. The grid voltage signal is injected into a second-order generalized integrator software phase lock loop (SOGI-SPLL) to generate the phase reference which is used to synchronize i_ref with the grid voltage. The instantaneous current reference i_{ref_inst} is compensated by a 3P3Z compensator. The result goes through a feedback linearization module and becomes the duty cycle which is used to generate PWM signal to control the inverter. The detail of the control method is described in another article and will not be discussed further.

3. Loss Analysis

The loss analysis is an essential way to improve the system efficiency. For low frequency inverter, the traditional calculation and approximation method are proven to be effective. However, when high speed switching is adopted, the losses, which are overlooked in low frequency condition, may become an indispensable part of the total losses and cause the inaccurate of loss analysis. In this section, the losses of inverter are systematically analyzed. The switching procedure, including the miller effect, is discussed in detail. The high frequency loss is thoroughly analyzed, some of which are not taken into consideration in low frequency applications. Moreover, the loss distribution based on the new method can offer a more accurate and detailed guide line for the improvement of high frequency application.

Before the analysis, several assumptions are made in order to simplify the procedure:

• The influence of some parasitic parameters such as leakage inductance is not considered.
• The temperature influence on device parameters is not discussed. If the parameter is temperature dependent, the calibration is only based on the datasheet. The analysis is conducted considering the inverter operating temperature is 60 °C.
• The parameters of the symmetry components are same and match the datasheet.
• The losses of the symmetry components are considered to be the same.

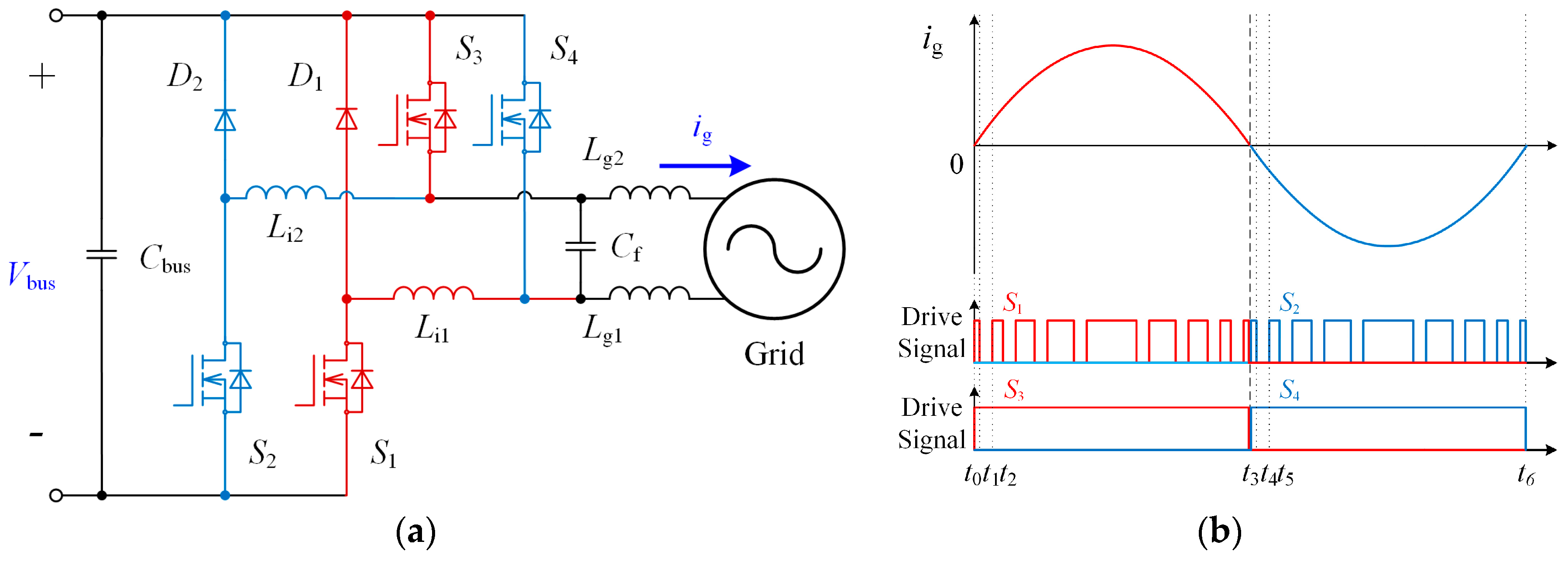
3.1. High Side MOSFET Loss

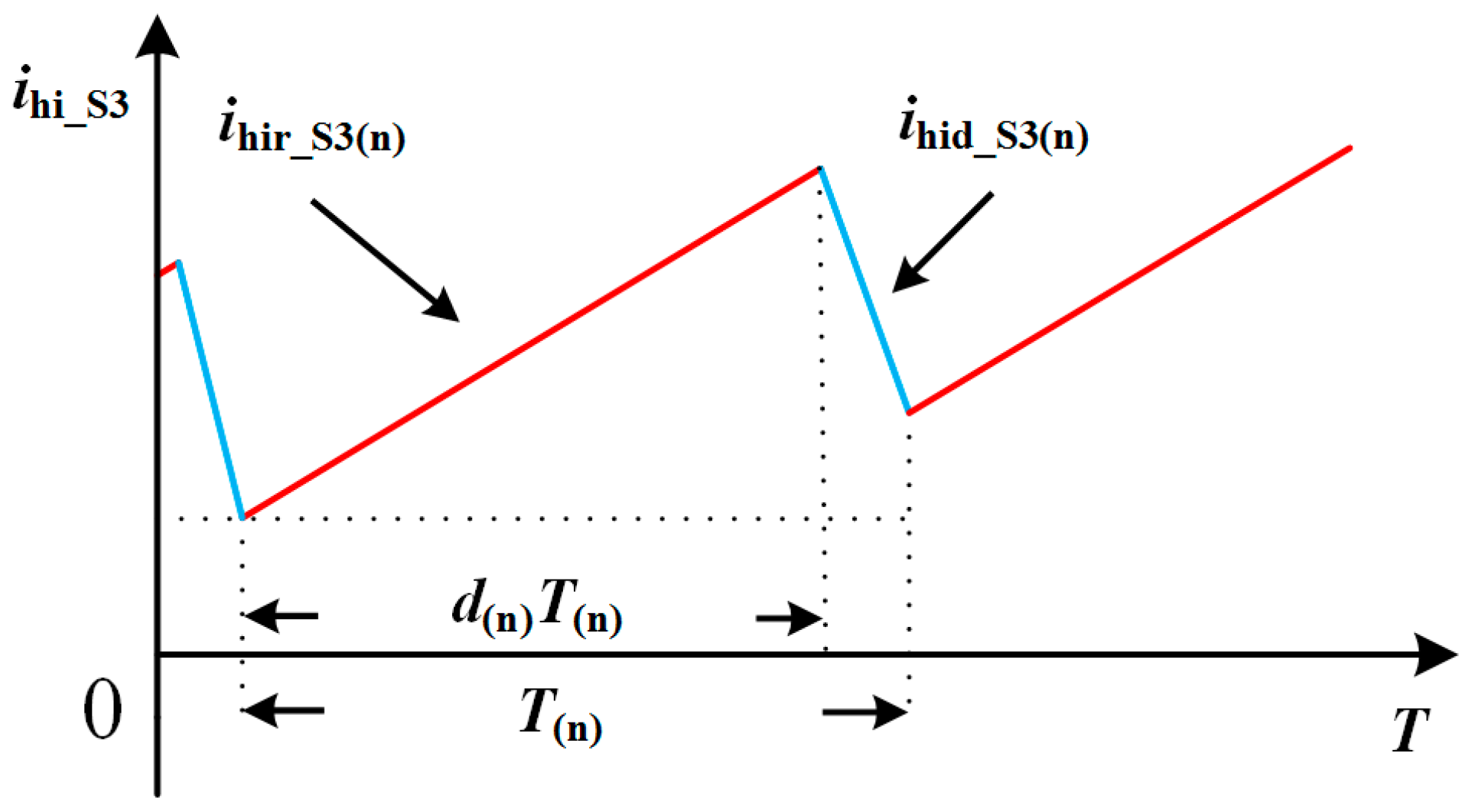
Basing on operation principles in Section 2, the high side MOSFETs S₃, S₄ are working at AC frequency. Comparing with the conduction loss, the switching loss can be ignored for their low switching frequency. The D-S current of the high side MOSFET S₃ i_{hi_S3} is shown in Figure 3.

When S₃ is turned on, the switching of the low side MOSFET S₁ divides i_{hi_S3} into two parts. When S₁ turns on, i_{hi_S3} rises, i_{hi_S3} flows through S₁, and the current is in rising period; when S₁ turns off, i_{hi_S3} falls, i_{hi_S3} flows through D₁, and the current is in falling period. The switching of S₁ causes the fluctuation of i_{hi_S3}. T_grid is the gird period. T(n) is the nth switching period of the low side switch S₁ and the duty cycle is d(n), the nth conducting time is d(n)T(n). i_{hir_S3(n)} is the nth rising period of i_{hi_S3} which is also the turn-on current of S₁. i_{hid_S3(n)} is the falling period which is also the free-wheeling current of D₁. N_s is the number of S₁ switching period which is contained in one AC period. The conduction loss of the high side MOSFET S₃ P_{hicon_S3} can be divided into two parts:

$$P_{\mathrm{h}\mathrm{i}\mathrm{r}\mathrm{c}\mathrm{o}\mathrm{n}\_\mathrm{S}3}=\frac{1}{T_{\mathrm{g}\mathrm{r}\mathrm{i}\mathrm{d}}}[{\displaystyle \sum _{\mathrm{n}=1}^{N_{\mathrm{s}}}({\displaystyle {\int }_0^{d(\mathrm{n})T(\mathrm{n})}{i}_{\mathrm{h}\mathrm{i}\mathrm{r}(\mathrm{n})}^2}}(t)R_{\mathrm{D}\mathrm{S}\_\mathrm{S}3}\mathrm{d}t)]$$

(1)

$$P_{\mathrm{hidcon}\_\mathrm{S}3}=\frac{1}{T_{\mathrm{grid}}}[{\displaystyle \sum _{\mathrm{n}=1}^{N_{\mathrm{s}}}(}{\displaystyle {\int }_0^{[1-d(\mathrm{n})]T(\mathrm{n})}{i}_{\mathrm{hid}(\mathrm{n})}^2(t)R_{\mathrm{DS}\_\mathrm{S}3}\mathrm{d}t})]$$

(2)

$$P_{\mathrm{hicon}\_\mathrm{S}3}=P_{\mathrm{hircon}\_\mathrm{S}3}+P_{\mathrm{hidcon}\_\mathrm{S}3}$$

(3)

where P_{hircon_S3} is the i_{hi_S3} rising period loss and P_{hidcon_S3} is the falling period loss, R_{DS_S3} is the D-S resistance of S₃ which can be obtained from datasheet.

3.2. Low Side MOSFET Loss

The conduction loss of the low side MOSFET S₁, P_{locon_S1} can be easily deduced from Equation (1). The conduction current is the same as P_{hircon_S3} and the only difference is the D-S resistance. R_{DS_S1} is the D-S resistance of S₁. P_{locon_S1} can be calculated as:

$$P_{\mathrm{locon}\_\mathrm{S}1}=\frac{1}{T_{\mathrm{grid}}}[{\displaystyle \sum _{\mathrm{n}=1}^{N_{\mathrm{s}}}({\displaystyle {\int }_0^{d(\mathrm{n})T(\mathrm{n})}{i}_{\mathrm{hir}\left(\mathrm{n}\right)}^2(t)R_{\mathrm{DS}\_\mathrm{S}1}\mathrm{d}t}})]$$

(4)

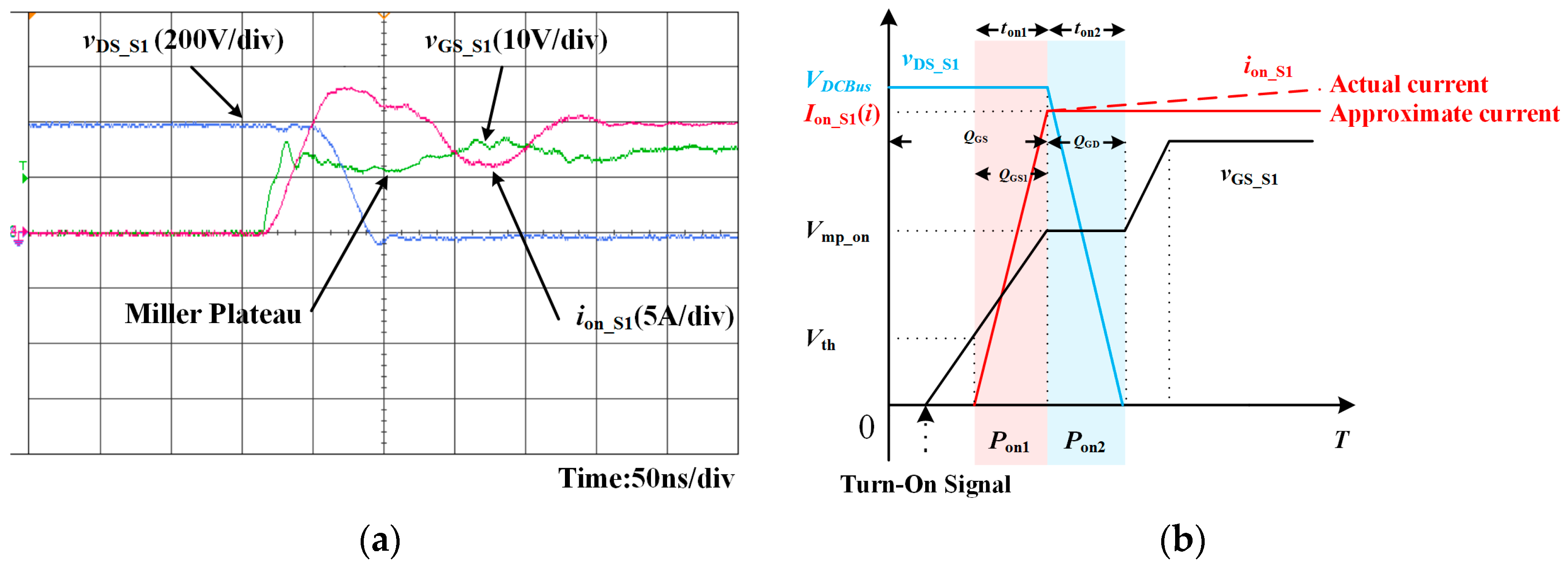
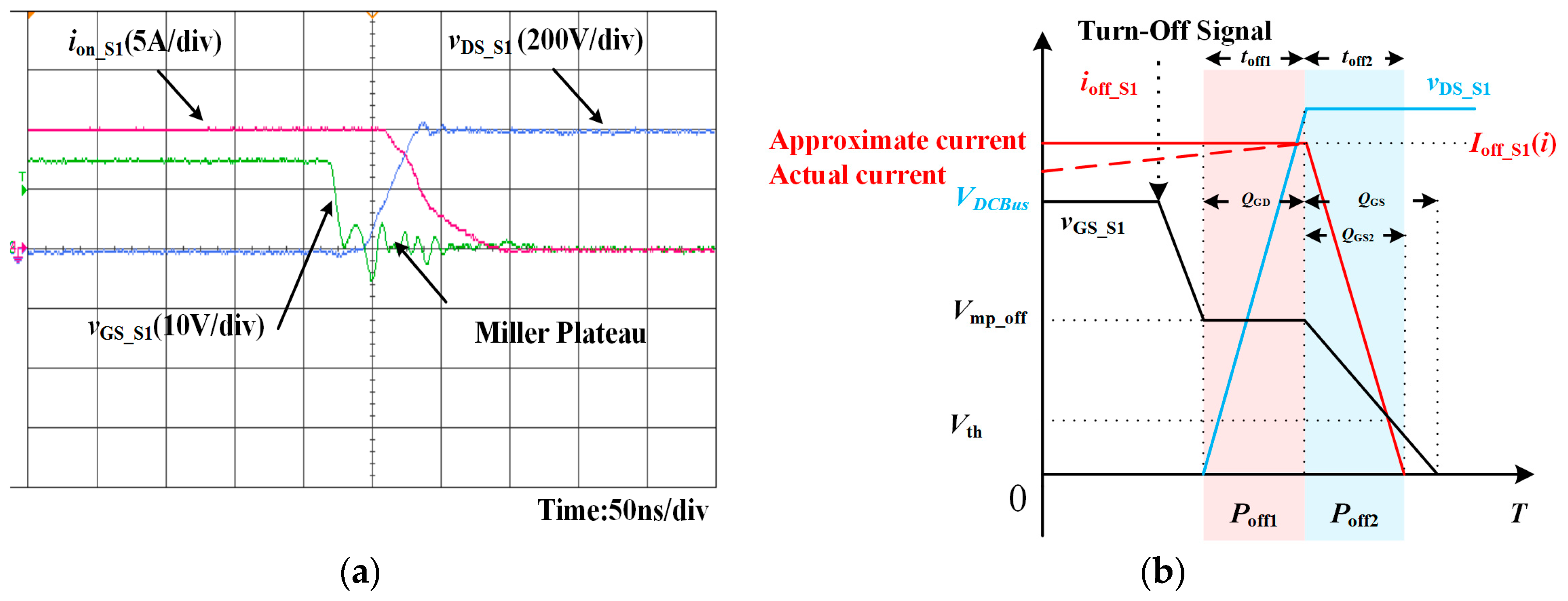
According to the operation principles, low side MOSFETs S₁, S₂ are working at 400 kHz. Figure 4a shows the voltage waveforms of S₁ during the turn-on transition and the Figure 4b is the simplified diagram of the transition.

As Figure 4b shows, an approximation is made in order to simplify the analysis. The D-S current of S₁ i_{on_S1} is considered to be a constant current after i_{on_S1} is fully turn-on. When a signal starts to turn on S₁, there is a time delay before G-S voltage of S₁ v_{GS_S1} increases to the gate threshold voltage V_th. Then, the output capacitance of S₁, C_{OSS_S1} begins to be charged. The output capacitance loss P_{OSS_S1} can be calculated as:

$$P_{\mathrm{OSS}\_\mathrm{S}1}=f_{\mathrm{SW}}\times {\displaystyle {\int }_0^{V_{\mathrm{DCBus}}}{v}_{\mathrm{DS}\_\mathrm{S}1}{C}_{\mathrm{OSS}\_\mathrm{S}1}}(v_{\mathrm{DS}\_\mathrm{S}1})\mathrm{d}{v}_{\mathrm{DS}\_\mathrm{S}1}$$

(5)

where f_SW is the switching frequency of S₁, V_DCBus is the input DC bus voltage and v_{DS_S1} is the D-S voltage of S₁. The output capacitance C_{OSS_S1} is a v_{DS_S1} related parameter which is provided by the datasheet.

When v_{GS_S1} reaches V_th, the i_{on_S1} starts to rise linearly. After the rising period, i_{on_S1} turns on completely, the v_{GS_S1} reaches the turn-on miller plateau voltage V_{mp_on} and the voltage v_{DS_S1} starts to decrease. The miller plateau is caused by the charging or discharging procedure of the capacitance between G-D, which is C_GD [20]. In actual waveform, as Figure 4a shows, miller plateau have a slope. The steepness of the slope is depending on the value of C_GD and C_GS, where C_GS is the capacitance between G-S. Typically, C_GD is larger than C_GS, the phenomenon appears as a plateau. The duration time can be considered as the charging time to charge Q_GD, which is the gate to drain charge.

At the end of the miller plateau, the v_{GS_S1} reduces to zero and the turn-on procedure is completed. During the turn-on transition, the turn-on loss P_on can be divided into two parts: P_on1 and P_on2. The v_{GS_S1} is constant and i_S1 is linearly changed during t_on1. Similarly, the i_S1 is constant and v_{GS_S1} is linearly changed within t_on2. The turn-on loss of S₁ P_{on_S1} can be deduced form Equation (6).

$$P_{\mathrm{on}\_\mathrm{S}1}=\frac{1}{T_{\mathrm{grid}}}{\displaystyle \sum _{\mathrm{n}=1}^{Ns}\frac{V_{\mathrm{DCBus}}{I}_{\mathrm{on}\_\mathrm{S}1(\mathrm{n})}}{2}(t_{\mathrm{on}1}+t_{\mathrm{on}2})}=\frac{1}{T_{\mathrm{grid}}}{\displaystyle \sum _{\mathrm{n}=1}^{Ns}\frac{V_{\mathrm{DCBus}}{I}_{\mathrm{on}\_\mathrm{S}1(n)}}{2}(\frac{Q_{\mathrm{GS}2}{R}_{\mathrm{Gon}}}{\frac{V_{\mathrm{mp}\_\mathrm{on}}+V_{\mathrm{th}}}{2}}+\frac{Q_{\mathrm{GD}}{R}_{\mathrm{Gon}}}{V_{\mathrm{mp}\_\mathrm{on}}})}$$

(6)

where I_{on_S1(n)} is the nth switching period turn-on current of S₁. Q_GS2 represents the corresponding charge during t_on1 which can be calculated according to the transfer characteristic figure of devices, R_Gon is the gate loop resistance during turn-on period.

Figure 5a shows the waveforms of S₁ during the turn-off transition and the Figure 5b is the simplified diagram of the transition. A similar approximation is made which considers the D-S turn-off current of S₁ i_{off_S1} to be constant before t_off2. When the signal starts to turn off S₁, v_{GS_S1} starts to decrease. The v_{GS_S1} begins to increases when v_{GS_S1} reaches the turn-off miller plateau voltage V_{mp_off}. At the end of the plateau, v_{GS_S1} stops increasing and i_{off_S1} starts to decrease. The turn-off transition is completed when v_{GS_S1} goes down to V_th and i_{off_S1} decreases to zero. The turn-off loss P_{off_S1} can be regarded as two parts: P_off1 during t_off1 and P_off2 during t_off2 which can be calculated by Equation (7).

$$P_{\mathrm{off}\_\mathrm{S}1}=\frac{1}{T_{\mathrm{grid}}}{\displaystyle \sum _{\mathrm{n}=1}^{Ns}\frac{V_{\mathrm{DCBus}}{I}_{\mathrm{off}\_\mathrm{S}1(\mathrm{n})}}{2}(t_{\mathrm{off}1}+t_{\mathrm{off}2})}=\frac{1}{T_{\mathrm{grid}}}{\displaystyle \sum _{\mathrm{n}=1}^{Ns}\frac{V_{\mathrm{DCBus}}{I}_{\mathrm{off}\_\mathrm{S}1(\mathrm{n})}}{2}(\frac{Q_{\mathrm{GD}}{R}_{\mathrm{Goff}}}{V_{\mathrm{mp}\_\mathrm{off}}}+\frac{Q_{\mathrm{GS}2}{R}_{\mathrm{Goff}}}{\frac{V_{\mathrm{mp}\_\mathrm{off}}+V_{\mathrm{th}}}{2}})}$$

(7)

where I_{off_S1(n)} is the nth switching period turn-off current of S₁. R_Goff is the gate loop resistance during turn-off period. The total loss of S₁ P_{loss_S1} is regarded as:

P_{loss_S1} = P_{locon_S1} + P_{OSS_S1} + P_{on_S1} + P_{off_S1}

(8)

3.3. Free-Wheeling Diode Loss

The conduction loss of the free-wheeling diode D₁, P_{dcon_D1} can be deduced from Equation (2), which is shown in Equation (9):

$$P_{\mathrm{dcon}\_\mathrm{D}1}=\frac{1}{T_{\mathrm{grid}}}[{\displaystyle \sum _{n=1}^{N_{\mathrm{s}}}(}{\displaystyle {\int }_0^{[1-d(\mathrm{n})]T(\mathrm{n})}{i}_{\mathrm{hid}(\mathrm{n})}{U}_{\mathrm{f}}\mathrm{d}t})]$$

(9)

U_f is the forward voltage of the diode. The turn-on loss of the diode P_{ond_D1} can be represented as (10):

$$P_{\mathrm{ond}\_\mathrm{D}1}=\frac{1}{T_{\mathrm{grid}}}{\displaystyle \sum _{\mathrm{n}=1}^{N_{\mathrm{s}}}\frac{1}{2}}{U}_{\mathrm{d}}{I}_{\mathrm{don}\left(\mathrm{n}\right)}{t}_{\mathrm{r}}\approx \frac{1}{T_{\mathrm{grid}}}{\displaystyle \sum _{\mathrm{n}=2}^{N_{\mathrm{s}}}\frac{1}{2}}{U}_{\mathrm{DCBus}}{I}_{\mathrm{off}\_\mathrm{S}1(\mathrm{n}-1)}{t}_{\mathrm{on}1}$$

(10)

where U_d is the voltage on the diode. I_don(n) is the nth diode turn-on current which can be approximated as the (n − 1)th turn-off current of S₁ I_{off_S1(n−1)}. t_r is the rising time of the S₁ which can be approximated as t_on1.The turn-on loss of the diode P_{offd_D1} can be represented as (11):

$$P_{\mathrm{offd}\_\mathrm{D}1}=\frac{1}{T_{\mathrm{grid}}}{\displaystyle \sum _{\mathrm{n}=1}^{N_{\mathrm{s}}}\frac{1}{2}}{U}_{\mathrm{d}}{i}_{\mathrm{RM}\left(\mathrm{n}\right)}{t}_{\mathrm{rr}}=\frac{1}{T_{\mathrm{grid}}}{\displaystyle \sum _{\mathrm{n}=1}^{N_{\mathrm{s}}}\frac{1}{2}}{U}_{\mathrm{DCBus}}{i}_{\mathrm{RM}\left(\mathrm{n}\right)}{t}_{\mathrm{rr}}$$

(11)

I_RM is the diode peak reverse current and t_rr is the reverse recovery time.

3.4. Inductor Loss

The copper loss P_LCu of filter inductor can be calculated as

$$P_{\mathrm{L}\mathrm{Cu}}=\frac{1}{T_{\mathrm{grid}}}{\displaystyle {\int }_0^{T_{\mathrm{grid}}}{i}_{\mathrm{L}}^2(t)R_{\mathrm{L}}\mathrm{d}t}$$

(12)

where i_L is the inductor current and the R_L is the resistance of the inductor winding.

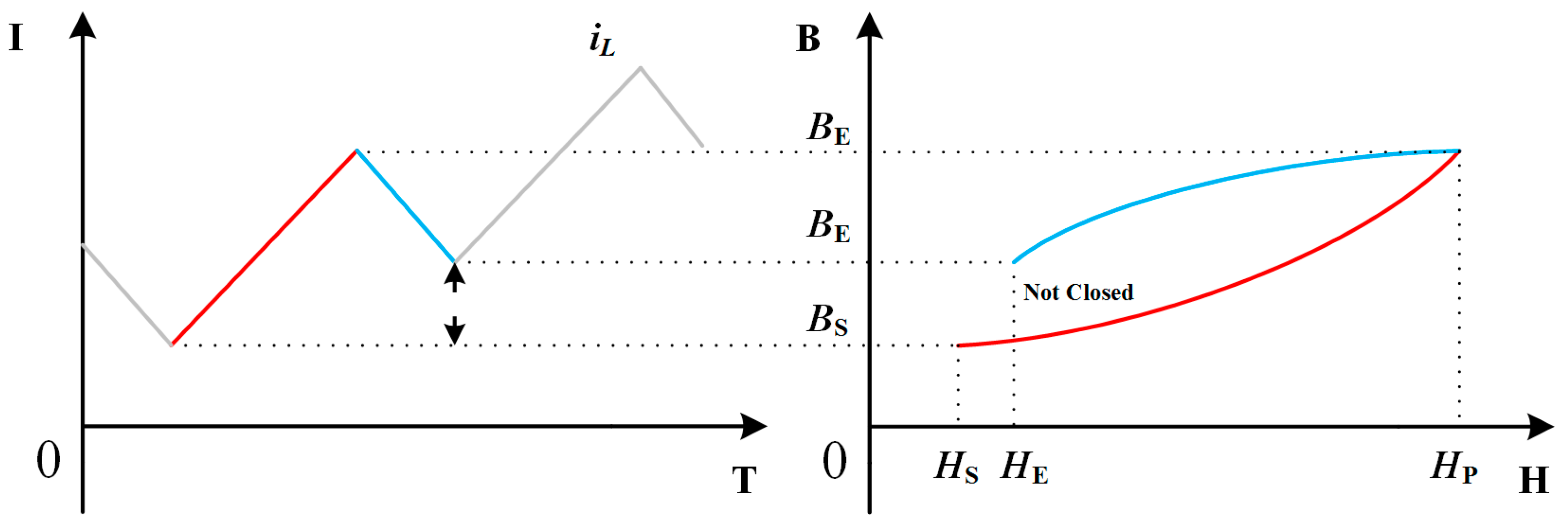
Figure 6 shows the trajectory of inductor current i_L on the B-H plane during one switching cycle. At the end of the switching cycle, the i_L is not the same as the initial value because the inverter is working in continuous current mode in order to follow the sinusoidal reference. The work mode leads to the unclosed B-H curve as Figure 6 shows. Accordingly, the traditional hysteresis loss calculation based on closed B-H curve is not suitable for inverter hysteresis loss calculation. The unclosed B-H curve should be adopted [21,22,23].

Magnetic flux density B can be obtained by integral of the inductor voltage u_L. The magnetic flux density at t_n can be calculated as:

$$B(t_{\mathrm{n}})=\frac{1}{N\cdot A}{\displaystyle {\int }_0^{t_{\mathrm{n}}}{u}_{\mathrm{L}}\mathrm{d}t}$$

(13)

where N is the number of winding turns and A is the cross-section area of the inductor core. i_L(t_n) is the inductor current at t_n, the magnetic field intensity H(t₁) can be obtained by:

$$H(t_{\mathrm{n}})=\frac{N{i}_{\mathrm{L}}(t_1)}{l}$$

(14)

where l is the length of the equivalent magnetic circuit. The hysteresis loss P_hysis can be calculated as:

$$P_{\mathrm{hysis}}=\frac{1}{T_{\mathrm{gird}}}{\displaystyle \sum _{n=1}^{N_{\mathrm{s}}}{\displaystyle {\int }_{B_{\mathrm{S}}}^{B_{\mathrm{P}}}HdB}-}{\displaystyle {\int }_{B_{\mathrm{P}}}^{B_{\mathrm{E}}}HdB}$$

(15)

3.5. Capacitor Loss

The loss which is caused by the leakage current of the capacitor P_cleak can be calculated as:

$$P_{\mathrm{cleak}}=U_{\mathrm{c}}\cdot I_{\mathrm{cleak}}$$

(16)

U_c is the voltage on the capacitor, and I_cleak is the leakage current of the capacitor, which is a U_c related parameter and can be found in the datasheet.

R_cs is the resistance of the capacitor lead and electrode, I_rip is the ripple current of the capacitor, and the loss on these conductors can be represented as:

$$P_{\mathrm{cs}}=I_{\mathrm{rip}}^2{R}_{\mathrm{cs}}$$

(17)

R_ESR is the equivalent series resistance of the capacitor, which can be deduced form dissipation factor tanδ:

$$R_{\mathrm{ESR}}=\frac{\tan \delta }{2\pi fC}$$

(18)

where f is the frequency which the ESR is calculated at. C is the capacitance of the capacitor. The ESR loss of the capacitor can be calculated as:

$$P_{\mathrm{ESR}}=I_{\mathrm{rip}}^2{R}_{\mathrm{ESR}}$$

(19)

The total losses on the capacitor is

$$P_{\mathrm{closs}}=P_{\mathrm{cleak}}+P_{cs}+P_{\mathrm{ESR}}$$

(20)

3.6. Loss Calculation Results

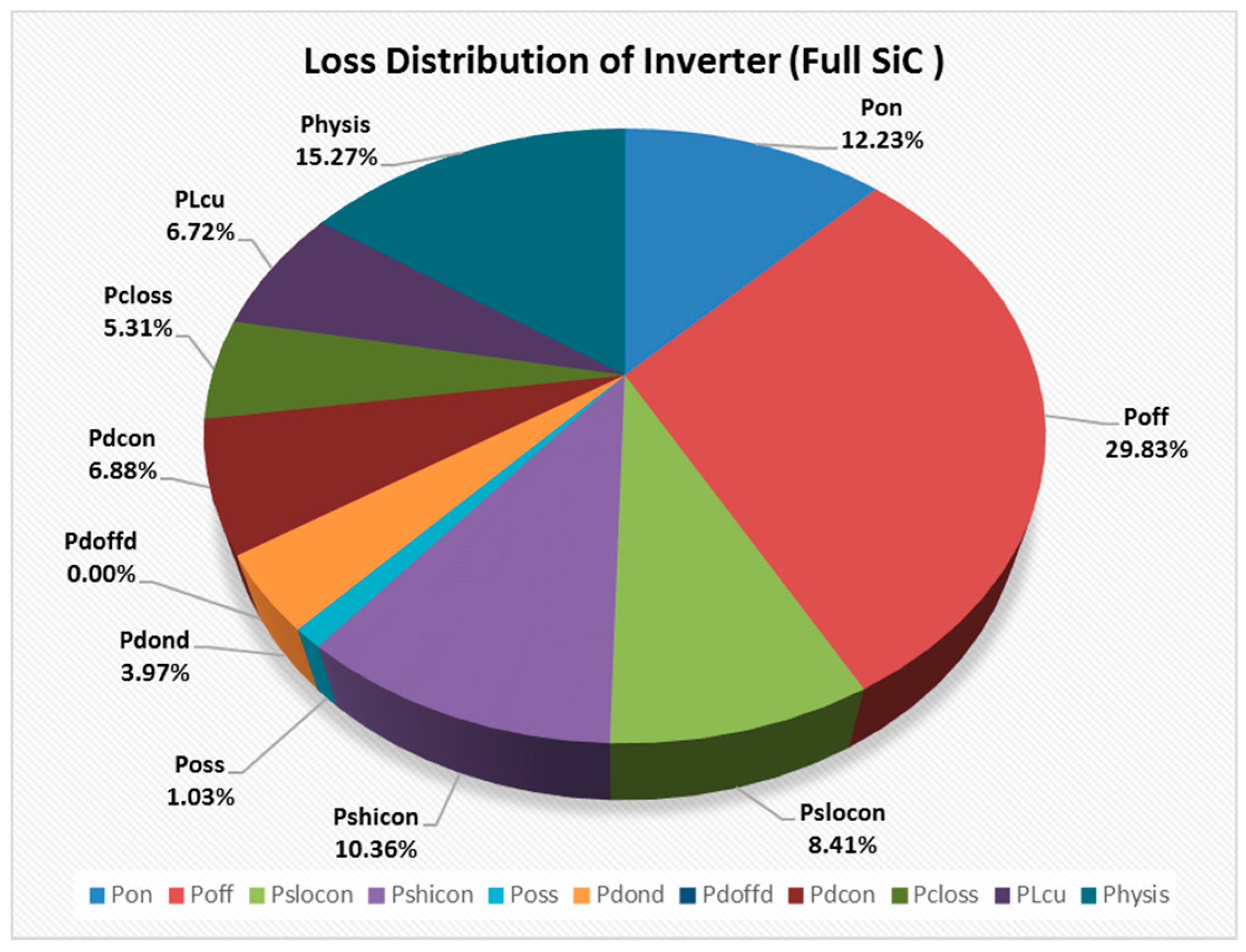
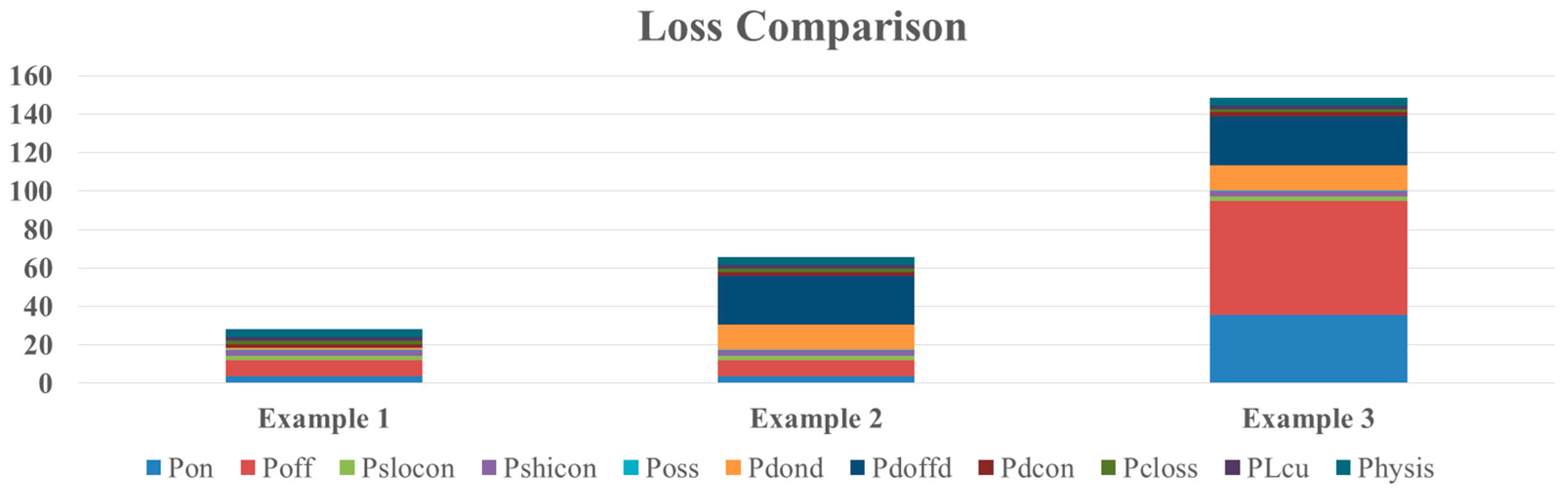
Based on the previous methods, the calculation results of the Full SiC power devices inverter losses are shown in Figure 7 as calculation Example 1.

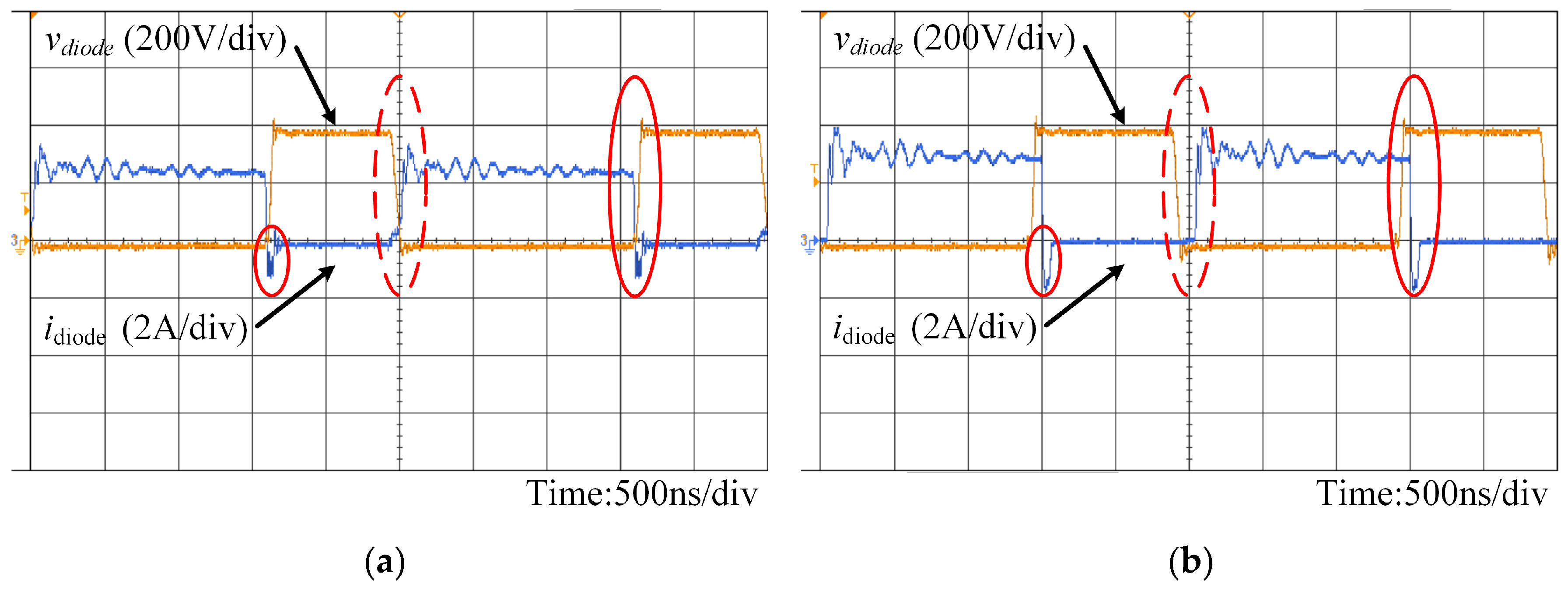
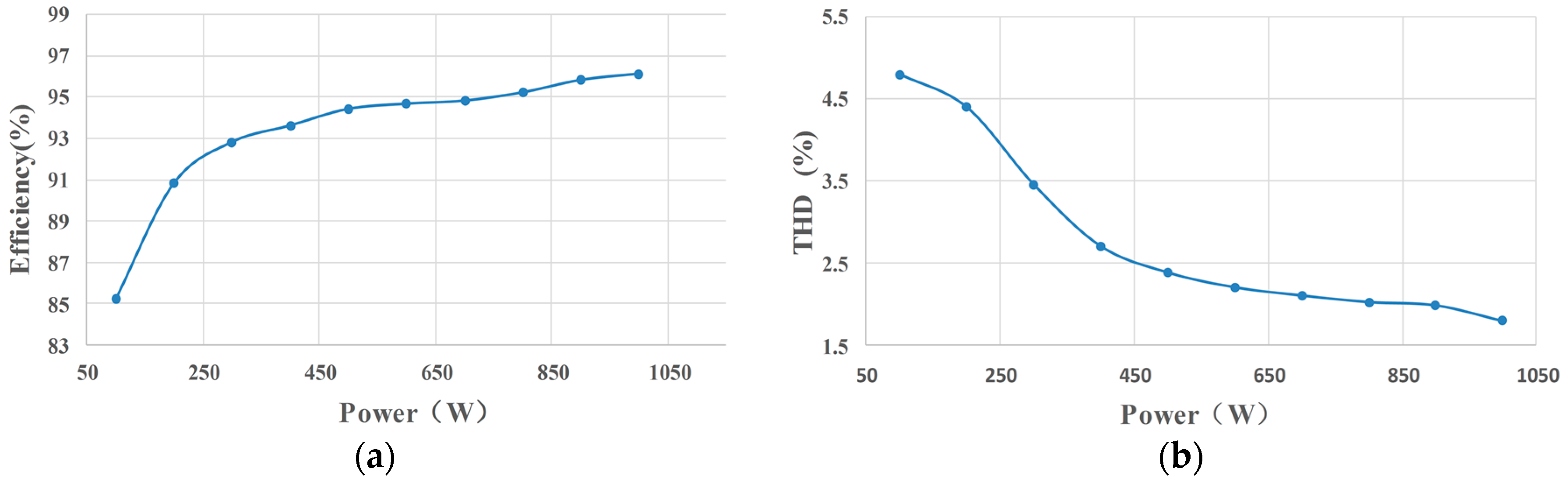
As we can see from Figure 7, the switching loss takes the major part of the total loss. The output capacitance loss P_OSS, which is often overlooked in low frequency loss analysis, is over 1% and should be taken account in high frequency application. For the special characteristic of the SiC diode, the reverse recovery time t_rr is consider to be 0. Hence, the free-wheeling diode turn-off loss P_doff is 0. This superiority, which is proven in later experiment, is vital for the total loss of the inverter. Finally, the calculation efficiency is 97.32% at rated power of 1 kW.

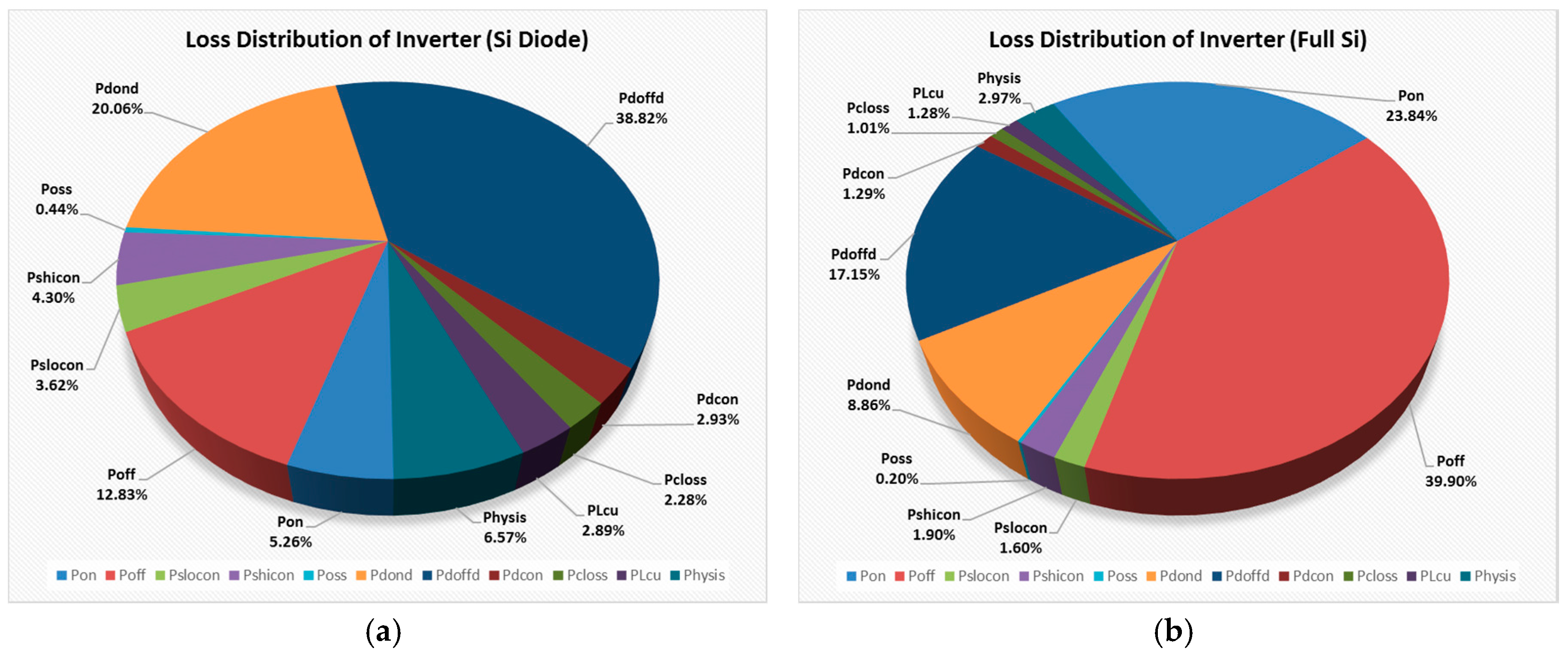
Two comparative calculation examples are set up. In Example 2, the free-wheeling diodes D₁, D₂ are replaced by two normal Si diodes. In Example 3, all the power devices are replaced by the normal Si devices. The loss distribution of the comparative calculation examples are shown in Figure 8.

As Figure 8a shows, when the SiC diodes are replace by the normal Si diodes, the total loss on the diodes is over 50%. The turn-on loss and the turn-off loss of the diodes contribute the most part of the losses increase. As a result, the calculation efficiency of Example 2 is down to 93.57% at 1 kW.

After all the power devices are replaced by the Si devices. The losses of the switches become the major part of the total losses. Consequently, as Figure 8 shows, the total loss of Example 3 is almost three times larger than Example 2. The calculation efficiency of Example 3 is 85.27% at 1 kW.

The total loss comparison is shown in Figure 9. For Example 2, the diode losses contribute the most. For Example 3, the losses on the switches are numerous. The total losses difference between the Full SiC and Full Si power device is over five times. These results are confirmed in later comparative experiments, which indicate that the Si power devices are not suitable for high frequency application.

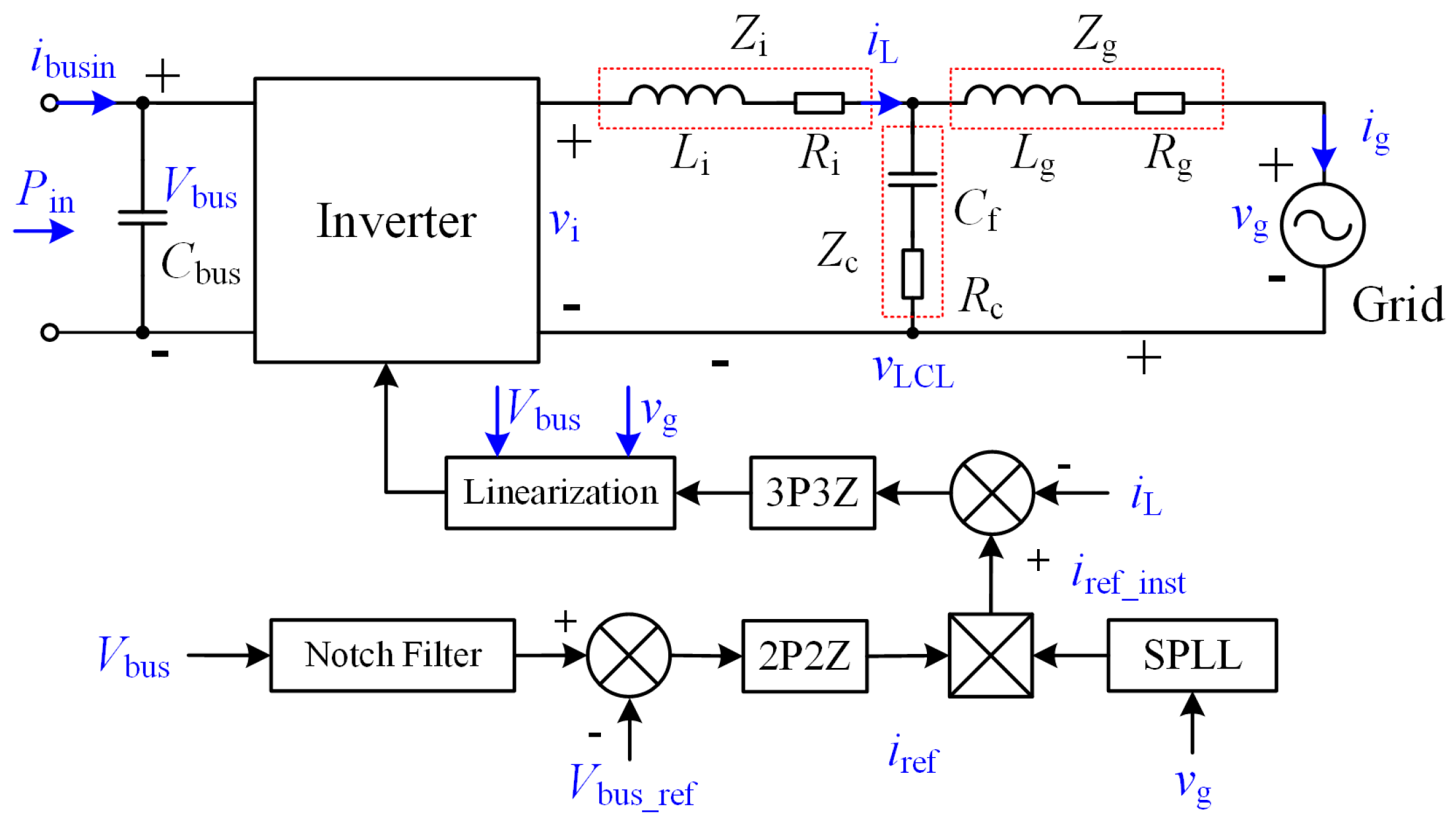
4. Improved Simulation Method

A simulation model is often built in software environment in order to verify the validity of theoretical analyses and accelerate the compensator tuning. In low frequency converting, the simplified component models are considered to be effective and timesaving. However, as the switching frequency increases, some details of the switching procedure may have a serious influence on the simulation, which could make the results become inaccurate, even unreliable. The inconsistency between the simulation results and experiment results emerges during the design process. The deviation between PWM control signal and switching response in high frequency switching is consider to be the reason which cause the inconsistency. The influence of the deviation on the simulation is verified by experiment. Moreover, based on the theoretical analysis and test results, a compensator method is proposed in order to minimize the deviation which is caused by the influence. Consequently, the simulation results are significantly improved. The improved simulation model is used in prototype design to verify the compensators. The method is proven to be effective by the experiments in later section.

4.1. Influence of High Frequency Switching

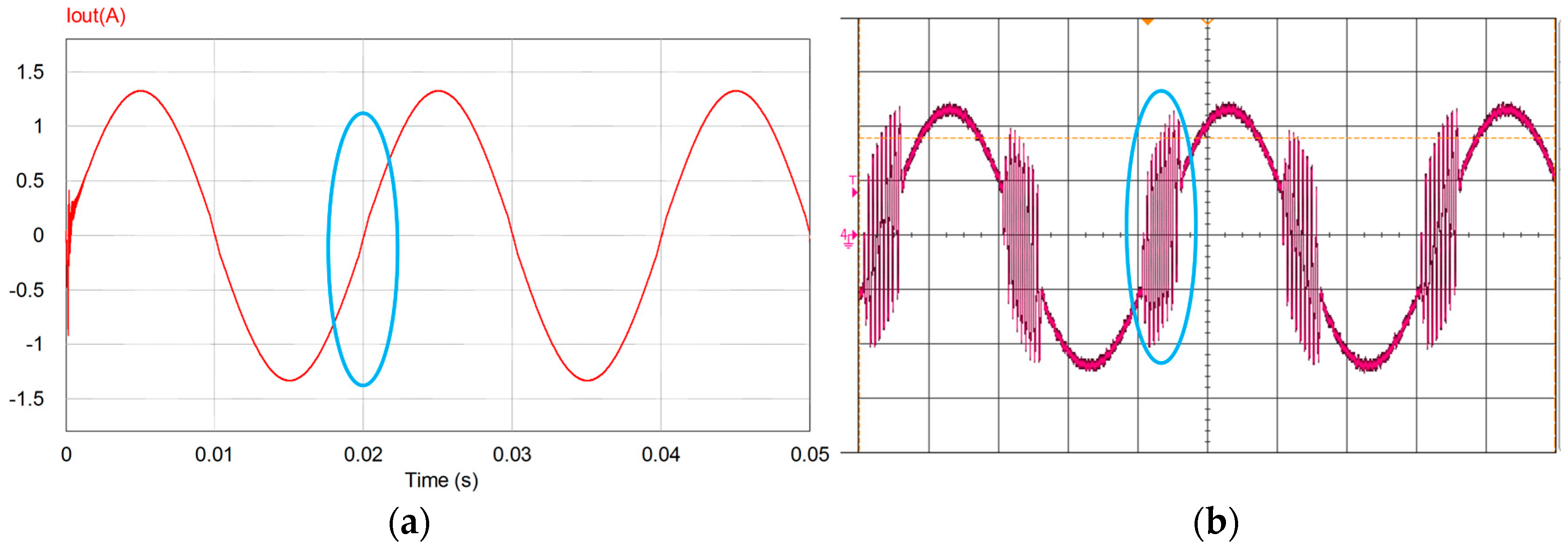
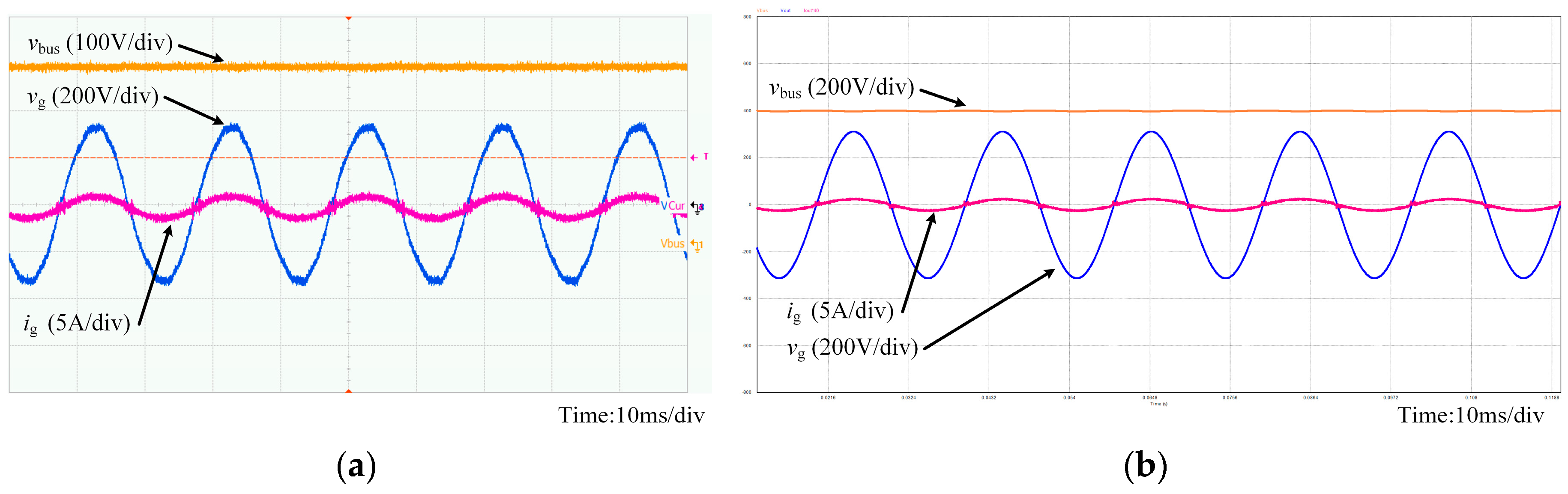
A simulation model is built in software environment of PSIM. The parameters of the components and control compensator are the same as the experimental prototype. The grid-connecting power experiments are carried out. The 3P3Z compensator in the current loop, which is designed to follow the current reference, are tuned and tested on the simulation model. As Figure 10a shows, the compensation effect is desirable. However, during the experiment, the same compensator, which has the same parameters, causes the current oscillation during zero-crossing procedure.

The same simulation method is used in the previous 50 kHz inverter design and no similar issue arises. Through analysis, the deviation between PWM control signal and switching response in high frequency switching, is the main reason which causes the simulation to be inaccurate.

4.2. Equivalent Opening Time

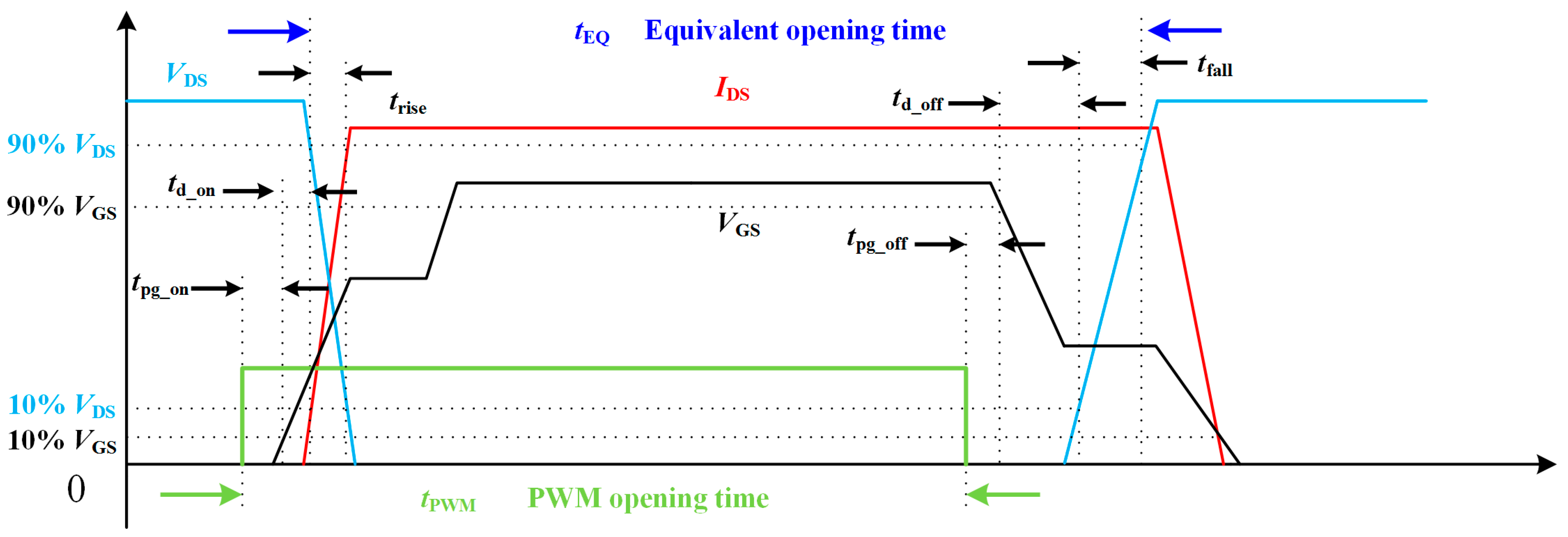
Figure 11 shows the waveforms of a complete switching cycle. The PWM signal is considered to be an ideal square wave. When the rising edge of the PWM signal begins to turn on the switch, there is a turn-on propagation delay t_{pg_on} before the G-S voltage starts to rise. The delay is caused by the drive circuits when converting the PWM signal into drive signal. When V_GS rises, the D-S voltage V_DS starts to descend. The time, which is from 10% V_GS to 90% V_DS, is defined as the turn-on delay t_{d_on}. The time, which is form 90% V_DS to 10% V_DS, is the rise time t_rise. The turn-off propagation delay t_{pg_off}, turn-off delay t_doff and fall time t_fall can be obtained by similar definitions. The equivalent opening time is define as the period which the V_DS fall below 90% then rise over 90%. As Figure 11 shows, the relationship between PWM opening time t_PMW and the equivalent opening time t_EQ can be represented as Eqaution (21)

$$t_{\mathrm{EQ}}=t_{\mathrm{PWM}}+[t_{\mathrm{pg}\_\mathrm{off}}-t_{\mathrm{pg}\_\mathrm{on}}]+[t_{\mathrm{d}\_\mathrm{off}}(V_{\mathrm{DS}})-t_{\mathrm{d}\_\mathrm{on}}(V_{\mathrm{DS}})]+t_{\mathrm{rise}}(V_{\mathrm{DS}})+t_{\mathrm{fall}}(V_{\mathrm{DS}})$$

(21)

The equivalent opening time t_EQ can be regarded as the actual respond of the switch under the control of PWM signal. In practical circuits, t_{pg_on} and t_{pg_off} are small and assumed to be equal. Hence, Equation (21) can be simplified as:

$$t_{\mathrm{EQ}}=t_{\mathrm{PWM}}+t_{\mathrm{d}\_\mathrm{off}}(V_{\mathrm{DS}})-t_{\mathrm{d}\_\mathrm{on}}(V_{\mathrm{DS}})+t_{\mathrm{rise}}(V_{\mathrm{DS}})+t_{\mathrm{fall}}(V_{\mathrm{DS}})=t_{\mathrm{PWM}}+t_{\mathrm{e}}(V_{\mathrm{DS}})$$

(22)

where t_e is the total extend time which is caused by the delay in the switching procedure. t_{d_on}, t_{d_off}, t_fall and t_rise are all V_DS related parameters provided by the datasheet. It is obvious that the PWM opening time is extended during the switching procedure. The proportions of the deviation in the equivalent opening time t_EQ under different switching frequencies and duty cycles are shown in

Table 1. The proportion of the deviation.

te	fsw	Duty Cycle	tPWM(ns)	tEQ(ns)	te/tEQ
92 ns	50 kHz	2%	400	492	18.70%
		50%	10,000	10,092	0.91%
		80%	16,000	16,092	0.57%
	400 kHz	2%	50	142	64.79%
		50%	1250	1342	6.86%
		80%	2000	2092	4.40%

.

As Table 1 shows, when the switching frequency is low, the proportion of t_e in t_EQ is very small. During the practical circuit design, this deviation is often ignored. However, in high frequency implementation, this time deviation may even larger than t_PWM. When the f_sw is at 400 kHz, at 2% duty cycle, the proportion of t_e is over 50%. t_PWM is extended about two times. This deviation may lead to the inconsistency between the output and control signal. This difference has an error accumulation effect, which can cause the error response of the controller. As a result, the compensator, which is tested in the simulation and consider to be valid, will fail on the prototype.

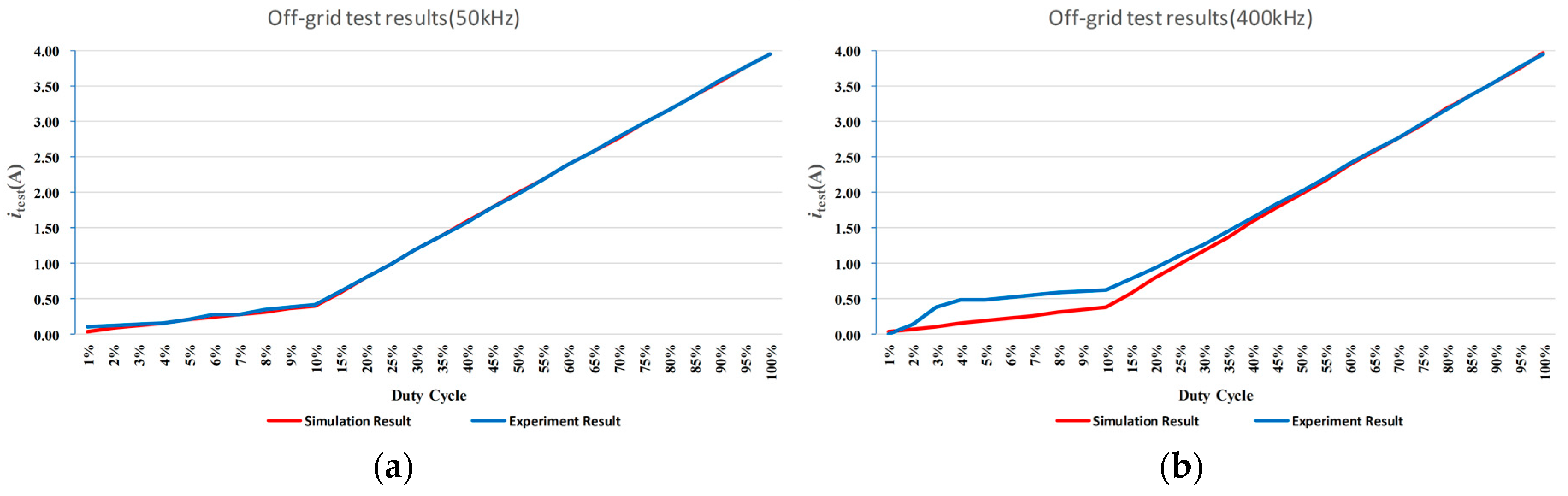
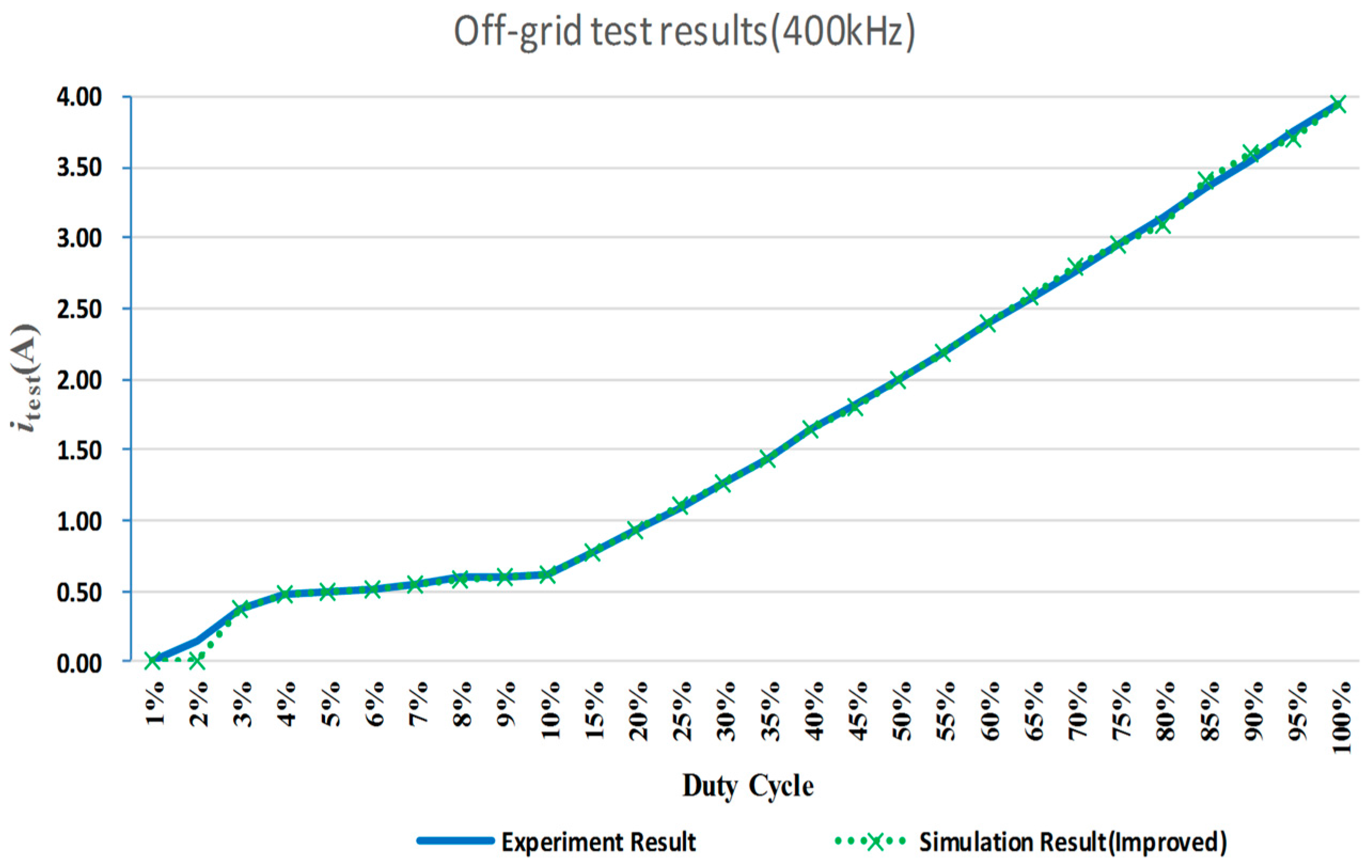
In order to verify the analysis, an off-grid DC experiment is set up, for the deviation is more obvious when the duty cycle is constant. The difference between the output currents can prove the pervious analysis. The prototype connects to a 100 Ω resistor instead of the gird, then runs at 50 kHz and 400 kHz respectively. A constant duty cycle is given to the inverter in order to run the inverter in DC output mode. The output current i_test is tested at each duty cycle at different switching frequency. Meanwhile, the same test is carried out on the simulation model. As Figure 12 shows, the output current at the same duty cycle of simulation and experiment are represented by two respective curves. There is almost no difference between the experiment results and simulation results when the switching frequency is at 50 kHz as Figure 12a shows. Because the proportion of the deviation in low frequency is very small, which can be ignored in traditional analysis. However, when the switching frequency is at 400 kHz as Figure 12b shows, there are significant differences between the simulation results and the experiment results. When the test duty cycle is under 45%, the experiment output current is apparently larger than the simulation results at the same duty cycle. This phenomenon can be explained as the control PWM signal in the prototype is extended by the delays which we talked above. The phenomenon is more obvious at low duty cycle which is consistent with previous analysis.

4.3. Compensating Method

Different from other researches, the proposed method focuses on the impact of the switching procedure on the output power. Instead of simulating the complex switching procedure in detail, a compensating module is used to improve the simulation results. The proposed method is simple and effective. Based on Equation (22), d_EQ is the duty cycle based on t_EQ and can be calculated as:

$$d_{\mathrm{EQ}}=\frac{d\cdot t_{\mathrm{sw}}+t_{\mathrm{d}\_\mathrm{off}}(V_{\mathrm{DS}})-t_{\mathrm{d}\_\mathrm{on}}(V_{\mathrm{DS}})+t_{\mathrm{rise}}(V_{\mathrm{DS}})+t_{\mathrm{fall}}(V_{\mathrm{DS}})}{t_{\mathrm{sw}}}$$

(23)

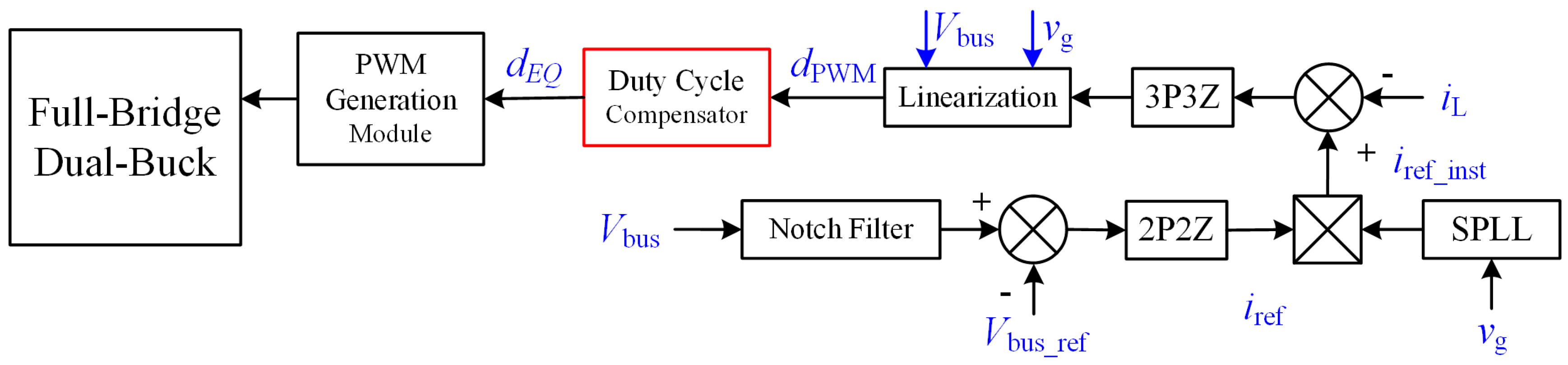
where t_sw is the switching period, and d_PWM is the duty cycle of the input PWM. The compensator is added between the Linearization module and PWM generating module (Figure 13).

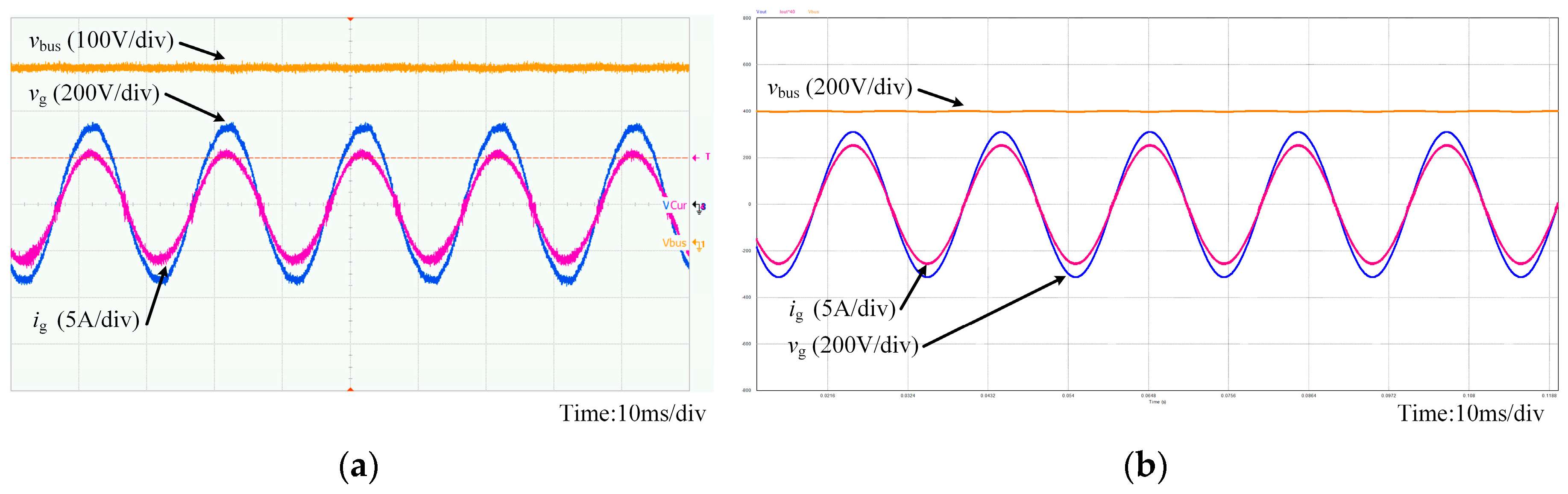
The linearization module [24,25,26] is used to generate the duty cycle d_PWM for controlling the switches. The duty cycle d_PWM is compensated by the duty cycle compensator. In order to test the compensation effect, the 400 kHz off-grid DC experiment is carried out on the improved simulation model. The simulation results are shown in Figure 14. Apparently, the compensator module is able to simulate the prototype output current correctly. The deviation of the output current between the simulation and experiment is minimized successfully.

Because of the deviation, the characteristic of compensator at low duty cycle have to be adjusted. Based on the improved simulation model, the characteristic of the inverter is re-analyzed. The compensator is redesign accordingly. The oscillation during zero-crossing is restrained by the new compensator in the simulation. The compensation effect is proven by the further experiment. The output waveforms of the experiments are shown in the later section.

5. Experiment Results

A 1-kW prototype is built in the laboratory (Figure 15). The parameters of the components are shown in

Table 2. Parameters of the proposed system.

Component	Manufacture	Model	Value
S1, S2, S3, S4	Wolfspeed	C2M0280120D
D1, D2	Wolfspeed	CVFD20065A
Li1, Li2	Magnetics	77439A7	800 μH
Lg1, Lg2	Magnetics	77548A7	215 μH
Cf	WIMA	MKP10	0.15 μF

. The control platform is TMS320F28377D from Texas Instruments. It is a high performance dual-core MCU running at 200 MHz.

5.1. Grid-Connected Experiment

Figure 16a shows the measured waveforms at 100 W and Figure 16b is the corresponding simulation waveforms. The output current i_g can track the grid voltage very well when the power output is low. The power factor is 0.99 and THD is 4.8%. The bus voltage is stabilized at 400 V and the ripple is within ±4 V. The zero-crossing oscillation which happens in pervious compensator design is efficiently restrained. The simulation waveforms in Figure 16b match the experiment results well.

Figure 17a shows the waveform at 1 kW and Figure 17b is the corresponding simulation waveforms. The RMS value of i_g is 4.5 A. Along with the increase of the output power, the waveform of the i_g rises significantly. The power factor is 0.99 and THD is down to 1.8%. The efficiency of the inverter is 96.1% at this moment.

Figure 18a shows the waveforms of the switch voltage and grid current at rated power of 1 kW. Figure 18b is the partial enlarged waveform of Figure 18a. i_g is the grid current. v_DS is the drain-to-source voltage of the switch S₁. v_GS is the drive signal of S₁. As the waveform shows, when i_g is above zero, S₁ is switched at high frequency of 400 kHz. The voltage stress of S₁ is 400 V; when i_g is below zero, S₁ is closed.

The relationships between efficiency, THD versus the output power are shown in Figure 19a,b, respectively. The THD decreases from 4.8% to 1.8% when the output power grows from 100 W to 1000 W, while the efficiency increases from 85.2% to 96.1%. Finally, the efficiency reaches the maximum efficiency of 96.1% at rated power. Thus, in small renewable energy application, the proposed inverter achieves an excellent performance, including relatively high conversion efficiency, high power factor and low THD.

5.2. Comparison Experiments of Power Loss

The comparative experiments are set up in order to verify the loss analyses in Section 3. The power devices of Prototype 1 are all SiC power devices. The free-wheeling diodes D₁ and D₂ are replaced by normal Si diodes on Prototype 2. All the power devices are replaced by normal Si devices on Prototype 3. The power devices used in each Prototype are shown in

Table 3. Power Devices of the Prototype.

Prototype	D1, D2	S1–S4
1	CVFD20065A	C2M0280120D
2	BYV29-600	C2M0280120D
3	BYV29-600	IPW60R040C7

.

The efficiency curves of the comparison experiments are shown in Figure 20. Prototype 1, which uses power devices that are full SiC components, reaches the rated power at 1 kW. When the temperature of the components is stable, the efficiency of Prototype 1 is 96.1%. Prototype 2, in which the diodes are replaced with Si diodes, reaches the rated power of 1 kW. However, the Si diodes break down within one minute. The efficiency of Prototype 2 at 1 kW is 91.83%. The voltage v_diode and current i_diode waveforms of the free-wheeling diode D₁ at 150 W in Prototype 1 and 2 are compared in Figure 21. Prototype 3 has the highest efficiency when the output power is low because the Si power devices used in the experiment have a lower conduction loss than the SiC. When the output power rises, Prototype 3 reaches the highest efficiency of 88.9% at 500 W. Then, the efficiency of Prototype 3 starts to decrease and the Si switches break down at 600 W. The efficiency of Prototype 3 at 1 kW cannot be measured. The experiment proves that the Si power devices are not suitable for high switching frequency application.

As Figure 21b shows, during the turn-on and turn-off procedure, the voltage and current of the Si diode in Prototype 2 have a large overlap area and big reverse recovery current, which means the switching losses of the diodes are very large. Comparing with the Si diode (Figure 21a), the SiC diode has a faster switching speed, which contributes to a low switching loss. Remarkably, the reverse recovery current of the SiC diode is not zero in the measured high frequency waveforms, but the reverse recovery loss is significantly smaller than Si diode due to the extremely short reverse recovery time.

The comparisons of experiment and calculation efficiencies are shown in

Table 4. Experiment and calculation efficiency.

Prototype	Calculation Efficiency (1 kW)	Experiment Efficiency (1 kW)	Deviation
1	97.32%	96.1%	1.22%
2	93.57%	91.83%	1.74%
3	85.27%	88.9% (at 500 W)	Unknown

. For prototype 1, the calculation efficiency at 1 kW is 97.32% and the corresponding experiment efficiency is 96.1%. The deviation between experiment and calculation is 1.02% which may be caused by the unmeasured losses such as the losses on the relay, fuse and so on. The calculation efficiency of Prototype 2 is 93.57% and the experiment efficiency at 1 kW is 91.83%. The deviation of Prototype 2 is 1.74%. Because the efficiency experiment of Prototype 2 does not reach a temperature stable state before the Si diodes breaks down, the unstable state of the main circuit may cause extra loss in Prototype 2. Prototype 3 cannot reach the rated power and breaks down at 600 W during the experiment; its efficiency is 88.9% at 500 W. Finally, the deviation between experiment and calculation efficiency is within acceptable range, which proves that the proposed loss calculation methodology is valid.

6. Conclusions

A 400 kHz dual-buck full-bridge inverter is proposed for small power renewable energy gird-connected generation. A current voltage dual-loop control strategy is employed, including a 3P3Z compensator in the inner current loop and a 2P2Z compensator in the outer voltage loop. Consequently, the inverter can deliver grid-tie power and regulate the DC bus voltage simultaneously. A systematic method for calculating the losses of high frequency inverter is presented. The influences of high frequency switching on loss analysis are discussed in detail. The loss distribution of the proposed inverter is obtained through the presented method. The simulation error, which is cause by the deviation between PWM control signal and switching response, is thoroughly analyzed. An improved simulation method is proposed in order to minimize the deviation which is caused by the delays of the switch in high frequency switching procedure. The loss analysis and simulation method are both validated by corresponding experiments. Finally, the power experiment of the inverter is finished at rated power of 1 kW, with the power factor above 0.99 and THD of 1.8%. The adoption of SiC power devices contributes to the highest efficiency of 96.1% at rated power. The experiment results prove that the proposed loss calculation method and improved simulation method is effective and suitable for high frequency inverter.