Neuro-Fuzzy Wavelet Based Adaptive MPPT Algorithm for Photovoltaic Systems

Abstract

An intelligent control of photovoltaics is necessary to ensure fast response and high efficiency under different weather conditions. This is often arduous to accomplish using traditional linear controllers, as photovoltaic systems are nonlinear and contain several uncertainties. Based on the analysis of the existing literature of Maximum Power Point Tracking (MPPT) techniques, a high performance neuro-fuzzy indirect wavelet-based adaptive MPPT control is developed in this work. The proposed controller combines the reasoning capability of fuzzy logic, the learning capability of neural networks and the localization properties of wavelets. In the proposed system, the Hermite Wavelet-embedded Neural Fuzzy (HWNF)-based gradient estimator is adopted to estimate the gradient term and makes the controller indirect. The performance of the proposed controller is compared with different conventional and intelligent MPPT control techniques. MATLAB results show the superiority over other existing techniques in terms of fast response, power quality and efficiency.

1. Introduction

As a kind of clean energy source, Photovoltaic (PV) systems have gained a prodigious popularity in the last few years, due to their high efficiency and low costs. As the output of the PV system depends on weather conditions, therefore, the voltage and current of the PV system need to be controlled for maximum power extraction [1]. In order to acquire the maximum advantage from the PV system, it is imperative to operate PV near the Maximum Power Point (MPP). Usually, an embedded DC-DC converter controlled with different control techniques with the PV array and the load is used to track the MPP [2,3]. The boost converter is highly recommended due to its advantages over the buck converter [4]. Due to nonlinear I-V and P-V characteristics of the PV array, the MPPT becomes more challenging. Such non-linear and non-minimum phase characteristics further confuse the MPPT of the boost converter [5]. To overcome these problems, different conventional and intelligent MPPT algorithms have been proposed such as Incremental Conductance (IC) [6,7,8], Open Circuit Voltage (OCV) [9], Short Circuit Current (SCC) [10], Perturb and Observe (P&O) [11], fuzzy logic [12,13,14,15], feedback linearization [16], neural network [17,18,19,20,21,22], neuro-fuzzy [23,24,25] and sliding mode [26,27]. Nevertheless, there still remains the concern of fast and accurately determining the locus of the MPP during high weather variations and external load changes occurring.

Moreover, both Fuzzy Logic (FL) and Neural Network (NN) controls have been preferred for the MPPT of the PV system over the last several years. The FL MPPT controller is one of the most promising control schemes for the unpredictable PV system, but it requires a priori knowledge of the system input/output relationship [28]. Similarly, the NN enhances the efficiency of the system by adopting a multilayer structure; though, each kind of PV array has to be periodically trained to formulate the control rules; therefore, its limitation is versatility [29]. The shortcomings of NN and FL are overwhelmed by hybridizing NN and FL in the Neuro-Fuzzy Controller (NFC) [24,30,31,32]. NFC combines the explicit knowledge of FC, which is understood with the implicit knowledge of NN, which is acquired by learning. The hybrid neuro-fuzzy is becoming the most preferred choice for tracking the MPP of PV over the last few decades.

Nevertheless, the neuro-fuzzy system have problems of getting trapped in local minima of the search space and low convergence speed [33]. In recent years, several researchers have developed different techniques for solving the local minima problem in the neuro-fuzzy system [34,35]. However, several studies have shown that the limitations of the neuro-fuzzy system are overcome by using wavelets in its consequent structure [36]. The multi-resolution property of wavelets is used to explore the non-stationary signals to find out their local characteristics with high accuracy [37]. All of the above stated control techniques are developed for a particular operating state and are not capable of adapting to a fluctuating non-linear environment. In the case of high fluctuation, the system parameters may go out of bounds, which may result in instability of the system. In such situations, an adaptive control is magnificently effective to solve nonlinear and time-varying uncertain control problems. An adaptive control is roughly divided into two categories, i.e., direct and indirect [38]. In indirect adaptive control, the model of the plant is identified online, which is used to synthesize the controller parameters [39]. While, in direct adaptive control, the adaptation signal is produced directly from a predefined control criterion, which guarantees the closed-loop system stability without the knowledge of system parameters [40,41]. In direct adaptive control, the instantaneous dynamics of the system cannot be captured online, which affects the system’s stability.

In this work, a high performance wavelet-based indirect adaptive neuro-fuzzy MPPT control method is proposed. A five-layer wavelet-based neuro fuzzy control is designed to track the MPP of the PV system. The information extracted from the fuzzy control is used to initialize the parameters of the proposed structure. An on-line learning algorithm based on the Hermite Wavelet-embedded Neural Fuzzy (HWNF) gradient-decent-based back-propagation algorithm is derived to update the parameters of the proposed structure adaptively. Compared with the conventional and intelligent MPPT algorithms, such as Proportional Integral Derivative (PID)-based IC, PID-based P&O and FL controllers, the proposed MPPT controller over performs in terms of efficiency, power quality and MPP error.

The paper is structured as follows: Section 2 focuses on the PV system. Section 3 presents the proposed controller design. Section 4 describes the performance of the proposed solution using detailed simulations, followed by the conclusion in Section 5.

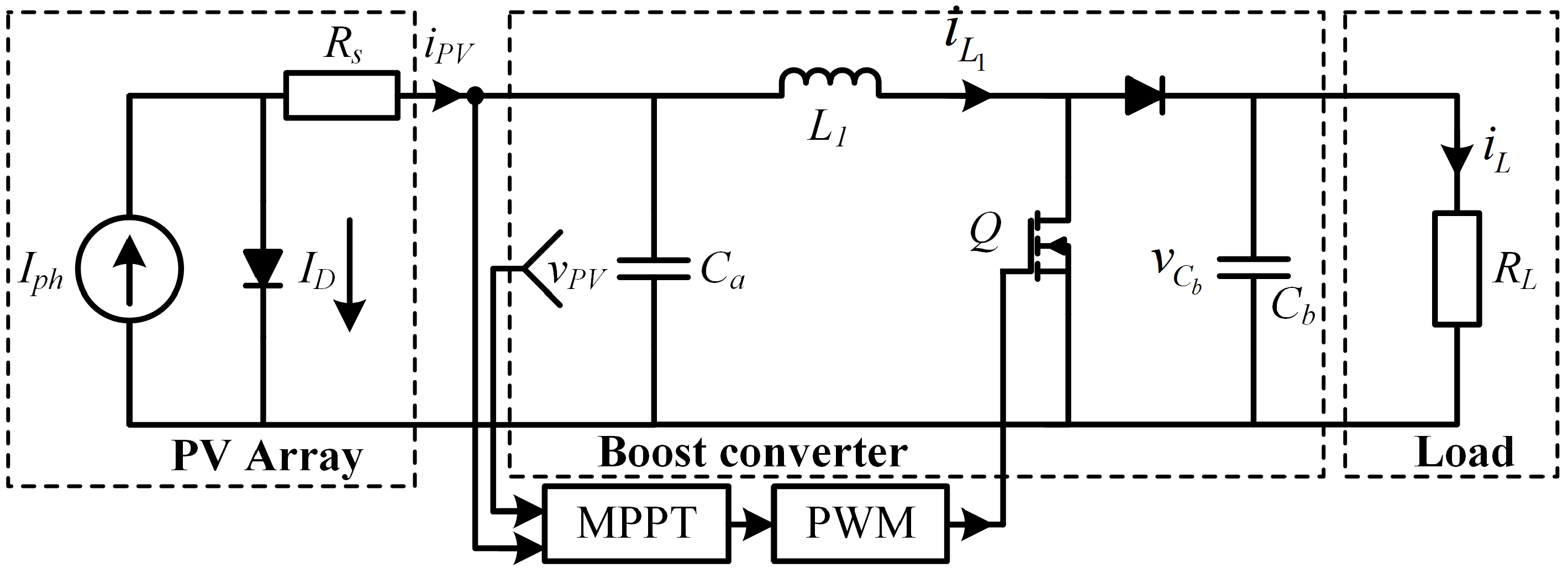
2. Photovoltaic Energy System

The PV system generates electricity from solar irradiance. The PV structural unit contains solar cells. The entire layout of the PV system interconnecting with the load is shown in Figure 1. The system is comprised of a DC-DC boost converter. The dynamic model of the PV system can be represented by three differential equations given as [42]:

$$\frac{d{v}_{PV}}{dt}=\frac{1}{C_a}(i_{PV}-i_{L_1})$$

(1)

$$\frac{d{i}_{L_1}}{dt}=\frac{1}{L_1}(v_{PV}-v{C}_b(1-D))$$

(2)

$$\frac{d{v}_{C_b}}{dt}=\frac{1}{C_b}\left(i_{L_1}(1-D)-\frac{v_{C_b}}{R_L}\right)$$

(3)

2.1. Photovoltaic Array

The I-V and P-V characteristic curves of the PV the array are non-linear in nature. As a function, this non-linearity is defined in terms of the voltage and current of the PV array as follows [43]:

$$i_{PV}=n_p{I}_{ph}-n_p{I}_D\left[\exp \left(\frac{v_{PV}+R_s{i}_{PV}}{n_s{v}_t}\right)-1\right]$$

(4)

where $n_s$ and $n_p$ are the number of cells connected in series/string and the number of parallel strings, whereas $v_t$ represents the terminal voltage.

The characteristics of the PV array are non-linear and time-variant in nature. The output power of the solar cell increases with an increase in solar irradiance level and decreases with an increase in temperature. There is a unique MPP on each P-V curve. The MPP must be tracked using a maximum power point tracker in order to extract maximum power from the PV array.

2.2. DC-DC Boost Converter

The schematic diagram of the DC-DC boost converter is shown in Figure 1. Basically, this converter is required to track the PV MPP by adjusting its duty cycle D between [0,1]. A Pulse Width Modulation (PWM) generator is used to generate the appropriate pulse signal to MOSFET Q according to the given duty cycle. The DC-DC boost converter is characterized by its non-linearity. The input equivalent resistance of DC-DC boost converter is given as [44]:

$$R_{eq}=R_i{(1-D)}^2$$

(5)

According to the power transfer theory, the power delivered to the load is maximized when the equivalent resistance $R_{eq}$ equals the output resistance of the PV array [45].

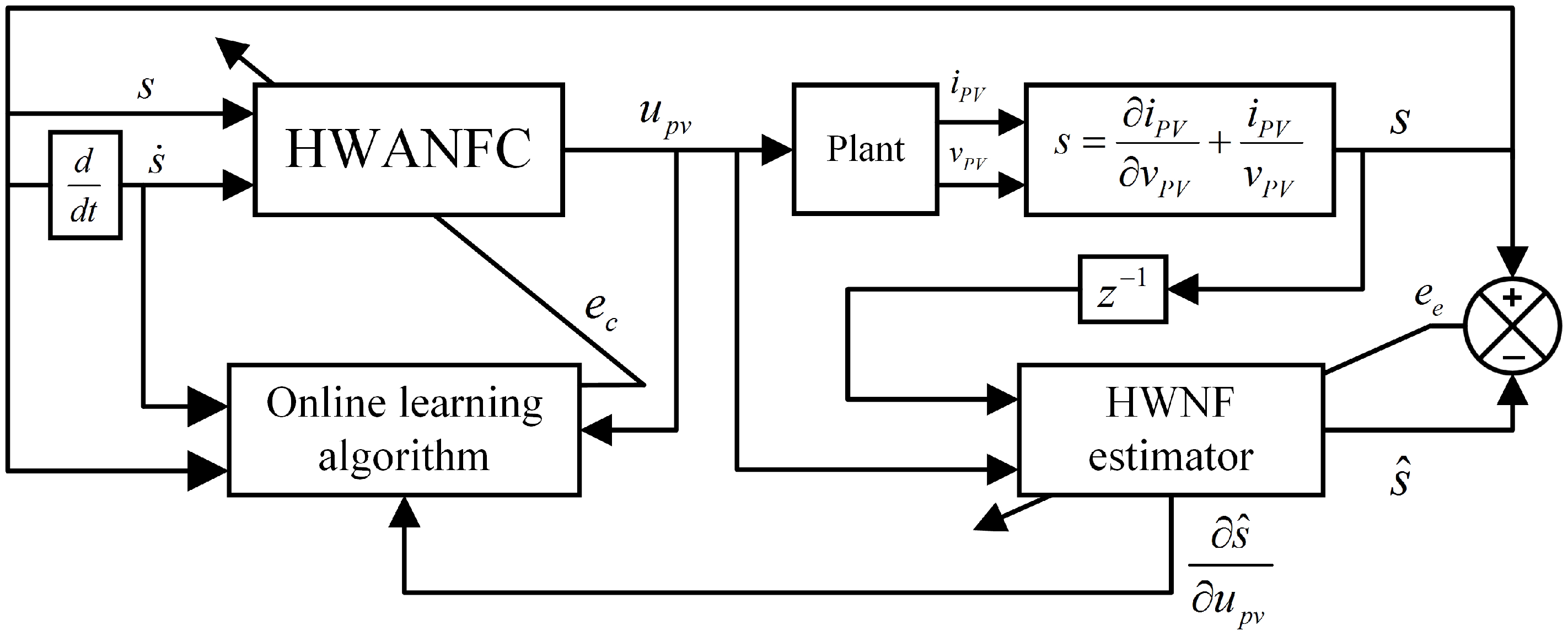
3. Proposed Adaptive Neural Fuzzy Control System

The indirect adaptive neural fuzzy control system is used to control PV output power. Initially, the Hermite Wavelet-based Adaptive Neural Fuzzy Controller (HWANFC) is adopted as the MPP tracker for the PV system. In the proposed system, the HWNF-based gradient estimator is adopted to estimate the gradient term and makes the controller indirect.

The proposed intelligent control system is shown in Figure 2. An HWANFC is used as an MPP tracker. The condition of a MPP is described as:

$$\frac{\partial P_{pv}}{\partial v_{pv}}=\frac{\partial v_{pv}{i}_{pv}}{\partial v_{pv}}=v_{pv}\frac{\partial i_{pv}}{\partial v_{pv}}+i_{pv}=0$$

(6)

Therefore, input error term s of the HWANFC is calculated as:

$$s=\frac{\partial i_{pv}}{\partial v_{pv}}+\frac{i_{pv}}{v_{pv}}\approx \frac{i_{pv}\left(N\right)-i_{pv}(N-1)}{v_{pv}\left(N\right)-v_{pv}(N-1)}+\frac{i_{pv}\left(N\right)}{v_{pv}\left(N\right)}$$

(7)

where N represents the number of iterations. In order to identify the input-output dynamic behavior of the proposed controlled plant, the HWNF-based gradient estimator is used such that it provides a reference signal for the HWANFC parameter tuning.

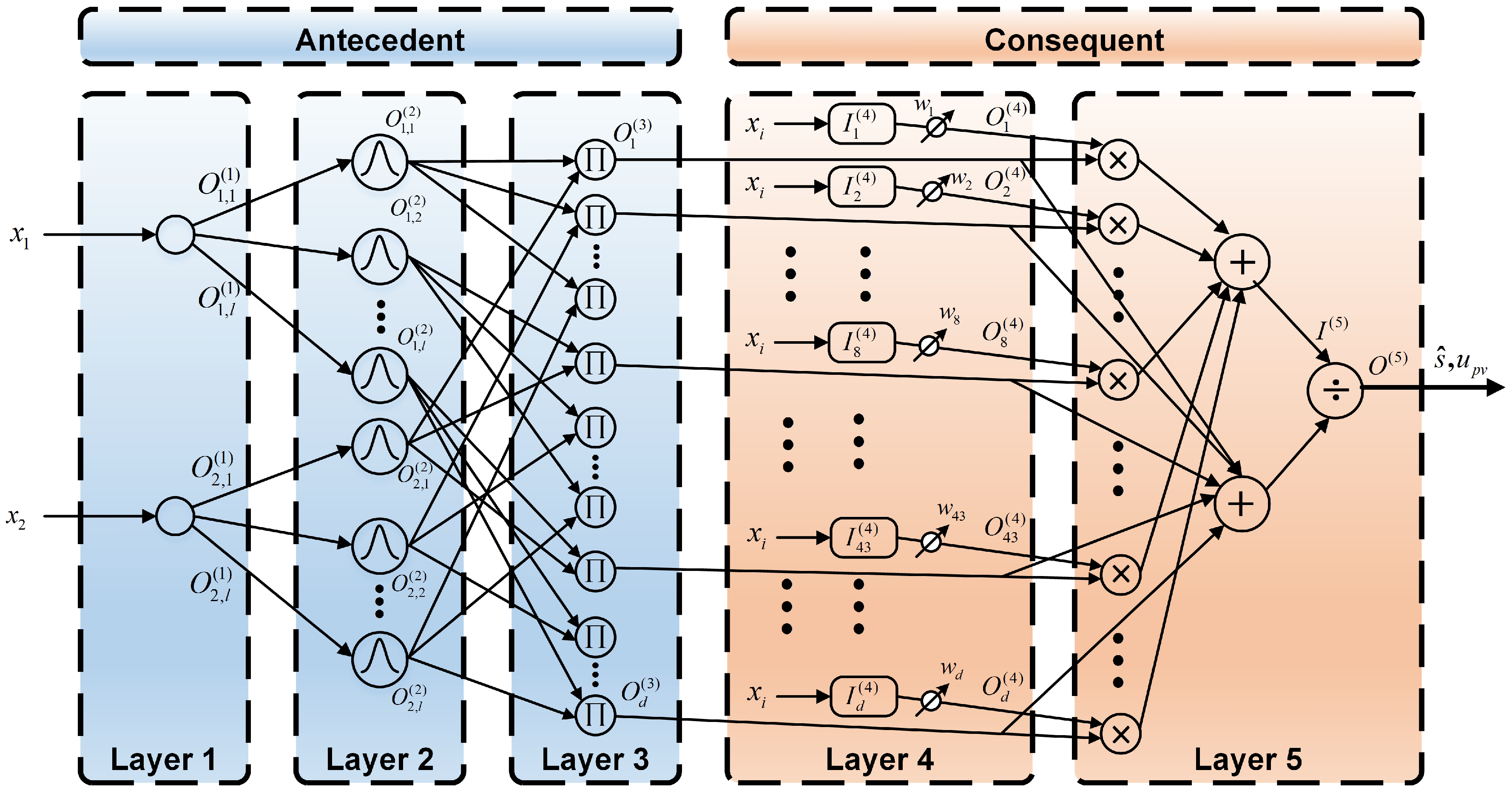
3.1. Structure of the HWANFC and HWNF-Based Gradient Estimator

The Hermite wavelet has a restriction-free input range, which makes it more appropriate for solving highly nonlinear problems with a wide search space [46,47]. Moreover, the series expansion of sufficient Hermite polynomials is used to represent any signal with a high degree of accuracy. The recursive relationships of Hermite polynomials and their first-order derivatives are efficiently used in the constructive network design. The Hermite polynomial $H_m\left(x\right)$ of order m is defined on the interval $[-\infty ,\infty ]$ and is given as:

$$H_0\left(x\right)=1,H_1\left(x\right)=2x,and H_{m+1}\left(x\right)=2x{H}_m\left(x\right)-2m{H}_{m-1}\left(x\right)$$

(8)

where $H_m\left(x\right)$ is orthogonal with respect to the weight function as:

$${\int }_{-\infty }^{\infty }{e}^{-x^2}{H}_m\left(x\right)H_n\left(x\right)=\left\{\begin{array}{cc}0,& m\ne n\\ n!2^n\sqrt{\pi }& m=n\end{array}\right.$$

(9)

Hermite wavelet ${\mathsf{\Psi }}_{n,m}\left(x\right)$ is defined on interval [0,1] by:

$${\mathsf{\Psi }}_{n,m}\left(x\right)=\{\begin{array}{cc}{2}^{k/2}\sqrt{\frac{1}{n!2^n\sqrt{\pi }}}{H}_m(2^{k}x-g)& \frac{g-1}{2^k}\le x\le \frac{g+1}{2^k}\\ 0,& otherwise\end{array}$$

(10)

where $n=1,2,.....,2^{k-1}$, $g=2n-1$, is the translation parameter, k is the positive integer, which represents the level of resolution, and $m=1,....,M-1$, is the degree of the polynomial.

Figure 3 depicts the HWANFC structure, which is a five-layer feedforward connectionist network [48].

(i) Layer 1, the input layer:

The input units in this layer for HWANFC are MPP tracking error $x_1=s$ and the change in error $x_2=\dot{s}$. Similarly, the input units for the HWNF-based gradient estimator are MPP tracking error $x_1=s$ and the output of HWANFC $x_2=u_{pv}$. The input $I_i^{\left(1\right)}$ and the output $Y_{i,j}^{\left(1\right)}$ for this layer are given as:

$$\left\{\begin{array}{cc}{I}_i^{\left(1\right)}=x_i,& i=1,2\\ O_{i,j}^{\left(1\right)}=I_i^{\left(1\right)}& j=1,2,...,l\end{array}\right.$$

(11)

where l represents the number of linguistic variables.

(ii) Layer 2, the linguistic term layer:

This layer uses a Gaussian membership function to fuzzify the inputs of antecedent part. The input-output relationship of this layer is defined as:

$$\left\{\begin{array}{c}{I}_{i,j}^{\left(2\right)}=-\frac{{(O_{i,j}^{\left(1\right)}-c_{i,j})}^2}{{\sigma }_{i,j}}\\ O_{i,j}^{\left(2\right)}=exp\left(I_{i,j}^{\left(2\right)}\right)\end{array}\right.$$

(12)

where $c_{i,j}$ and $s_{i,j}$ denote the center and width of Gaussian function, respectively.

(iii) Layer 3, the rule layer

This layer utilizes the product T-norm in order to compute the firing strength of each rule as follows:

$$\left\{\begin{array}{c}{I}_{(j-1)l+f}^{\left(3\right)}=O_{1,j}^{\left(2\right)}{O}_{2,f}^{\left(2\right)},f=1,2,\dots ,l\\ O_h^{\left(3\right)}=I_h^{\left(3\right)},h=1,2,\dots ,d(=l^2)\end{array}\right.$$

(13)

(iv) Layer 4, the consequent layer

This layer presents the Hermite wavelet function in each node. The weighted consequent value is given by:

$$\left\{\begin{array}{c}{I}_{(j-1)l+f}^{\left(4\right)}={\mathsf{\Psi }}_{j,f}(x_1,x_2)\\ O_h^{\left(4\right)}=w_h{I}_h^{\left(4\right)},h=1,2,\dots ,d(=l^2)\end{array}\right.$$

(14)

(v) Layer 5, the output layer

This layer performs the centroid defuzzification in order to obtain the inference output as follows:

$$\left\{\begin{array}{c}{I}^{\left(5\right)}={\sum }_{h=1}^d{O}_h^{\left(3\right)}{O}_h^{\left(4\right)}\\ O^{\left(5\right)}=\frac{I^{\left(5\right)}}{{\sum }_{h=1}^d{O}_h^{\left(3\right)}}\end{array}\right.$$

(15)

where $O^{\left(5\right)}\in \left\{\widehat{s},u_{pv}\right\}$, is the output of the Hermite wavelet network such that $\widehat{s}$ is the output of the HWNF-based gradient estimator and $u_{pv}$ is the output of HWANFC referred to as the duty cycle of the signal fed to switch.

3.2. Adaptive Mechanism for the HWNF-Based Gradient Estimator

Once an HWNF-based gradient estimator has been constructed, the adaptive mechanism aims at determining appropriate values for the parameters of the Gaussian membership functions $(c_{i,j},{\sigma }_{i,j})$ and linking weights $\left(w_{i,j}\right)$. In order to initialize these parameters in this study, the expert knowledge from traditional fuzzy control is used [2,48]. Using their initialization, the HWNF-based estimator gives stable starting, rather than random initialization. After the initialization process, a gradient-decent-based back-propagation algorithm is embedded to adjust the control parameters.

The error function to adjust the HWNF-based Gradient Estimator (HWNFGE) is given as:

$$e_e=(\widehat{s}\left(t\right)-s\left(t\right))$$

(16)

where $s\left(t\right)$ is the PV plant output (MPP tracking error) and $\widehat{s}\left(t\right)$ is one of the HWNFGE outputs. The generalized parameters update law is written as:

$${\mathrm{\Xi }}_{i,j}(t+1)={\mathrm{\Xi }}_{i,j}\left(t\right)+\gamma e_e\left(t\right)\frac{\partial \widehat{s}\left(t\right)}{\partial {\mathrm{\Xi }}_{i,j}\left(t\right)}$$

(17)

where ${\mathrm{\Xi }}_{i,j}\in \left\{c_{i,j},{\sigma }_{i,j}\right\}$ and γ is the learning rate. The update law for linking variable $w_h$ is given as:

$$w_h(t+1)=w_h\left(t\right)+\gamma e_e\left(t\right)\frac{\partial \widehat{s}\left(t\right)}{\partial w_h\left(t\right)}$$

(18)

The differential term $\frac{\partial \widehat{s}\left(t\right)}{\partial {\mathrm{\Xi }}_{i,j}\left(t\right)}$ is simplified for the respective parameter by applying the chain rule as follows.

For linking weight $\left(w_h\right)$:

$$\frac{\partial \widehat{s}}{\partial w_h}=\frac{\partial \widehat{s}}{\partial O_h^{\left(4\right)}}\frac{\partial O_h^{\left(4\right)}}{\partial w_h}=\frac{O_h^{\left(3\right)}}{{\sum }_{h=1}^d{O}_h^{\left(3\right)}}{I}_h^{\left(4\right)}$$

(19)

For the center of Gaussian function $\left(c_{i,j}\right)$:

$$\frac{\partial \widehat{s}}{\partial c_{i,j}}=\frac{\partial \widehat{s}}{\partial O_h^{\left(3\right)}}\frac{\partial O_h^{\left(3\right)}}{\partial O_{i,j}^{\left(2\right)}}\frac{\partial O_{i,j}^{\left(2\right)}}{\partial c_{i,j}}=\frac{(O_h^{\left(4\right)}-\widehat{s})}{{\sum }_{h=1}^d{O}_h^{\left(3\right)}}{O}_h^{\left(3\right)}\frac{(x_i-c_{i,j})}{{\sigma }_{i,j}^2}$$

(20)

For the spread of Gaussian function $\left({\sigma }_{i,j}\right)$:

$$\frac{\partial \widehat{s}}{\partial {\sigma }_{i,j}}=\frac{\partial \widehat{s}}{\partial O_h^{\left(3\right)}}\frac{\partial O_h^{\left(3\right)}}{\partial O_{i,j}^{\left(2\right)}}\frac{\partial O_{i,j}^{\left(2\right)}}{\partial {\sigma }_{i,j}}=\frac{(O_h^{\left(4\right)}-\widehat{s})}{{\sum }_{h=1}^d{O}_h^{\left(3\right)}}{O}_h^{\left(3\right)}\frac{{(x_i-c_{i,j})}^2}{{\sigma }_{i,j}^3}$$

(21)

After putting the above differential term in the update law, the final updated equations are given as:

$$w_h(t+1)=w_h\left(t\right)+\gamma (\widehat{s}\left(t\right)-s\left(t\right))\left[\frac{O_h^{\left(3\right)}}{{\sum }_{h=1}^d{O}_h^{\left(3\right)}}\right]$$

(22)

$$c_{i,j}(t+1)=c_{i,j}\left(t\right)+\gamma (\widehat{s}\left(t\right)-s\left(t\right))\left[\frac{(O_h^{\left(4\right)}-\widehat{s})}{{\sum }_{h=1}^d{O}_h^{\left(3\right)}}{O}_h^{\left(3\right)}\frac{(x_i-c_{i,j})}{{\sigma }_{i,j}^2}\right]$$

(23)

$${\sigma }_{i,j}(t+1)={\sigma }_{i,j}\left(t\right)+\gamma (\widehat{s}\left(t\right)-s\left(t\right))\left[\frac{(O_h^{\left(4\right)}-\widehat{s})}{{\sum }_{h=1}^d{O}_h^{\left(3\right)}}{O}_h^{\left(3\right)}\frac{{(x_i-c_{i,j})}^2}{{\sigma }_{i,j}^3}\right]$$

(24)

From the input-output relationship between $\widehat{s}$ and $u_{pv}$ of the HWNFGE, we can get the required gradient information for HWANFC as:

$$\frac{\partial s}{\partial u_{pv}}\approx \frac{\partial \widehat{s}}{\partial u_{pv}}=\frac{{\sum }_{h=1}^d{O}_h^{\left(3\right)}\left[-\left(\frac{u_{pv}-c_{i,j}}{{\sigma }_{i,j}^2}\right)O_h^{\left(4\right)}-\widehat{s}+2\sqrt{\frac{2}{\pi }}\left\{8{\Omega }_{11}^j+{\Omega }_{12}^j(128u_{pv}-\Gamma )\right\}\right]}{{\sum }_{h=1}^d{O}_h^{\left(3\right)}}$$

(25)

where Γ is given as:

$$\left\{\begin{array}{cc}\Gamma =32,& 0\le u_{pv}\le 1/2\\ \Gamma =48,& 1/2\le u_{pv}\le 1\end{array}\right.$$

(26)

3.3. On-Line Learning Algorithm for HWANFC

For HWANFC, the update parameters are the same as HWNFGE, i.e., Gaussian membership functions $({\nu }_{i,j},s{s}_{i,j})$ and linking weights $\left({\kappa }_{i,j}\right)$. In this online algorithm, the initial parameters are also taken based on expert knowledge. However, the error function for HWANFC adaptation is slightly changed from HWNFGE and given as follows:

$$e_c=(r\left(t\right)-s\left(t\right))$$

(27)

where $r\left(t\right)$ is the reference input. The parameters of the HWANFC are updated by minimizing the following cost function:

$${\mathrm{\Theta }}_c=\frac{1}{2}\left[e_c^2\left(t\right)+\zeta u_{pv}^2\left(t\right)\right]$$

(28)

where ${\mathrm{\Theta }}_c$ is the cost function and ζ is the learning rate. Therefore, the generalized adaptive law can be written as:

$${\wp }_{i,j}(t+1)={\wp }_{i,j}\left(t\right)+\zeta \frac{\partial {\mathrm{\Theta }}_c\left(t\right)}{\partial {\wp }_{i,j}\left(t\right)}+\zeta \Delta e_c\left(t\right)$$

(29)

where ${\wp }_{i,j}\in \left\{{\nu }_{j,j},s{s}_{i,j}\right\}$ is the update parameter vector of HWANFC, and these parameters are updated via the gradient-decent algorithm. The update law for linking variable ${\kappa }_h$ is given as:

$${\kappa }_h(t+1)={\kappa }_h\left(t\right)+\zeta \frac{\partial {\mathrm{\Theta }}_c\left(t\right)}{\partial {\kappa }_h\left(t\right)}+\zeta \Delta e_c\left(t\right)$$

(30)

The term $\frac{\partial {\mathrm{\Theta }}_c\left(t\right)}{\partial {\wp }_{i,j}\left(t\right)}$ can be simplified using the following equation:

$$\frac{\partial {\mathrm{\Theta }}_c\left(t\right)}{\partial {\wp }_{i,j}\left(t\right)}=\left[e_c\left(t\right)\frac{\partial \widehat{s}}{\partial u_{pv}}-\zeta u_{pv}\right]\frac{\partial u_{pv}}{\partial {\wp }_{i,j}\left(t\right)}$$

(31)

The term $\frac{\partial \widehat{s}}{\partial u_{pv}}$ is calculated by HWNFGE and given by (25). The differential term $\frac{\partial u_{pv}}{\partial {\wp }_{i,j}\left(t\right)}$ from Equation (31) is simplified for the respective parameter by applying the chain rule as follows;

For linking weight $\left({\kappa }_h\right)$:

$$\frac{\partial u_{pv}}{\partial {\kappa }_h}=\frac{\partial u_{pv}}{\partial O_h^{\left(4\right)}}\frac{\partial O_h^{\left(4\right)}}{\partial {\kappa }_h}=\frac{O_h^{\left(3\right)}}{{\sum }_{h=1}^d{O}_h^{\left(3\right)}}{I}_i^{\left(4\right)}$$

(32)

For the center of Gaussian function $\left({\nu }_{i,j}\right)$:

$$\frac{\partial u_{pv}}{\partial {\nu }_{i,j}}=\frac{\partial u_{pv}}{\partial O_h^{\left(3\right)}}\frac{\partial O_h^{\left(3\right)}}{\partial O_{i,j}^{\left(2\right)}}\frac{\partial O_{i,j}^{\left(2\right)}}{\partial {\nu }_{i,j}}=\frac{(O_h^{\left(4\right)}-u_{pv})}{{\sum }_{h=1}^d{O}_h^{\left(3\right)}}{O}_h^{\left(3\right)}\frac{(x_i-{\nu }_{i,j})}{s{s}_{i,j}^2}$$

(33)

For the spread of Gaussian function $\left(s{s}_{i,j}\right)$:

$$\frac{\partial u_{pv}}{\partial s{s}_{i,j}}=\frac{\partial u_{pv}}{\partial O_h^{\left(3\right)}}\frac{\partial O_h^{\left(3\right)}}{\partial O_{i,j}^{\left(2\right)}}\frac{\partial O_{i,j}^{\left(2\right)}}{\partial s{s}_{i,j}}=\frac{(O_h^{\left(4\right)}-u_{pv})}{{\sum }_{h=1}^d{O}_h^{\left(3\right)}}{O}_h^{\left(3\right)}\frac{{(x_i-{\nu }_{i,j})}^2}{s{s}_{i,j}^3}$$

(34)

After putting the above differential term into the general update law, the final updated equations are given as:

$${\kappa }_h(t+1)={\kappa }_h\left(t\right)+\zeta \left((r\left(t\right)-s\left(t\right))\frac{\partial \widehat{s}}{\partial u_{pv}}-\zeta u_{pv}\right)\left[\frac{O_h^{\left(3\right)}}{{\sum }_{h=1}^d{O}_h^{\left(3\right)}}\right]$$

(35)

$${\nu }_{i,j}(t+1)={\nu }_{i,j}\left(t\right)+\zeta \left((r\left(t\right)-s\left(t\right))\frac{\partial \widehat{s}}{\partial u_{pv}}-\zeta u_{pv}\right)\left[\frac{(O_h^{\left(4\right)}-u_{pv}\left(t\right))}{{\sum }_{h=1}^d{O}_h^{\left(3\right)}}{O}_h^{\left(3\right)}\frac{(x_i-{\nu }_{i,j})}{s{s}_{i,j}^2}\right]$$

(36)

$$s{s}_{i,j}(t+1)=s{s}_{i,j}\left(t\right)+\zeta \left((r\left(t\right)-s\left(t\right))\frac{\partial \widehat{s}}{\partial u_{pv}}-\zeta u_{pv}\right)\left[\frac{(O_h^{\left(4\right)}-u_{pv}\left(t\right))}{{\sum }_{h=1}^d{O}_h^{\left(3\right)}}{O}_h^{\left(3\right)}\frac{{(x_i-{\nu }_{i,j})}^2}{s{s}_{i,j}^3}\right]$$

(37)

where $x_i=e_c\left(t\right)$ or, also, $x_i=\Delta e_c\left(t\right)$.

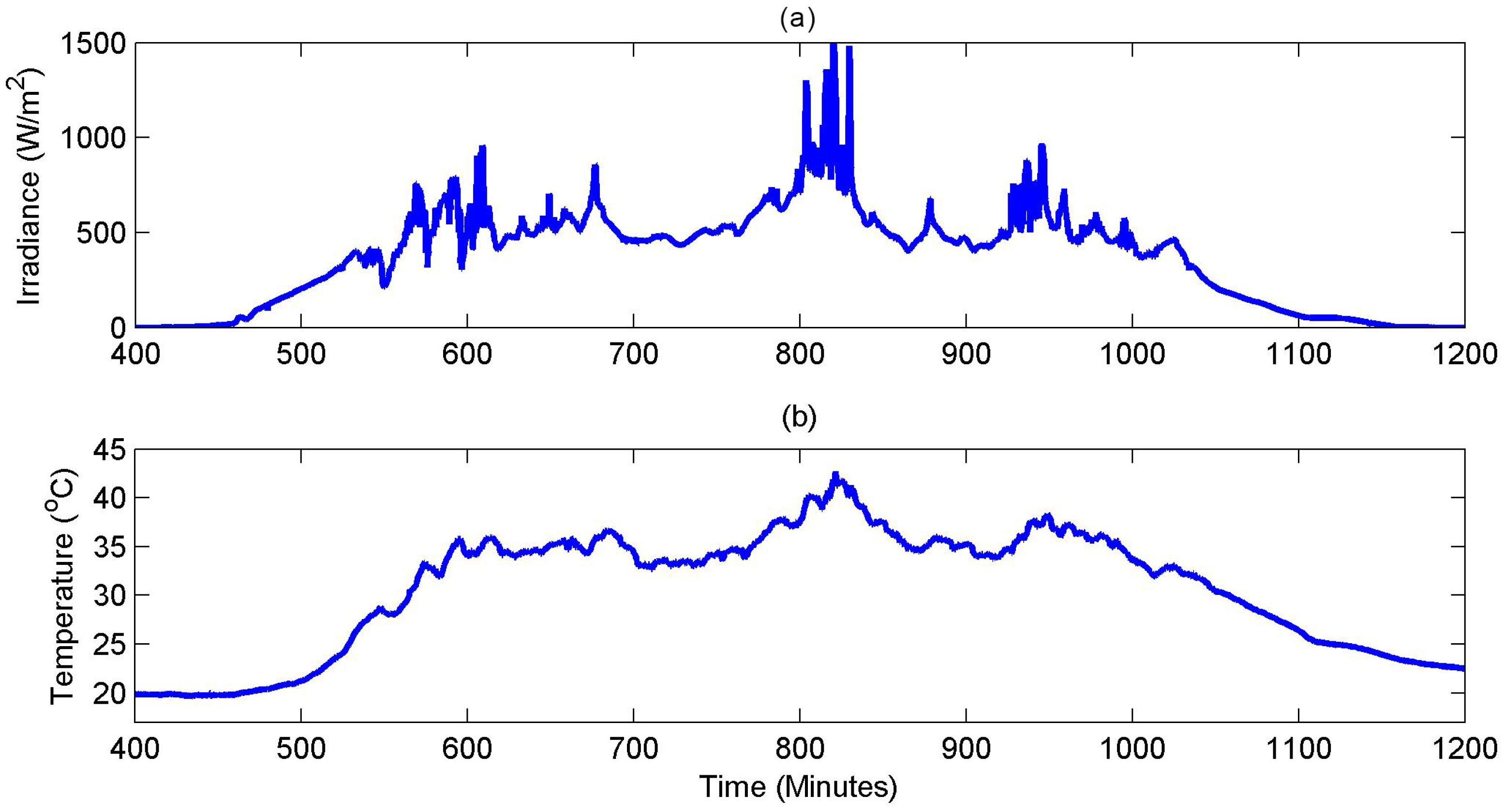
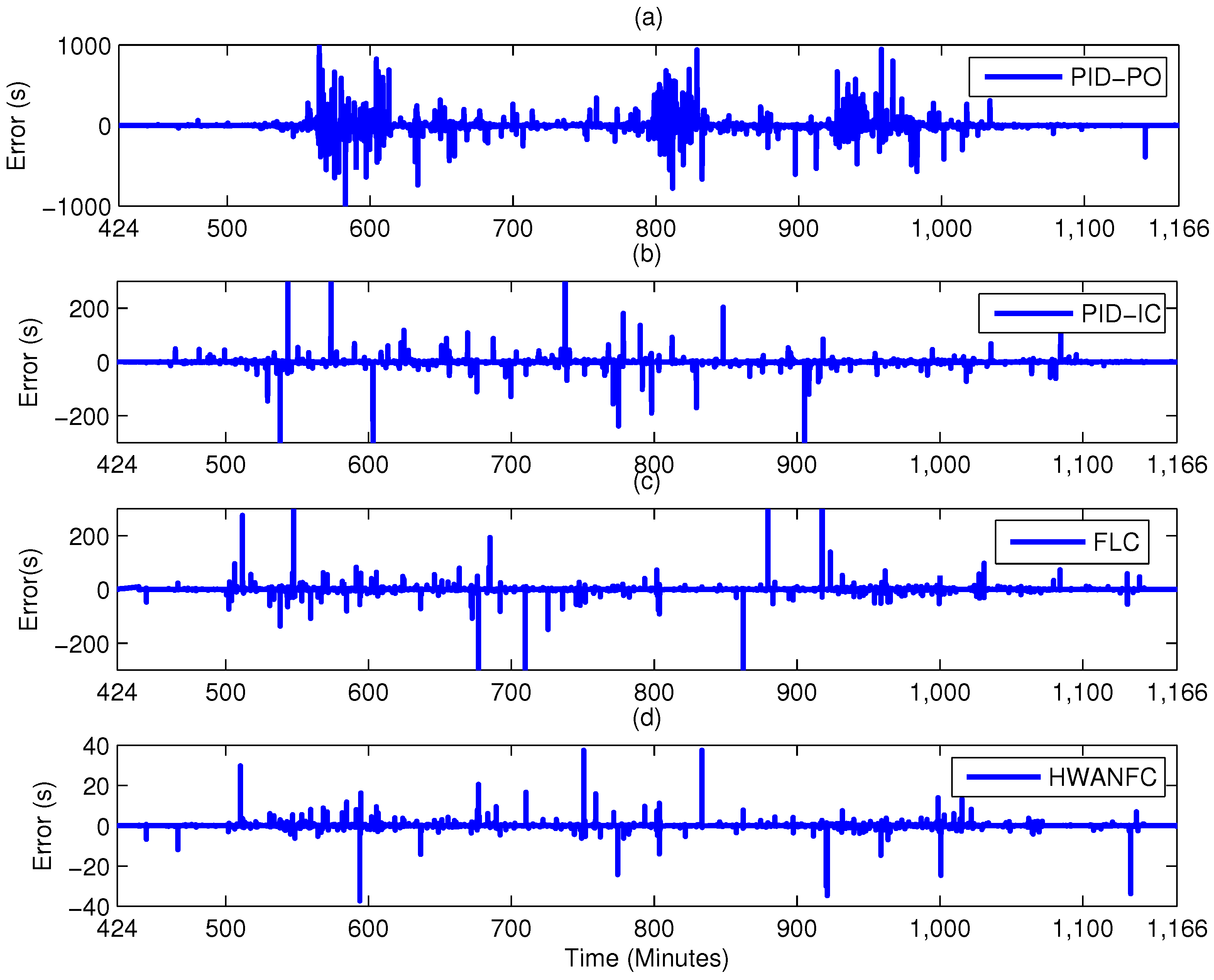
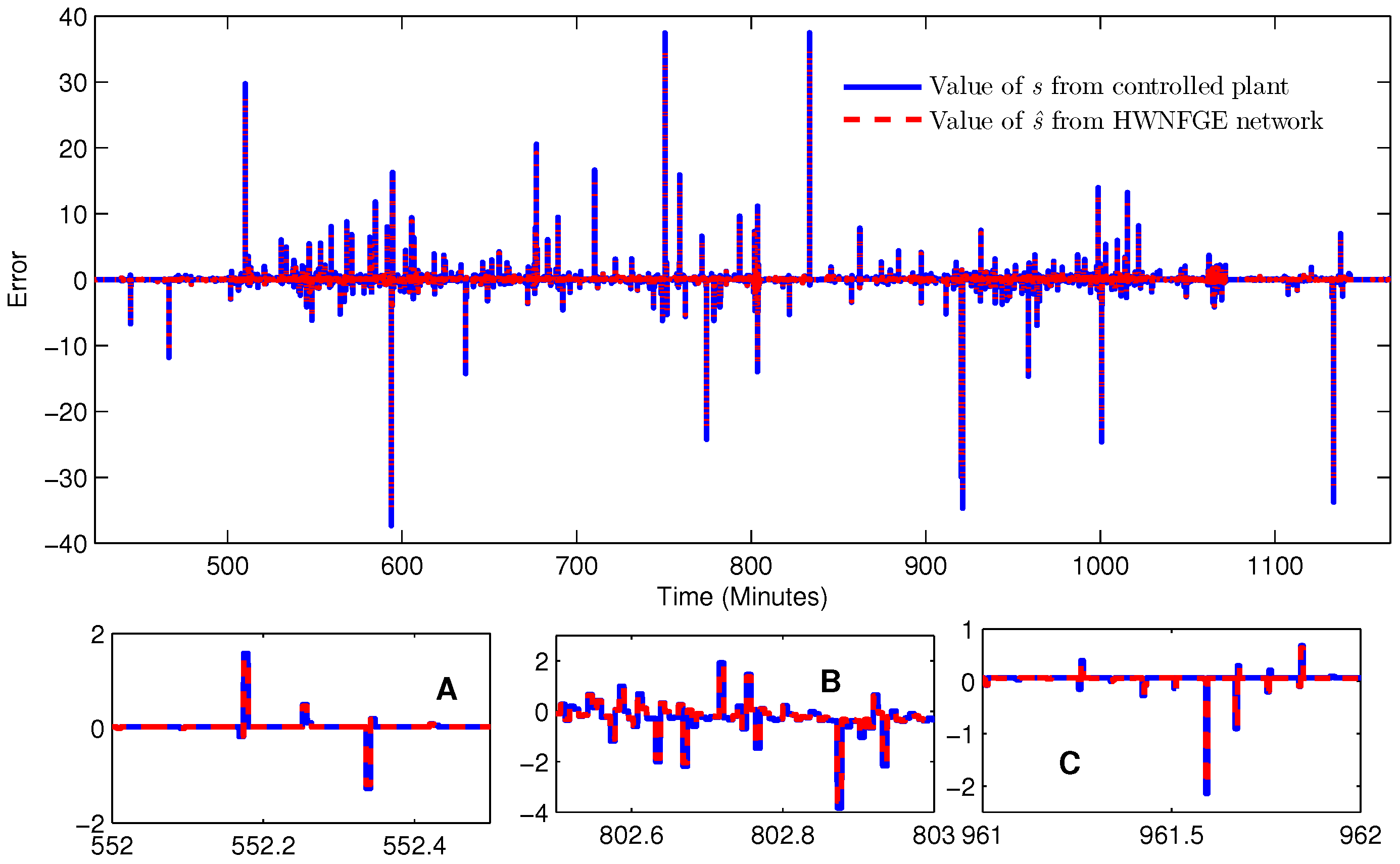
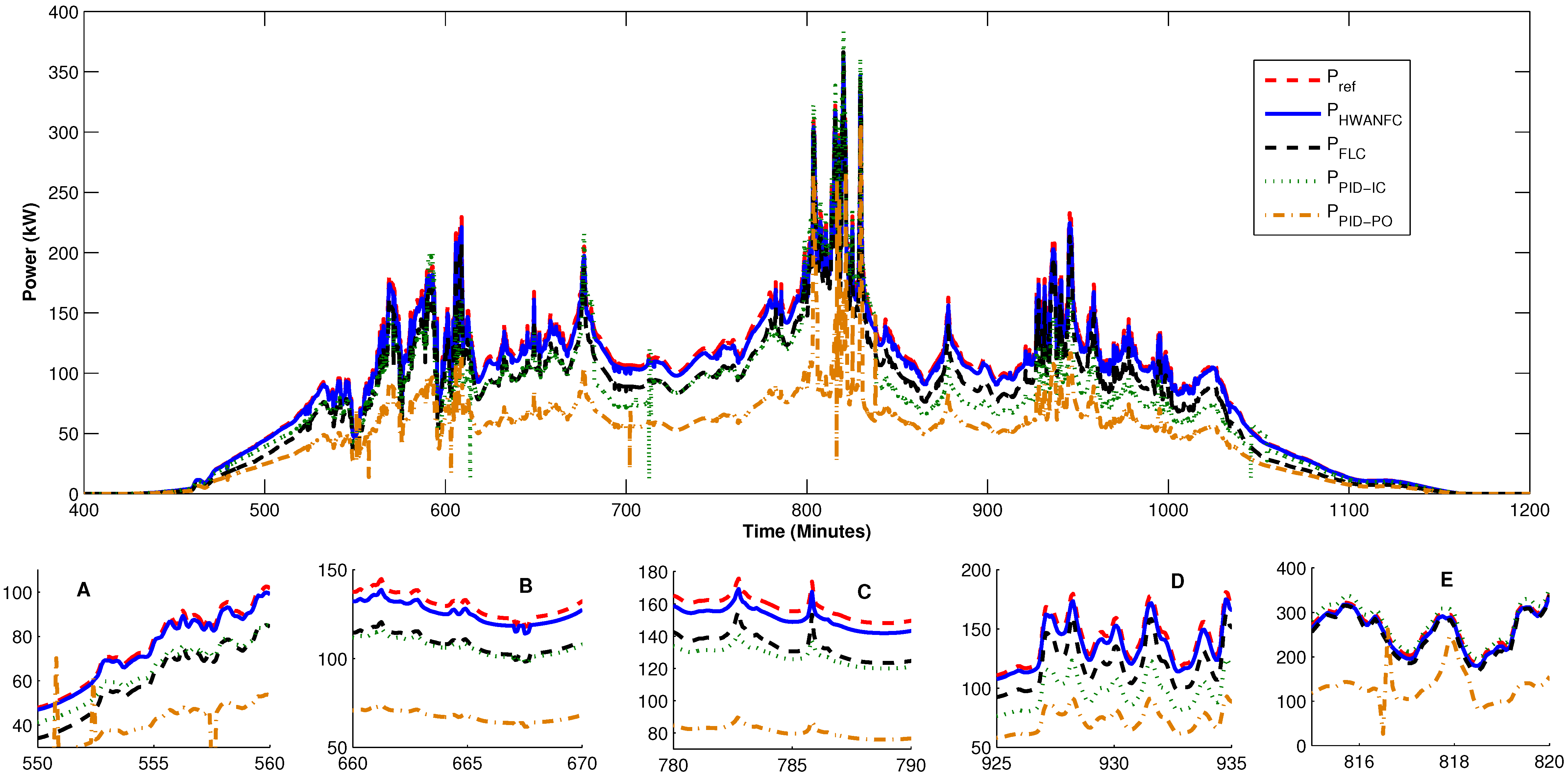
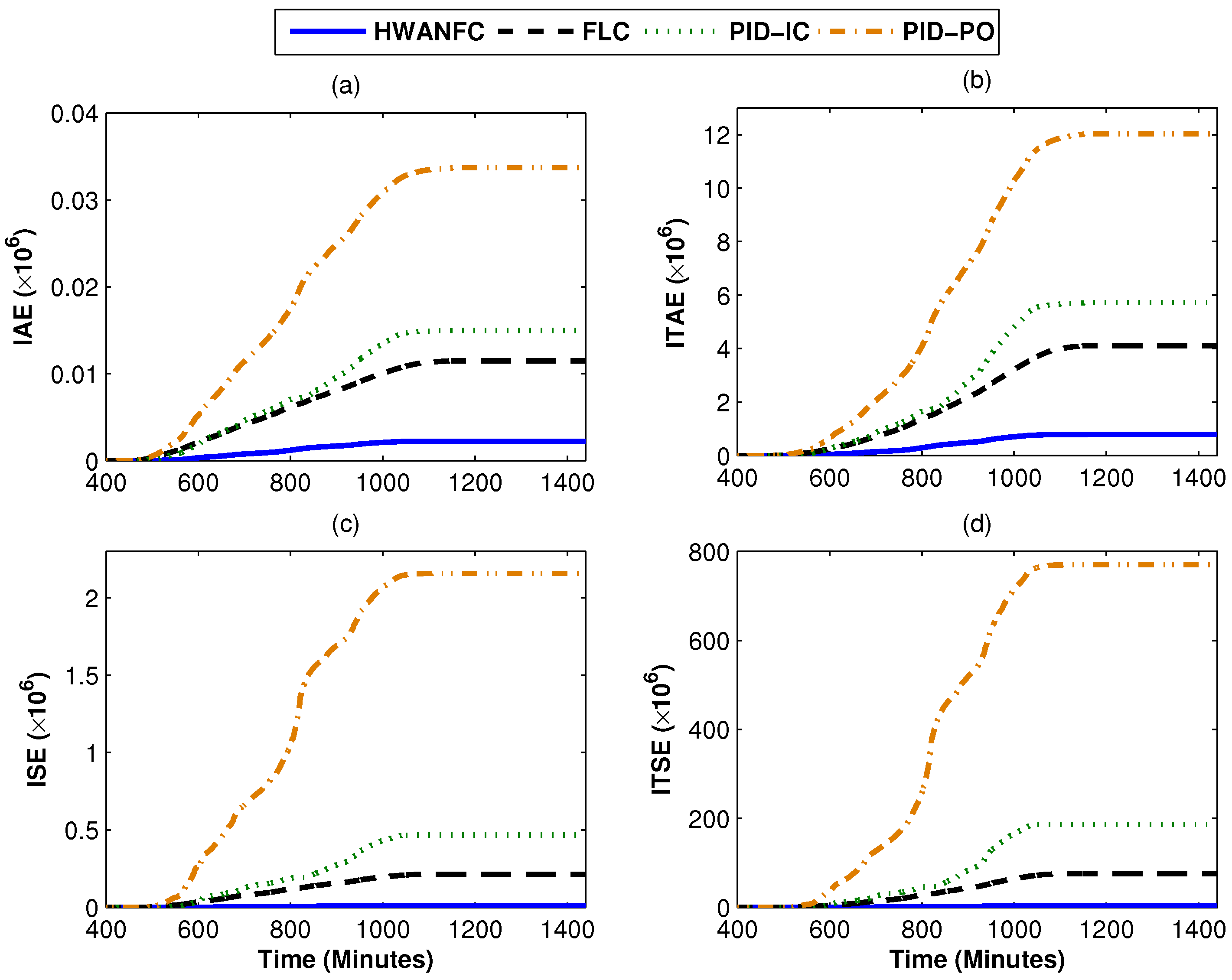
4. Results and Discussion

In order to observe the performance of the proposed controller, it is designed in MATLAB/Simulink. Initially, the proposed HWANFC is developed to track the MPP of the PV array. The parameters in the HWANFC are initialized as follows:

$$\begin{array}{c}l=7,\zeta =0.2,[s{s}_{1,0}\left(0\right),s{s}_{1,1}\left(0\right),....,s{s}_{1,7}\left(0\right),s{s}_{2,0}\left(0\right),s{s}_{2,1}\left(0\right),....,s{s}_{2,7}\left(0\right)]=\hfill \\ \left[0.01,0.011,0.012,0.013,0.017,0.019,0.02,0.03,0.034,0.0375,0.041,0.046,0.0491,0.05\right]\hfill \\ \left[{\nu }_{1,0}\left(0\right),{\nu }_{1,1}\left(0\right),....,{\nu }_{1,7}\left(0\right),{\nu }_{2,0}\left(0\right),{\nu }_{2,1}\left(0\right),....,{\nu }_{2,7}\left(0\right)\right]=\hfill \\ \left[0.02,0.021,0.023,0.024,0.028,0.031,0.34,0.035,0.038,0.0395,0.044,0.050,0.0531,0.054\right]\hfill \end{array}$$

The initial linking weights $w_h$ and ${\kappa }_h$ are given in

Table 1. Initial linking weights of HWANFC and the HWNF-based Gradient Estimator (HWNFGE).

${\mathit{x}}_2$	${\mathit{x}}_1$
	LN	MN	SN	ZE	SP	MP	LP
LN	1.00 ($w_1,{\kappa }_1$)	1.00 ($w_8,{\kappa }_8$)	0.66	0.66	0.33	0.33	0.00
MN	1.00 ($w_2,{\kappa }_2$)	0.66	0.66	0.33	0.33	0.00	−0.33
SN	0.66	0.66	0.33	0.33	0.00	−0.33	−0.33
ZE	0.66	0.33	0.33	0.00	−0.33	−0.33	−0.66
SP	0.33	0.33	0.00	−0.33	−0.33	−0.66	−0.66
MP	0.33	0.00	−0.33	−0.33	−0.66	−0.66	−1.00 ($w_{48},{\kappa }_{48}$)
LP	0.00	−0.33	−0.33	−0.66	−0.66	−1.00 ($w_{42},{\kappa }_{42}$)	−1.00 ($w_{49},{\kappa }_{49}$)

.

The initial parameters for HWNFGE are given as:

$$\begin{array}{c}l=7,\gamma =0.4,\left[{\sigma }_{1,0}\left(0\right),{\sigma }_{1,1}\left(0\right),....,{\sigma }_{1,7}\left(0\right),{\sigma }_{2,0}\left(0\right),{\sigma }_{2,1}\left(0\right),....,{\sigma }_{2,7}\left(0\right)\right]=\hfill \\ \left[0.011,0.013,0.014,0.016,0.019,0.022,0.024,0.035,0.039,0.042,0.047,0.052,0.0591,0.062\right]\hfill \\ \left[c_{1,0}\left(0\right),c_{1,1}\left(0\right),....,c_{1,7}\left(0\right),c_{2,0}\left(0\right),c_{2,1}\left(0\right),....,c_{2,7}\left(0\right)\right]=\hfill \\ \left[0.021,0.023,0.027,0.028,0.031,0.035,0.39,0.044,0.050,0.052,0.054,0.059,0.0631,0.0654\right]\hfill \end{array}$$

The PV array containing 66 series with 13 parallel strings is constructed via the Simpower System toolbox. The overall power rating of the PV array is 261 kW. In order to prove the effectiveness of the proposed control algorithm, a traditional Fuzzy Logic Controller (FLC) based on the IC algorithm, a PID controller based on IC and the P&O algorithm are also used to track MPP. In this research, the Defense Housing Authority (DHA), Islamabad, Pakistan, is taken as a case study. The minute basis irradiance (W/m²) and ambient temperature (${}^{\circ }$C) levels are recorded by the Pakistan Meteorological Department (PMD) for a complete summer day, as shown in Figure 4.

The irradiance level varies over a day depending on the appearance of sun. From Figure 4, the Sun rises at 6:04 h (424 min) and sets at 19:26 h (1166 min). During the day time, the average solar irradiance level reaches 1000 W/m². Similarly, the average temperature during the night time is 20 ${}^{\circ }$C, while in the day time, it reaches up to 42 ${}^{\circ }$C. The HWANFC for the PV system tracks the MPP by keeping the slope close to zero. In order to analyze the performance of HWANFC, a PID controller-based IC and P&O and FLC are also used to track the MPP of the PV system. Figure 5 shows the performance of different controllers. The random spikes are due to the rapid change of solar irradiance. As the irradiance level changes, the MPP alters its position, which in turn changes the value of s. After that, the controller tries to minimize this error by adjusting the duty cycle. From the figure, the P&O algorithm-based PID controller error is up to 1000. Similarly, with IC-PID and FLC, the maximum error reduces to 250, while the HWANFC achieves the MPP so quickly and efficiently that the maximum error spike does not exceed 40.

The comparison between error term s acquired by the controlled plant and the HWNFGE generated error $\widehat{s}$ is illustrated in Figure 6. From the figure, it is clearly observed that the HWNFGE accurately identifies the network and calculates the error term efficiently. However, at large values of s (due to the rapid change in irradiance level), the value of $\widehat{s}$ is slightly less than the experimental error. In order to analyze the error difference more accurately, various zoomed sub-figures at different timings are shown in Figure 6A–C.

The output power comparison of the PV array regulated with HWANFC, FLC, PID-based IC and PID-based P&O along with reference power are shown in Figure 7. Throughout the day, the various undershoots and poor response of P&O and the IC technique are clearly analyzed from Figure 7. At t = 785 min (Subfigure C), the power loss between the reference power, P&O and IC technique reaches 80 kW and 30 kW, respectively. The FLC response is comparatively better than the IC technique. However, the proposed HWANFC out-performs the FLC.

Based on the output power of the PV from various controllers, the PV efficiency (${\eta }_{PV}$) and PV average efficiency (${\eta }_{PV-av}$) are calculated as follows:

$${\eta }_{PV}=\frac{{\int }_0^t{P}_{PV}\left(t\right)dt}{{\int }_0^t{P}_{ref}\left(t\right)dt}\times 100\%$$

(38)

$${\eta }_{PV-av}=\frac{1}{T}{\eta }_{PV}$$

(39)

Similarly, in order to test the dynamic performance of the proposed controller, the following comparison indexes were used [49]: Mean Relative Error (MRE), Integral Absolute Error (IAE), Integral Time Absolute Error (ITAE), Integral Square Error (ISE) and Integral Time Square Error (ITSE):

$$MRE=\frac{1}{T}\sum _{t=1}^T\frac{P_{ref}-P_{PV}}{P_{PV}}$$

(40)

$$IAE={\int }_0^t\left|e\left(t\right)\right|dt$$

(41)

$$ITAE={\int }_0^{t}t\left|e\left(t\right)\right|dt$$

(42)

$$ISE={\int }_0^t{e}^2\left(t\right)dt$$

(43)

$$ITSE={\int }_0^{t}t{e}^2\left(t\right)dt$$

(44)

where $e\left(t\right)=P_{ref}\left(t\right)-P_{PV}\left(t\right)$. Figure 8 shows the simulation results of ${\eta }_{PV}$ and ${\eta }_{PV-av}$, whereas Figure 9 corresponds to IAE, ITAE, ISE and ITSE. From Figure 8a, the PV efficiency for HWANFC reaches 96.81 and then keeps constant, while other controllers’ efficiencies fluctuate with time. Similarly, the mean efficiency for HWANFC linearly increases with a certain slope with respect to the others. In Figure 9, as time increases, the accumulative error of each controller increases. However, the proposed HWANFC index is less among all other controllers.

Table 2. PV efficiencies and performance parameters. FLC, Fuzzy Logic Controller; P&O, Perturb and Observe.

Controllers	${\mathit{\eta }}_{\mathit{PV}}$ (%age)	${\mathit{\eta }}_{\mathit{PV}-\mathit{av}}$ (%age)	MRE (103)	IAE (106)	ITAE (106)	ISE (106)	ITSE (106)
HWANFC	96.81	94.04	0.0029	0.00243	0.7934	0.01043	3.666
FLC	83.66	76.63	0.0276	0.01149	4.11	0.2146	75.66
PID-IC	80.13	75.56	3.147	0.01498	5.72	0.4669	186.8
PID-P&O	52.06	48.57	1.242	0.0337	12.04	2.158	770.3

depicts the values of various indexes and efficiencies based on a 1440-min simulation with a sampling time of 10⁻⁶ s. The PV efficiency of the proposed HWANFC is high among other controllers, and the error indexes are also lower than those of FLC/PID-IC/PID-P&O. According to the results, the proposed HWANFC shows a better MPP tracking and efficiency improvement than other controllers.

5. Conclusions

In this work, an intelligent wavelet-based neuro-fuzzy indirect method with high adaptive capability is designed for the MPPT of a PV system. A five-layer NFC is adopted as the process feedback controller. The proposed control is initialized from the traditional fuzzy control by means of expert knowledge, which decreases the weight of the lengthy pre-learning. With a derived learning scheme, the parameters are updated in the proposed structure adaptively by observing and adjusting the tracking error. A neural network is developed to provide the HWANFC with the gradient information. The Hermite wavelets are integrated to improve the performance of the proposed controller. Various simulation results and comparison indexes have shown that the HWANFC can track the MPP quickly with high robustness to the parameter variations and external load disturbances and out-performs compared with the traditional MPPT techniques.