Development of a Leader-End Reclosing Algorithm Considering Turbine-Generator Shaft Torque
Abstract
:1. Introduction
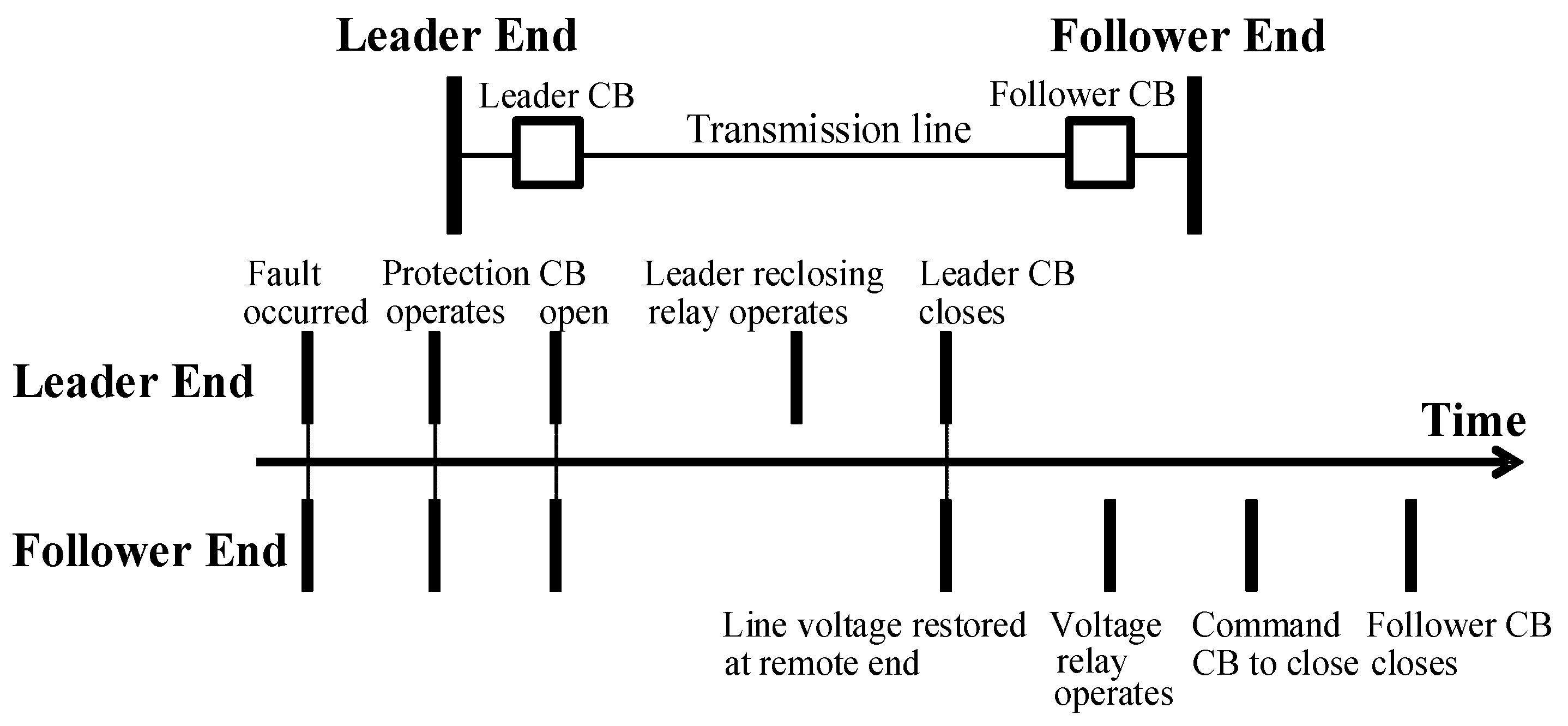
2. Leader-Follower Reclosing Scheme
3. Power System Modeling and Assumption
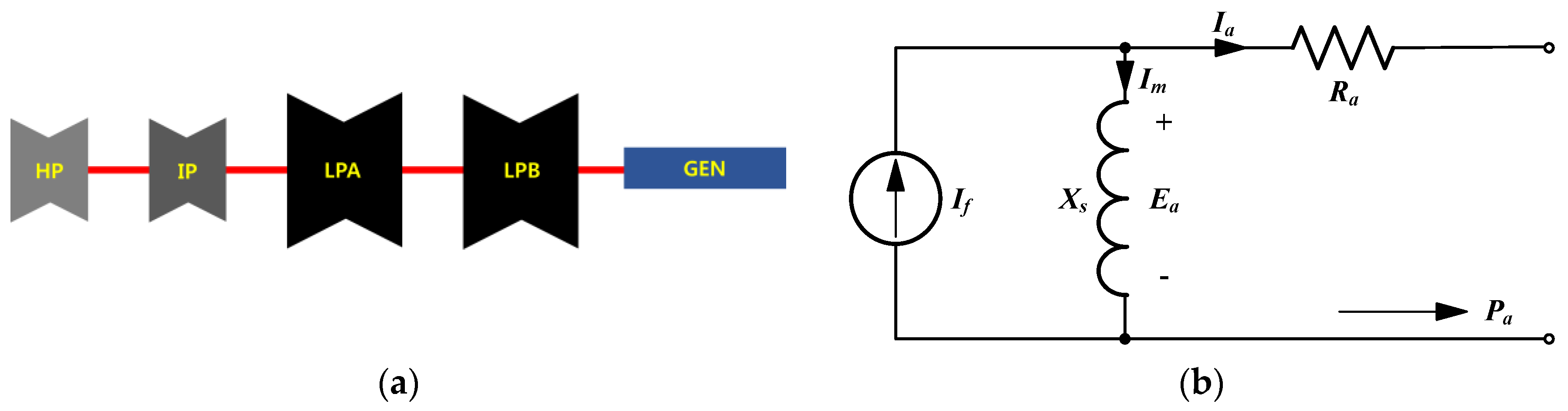
3.1. Modeling of the Power System and Turbine-Generator
3.2. Torque and Power Delivery Characteristics of the Synchronous Generator
3.3. Assumptions for Simulation
- In all cases, the fault resistance of the permanent ground fault was set to zero Ohm for the purpose of analyzing the mechanical stress on the turbine-generator shaft under the most severe condition.
- We calculated the peak-to-peak transient shaft torque beyond the moment of the leader reclosing failure to determine the quantity of the mechanical stress that was applied to the turbine shaft. The shaft torque calculation point was between the LPB and GEN because the maximum transient shaft torque during disturbances typically occurs at this point.
4. Analysis of Turbine-Generator-Shaft Torque According to Leader Reclosing
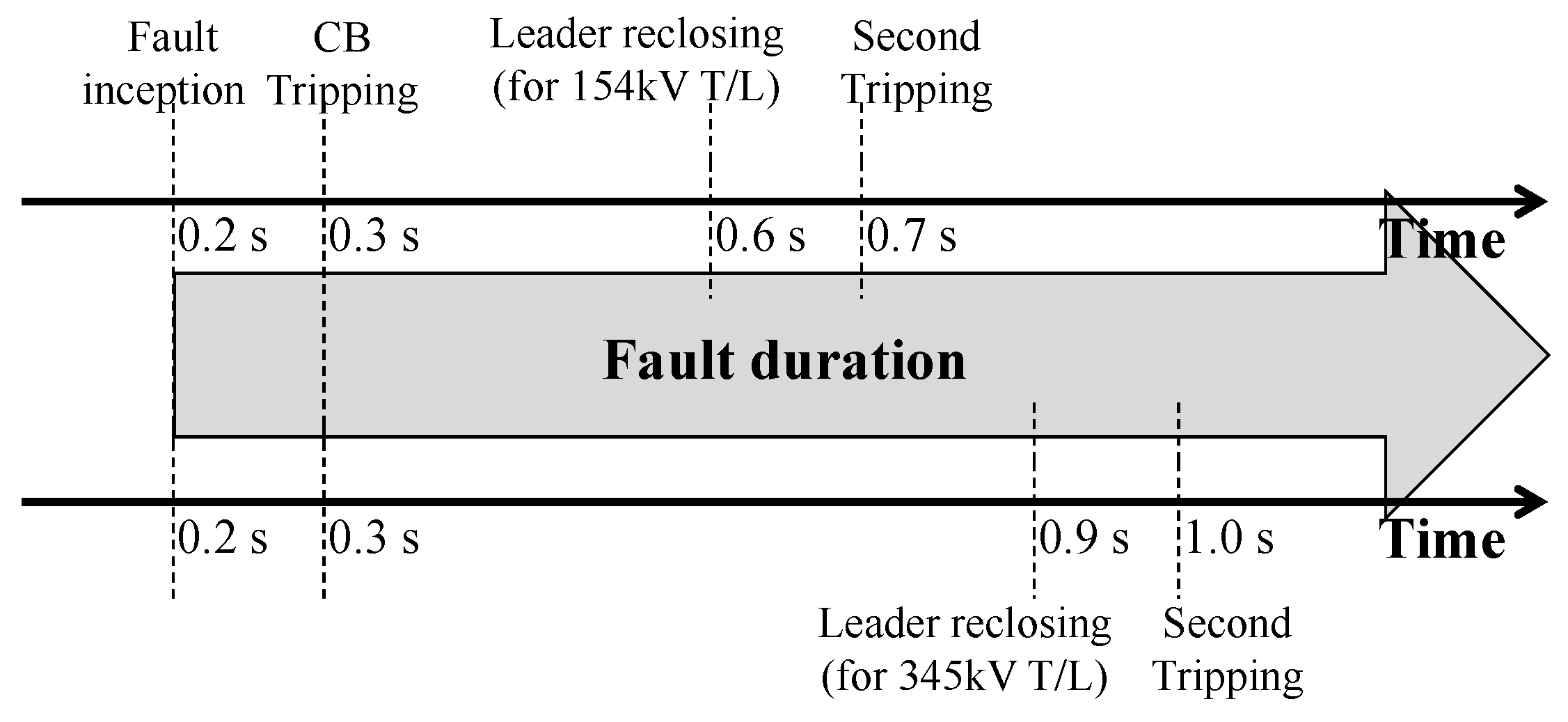
4.1. Simulation Cases
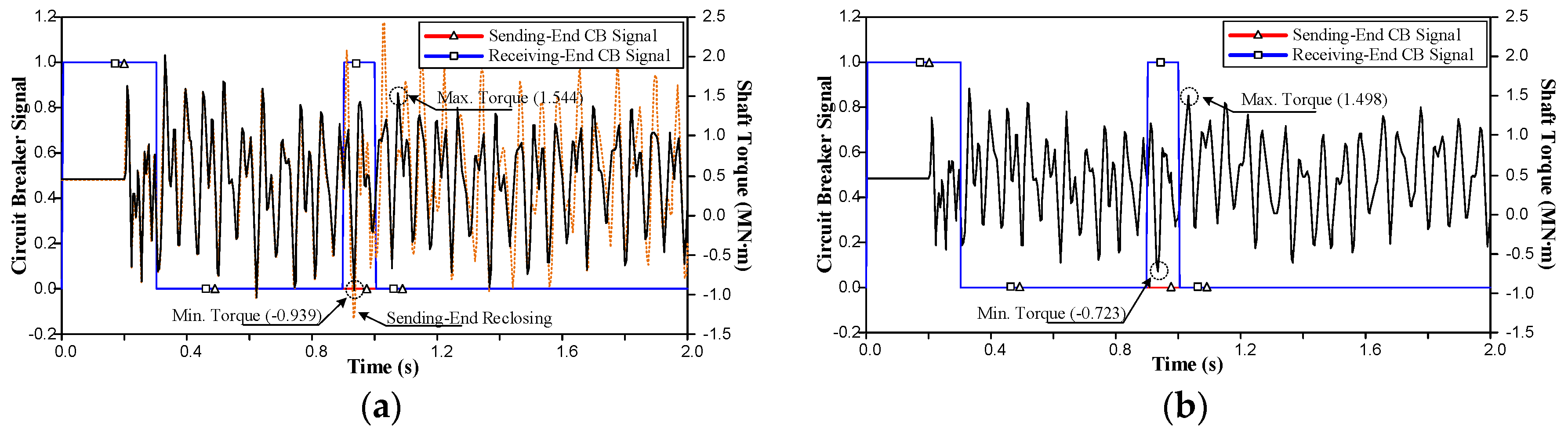
4.2. Simulation Result for the Three-Phase Fault
4.3. Simulation Result for the Single-Phase Fault
4.4. Additional Simulation Result of the Three-Phase Fault for Determining the Preferable Leader-End
5. Development of the Leader-End Reclosing Algorithm
5.1. Outline of the Algorithm
- Common memory section.
- Common services.
- Used external services or objects.
- Internal function definitions.
- Exported function definitions.
5.2. Verification of the Algorithm
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Tables of Each Turbine-Generator Parameters
| Rating | 2 Pole, 246 MVA, 3-Phase, 19.6 kV | ||
|---|---|---|---|
| Electrical Parameters | Reactance [p.u.] | ||
| Time Constant [s] | |||
| Mechanical Parameters | Moment of Inertia [] | HP = 380.609 | LPB = 3622.785 |
| IP = 637.580 | GEN = 3558.311 | ||
| LPA = 3517.856 | |||
| Spring Constant [] | HP-IP = 14.898 | LPA-LPB = 40.162 | |
| IP-LPA = 26.958 | LPB-GEN = 54.687 | ||
| Rating | 2 Pole, 612 MVA, 3-Phase, 22 kV | ||
|---|---|---|---|
| Electrical Parameters | Reactance [p.u.] | ||
| Time Constant [s] | |||
| , | . | ||
| Mechanical Parameters | Moment of Inertia [. ] | HP = 773.61 | LPB = 7363.54 |
| IP = 1295.72 | GEN = 7232.66 | ||
| LPA = 7150.74 | |||
| Spring Constant [. ] | HP-IP = 30.281 | LPA-LPB = 81.634 | |
| IP-LPA = 54.794 | LPB-GEN = 111.158 | ||
References
- EPRI Solutions. Torsional Interaction between Electrical Network Phenomena and Turbine-Generator Shafts; EPRI Technical Report; EPRI: Palo Alto, CA, USA, 2006. [Google Scholar]
- Hammons, T.J.; Canay, I.M. Effect of damper modeling and the fault clearing process on response torque and stressing of turbine-generator shafts. IEEE Trans. Energy Convers. 1986, EC-1, 113–121. [Google Scholar] [CrossRef]
- Canay, I.M.; Rohrer, H.J.; Schnirel, K.E. Effect of electrical disturbances, grid recovery voltage and generator inertia on maximization of mechanical torques in large turbogenerator sets. IEEE Trans. Power Appar. Syst. 1980, PAS-99, 1357–1370. [Google Scholar]
- Hammons, T.J.; Chanal, L. Measurement of torque in steam turbine-generator shafts following severe disturbances on the electrical supply system-analysis and implementation. IEEE Trans. Energy Convers. 1991, 6, 193–203. [Google Scholar] [CrossRef]
- Oh, Y.S.; Seo, H.C.; Yang, J.J.; Kim, C.H. Development of a reclosing scheme for reduction of turbine generator shaft torsional torques: A decision method to achieve optimal reactor capacity. J. Electr. Eng. Technol. 2014, 9, 742–750. [Google Scholar] [CrossRef]
- IEEE Working Group. Effects of switching network disturbances on turbine-generator shaft systems. IEEE Trans. Power Appar. Syst. 1982, PAS-101, 3151–3157. [Google Scholar]
- Chyn, C.; Wu, R.-C.; Tsao, T.P. Torsional fatigue of turbine-generator shafts owing to network faults. IEE Proc. Gener. Transm. Distrib. 1996, 143, 479–486. [Google Scholar] [CrossRef]
- Abolins, A.; Lambrecht, D.; Joyce, J.S.; Rosenberg, L.T. Effect of clearing short circuits and automatic reclosing on torsional stress and life expenditure of turbine-generator shafts. IEEE Trans. Power Appar. Syst. 1976, PAS-95, 14–25. [Google Scholar] [CrossRef]
- Joyce, J.S.; Kulig, T.; Lambrecht, D. The impact of high-speed reclosure of single and multi-phase system faults on turbine-generator shaft torsional fatigue. IEEE Trans. Power Appar. Syst. 1980, PAS-99, 279–291. [Google Scholar] [CrossRef]
- Joyce, J.S.; Kulig, T.; Lambrecht, D. Torsional fatigue of turbine-generator shafts caused by different electrical system faults and switching operations. IEEE Trans. Power Appar. Syst. 1978, PAS-97, 1965–1977. [Google Scholar] [CrossRef]
- IEEE Power System Relaying Committee Working Group. Single phase tripping and auto reclosing of transmission lines IEEE committee report. IEEE Trans. Power Deliv. 1992, 7, 182–192. [Google Scholar]
- Ahn, S.P.; Kim, C.H.; Aggarwal, R.K.; Johns, A.T. An alternative approach to adaptive single pole auto-reclosing in high voltage transmission systems based on variable dead time control. IEEE Trans. Power Deliv. 2001, 16, 676–686. [Google Scholar] [CrossRef]
- Berdy, J.; Brown, P.G.; Andrichak, J.G.; Wilkinson, S.B. High-Speed Reclosing System and Machine Considerations. Available online: http://store.gedigitalenergy.com/faq/Documents/750_760/GER-3224.pdf (accessed on 2 March 2017).
- IEEE Guide for Automatic Reclosing of Circuit Breakers for AC Distribution and Transmission Lines; IEEE Std. C37.104; IEEE: New York, NY, USA, 2012.
- Anderson, P.M. Power System Protection, 1st ed.; Wiley-IEEE Press: Hoboken, NJ, USA, 1998. [Google Scholar]
- Sen, P.C. Principles of Electric Machines and Power Electronics, 3rd ed.; John Wiley & Sons Press: Chichester, UK, 1989. [Google Scholar]
- Myongji University and Korea Power eXchange. A Study on Establishment of Protective Relay Setting Rules; Final Report; Korea Power eXchange: Seoul, Korea, 2003. [Google Scholar]
- Jo, Y.H.; Xiang, L.; Choi, M.S.; Park, J.S.; Lim, S.I.; Kim, S.T.; Lee, S.J. A Fast Algorithm of the Apparent Factor Calculation for Distance Relay Setting without Fault Analysis. J. Electr. Eng. Technol. 2013, 8, 64–69. [Google Scholar] [CrossRef]
- Seyedi, H.; Behroozi, L. New distance relay compensation algorithm for double-circuit transmission line protection. IET Gener. Transm. Distrib. 2011, 5, 1011–1018. [Google Scholar] [CrossRef]
- Dubey, R.; Samantaray, S.R. Wavelet singular entropy-based symmetrical fault-detection and out-of-step protection during power swing. IET Gener. Transm. Distrib. 2013, 7, 1123–1134. [Google Scholar] [CrossRef]
- Ahn, Y.J. Distance Relay for Protection of Transmission Line Having Minimized Reactance Effect. U.S. Patent 06661630, 9 December 2003. [Google Scholar]
- Janne, A.; Ari, W. System and Method for Determining Location of Phase-to-Earth Fault. U.S. Patent US7514933 B2, 7 April 2009. [Google Scholar]
- Mahseredjian, J. DLL Programming in EMTP (EMTP-EMTPWorks Help Files); Powersys: Le Puy-Sainte-Réparade, France, 2012; pp. 1–24. [Google Scholar]
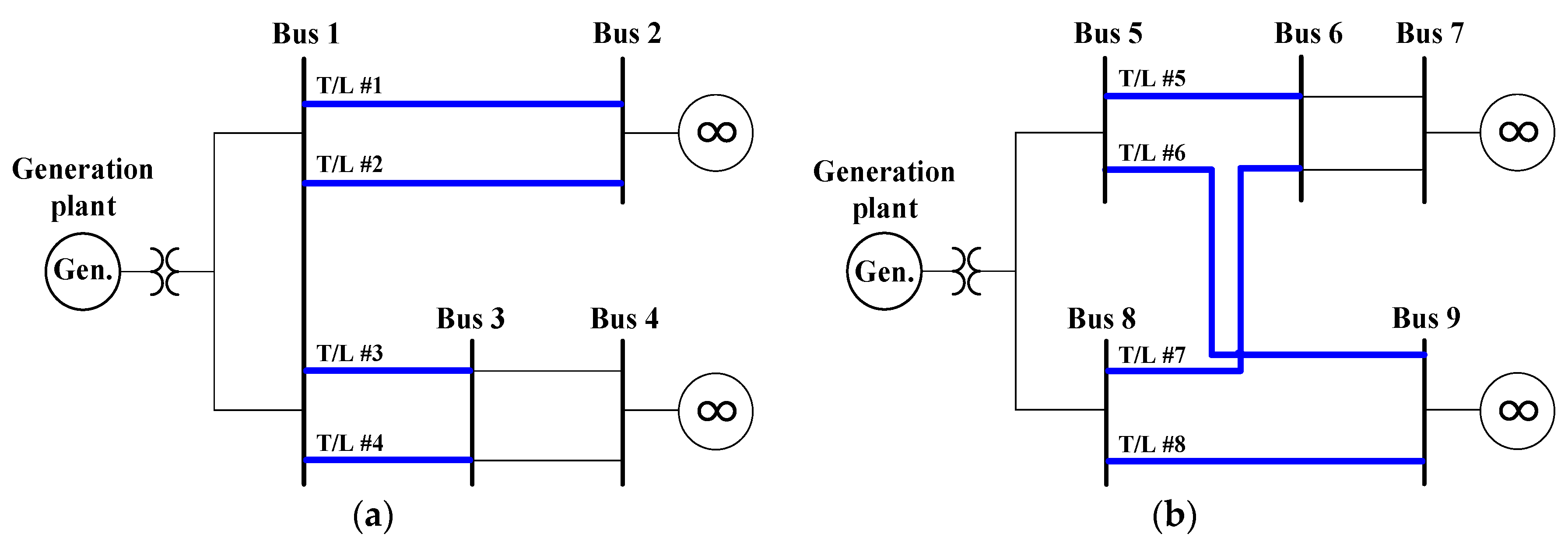




| Case | Voltage Level | Faulted Line | Fault Type | Fault Location | |
|---|---|---|---|---|---|
| 1 | 1-1 | 154 kV | T/L #1 | 3-phase permanent Fault | 10% 50% 90% of each T/L |
| 1-2 | T/L #2 | ||||
| 1-3 | T/L #3 | ||||
| 1-4 | T/L #4 | ||||
| 2 | 2-1 | T/L #1 | single-phase permanent Fault | ||
| 2-2 | T/L #2 | ||||
| 2-3 | T/L #3 | ||||
| 2-4 | T/L #4 | ||||
| 3 | 3-1 | 345 kV | T/L #5 | 3-phase permanent Fault | |
| 3-2 | T/L #6 | ||||
| 3-3 | T/L #7 | ||||
| 3-4 | T/L #8 | ||||
| 4 | 4-1 | T/L #5 | single-phase permanent Fault | ||
| 4-2 | T/L #6 | ||||
| 4-3 | T/L #7 | ||||
| 4-4 | T/L #8 | ||||
| Fault Location [%] | Peak-to-Peak Shaft Torque [MNm] | |||||||
|---|---|---|---|---|---|---|---|---|
| Case 1-1 | Case 1-2 | Case 1-3 | Case 1-4 | |||||
| S | R | S | R | S | R | S | R | |
| 10 | 2.103 | 1.272 | 2.103 | 1.272 | 2.188 | 1.300 | 2.188 | 1.300 |
| 50 | 1.278 | 0.910 | 1.278 | 0.910 | 1.418 | 1.016 | 1.418 | 1.016 |
| 90 | 1.025 | 1.021 | 1.025 | 1.021 | 1.173 | 1.270 | 1.173 | 1.270 |
| Case 3-1 | Case 3-2 | Case 3-3 | Case 3-4 | |||||
| 10 | 3.801 | 2.539 | 3.655 | 2.564 | 3.739 | 2.483 | 3.596 | 2.517 |
| 50 | 2.710 | 1.922 | 2.603 | 1.874 | 2.543 | 1.817 | 2.440 | 1.760 |
| 90 | 2.322 | 2.151 | 2.211 | 2.005 | 2.239 | 2.327 | 2.120 | 2.171 |
| Fault Location [%] | Peak-to-Peak Shaft Torque [MNm] | |||||||
|---|---|---|---|---|---|---|---|---|
| Case 2-1 | Case 2-2 | Case 2-3 | Case 2-4 | |||||
| S | R | S | R | S | R | S | R | |
| 10 | 0.535 | 0.324 | 0.535 | 0.324 | 0.540 | 0.321 | 0.540 | 0.321 |
| 50 | 0.277 | 0.205 | 0.277 | 0.205 | 0.287 | 0.208 | 0.287 | 0.208 |
| 90 | 0.213 | 0.202 | 0.213 | 0.202 | 0.228 | 0.233 | 0.228 | 0.233 |
| Case 4-1 | Case 4-2 | Case 4-3 | Case 4-4 | |||||
| 10 | 0.937 | 0.588 | 0.903 | 0.570 | 1.068 | 0.672 | 1.016 | 0.648 |
| 50 | 0.482 | 0.338 | 0.453 | 0.330 | 0.502 | 0.351 | 0.453 | 0.325 |
| 90 | 0.364 | 0.328 | 0.364 | 0.373 | 0.367 | 0.321 | 0.351 | 0.349 |
| Fault Location [%] | Peak-to-Peak Shaft Torque [MNm] | |||
|---|---|---|---|---|
| T/L #3 of 154 kV System | T/L #4 of 154 kV System | |||
| S | R | S | R | |
| 81% of T/L | 1.186 | 1.154 | 1.186 | 1.154 |
| 82% of T/L | 1.183 | 1.164 | 1.183 | 1.164 |
| 83% of T/L | 1.181 | 1.173 | 1.181 | 1.173 |
| 84% of T/L | 1.179 | 1.183 | 1.179 | 1.183 |
| 85% of T/L | 1.178 | 1.194 | 1.178 | 1.194 |
| T/L #6 of 345 kV System | T/L #8 of 345 kV System | |||
| 85% of T/L | 2.224 | 2.161 | 2.114 | 2.013 |
| 86% of T/L | 2.226 | 2.192 | 2.114 | 2.041 |
| 87% of T/L | 2.229 | 2.223 | 2.116 | 2.070 |
| 88% of T/L | 2.231 | 2.255 | 2.116 | 2.103 |
| 89% of T/L | 2.234 | 2.289 | 2.117 | 2.137 |
| Case | Fault Type | Transmission Line and “” | Fault Location [%] | |
|---|---|---|---|---|
| 5 | 5-1 | 3-Phase Permanent Fault | T/L #3 of the 154 kV System “” = 84% | 10 |
| 5-2 | 83 | |||
| 5-3 | 84 | |||
| 5-4 | 90 | |||
| 6 | 6-1 | 3-Phase Permanent Fault | T/L #6 of the 345 kV System “” = 88% | 10 |
| 6-2 | 87 | |||
| 6-3 | 88 | |||
| 6-4 | 90 | |||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cho, G.-J.; Park, J.-K.; Sohn, S.-H.; Chung, S.-J.; Gwon, G.-H.; Oh, Y.-S.; Kim, C.-H. Development of a Leader-End Reclosing Algorithm Considering Turbine-Generator Shaft Torque. Energies 2017, 10, 622. https://doi.org/10.3390/en10050622
Cho G-J, Park J-K, Sohn S-H, Chung S-J, Gwon G-H, Oh Y-S, Kim C-H. Development of a Leader-End Reclosing Algorithm Considering Turbine-Generator Shaft Torque. Energies. 2017; 10(5):622. https://doi.org/10.3390/en10050622
Chicago/Turabian StyleCho, Gyu-Jung, Ji-Kyung Park, Seung-Hyun Sohn, Se-Jin Chung, Gi-Hyeon Gwon, Yun-Sik Oh, and Chul-Hwan Kim. 2017. "Development of a Leader-End Reclosing Algorithm Considering Turbine-Generator Shaft Torque" Energies 10, no. 5: 622. https://doi.org/10.3390/en10050622
APA StyleCho, G.-J., Park, J.-K., Sohn, S.-H., Chung, S.-J., Gwon, G.-H., Oh, Y.-S., & Kim, C.-H. (2017). Development of a Leader-End Reclosing Algorithm Considering Turbine-Generator Shaft Torque. Energies, 10(5), 622. https://doi.org/10.3390/en10050622







