Presentation and Performance Evaluation of a Novel Stator-Permanent-Magnet Hybrid Stepping Motor

Abstract

In this paper, a new type of hybrid stepping motor (HSM) with permanent magnets (PMs) embedded in the stator, namely the stator-permanent-magnet hybrid stepping motor (SHSM), is presented. It has the same operation principles as the traditional HSM, with a 2-D distributed magnetic field nature and superiorities such as simpler rotor structure, easier PM cooling, higher torque and power density, and higher power grade. Its structural topology and operation principles are initially presented. Then an investigation on the performance comparison between the HSM and the SHSM, in terms of PM flux density, PM torque, detent torque, positional holding accuracy, stator core saturation issue, PM flux leakage, and PM utilization rate is carried out theoretically to make an assessment of the performance superiorities of the SHSM. A prototype of a 2-phase 8-pole 50-rotor-tooth SHSM is fabricated and experimentally compared with the HSM by using finite element analysis (FEA) to verify the motor’s operational feasibility and the theoretical analysis. The FEA and experimental results show that the proposed SHSM has performance advantages such as higher torque density, higher power grade, and higher pull-out torque, holding torque, and torque-speed property, although it has performance defects such as higher torque ripple and relatively lower positional holding accuracy in the open-loop operation than the conventional HSM. Consequently, this novel SHSM is more suitable for electromechanical energy conversion applications rather than positioning mechanisms, especially taking into account the open-loop control advantage.

1. Introduction

Stepping motors are typically classified into three categories: variable-reluctance (VR), permanent-magnet (PM), and hybrid (HSM). The HSM benefits merit its use over the PM and VR stepping motors. It can achieve small step sizes easily along with a simpler magnet structure, and requires less excitation to achieve a given torque, due to the utilization of PMs [1]. Therefore, it is quite suitable for high-precision and high-torque positioning applications, becoming so far the most widely used stepping motor type in automation applications. However, it still suffers from some defects mainly due to the rotor-permanent-magnet structure and the 3-D distributed magnetic field nature, which limits its performance improvement, capability enhancement, and therefore its further development. For example, the PM field has to travel vertically through core laminations and inter-lamination air-gaps to form a closed magnetic circuit [2], leading to a low utilization rate of the PM and core materials; Moreover, it is difficult to control the temperature rise of the rotor-PM, which increases the risk of irreversible demagnetization; Additionally, since the PM size is restricted by the rotor’s diameter, the multi-stack rotor and more than one PM should be adopted to supply an adequate PM field when the core stack length is long enough, which in turn complicates the motor’s structure and manufacture and lowers the mechanical robustness.

Historically, much work was done for the modeling, control, calculations, design, and analysis of the HSM. For example, Betin et al. [3] applied the fuzzy logic principle to the closed-loop control with feedback of a stepping motor drive. Tsui et al. [4] proposed a novel modeling approach and also the model-based damping algorithms for open-loop and servo control to eliminate the low-speed resonance and vibration. Matsui et al. [5] established the equivalent magnetic circuit of a two-phase HSM with permeances determined by the analytical method, based on which, the instantaneous torque was calculated and analyzed under the sinusoidal current drive. Stuebig et al. [6] presented a summative work on the comparison of calculation methods, i.e., the analytical method, the numerical method (mainly the finite element method (FEM)), and the combined analytical-numerical method for the HSM. In addition, Jenkins et al. [7] presented a design methodology for the HSM, taking into account the saturation throughout the motor and allowing for variations of the magnet working point. De Silva [8] developed two design equations for stepping motors in terms of equal and unequal stator and rotor tooth pitch. Rajagopal et al. [9] studied the design of optimal tooth-geometry for an HSM to satisfy specific performance requirements.

On the other hand, recent research interests are increasingly focused on motors with stator- permanent-magnet structures, such as doubly salient permanent magnet (DSPM) motors [10,11], flux reversal permanent magnet (FRPM) motors [12,13], and flux-switching permanent magnet (FSPM) motors [14,15]. Studies have shown that these motors have a lot of advantages, e.g., simpler rotor structure, easier PM heat dissipation, higher fault-tolerant ability, higher torque, power density, and efficiency, and so on [16,17]. Nevertheless, few studies related to breakthroughs in structures and topologies for stepping motors, especially the ones with the stator-permanent-magnet configuration, are available to the authors’ best knowledge, except for the two preliminary works published in [18,19] by the authors’ research group. In [18], basic structural characteristics of the stator-permanent-magnet hybrid stepping motor (SHSM) were presented, and the field-circuit coupled method was employed to compute the motor behavior; in [19], the general design of the SHSM was proposed based on the normalized analysis method and the motor’s 2-D distributed magnetic field nature.

In order to enhance the operating performance of the HSM, and eliminate the defects of its rotor-PM construction, a novel structure of HSM with PMs embedded in the stator, namely the SHSM, is proposed. In this paper, a comprehensive description of the proposed SHSM, in terms of structural equivalent transformation, topologies, operational principle, and performance superiorities is initially presented. Then a thorough investigation on performance comparison between the novel SHSM and the normal HSM, such as PM flux density, PM torque, detent torque, positional holding accuracy, stator core saturation issue, PM grade, PM flux leakage, and PM utilization rate is carried out theoretically to make a reasonable performance assessment of the SHSM. A prototype of the 2-phase 8-pole 50-rotor-tooth SHSM has been fabricated for the experiments, with corresponding simulation models built and calculated by using finite element analysis (FEA), in order to verify the validity of the theoretical analysis and to evaluate the operation performance of the proposed SHSM.

2. Description of the SHSM

2.1. Structural Equivalent Transformation

Figure 1a shows the configuration of the most commonly used 2-phase 8-pole 50-rotor-tooth HSM, in which concentrated windings are adopted, two identical rotor stacks are displaced axially along the rotor and staggered in angle by one-half the rotor tooth pitch, while the stator pole structure is continuous along the length of the rotor. Unlike the multi-stack VR stepping motor, in the HSM, the two rotor stacks are separated by an axially magnetized PM. As a result, one end of the rotor can be considered as a north magnetic pole and the other end as a south magnetic pole. In addition, the motor configuration with multiple PMs and rotor stacks is generally adopted for an increased stator core length [20], as shown in Figure 1b, in order to improve the torque producing ability.

An equivalent transformation from the normal HSM to the novel SHSM is shown in Figure 2. Figure 2a,b show the schematic end view of the HSM. By symmetry, Figure 2a can be divided into two identical parts, i.e., I = II, so for Figure 2b III = IV. Supposing the rotor in Figure 2b rotates one-half a tooth pitch, and simultaneously all the stator windings are inversely supplied, then Figure 2c can be obtained. It can be seen that Figure 2c is exactly equivalent to Figure 2b, and that it can be identically divided into two parts, i.e., V = VI. Interestingly, Figure 2a has the same rotor position as that of Figure 2c. It is suitable to select one part of each, e.g., part I and part VI, and assemble them together to constitute a novel motor structure, in which the polarities of both the stator and rotor poles can be produced by using two PMs symmetrically embedded in the stator yoke and magnetized in the opposite direction, as shown in Figure 2d; thus, the novel SHSM is finally obtained. It should be emphasized that the saturated magnetic bridge shown in Figure 2d is usually adopted to keep the stator lamination sheets in one piece and solve problems in series manufacturing while maintaining the very small desired air-gap, and that the width of the magnetic bridge is designed to be as small as possible to reduce the PM flux leakage.

2.2. Topologies and Operational Principle

Multiple motor topologies are available to the SHSM, due to various combinations of the stator, rotor teeth, and stator PMs. Figure 3 shows two typical combinations for analysis.

Supposing that m is the number of phases, p is the number of stator poles per phase, n is the number of PMs, and Z_r is the number of rotor teeth, the motor topologies can be expressed as follows:

• For topology 1, p must be a multiple of 4, n = p/2, and,

  $$k\frac{360}{Z_r}\pm j\frac{360}{2m{Z}_r}=\frac{360}{mp},j\le m$$

  (1)

  $$Z_r=p(km\pm \frac{j}{2}),j\le m$$

  (2)
• For topology 2, p must be an even number and m ≥ 3, n = p, and,

  $$k\frac{360}{Z_r}\pm j\frac{360}{m{Z}_r}=\frac{360}{mp},j\le m$$

  (3)

  $$Z_r=p(km\pm j),j\le m$$

  (4)

where k and j are positive integers which include the motor topologies in [18,19].

The proposed SHSM has the same operational principle as that of the HSM, due to structure equivalent transformation. Figure 4 shows the theoretical waveforms of the PM flux ψ_pm and current i of one phase with respect to the rotor position θ (electrical angle), and,

$${\mathsf{\psi }}_{pm}=\frac{1}{2}[({\mathsf{\psi }}_{\max }+{\mathsf{\psi }}_{\min })-({\mathsf{\psi }}_{\max }-{\mathsf{\psi }}_{\min })\cos \theta ]$$

(5)

$$i=I_m\cos (\theta +\delta )$$

(6)

where I_m is the amplitude of the phase current, and δ is the torque angle [19].

The energy stored in the magnetic field can be expressed as

$$W_f=W_{pm}+W_w=W_{pm}+\frac{1}{2}{I}^{\mathrm{T}}LI$$

(7)

where W_pm is the PM energy, W_w is the winding energy at I, I = [i_a, i_b,..., i_m]^T is the matrix of phase currents, and L = [L_xy] (x = a, b,..., m; y = a, b,..., m) is the matrix of phase inductances. By employing the coenergy method, the expression of the total torque T is obtained as [5,21]

$$T=\frac{\partial (I^{\mathrm{T}}\mathsf{\psi }-W_f)}{\partial \theta }{Z}_r=(I^{\mathrm{T}}\frac{\mathrm{d}{\mathsf{\psi }}_{pm}}{\mathrm{d}\theta }+\frac{1}{2}{I}^{\mathrm{T}}\frac{\partial L}{\partial \theta }I-\frac{\mathrm{d}{W}_{pm}}{\mathrm{d}\theta })Z_r=T_{pm}+T_r-T_{cog}$$

(8)

in which ψ = LI + ψ_pm is the matrix of total fluxes produced by the phase currents and PMs, ψ_pm = [ψ_pma, ψ_pmb, , ψ_pmm]^T is the matrix of the PM fluxes, T_pm is the PM torque component due to the interaction between the phase current and the PM flux, T_r is the reluctance torque component due to the variation of inductances, and T_cog is the cogging torque (detent torque) due to the variation of the PM energy with respect to the rotor position. According to Equations (5)–(8), T_pm can be derived when the m phases are energized with sinusoidal currents as

$$T_{pm}=\frac{m}{4}{Z}_r{I}_m({\mathsf{\psi }}_{\max }-{\mathsf{\psi }}_{\min })\sin \delta =\frac{m}{4}{Z}_r{I}_m\Delta {\mathsf{\psi }}_{pm}\sin \delta$$

(9)

2.3. Performance Superiorities

Compared to the conventional HSM, the novel SHSM with structure innovation has advantages in following aspects:

• PMs are embedded in the stator yoke, and a single-stack rotor is merely required, thus the manufacturing difficulties and costs are reduced.
• The PM magnetic circuit is located in the radial-circumferential plane, which eliminates the defects that the PM flux has to go vertically through, such as the core laminations and inter-lamination air-gaps [2]. As a result, the utilization rate of PMs and core materials is improved, which increases the output torque and power for the given current.
• The axial length of the motor can be chosen at any range since the number of core laminations has nothing to do with the utilization rate of the PMs, hence the motor’s power grade can be easily enhanced by simply increasing the core stack length.
• It is easier to realize the heat dissipation of the PMs which are embedded in the stator, such as the protection of the PMs [16].
• The PM and current magnetic field are coupled in the same radial-circumferential plane. A 2-D distribution of electromagnetic field can thus be considered for the motor design and analysis assuming a negligible end effect, which proves to be time-saving and features high accuracy.

All the above advantages make it possible to not only be applied in the high-precision positioning systems like an HSM, but also in the high-power electromechanical energy conversion areas like a DSPM motor. Moreover, when taking into account the open-loop control advantage for the motor-drive system, the novel SHSM will have a favorable position in competitions with other types of motor.

3. Performance Comparison between HSM and SHSM

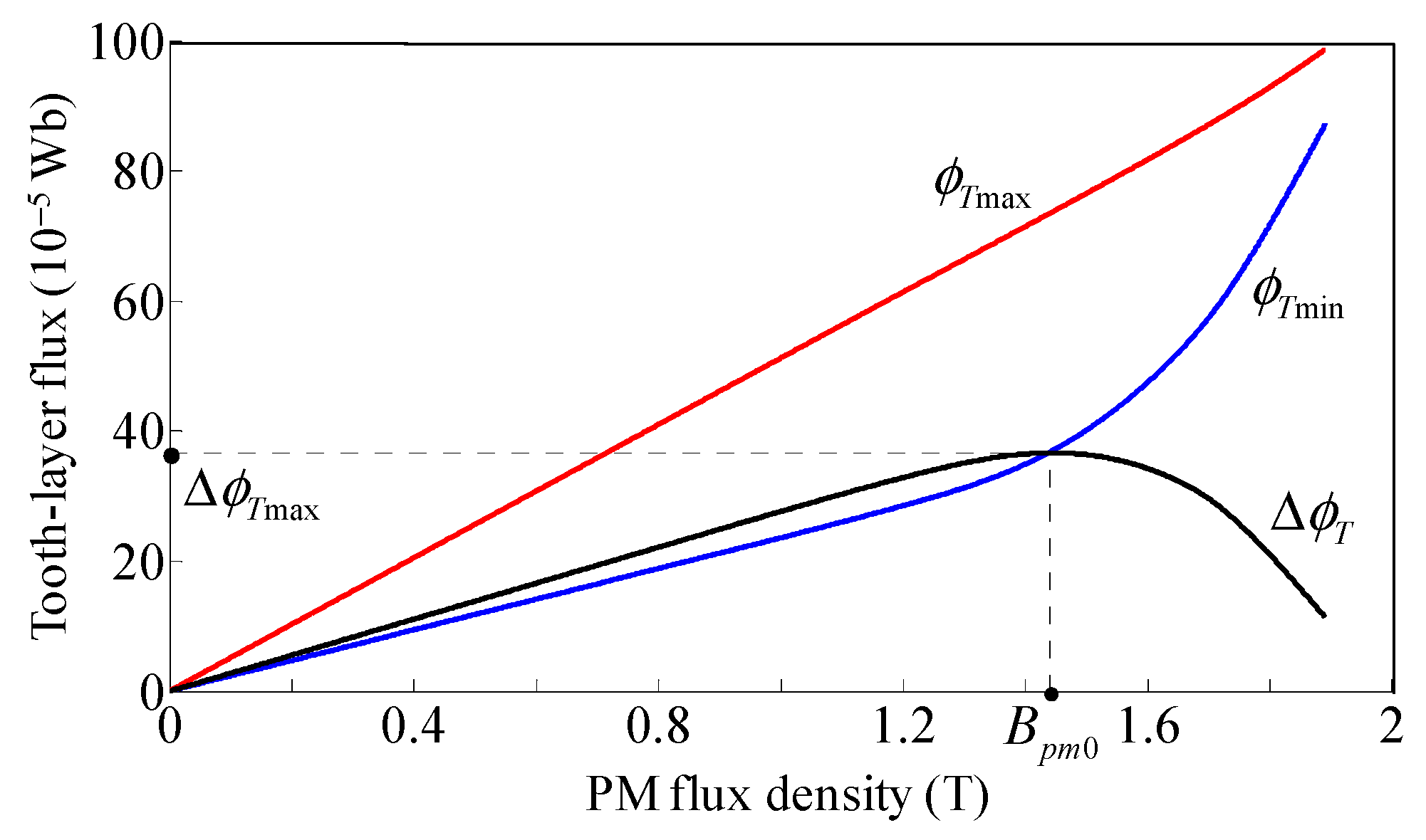
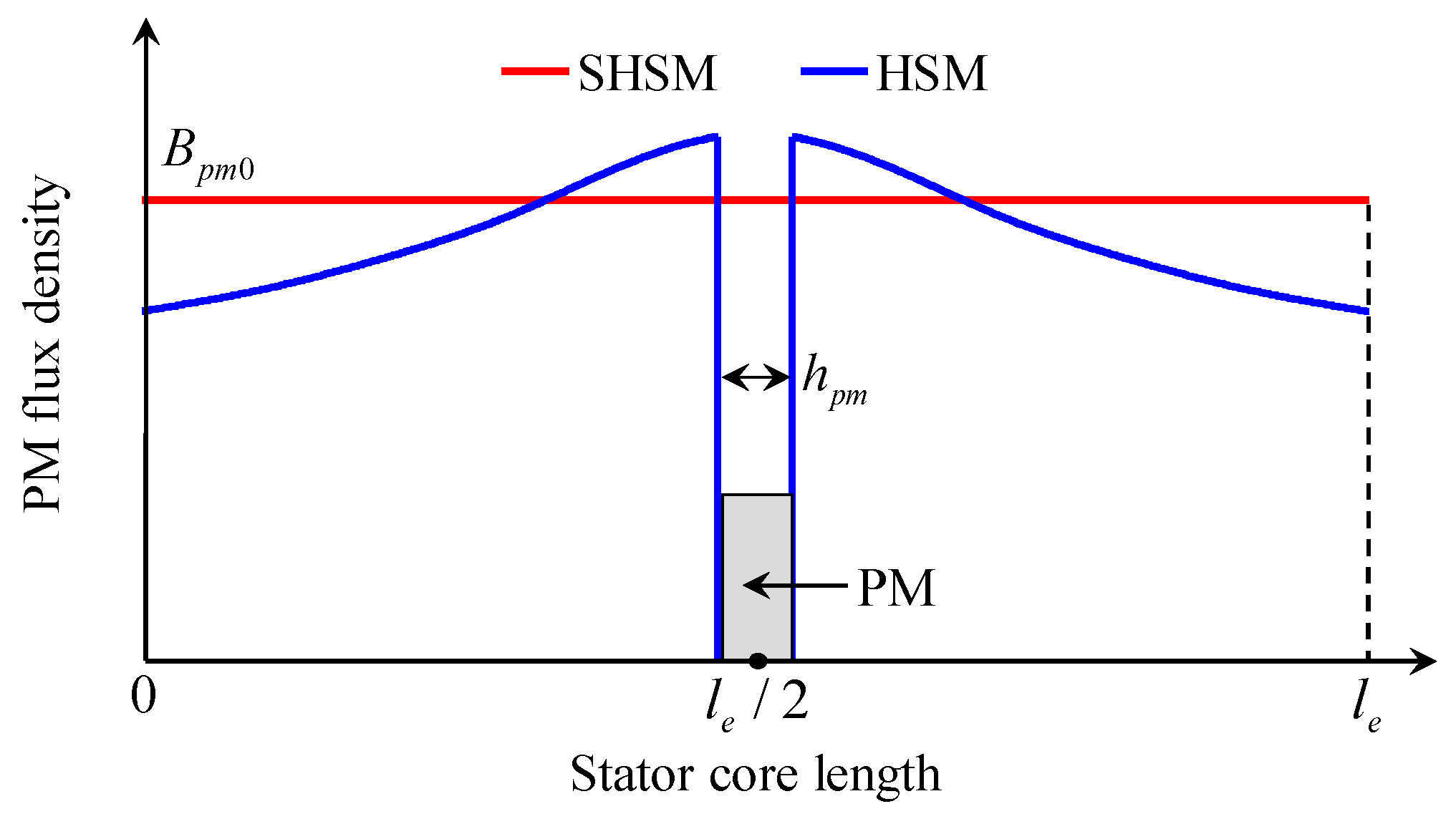
3.1. PM Flux Density

Based on the operational principle of the HSM and the SHSM, the PM torque T_pm is proportional to ∆ψ_pm once the motor structure and current excitation are determined, and ∆ψ_pm can be derived as

$$\Delta {\mathsf{\psi }}_{pm}=N_{ph}{Z}_s\Delta {\varphi }_T=N_{ph}{Z}_s({\varphi }_{T\max }-{\varphi }_{T\min })$$

(10)

where N_ph is the phase winding turns, Z_s is the stator teeth per stator pole, and ϕ_Tmax and ϕ_Tmin represent the tooth-layer PM flux at the tooth-tooth position and tooth-gap position, respectively. Figure 5 shows the relationships of ∆ϕ_T, ϕ_Tmax, and ϕ_Tmin with respect to the air-gap PM flux density B_pm obtained by 2-D FEA, in which t is the tooth width, g is the air-gap length, and λ is the tooth pitch. It can be found that ∆ϕ_T reaches its maximum value ∆ϕ_Tmax when B_pm = B_pm0, signifying the maximum PM torque according to Equations (9) and (10), and B_pm0 can thus be defined as the optimal PM flux density.

In terms of [2,18], the axial distribution of B_pm along the stator core length in the HSM (with single PM and two rotor stacks) is non-uniform and would take the form of Figure 6, where h_pm is the PM height in the magnetizing direction, taking into account the inter-lamination air-gaps. On the contrary, the axial distribution of B_pm along the stator core length is uniform in the SHSM, which can be designed as B_pm0 by using 2-D FEA or even the more accurate 3-D FEA.

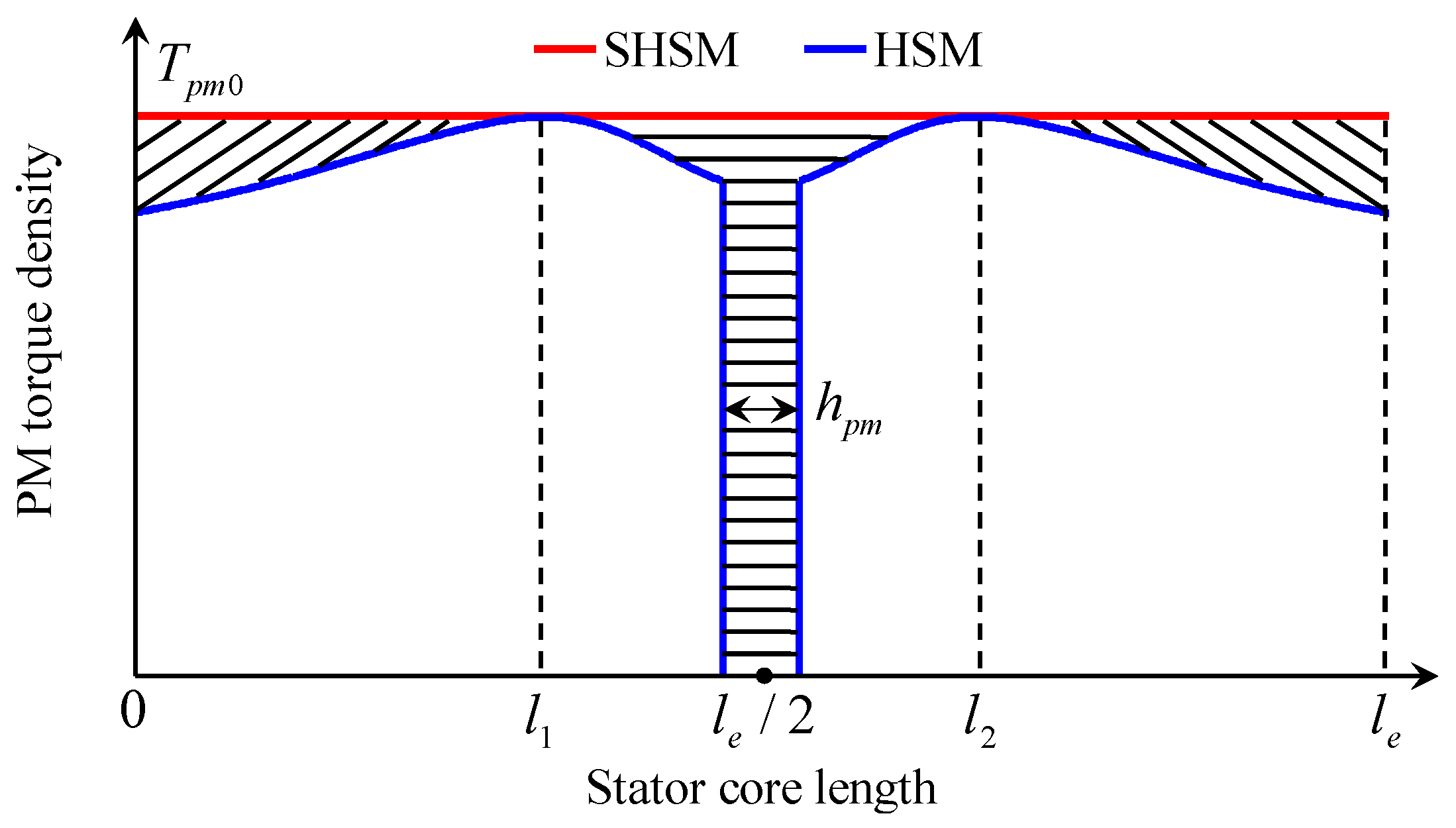
3.2. PM Torque

According to Figure 6, the optimal stator core length, corresponding to B_pm0 and the maximum T_pm, can be chosen at any range in the SHSM. Nevertheless, the situation is more complex when it comes to the HSM. For convenience, the simplest configuration of HSM, one with a single PM and two rotor stacks, is taken into account and analyzed. As shown in Figure 1, the PM surface area S_pm is restricted by the inner and outer rotor diameter, resulting in limited PM flux. As a result, there exists an optimal stator core length l_e0 corresponding to the maximum S_pm and T_pm, which can be determined by using 3-D FEA, taking into account the inter-lamination air-gaps, the saturation effect, and the end effect.

Figure 7 shows the axial distribution of the PM torque density of the two motors based on Figure 6, in which T_pm0 represents the maximum PM torque of the unit stator core length (1 m) corresponding to the optimal PM flux density B_pm0, l₁ and l₂ represent the axial position where the PM flux density of the two motors are the same, and the shaded area represents the torque losses of the HSM compared to the SHSM.

Supposing that l_e is the actual stator core length, according to the axial distribution characteristics of PM flux density and PM torque density shown in Figure 6 and Figure 7, the PM torque comparison between the HSM and the SHSM is carried out in three cases:

• l_e ≤ l_e0/2. B_pm is almost uniformly distributed in the HSM, and S_pm can be suitably selected to make B_pm = B_pm0, thus the torque density ratio of the two motors is ρ = (l_e − h_pm)/l_e.
• l_e0/2 < l_e ≤ l_e0. B_pm is non-uniformly distributed in the HSM, and S_pm can be suitably selected to make the average value of B_pm equal to B_pm0, thus ρ = (l_e − S_s/T_pm0)/l_e, where S_s is the shaded area as shown in Figure 7.
• l_e > l_e0. Multiple PMs and rotor stacks can be used in the HSM to improve the torque producing capability. Supposing that N_pm is the number of PMs, ρ can be determined by either case1 as ρ = (l_e − N_pmh_pm)/l_e when l_e/N_pm ≤ l_e0/2 or case2 as ρ = (l_e − N_pmS_s/T_pm0)/l_e when l_e0/2 < l_e/N_pm ≤ l_e0.

Consequently, the SHSM benefits from the advantages of higher output torque (power) density than the HSM, no matter what the motor’s configuration and stack length is.

3.3. Stator Core Saturation Issue

The 2-D electromagnetic field distribution can bring the advantage of higher torque density to the SHSM as analyzed above. However, it will inevitably cause the additional saturation issue of the stator core compared with the HSM, due to the different magnetic field distribution characteristics of the two motors. The magnetic field analysis in terms of the stator pole and stator yoke of the two motors is carried out, taking the 2-phase 8-pole 50-rotor-tooth motor configuration, as shown in Figure 8. The stator pole and yoke region under investigation and the positive direction of magnetic flux are shown in Figure 8a,b. Moreover, the simplified equivalent magnetic circuits corresponding to half of the HSM in Figure 8a and the whole SHSM in Figure 8b are built [18], as shown in Figure 9.

The parameters are defined as follows: ϕ_p is the total magnetic flux passing the stator pole; ϕ_ys is the total magnetic flux passing the stator yoke; F_a = N_pi_a and F_b = N_pi_b are the magnetomotive force (MMF) sources of the winding currents, where N_p is the winding turns per stator pole; F_pm is the MMF source of the PM; F_δ is the air-gap MMF drop of the PM; Λ_pm and Λ_σ are the main and leakage permeance of the PM; and Λ_a, Λ_b, Λ_a−, and Λ_b− are the parallel tooth-layer permeances at different stator poles.

The magnetic circuits show in Figure 9 can be solved according to the derivation process in Appendix A, and the ϕ_p and ϕ_ys are given as

$$\{\begin{array}{l}{\varphi }_{p,\mathrm{HSM}}=Z_s{l}_e{F}_{\delta }{\Lambda }_{t1}\cos \theta +Z_s{l}_e{{\rm N}}_p{{\rm I}}_m{\Lambda }_{t0}\cos (\theta +\delta )\\ {\varphi }_{p,\mathrm{SHSM}}=Z_s{l}_e{F}_{\delta }({\Lambda }_{t0}+{\Lambda }_{t1}\cos \theta )+Z_s{l}_e{{\rm N}}_p{{\rm I}}_m({\Lambda }_{t0}+\frac{{\Lambda }_{t1}}{2}\cos \theta )\cos (\theta +\delta )\\ {\varphi }_{ys,\mathrm{HSM}}=\frac{Z_s{l}_e{F}_{\delta }{\Lambda }_{t1}}{2}(\sin \theta -\cos \theta )+\frac{Z_s{l}_e{{\rm N}}_p{{\rm I}}_m{\Lambda }_{t0}}{2}[\sin (\theta +\delta )-\cos (\theta +\delta )]\\ {\varphi }_{ys,\mathrm{SHSM}}=Z_s{l}_e{F}_{\delta }({\Lambda }_{t0}-{\Lambda }_{t1}\cos \theta )-Z_s{l}_e{{\rm N}}_p{{\rm I}}_m({\Lambda }_{t0}+\frac{{\Lambda }_{t1}}{2}\cos \theta )\cos (\theta +\delta )\end{array}$$

(11)

Assuming that the two motors have the same stator pole width w_p and minimum stator yoke thickness h_ys (as shown in Figure 8), the maximum flux density of the stator pole B_pmax and stator yoke B_ysmax can be determined according to Equation (11) and compared as

$$\frac{B_{p\max ,\mathrm{SHSM}}}{B_{p\max ,\mathrm{HSM}}}=1+\frac{F_{\delta }+\frac{c}{2}{{\rm N}}_p{{\rm I}}_m}{c{F}_{\delta }+{{\rm N}}_p{{\rm I}}_m},\frac{B_{ys\max ,\mathrm{SHSM}}}{B_{ys\max ,\mathrm{HSM}}}=\sqrt{2}\left[1+\frac{F_{\delta }(1-c)}{c{F}_{\delta }+{{\rm N}}_p{{\rm I}}_m}\right]$$

(12)

where c = Λ_t1/Λ_t0 can be determined in terms of [5], and c < 0.6 at the range of g/λ = 0.02–0.1. It indicates that the maximum flux density of the stator pole and yoke region of the SHSM is higher than that of the HSM, whether the phase windings are energized or not. In other words, the SHSM suffers higher stator core saturation than the HSM, which may influence the operation performance, e.g., reducing the maximum output torque to a certain extent.

3.4. Detent Torque and Positional Holding Accuracy

In the SHSM, any two stator poles separated by 180° are of inverse symmetry and have the same electromagnetic properties, as shown in Figure 8b. Moreover, the air-gap PM flux density of the stator poles nearer to the PMs is higher than that of the others, due to the shorter PM magnetic circuit. Therefore, the actual air-gap PM MMF drop of the stator poles nearer and farther from the PMs can be approximately determined as (F_δ + ∆F) and (F_δ − ∆F), where ∆F is the extra MMF drop considering the asymmetrical distribution of the PM magnetic circuit. As a result, the detent (cogging) torque of the HSM and the SHSM can be expressed according to the derivation in Appendix B as

$$\begin{array}{cc}\hfill T_{cog,\mathrm{HSM}}& =-4Z_s{Z}_r{l}_e{F}_{\delta }^2{\displaystyle \sum _{n=1}^{\infty }4n{\Lambda }_{t4n}\sin 4n\theta }\hfill \\ & \approx -16Z_s{Z}_r{l}_e{F}_{\delta }^2{\Lambda }_{t4}\sin 4\theta \hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill T_{cog,\mathrm{SHSM}}& =-4Z_s{Z}_r{l}_e\{F_{\delta }^2{\displaystyle \sum _{n=1}^{\infty }4n{\Lambda }_{t4n}}\sin 4n\theta +F_{\delta }\Delta F{\displaystyle \sum _{n=1}^{\infty }(2n-1){\Lambda }_{t(2n-1)}}[\sin (2n-1)\theta +{(-1)}^{n-1}\cos (2n-1)\theta ]\}\hfill \\ & \approx -16Z_s{Z}_r{l}_e{F}_{\delta }^2{\Lambda }_{t4}\sin 4\theta -4Z_s{Z}_r{l}_e{F}_{\delta }\Delta F{\Lambda }_{t1}(\sin \theta +\cos \theta )\hfill \end{array}$$

(14)

Accordingly, the maximum value of the detent torque of the two motors is compared as

$$\frac{T_{cog\max ,\mathrm{SHSM}}}{T_{cog\max ,\mathrm{HSM}}}\approx 1+\frac{\sqrt{2}\Delta F{\Lambda }_{t1}}{4F_{\delta }{\Lambda }_{t4}}$$

(15)

Since sinusoidal currents are employed for driving the motor, the drive must be based on the so-called micro-stepping principle [22]. In the open-loop operation, assuming that the ideal sinusoidal currents i_a = I_mcos (θ + δ), i_b = I_msin (θ + δ) are employed, the ideal micro-step angle is infinitesimal, and then the relationships with respect to the given rotor position θ, given load torque T_l, given torque angle δ, and actual rotor position θ’ can be derived in terms of Equations (8) and (9) as

$$T_l=T_{pm}(\delta )=T_{pm}(\Delta \theta +\delta )+T_r({\theta }^{\prime },\delta )+T_{cog}({\theta }^{\prime })$$

(16)

where ∆θ = θ’ − θ represents the positional holding accuracy, as schematically shown in Figure 10.

3.5. PM Grade, PM Flux Leakage, and PM Utilization Rate

As it is known, the temperature rise of magnets located on the stator is much easier to control than those located on the rotor [16]. Therefore, the requirements for temperature rise of PMs can be reduced in the SHSM. In addition, much more installation space is available for the PMs embedded in the stator yoke, especially for the motor configuration with more than two PMs. As a result, the PM width in the radial length and PM height in the magnetizing direction can be increased to achieve the same PM flux; that is to say, the utilized PM grade or cost would be reduced. Taking the 2-phase 16-pole 100-rotor-tooth SHSM for instance, its configurations with high-grade (high residual flux density B_r and high coercive force H_c) and low-grade PMs are schematically shown in Figure 11.

Unlike the DSPM motor [16], the saturated magnetic bridge (see Figure 2d) is usually adopted in the SHSM to keep the stator lamination complete and to solve problems in series manufacturing due to the small desired air-gap. Although the magnetic bridge works in highly saturated conditions, the relative permeability of the bridge is still higher than the PMs (nearly equal to air), which can be proved by the nonlinear FEA. As a result, it suffers from the defect of relatively high flux leakage of the PMs embedded in the stator of the SHSM, which would reduce the PMs’ utilization rate.

Comparison of the PM utilization rate between HSM and SHSM is analyzed by taking the 2-phase 8-pole 50-rotor-tooth configuration as a example. Figure 12 provides the simplified equivalent magnetic circuits for the PM, in which R_lam is the total reluctance of the core laminations along the axial direction taking into account the inter-lamination air-gaps, and supposing that ϕ_m and ϕ_σ are the main and leakage flux of the PM, and ϕ_δ is the air-gap flux. The magnetic leakage factor σ can be defined as σ = ϕ_m/ϕ_δ [23].

Assuming that R_pm, R_δ, and ϕ_δ of the two motors are designed to be the same [19], ϕ_m can be thus obtained as

$${\varphi }_{m,\mathrm{HSM}}=S_{pm,\mathrm{HSM}}{B}_r\frac{{\sigma }_{\mathrm{HSM}}{R}_{pm}}{2R_{\delta }+R_{lam}+{\sigma }_{\mathrm{HSM}}{R}_{pm}},{\varphi }_{m,\mathrm{SHSM}}=S_{pm,\mathrm{SHSM}}{B}_r\frac{{\sigma }_{\mathrm{SHSM}}{R}_{pm}}{2R_{\delta }+{\sigma }_{\mathrm{SHSM}}{R}_{pm}}$$

(17)

Moreover, R_pm can be expressed as R_pm = (H_ch_pm)/(B_rS_pm), thus the ratio of the total utilized PM volume of the two motors is derived as

$$\frac{V_{pm,\mathrm{SHSM}}}{V_{pm,\mathrm{HSM}}}=\frac{h_{pm,\mathrm{SHSM}}{S}_{pm,\mathrm{SHSM}}}{h_{pm,\mathrm{HSM}}{S}_{pm,\mathrm{HSM}}}={(\frac{2R_{\delta }+{\sigma }_{SHSM}{R}_{pm}}{2R_{\delta }+{\sigma }_{HSM}{R}_{pm}+R_{lam}})}^2$$

(18)

It indicates that the SHSM benefits from the advantage of the higher PM utilization rate and therefore PM volume-saving compared to the HSM under the condition that the PM leakage factor of the two motors is designed to be nearly the same.

4. Experimental and FEA Verification

To verify the operation feasibility and the theoretical analysis of the proposed SHSM, a 2-phase 8-pole 50-rotor-tooth prototype machine has been fabricated for experimentation as shown in Figure 13, and the associated nonlinear FEA has also been carried out. The detailed specifications and main design parameters of the prototype machine are listed in

Table 1. Design specifications of the prototype machine.

Parameters	Values	Parameters	Values
Rated power (W)	200	Outer diameter of stator(mm)	144
Rated speed (r/min)	600	Inner diameter of stator (mm)	63.5
Rated torque (N·m)	3.2	Air-gap length (mm)	0.25
Rated current (A)	3	Stack length (mm)	60
No. of phase turns	160	Tooth width (mm)	1.6
No. of stator poles	8	Tooth height (mm)	1.6
No. of stator pole-teeth	5	PM dimensions (mm3)	3 × 20 × 60
No. of rotor teeth	50	PM material	N35SH

.

4.1. Experiments

Figure 14 shows the calculated and measured waveform of the no-load back electromotive force (EMF). It can be found that the amplitude of the calculated one (about 24.5 V) is slightly greater than that of the measured one (about 22 V), mainly due to the fact that the motor’s end effect is neglected in the 2-D FEA. To take the end effect into account, the end coefficient k_end can be adopted to modify the calculated results [24], which can be determined as k_end = 0.9 according to the results in Figure 14.

The transient current can be derived as [18,24]

$$i(t)=I_0{e}^{\frac{-t(R+R_s+{\omega }_r\frac{dL}{d\theta })}{L}}+\frac{U_{\mathrm{DC}}-{\omega }_r\frac{d{\mathsf{\psi }}_{pm}}{d\theta }}{R+R_s+{\omega }_r\frac{dL}{d\theta }}(1-e^{\frac{-t(R+R_s+{\omega }_r\frac{dL}{d\theta })}{L}})$$

(19)

where R and L are respectively the winding resistance and inductance, R_s is the sampling resistance used for detecting the winding currents, and ω_r is the mechanical angular velocity, U_DC is the DC-bus voltage. Supposing that I_g is the given current amplitude and T_i = 2π/(Z_rω_r) is the current period time, in the initial state when the current i is established from I₀ = 0, the actual current amplitude I_m applied to the phase winding can be approximately expressed as

$$I_m=\{\begin{array}{ll}{I}_g,& i(\frac{T_i}{4})\ge I_g\\ \frac{U_{\mathrm{DC}}-k_E{\omega }_r}{R+R_s+k_L{\omega }_r}(1-e^{\frac{-T_i(R+R_s+k_L{\omega }_r)}{4L}}),& i(\frac{T_i}{4})<I_g\end{array}$$

(20)

where the coefficients k_E and k_L represent the amplitude of (dψ_pm/dθ) and (dL/dθ), respectively.

In the designed motor-drive system, the required parameters are measured: R = 1.2 Ω (at room temperature), L = 16.6 mH (in average), R_s = 0.5 Ω, U_DC = 300 V, and the given current amplitude is I_g = 4.2 A. Moreover, the values of k_E and k_L can be determined by 2-D FEA as k_E = 0.7 and k_L = 0.024. Both the calculated and measured current-speed characteristics of the prototype are shown in Figure 15a. It can be seen that the calculated result coincides well with the experimental one.

Based on the current-speed characteristic, the maximum pull-out torque at different speeds can be calculated by 2-D FEA. In addition, the torque-speed characteristic can be measured by adding maximum load to the prototype at different speeds via the MTS-II Motor Measurement System as shown in Figure 13d. Figure 15b shows the comparison of the calculated and measured torque-speed characteristics, supposing a negligible friction factor and taking into account the end effect. It can be seen that the calculation result can well predict the measured one, which is of significant importance in computing the motor’s dynamic performance.

4.2. FEA Results

To verify the theoretical analysis and evaluate the performance of the proposed SHSM, two comparative FEM models are established. One is the SHSM with the configuration shown in Figure 8b and the parameters shown in Table 1, apart from the fact that the stator outer diameter is changed to 125 mm and the PM radial length is changed to 34 mm, aimed to achieve the optimal PM flux density B_pm0. The other one is the HSM with the configuration shown in Figure 8a and the same dimensions as the SHSM except for the PM surface area. The two models have the same stator pole width w_p = 12 mm, stator yoke thickness h_ys = 12.5 mm, and the same stacking factor k_Fe = 0.95.

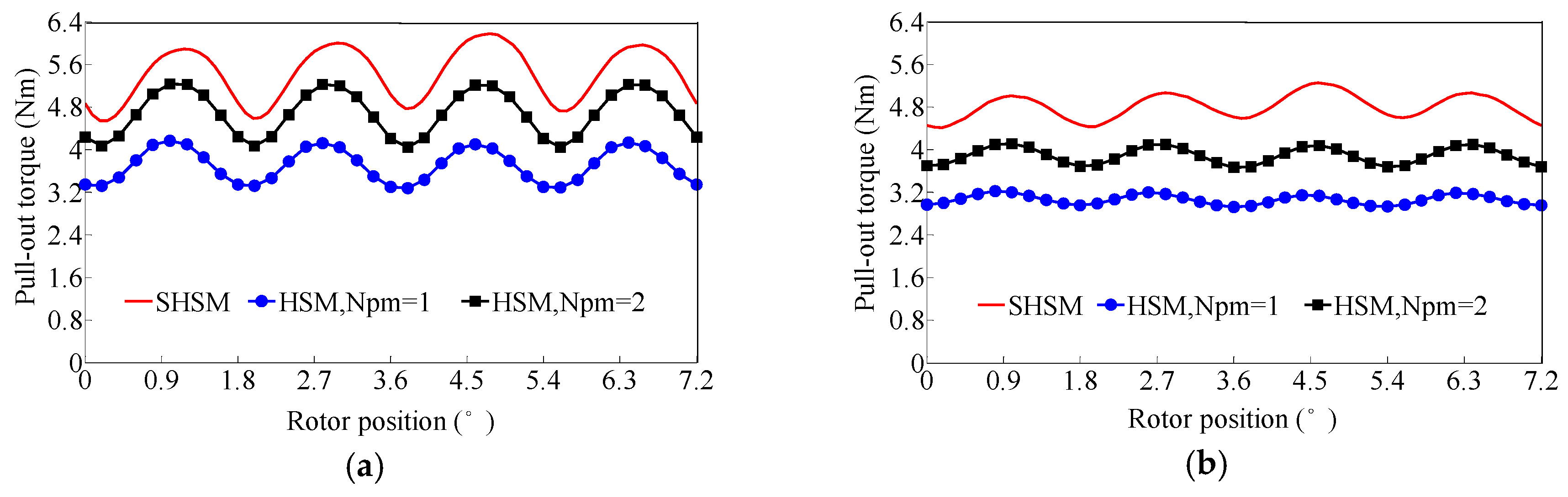
4.2.1. PM Flux Density and Pull-Out Torque

Figure 16 shows the comparison of the PM flux density characteristics, in which the calculation results of the HSM are obtained by 3-D FEA, whilst the optimal PM flux density B_pm0 = 1.4 T of the SHSM is determined by 2-D FEA. For N_pm = 1, the maximum PM surface area is selected, and the calculated results can well verify the theoretical analysis. For N_pm = 2, the PM surface area is adjusted to obtain the similar PM flux density characteristic to the SHSM.

Figure 17a shows the comparison of the pull-out torque under rated currents with δ = π/2. It can be seen that the average pull-out torque of the HSM reaches about 4.8 N·m when N_pm = 2, which is still lower than that of the SHSM of about 5.5 N·m. The FEA calculated pull-out torque density ratio is about ρ = 0.87, which coincides well with the theoretical one ρ = (l_e − N_pmh_pm)/l_e = 0.9. In addition, the unequal-tooth-pitch method [9] is usually adopted to reduce the torque ripples for stepping motors accordingly, and the pull-out torque calculation results with λ_s = 6.8° (stator tooth pitch) and λ_r = 7.2° (rotor tooth pitch) are shown in Figure 17b.

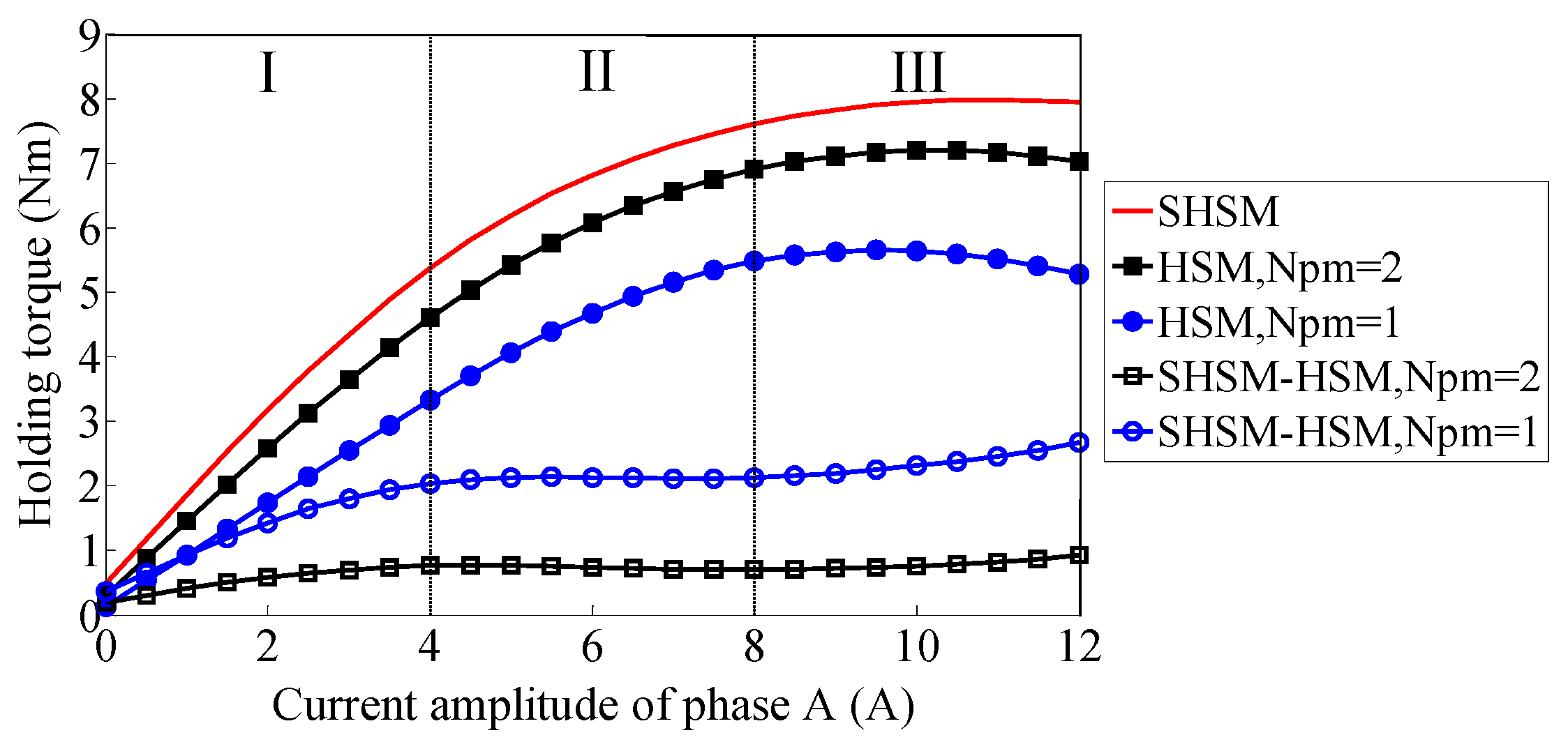
4.2.2. Stator Core Saturation and Holding Torque

Figure 18 shows the comparison of flux density in the stator pole and stator yoke region by using the analytical method and FEA. Λ_t0 and Λ_t1 in Equation (11) can be accurately determined as Λ_t0 = 8.1 × 10⁻⁶ (Wb/A) and Λ_t1 = 2.4 × 10⁻⁶ (Wb/A) by 2-D FEA [18,25], and F_δ = gB_pm0/µ₀ = 280 A. It can be seen that the analytical method can well predict the flux variation in the stator pole and yoke region, although some errors occur mainly due to the saturation effect.

The FEA results show that the stator core saturation level of the HSM is lower than that of the SHSM due to the existence of the axial PM magnetic circuit, which verifies the theoretical analysis. Further discussion should be carried out with regards to this flux density comparison. For the SHSM, the total magnetic flux generated by winding currents and PMs is distributed in the same radial-circumferential plane, and the calculated results can well reflect the actual stator core saturation level. Nevertheless, for the HSM, the flux is non-uniformly distributed in the stator pole and yoke region, due to the 3-D distributed PM field and the influence of inter-lamination air-gaps, thus the calculated results can only reflect the average stator core saturation level. To investigate the actual flux distribution characteristic of the HSM, and to reasonably evaluate the influence of the stator core saturation on the torque producing ability, much more research regarding the magnetic field calculations and analyses needs to be performed by using 2-D and 3-D FEA, which will be presented in future works.

In this work, a comparison of the holding torque is carried out under the most idealized situation, namely, the saturation effect of the stator core except for the stator tooth region which is neglected in the HSM, with the results shown in Figure 19. It can be found that the torque difference of the two models increases almost linearly in region I, due to the lower iron saturation. In region II, the torque difference is almost unchanged, due to the influence of the relatively higher stator core saturation of the SHSM. In region III, the holding torque hardly increases and even decreases due to the oversaturation of the tooth-layer (see Figure 5), whereas the torque difference rises again since the tooth-layer saturation level of the SHSM is lower than that of the HSM due to the high saturation of the stator pole and yoke.

4.2.3. Detent Torque and Positional Holding Accuracy

Figure 20 shows the comparison of detent torque (N_pm = 2 in the HSM) obtained by the analytical method and FEA. Λ_t4 and ∆F in Equations (13)–(15) are determined as Λ_t4 = 2.5 × 10⁻⁸ (Wb/A) and ∆F = 5 A by 2-D FEA. It can be seen that the detent torque of the SHSM is non-uniformly distributed in a tooth-pitch cycle and is slightly higher than that of the HSM due to the asymmetric distribution of the PM magnetic circuit, and the analytical calculation can well predict this variation, which verifies the theoretical analysis. In addition, the primary 4th harmonic torque component can be effectively reduced by using the unequal-tooth-pitch method.

Figure 21 shows the comparison of the positional holding accuracy obtained by FEA according to Equation (16). It can be seen that the positional holding accuracy (∆θ) of the SHSM is lower than that of the HSM due to the higher torque ripple, especially under the unequal-tooth-pitch situation. On the other hand, the ∆θ shown in Figure 21b can hardly be improved in the open-loop operation, since the ideal sinusoidal currents have been employed and the torque ripple can hardly be reduced. In other words, the micro-stepping driving mode reaches the highest positioning accuracy of about ∆θ = 0.11° (HSM) and ∆θ = 0.22° (SHSM) for the specific torque angle δ even with infinite subdivisions, due to the limitations of the motor structure and operation principle.

4.2.4. PM Flux Leakage and PM Utilization Rate

Figure 22 gives the PM flux leakage of the SHSM obtained by 2-D FEA. It can be seen that the leakage factor takes the value of σ = 1.1–1.16 at g = 0.1–0.25 mm without the magnetic bridge, which is much smaller than that of the DSPM motor [23] due to the very small desired air-gap. Moreover, it increases almost linearly with respect to the magnetic bridge thickness t_bge to about the same value of σ = 1.46 at t_bge = 3 mm. On the other hand, the utilized PM volume with g = 0.1 mm (which is the more general design case) is reduced significantly more than that with g = 0.25 mm due to the decrease of R_δ according to Equations (17) and (18), indicating a much higher PM utilization rate.

4.2.5. Mechanical Force Analysis

For the requirements of practical application, it is of high necessity to conduct the mechanical force analysis for the SHSM due to the asymmetrical excitation of the PM location. Taking the SHSM in Figure 8b for instance, any two stator poles separated in angle by 180° have the same tooth-tooth position, the same PM field intensity, and the same superimposed excitation by the PMs and winding currents. As a result, these two stator poles would suffer the mechanical force with same magnitude and opposite direction according to Equation (8), and therefore the motor’s resultant force is zero. Figure 23 shows the 2-D FEA calculation results, which verifies the theoretical analysis.

5. Conclusions

This paper presented a novel stator-permanent-magnet hybrid stepping motor (SHSM). Taking a comprehensive consideration of the theoretical analysis, FEA simulations, and experimental studies, the following conclusions can be obtained:

• The proposed SHSM has the same operational principle and control method as the traditional HSM, with superiorities such as simpler rotor structure, easier manufacturing and PM cooling, higher mechanical robustness, higher PM utilization rate, and higher torque, power density, and power grade.
• The proposed SHSM benefits from a 2-D distributed electromagnetic field nature, which simplifies the design, analysis, and calculations for this kind of machine with a relatively high accuracy and time-saving advantages.
• The proposed SHSM suffers from higher stator core saturation and higher detent torque and torque ripple compared with the HSM, since the total flux generated by the PMs and winding currents is distributed in the same radial-circumferential plane and is mutually superimposed, and the PM magnetic circuit is asymmetrically distributed with respect to the PMs, which may lead to a reduction of operation performance to certain extent.
• The proposed SHSM suffers from relatively lower positioning accuracy compared with the HSM, especially under the unequal-tooth-pitch situation, and therefore it is more suitable for electro-mechanical energy conversion applications rather than positioning mechanisms.