Investigation on the Development of a Sliding Mode Controller for Constant Power Loads in Microgrids
Abstract
:1. Introduction
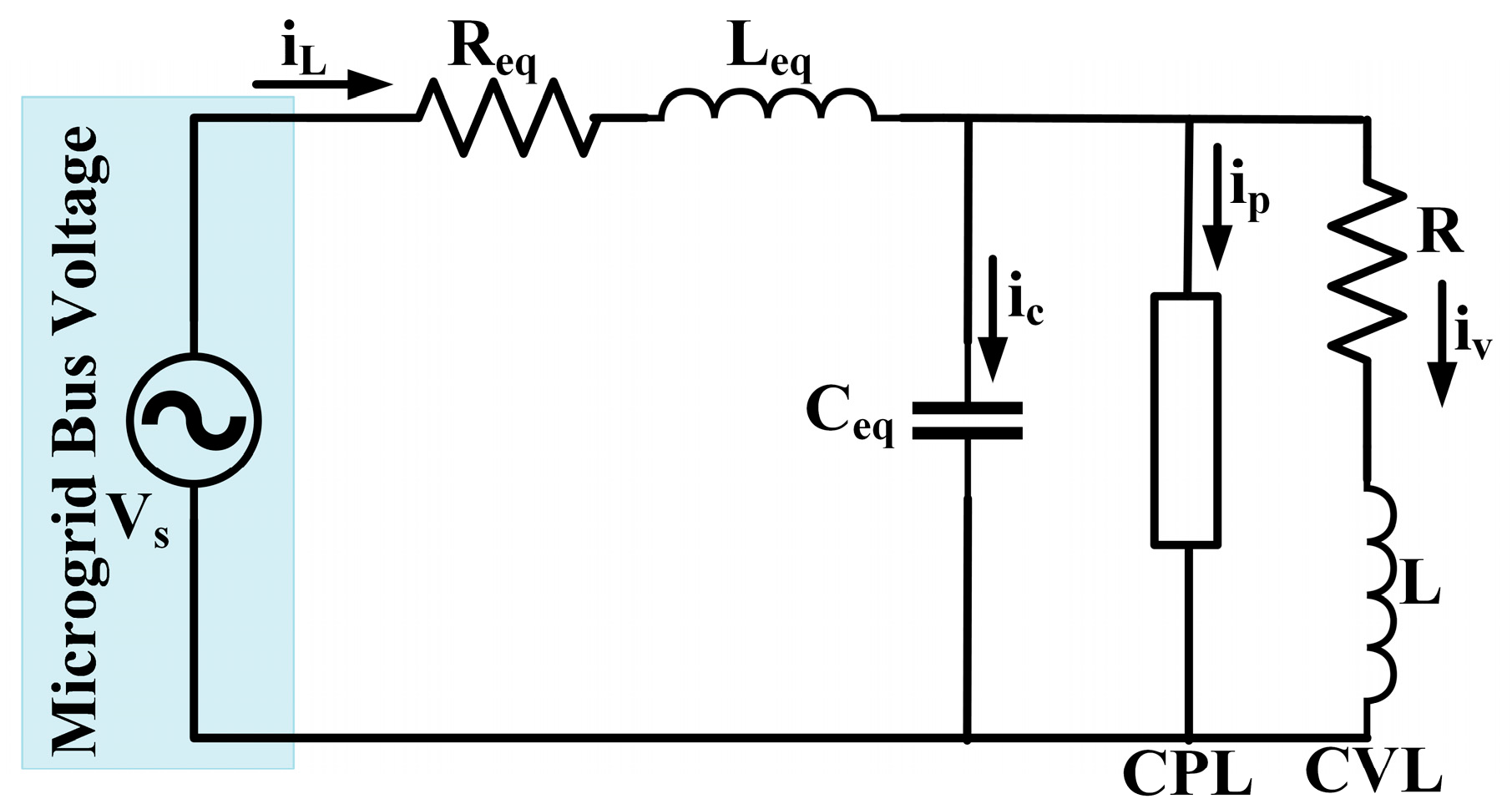
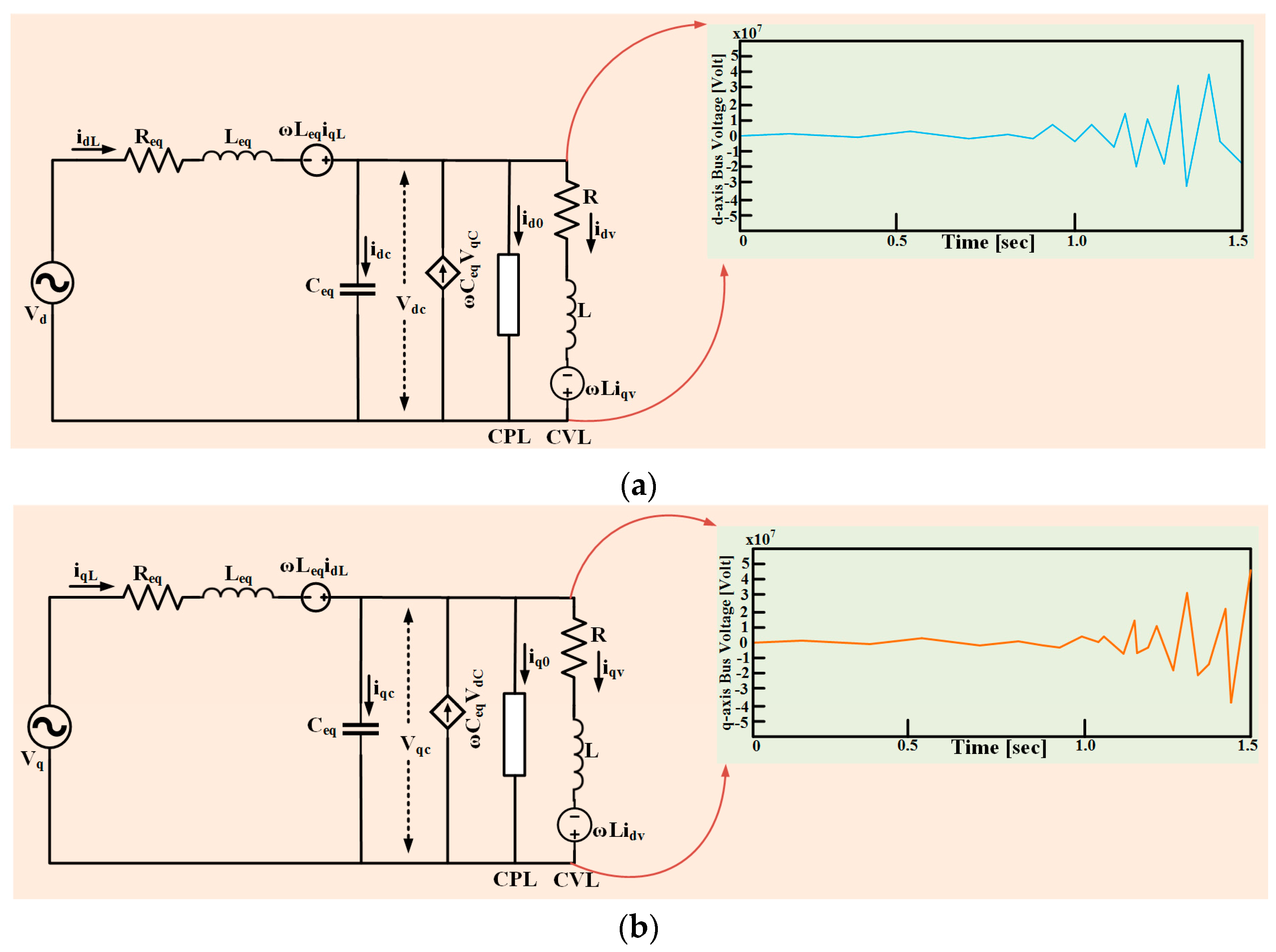
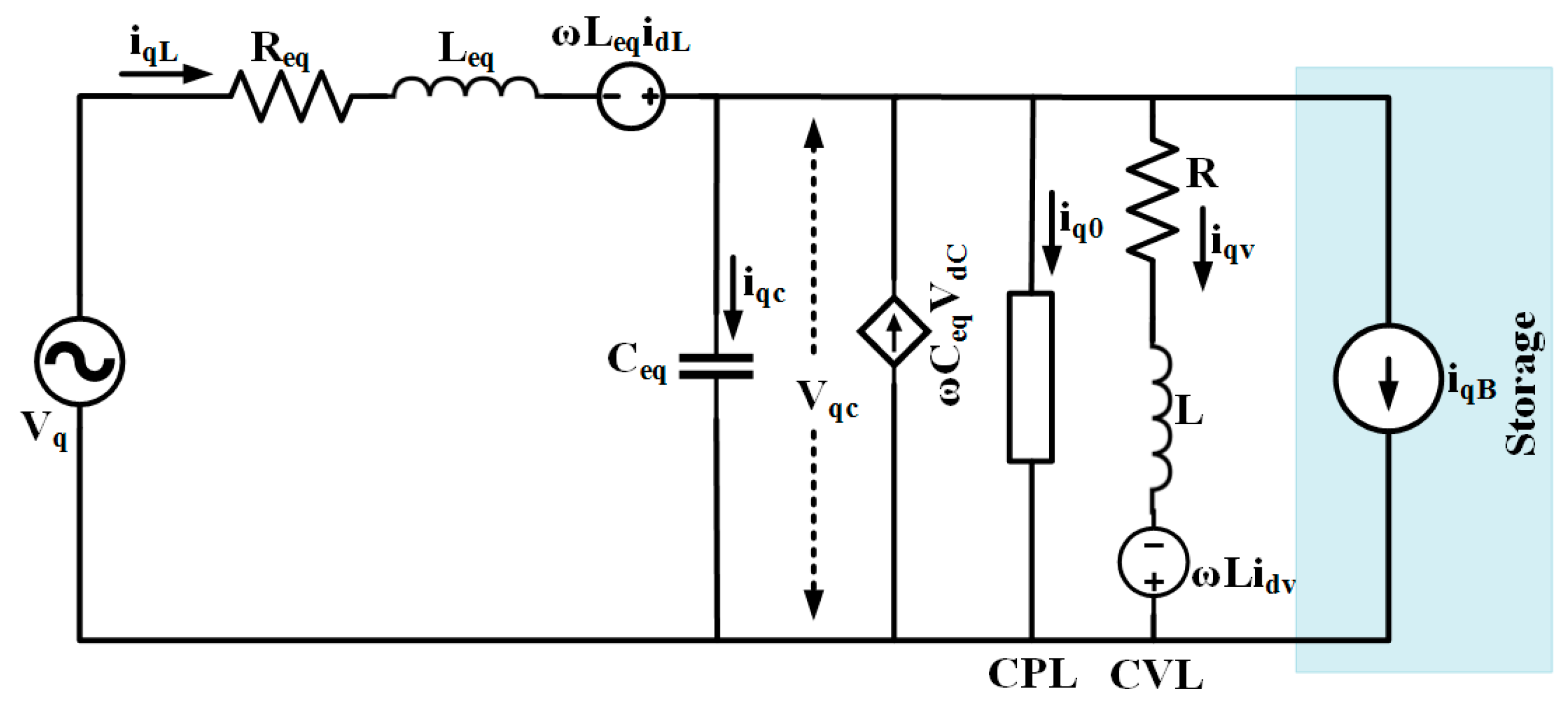
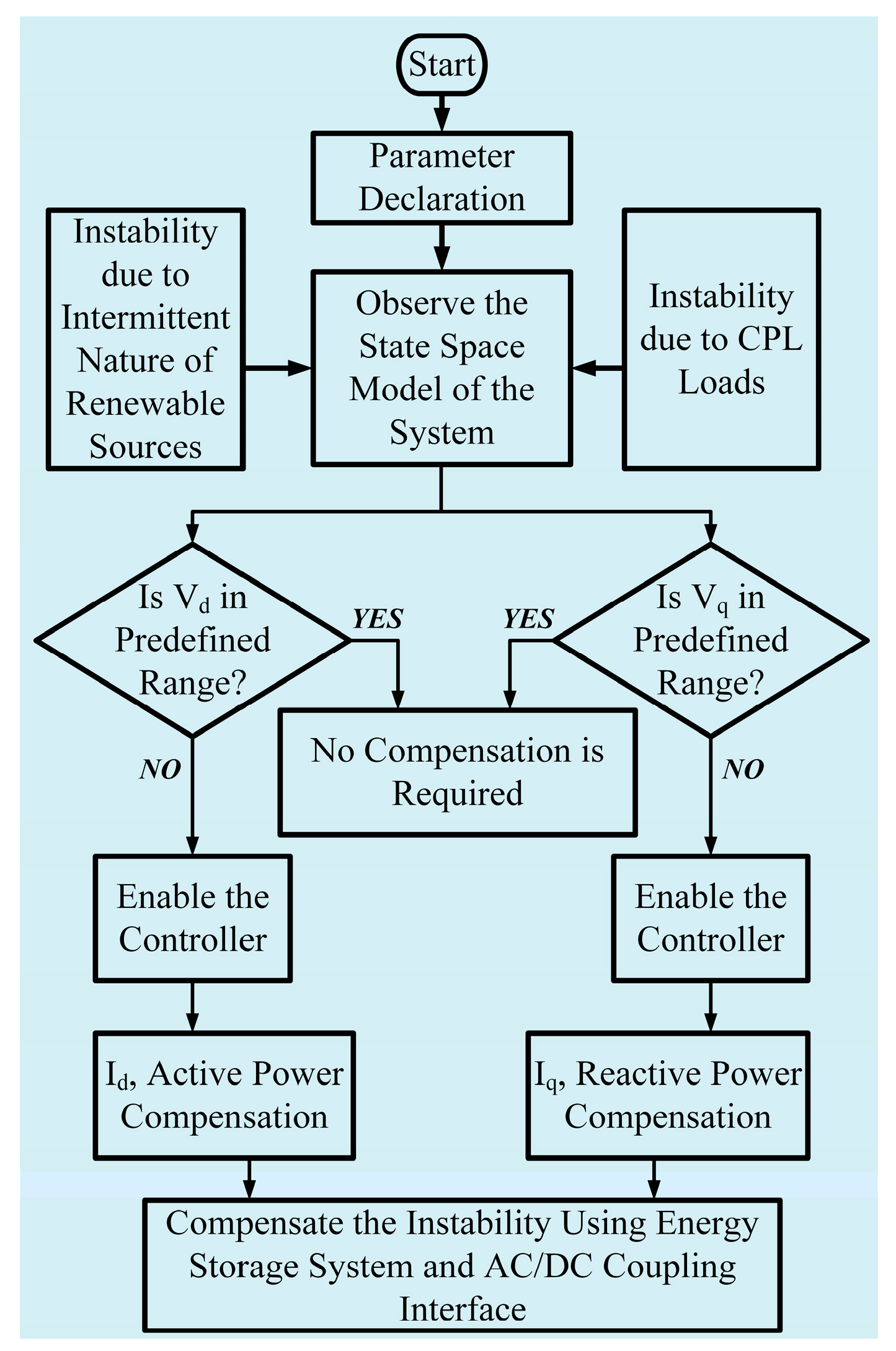
2. Modeling of Microgrid with CPL
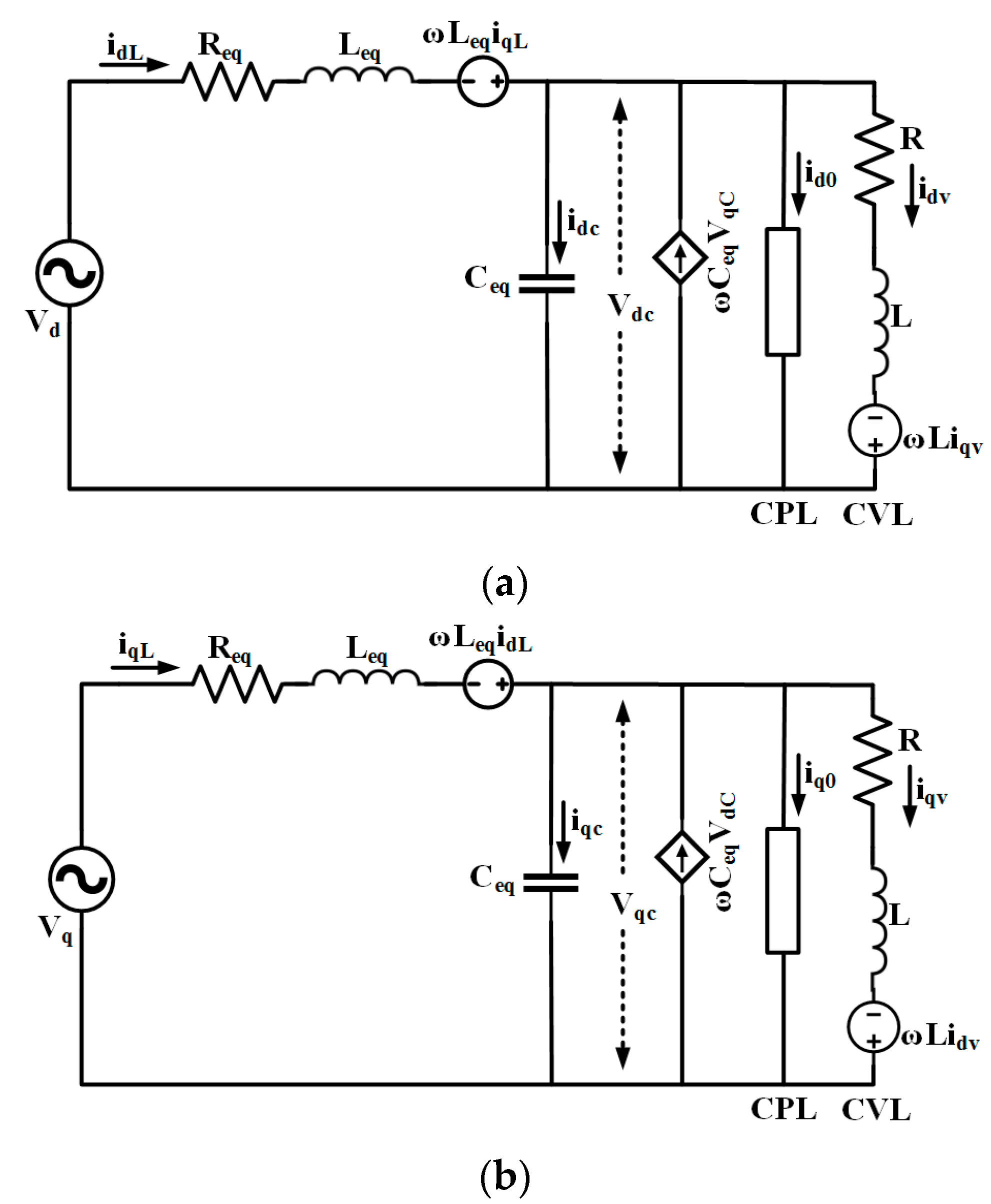
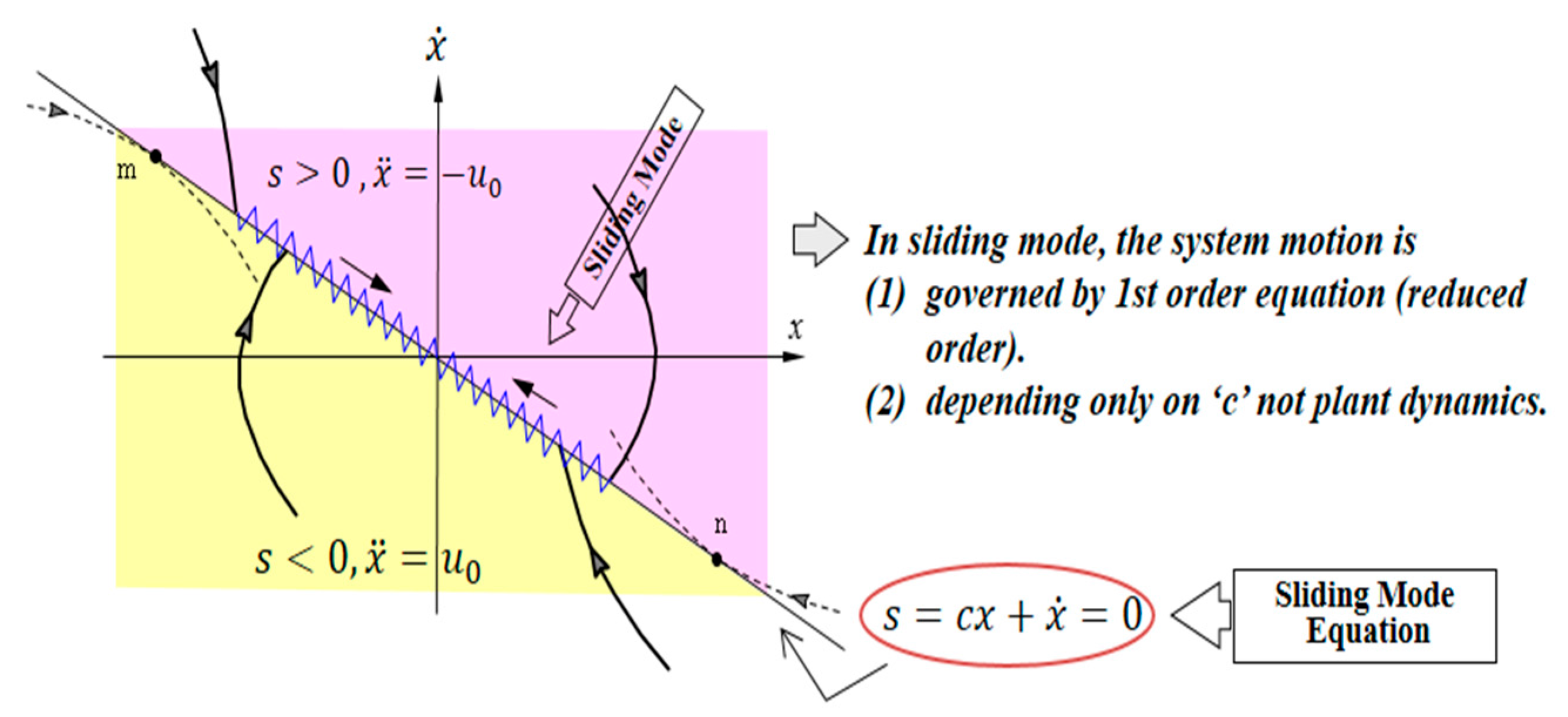
3. Sliding Mode Controller Design
- State trajectories are toward the switching line s = 0
- State trajectories cannot leave and belong to the switching line s = 0
- After sliding mode starts, further motion is governed by
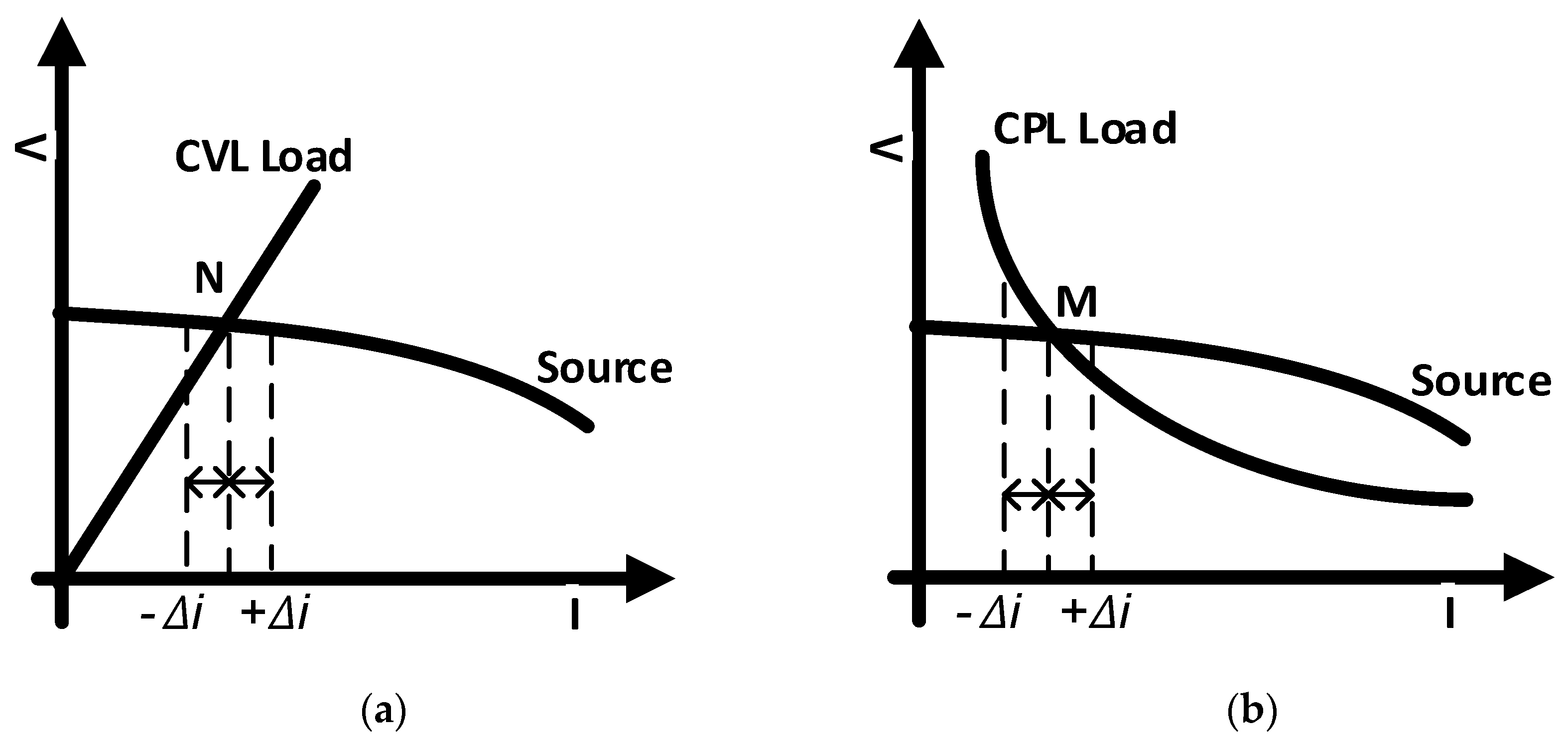
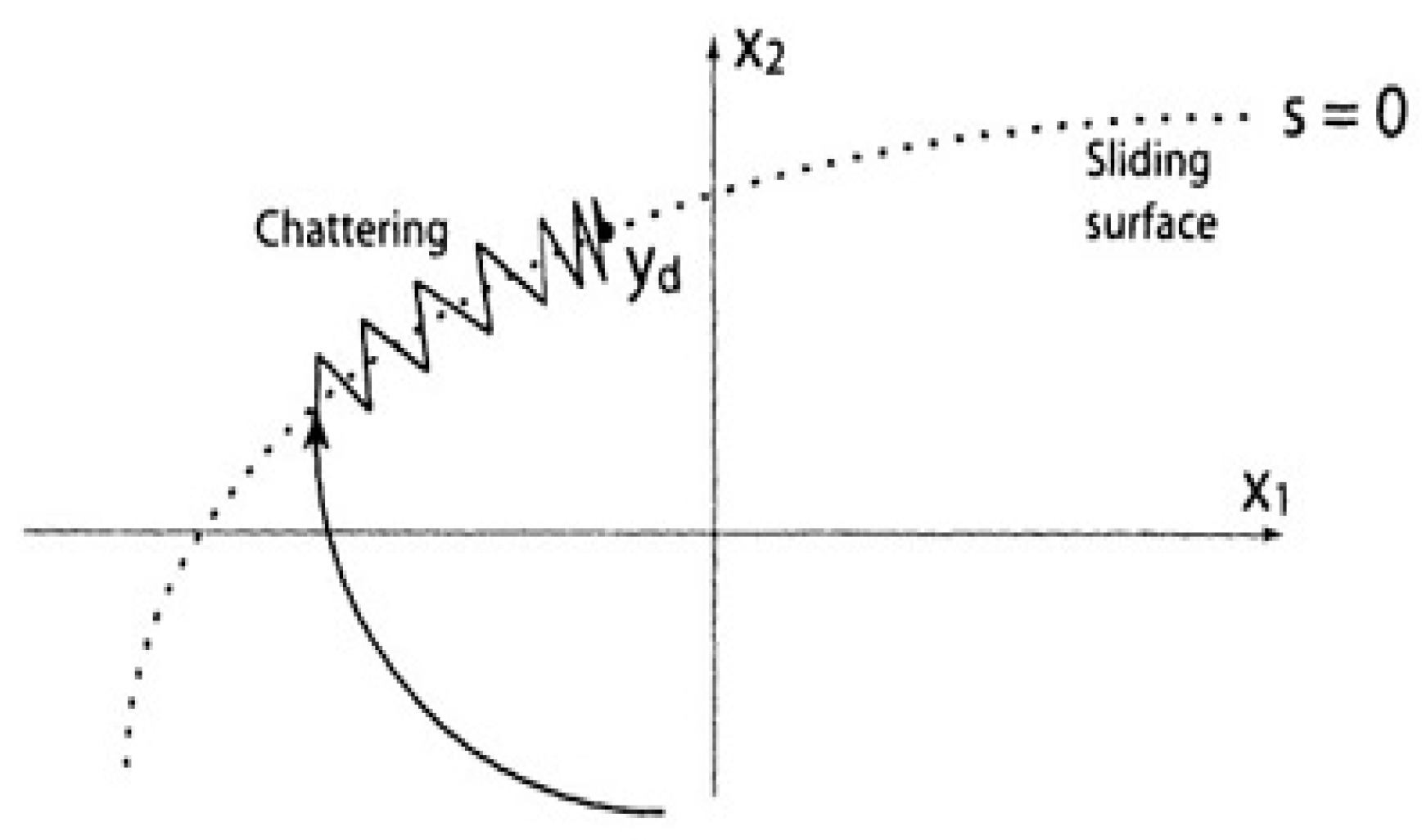
3.1. Chattering
3.2. Chattering Reduction
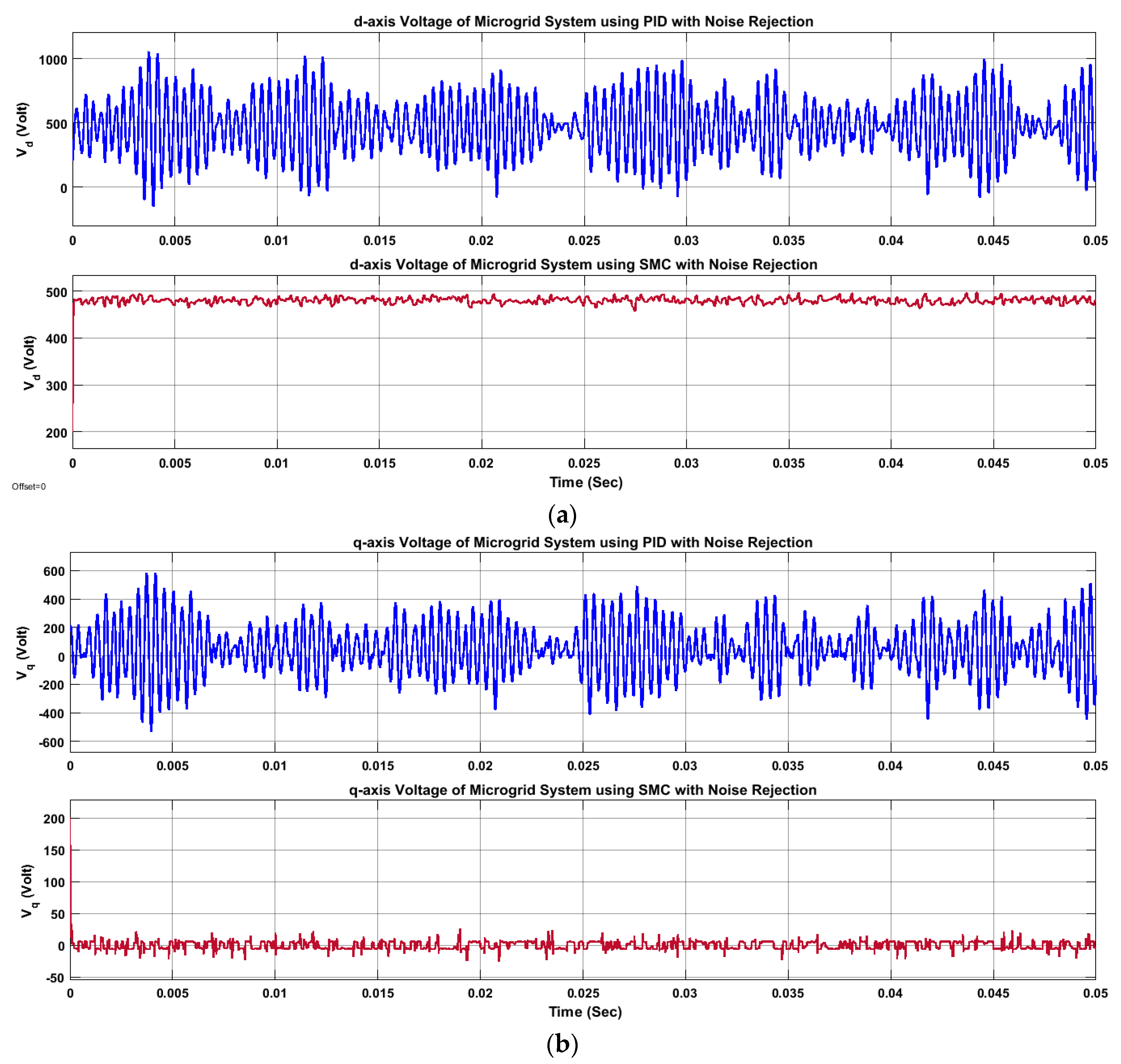
3.3. Selection of Sliding Mode Control over PID Control Technique
- Characteristically, the microgrid system is significantly nonlinear with time-varying parameters as well as system uncertainties. Hence, using PID control technique may hamper system stability due to the possible overlinearization of the system. On the other hand, an SMC controller doesn’t ignore the system nonlinearity during controller design.
- The efficiency of the entire system depends cardinally on the loading conditions. In the case of modeling imprecision, the SMC controller offers a systematic way to address the complication of retaining stability as well as the desired consistent performance.
- The sliding mode control technique is easy to implement. It requires implementation of short computational and numerical algorithms in the microcontroller. It is readily compatible with the standard communication protocols such as Ethernet/IP, RS-232, and the Modbus.
- In the case of harsh industrial environments, where stability, as well as high performance, is required despite the presence of high nonlinearity, the lifetime of the hardware components can be reduced considerably in the application of PID controllers. Unlike the PID control technique, SMC requires significantly less equipment and maintenance costs.
- Compared to the PID control technique, SMC offers robust performance against parametric variations and any disturbance and better response time to retain microgrid stability.
3.4. Controller Design
4. Robustness Analysis of SMC
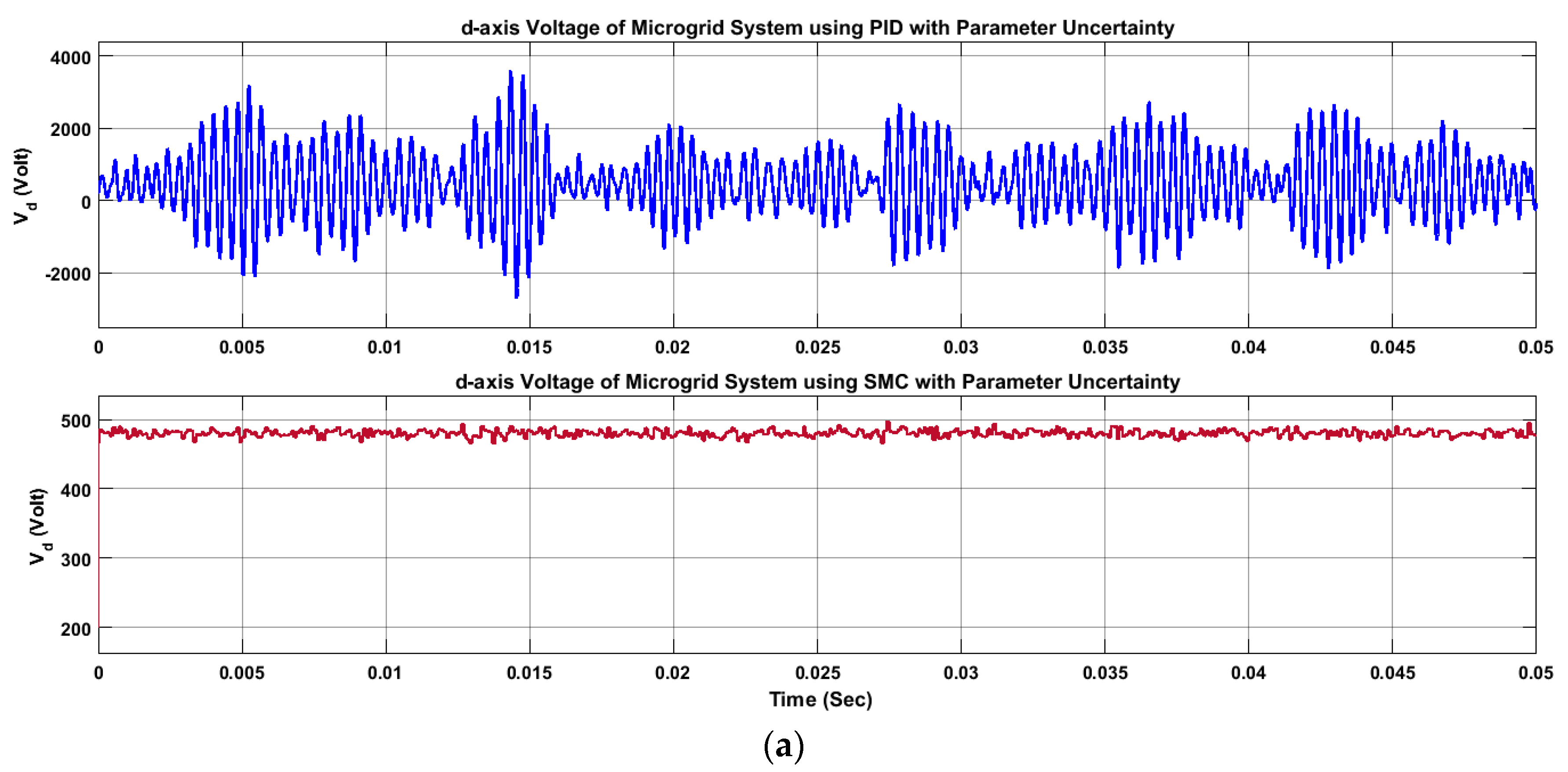
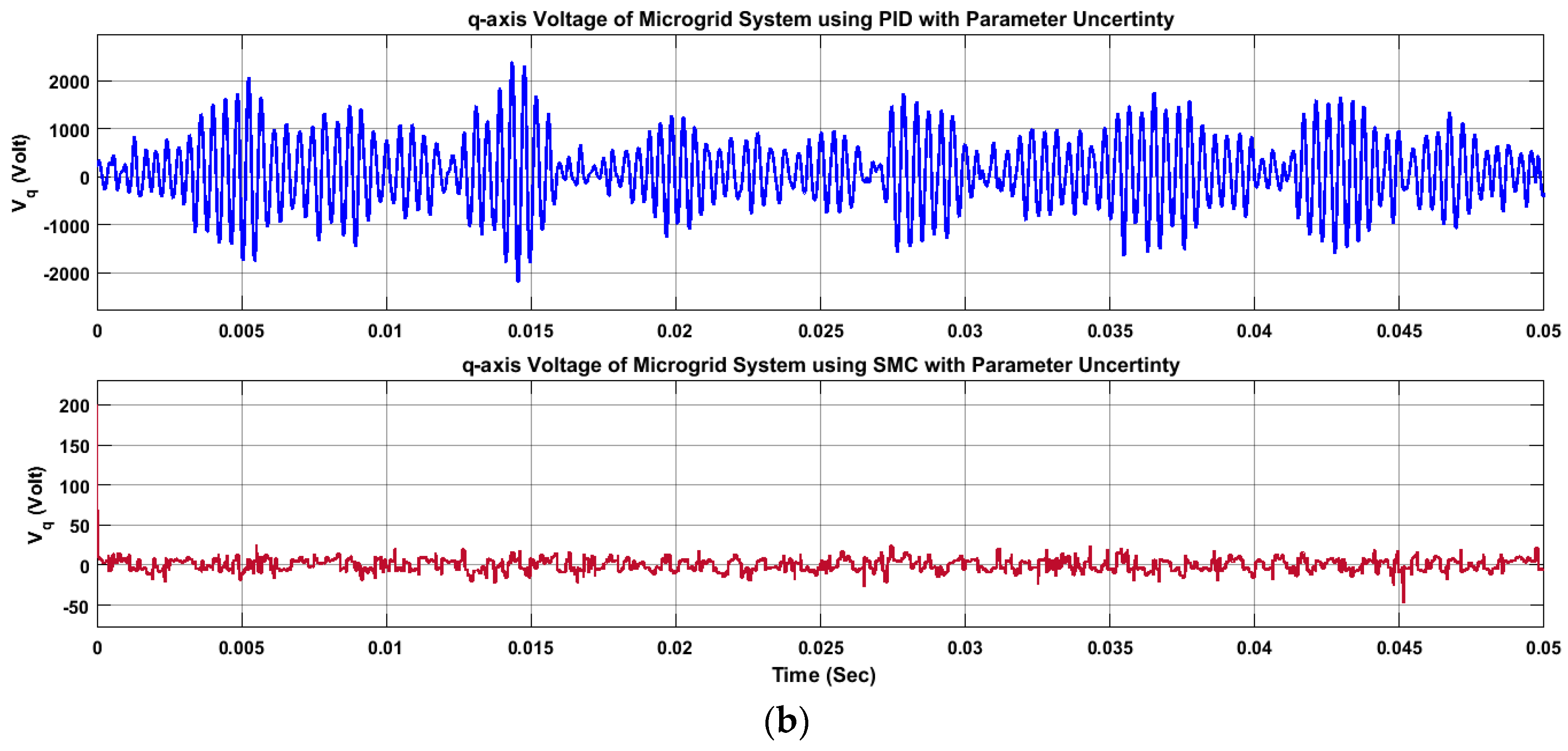
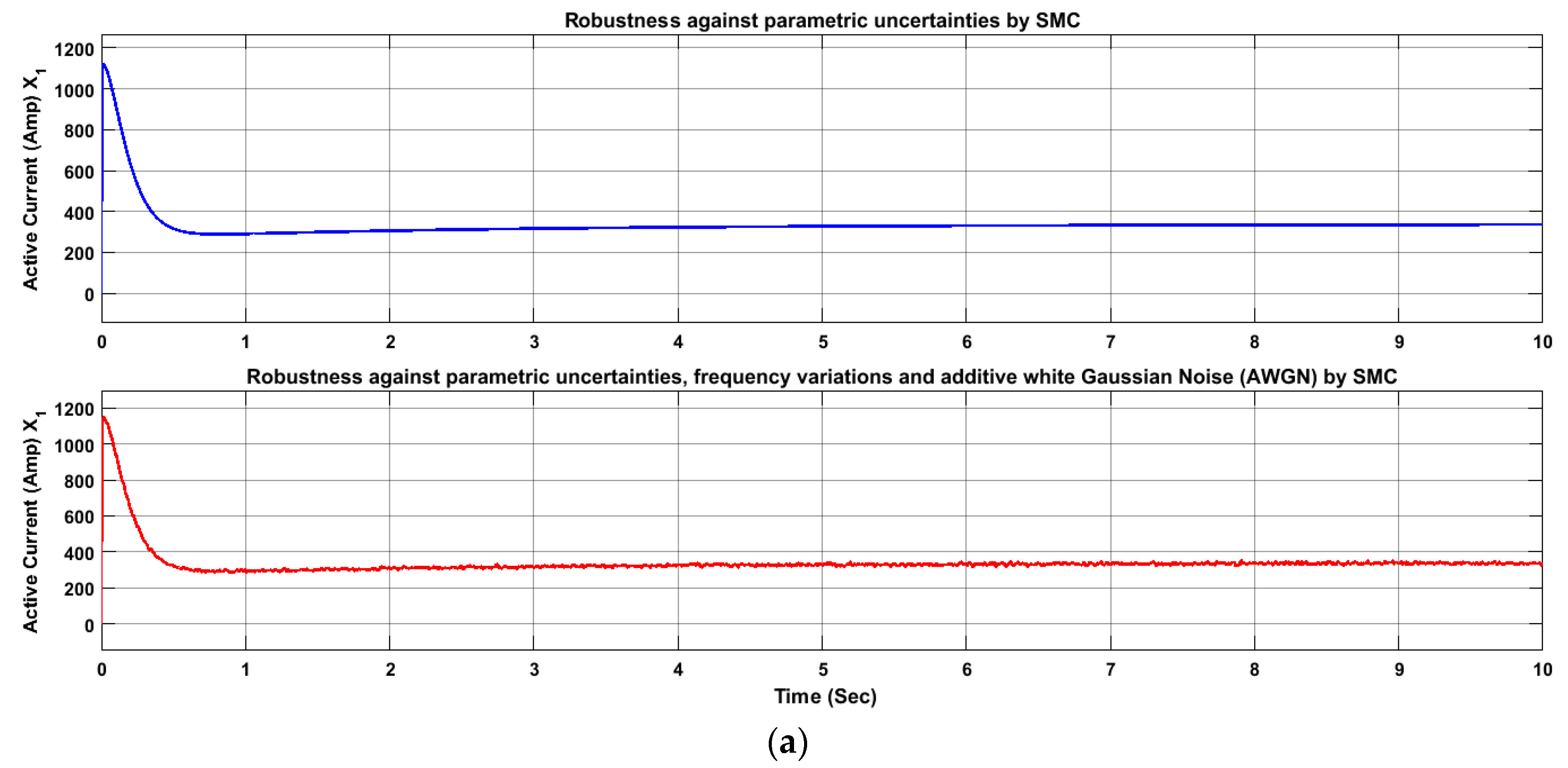
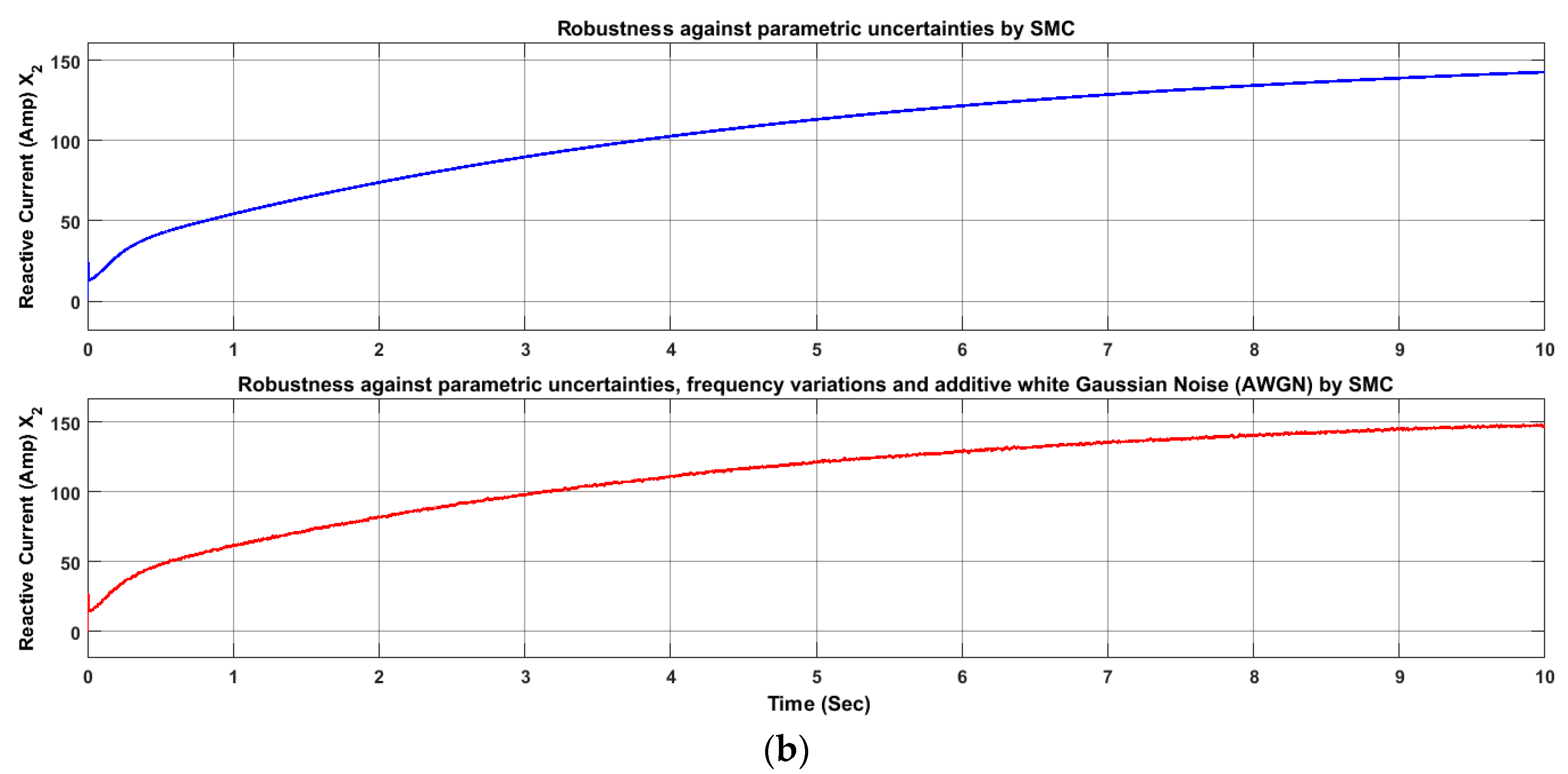
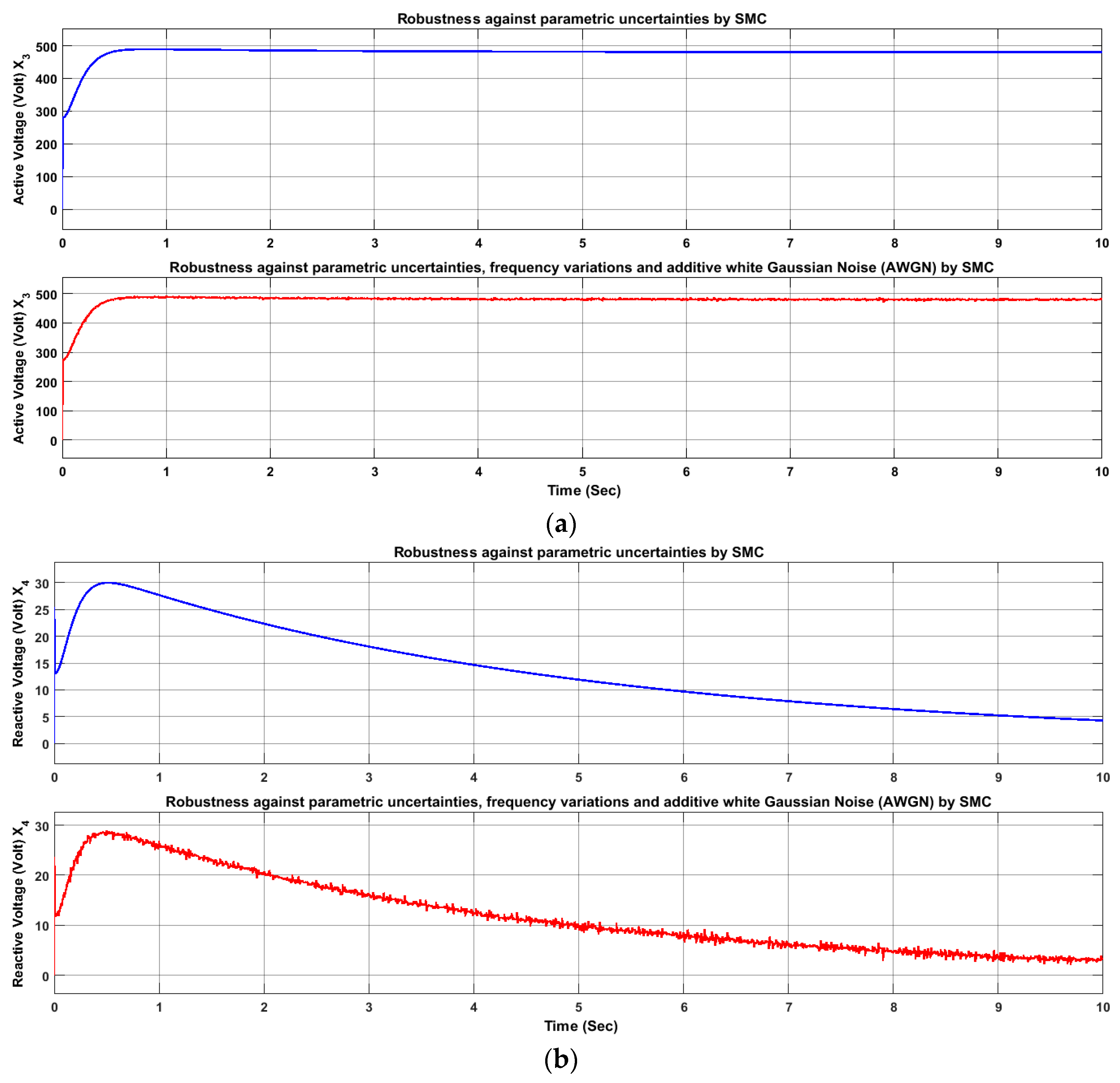
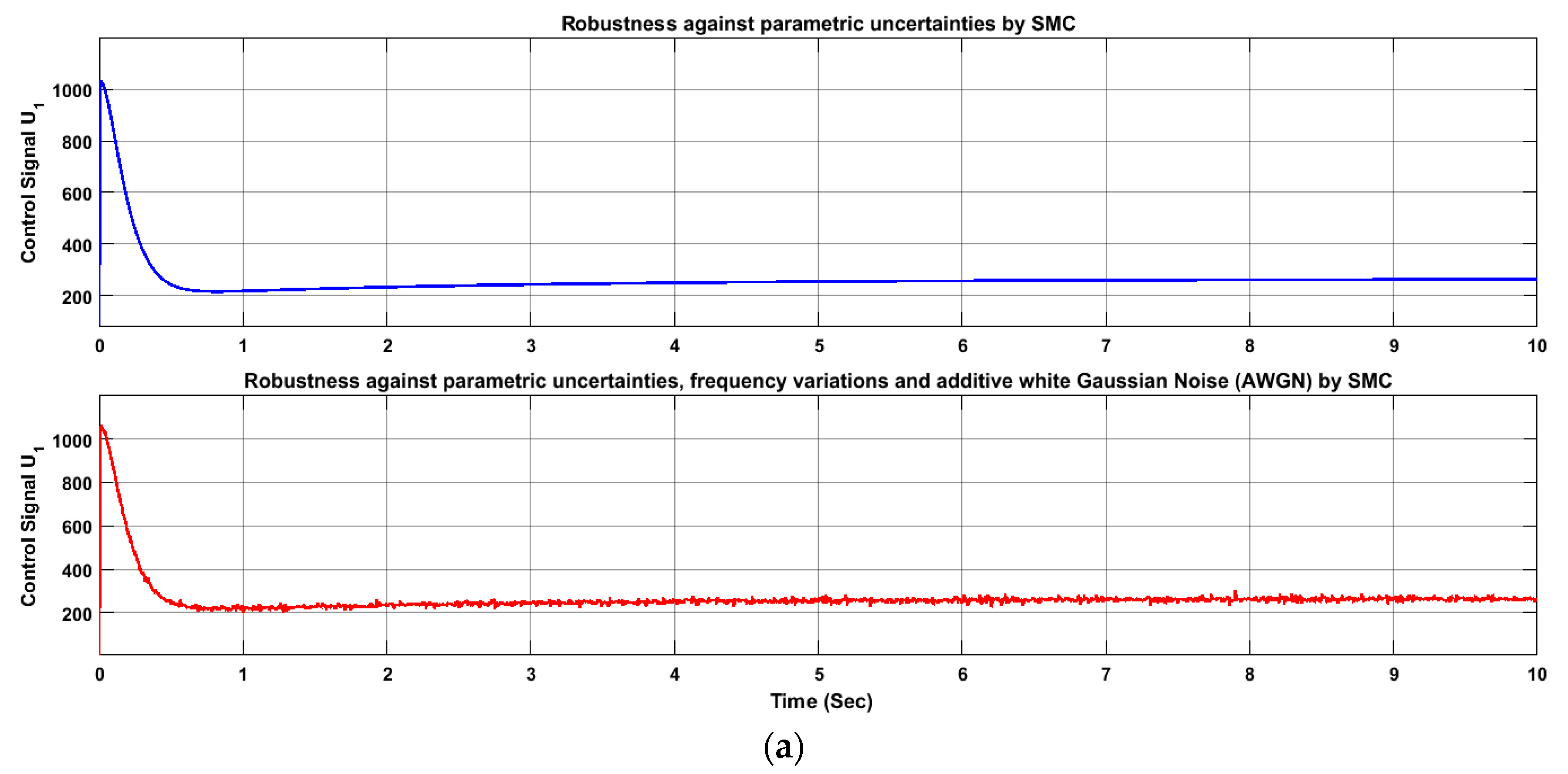
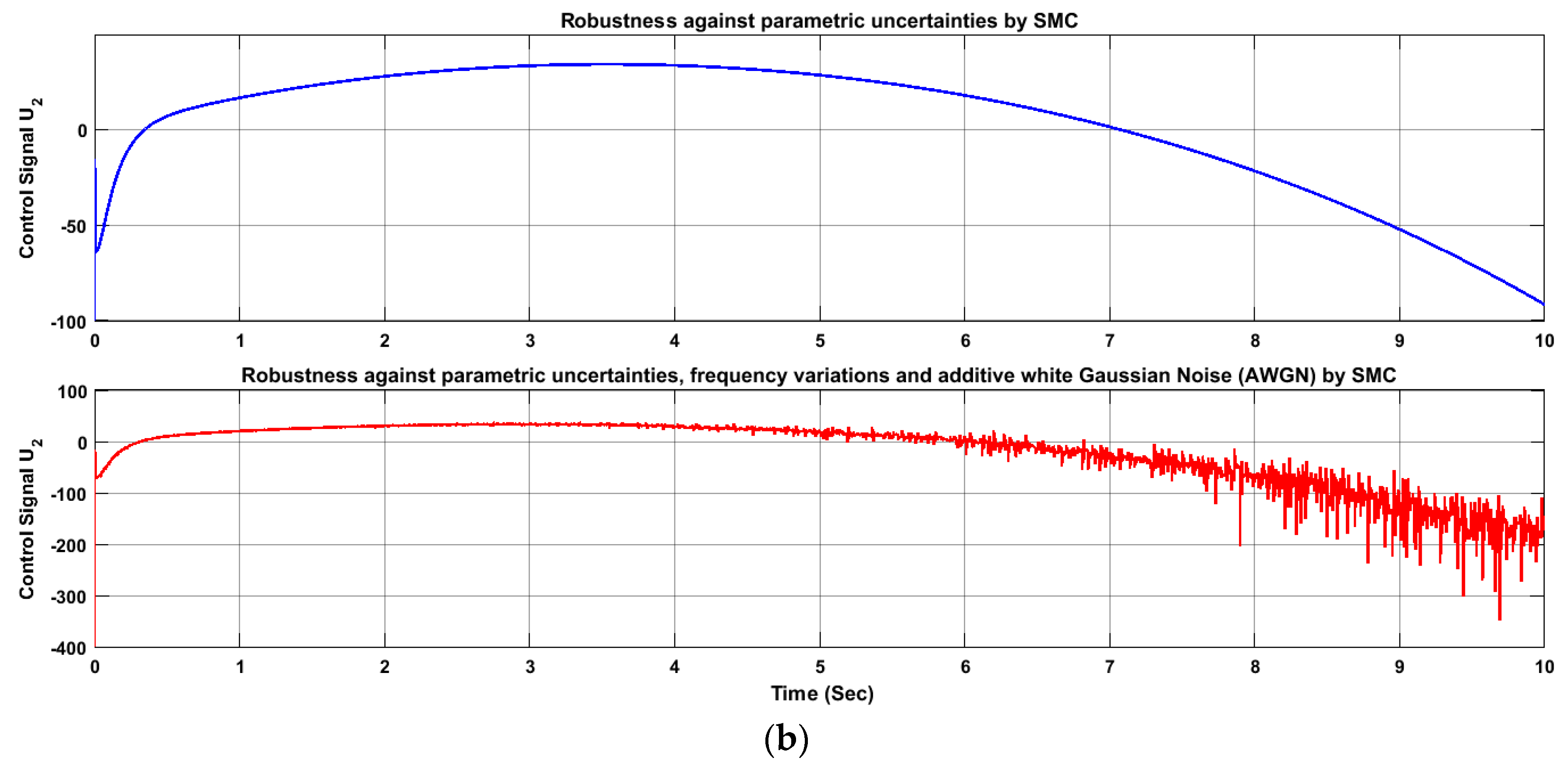
4.1. Sliding Mode Controller, Robustness Against Parametric Uncertainties
4.2. Sliding Mode Controller Robustness Against Parametric Uncertainties, Frequency Variations and Additive White Gaussian Noise (AWGN)
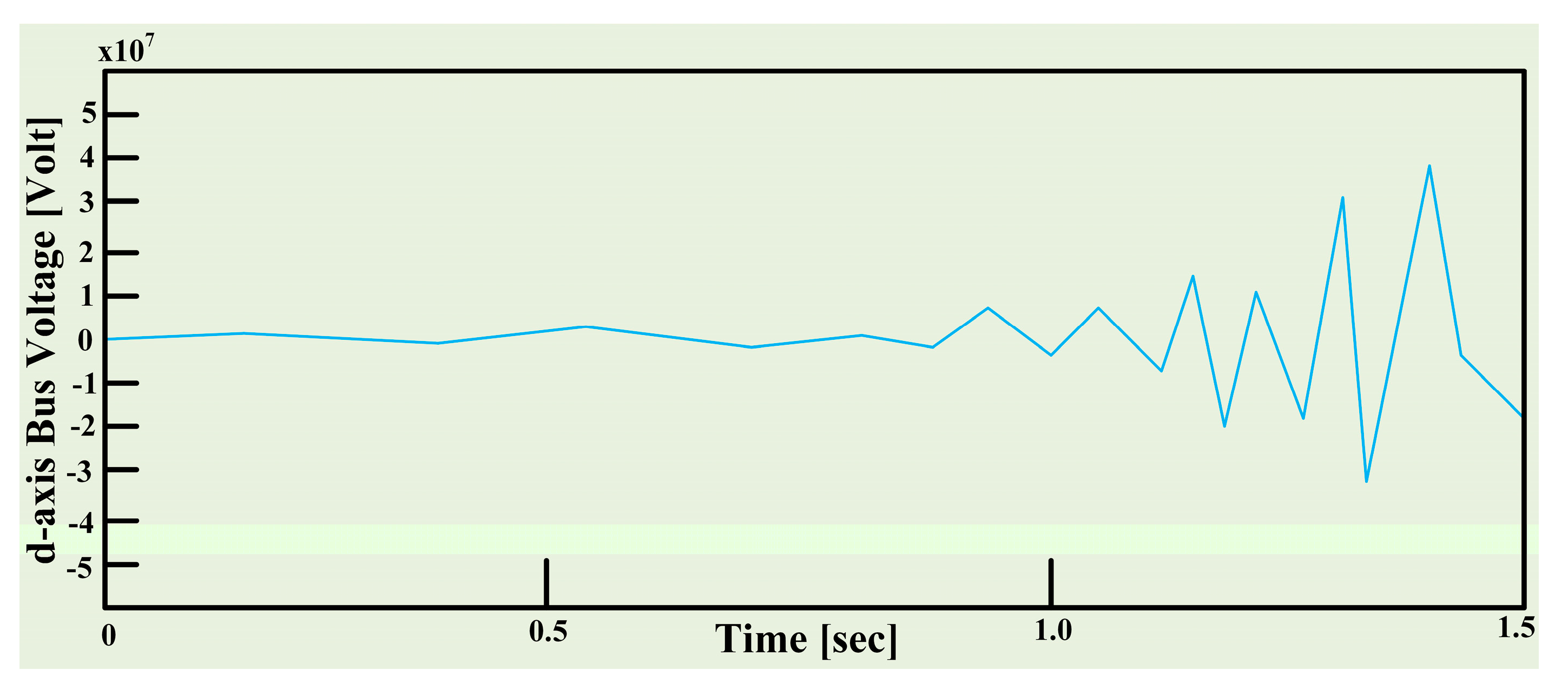
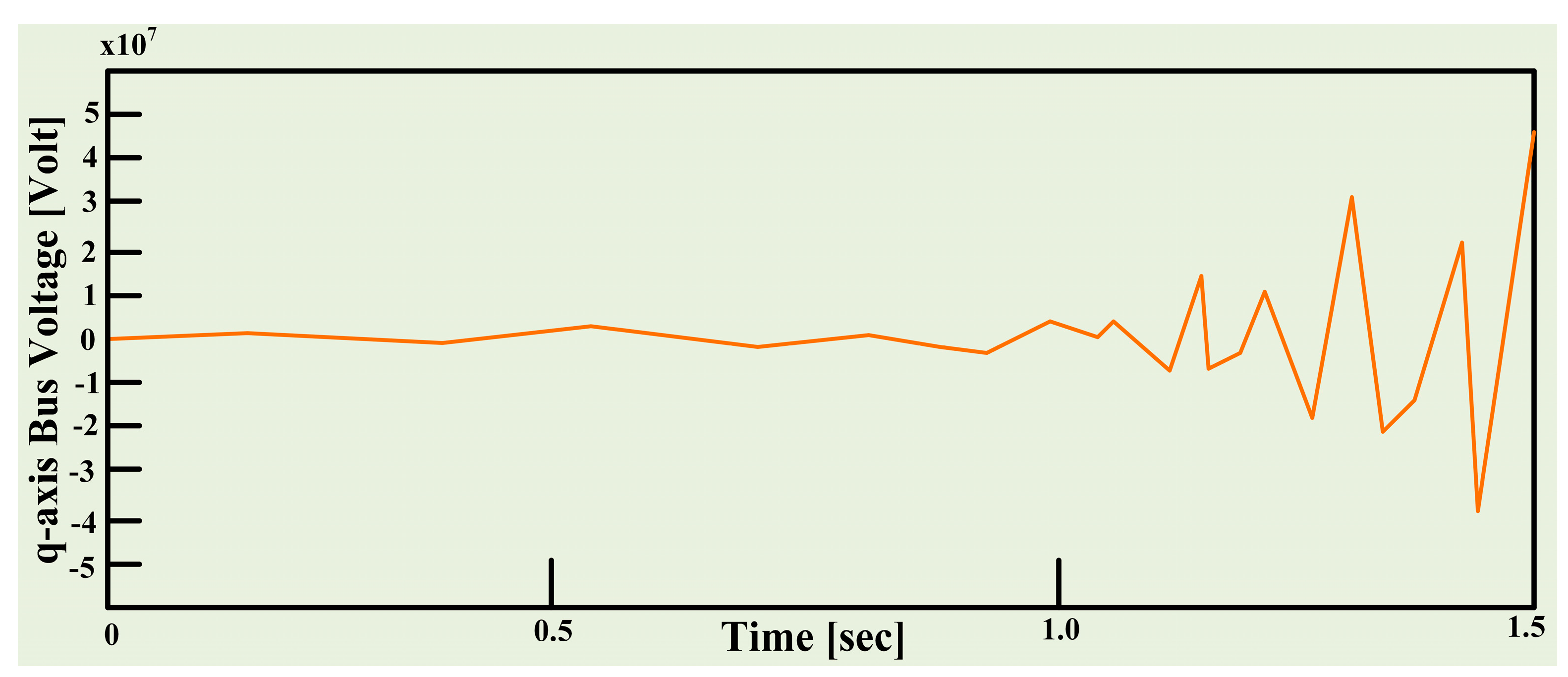
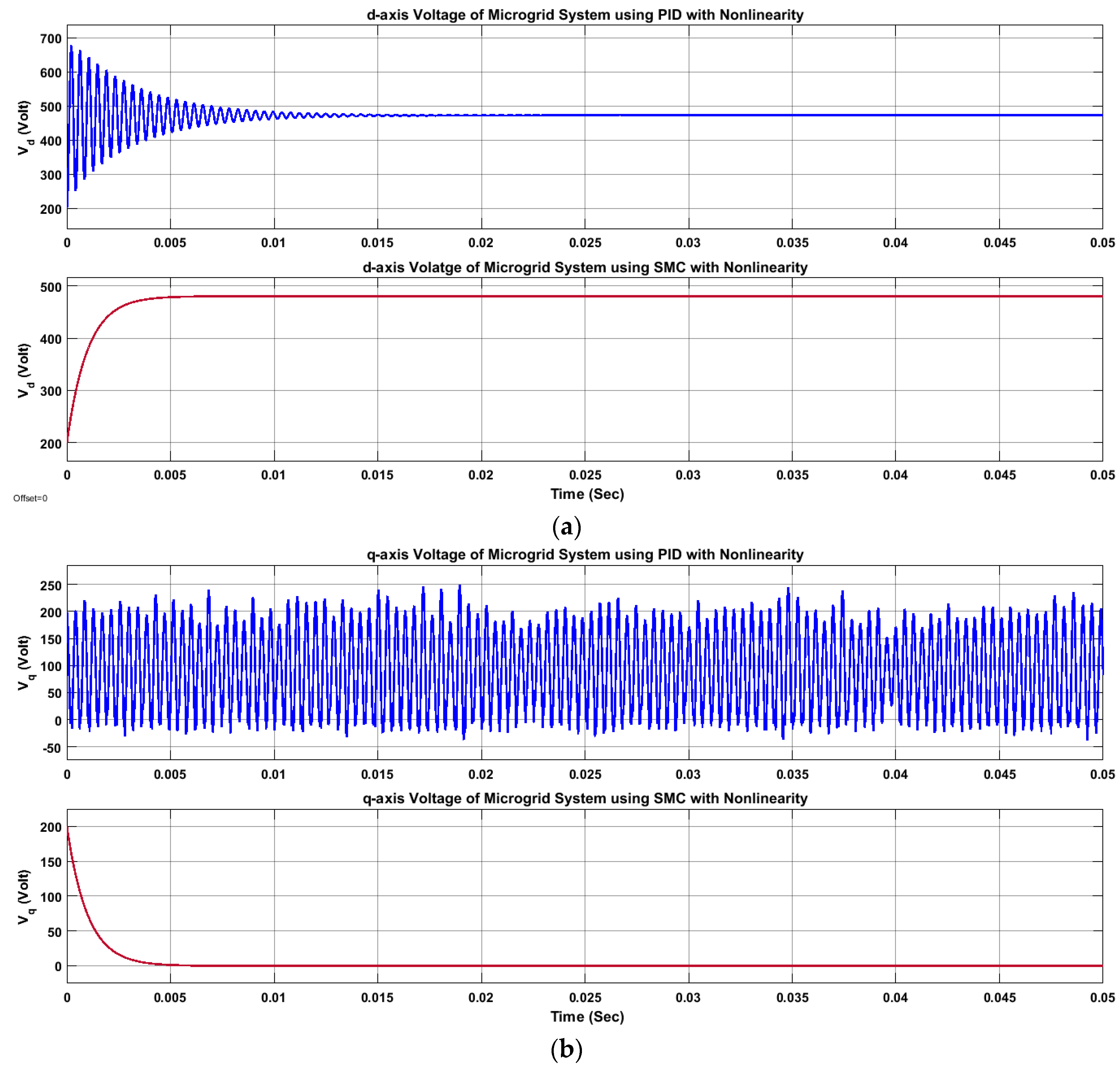
5. Results
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hossain, E.; Kabalci, E.; Bayindir, R.; Perez, R. Microgrid testbeds around the world: State of art. Energy Convers. Manag. 2014, 86, 132–153. [Google Scholar] [CrossRef]
- Evangelopoulos, V.A.; Georgilakis, P.S.; Hatziargytious, N.D. Optimal operation of smart distribution networks—A review of models, methods and future research. Electr. Power Syst. Res. 2016, 140, 95–106. [Google Scholar] [CrossRef]
- Ali Memon, A.; Kauhaniemi, K. A critical review of AC Microgrid protection issues and available solutions. Electr. Power Syst. Res. 2016, 129, 23–31. [Google Scholar] [CrossRef]
- Malik, F.H.; Lehtonen, M. A review: Agents in smart grids. Electr. Power Syst. Res. 2016, 131, 71–79. [Google Scholar] [CrossRef]
- Papadimitriou, C.N.; Zountouridou, E.I.; Hatziargyriou, N.D. Review of hierarchical control in DC microgrids. Electr. Power Syst. Res. 2015, 122, 159–167. [Google Scholar] [CrossRef]
- Sanchez, S.; Ortega, R.; Griño, R.; Bergna, G.; Molinas, M. Conditions for Existence of Equilibria of Systems with Constant Power Loads. IEEE Circuits Syst. I Regul. Pap. 2014, 61, 2204–2211. [Google Scholar] [CrossRef]
- Li, Y.; Vannorsdel, K.R.; Zirger, A.J.; Norris, M.; Maksimovic, D. Current Mode Control for Boost Converters with Constant Power Loads. IEEE Trans. Circuits Syst. I Regul. Pap. 2012, 59, 198–206. [Google Scholar] [CrossRef]
- Sanchez, S.; Molinas, M. Assessment of a stability analysis tool for constant power loads in DC-grids. In Proceedings of the International Power Electronics and Motion Control Conference (EPE/PEMC), Novi Sad, Serbia, 4–6 September 2012; pp. DS3b.2-1–DS3b.2-5. [Google Scholar]
- Barabanov, N.; Ortega, R.; Griñó, R.; Polyak, B. On Existence and Stability of Equilibria of Linear Time-Invariant Systems with Constant Power Loads. IEEE Trans. Circuits Syst. I Regul. Pap. 2016, 63, 114–121. [Google Scholar] [CrossRef]
- Trias, A.; Marín, J.L. The Holomorphic Embedding Load flow Method for DC Power Systems and Nonlinear DC Circuits. IEEE Trans. Circuits Syst. I Regul. Pap. 2016, 63, 322–333. [Google Scholar] [CrossRef]
- Wu, M.; Lu, D.D.C. A Novel Stabilization Method of LC Input Filter with Constant Power Loads without Load Performance Compromise in DC Microgrids. IEEE Trans. Ind. Electron. 2015, 62, 4552–4562. [Google Scholar] [CrossRef]
- Kwasinski, A.; Onwuchekwa, C.N. Dynamic Behavior and Stabilization of DC Microgrids with Instantaneous Constant-Power Loads. IEEE Trans. Power Electron. 2011, 26, 822–834. [Google Scholar] [CrossRef]
- Huddy, S.R.; Skufca, J.D. Amplitude Death Solutions for Stabilization of DC Microgrids with Instantaneous Constant-Power Loads. IEEE Trans. Power Electron. 2013, 28, 247–253. [Google Scholar] [CrossRef]
- Sanchez, S.; Molinas, M. Large Signal Stability Analysis at the Common Coupling Point of a DC Microgrid: A Grid Impedance Estimation Approach Based on a Recursive Method. IEEE Trans. Energy Convers. 2015, 30, 122–131. [Google Scholar] [CrossRef]
- Marx, D.; Magne, P.; Nahid-Mobarakeh, B.; Pierfederici, S.; Davat, B. Large Signal Stability Analysis Tools in DC Power Systems With Constant Power Loads and Variable Power Loads—A Review. IEEE Trans. Power Electron. 2012, 27, 1773–1787. [Google Scholar] [CrossRef]
- Magne, P.; Marx, D.; Nahid-Mobarakeh, B.; Pierfederici, S. Large-Signal Stabilization of a DC Link Supplying a Constant Power Load Using a Virtual Capacitor: Impact on the Domain of Attraction. IEEE Trans. Ind. Appl. 2012, 48, 878–887. [Google Scholar] [CrossRef]
- Jelani, N.; Molinas, M.; Bolognani, S. Reactive Power Ancillary Service by Constant Power Loads in Distributed AC Systems. IEEE Trans. Power Deliv. 2013, 28, 920–927. [Google Scholar] [CrossRef]
- Singh, S.; Fulwani, D.; Kumar, V. Robust sliding-mode control of dc/dc boost converter feeding a constant power load. IEEE Trans. Power Electron. 2015, 8, 1230–1237. [Google Scholar] [CrossRef]
- Gautam, A.R.; Singh, S.; Fulwani, D. DC bus voltage regulation in the presence of constant power load using sliding mode controlled dc-dc Bi-directional converter interfaced storage unit. In Proceedings of the IEEE First International Conference on DC Microgrids (ICDCM), Atlanta, GA, USA, 7–10 June 2015; pp. 257–262. [Google Scholar]
- Stramosk, V.; Pagano, D.J. Nonlinear control of a bidirectional dc-dc converter operating with boost-type Constant-Power Loads. In Proceedings of the Power Electronics Conference (COBEP), Brazilian, Brazil, 27–31 October 2013; pp. 305–310. [Google Scholar]
- Liu, Z.; Liu, J.; Bao, W.; Zhao, Y. Infinity-Norm of Impedance-Based Stability Criterion for Three-Phase AC Distributed Power Systems with Constant Power Loads. IEEE Trans. Power Electron. 2015, 30, 3030–3043. [Google Scholar] [CrossRef]
- Jelani, N.; Molinas, M. Asymmetrical Fault Ride Through as Ancillary Service by Constant Power Loads in Grid-Connected Wind Farm. IEEE Trans. Power Electron. 2015, 30, 1704–1713. [Google Scholar] [CrossRef]
- Emadi, A. Modeling of power electronic loads in AC distribution systems using the generalized State-space averaging method. IEEE Trans. Ind. Electron. 2004, 51, 992–1000. [Google Scholar] [CrossRef]
- Karimipour, D.; Salmasi, F.R. Stability Analysis of AC Microgrids with Constant Power Loads Based on Popov’s Absolute Stability Criterion. IEEE Trans. Circuits Syst. II Express Briefs 2015, 62, 696–700. [Google Scholar] [CrossRef]
- Jian, S. Small-signal methods for AC distributed power systems—A review. IEEE Trans. Power Electron. 2009, 24, 2545–2554. [Google Scholar] [CrossRef]
- Vilathgamuwa, D.M.; Zhang, X.N.; Jayasinghe, S.D.G.; Bhangu, B.S.; Gajanayake, C.J.; Tseng, K.J. Virtual resistance based active damping solution for constant power instability in AC microgrids. In Proceedings of the IECON 2011—37th Annual Conference on IEEE Industrial Electronics Society, Melbourne, Australia, 7–10 November 2011; pp. 3646–3651. [Google Scholar]
- Ganjefar, S.; Sarajchi, M.H.; Mahmoud Hoseini, S. Teleoperation Systems Design Using Singular Perturbation Method and Sliding Mode Controllers. ASME. J. Dyn. Syst. Meas. Control 2017, 136, 051005. [Google Scholar] [CrossRef]
- Khalil, H.K. Nonlinear Systems, 3rd ed.; Prentice-Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Elhalwagy, Y.Z.; Tarbouchi, M. Fuzzy logic sliding mode control for command guidance law design. ISA Trans. 2004, 43, 231–242. [Google Scholar] [CrossRef]
- Torchani, B.; Sellami, A.; Garcia, G. Sliding mode control of saturated systems with norm bounded uncertainty. In Proceedings of the 16th IEEE Mediterranean Electrotechnical Conference, Yasmine Hammamet, Tunisia, 25–28 March 2012; pp. 15–18. [Google Scholar]
- Sliding Mode Control. Available online: https: //theses.lib.vt.edu/theses/available/etd5440202339731121/unrestricted/CHAP4_DOC.pdf (accessed on 10 May 2017).
- Wang, D.; Zhang, Q.; Wang, A. Robust nonlinear control design for ionic polymer metal composite based on sliding mode approach. In Proceedings of the UKACC International Conference on Control (CONTROL), Loughborough, UK, 8–14 July 2014; pp. 519–524. [Google Scholar]
- Santi, E.; Li, D.; Monti, A.; Stankovic, A.M. A Geometric Approach to Large-signal Stability of Switching Converters under Sliding Mode Control and Synergetic Control. In Proceedings of the IEEE 36th Power Electronics Specialists Conference, Recife, Brazil, 12–16 June 2005; pp. 1389–1395. [Google Scholar]
- Farrell, J.A.; Polycarpou, M.M. Adaptive Approximation Based Control: Unifying Neural, Fuzzy and Traditional Adaptive Approximation Approaches; John Wiley & Sons: Hoboken, NJ, USA, 2006; Volume 48. [Google Scholar]
- Bharatiraja, C.; Sanjeevikumar, P.; Siano, P.; Ramesh, K.; Raghu, R. Real Time Foresting of EV Charging Station Scheduling for Smart Energy System. Energies 2017, 10, 377. [Google Scholar]
- Ozsoy, E.; Sanjeevikumar, P.; Mihet-Popa, L.; Fedák, V.; Ahmad, F.; Akhtar, R.; Sabanovic, A. Control Strategy for Grid Connected Inverters under Unbalanced Network Conditions—A DOb Based Decoupled Current Approach. Energies 2017, 10, 1067. [Google Scholar] [CrossRef]
- Vavilapalli, S.; Sanjeevikumar, P.; Umashankar, S.; Mihet-Popa, L. Power Balancing Control for Grid Energy Storage System in PV Applications—Real Time Digital Simulation Implementation. Energies 2017, 10, 928. [Google Scholar] [CrossRef]
- Awasthi, A.; Karthikeyan, V.; Rajasekar, S.; Sanjeevikumar, P.; Siano, P.; Ertas, A.H. Dual Mode Control of Inverter to Integrate Solar-Wind Hybrid fed DC-Grid with Distributed AC grid. In Proceedings of the 16th IEEE International Conference on Environment and Electrical Engineering, Florence, Italy, 7–10 June 2016. [Google Scholar]
- Hussain, S.; Alammari, R.; Jafarullah, M.; Iqbal, A.; Sanjeevikumar, P. Optimization Of Hybrid Renewable Energy System Using Iterative Filter Selection Approach. IET Renew. Power Gener. 2017. [Google Scholar] [CrossRef]
- Hajizadeh, A.; Norum, L.N.; Hassanzadehc, F.; Sanjeevikumar, P. An Intelligent Power Controller for Hybrid DC Micro Grid Power System. In Lecture Notes in Electrical Engineering; Springer: Berlin, Germany, 2017. [Google Scholar]
- Swaminathan, G.; Ramesh, V.; Umashankar, S.; Sanjeevikumar, P. Fuzzy Based Micro Grid Energy Management System using Interleaved Boost Converter and Three Level NPC Inverter with Improved Grid Voltage Quality. In Lecture Notes in Electrical Engineering; Springer: Berlin, Germany, 2017. [Google Scholar]
- Swaminathan, G.; Ramesh, V.; Umashankar, S.; Sanjeevikumar, P. Investigations of Microgrid Stability and Optimum Power sharing using Robust Control of grid tie PV Inverter. In Lecture Notes in Electrical Engineering; Springer: Berlin, Germany, 2017. [Google Scholar]
- Samee, S.; Khan, S.; Vengatesan, K.; Bhaskar, M.S.; Sanjeevikumar, P.; Jaspreetkuar, P. Smart City Automatic Garbage Collecting System for a Better Tomorrow. In Lecture Notes in Electrical Engineering; Springer: Berlin, Germany, 2017. [Google Scholar]
- Tiwaria, R.; Ramesh Babu, N.; Sanjeevikumar, P. A Review on GRID CODES—Reactive power management in power grids for Doubly-Fed Induction Generator in Wind Power application. In Lecture Notes in Electrical Engineering; Springer: Berlin, Germany, 2017. [Google Scholar]
- Tiwari, R.; Ramesh Babu, N.; Arunkrishna, R.; Sanjeevikumar, P. Comparison between PI controller and Fuzzy logic based control strategies for harmonic reduction in Grid integrated Wind energy conversion system. In Lecture Notes in Electrical Engineering; Springer: Berlin, Germany, 2017. [Google Scholar]


© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hossain, E.; Perez, R.; Padmanaban, S.; Siano, P. Investigation on the Development of a Sliding Mode Controller for Constant Power Loads in Microgrids. Energies 2017, 10, 1086. https://doi.org/10.3390/en10081086
Hossain E, Perez R, Padmanaban S, Siano P. Investigation on the Development of a Sliding Mode Controller for Constant Power Loads in Microgrids. Energies. 2017; 10(8):1086. https://doi.org/10.3390/en10081086
Chicago/Turabian StyleHossain, Eklas, Ron Perez, Sanjeevikumar Padmanaban, and Pierluigi Siano. 2017. "Investigation on the Development of a Sliding Mode Controller for Constant Power Loads in Microgrids" Energies 10, no. 8: 1086. https://doi.org/10.3390/en10081086
APA StyleHossain, E., Perez, R., Padmanaban, S., & Siano, P. (2017). Investigation on the Development of a Sliding Mode Controller for Constant Power Loads in Microgrids. Energies, 10(8), 1086. https://doi.org/10.3390/en10081086







