Assessment of Capacitance for Self-Excited Induction Generator in Sustaining Constant Air-Gap Voltage under Variable Speed and Load

Abstract

The concept of a Self-Excited Induction Generator (SEIG) has introduced the concept of the placement of an induction machine for power generation in an isolated mode with external capacitance. The produced output voltage and generated frequency in an SEIG greatly depends on speed, load, and terminal capacitance. To maintain constant air-gap voltage against a varying speed and load, a corresponding supply of reactive power through capacitors is needed. The selection of the required capacitance while there is continuous variation of vital parameters needs a rigorous random-selection method. In this paper, an intelligent selection of suitable additional capacitance has been made by using the Fuzzy Logic Technique for a Three-Phase 5.0 HP SEIG. Additional capacitance in the range of 14.79–22.47 μF is compulsory under a varying load of 427−101 ohms, and additional capacitance in the range of 13.70–22.59 μF is essential for a varying speed of 1349 to 1672 RPM. With this promising result, we propose the implementation of this intelligent technique in place of analytical and standard methods for capacitance selection.

1. Introduction

The indiscriminate utilization of fossil fuels to meet the ever-growing energy demand of the worldwide population has in all increased the total global figure for the production of greenhouse gases (GHG) by three quarters [1]. These GHG emissions are a major contributor to global warming and stand as the biggest hurdle for upcoming generations. The changing scene of ultramodern living and a manyfold population rise has raised energy demands. To fulfill these rising energy demands, alternative sources of energy need to be identified and exploited on a large scale. It has also necessitated the need for a sustainable and green energy source. Renewable-energy sources, such as solar, wind, biomass, and hydro are sustainable, environmentally safe, and green sources of energy. Additionally, the recent development of deregulation and decentralization of the power-generation system has given birth to the concept of distributed generation by using renewable-energy resources [2]. Commissioning distributed generation through the exploitation of renewable energy resources near load centers requires a conversion-efficiency device like a generator. Usage of an induction machine as generator is well-received as a renewable energy resource [3,4,5,6,7]. Induction machines, coupled to an external prime mover and running at a speed above the synchronous speed with grid frequency, are capable of generating power at a negative slip. In the negative-slip region, the induced torque direction is reversed, the machine starts behaving as an induction generator, and it draws a current that lags behind the voltage with an angle greater than 90° [8]. This indicates the outflow of real power from the machine, but to maintain real and reactive power balance, the machine needs the reactive power. For the induction generator, sufficient voltage buildup across generator terminals requires a means for excitation, and, consequently, the generator can work in grid-connected mode or -isolated mode. For grid-connected induction generators, the extraction of reactive power can be done through the grid, but this burdens the grid. The remedial measure for the same could be by connecting the capacitor bank across generator terminals. For the isolated mode of an induction generator, an appropriate capacitor bank must be connected across generator terminals, and the phenomenon of connecting capacitors is known as capacitor self-excitation. This induction generator is called a Self-Excited Induction Generator (SEIG) [9,10,11].

1.1. Self-Excited Induction Generator

The conception of self excitation of induction machines emerged in 1935 with the notion that an induction machine in isolated mode can act as an induction generator with an external capacitor. The function of capacitance connected at stator terminals is to provide the required reactive power to fulfill the needs of the generator and load. SEIGs have the advantages of a small size, single excitation, and self-protection capability, and have wide applications in wind-power generation. In SEIGs, there is no issue of synchronization of the generated voltage with the bus-bar voltage of the system. The dependence of vital parameters, such as output voltage and frequency of SEIG on speed, load, and terminal capacitance imposes a restriction on its usage. An SEIG with a fixed value of capacitance rises to a difference between reactive powers supplied by shunt capacitors and required by the load, which further leads to poor voltage regulation [12,13]. So, at all possible speeds and loadings, a fixed capacitor cannot provide sufficient amount of reactive power. Even the average capacitances provided by fixed capacitors might not be helpful due to excessive overvoltages. Inadequate capacitance does not allow the generator to build up voltage, and over-rated capacitance suddenly raises the voltage on load removal and transient temperature. Hence, the selection of additional or suitable capacitance under varying generator speed and loads needs artificial intelligence or optimization techniques to counter the two listed major drawbacks of induction generators. For the selection of suitable capacitance information of performance characteristics, operating conditions, parameters, and terminal conditions are prerequisites.

1.2. Literature Review

Hammad et al., (1977) introduced the concept of designing thyristor phase-controlled voltage regulators for cost-effective voltage regulation at frequency-sensitive varying loads for optimized output voltage [13]. Ooi et al., (1979) proposed the synchronous condenser to compensate for machines’ reactive power requirements for wind-turbine power [14]. Singh et al., (1990) developed an algorithm for the number of capacitors required to generate voltage for the rated capacity loading of a machine [15]. Murthy et al., (1993) examined the capacitance requirements of an SEIG with the addition of a single parallel capacitor for each phase [16]. Bhim et al., (1995) performed approximate analysis for a long-shunt SEIG for series estimation and for shunt capacitors to meet reactive-power requirements [17]. Ojo et al., (1996) stated that with the addition of short-shunt and long-shunt excitation connections, the performance of single-phase induction generators could be improved [18]. Wang et al., (1999) suggested that, if an SEIG is supplying a constant load at a fixed speed, then a single capacitor is ideal for reactive power requirements [19]. Chan et al., (2002) presented a practical method for the computation of minimum capacitance to initiate voltage buildup for SEIG using the iterative secant method [20]. Seyoum et al., (2003) said that intricate excitation and control strategies are required due to fluctuating output voltage and frequency [21]. Ahmed et al., (2003) introduced the nodal admittance approach steady-state frequency-domain analysis for determining minimum excitation capacitance. A static VAR compensator (SVC) has been in parallel to a thyristor-phase control reactor (TCR) and thyristor switched capacitor (TSC) for reactive power compensations [22]. Singh et al., (2009) took the multivariable unconstrained nonlinear optimization problem for minimum excitation capacitance [23]. Khela et al., (2011) applied the Artificial Neural Network (ANN) model for estimation of capacitance requirements with a variable load [24]. Haque et al., (2012) presented the determination of excitation capacitance for building no-load voltage for off-grid SEIG operations [25]. Kumar et al., (2013) introduced a new, simple, and direct method of analyzing the complex impedance matrix of generators while being connected with an R-L load to predict the minimum capacitance value [26]. A. Abbou et al., (2013) applied the loop and nodal analysis method, named direct method, to obtain the criteria for maintaining performance characteristics of a three-phase SEIG in isolated mode [27]. Faisal et al., (2014) presented a steady-state model and analysis for single-phase SEIGs for optimum capacitance against inductive and resistive loads [28]. Alok et al., (2016) presented a mathematical model using node admittance for six-phase induction generators for excitation capacitance by using a genetic algorithm [29]. Mhamdi Taoufik et al., (2017) developed a wind generator for rural electrification, and many experimental tests were performed to define parameters and convenient capacitor bank [30]. Khaled S Sakkoury et al., (2017) performed analysis, modeling, and simulation of wind-driven SEIGs under dynamic conditions [31].

1.3. Paper Overview

The present paper is divided into four broad sections. Section 1 introduces SEIGs and the literature review relevant to the paper subject. Section 2 describes the need and reasons for standard tests, and applies an analytical technique for analysis of SEIG. It introduces a new fuzzy-logic technique for analysis and determination of capacitance requirements for maintaining of a constant air-gap voltage. Section 3 reports the available data required for further computation and presenting the result outcomes with the implementation of the above-quoted techniques. Section 4 evidently concludes capacitance requirements for the maintenance of a constant air gap.

This paper proposes the artificial-intelligence fuzzy-logic technique for determination of intelligently selected capacitance to maintain a constant air gap under varying speed and load. Optimized capacitance values were verified with the analytical and standard test method, and they were experimented on a four-pole three-phase self-excited induction generator of a 5.0 HP power rating. The chief purpose of the application of the fuzzy-logic technique on SIEGs is to generalize the algorithm for all ratings and types of SEIGs without long calculations of analytical methods and randomized experimental selection of appropriate capacitance. The benefit of the fuzzy-logic technique is that it is a simple rule-based technique on membership-function formation. The main point behind the experimental verification of selected capacitance was for testing and validating fuzzy-logic results.

2. Materials and Methods

The schematic of an SEIG shows that it has four parts: the prime mover, machine, load, and capacitance for the purpose of self-excitation, as shown in Figure 1. To keep the machine acting as an induction generator, reactive power is fed, as per the simple principle.

Real power generated (P_g) = real power consumed by load (P_L).

Reactive power for load = reactive power supplied by capacitor-Reactive power for generator

Q_L = Qc − Qg

Steady-state analysis of any machine is always curious from a design and operation point of view. Similarly for an SEIG, when it operates in isolated mode, terminal voltage and frequency are unidentified and based on known or measured parameters that need to be computed at a given speed, load impedance, and capacitance. A large number of researchers have presented their work on SEIG steady-state analysis [32,33,34,35,36,37]. Various models, such as the D-q Reference Model, Impedance-Based, Admittance-Based, Operational Circuit-Based, and Power Equations-Based models have been presented by researchers for SEIG analysis [34,38,39,40,41]. The above methods engage advanced polynomial equations for generated frequency and magnetizing reactance, the coefficients of which can be solved using an SEIG impedance network. The commonly used methods for steady-state analysis of any induction machine are the standard-test method and analytical method. By performing the standard test on a machine, unknown parameters can be measured or calculated. In the second method, the parameters of an equivalent machine circuit are determined by solving the equivalent machine circuit. Both of these methods have been applied on the machine under study.

2.1. Standard Tests for Analysis of Self-Excited Induction Generator

For the SEIG analysis, the data about its performance characteristics at any load must be known, which is possible through a standard No-Load or Block-Rotor Test, or can be taken from design data. The purpose of this standard test is to predetermine the performance characteristics of a machine at any load without actually loading it. An experimental approach has been adopted in this study for determination of stator resistance, rotor resistance, stator leakage reactance, rotor leakage referred to stator, magnetizing reactance (unsaturated), magnetizing reactance (saturated), and equivalent resistance in place of the generator’s core-loss branch [42,43]. The new addition of magnetizing reactance (saturated) is due to the self-excitation of an induction generator. Voltage build-up in a generator is only possible when it enters into the saturated region. The state of entering this region relies on its speed, excitation capacitance, and load. For a particular machine, there exists a definite relationship between air-gap-induced voltage and saturated magnetizing reactance, which further depends on the magnetizing characteristics of the magnetic material used for stator and rotor. To establish the relationship between these two vital parameters, a Synchronous Run Test was performed on the machine by running the induction motor at synchronous speed corresponding to the supply frequency.

The detailed procedure to perform a synchronous run test on the machine under study was as follows. The schematic of this setup is shown in Figure 2, depicting that the three-phase induction motor, coupled with the prime mover, was attached to a power-quality analyzer to measure input voltage, current, power, and power factor. Here, the machine ran as a motor at no load by supplying power at a rated voltage and frequency. Then, the prime mover was supplied to provide torque to the induction motor in same direction. The speed of the prime mover was adjusted to achieve synchronous speed of setup at rated frequency. The input voltage was then varied from low to rated voltage against synchronous speed at a rated frequency, and measurements were made at each step to demonstrate magnetizing characteristics. At that stage, the induction machine drew only the magnetizing current from the supply that maintains air-gap voltage. In this case, active power drawn by the stator was zero, owing to the zero power factor of the stator current. From these experimental data, air-gap voltage and the corresponding value of magnetizing reactance was determined as mentioned below:

Magnetizing Current I_m = Phase Current I_ph

(1)

Per Phase Stator Impedance Z_ph = V_ph/I_ph

(2)

Air-gap Voltage per phase at rated frequency E₁ = V_ph – (R_s + jX_ls) (−jI_m)

(3)

Saturated Reactance X_m = E₁/I_m

(4)

Saturated Reactance X_m = (Z_ph² − R_s²)^1/2 − X_ls

(5)

V_ph = per phase applied voltage, X_ls = stator leakage reactance, R_s = Stator resistance.

The relationship of X_m and E₁ was established by using a piecewise linearization technique. This model was further used for SEIG performance analysis under different loading conditions.

2.2. Analytical Technique for Analysis of Self-Excited Induction Generator

For implementation of the analytical technique, the per-phase SEIG-equivalent circuit with rotor parameters referred to the stator side is shown in Figure 3. A core-loss branch was included in the equivalent circuit, though its effect was insignificant on machine performance. This equivalent circuit was with reference to the rated machine frequency and making the resistance parameters of circuit as frequency-sensitive [11,44]. From the circuit, the impedances of different branches seen from respective nodes are:

Z_AH = R_L/a + jX_L, Z_BG = −jX_c/a²

Z_BC = R_s/a + jX_s; Z_CF = R_e/a||jX_m

Z_CE = R_r/(a − b) + jX_r

Z _Total = [(R_e/a||jX_m)||(R_r/(a − b) + jX_r)] + R_s/a + jX_s + [(R_L/a + jX_L) + (−jX_c/a²)]

(6)

The equivalent circuit results in a single-loop equation:

Is × Z_Total = 0

(7)

For successful voltage build-up, Is ≠ 0, Thus

Z_Total = 0

(8)

The details of equivalent circuit parameters are in Nomenclature. By separating the real and imaginary components of the equation, two nonlinear simultaneous equations were obtained in terms of machine parameters, speed, capacitive reactance, load resistance, magnetizing reactance, and generated frequency. By putting the real and imaginary part of the equation separately equal to zero, the obtained equations are:

Real (X_m,a) = P₁X_ma⁵ + P₂X_ma⁴ + (P₃X_m + P₄) a³ + (P₅X_m + P₆) a² + (P₇X_m + P₈) a+ P₉X_m + P₁₀

(9)

Imaginary (X_m,a) = (Q₁X_m + Q₂) a⁴ + (Q₃X_m + Q₄) a³ + (Q₅X_m + Q₆)a² + (Q₇X_m + Q₈)a + Q₉

(10)

The coefficients P₁–P₁₀ and Q₁–Q₉ of the two equations were obtained using MATLAB and are given in Nomenclature. These are solved using the Newton Raphson Method in MATLAB, and the value of ‘X_m’ and ‘a’ was calculated. The value of ‘E₁’ was determined from magnetizing characteristics. To determine ‘X_m’ and ‘a’ with this technique, we engaged tedious mathematical computations and lengthy computer programming.

The branch currents, terminal voltages, and output power of SEIG were determined as follows:

Stator Current I_s = (E₁/a)/Z_BC + (Z_BG + Z_AH)

(11)

Rotor Current I_r = (−E₁/a)/Z_CE

(12)

Magnetizing Current I_m = (E₁/a)/j X_m

(13)

Core-Loss Branch Current I_e = (E₁/a)/(R_e/a)

(14)

Load Current I_L = Is*(−jX_c/a²)/[R_L/a + j(X_L − X_c/a²)]

(15)

Terminal Voltage V_t/a = (E₁/a) − I_s (R_s/a + jX_ls)

(16)

Generated Power Po = 3I_L²R_L/a

(17)

2.3. Fuzzy Technique for Analysis and Determination of Capacitance to Maintain Constant Air-Gap Voltage of Self-Excited Induction Generator

To solve the polynomial equations of analytical techniques, rigorous calculations were involved, which is quite a time-consuming task and may lead to calculation errors. Fuzzy technique is a tool that resolves all these issues and makes the determination of parameters simple, fast, and accurate. It is used here to find the per-unit value of generated frequency ‘a’ and saturated magnetizing reactance ‘X_m’. A rule-based method was used, limits on each parameter were fixed, and fuzzy sets were classified into various linguistic variables; from that, membership functions were formed.

• The 9 given inputs were stator-leakage reactance X_s, rotor-leakage reactance X_r, stator resistance R_s, rotor resistance R_r, core-loss resistance R_c, speed N, power factor PF, capacitance C, and load admittance Y.
• The 2 outputs were generated frequency ‘a’ and magnetizing reactance X_m. All input and output parameters are in per-unit values.
• The range and naming of input membership functions and output membership functions were extreme low (EL), very low (VL), low (L), medium (M), high (H), and very high (VH). By adjusting the range of the membership functions, more rules are formed and high rate of result accuracy can be achieved.

The input–output parameters calculated from the analytical technique or by using any standard method are proposed as the fuzzy rule. To find the input parameters, MATLAB programming was used, and the parameter range was selected as per the real-time SEIG applications.

The fuzzy model was implemented to find the generated frequency and magnetic reactance requirements of SEIG under varying stator and rotor resistance, and stator and rotor reactance.

The excitation process of SEIG is greatly influenced by variation in terminal parameters like speed and load, which leads to a reduction in terminal voltage. When an induction generator runs in isolated mode, its terminal voltage decreases due to a decrease in air-gap voltage. To maintain this air-gap voltage, minimum excitation capacitance for excitation and additional capacitance are required. To regulate this capacitance requirement, the fuzzy model was proposed for implementation that would compute the capacitance requirement to maintain constant air-gap voltage. In the previous fuzzy model for parameter determination, 9 inputs and 2 outputs were taken. In the present model, an additional input of change in capacitance ΔC was taken. For constant air-gap magnetizing, reactance should be constant.

For maintaining constant air-gap voltage for varying speed under constant load and excitation capacitance, the membership function for all parameters except speed and change in capacitance were kept as constant. Speed membership functions are extreme low (EL), very low (VL), medium (M), high (H), and very high (VH), and membership functions for change in capacitance are negatively large (NL), negatively medium (NM), negatively small (NS), positively small (PS), and positively large (PL). For implementation of the fuzzy rule for a constant air gap, 25 rules were made. The first rule, when speed is extremely low (EL) and ΔC is negatively small, magnetizing reactance is high and generated frequency is low. The other rules are similarly defined and used in the implementation of the model.

It is observed that no-load voltage of SEIG generally varies (110–125%) and the generator fails to excite when its saturated magnetizing reactance attains a value close to unsaturated magnetizing reactance. So, limits have been suggested to impose based on the standard limits of other machines. For unsaturated magnetizing reactance X_m, minimum magnetizing reactance X_min, maximum no-load air-gap voltage E_max, and minimum air-gap voltage at rated load E_min, the limits are 2.0–5.0 p.u., 0.45–0.65 p.u., 1.10–1.50 p.u., and 0.45–0.65 p.u., respectively.

3. Data Reporting and Results

SEIG has the capability to work in two modes, i.e., grid-connected and isolated mode. In both modes, the smooth operation of the induction generator is the utmost priority for the generation of terminal voltage and power. For the successful operation of an SEIG in isolated mode, it is important to meet the reactive power requirements, which is possible by integrating the minimum value of capacitance. Before the intelligent selection of appropriate capacitance, the prerequisite is to determine the unknown parameters of the SEIG-equivalent circuit. The step-by-step results of this study are presented below:

3.1. Specifications of Induction Machine

For the present research work, a Squirrel-Cage Three-Phase Induction Machine was selected, and

Table 1. Specifications of induction machine.

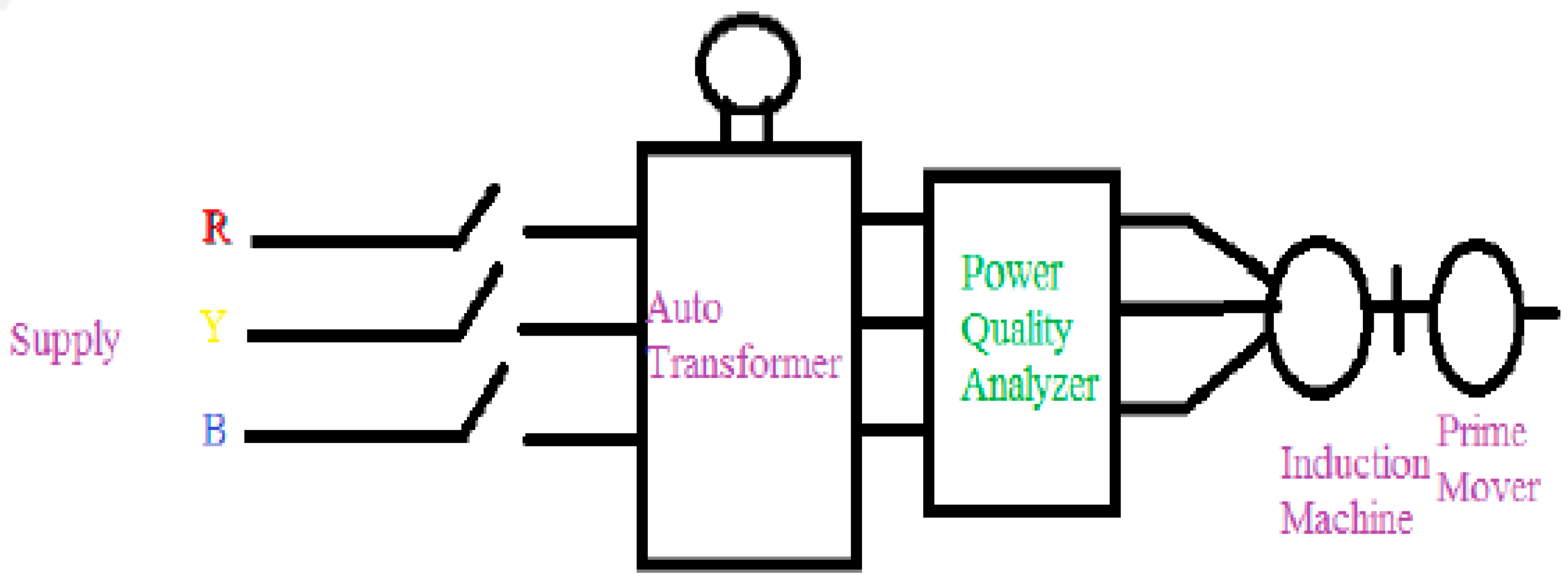
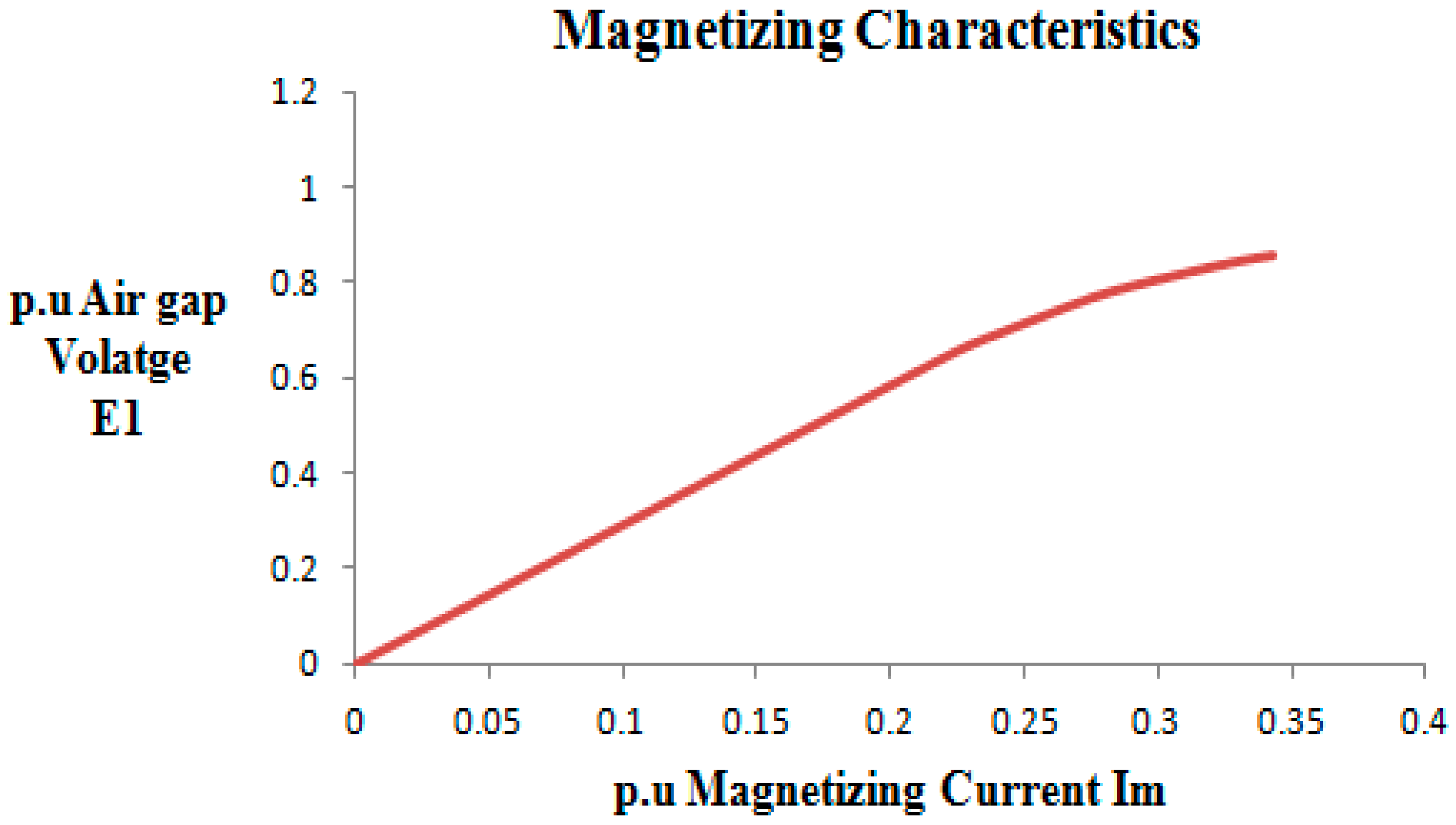
Type of Machine	Power Rating (HP)	Voltage Rating (volt)	Current Rating (Amp)	Speed (RPM)	No. of Poles	Type of Connection
Three-Phase Induction Machine	5.0	415	7.60	1500	4	Delta

presents the information about its machine specifications:

3.2. Determination of Machine Parameters and Magnetizing Characteristics with Standard Test

For the determination of the machine’s technical parameters, the No-load and Block-Rotor Test were performed on the machine under study, and results are tabulated in

Table 2. Base parameters of induction machine.

Voltage (Volt)	Current (Amp)	Power (VA)	Frequency (Hz)	Speed (RPM)	Impedance (Ohm)	Admittance (Mho)	Capacitance (μF)
415	4.33	1797	50	1500	95.84	0.010	25.46

and

Table 3. Parameters of induction machine.

Stator Resistance (p.u)	Rotor Resistance (p.u)	Stator-Leakage Reactance (p.u)	Rotor Leakage Reactance (p.u)	Core-Branch Resistance (p.u)	Magnetizing Reactance Unsaturated (p.u)
0.061	0.0437	0.097	0.097	32.53	2.973

.

The experimental-data relationship of magnetizing reactance ‘X_m’ and corresponding air-gap voltage ‘E₁’ of induction machine is established with a synchronous run test, and determination of these two parameters was done as follows. Characteristics are shown in Figure 4.

X_m < 2.693 p.u, E₁ = 1.3818 − 0.2117 X_m p.u

X_m < 2.838 and X_m ≥ 2.693, E₁ = 2.1679 − 0.5057 X_m p.u

X_m < 2.971 and ≥ 2.838, E₁ = 3.8732 − 1.1057 X_m p.u

X_m > 2.9716, E₁ = 0

All mesurements are done on standard measuring devices of OSAW Company and Power Quality Analyzer Model No. C.A.8332, CHAUVIN ARNOUX MAKE.

For the performance analysis of any system or machine, per unit values are the preferred method of data demonstration, so base values of machine has been determined to define p.u values. As magnetizing current of machine increases in steps the voltage build-up starts in machine and simultaneously air gap voltage increases and finally reaches close to 1.0 p.u.

3.3. Determination of Machine Parameters with Analytical Technique

The conventional equivalent circuit of machine for SEIG is solved by using the Equations (6)–(17) and results with analytical technique for magnetizing reactance, generated frequency, terminal voltage and output power with varying load, speed and excitation capacitance are described in

Table 4. Magnetizing Reactance and Generated Frequency of SEIG with varying Load for Analytical and Fuzzy Techniques, Speed = 1485 RPM, Excitation Capacitance = 27.57 μF.

Load Admittance (p.u)	Magnetizing Reactance (p.u) Analytical	Magnetizing Reactance (p.u) Fuzzy	Generated Frequency 9 (p.u) Analytical	Generated Frequency (p.u) Fuzzy
0.225	1.232	1.227	0.975	0.976
0.538	1.434	1.430	0.961	0.962
0.6389	1.526	1.525	0.957	0.956
0.871	1.817	1.827	0.947	0.947

,

Table 5. Magnetizing reactance and SEIG-generated frequency with varying speed for analytical and fuzzy techniques. Load = 230 Ohm, excitation capacitance = 22.00 μF.

Speed (p.u.)	Magnetizing Reactance (p.u.) Analytical	Magnetizing Reactance (p.u.) Fuzzy	Generated Frequency (p.u.) Analytical	Generated Frequency (p.u.) Fuzzy
0.923	1.969	1.9698	0.903	0.903
0.953	1.844	1.846	0.932	0.932
1.014	1.623	1.621	0.991	0.992
1.071	1.448	1.443	1.047	1.047

,

Table 6. Magnetizing reactance and SEIG-generated frequency with varying capacitance for analytical and fuzzy techniques. Speed = 1430 RPM, load = 178 Ohm.

Capacitance (p.u.)	Magnetizing Reactance (p.u.) Analytical	Magnetizing Reactance (p.u.) Fuzzy	Generated Frequency (p.u.) Analytical	Generated Frequency (p.u.)n Fuzzy
0.608	2.200	2.204	0.997	0.997
0.665	1.985	1.986	0.997	0.997
0.764	1.698	1.696	0.996	0.996
0.830	1.549	1.547	0.995	0.996

and

Table 7. Determination of capacitance requirement at constant air-gap voltage with varying load. Speed = 1485 RPM, excitation capacitance = 25.46 μF.

Load Admittance (p.u)	Air-Gap Voltage (p.u)	Additional Capacitance (p.u) Fuzzy	Additional Capacitance (p.u) Analytical	Additional Capacitance (p.u) Standard Test
0.225	1.0	0.581	0.580	0.590
0.413	1.0	0.633	0.632	0.651
0.538	1.0	0.694	0.693	0.719
0.580	1.0	0.694	0.693	0.719
0.638	1.0	0.719	0.718	0.743
0.819	1.0	0.805	0.806	0.832
0.871	1.0	0.838	0.835	0.855
0.948	1.0	0.882	0.881	0.895

.

3.4. Determination of Machine Parameters with Fuzzy-Logic Technique

For the implementation of fuzzy technique on the machine under study, three cases are considered, in first case all parameters of machine are kept constant and load is varied in steps from no load to full load. The machine parameters as input to fuzzy logic are: stator and rotor resistance vary from 0.01–0.11 p.u, stator and rotor leakage reactance from 0.03–0.17 p.u. The load power factor range is restricted to 0.85–1.0. In second case all parameters of machine are kept constant and speed is varied 85–120% of base speed matching to rated frequency and load is kept at unity power factor. In third case all other parameters are kept constant and capacitance is varied from 65–110% of base capacitance. The results of these three cases are presented in Table 4, Table 5 and Table 6 and compared with analytical results.

At constant speed and a fixed excitation capacitance, as the machine load decreases, the machine’s magnetizing reactance increases with a corresponding decrease in generated frequency.

At a constant load and fixed excitation capacitance, as machine speed increases, its magnetizing reactance decreases with a corresponding increase in generated frequency.

At constant speed and a fixed load, as machine excitation capacitance increases, its magnetizing reactance decreases with corresponding almost constantly generated frequency.

3.5. Determination of Capacitance Requirement for Maintenance of Air-Gap Voltage

After implementation of the fuzzy-logic model, the results are tabulated in Table 7,

Table 8. Determination of terminal voltage and output power at constant air-gap voltage with varying load. Speed = 1485 RPM, excitation capacitance = 25.46 μF.

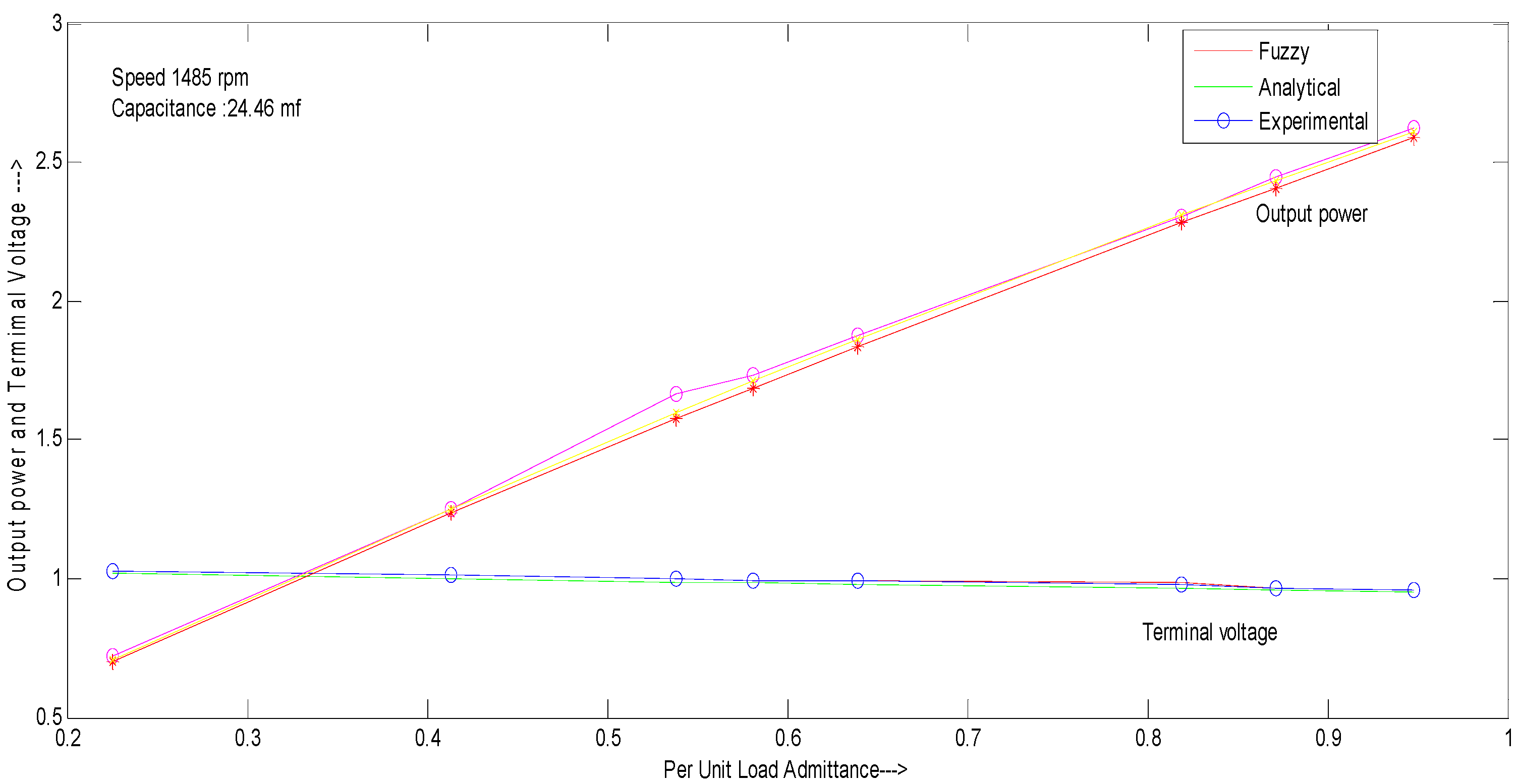
Load Admittance (p.u.)	Terminal Voltage (p.u.) Fuzzy	Terminal Voltage (p.u.) Analytical	Terminal Voltage (p.u.) Standard Test	Output Power (p.u.) Fuzzy	Output Power (p.u.) Analytical	Output Power (p.u.) Standard Test
0.225	1.031	1.017	1.028	0.718	0.698	0.709
0.413	1.015	0.998	1.014	1.251	1.236	1.249
0.538	0.996	0.987	0.997	1.665	1.574	1.600
0.580	0.995	0.983	0.995	1.732	1.686	1.710
0.638	0.993	0.978	0.992	1.875	1.836	1.861
0.819	0.987	0.964	0.980	2.305	2.283	2.308
0.871	0.966	0.959	0.966	2.443	2.408	2.431
0.948	0.956	0.954	0.956	2.621	2.590	2.610

,

Table 9. Determination of capacitance requirement at constant air-gap voltage with varying speed. Load = 165 Ohm, excitation capacitance = 25.46 μF.

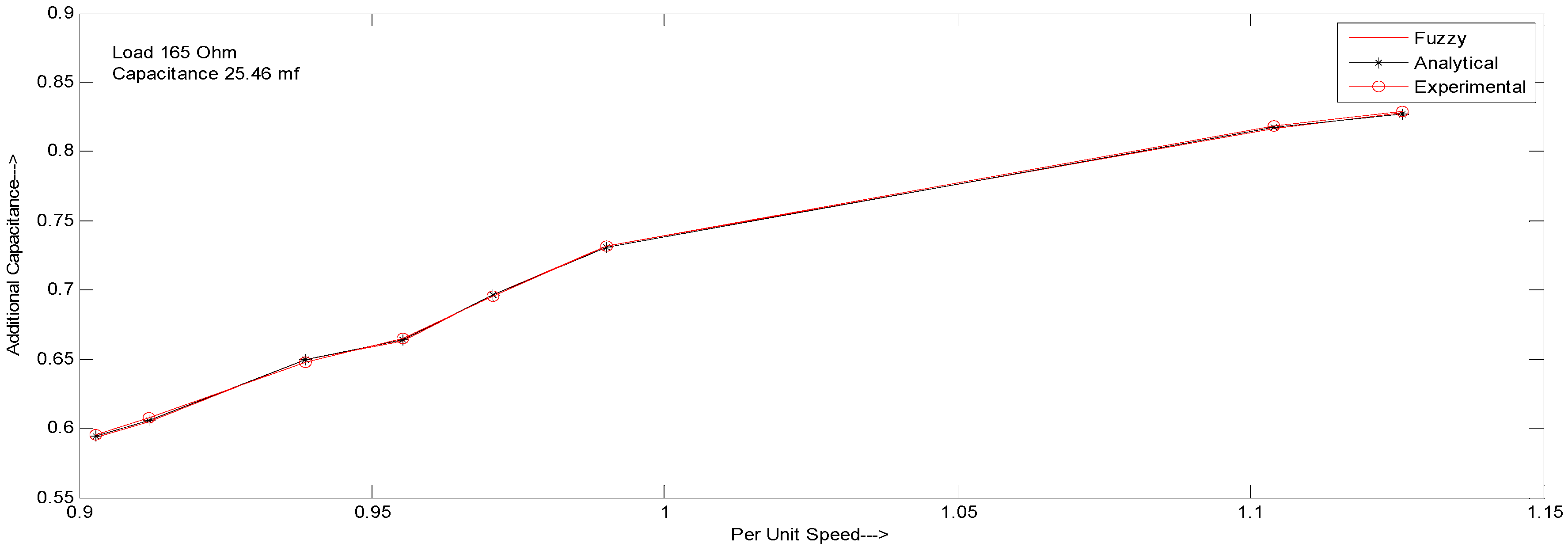
Speed (p.u)	Air gap Voltage (p.u.)	Additional Capacitance (p.u.) Fuzzy	Additional Capacitance (p.u.) Analytical	Additional Capacitance (p.u.) Standard Test
0.903	1.0	0.583	0.583	0.583
0.912	1.0	0.644	0.643	0.634
0.938	1.0	0.649	0.648	0.648
0.955	1.0	0.703	0.703	0.704
0.970	1.0	0.726	0.726	0.725
0.990	1.0	0.791	0.790	0.791
1.104	1.0	0.837	0.837	0.837
1.036	1.0	0.887	0.887	0.888
	(18)

and

Table 10. Determination of terminal voltage andoOutput power at constant air-gap voltage with varying speed. Load = 165 Ohm, excitation capacitance = 25.46 μF.

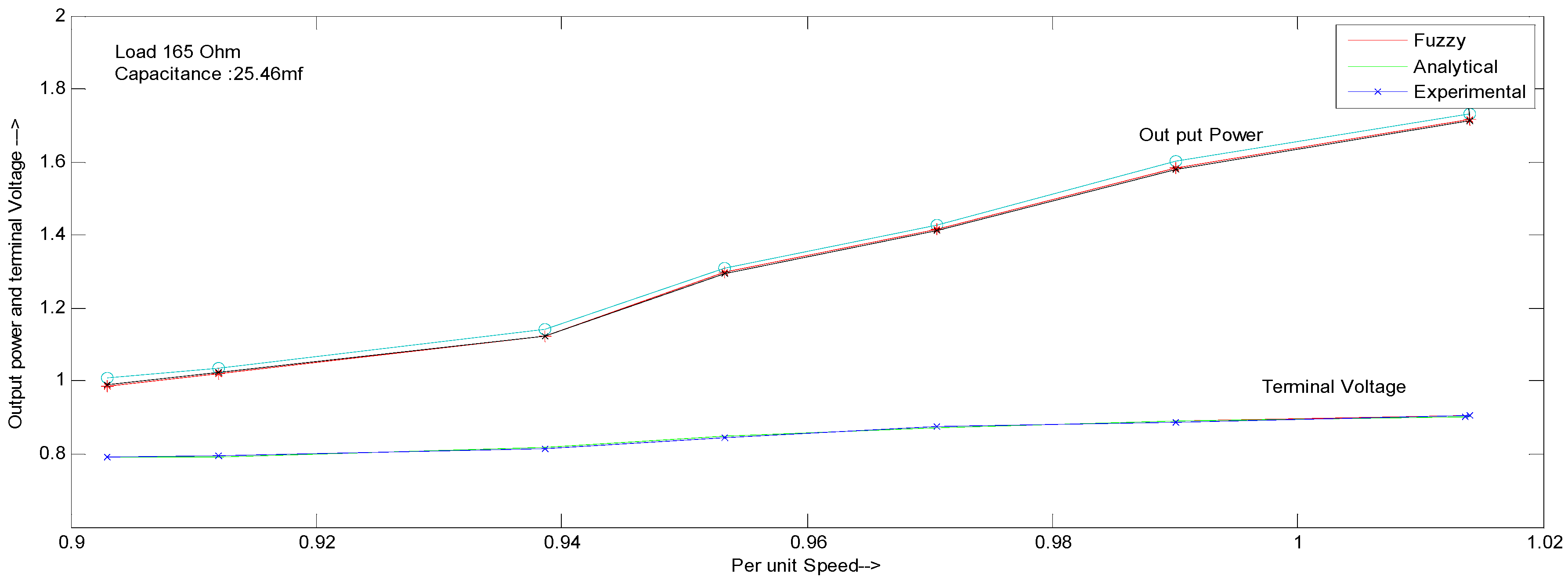
Speed (p.u)	Terminal Voltage (p.u) Fuzzy	Terminal Voltage (p.u) Analytical	Terminal Voltage (p.u) Standard Test	Output Power (p.u) Fuzzy	Output Power (p.u) Analytical	Output Power (p.u) Standard Test
0.903	0.792	0.792	0.793	1.0078	0.9861	0.9917
0.912	0.792	0.792	0.795	1.0373	1.0189	1.0234
0.938	0.818	0.818	0.815	1.1436	1.123	1.1235
0.953	0.849	0.849	0.845	1.3083	1.2972	1.2944
0.970	0.873	0.873	0.876	1.4263	1.4162	1.4124
0.990	0.889	0.889	0.887	1.6021	1.5849	1.581
1.104	0.905	0.901	0.905	1.7323	1.7173	1.7145
1.036	0.906	0.905	0.903	1.8703	1.857	1.8575

.

At constant speed and fixed excitation capacitance against the maintenance of constant air-gap voltage, as load admittance increases, the corresponding requirement of additional capacitance also increases.

At constant speed and fixed excitation capacitance against the maintenance of constant air-gap voltage, as load admittance increases, the corresponding terminal voltage decreases and output power increases, as described in Figure 5 and Figure 6.

At a constant load and fixed excitation capacitance against the maintenance of constant air-gap voltage, as the speed increases, the corresponding terminal voltage and output power increase, as described in Figure 7 and Figure 8.

For sustainability of constant air-gap voltage under variable or operating conditions, the combination of parameter values is the most important factor. Fuzzy logic is fairly intelligent at handling these variations or transient conditions, with a careful selection of a parameter range in fuzzy rules, such as stator resistance, rotor resistance, and inductances of stator and rotor, which has significant effect on initialization and early transient settlement. The occurrence of overvoltages and overcurrents due to transients or due to unpractical changes in excitation capacitance may lead the machine out of synchronism and generation capability.

3.6. Comparison of Heuristic Methods

Heuristic methods are experience-based methods that reduce the effort of calculations and time for any particular machine or equipment under different operating conditions. The fuzzy-logic technique is basically a heuristic method as, when accurate decisions are not possible due to complexity in system parameters, an optimal, flexible, and smooth decision can be met out of fuzzy decision-making. Similar soft computation-based techniques, like artificial intelligence and optimization techniques, are implemented in SEIG by various researchers for performance analysis, evaluation of frequency, air-gap voltage, and capacitance requirements. Joshi et al (2006) used an Artificial Neural Network for SEIG performance analysis [45]. Khela et al., (2011) implemented the Artificial Neural Network model for capacitance estimation to maintain constant air-gap voltage [24]. Mohamed Enany (2014) conducted steady-state SEIG modeling and analysis by using an Adaptive Neurofuzzy Inference System (ANFIS) [46]. The present paper has proposed and implemented the fuzzy technique for capacitance assessment in sustaining constant air-gap voltage under variable conditions. All contributions of researchers evidently support the applications of these techniques for SEIG analysis, but results might not be compared directly, as parameters of the machine under study vary for each study.

4. Conclusions

A Self-Excited Induction Generator has the capacity to work in an isolated mode for power generation as distributed generation in remote locations or near load centers. For the generation of enough voltage and sufficient frequency, the chief requirement of this generator is reactive power, which can be met by installing a capacitor bank on stator terminals. However, the dependence of these essential parameters, output voltage, and frequency on speed, load, and capacitance, imposes a restriction on its usage. During operation of an SEIG, speed, load, and capacitance are continuously varying parameters, which further affect output voltage and frequency. To determine suitable capacitance under varying speed and load conditions, a fuzzy-logic technique has shown promising results. The result shows that at constant air-gap voltage 1.0 p.u. and rated frequency, the required capacitance range is 0.581–0.882 p.u., corresponding to a varying load of 0.225–0.948 p.u. At this stage, the terminal voltage and output power available at generator terminals are in the range of 1.01–0.950 p.u. and 0.718–2.621 p.u., respectively. Further, at constant air-gap voltage, 1.0 p.u. and rated frequency, the required capacitance range is 0.583–0.887 p.u. corresponding to a varying speed of 0.903–1.036 p.u. During this, the terminal voltage and output power available at generator terminals are in the range of 0.792–0.906 p.u. and 0.698–2.594 p.u., respectively. Hence, this study concludes that, to maintain constant air-gap voltage, a total capacitance of 14.79 to 22.47 μF is required under a varying load of 427 to 101 ohms, and total capacitance of 13.70 to 22.59 μF is required under a varying speed of 1349 to 1672 RPM.

To test the fuzzy results, the same SEIG was also placed for analytical and standard-test techniques. The results collected from all the three techniques are comparable. For the verification of the fuzzy-logic technique for an SEIG, the determination of machine parameters was done through standard tests and analytical technique, and results verified with the implementation of the fuzzy model. It is valid that the fuzzy-logic technique of artificial intelligence has enough intelligence to select suitable capacitance for any SEIG without following conventional analytical and standard-test techniques.