Abstract
Smart grid architecture is one of the difficult constructions in electrical power systems. The main feature is divided into three layers; the first layer is the power system level and operation, the second layer is the sensor and the communication devices, which collect the data, and the third layer is the microprocessor or the machine, which controls the whole operation. This hierarchy is working from the third layer towards first layer and vice versa. This paper introduces an eco unit commitment study, that scheduling both conventional power plants (three IEEE) thermal plants) as a dispatchable distributed generators, with renewable energy resources (wind, solar) as a stochastic distributed generating units; and plug-in electric vehicles (PEVs), which can be contributed either loads or generators relied on the charging timetable in a trustworthy unit commitment. The target of unit commitment study is to minimize the combined eco costs by integrating more augmented clean and renewable energy resource with the help of field programming gate array (FPGA) layer installation. A meta-heuristic algorithm, such as the Gravitational Search Algorithm (GSA), proves its accuracy and efficiency in reducing the incorporated cost function implicating costs of CO2 emission by optimally integrating and scheduling stochastic resources and charging and discharging processes of PEVs with conventional resources power plants. The results obtained from GSA are compared with a conventional numerical technique, such as the Dynamic Programming (DP) algorithm. The feasibility to implement GSA on an appropriate hardware platform, such as FPGA, is also discussed.
1. Introduction
Unit commitment concentrates on optimally reducing the production cost, which basically relies on the fuel cost. On the other side, the increase of fuel cost leads to the increase of the CO2 emissions. Decarbonizing the limit of CO2 emission in electric networks is mainly the aim of this study, while supplying the required demands, which can be applied by the unit commitment problem. The definition of the unit commitment study is optimally scheduling the generation power, which is obtained from different energy resources. The set of the priority list of the generating units can be achieved by using conventional and meta-heuristic techniques to find the unit commitment’s solution, so that the combined cost of emissions can be optimally reduced [1,2].
Furthermore, the greenhouse gas emissions (GHGEs) is roughly from electricity production. However, the fossil-burnt fuel power plants can be early excluded, a critical issue is remained for decision-makers who liken the cost of fossil-burnt fuels with zero-carbon energy electric power resources. Several renewable energies, such as windmills, photovoltaic power, concentrated solar power, large dams and small hydropower; and fuel shifting technologies, such as plug-in electric hybrid vehicles in the transportation sector can be used to generate carbon–neutral electricity [3]. Customers will be attracted to use the renewable resources in case they are contributing to pay the actual price of electricity production, which includes the cost of generation, in addition to the transmission, distribution, and indirect cost of environmental cleanup and health effects [4].
It is expected that plug-in electric vehicles will be spread in the upcoming decades for many reasons. Passengers will be encouraged to use plug-in electric vehicles (PEVs) for many optimistic forestations of PEVs that can facilitate supplying the demand in suspicious situations and shifting peak load [5,6]. The connotation of battery energy storage systems can represent the PEVs, in which external electrical source will power the electric motor of vehicles. From a grid point of view, two basic types of electric vehicles (EVs) are typically referred to PEVs, as the battery is taken into consideration as a primary source of power in EVs, or plug-in hybrid electric vehicles (PHEVs), which are incorporated with a secondary drive option. Some models manifest the internal combustion engine (ICE), which is a gasoline-powered engine. However, charge and discharge process in the battery of PEVs may rise unexpected sharp spikes in the consumption of electric power and cause potential grid issues [7]. PEVs provide energy storage batteries having the manner of vehicle to grid (V2G) to enhance grid operation and decrease the uncertain behavior of renewable energy resources, such as solar and wind power [8]. PEVs can be charged during weekends, at night, when electricity prices are quite low and when vehicles are parked and not used. However, some PEVs charging will be required during the daylight and even during peak demand or rush hour periods when the grid already supplies the maximum capacity of the electric power [9,10,11].
An efficient optimization technique is needed, due to the complexity of the problem in order to obtain the optimal solution, which fulfils the objective function under certain constraints. The economical emission dispatch unit commitment is solved by the gravitational search algorithm, which is counted as a new meta-heuristic technique. The obtained results from the new technique will be matched with a conventional numerical technique, such as the Dynamic Programming (DP) algorithm [12,13,14,15,16].
This paper’s purpose is to schedule the renewable energy resources (RERs), such as wind or solar, power plants and PEVs, which are integrated as stochastic distributed generators, either load (G2V) or generator (V2G), and the thermal generating units, which is integrating as dispatchable distributed generators in an optimization framework. The sporadic intermittent RERs can be handled by this optimally scheduling coordination and PEVs passengers will be encouraged to participate in the demand response program while hourly charges are optimally pre-defined. The emission cost is not considered as a penalty cost, but it is included in the construction of the optimization function as a cost that should be paid [17], implementing by the GSA in a new field to advocate its fulfilment with regards to other conventional and intelligent programming techniques. The aim of the unit commitment in this paper is to reduce emission cost for the sake of better environmental conditions. Studying the feasibility of implementing the decarbonized commitment unit on field programming gate array (FPGA) is also presented. This study is based on introducing the various usage of FPGA as a fast, reliable and low cost hardware implementation for different components in the smart grid.
The sections in this paper are organized as follows. Section 2 formulates the Unit Commitment objective function. Section 3 introduces different Unit Commitment Techniques. Section 4 presents a suggested proposal of FPGA hardware implementation for the GSA. Section 5 shows System Data. Section 6 reports and discusses results concerning four case studies. Section 7 closes the paper, providing the remarks’ conclusion.
2. Unit Commitment Objective Function
In this study, the unit commitment is formulated as a multi-objective, single function representation optimization problem, which seeks to optimally reduce both the emission cost, operation, and the total transmission losses. Not only the RERs, such as clean resources (wind, solar), can be supplemented to the electric industry to reduce the emission, but the PEVs can be supplemented as well. The PEVs will be employed to decrease both the emission and the cost in the electricity and transportation sectors:
where; is the output power of each thermal generator “i” at each hour. NG is the number of thermal generators, α is CO2 emission factor that considers the ratio between the quantity of gas emitted (in ton) per unit of energy production (in kWh). Table 1 describes the CO2 emission factor (α) with the different energy resources. According to the World Bank’s annual Carbon Pricing Watch Report 2017, is the emission penalty factor in unpaid markets for planning purposes. Its value is around 10–15 $/ton CO2 by the end of 2017 [18].

Table 1.
CO2 emission factor “α” for different energy resources [19].
Under the power balance constraint:
where; Plosses is the total active transmission line losses of the system at each hour.
where; is the current of each feeder “i”, Rli is the transmission line resistance of each feeder in the system at each hour and is the total number of feeders in the IEEE 30 bus system.
2.1. Operating Constraints of PEVs
Dispatchable generators, stochastic energy resources and PEVs, which smartly integrate as loads, energy storages or small portable power plants (energy sources) should subtend and supply the whole load demand (hour) and the system losses, which are represented as follows:
If PEVs are operated as an energy resource or a small power plant:
If PEVs are combined to the demand as loads:
where; is the output power for individual thermal unit “i” at each hour. Pwind/solar is the output power gained from solar or wind plants at each hour; is defined as the coefficient of a linearized fuel cost function of (wind/solar) plans at each hour: is the power of each vehicle j, and is the efficiency of PEVs system. is vehicles’ number that are joined the network at this hour. is units’ number that are on in the unit commitment problem at each hour. and are the present and the departure state of charge (SOC) respectively.
2.2. Some Other Constraints
Each thermal generator should supply output electric power within the minimum and maximum limits:
where; and are the minimum and maximum output limits of the i-th thermal unit respectively, considering minimum up/down time, ramp up/down rate and the spinning reserve of the system at each hour, which should maintain the reliability and the efficiency of the system. Only the registering vehicles will participate in the smart grid according to predetermined scheduling intervals:
where; is the vehicles’ number joined the network at this hour. is the total number of vehicles in the network.
To maintain the battery life:
where; is the storage energy depletion at minimum level. is the charging up to maximum level.
The optimization of the multi-objective function for Cost Emission Economical Dispatch (CEED), which should be minimized in the smart grid is defined as follows:
where, is on/off state of each unit i.
3. Unit Commitment Techniques
Figure 1 shows a flowchart for optimally reducing the objective function using both the conventional units, PEVs and RERs to decrease the operating cost and decarbonize the emission in the smart grid through T = 24 h.
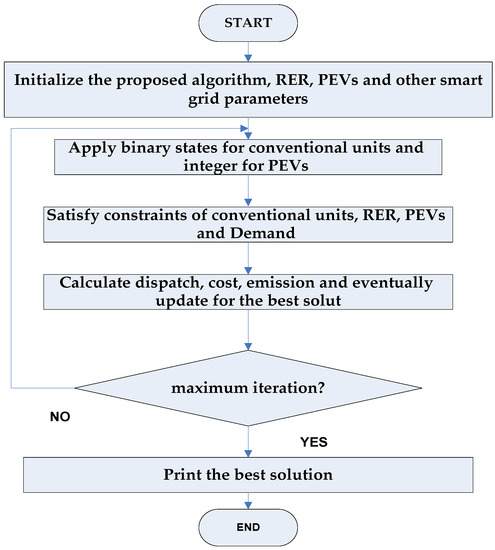
Figure 1.
The flowchart for minimizing both emission and cost by utilizing plug-in electric vehicles (PEVs) and renewable energy resources (RERs).
3.1. Unit Commitment Solution Dynamic Programming Technique Based
The theory of dynamic programming (DP) was explicated by Bellman in 1957. Considering a set of various generating units as the states, which require to be determined. Two directions are attainable to look for the optimum result for each time interval (hour) [16].
Step by Step Transition for Forward Dynamic Programming
The definition of the dynamic programming in a forward direction is the track or path from one state at a given certain hour to a state at the next hour. The state Xi(t) is the i-th combination in hour t, where N is the strategies’ number to store at each step and L is the states’ number to treat each period. The maximum value of L or N is 2N − 1. In Figure 2, there is a the step by step execution and the flowchart of the dynamic programming method.
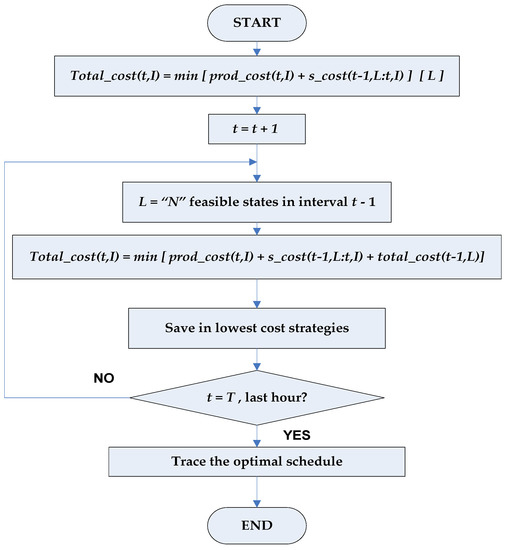
Figure 2.
The flowchart of forward dynamic programming algorithm.
3.2. The Gravitational Search Algorithm (GSA)
The Gravitational Search Algorithm (GSA) is a heuristic algorithm discovered by Esmat Rashedi et al. in 2009 on the basis of Newton gravitation theories [12,13,14,15]. In GSA, each solution in the search space is called agent; each agent reacts with other agents through the gravity force. The performance of each agent is determined by its mass. Therefore, each agent is represented by a particle with specific features. Due to the force of gravity, an overall motion of all particles towards the particles with heavier masses is achieved. The weighty masses that move slowly than the other particles are deemed as good solutions. GSA explores the optimal solution by tuning the gravitational mass and the inertial mass properly. In order to explain the mechanism of GSA, let N agents is considered for describing a certain system. The location of each agent in a search space of n-dimension is defined by:
where; presents the location of agent i in d-dimension at time t. The algorithm is started by setting initial values of the gravitational constant G according to Equation (11):
where; and α are set in the launch of the search and their amounts are decreased over the process of the algorithm. T is the total number of iterations. It is important to determine the gravitational force that attracts two agents to each other at a specific time t. If it is presumed that agent j acts on agent i, so the gravitational force between them can be found from the following Equation (12):
where; is the active gravitational mass of agent i, is the passive gravitational mass of agent i, is the Euclidian distance between agent i and agent j and ε is a constant [13]. Then, Equation (12) is modified as follows:
where; randj is a number randomly chosen between 0 and 1. Thus, the acceleration is specified as follows:
where; is the inertia mass of agent i.
During the search, agent i update its velocity and location as illustrated in Equations (15) and (16), respectively:
where; randi is a number randomly chosen between 0 and 1. The flow chart of the GSA is illustrated in Figure 3.
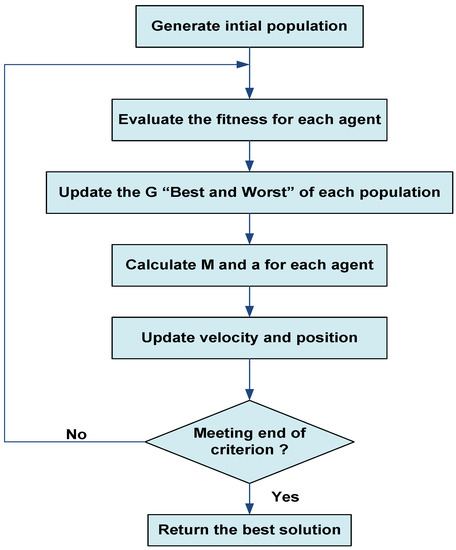
Figure 3.
The flowchart of the Gravitational Search Algorithm (GSA).
In order to achieve the optimum solution of the research problem, the algorithm used parameters are shown in Table 2.

Table 2.
GSA applied parameters.
4. Hardware Implementation Based on FPGA
The smart grid integrates different technologies, such as RERs (wind, solar), energy storage batteries, with cyber elements, such as computation cores, advanced metering infrastructure (AMI) and communication network [20,21]. Accordingly, effective microgrid controllers and reliable computational core are essential to achieve an effective operation. Nowadays, incorporation between power grid equipment’s and advanced technology, such as FPGA is essential to provide more reliability, high performance, and low cost. The smart grid is growing and adopting new communication protocols and optimization algorithms, and hence each design platform utilized in the SMG power management needs flexibility. FPGA is a flexible platform as it can reprogrammed easily to change its functionality. Reliability is another advantage where FPGA can integrate more than processors and other devices to perform reliable functions [20]. Moreover, FPGA integrates central processing unit (CPU) based processor cores, which offers the ability to perform the processing between logic programmable blocks in FPGA and Processor core to combine between processor flexibility and fast percussing, due to FPGA parallel architecture. Analog cores, such as digital to analog converters (DAC) and analog digital converters (ADC) can also integrated in FPGA, which can facilitate the interface with different signals.
One of the main features of a smart micro grid is its ability to manage its operation, based on the grid parameters with fast response. Reference [22] utilized the FPGA to implant a dynamic energy management schemes, which controls the charge/discharge transactions of the energy storage elements in the grid. The FPGA platform has a highly parallelism operation, which provide a fast response cope with SMG requirements [22].
Reference [23] introduced a prototype micro-grid controller that controls the power balance between load and generator. This power management algorithm has been configured on FPGA. The controller integrates the outputs of different type of RERs and also isolates load and source control features to get efficient load management and actual source use.
Smart substation is a vital component in smart gird, which consists of electronic current transformers, smart circuit breakers and Ethernet communication circuit with high speed, which governed by International Electrotechnical Commission (IEC 61850) series communication standards [24]. To achieve a high development in the smart substation, a dynamic performance test of its components is required. A real time digital simulator (RTDS) plays an important role to complete this test and improve the smart substation. FPGA is considered as the best candidate for implementing RTDS, due to its parallel processing hardware structure, which allows implementing different algorithms with reducing the sequencing of operation comparing with CPUs implementation. In addition, FPGA-RTDS offers more specifications, which required for accurate real time simulation, such as lower I/O latency, higher frequency bandwidth and lower sampling rate below 1 µs typically [25,26]. Reference [24] utilized an FPGA-RTDS as a part of smart replacement real-time hardware-in-the-loop simulation platform.
Another FPGA contribution is implementing a real time simulator for microgrid based on FPGA and orders [27]. One of the challenges in real time simulator is the simulation steps, which required to be in microsecond or less to be compatible with the switching frequency of power electronic switching devices in SG. The proposed real time simulator in Reference [27] has the capability of parallel computing, multivalued coefficient prestorage algorithm, and real time solver for multirate simulation algorithm. In addition, the proposed simulator is suggested as order generator for auto scheduling. The proposed system is compared with Power System Computer Aided Design (PSCAD) by applying the same simulation parameters and model on both solver. The real time solver based on FPGA shows a 5% improvement than PSCAD, which is considerably high value [27].
Figure 4 shows the proposal for the FPGA hardware implementation for GSA. It composes of four main modules, system parameters memory module, gravitational force module, force_velocity module, and location adder module. The system parameters memory module is utilized to store all the system initial parameters, which are required for other modules. The gravitational force module composes of lookup table, which stores all values of G(t). The address of this lookup table is delivered from hour_conter. The final block is calculation module, which calculates the value, as indicated in Equation (12). The role of force_velocity module is to calculate both the force and the velocity . As indicated in Equations (13) and (15), a random generator and a multiplier are required to get the values of and . Accordingly, the multiplexer 2:1 in this module allows to use single rand generator and multiplier to calculate both quantities and hence safe more area required. The final main module in GSA is location_ Adder, which responsible for calculating the new location , which is defined by Equation (16).
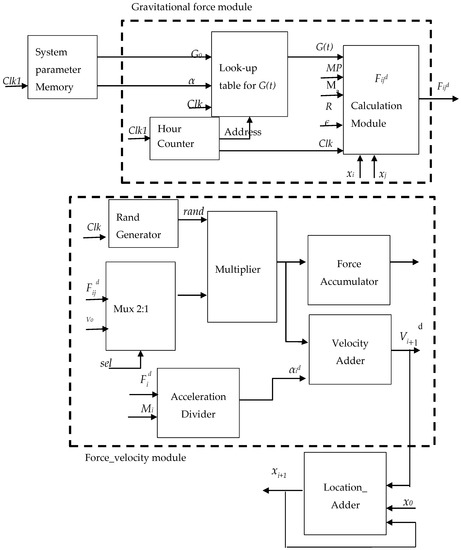
Figure 4.
The proposed field programming gate array (FPGA) hardware implementation of GSA unit.
5. System Data
5000 PEVs and RERs are simulated with three thermal units. Coal-fired generators are used, due to their low operational costs; and the range of heat rates of these generating units is typically from 9000 Btu/kWh to 11,000 with (fuel price = 1 $/MBtu). Table 3 and Table 4 represent the thermal power plant data, from Reference [28]. Table 5 represents wind and solar power plants data, from Reference [29].

Table 3.
Thermal generator data.

Table 4.
Thermal generator energy data.

Table 5.
RERs (wind, solar) power plants.
Random model parameters of PEVs are: Anticipated total number of PEVs in the smart grid = 5000; Maximum battery capacity = 25 kWh; Minimum battery capacity = 10 kWh; Average battery capacity “Pavg” = 15 kWh; Charging/discharging frequency = 1 per day; Departure state of charge (SOC) “Ψdep” = 50%; Efficiency “η” = 85%. A typical PEV requires about 2.6 $/gallon (fuel price = 1 $/MBtu) for gasoline price, 8.22 kWh/day (41.1 MWh/day) for 5000 vehicles. The emission factor for fuel oil is from Table 1, presuming the scenario for simulation of PEVs according to the demand, which is comparatively low during hours 1–7, 16–19 and 23–24 (a total of 12 h). PEVs can be charged during the off-peak load. In Figure 5, an additional 41.1 MWh load for 5000 vehicles. Estimating at each hour certain vehicles’ number will be charged [29]. The batteries’ cost function of PEVs is represented as a linear function of the absolute of its discharged power at each hour, as shown in Equation (17):
where and are the operational cost coefficients of the batteries of PEVs, which are generally associated with the maintenance costs. The parameters are assumed as follows [8]:
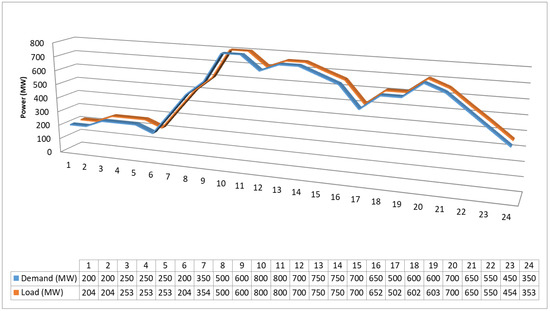
Figure 5.
PEVs Load leveling. Note: The PEVs is considered as load during off peak excluding hour 8, until hour 15, and hour 20 until hour 22.
The operation cost for solar energy is (14.597 $/MW) and for wind energy is (10 $/MW), which are obtained from the International Renewable Energy Agency (IRENA) [30].
6. Simulation Results
Six generators are represented in this paper to find the solution of the CEED problem. They are connected to IEEE 30 bus, which is illustrated in Figure 6. The three thermal (coal-fired) generators are installed on busses 1, 2, 3; PEVs are installed on bus 5; one wind plant is installed on bus 8; and one solar plant is installed on bus 13. The different demand values for 24 h are considered:
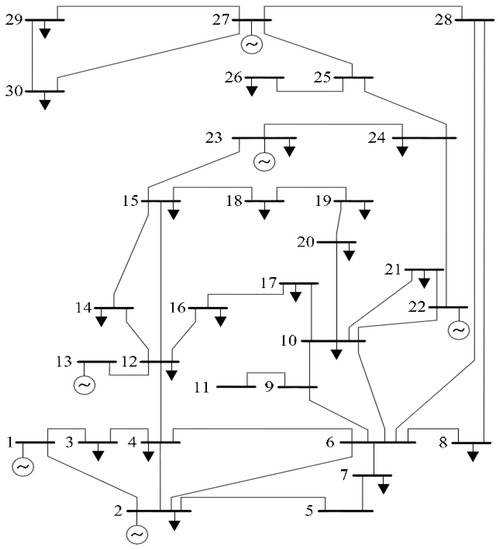
Figure 6.
IEEE 30 bus system. Note: Generators are on buses—1, 2, 5, 8, 11, and 13.
Demand (hour) = [200; 200; 250; 250; 250; 200; 350; 500; 600; 800; 800; 700; 750; 750; 700; 650; 500; 600; 700; 650; 550; 450; 350].
The transmission losses of the system are calculated by Newton Raphson method, using MATLAB. The parameters of the proposed algorithm (GSA) are illustrated in Table 2. Four scenarios are being applied and the results from the proposed algorithm (GSA) are compared with and Dynamic Programming (DP). The CEED problem is simulated in MATLAB R2016a (The MathWorks, Inc., Natick, MA, USA).
6.1. Scenario 1 (Base Case)
Scenario 1 shows the scheduling unit commitment for only the three thermal units, which are installed on busses 1, 2 and 5, by considering the transmission line losses of the IEEE 30 bus system, as shown in Table 6.

Table 6.
Base case of 3 coal-fired generators implementing by the GSA.
6.2. Scenario 2 (PEVs and the Three Coal-Fired Units)
Scenario 2 represents the integration of 5000 PEV (V2G/G2V), which are installed on bus 8, with the three thermal units. Load is leveled when the load of PEVs (G2V) is appended to demand, Positive and negative values mention as V2G/G2V (discharging/charging) respectively. By comparing both Scenario 1 and Scenario 2, start-up and fuel cost excess when integrating PEVs with the three coal-fired generating units by 3500 $/day; 38,021.398 $/day. However, the emission and the losses are decreased by 80.747 ton/day; 117.816 MW/day from the dispatchable generating units and PEVs when supplying the demand.
6.3. Scenario 3 (RERs, and Three Coal-Fired Units)
Scenario 3 represents the integration of the RERs (wind and solar), which are installed on busses 11 and 13, with the coal-fired power plants, simulation results by using the GSA. Integrating RERs (wind, solar) to partially exchange the conventional units will participate in decreasing both the emission and losses costs. The operation and maintenance prices significantly reducing in spite of the relatively high production costs of renewable energy resources, so that this can encourage the use of energy resources and also decarbonize the emissions in the smart grid.
6.4. Scenario 4 (RERs, PEVs, and the Three Coal-Fired Units)
Both wind and solar plants are installed on busses 11 and 13 respectively to lower emissions from both the coal-fired generators and PEVs. Moreover, PEVs are installed on bus 8 to handle the intermittency of RERs. Subsequently, the reliability and adequacy of the smart grid can be improved against any unanticipated uncertainty behavior for RERs by installing both RES and PEVs in the smart grid. A considerable reduction in losses by installed both RERs and PEVs with the thermal generators into the smart grid manifested, which fell to 11.717 MW/day as compared to installing RERs with the three coal-fired generators. Emission cost fell to 1323.308 ton/day as compared to integrating PEVs into the coal-fired generators. Table 7 illustrates the total system losses, emission and emission cost. Comparing the results are attained from the intended technique (GSA) with the forward dynamic programming (DP). The whole comparison in Table 7 illustrates the efficiency of the GSA in finding the unit commitment’s solution. The GSA execution time is less than that of the DP. As the complexity of the problem increases from scenario 3 to scenario 4, DP has needed a computer with higher specifications for execution. The emission cost is increased inconsiderable by integrating combined PEVs, but PEVs enhance wind and solar units. Therefore, it is worthy to exploit in the PEVs (electrically based), which will produce more lowering in the cost of emissions and losses of the system. Concentrating on the production cost in any case is to reduce the cost to 2/3 of its total cost, but the operation cost will be excessed on the long-dated.

Table 7.
Results synopsis for GSA and Dynamic Programming (DP) (implicating emission cost and losses of the system).
Considering losses of IEEE 30 bus system and comparing the obtained results in Table 7 with Table 8 in Reference [31] without considering transmission line losses, it is found that:

Table 8.
Results summary for GSA (including emission cost without considering losses of the system) [23].
- In case 1: The start-up cost, and emission is significantly increasing by 800 $/day, 866.869 ton/day.
- In case 2: The start-up cost, and emission is significantly increasing by 3000 $/day, 754.354 ton/day.
- In case 3: The start-up cost, and emission is significantly increasing by 500 $/day, 768.636 ton/day.
- In case 4: A significant reduction in the start-up cost by1800 $/day. However, the emission is significantly increasing by 829.781 ton/day.
7. Conclusions
The unit commitment problem in this study has been explained in four different scenarios with two algorithms, considering the transmission line losses of the IEEE 30 bus system, fitted with results and analysis to fulfil; (i) Lowering both the losses and total production cost inclosing the emission cost; (ii) The emissions are decarbonized from both the dispatchable generating units and the transportation sector; (iii) A new technology is provided by replacing fuel-fired vehicles with electric motor vehicles with environment-friendly batteries and stimulating the EV-owners to participate in the demand response program and provide the grid with electrical power during the rush hour periods. The new algorithm, GSA fulfilment is promising better solutions than DP technique. In the four scenarios, the GSA submits competitive solutions with agreeable degree of accuracy in the results. The conclusion from this study is that, integrating both PEVs and RERs with the dispatchable generating units fulfilled many objectives; (i) The adequacy of the smart electric network shows a significant improvement; (ii) The emissions from the electricity sector and transportation sector is decarbonized by nearly 11.2% of the base case emissions; (iii) New types of unit commitment sources is scheduled with different coordinate actions by environment-friendly electrical energy storage, such as PEVs (V2G) to encourage the customers to provide electric energy to power the network during the peak demand intervals; (iv) Taking both losses and emission costs into consideration reduce significantly in the amount of power generation from the thermal units for the sake of power generated from RERs and PEVs. Implementing the Decarbonized Unit Commitment on FPGA can provide a fast response, due to FPGA parallel architecture. This can be appropriate with the real time operation, as the FPGA can perform all calculations in order of microseconds. Flexibility and reprogramming also can be achieved, which allow to perform simply any modifications/upgrading on the proposed algorithm without affecting the whole system. In addition, the smaller I/O latency, lower sampling rate required and integrating an ADC/DAC with the FPGA give other essential aspects can be achieved from this hardware platform. Accordingly, integrating the proposed unit with the smart substation section in the smart grid or as a controller in smart microgid can be easily attained by realizing it on a suitable FPGA platform.
Author Contributions
The six authors contribute in the whole work. Conceptualization, R.A.S. and N.H.E.-A.; Data curation, A.B.; Formal analysis, H.-A.I.E.; Investigation, H.H.I. and H.K.T.; Methodology, R.A.S.; Project administration, N.H.E.-A.; Resources, A.B.; Software, H.H.I.; Supervision, R.A.S., A.B. and H.K.T.; Validation, H.-A.I.E.; Writing—original draft, H.-A.I.E. and H.H.I.; Writing—review & editing, N.H.E.-A. and H.K.T.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| PGi | the output power of each thermal generator “i” at each hour |
| , | the minimum and maximum output limits of the i-th thermal generator respectively |
| the total active transmission line losses of the system at each hour | |
| the current of each feeder i at each hour in the system | |
| the transmission line resistance of each feeder in the system at each hour. | |
| the total number of feeders in the IEEE 30 bus electric system | |
| A, B, C | a quadratic fuel cost function coefficients of each thermal generator |
| NG | the conventional thermal generators’ number |
| the output power from a wind plant at each hour | |
| the output power from a solar plant at each hour | |
| A | CO2 emission factor |
| the emission penalty factor | |
| the power of each vehicle j | |
| , | the operational and maintenance cost coefficients of the batteries of PEVs. |
| the electric network’s efficiency | |
| Vehicles’ number that are linked to the network at this hour. | |
| the total vehicles in the network | |
| NG | number of conventional thermal generating units that operate at each hour in the unit commitment objective function |
| the present state of charge (SOC) | |
| the departure state of charge (SOC) | |
| the storage energy depletion at minimum level | |
| the charging up to maximum level | |
| on/off state of each unit “i” | |
| L | the states’ number to look for each interval in DP algorithm |
| N | the number of strategies to save at each step in DP algorithm |
| 2N − 1 | maximum value of X or N in DP algorithm |
References
- Lopez, C.J.; Ano, O.; Esteybar, D.O. Stochastic unit commitment & optimal allocation of reserves: A hybrid decomposition approach. IEEE Trans. Power Syst. 2018. [Google Scholar] [CrossRef]
- Elsayed, A.M.; Maklad, A.M.; Farrag, S.M. A New Priority List Unit Commitment Method for Large-Scale Power Systems. In Proceedings of the 2017 Nineteenth International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 19–21 December 2017; pp. 359–367. [Google Scholar]
- Venayagamoorthy, G.K.; Braband, G. Carbon reduction potential with intelligent control of power systems. In Proceedings of the 17th World Congress: International Federation of Automatic Control, Seoul, Korea, 6–11 July 2008. [Google Scholar]
- Nguyen, D.T.; Le, L.B. Risk-constrained profit maximization for microgrid aggregators with demand response. IEEE Trans. Smart Grid 2015, 6, 135–146. [Google Scholar] [CrossRef]
- Center for Climate and Energy Solution. Climate Solution, Technology Solution, Electrical Vehicles. Available online: www.c2es.org/content/electric-vehicles/ (accessed on 3 March 2018).
- Little, A.D.; Browning, L.; Santini, D.; Vyas, A.; Taylor, D.; Markel, T.; Duvall, M.; Graham, R.; Miller, A.; Frank, A.; et al. Comparing the Benefits and Impacts of Hybrid Electric Vehicle Options for Compact Sedan and Sport Utility Vehicles; Final Report 1006892; Electric Power Research Institute (EPRI): Palo Alto, CA, USA, 2002; Available online: http://www.evworld.com/library/EPRI_sedan_options.pdf (accessed on 13 March 2018).
- Corrigan, D.; Masias, A. Batteries for Electric and Hybrid Vehicles. In Linden’s Handbook of Batteries, 4th ed.; Reddy, T.B., Ed.; McGraw Hill: New York, NY, USA, 2011. [Google Scholar]
- Ghasemi, A.; Mortazavi, S.S.; Mashhour, E. Hourly demand response and battery energy storage for imbalance reduction of smart distribution company embedded with electric vehicles and wind farms. Renew. Energy 2016, 85, 124–136. [Google Scholar] [CrossRef]
- Morais, H.; Sousa, T.; Soares, J.; Faria, P.; Vale, Z. Distributed energy resources management using plug-in hybrid electric vehicles as a fuel-shifting demand response resource. Energy Convers. Manag. 2015, 97, 78–93. [Google Scholar] [CrossRef]
- Un-Noor, F.; Padmanaban, S.; Mihet-Popa, L.; Mollah, M.N.; Hossain, E. A Comprehensive Study of Key Electric Vehicle (EV) Components, Technologies, Challenges, Impacts, and Future Direction of Development. Energies 2017, 10, 1217. [Google Scholar] [CrossRef]
- Li, K.; Xue, Y.; Cui, S.; Niu, Q.; Yang, Z.; Luk, P. Advanced computational methods in energy, power, electric vehicles and their integration. In Proceedings of the International Conference on Life System Modeling and Simulation (LSMS2017) and International Conference on Intelligent Computing for Sustainable Energy and Environment (ICSEE 2017), Nanjing, China, 22–24 September 2017; Part III. Springer: Berlin, Germany, 1842. [Google Scholar]
- Rashed, E.; Nezamabadi-Pour, H.; Saryazd, S. GSA: A Gravitational Search Algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Rashedi, E.; Rashedi, E.; Nezamabadi-Pour, H. A comprehensive survey on gravitational search algorithm. Swarm Evolut. Comput. 2018, in press. [Google Scholar] [CrossRef]
- Mahdad, B.; Srairi, K. Interactive gravitational search algorithm and pattern search algorithms for practical dynamic economic dispatch. Int. Trans. Electr. Energy Syst. 2015, 25, 2289–2309. [Google Scholar] [CrossRef]
- Jiang, S.; Wang, Y.; Ji, Z. Convergence analysis and performance of an improved gravitational search algorithm. Appl. Soft Comput. 2014, 24, 363–384. [Google Scholar] [CrossRef]
- Thakur, N.; Titare, L.S. Determination of unit commitment problem using dynamic programming. Int. J. Nov. Res. Electr. Mech. Eng. 2016, 3, 24–28. [Google Scholar]
- Krishnamurthy, S.; Tzoneva, R. Comparative analyses of Min-Max and Max-Max price penalty factor approaches for multi criteria power system dispatch problem with valve point effect loading using Lagrange’s method. In Proceedings of the 2011 IEEE International Conference on Power and Energy Systems (ICPS), Chennai, India, 22–24 December 2011. [Google Scholar]
- World Bank and Ecofys. Carbon Pricing Watch 2017. 2017. Available online: https://openknowledge.worldbank.org/handle/10986/26565 (accessed on 3 March 2018).
- Brigatto, G.A.A.; Carmargo, C.C.B.; Sica, E.T. Multi-Objective Optimization of Distributed Generation Portofolio Insertion Strategies. In Proceedings of the 2010 IEEE/PES Transmission and Distribution Conference and Exposition: Latin America (T&D-LA), Sao Paulo, Brazil, 8–10 November 2010. [Google Scholar]
- Altera Corporation. Overcoming Smart Grid Equipment Design Challenges with FPGAs; Altera Corporation: San Jose, CA, USA, 2013. [Google Scholar]
- Yang, Q.; An, D.; Yu, W.; Tan, Z.; Yang, X. Towards Stochastic Optimization-Based Electric Vehicle Penetration in a Novel Archipelago Microgrid. Sensors 2016, 16, 907. [Google Scholar] [CrossRef] [PubMed]
- Vadana, D.P.; Kottayil, S.K. Autonomous Control of Smart Micro Grid in Islanding Mode. Procedia Technol. 2015, 21, 204–211. [Google Scholar] [CrossRef]
- Wang, Y.; Dinavahi, V. Real-time digital multi-function protection system on reconfigurable hardware. IET Gener. Transm. Distrib. 2016, 10, 2295–2305. [Google Scholar] [CrossRef]
- Zhang, B.; Wu, Y.; Jin, Z.; Wang, Y. A Real-Time Digital Solver for Smart Substation Based on Orders. Energies 2017, 10, 1795. [Google Scholar] [CrossRef]
- Razzaghi, R.; Mitjans, M.; Rachidi, F.; Paolone, M. An automated FPGA real-time simulator for power electronics and power systems electromagnetic transient applications. Electr. Power Syst. Res. 2016, 141, 147–156. [Google Scholar] [CrossRef]
- Dufour, C.; Cense, S.; Jalili-Marandi, V.; Bélanger, J. Review of state-of-the-art solver solutions for HIL simulation of power systems, power electronic and motor drives. In Proceedings of the 15th European Conference on Power Electronics and Applications (EPE), Lille, France, 2–6 September 2013; pp. 1–12. [Google Scholar]
- Zhang, B.; Fu, S.; Jin, Z.; Hu, R. A Novel FPGA-Based Real-Time Simulator for Micro-Grids. Energies 2017, 10, 1239. [Google Scholar] [CrossRef]
- He, D.; Tan, Z.; Harley, R.G. Chance constrained unit commitment with wind generation and superconducting magnetic energy storages. In Proceedings of the IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012. [Google Scholar]
- Saber, A.Y.; Venayagamoorthy, G.K. Efficient utilization of renewable energy sources by gridable vehicles in cyber-physical energy systems. IEEE Syst. J. 2010, 4, 285–294. [Google Scholar] [CrossRef]
- International Renewable Energy Agency (IRENA). Renewable Power Generation Costs in 2017; International Renewable Energy Agency: Abu Dhabi, UAE, 2018; Available online: http://www.irena.org/publications/2018/Jan/Renewable-power-generation-costs-in-2017 (accessed on 18 March 2018).
- ElAzab, H.-A.I.; Swief, R.A.; El-Amary, N.H.; Temraz, H.K. Unit Commitment Towards Decarbonized Network Facing Fixed and Stochastic Resources Applying Water Cycle Optimization. Energies 2018, 11, 1140. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).