Influence of Blade Leading-Edge Shape on Cavitation in a Centrifugal Pump Impeller
Abstract
:1. Introduction
2. Numerical Method
3. Case and Setup
3.1. Impeller Geometry
3.2. Domain Modeling and Meshing
3.3. Computational Setup
4. Model Tuning
4.1. Tuning Process
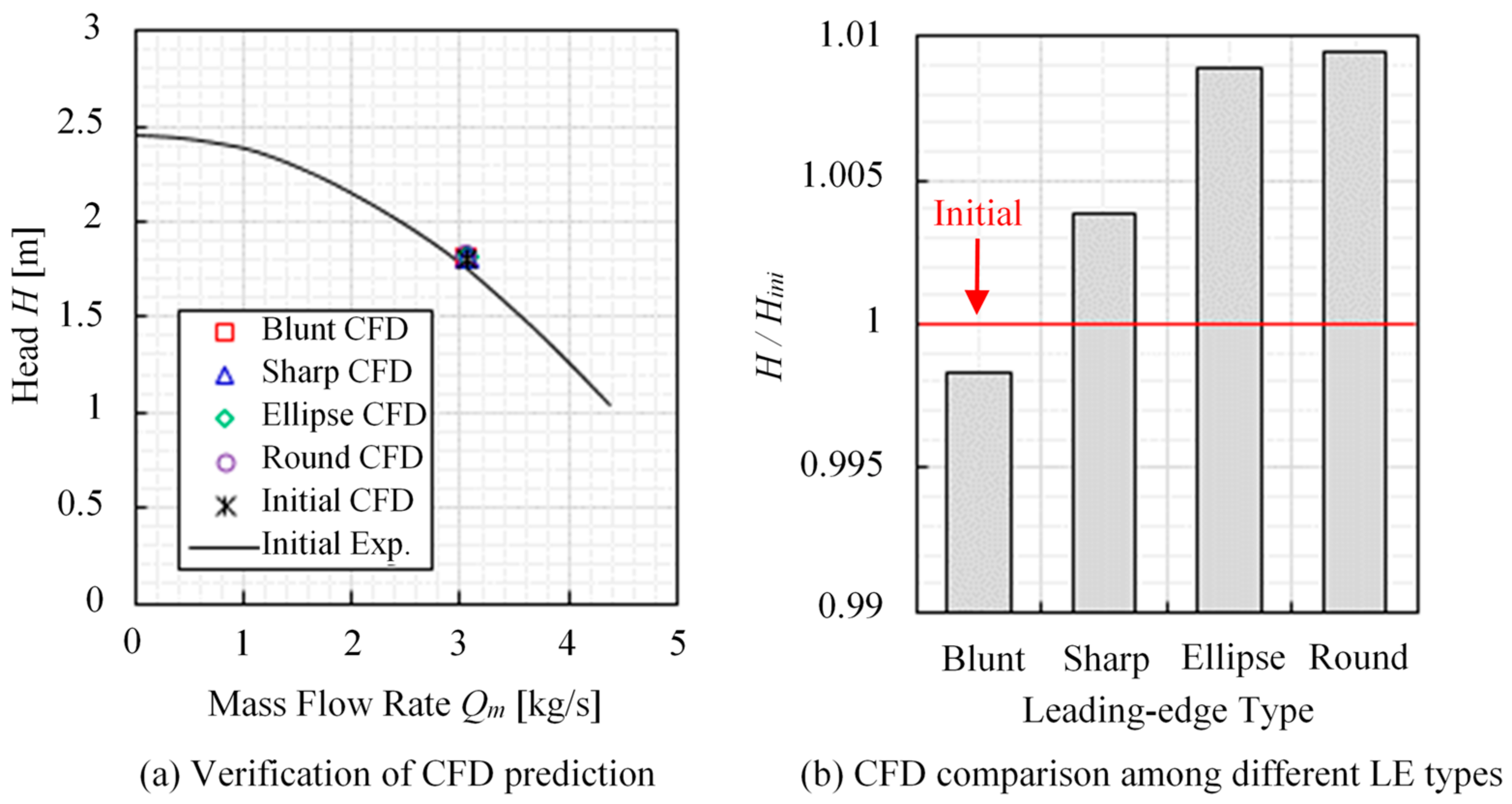
4.2. Verification of Tuning
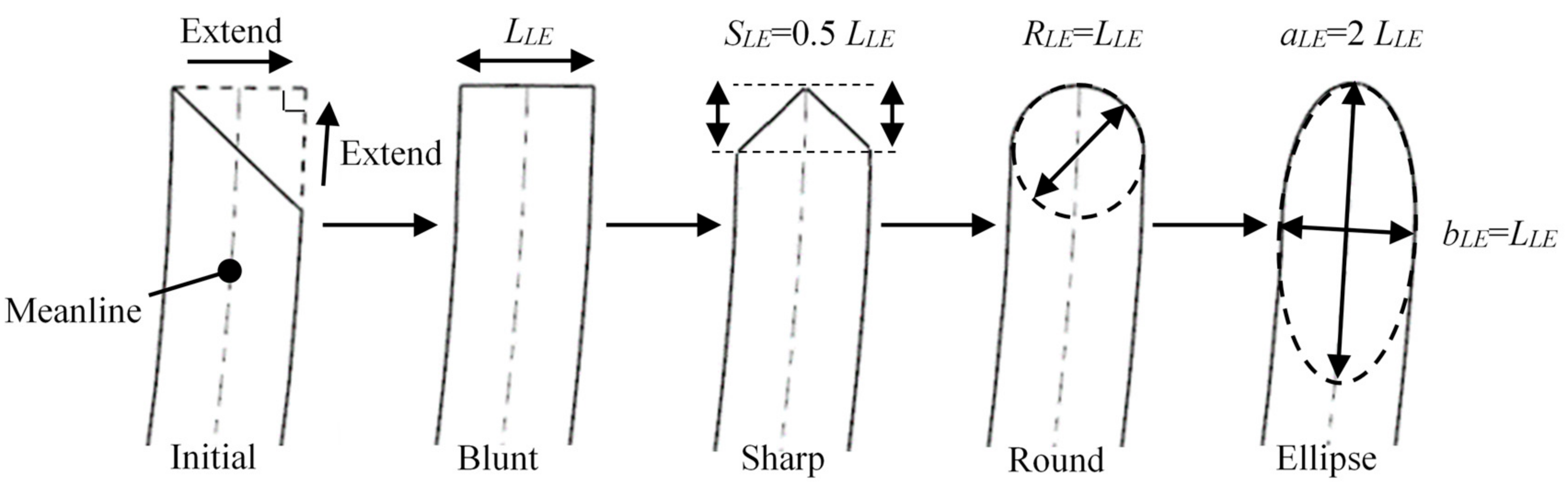
5. Leading-Edge Reshaping
6. Comparative Analyses
6.1. Pump Performance
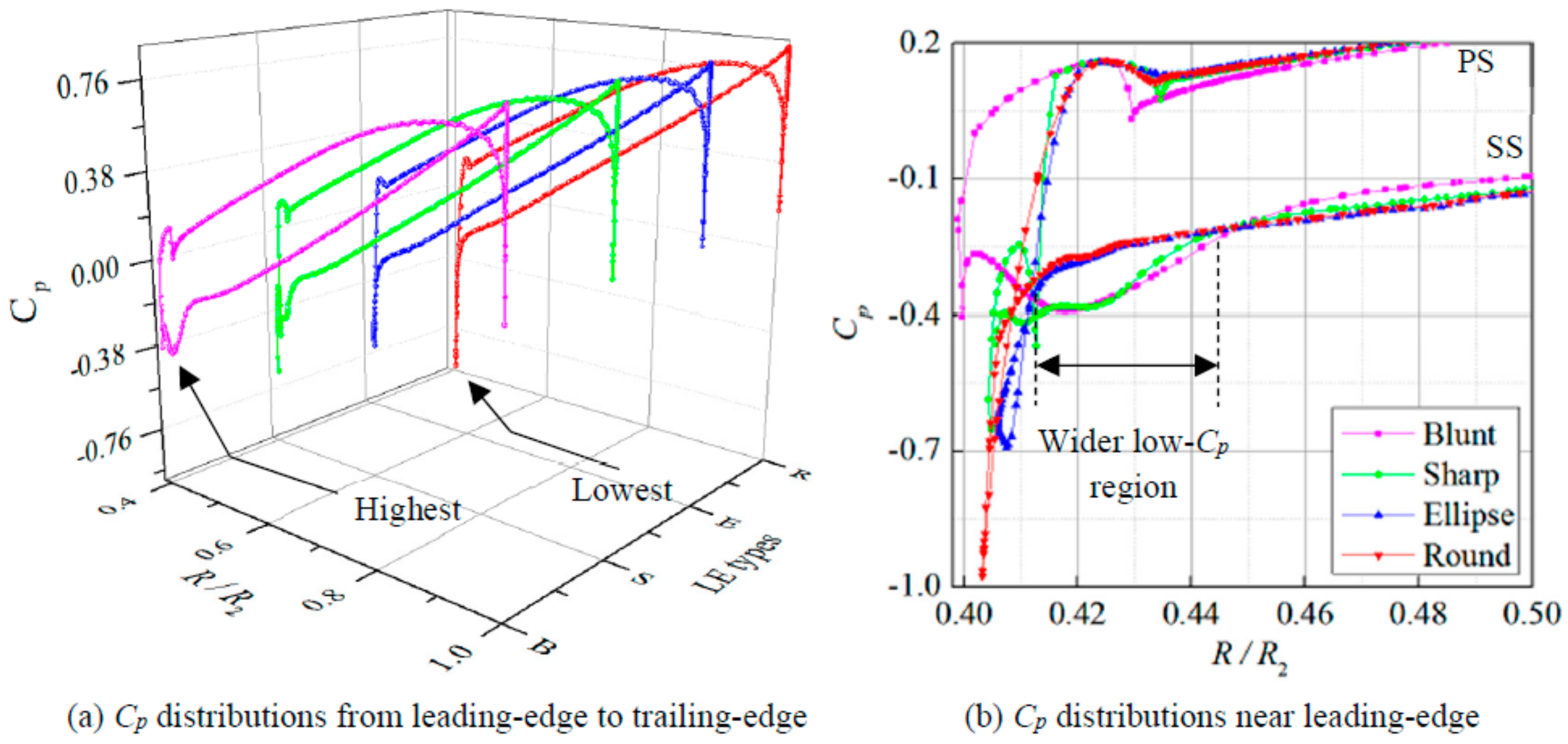
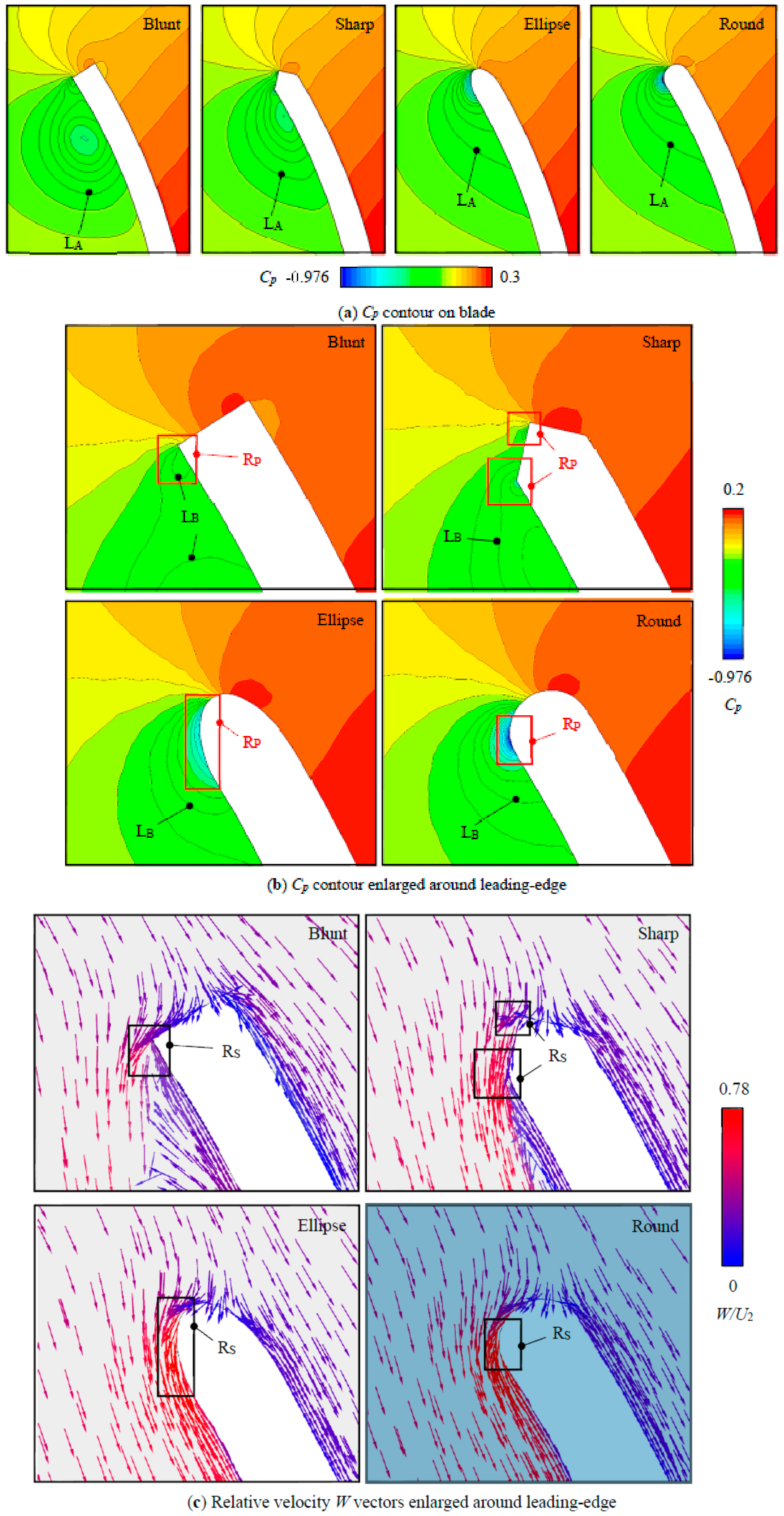
6.2. Pressure Distribution
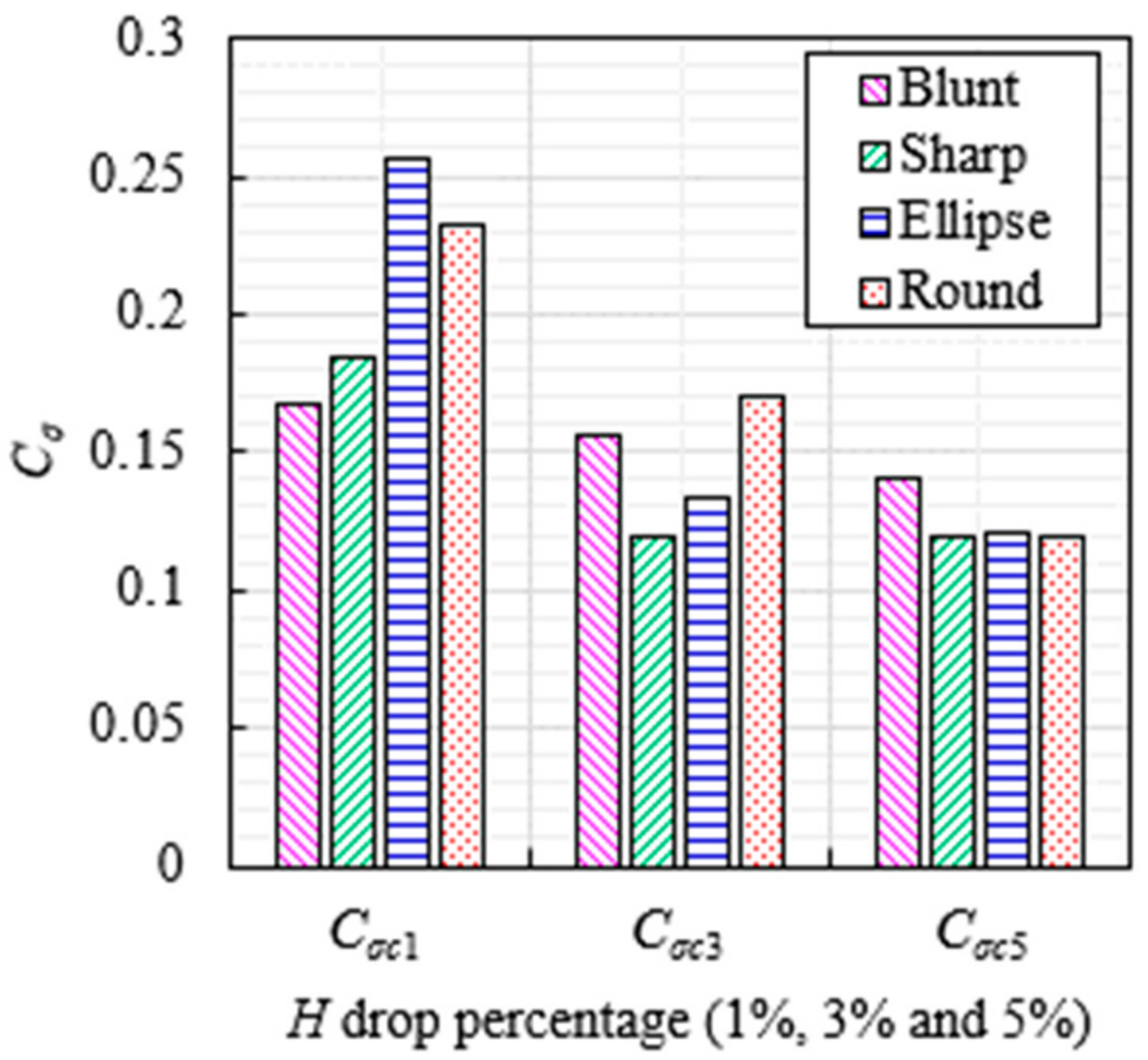
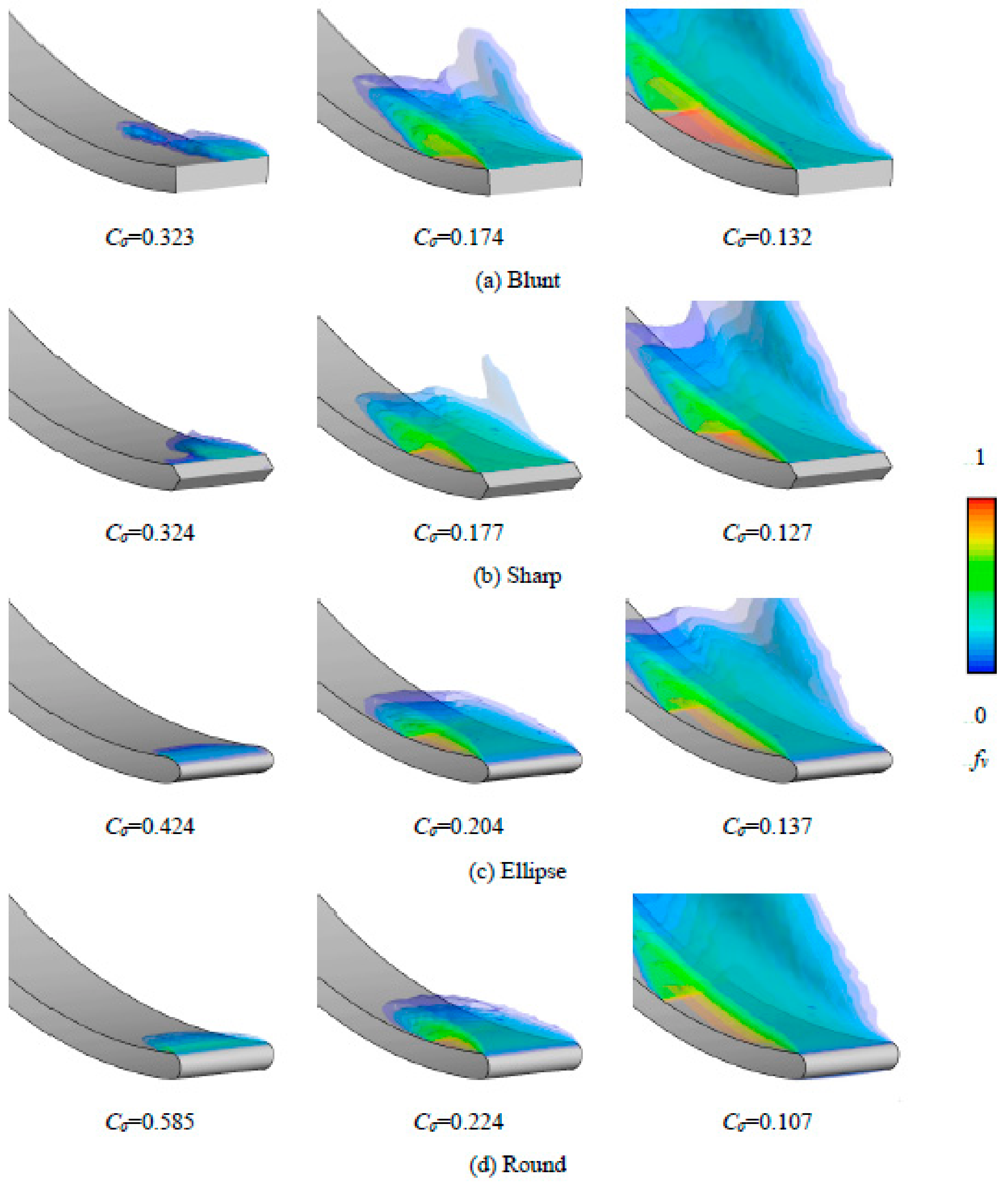
6.3. Development of Cavitation Scale
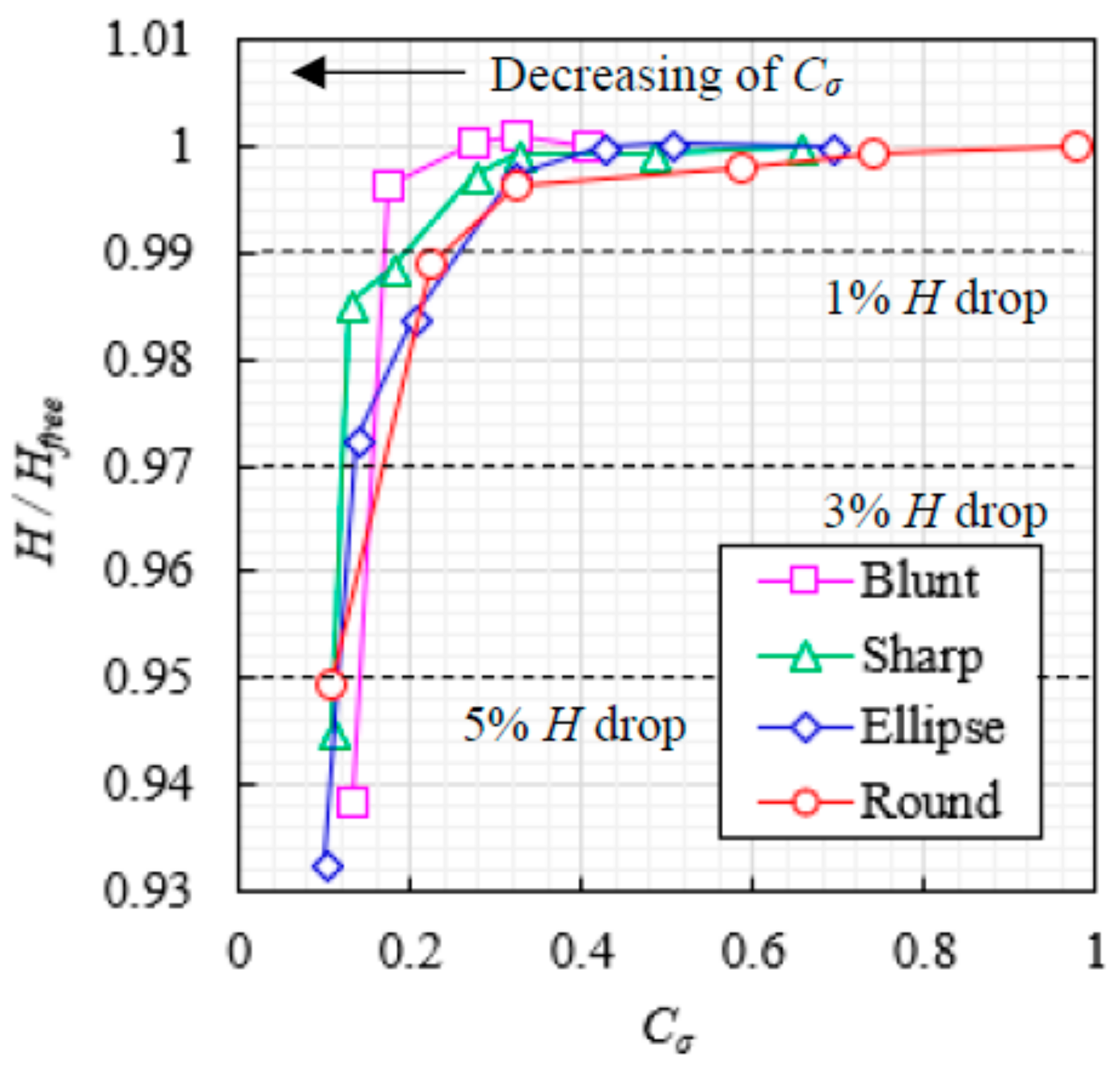
6.4. Cavitation-Induced Performance Drop
6.5. Flow Field Analyses
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Franc, J.P.; Michel, J.M. Fundamentals of Cavitation; Springer: Heidelberg, Germany, 2010. [Google Scholar]
- Brennen, C.E. Cavitation and Bubble Dynamics; Oxford University Press: New York, NY, USA, 1995. [Google Scholar]
- Henry, W. Experiments on the quantity of gases absorbed by water, at different temperatures, and under different pressures. Philos. Trans. R. Soc. Lond. 1803, 93, 29–274. [Google Scholar] [CrossRef]
- Arndt, R.E.A. Cavitation in fluid machinery and hydraulic structures. Annu. Rev. Fluid Mech. 1981, 13, 273–326. [Google Scholar] [CrossRef]
- Wu, Q.; Huang, B.; Wang, G.; Cao, S.; Zhu, M. Numerical modelling of unsteady cavitation and induced noise around a marine propeller. Ocean Eng. 2018, 160, 143–155. [Google Scholar] [CrossRef]
- Valentín, D.; Presas, A.; Egusquiza, M.; Valero, C.; Egusquiza, E. Transmission of high frequency vibrations in rotating systems. Application to cavitation detection in hydraulic turbines. Appl. Sci. 2018, 8, 451. [Google Scholar] [CrossRef]
- Mouvanal, S.; Chatterjee, D.; Bakshi, S.; Burkhardt, A.; Mohr, V. Numerical prediction of potential cavitation erosion in fuel injectors. Int. J. Multiph. Flow 2018, 104, 113–124. [Google Scholar] [CrossRef]
- Hao, Y.; Tan, L. Symmetrical and unsymmetrical tip clearances on cavitation performance and radial force of a mixed flow pump as turbine at pump mode. Renew. Energy 2018, 127, 368–376. [Google Scholar] [CrossRef]
- Hirschi, R.; Dupont, P.; Avellan, F.; Favre, J.N.; Guelich, J.F.; Parkinson, E. Centrifugal pump performance drop due to leading edge cavitation: Numerical predictions compared with model tests. J. Fluids Eng. Trans. ASME 1998, 120, 705–711. [Google Scholar] [CrossRef]
- Guennoun, F.; Farhat, M.; Ait Bouziad, Y.; Avellan, F.; Pereira, F. Experimental investigation of a particular traveling bubble cavitation. In Proceedings of the 5th International Symposium on Cavitation, Osaka, Japan, 1–4 November 2003. [Google Scholar]
- Dijkers, R.J.; Fumex, B.; de Woerd, J.O.; Kruyt, N.P.; Hoeijmakers, H.W. Prediction of sheet cavitation in a centrifugal pump impeller with the three-dimensional potential-flow model. In Proceedings of the 2005 ASME Fluids Engineering Division Summer Meeting and Exhibition, Houston, TX, USA, 1 January 2005. [Google Scholar]
- Shi, L.; Zhang, D.; Zhao, R.; Shi, W.; BPM, B.V. Visualized observations of trajectory and dynamics of unsteady tip cloud cavitating vortices in axial flow pump. J. Fluid Sci. Technol. 2017, 12, JFST0007. [Google Scholar] [CrossRef]
- Epps, B.; Víquez, O.; Chryssostomidis, C. A method for propeller blade optimization and cavitation inception mitigation. J. Ship Prod. Des. 2015, 31, 88–99. [Google Scholar] [CrossRef]
- Tuzson, J. Centrifugal Pump Design; Wiley-Interscience: Hoboken, NJ, USA, 2000. [Google Scholar]
- Han, X.; Kang, Y.; Li, D.; Zhao, W. Impeller Optimized Design of the Centrifugal Pump: A Numerical and Experimental Investigation. Energies 2018, 11, 1444. [Google Scholar] [CrossRef]
- Xie, H.; Song, M.; Liu, X.; Yang, B.; Gu, C. Research on the Simplified Design of a Centrifugal Compressor Impeller Based on Meridional Plane Modification. Appl. Sci. 2018, 8, 1339. [Google Scholar] [CrossRef]
- Li, P.; Han, Z.; Jia, X.; Mei, Z.; Han, X. Analysis of the Effects of Blade Installation Angle and Blade Number on Radial-Inflow Turbine Stator Flow Performance. Energies 2018, 11, 2258. [Google Scholar] [CrossRef]
- Guan, X. Modern Pumps Theory and Design; China Astronautics Publishing House: Beijing, China, 2011. [Google Scholar]
- Wei, W.; Pengbo, L.; Xiaofang, W. Blade optimal design and cavitation investigation based on state equation model of mixed-flow pump. J. Dalian Univ. Technol. 2013, 53, 189–194. [Google Scholar]
- Ruan, H.; Luo, X.; Liao, W.; Zhao, Y. Effects of low pressure edge thickness on cavitation performance and strength for pump-turbine. Trans. Chin. Soc. Agric. Eng. 2015, 31, 32–39. [Google Scholar]
- Tao, R.; Xiao, R.; Wang, F.; Liu, W. Cavitation behavior study in the pump mode of a reversible pump-turbine. Renew. Energy 2018, 125, 655–667. [Google Scholar] [CrossRef]
- IH, S.; JW, A. Influence of the leading edge shape of a 2-dimensional hydrofoil on cavitation characteristics. J. Soc. Nav. Arch. Korea 2000, 37, 60–66. [Google Scholar]
- Kang, C.; Yang, M.; Wu, G.; Liu, H. Cavitation analysis near blade leading edge of an axial-flow pump. In Proceedings of the 2009 International Conference on Measuring Technology and Mechatronics Automation, Zhangjiajie, China, 11 April 2009. [Google Scholar]
- Hofmann, M.; Stoffel, B.; Friedrichs, J.; Kosyna, G. Similarities and geometrical effects on rotating cavitation in two scaled centrifugal pumps. In Proceedings of the 4th International Symposium on Cavitation, Pasadena, CA, USA, 20–23 June 2001. [Google Scholar]
- Christopher, S.; Kumaraswamy, S. Identification of critical net positive suction head from noise and vibration in a radial flow pump for different leading edge profiles of the vane. J. Fluids Eng. Trans. ASME 2013, 135, 121301. [Google Scholar] [CrossRef]
- Balasubramanian, R.; Sabini, E.; Bradshaw, S. Influence of impeller leading edge profiles on cavitation and suction performance. In Proceedings of the 27th International Pump Users Symposium, Houston, TX, USA, 12–15 September 2011. [Google Scholar]
- Bakir, F.; Kouidri, S.; Noguera, R.; Rey, R. Experimental analysis of an axial inducer influence of the shape of the blade leading edge on the performances in cavitating regime. J. Fluids Eng. Trans. ASME 2003, 143, 691–696. [Google Scholar] [CrossRef]
- Menter, F.R. Zonal two equation k-turbulence models for aerodynamic flows. AIAA Pap. 1993, 7, 2906. [Google Scholar]
- Menter, F.R. Ten years of experience with the SST turbulence model. Turbul. Heat Mass Transf. 2003, 4, 625–632. [Google Scholar]
- Launder, B.E.; Sharma, B.I. Application of the energy-dissipation model of turbulence to the calculation of flow near a spinning disc. Lett. Heat Mass Transf. 1974, 1, 131–137. [Google Scholar] [CrossRef]
- Wilcox, D.C. Re-assessment of the scale-determining equation for advanced turbulence models. AIAA J. 1988, 26, 1299–1310. [Google Scholar] [CrossRef]
- Spalart, P.R.; Shur, M. On the sensitization of turbulence models to rotation and curvature. Aerosp. Sci. Technol. 1997, 1, 297–302. [Google Scholar] [CrossRef]
- Pedersen, N.; Jacobsen, C.B.; Larsen, P.S. Flow in a centrifugal pump impeller at design and off-design conditions-part I: Particle image velocimetry (PIV) and laser Doppler velocimetry (LDV) measurements. J. Fluids Eng. Trans. ASME 2003, 125, 61–72. [Google Scholar] [CrossRef]
- Byskov, R.K.; Jacobsen, C.B.; Pedersen, N. Flow in a centrifugal pump impeller at design and off-design conditions-part II: Large eddy simulations. J. Fluids Eng. Trans. ASME 2003, 125, 73–83. [Google Scholar] [CrossRef]
- Zhang, W.; Ma, Z.; Yu, Y.C.; Chen, H.X. Applied new rotation correction k-ω SST model for turbulence simulation of centrifugal impeller in the rotating frame of reference. J. Hydrodyn. Ser. B 2010, 22, 404–407. [Google Scholar] [CrossRef]
- Huang, X.; Liu, Z.; Yang, W. Comparative study of SGS models for simulating the flow in a centrifugal-pump impeller using single passage. Eng. Comput. 2015, 32, 2120–2135. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, F.; Zhou, P. Evaluation of subgrid-scale models in large-eddy simulations of turbulent flow in a centrifugal pump impeller. Chin. J. Mech. Eng. 2012, 25, 911–918. [Google Scholar] [CrossRef]
- Zwart, P.J.; Gerber, A.G.; Belamri, T. A two-phase flow model for predicting cavitation dynamics. In Proceedings of the 5th International Conference on Multiphase Flow, Yokohama, Japan, 30 May–4 June 2004. [Google Scholar]

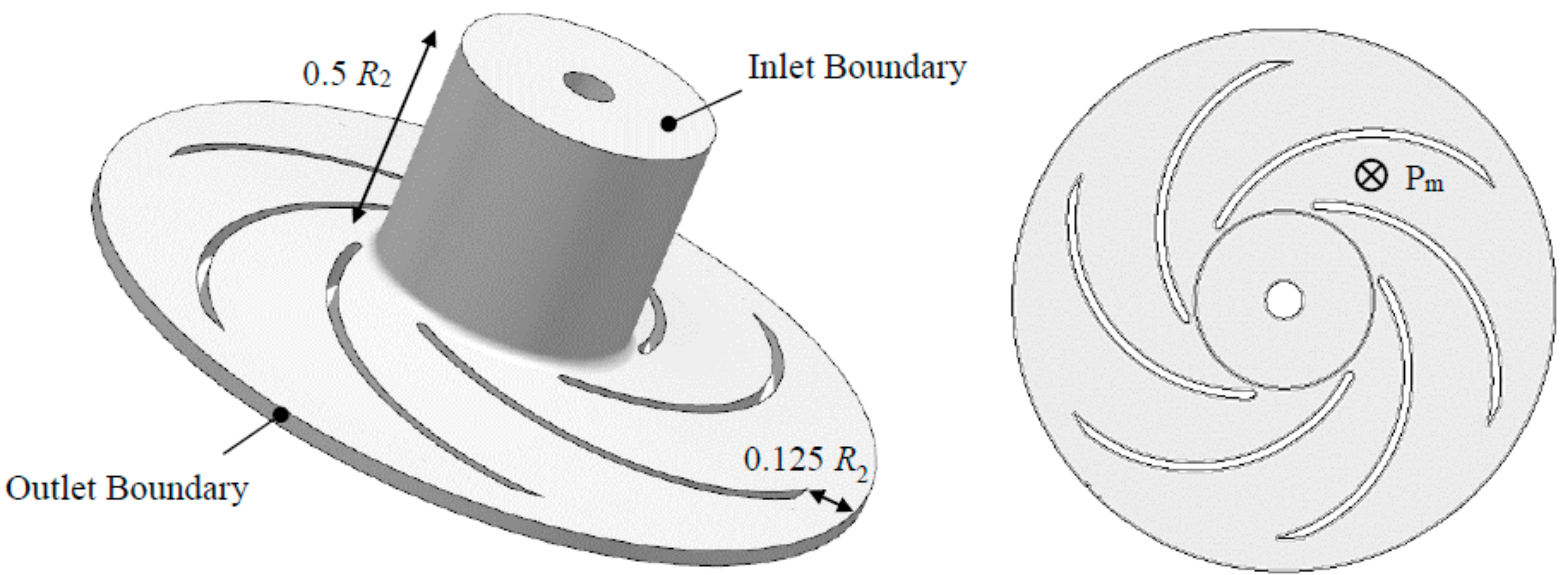
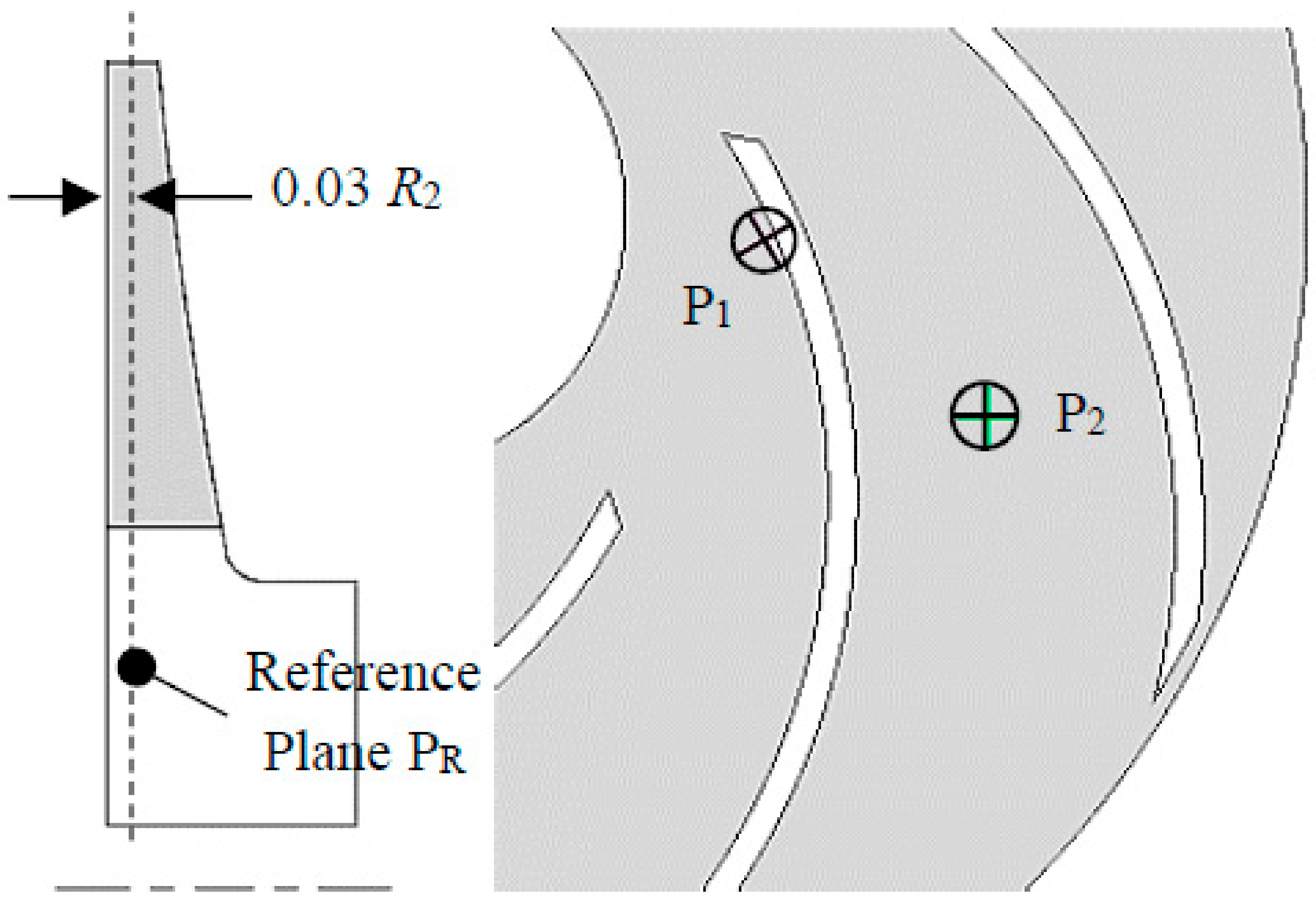
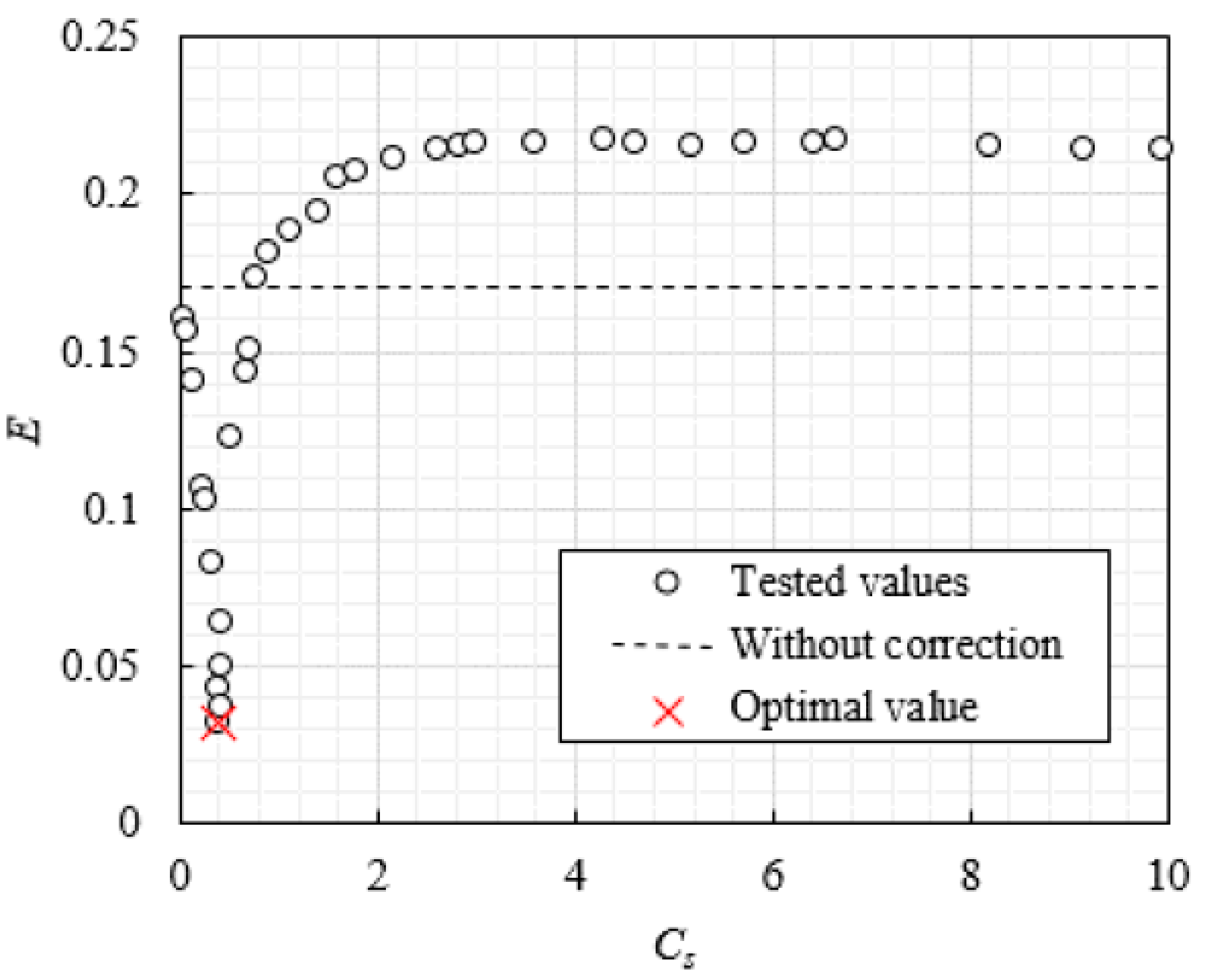

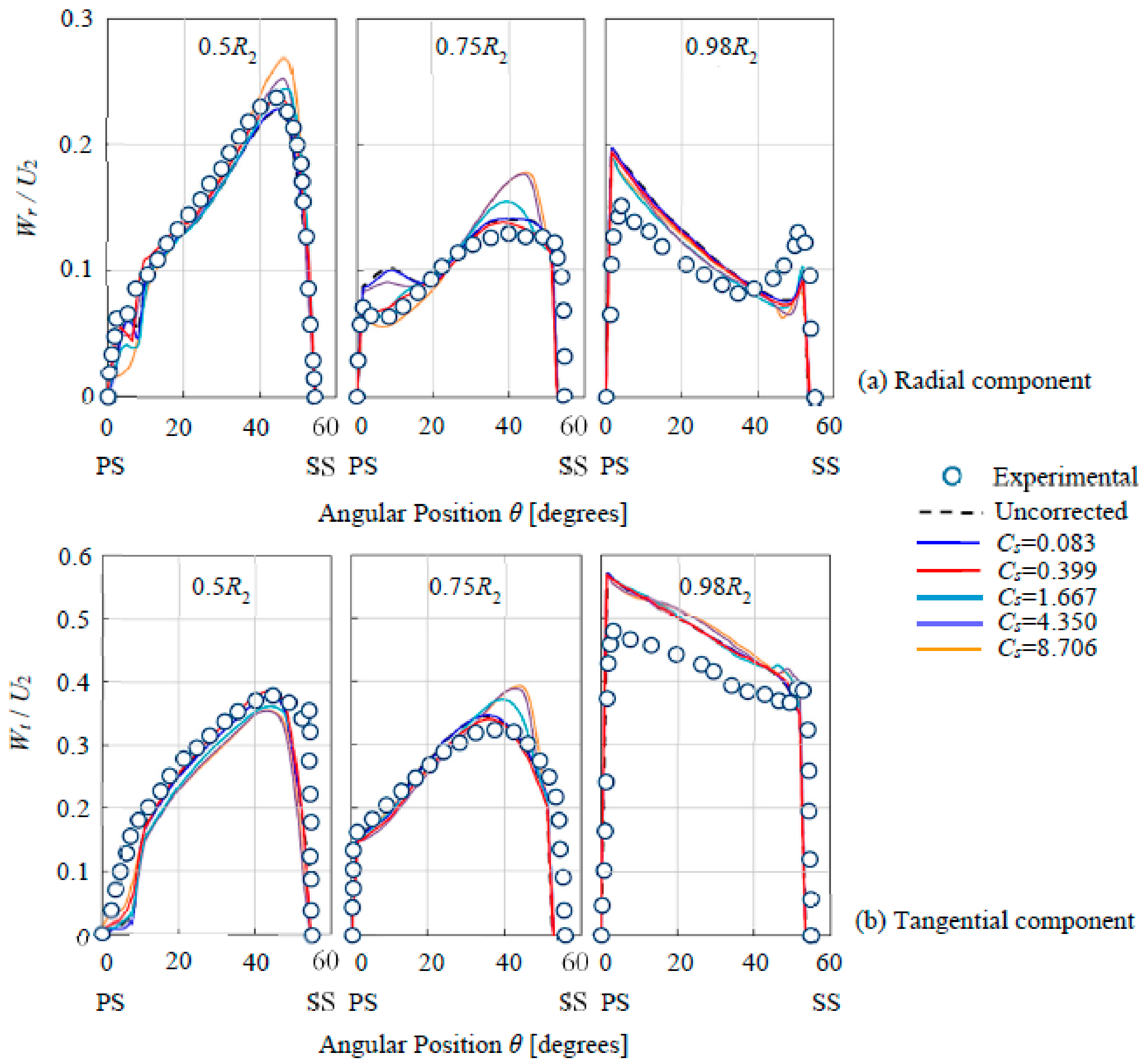

| No. | Mesh | Nodes | k2D on Pm [m2/s2] | Residual Against Mesh No. 1 |
|---|---|---|---|---|
| 1 | Very Coarse | 41308 | 1.5861 × 10−2 | - |
| 2 | Coarse | 82528 | 1.5383 × 10−2 | 3.014% |
| 3 | Medium | 159836 | 1.5130 × 10−2 | 1.645% |
| 4 | Fine | 323332 | 1.5082 × 10−2 | 0.317% |
| 5 | Very Fine | 602024 | 1.5083 × 10−2 | 0.007% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tao, R.; Xiao, R.; Wang, Z. Influence of Blade Leading-Edge Shape on Cavitation in a Centrifugal Pump Impeller. Energies 2018, 11, 2588. https://doi.org/10.3390/en11102588
Tao R, Xiao R, Wang Z. Influence of Blade Leading-Edge Shape on Cavitation in a Centrifugal Pump Impeller. Energies. 2018; 11(10):2588. https://doi.org/10.3390/en11102588
Chicago/Turabian StyleTao, Ran, Ruofu Xiao, and Zhengwei Wang. 2018. "Influence of Blade Leading-Edge Shape on Cavitation in a Centrifugal Pump Impeller" Energies 11, no. 10: 2588. https://doi.org/10.3390/en11102588
APA StyleTao, R., Xiao, R., & Wang, Z. (2018). Influence of Blade Leading-Edge Shape on Cavitation in a Centrifugal Pump Impeller. Energies, 11(10), 2588. https://doi.org/10.3390/en11102588






