Power and Fuel Economy of a Radial Automotive Thermoelectric Generator: Experimental and Numerical Studies
Abstract
:1. Introduction
2. Experimental Analysis
2.1. Radial ATEG
2.2. Experimental Set Up
2.3. Experimental Cases
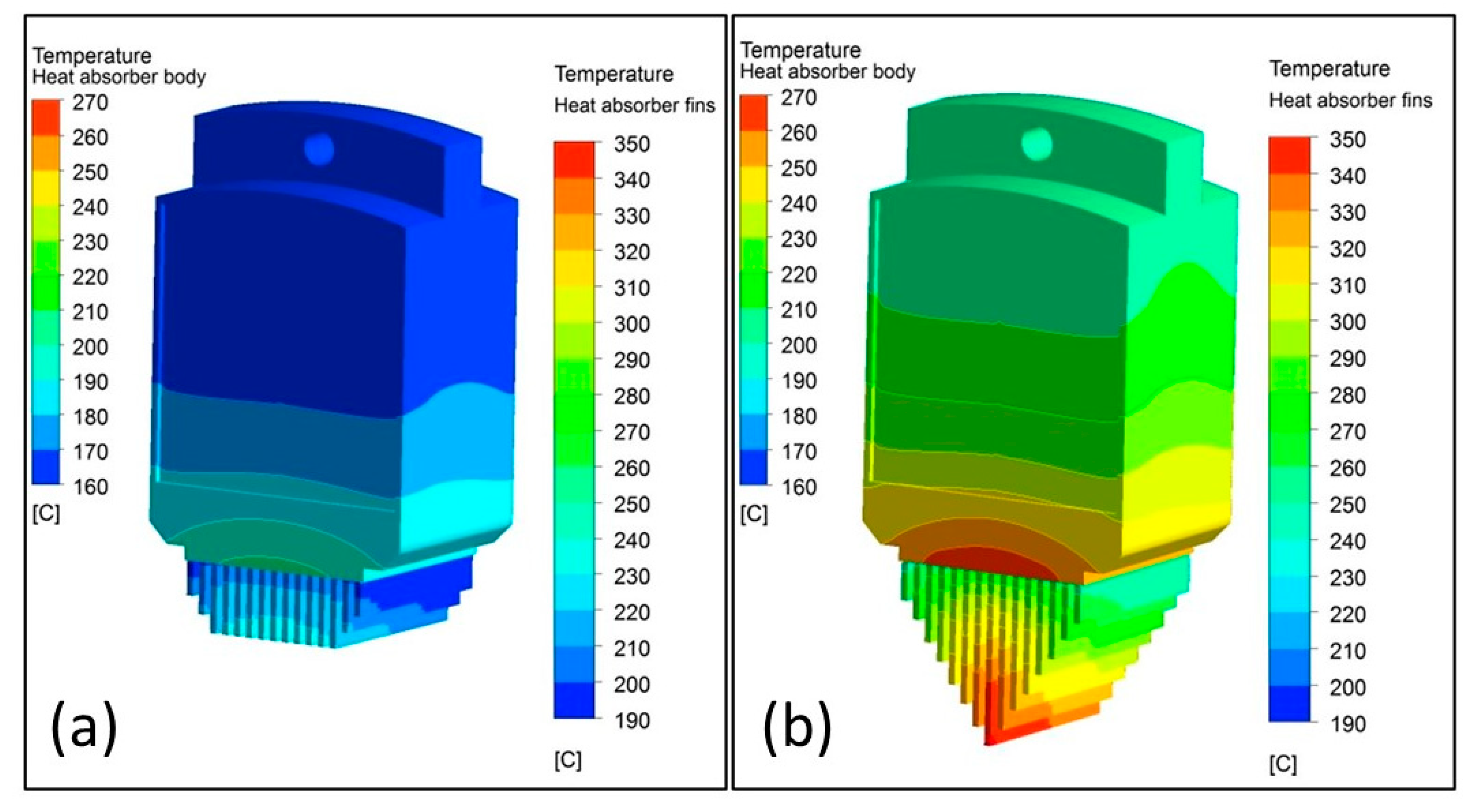
3. Numerical Model
3.1. Simulation Set Up
3.2. Model Validation
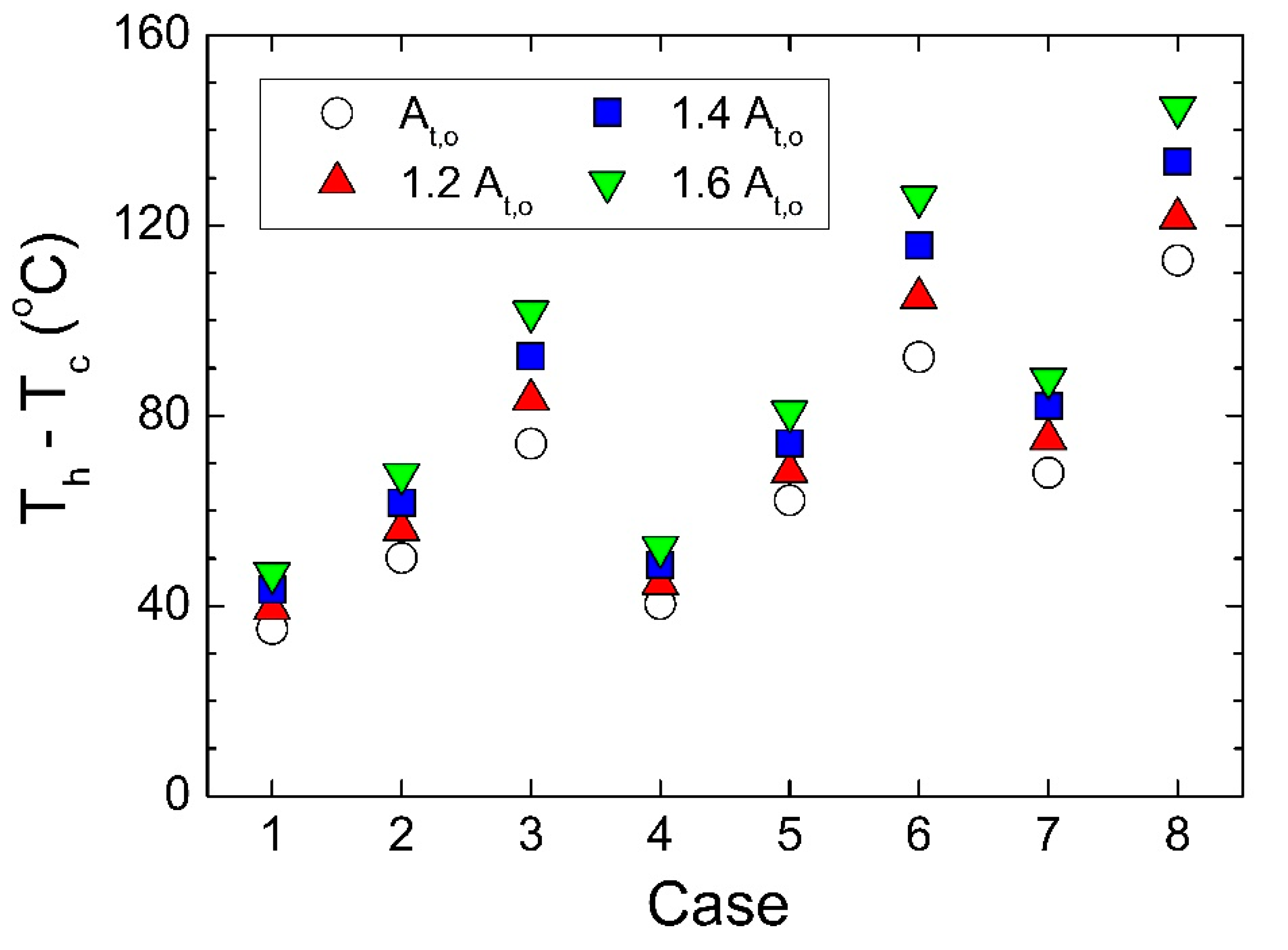
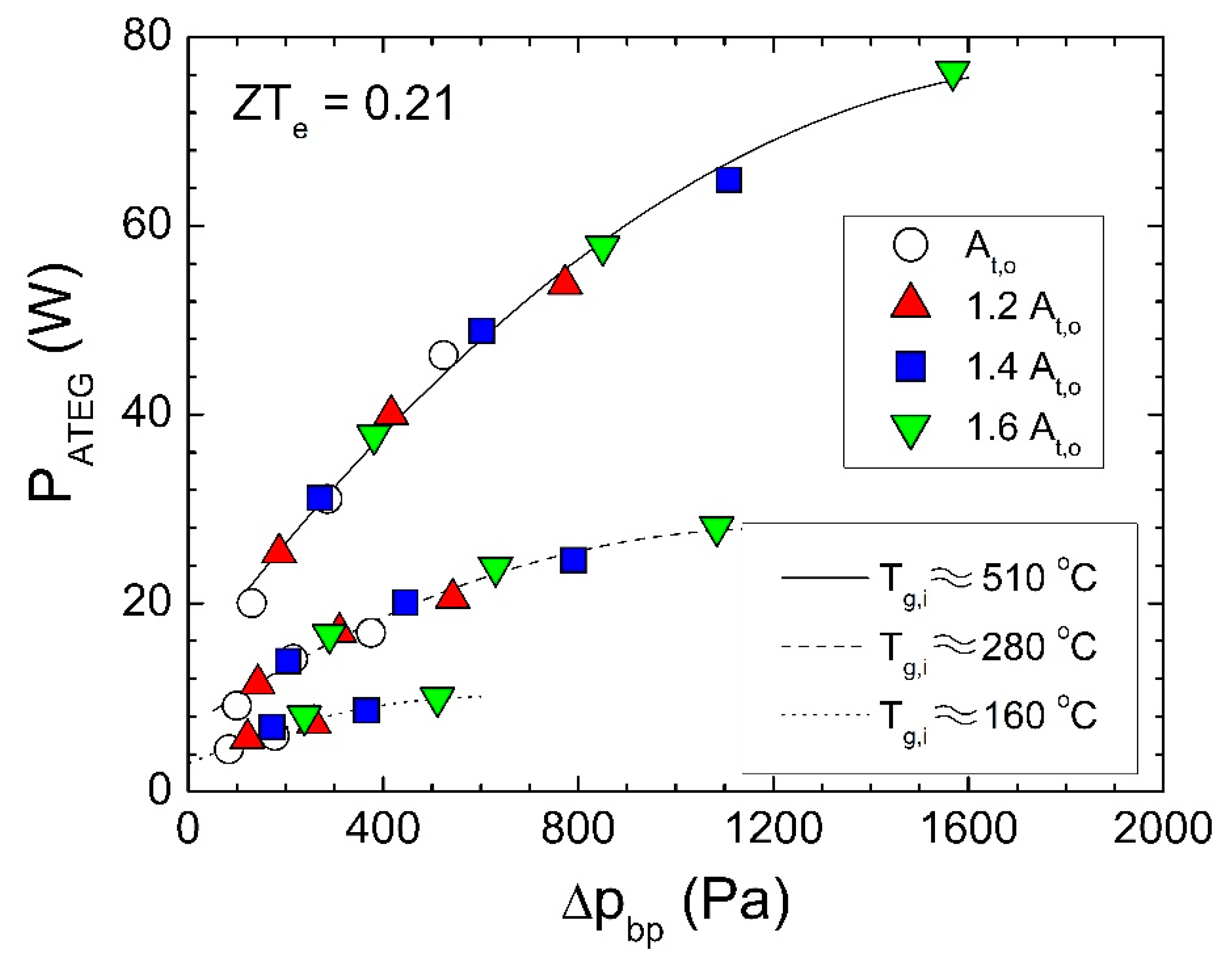
4. Results and Discussion
4.1. Electrical Power Output
4.2. Fuel Economy
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- The World Bank. Available online: https://data.worldbank.org/indicator/en.co2.tran.zs?end=2014&start=1960 (accessed on 5 September 2018).
- European Environment Agency. Available online: https://www.eea.europa.eu/data-and-maps/indicators/transport-emissons-of-greenhouse-gases/transport-emissions-of-greenhouse-gases-10 (accessed on 5 September 2018).
- European Comission. Available online: https://ec.europa.eu/clima/policies/transport_en (accessed on 5 September 2018).
- European Commission. Clean Power for Transport: A European Alternative Fuels Strategy. Communication from the Commission to the European Parliament, the Council, the European Economic and Social Committee and the Committee of the Regions; COM(2013) 17; European Commission: Brussels, Belgium, 2013. [Google Scholar]
- Rahman, A.; Razzak, F.; Afroz, R.; AKM, M.; Hawlader, M.N.A. Power generation from waste IC engines. Renew. Sustain. Energy Rev. 2015, 51, 382–395. [Google Scholar] [CrossRef]
- Karvonen, M.; Kapoor, R.; Uusitalo, A.; Ojanen, V. Technology competition in the internal combustion engine waste heat recovery: a patent landscape analysis. J. Clean. Prod. 2016, 112, 3735–3742. [Google Scholar] [CrossRef]
- Massaguer, A.; Massaguer, E.; Comamala, M.; Pujol, T.; Montoro, L.; Cardenas, M.D.; Carbonell, D.; Bueno, A.J. Transient behavior under a normalized driving cycle of an automotive thermoelectric generator. Appl. Energy 2017, 206, 1282–1296. [Google Scholar] [CrossRef]
- Frobenius, F.; Gaiser, G.; Rusche, U.; Weller, B. Thermoelectric generators for the integration into automotive exhaust systems for passenger cars and commercial vehicles. J. Electron. Mater. 2016, 45, 1433–1440. [Google Scholar] [CrossRef]
- Kim, T.Y.; Kwak, J.; Kim, B.W. Energy harvesting performance of hexagonal shaped thermoelectric generator for passenger vehicle applications: An experimental approach. Energy Convers. Manag. 2018, 160, 14–21. [Google Scholar] [CrossRef]
- Fernández-Yáñez, P.; Armas, O.; Kiwan, R.; Stefaopoulou, A.G.; Boehman, A.L. A thermoelectric generator in exhaust systems of spark-ignition and compression-ignition engines. A comparison with an electric turbo-generator. Appl. Energy 2018, 229, 80–87. [Google Scholar]
- Stobart, R.; Wijewardane, M.A.; Yang, Z. Comprehensive analysis of thermoelectric generation systems for automotive applications. Appl. Therm. Eng. 2017, 112, 1433–1444. [Google Scholar] [CrossRef]
- Wang, Y.; Li, S.; Xie, X.; Deng, Y.; Liu, X.; Su, C. Performance evaluation of an automotive thermoelectric generator with inserted fins or dimpled-surface hot heat exchanger. Appl. Energy 2018, 218, 391–401. [Google Scholar] [CrossRef]
- Orr, B.; Akbarzadeh, A.; Lappas, P. An exhaust heat recovery system utilizing thermoelectric generators and heat pipes. Appl. Therm. Eng. 2017, 126, 1185–1190. [Google Scholar] [CrossRef]
- Lan, S.; Yang, Z.; Chen, R.; Stobart, R. A dynamic model for thermoelectric generator applied to vehicle waste heat recovery. Appl. Energy 2018, 210, 327–338. [Google Scholar] [CrossRef]
- Crane, D.; Lagrandeur, J.; Jovovic, V.; Ranalli, M.; Adldinger, M.; Poliquin, E.; Dean, J.; Kossakovski, D.; Mazar, B.; Maranville, C. TEG on-vehicle performance and model validation and what it means for further TEG development. J. Electron. Mater. 2013, 42, 1582–1591. [Google Scholar] [CrossRef]
- Saidur, R.; Rezai, M.; Muzammil, W.K.; Hassan, M.H.; Paria, S.; Hasanuzzaman, M. Technologies to recover exhaust heat from internal combustion engines. Renew. Sustain. Energy Rev. 2012, 16, 5649–5659. [Google Scholar] [CrossRef]
- Di Battista, D.; Mauriello, M.; Cipollone, R. Waste heat recovery of an ORC-based power unit in a turbocharged diesel engine propelling a light duty vehicle. Appl. Energy 2015, 152, 109–120. [Google Scholar] [CrossRef]
- Dávila Pineda, D.; Rezania, A. Thermoelectric Energy Conversion. Basic Concepts and Device Applications, 1st ed.; Wiley-VCH Verlag GmbH&Co.: Weihheim, Germany, 2017. [Google Scholar]
- Ming, T.; Wang, Q.; Peng, K.; Cai, Z.; Yang, W.; Wu, Y.; Gong, T. The influence of non-uniform high heat flux on thermal stress of thermoelectric power generator. Energies 2015, 8, 12584–12602. [Google Scholar] [CrossRef]
- Crystal Ltd. Available online: www.crystalltherm.com (accessed on 4 May 2018).
- Cózar, I.R.; Pujol, T.; Lehocky, M. Numerical analysis of the effects of electrical and thermal configurations of thermoelectric modules in large-scale thermoelectric generators. Appl. Energy 2018, 229, 264–280. [Google Scholar] [CrossRef]
- Chen, J.; Li, K.; Liu, C.; Li, M.; Lv, Y.; Jia, L.; Jiang, S. Enhanced efficiency of thermoelectric generator by optimizing mechanical and electrical structures. Energies 2017, 10, 1329. [Google Scholar] [CrossRef]
- National Instruments. Available online: http://www.ni.com (accessed on 2 May 2018).
- Omega. Available online: http://www.omega.com (accessed on 2 May 2018).
- Sensus. Available online: http://www.sensus.com (accessed on 2 May 2018).
- Su, C.Q.; Tong, N.Q.; Xu, Y.M.; Chen, S.; Liu, X. Effect of the sequence of the thermoelectric generator and the three-way catalytic converter on exhaust gas conversion efficiency. J. Electron. Mater. 2013, 42, 1877–1881. [Google Scholar] [CrossRef]
- Wang, Y.; Li, S.; Zhang, Y.; Yang, X.; Deng, Y.; Su, C. The influence of inner topology of exhaust heat exchanger and thermoelectric module distribution on the performance of automotive thermoelectric generator. Energy Convers. Manag. 2016, 126, 266–277. [Google Scholar] [CrossRef]
- Bergman, T.L.; Lavine, A.S.; Incropera, F.P.; DeWitt, D.P. Fundamentals of Heat and Mass Transfer, 7th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2011. [Google Scholar]
- Celik, I.B.; Ghia, U.; Roache, P.J.; Freitas, C.J.; Coleman, H.; Raad, P.E. Procedure for estimation and reporting of uncertainty due to discretization in CFD applications. J. Fluids Eng. 2008, 130. [Google Scholar] [CrossRef]
- Massaguer, A.; Massaguer, E.; Comamala, M.; Pujol, T.; González, J.R.; Cardenas, M.D.; Carbonell, D.; Bueno, A.J. A method to assess the fuel economy of automotive thermoelectric generators. Appl. Energy 2018, 222, 42–58. [Google Scholar] [CrossRef]
- Karri, M.A.; Thacher, E.F.; Helenbrook, B.T. Exhaust energy conversion of thermoelectric generator: Two case studies. Energy Convers. Manag. 2011, 52, 1596–1611. [Google Scholar] [CrossRef]














| Engine 1 | ATEG Design 2 | #TEMs | Tg,I (°C) | Tc,I (°C) | Heat Absorber | mATEG (kg) | PATEG (W) | Δpbp (Pa) | Fe (%) | Reference |
|---|---|---|---|---|---|---|---|---|---|---|
| 1.4 L SI | 2PP | 12 | 709 | 74 | Circular tubes | 7 | 111 | 3653 | [7] | |
| HDV | 2PP | 224 | 80 | Fins | 416 | [8] | ||||
| 2.0 L SI | HexS | 18 | 611 | 80 | Fins | 99 | 2100 | [9] | ||
| 1.6 L SI | 2PP | 80 | 719 | 50 | Fins | 137 | 318 | 1.1 * | [10] | |
| 1.9 L CI | 4SSP | 8 | 427 | 7 | Radial fins | 30 | 149 | [11] | ||
| 3.9 L CI | 2PP | 240 | 290 | 80 | Fins/dims | 200 | 618 | 1348 | [12] | |
| 3.0 L SI | HP | 8 | 350 | 30 | Heat pipes | 38 | 135 | [13] | ||
| 6.6 L CI | 2PP | 4 | 200 | 10 | 8 | [14] | ||||
| 1.8 L CI | Radial | 10 | 540 | 28 | Fins | 4.8 | 40 | 524 * | 0.0 * | Present |
| Equipment | Accuracy | Reference |
|---|---|---|
| Current (NI 9227) | ±(169.7 mA + 5% of reading) | [23] |
| Voltage (NI 9215) | ±(85.3 mV + 1.05% of reading) | [23] |
| Temperature (NI 9211) | ± 0.6 °C | [23] |
| Type K thermocouple | ± 1.5 °C | [24] |
| Sensus 405 S water meter | ± 0.05 L | [25] |
| Manometer | ± 10 Pa | |
| Calibrated volume cylinder | ± 10 cm3 |
| Case | Regime (rpm) | Torque (N m) | (g/s) | Tg,I (°C) | Tw,I (°C) | Tamb (°C) |
|---|---|---|---|---|---|---|
| 1 | 1500 | 21.4 ± 0.1 | 24.1 ± 0.6 | 158.5 ± 1.6 | 19.1 ± 1.6 | 20.0 ± 1.6 |
| 2 | 1500 | 50.0 ± 0.1 | 24.0 ± 0.6 | 259.7 ± 1.6 | 20.2 ± 1.6 | 20.9 ± 1.6 |
| 3 | 1500 | 79.1 ± 0.1 | 24.1 ± 0.7 | 454.8 ± 1.6 | 20.3 ± 1.6 | 23.4 ± 1.6 |
| 4 | 2200 | 14.4 ± 0.1 | 34.5 ± 0.4 | 159.5 ± 1.6 | 21.8 ± 1.6 | 24.6 ± 1.6 |
| 5 | 2200 | 45.0 ± 0.1 | 34.2 ± 0.5 | 282.9 ± 1.6 | 22.2 ± 1.6 | 25.5 ± 1.6 |
| 6 | 2200 | 72.3 ± 0.1 | 34.1 ± 0.7 | 510.5 ± 1.6 | 22.9 ± 1.6 | 27.6 ± 1.6 |
| 7 | 2700 | 43.3 ± 0.1 | 44.7 ± 0.4 | 285.8 ± 1.6 | 25.1 ± 1.6 | 27.7 ± 1.6 |
| 8 | 2700 | 76.2 ± 0.1 | 44.8 ± 0.7 | 539.1 ± 1.6 | 24.8 ± 1.6 | 29.4 ± 1.6 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Comamala, M.; Pujol, T.; Cózar, I.R.; Massaguer, E.; Massaguer, A. Power and Fuel Economy of a Radial Automotive Thermoelectric Generator: Experimental and Numerical Studies. Energies 2018, 11, 2720. https://doi.org/10.3390/en11102720
Comamala M, Pujol T, Cózar IR, Massaguer E, Massaguer A. Power and Fuel Economy of a Radial Automotive Thermoelectric Generator: Experimental and Numerical Studies. Energies. 2018; 11(10):2720. https://doi.org/10.3390/en11102720
Chicago/Turabian StyleComamala, Martí, Toni Pujol, Ivan Ruiz Cózar, Eduard Massaguer, and Albert Massaguer. 2018. "Power and Fuel Economy of a Radial Automotive Thermoelectric Generator: Experimental and Numerical Studies" Energies 11, no. 10: 2720. https://doi.org/10.3390/en11102720
APA StyleComamala, M., Pujol, T., Cózar, I. R., Massaguer, E., & Massaguer, A. (2018). Power and Fuel Economy of a Radial Automotive Thermoelectric Generator: Experimental and Numerical Studies. Energies, 11(10), 2720. https://doi.org/10.3390/en11102720





