Day-Ahead Hierarchical Steady State Optimal Operation for Integrated Energy System Based on Energy Hub
Abstract
:1. Introduction
2. Inner Layer Modeling and Optimization
2.1. Modeling of Energy Hub
2.2. Inner Layer Optimization Model
2.2.1. Power Balance Constraint
2.2.2. Equipment Capacity and Climbing Rate Constraints
3. Outer Layer Modeling and Optimization
3.1. Steady State Operation Modeling of Integrated Energy System
3.1.1. Electricity Transmission System
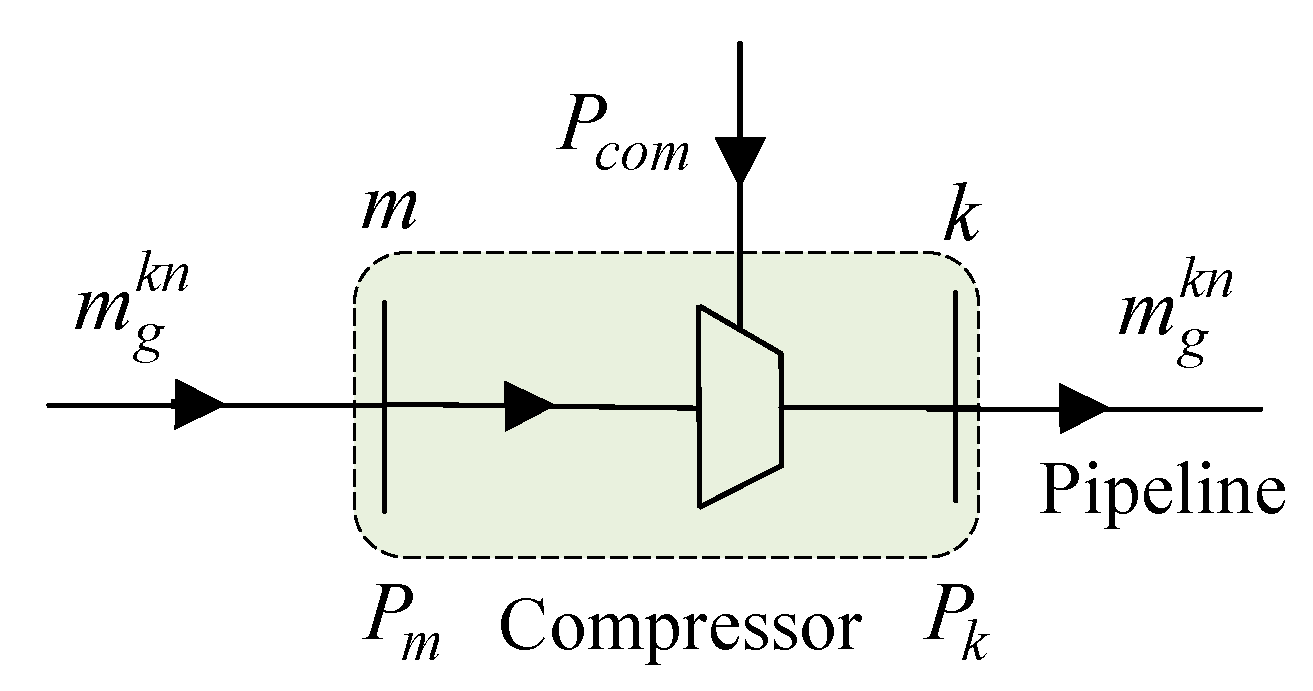
3.1.2. Natural Gas System
3.1.3. District Heating System
3.2. Outer Layer Optimization Model
4. Case Study
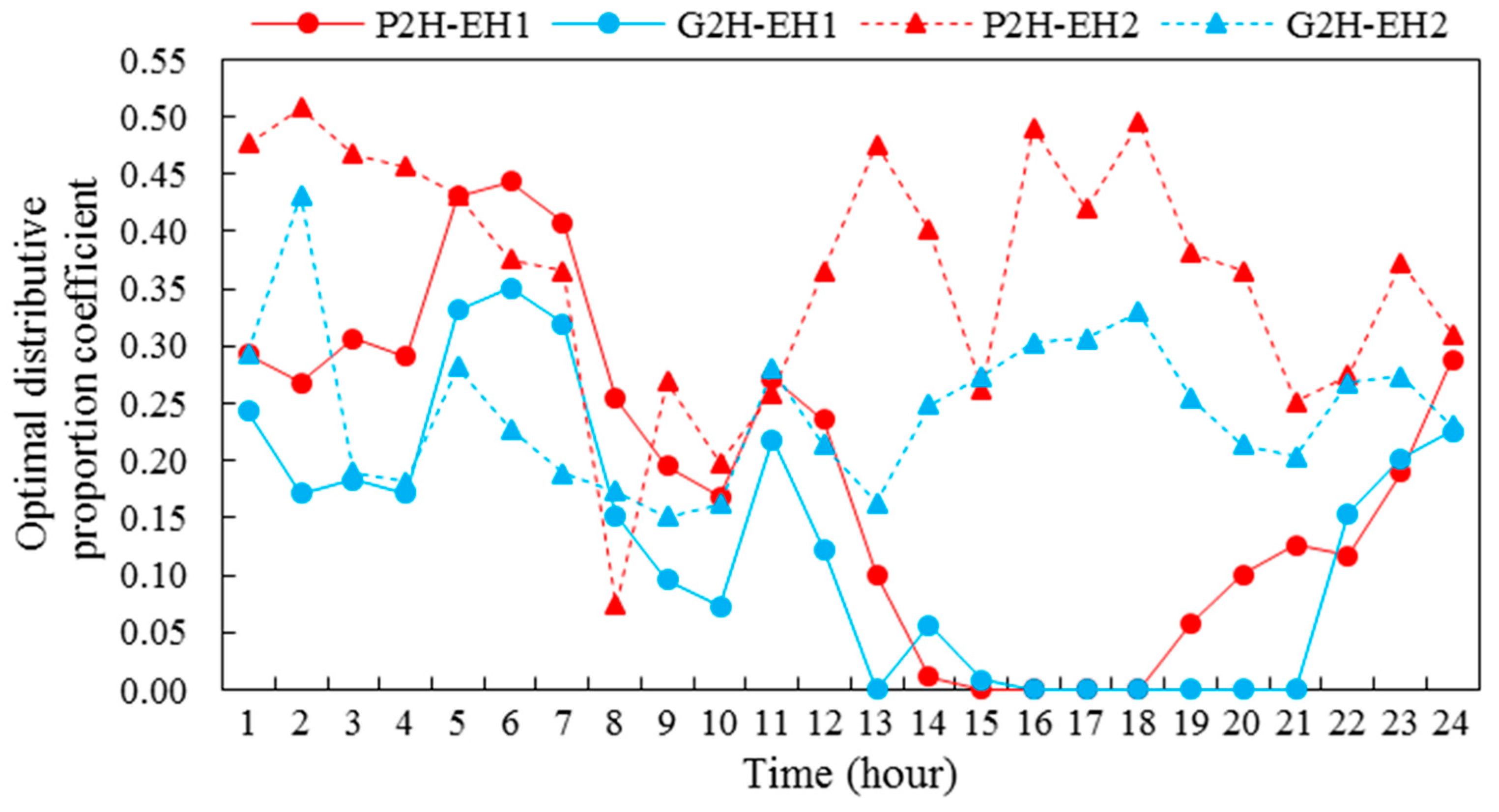
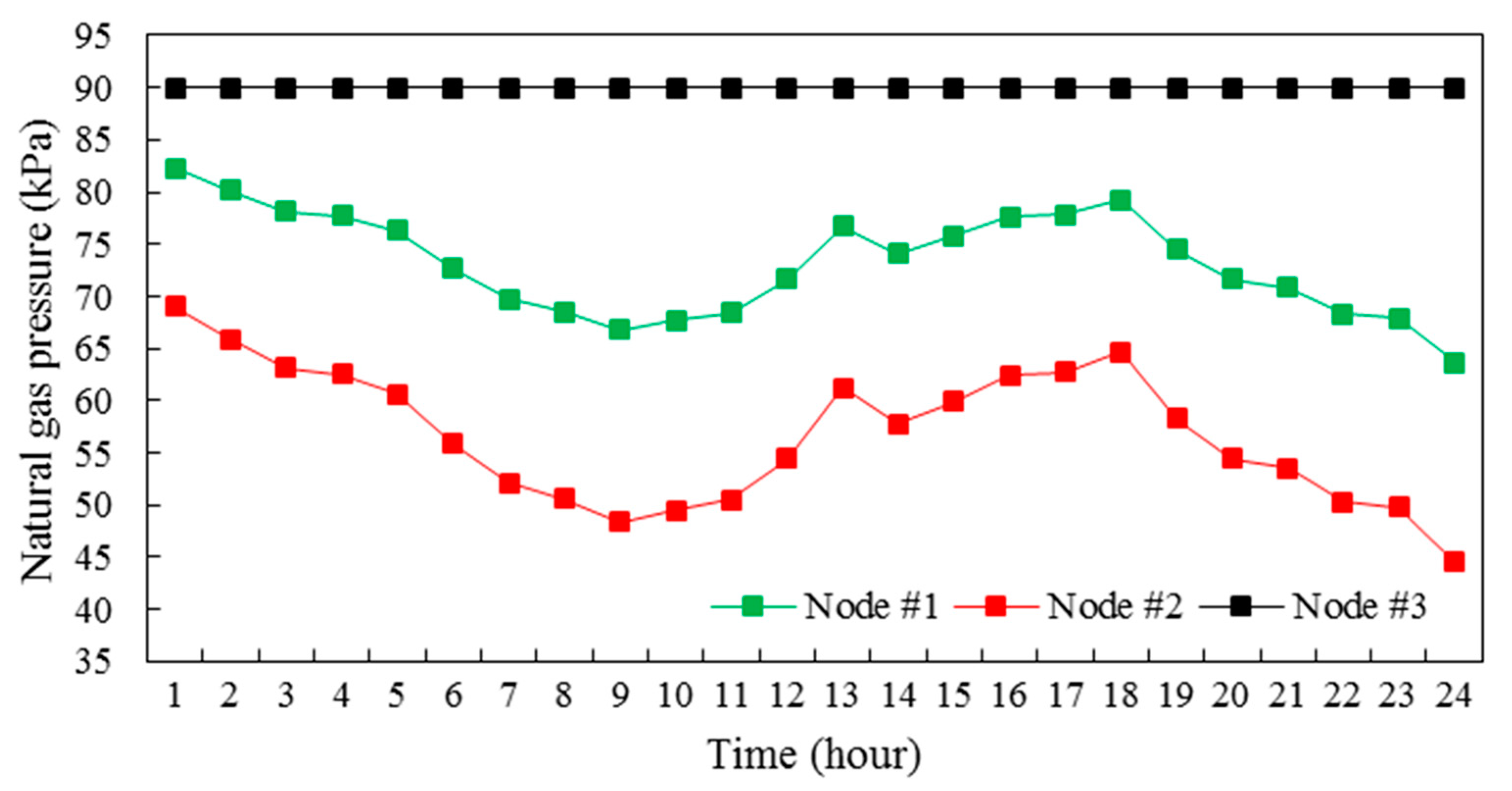
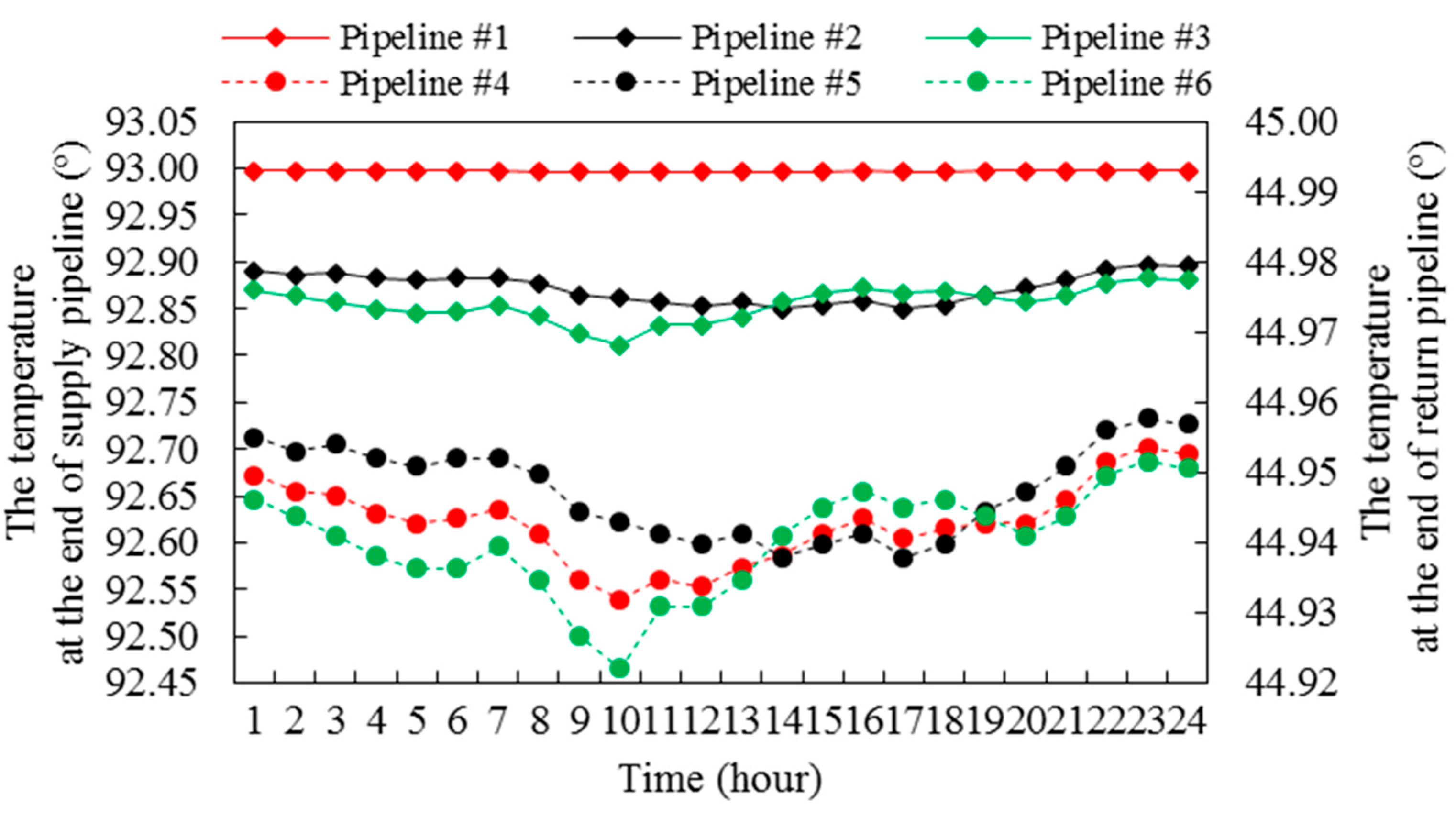
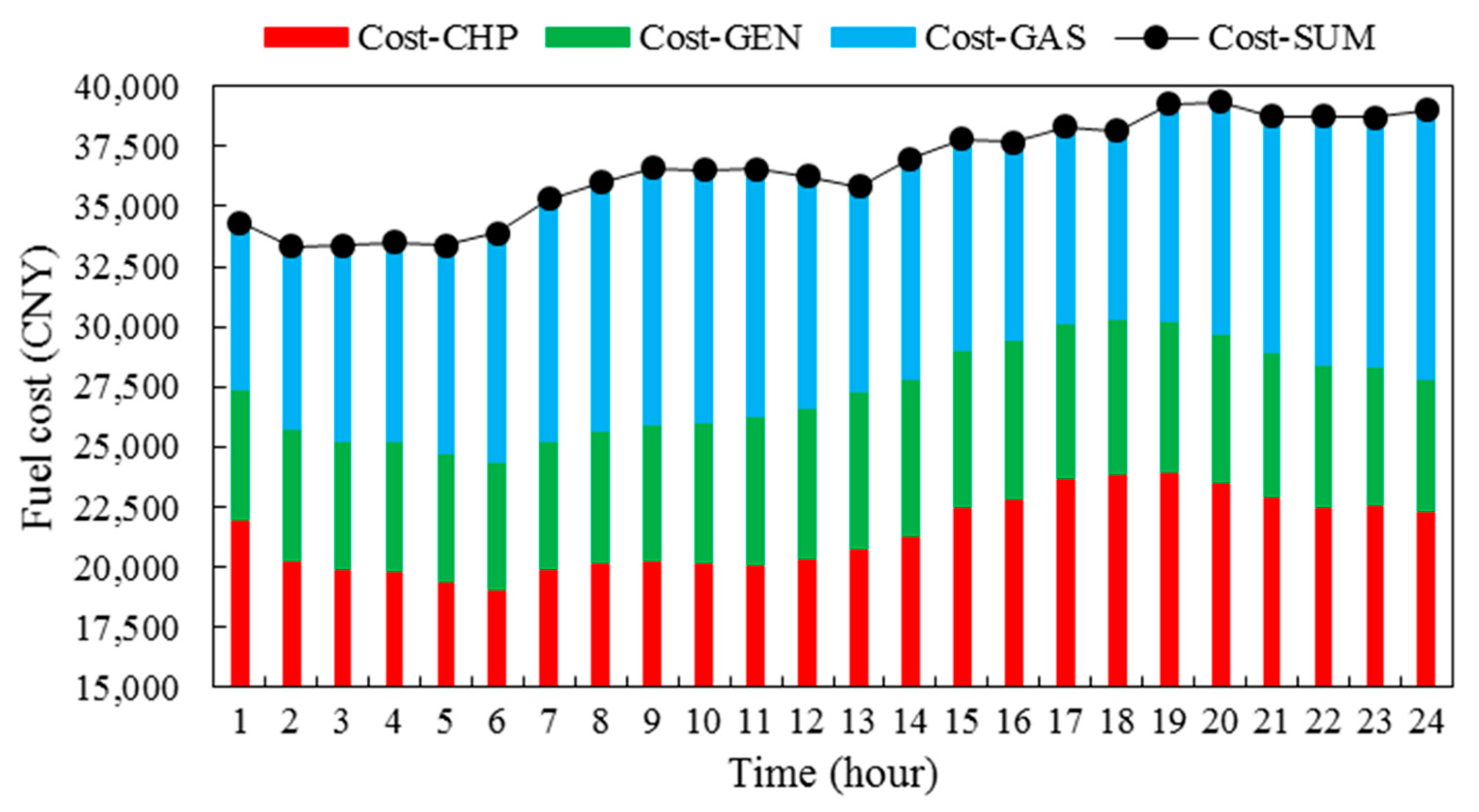
4.1. Results and Analyses
4.2. Discussions
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gil, M.; Dueñas, P.; Reneses, J. Electricity and natural gas interdependency: Comparison of two methodologies for coupling large market models within the European regulatory framework. IEEE Trans. Power Syst. 2015, 31, 361–369. [Google Scholar] [CrossRef]
- Clegg, S.; Mancarella, P. Integrated modeling and assessment of the operational impact of power-to-gas (P2G) on electrical and gas transmission networks. IEEE Trans. Sustain. Energy 2015, 6, 1234–1244. [Google Scholar] [CrossRef]
- Linna, N.; Liu, W.; Wen, F.; Xue, Y.; Dong, Z.; Zheng, Y.; Zhang, R. Optimal operation of electricity, natural gas and heat systems considering integrated demand responses and diversified storage devices. J. Mod. Power Syst. Clean Energy 2018, 6, 423–437. [Google Scholar]
- Zeng, Q.; Zhang, B.; Fang, J.; Chen, Z. Coordinated operation of the electricity and natural gas systems with bi-directional energy conversion. Energy Procedia 2017, 105, 492–497. [Google Scholar] [CrossRef]
- Xu, X.; Jia, H.; Chiang, H.; Yu, D.; Wang, D. Dynamic modeling and interaction of hybrid natural gas and electricity supply system in microgrid. IEEE Trans. Power Syst. 2015, 30, 1212–1221. [Google Scholar] [CrossRef]
- Qadrdan, M.; Wu, J.; Jenkins, N.; Ekanayake, J. Operating strategies for a GB integrated gas and electricity network considering the uncertainty in wind power forecasts. IEEE Trans. Sustain. Energy 2013, 5, 128–138. [Google Scholar] [CrossRef]
- Zhang, X.; Shahidehpour, M.; Alabdulwahab, A.; Abusorrah, A. Optimal expansion planning of energy hub with multiple energy infrastructures. IEEE Trans. Smart Grid 2017, 6, 2302–2311. [Google Scholar] [CrossRef]
- Erdener, B.; Pambour, K.; Lavin, R.; Dengiz, B. An integrated simulation model for analyzing electricity and gas systems. Int. J. Electr. Power Energy Syst. 2014, 61, 410–420. [Google Scholar] [CrossRef]
- Martinez-Mares, A.; Fuerte-Esquivel, C. A unified gas and power flow analysis in natural gas and electricity coupled networks. IEEE Trans. Power Syst. 2012, 27, 2156–2166. [Google Scholar] [CrossRef]
- Yang, L.; Zhao, X.; Li, X.; Yan, W. Probabilistic steady-state operation and interaction analysis of integrated electricity, gas and heating systems. Energies 2018, 11, 917. [Google Scholar] [CrossRef]
- Fan, S.; Ai, Q.; Piao, L.; Fan, Q.; Piao, L. Hierarchical energy management of micro-grids including storage and demand response. Energies 2018, 11, 1111. [Google Scholar] [CrossRef]
- Brahman, F.; Honarmand, M.; Jadid, S. Optimal electrical and thermal energy management of a residential energy hub, integrating demand response and energy storage system. Energy Build. 2015, 90, 65–75. [Google Scholar] [CrossRef]
- Anvari-Moghaddam, A.; Monsef, H.; Rahimi-Kian, A. Optimal smart home energy management considering energy saving and a comfortable lifestyle. IEEE Trans. Smart Grid 2017, 6, 324–332. [Google Scholar] [CrossRef]
- Wang, R.; Wang, P.; Xiao, G. A robust optimization approach for energy generation scheduling in micro-grids. Energy Convers. Manag. 2015, 106, 597–607. [Google Scholar] [CrossRef]
- Wang, C.; Jiao, B.; Guo, L.; Tian, Z.; Niu, J.; Li, S. Robust scheduling of building energy system under uncertainty. Appl. Energy 2016, 167, 366–376. [Google Scholar] [CrossRef]
- Nižetić, S.; Papadopoulos, A.; Tina, G.; Rosa-Clot, M. Hybrid energy scenarios for residential applications based on the heat pump split air-conditioning units for operation in the Mediterranean climate conditions. Energy Build. 2017, 140, 110–120. [Google Scholar] [CrossRef]
- Zlotnik, A.; Roald, L.; Backhaus, S.; Chertkov, M.; Andersson, G. Coordinated scheduling for interdependent electric power and natural gas infrastructures. IEEE Trans. Power Syst. 2017, 32, 600–610. [Google Scholar] [CrossRef]
- Wang, L.; Li, Q.; Sun, M.; Wang, G. Robust optimization scheduling of CCHP systems with multi-energy based on minimax regret criterion. IET Gener. Transm. Distrib. 2016, 10, 2194–2201. [Google Scholar] [CrossRef]
- Geidl, M.; Andersson, G. Optimal power flow of multiple energy carriers. IEEE Trans. Power Syst. 2007, 22, 145–155. [Google Scholar] [CrossRef]
- Moeini-Aghtaie, M.; Abbaspour, A.; Fotuhi-Firuzabad, M.; Hajipour, E. A decomposed solution to multiple-energy carriers optimal power flow. IEEE Trans. Power Syst. 2014, 29, 707–716. [Google Scholar] [CrossRef]
- Lin, G.; Chen, Y.; Liu, Y.; Xiong, W.; Tang, L.; Pan, Z.; Guo, Q. Coordinative optimization of multiple energy flows for microgrid with renewable energy resources and case study. Electr. Power Autom. Equip. 2017, 37, 275–281. [Google Scholar]
- Feng, Z.; Zhang, C.; Sun, B.; Wei, D. Three-stage collaborative global optimization design method of combined cooling heating and power. Proc. CSEE 2015, 35, 3785–3793. [Google Scholar]
- Shao, C.; Wang, X.; Shahidehpour, M.; Wang, X.; Wang, B. An MILP-based optimal power flow in multicarrier energy systems. IEEE Trans. Sustain. Energy 2017, 8, 239–248. [Google Scholar] [CrossRef]
- Piperagkas, G.; Anastasiadis, A.; Hatziargyriou, N. Stochastic PSO-based heat and power dispatch under environmental constraints incorporating CHP and wind power units. Electr. Power Syst. Res. 2011, 81, 209–218. [Google Scholar] [CrossRef]
- Liu, X.; Jenkins, N.; Wu, J.; Bagdanavicius, A. Combined analysis of electricity and heat networks. Energy Procedia 2014, 61, 155–159. [Google Scholar] [CrossRef]
- Shi, J.; Wang, L.; Wang, Y.; Zhang, J. Generalized energy flow analysis considering electricity gas and heat subsystems in local-area energy systems integration. Energies 2017, 10, 514. [Google Scholar] [CrossRef]
- Morvaj, B.; Evins, R.; Carmeliet, J. Optimization framework for distributed energy systems with integrated electrical grid constraints. Appl. Energy 2016, 171, 296–313. [Google Scholar] [CrossRef]
- Xu, X.; Jin, X.; Jia, H.; Yu, X.; Li, K. Hierarchical management for integrated community energy systems. Appl. Energy 2015, 160, 231–243. [Google Scholar] [CrossRef]
- Shabanpour-Haghighi, A.; Seifi, A. Simultaneous integrated optimal energy flow of electricity, gas, and heat. Energy Convers. Manag. 2015, 101, 579–591. [Google Scholar] [CrossRef]
- Liu, X.; Mancarella, P. Modelling, assessment and Sankey diagrams of integrated electricity-heat-gas networks in multi-vector district energy systems. Appl. Energy 2016, 167, 336–352. [Google Scholar] [CrossRef]
- Clegg, S.; Mancarella, P. Integrated electricity-heat-gas modelling and assessment, with applications to the Great Britain system. Part I: High-resolution spatial and temporal heat demand modelling. Energy 2018. [Google Scholar] [CrossRef]
- Clegg, S.; Mancarella, P. Integrated electricity-heat-gas modelling and assessment, with applications to the Great Britain system. Part II: Transmission network analysis and low carbon technology and resilience case studies. Energy 2018. [Google Scholar] [CrossRef]
- Li, G.; Zhang, R.; Jiang, T.; Chen, H.; Bai, L.; Li, X. Security-constrained bi-level economic dispatch model for integrated natural gas and electricity systems considering wind power and power-to-gas process. Appl. Energy 2016, 194, 696–704. [Google Scholar] [CrossRef]
- Bai, L.; Li, F.; Cui, H.; Jiang, T.; Sun, H.; Zhu, J. Interval optimization based operating strategy for gas-electricity integrated energy systems considering demand response and wind uncertainty. Appl. Energy 2016, 167, 270–279. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.; Wang, D.; Jia, H.; He, G.; Hu, Q.; Sui, P.; Fan, M. Performance evaluation of a hydrogen-based clean energy hub with electrolyzers as a self-regulating demand response management mechanism. Energies 2017, 10, 1211. [Google Scholar] [CrossRef]



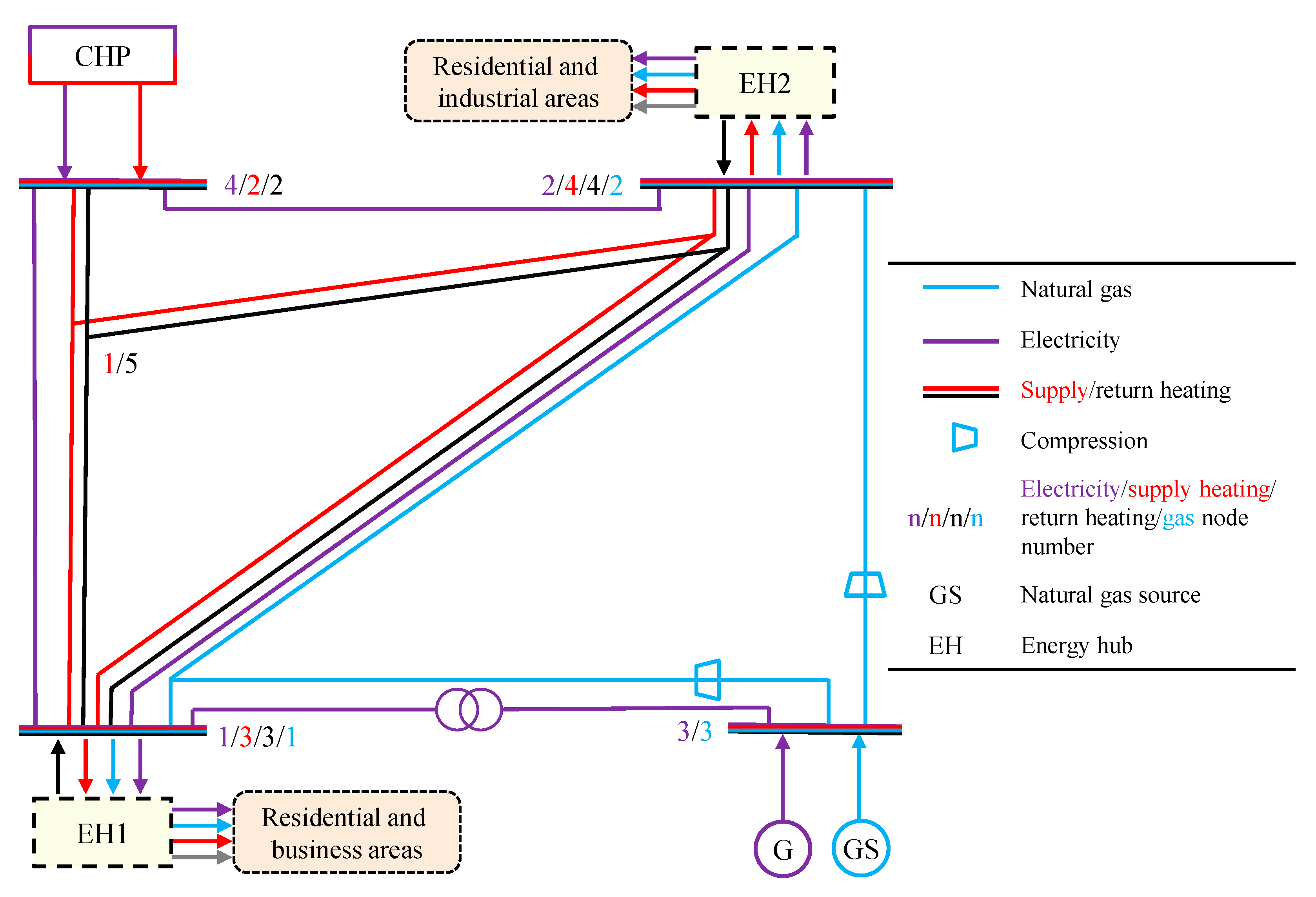


| Electricity Transmission System | Branch/line | From node | To node |
| 1 | 1 | 2 | |
| 2 | 1 | 4 | |
| 3 | 2 | 4 | |
| 4 | 1 | 3 | |
| District Heating System | Branch/pipeline | From node | To node |
| 1 | 2 | 1 | |
| 2 | 1 | 3 | |
| 3 | 1 | 4 | |
| 4 | 5 | 2 | |
| 5 | 3 | 5 | |
| 6 | 4 | 5 | |
| 7 | 3 | 4 | |
| 8 | 4 | 3 | |
| Natural Gas System | Branch/pipeline | From node | To node |
| 1 | 3 | 1 | |
| 2 | 3 | 2 | |
| 3 | 1 | 2 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhong, Y.; Xie, D.; Zhai, S.; Sun, Y. Day-Ahead Hierarchical Steady State Optimal Operation for Integrated Energy System Based on Energy Hub. Energies 2018, 11, 2765. https://doi.org/10.3390/en11102765
Zhong Y, Xie D, Zhai S, Sun Y. Day-Ahead Hierarchical Steady State Optimal Operation for Integrated Energy System Based on Energy Hub. Energies. 2018; 11(10):2765. https://doi.org/10.3390/en11102765
Chicago/Turabian StyleZhong, Yongjie, Dongliang Xie, Suwei Zhai, and Yonghui Sun. 2018. "Day-Ahead Hierarchical Steady State Optimal Operation for Integrated Energy System Based on Energy Hub" Energies 11, no. 10: 2765. https://doi.org/10.3390/en11102765




