1. Introduction
The significant progress in microelectronics, combined with the increasing demand from numerous industrial fields, makes the embedded autonomous wireless sensors and portable smart devices very popular due to their wide potential applications and ability to be employed in inaccessible and hostile environments. Conventional batteries are the main power source of such devices, but they some limitations, including a finite lifetime, need for periodic replacement, environment pollution and bulky nature [
1,
2,
3,
4]. In the last two decades, energy harvesting from ambient vibration sources has been revealed to be a realistic alternative to conventional batteries owing to its relative high energy density and availability in real indoor and outdoor applications. Nowadays, piezoelectric (PE), electromagnetic (EM) and electrostatic methods are the most commonly pursued vibratory energy harvesting mechanisms.
The piezoelectric (PE) energy harvester and electromagnetic (EM) energy harvester have received great attention as they have high electromechanical coupling effect and no external voltage source requirements [
5,
6,
7,
8,
9,
10]. In a given scenario, the two different schemes can be combined in one system such that one assists the other for vibration energy harvesting [
11,
12,
13,
14]. Compared with stand-alone PE or EM vibration energy harvesting, the hybrid harvesting technique based on combining piezoelectric and electromagnetic principles also takes advantage by sufficiently utilizing the limited space for fabrication and obtaining better output performance. Besides, due to the low-frequency and narrow-band characteristics of the practical vibration sources, hybrid energy harvesting mechanisms seem to be reasonable candidates for capturing energy. Nowadays a number of informative studies and developments have been presented in this area [
15,
16,
17]. Most reported references have investigated hybrid PE and EM energy harvesters through numerical analysis, finite element simulation and experimental methods [
18,
19,
20,
21,
22]. Only a few researchers have established mathematical models for hybrid PE and EM energy harvester designs [
23,
24,
25]. The aforementioned studies mainly focus on the response of hybrid energy harvesting devices subjected to sinusoidal excitations. However, many ambient vibrations sources can actually be somewhat stochastic in nature. Like white light, white excitation has equal intensity at different frequencies, giving it a constant power spectral density and broadband properties. Other non-white excitations can be defined as narrow-band (colored) excitation. Li et al. proposed electroelastic modeling, analysis and simulation solutions, and experimental validation of a hybrid PE and EM energy harvester under white Gaussian excitation [
26]. Nevertheless, many environmental excitations have most of their energy trapped within a narrow bandwidth, which is also a characteristic of colored excitation. As a result, a narrow-band (colored) excitation could be more representative of key ambient vibration sources [
27,
28,
29].
As reported in the available literature, designing energy harvesters excited by steady-state harmonic input with nonlinearities could be more frequency-robust in frequency variable situations and could improve the output performance over a wider bandwidth as well [
30,
31]. However, it has been indicated theoretically, numerically and experimentally that for energy harvesters with a single mechanism, introducing stiffness-type nonlinearities will not provide any enhancement in energy harvesting under both white Gaussian excitation and colored (narrow-band) excitation. Daqaq et al. [
32,
33,
34] analyzed that a white Gaussian excited Duffing-type PE or EM energy harvester cannot improve the power generation over linear harvesters. Sebald et al. [
35] and Green et al. [
36] corroborated these findings and showed that linear and nonlinear energy harvesters will produce exactly the same power levels when both are excited with white noise. Under (band-limited) colored excitation, generating nonlinear stiffness in a PE or EM energy harvester will even hinder power output. Daqaq et al. [
32] demonstrated that the expected value of the output power will decrease with the stiffness-type nonlinearity. After verification through numerical and experimental methods, Sebald et al. [
35,
37] reached a similar conclusion for a Duffing-type PE oscillator under colored excitation. Nevertheless, the effects of introducing nonlinear stiffness into a randomly excited hybrid PE and EM energy harvester on output characteristics could be quite different. Li et al. [
38] and Zhou et al. [
39] showed that a nonlinear hybrid energy harvester excited by white Gaussian noise could theoretically outperform its linear counterpart, which was validated by numerical and experimental methods, respectively. However, to the best of the authors’ knowledge, there are no related studies for the response of a nonlinear hybrid piezoelectric-electromagnetic energy harvester when subjected to colored excitation, which represents a more realistic simulation of a practical vibration environment.
Combining the basic assumption from our previous work [
39] and extending the approximate analytical Fokker-Planck (FP) theory from Daqaq et al [
32], which was concentrated on energy harvester with a single harvesting mechanism, the main contribution of this paper is to obtain the effects of introducing stiffness-type nonlinearity into a hybrid PE and EM energy harvester under colored excitation. Along with Monte Carlo (MC) simulation, the theoretical output characteristics of a nonlinear hybrid PE and EM energy harvester subjected to colored excitation are presented and compared. The content of this article is organized as follows:
Section 2 introduces the basic structure of a nonlinear hybrid energy harvester. The mathematical and numerical modeling of a colored noise excited nonlinear hybrid energy harvester is described in
Section 3. Verification with numerical solutions, theoretical output performances for nonlinear and linear hybrid energy harvesters with the variation of load resistances, spectral density (SD), bandwidth and center frequency under colored excitation are presented in
Section 4. In particular, for a case with colored excitation approaching white Gaussian excitation, theoretical results are discussed and compared with that from our previous Fokker-Planck expressions for a hybrid energy harvester under white noise excitation [
39]. Concluding comments are then provided in
Section 5.
2. Basic Structure
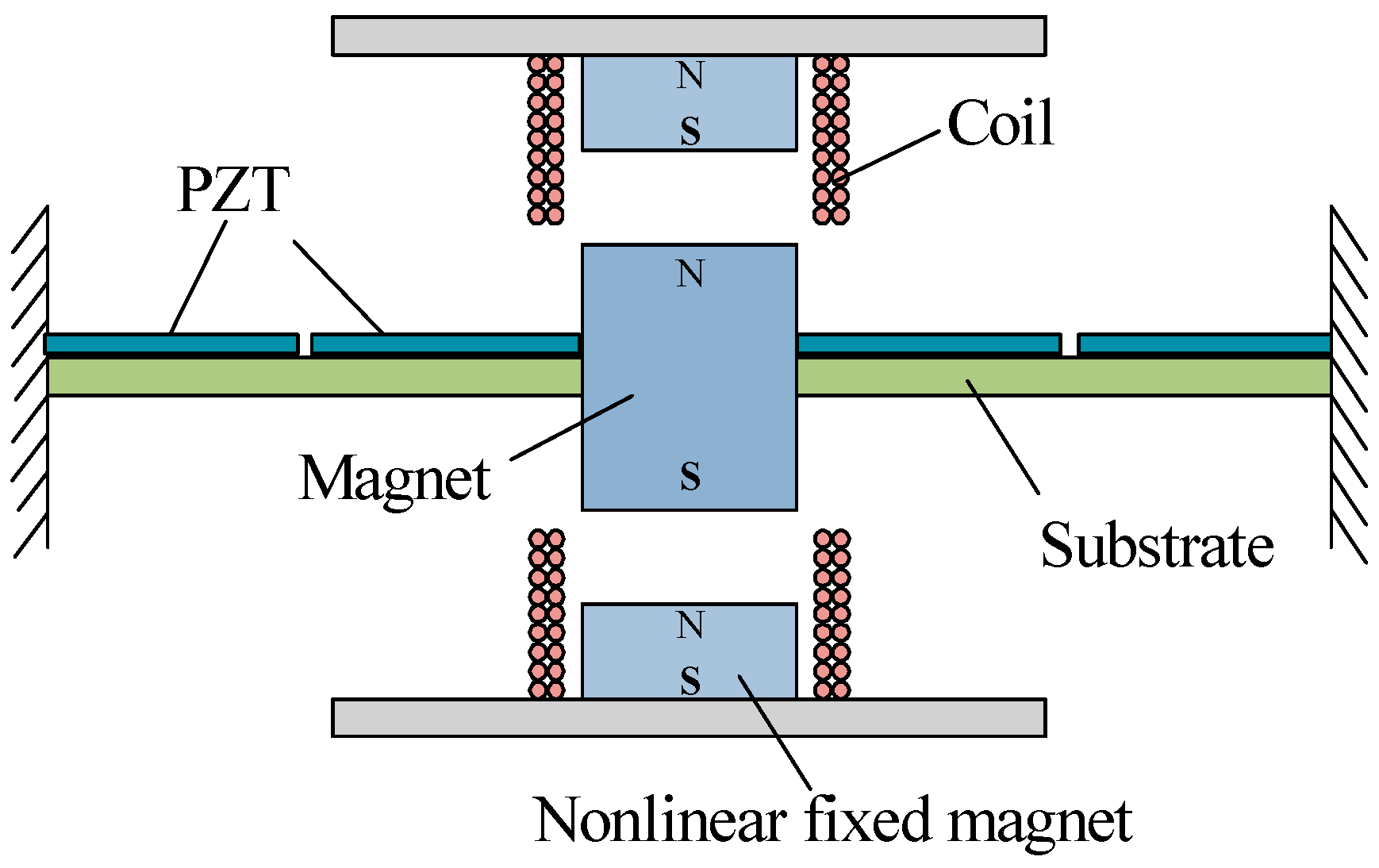
The adopted traditional hybrid PE and EM energy harvester consists of a piezoelectric element and an electromagnetic element. In the PE element, a doubly-clamped piezoelectric cantilever beam is excited at the support. The vibratory beam changes the stress distribution of the PZT layer, thus generating the output power through the piezoelectric effect. Electromagnetic power output is mainly realized by placing coils near the mass magnet due to Faraday’s law of electromagnetic induction. In order to generate a nonlinear hybrid PE and EM energy harvester, two permanent magnets are used, located symmetrically on the mass magnet (see
Figure 1). Introducing magnets as nonlinear component into hybrid piezoelectric and electromagnetic energy harvester will produce a linear factor
and nonlinear factor
based on references [
38,
39,
40,
41,
42], hence it becomes a nonlinear hybrid piezoelectric and electromagnetic energy harvester, and its governing equation can be obtained as follows:
where
z is the amplitude of mass magnet,
me is the equivalent mass and
ke is the stiffness of the beam,
cm is the damping coefficient;
k1 is the linear factor and
k3 is the nonlinear factor caused by the nonlinear magnetic force;
Rp,
Rm are load resistance of PE and EM element respectively;
Cp is the equivalent capacitance of the PE layer;
Vp is the output voltage of the PE energy harvesting element;
Iem is the output current of the EM energy harvesting element;
Rc and
Lc refer to the resistance and inductance of coils;
θ and
gem are the PE and EM transfer factors, respectively.
3. Colored Noise Excited Nonlinear Hybrid Piezoelectric and Electromagnetic Energy Harvester Modeling
Based on previous studies on both linear and nonlinear energy harvesters under random excitation [
26,
34,
36,
38,
39], the inductance of coils is usually ignored in order to simplify the theoretical analysis. Hence Equation (2) can be expressed as:
Following our former research on nonlinear hybrid PE and EM energy harvesters subjected to white Gaussian excitation [
39], an equivalent resistance is used to substitute the equivalent capacitance of the piezoelectric layer by considering the equality of modulus. The basic assumption is validated by both Fokker-Planck analysis and Monte Carlo simulation for white Gaussian noise excitation cases. Therefore for colored excitation, we still apply this assumption for our theoretical analysis, that is:
Thus Equation (3) becomes:
As it introduced before, narrow-band (colored) excitation characterized by three parameters—bandwidth, center frequency and spectral density—could better represent the excitation from practical vibration sources. Considering using the same excitation model as in reference [
32], choosing white Gaussian noise excitation through a second-order filter to obtain colored excitation, the relation between colored acceleration excitation
F(
t) and white Gaussian excitation
f(
t) can be derived as:
where
ωc,
γ are the center frequency and the bandwidth of the colored excitation, respectively.
The correlation function and spectral density of White Gaussian excitation
f(
t) are defined as:
where
S0 is the spectral density of the excitation, and
δ is the Dirac-delta function.
Fourier transform for Equation (7) gives:
The frequency response function of
F(
t) versus
f(
t) can be expressed as:
Then the spectrum of
F(
t) can be obtained:
According to reference [
32], an important characteristic of this selected excitation type is that the variance of
F(
t) is a constant, which is only related to
S0. As a result,
E(
F2) is independent of the center frequency and the bandwidth of the colored excitation.
The normal white noise can be considered as the derivative of the corresponding Wiener process, that is:
Introducing
and substituting Equations (4) and (5) into Equation (1), one may obtain:
Then the corresponding two-dimensional Kolmogorov equation is given as:
where:
In order to obtain concise expressions, introducing that:
It should be pointed out that here variable ce is obviously involved with cg and cθ, thus it relates to the electromagnetic transfer factor gem and piezoelectric transfer factor θ. In addition, according to Equations (5) and (17), the introduction of nonlinear magnetic forces, which brings linear factor k1 and nonlinear factor k3, will affect the natural frequency ωn. Thus it will change equivalent resistance R and damping coefficient cm, and hence finally will influence ce.
Then Equation (16) can be rewritten as:
where
p =
p(
x1,
x2,
x3,
x4,
t|
x10,
x20,
x40,
t0) is the is transition probability density function of random variable
x1,
x2,
x3,
x4 at time
t.
Equation (18) has the following boundary condition:
The exact solution of Equation (18) cannot be attainable. According to the effort made by Daqaq for nonlinear unimodal Duffing-type harvesters [
32], Van Kampen expansion can be used to derive an approximate solution when the mean square value of
xi is a measure of the response amplitude. In the former studies of our research [
39], it indicated that for the designed nonlinear hybrid piezoelectric and electromagnetic energy harvester,
E(
xi2) is proportional to
S as well. Consequently, we could use Van Kampen expansion similarly to calculate output for nonlinear hybrid energy harvester. That is:
Then the transition probability density function can be derived as a new function of
X1,
X2,
X3,
X4 and
t:
The corresponding two-dimensional Kolmogorov equation can be rearranged as:
with its boundary condition
p1(−∞,
t) =
p1(+∞,
t) = 0.
Following a similar manner described in Daqaq’s work [
32], after only considering less than fourth order moments and setting the time derivatives to zero, we can derive 45 linearly coupled algebraic equations with 45 unknown variables including
E(
xi2) that need to be solved together. These equations are listed in details in
Appendix A.
Based on Equations (4) and (6), the variance of output voltage of PE element and output current of EM element can be calculated as:
Thus mean power output of PE and EM element of nonlinear hybrid energy harvester are illustrated as:
Employing E(xi2) in Equations (23) and (24), the output characteristics of our nonlinear hybrid piezoelectric and electromagnetic energy harvester under colored excitation can be presented.
In order to validate the proposed theoretical method, Monte Carlo simulation [
39,
43] was used to analyze the responses of the designed nonlinear hybrid piezoelectric and electromagnetic energy harvester under colored excitation.
The normal White noise can be considered as the derivative of the corresponding Wiener process. As a result, after introducing
and substituting them into governing equations Equations (1)–(3) and excitation properties Equations (7) and (8) gives:
where
dB(
t) is the corresponding Wiener process, which has zero mean and 2
πS0 variance.
According to Euler-Maruyama scheme, Equation (25) can be expressed in time discrete form:
Using the randn function
N(0, 1) generated by Matlab, the distributed independent random variables Δ
Bn can be derived as:
Employing Equation (26) to obtain
, the expectations can be estimated by Monte Carlo simulation:
On the average, the Euler scheme discrete was calculated from 30,000 realizations and the transition probability density function from a simulation of 20,000 realizations with a time step 10−5.
4. Results and Discussion
Under colored excitation, output performances of hybrid piezoelectric and electromagnetic energy harvester can be influenced by characteristics of excitation signal, that is, the bandwidth γ, center frequency ωc and constant spectral density S0 within a certain frequency range. Meanwhile, output voltage and current of load resistance are considered as a measure of power output. Therefore, the output characteristics of the designed hybrid energy harvester can be associated with load resistances in PE element and EM element (Rp and Rm). As mentioned before, introducing nonlinear magnetic forces into the traditional hybrid PE and EM energy harvester will bring a linear factor term and a nonlinear factor term into the governing equation (Equation (1)). Consequently, the natural frequency of the vibrator will change and hence it will affect the value of so-called equivalent resistance for capacity of PZT layer based on Equation (5) and damping coefficient. Accordingly, the related coefficients of 45 linearly coupled algebraic equations will be changed and the output performances will eventually be affected.
It should be pointed out that here acceleration’s spectral density
S0 refers to the fixed value of spectral density of colored excitation within the following frequency range:
with the other frequencies, the spectral density of colored excitation remains zero.
The structural parameters, material properties and parameters of original differential equations for the nonlinear hybrid energy harvester are listed in
Table 1,
Table 2 and
Table 3. For comparative analysis, a linear hybrid case with same structural parameters and material properties is chosen. The only difference between linear and nonlinear hybrid energy harvester is whether it has two nonlinear fixed magnets (which brings linear and nonlinear factors into governing equation) or not. Thus for the linear case, variables
k1 and
k3 in the theoretical analysis and Monte Carlo simulation are zeros, and its natural frequency and damping coefficient will also be different from the nonlinear case. Then effects of introducing nonlinear magnets into hybrid energy harvester could be obtained and discussed.
4.1. Effects of Load Resistances and the Excitation’s Spectral Density
In this section, when the bandwidth
γ and center frequency
ωc are constant, the variation of the mean output powers of colored noise excited nonlinear and linear hybrid energy harvesters with load resistance of PE element,
Rp, load resistance of EM element,
Rm and acceleration’s spectral density value
S0 are presented and discussed using both the Fokker-Planck equation and Monte Carlo simulation. The output characteristics for nonlinear and linear hybrid energy harvesters with load resistances when
γ = 1 Hz,
ωc =
ωn and
S0 = 0.1 m
2/s
4·Hz are shown in
Figure 2 and some important values that are worth discussing are listed in
Table 4.
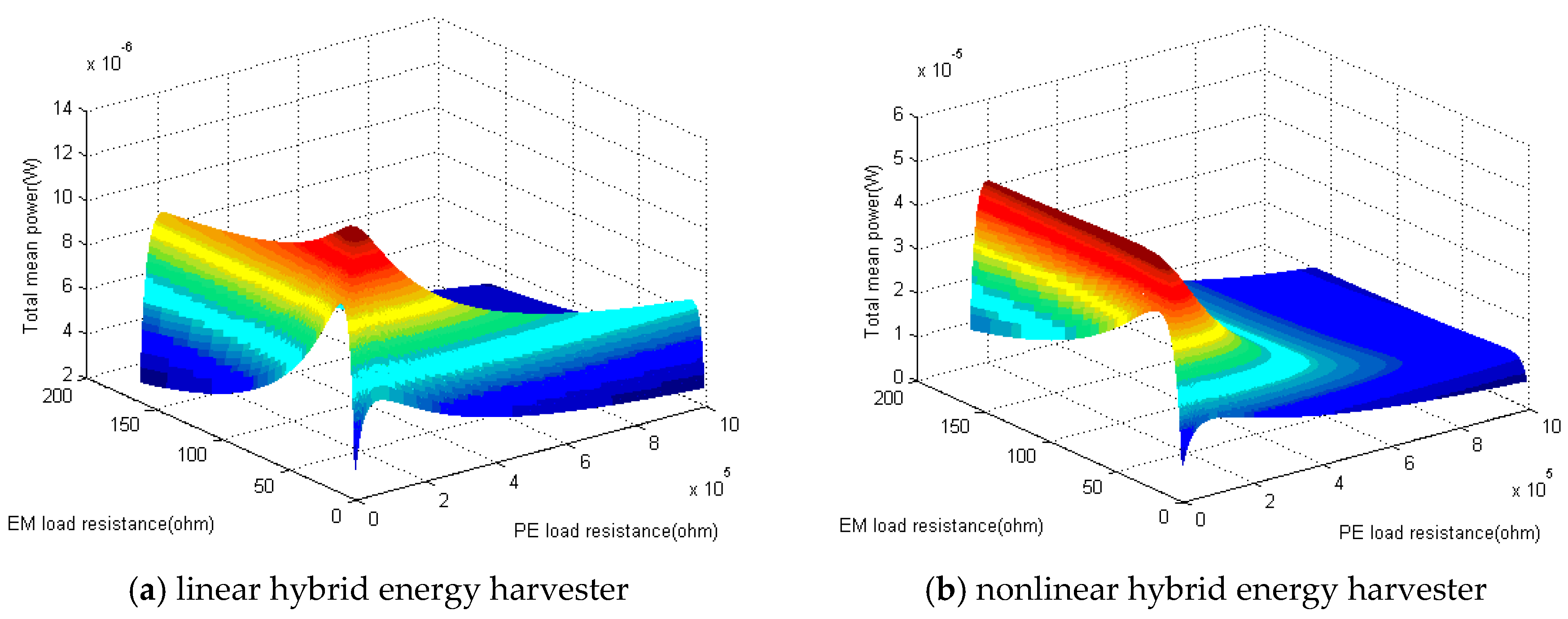
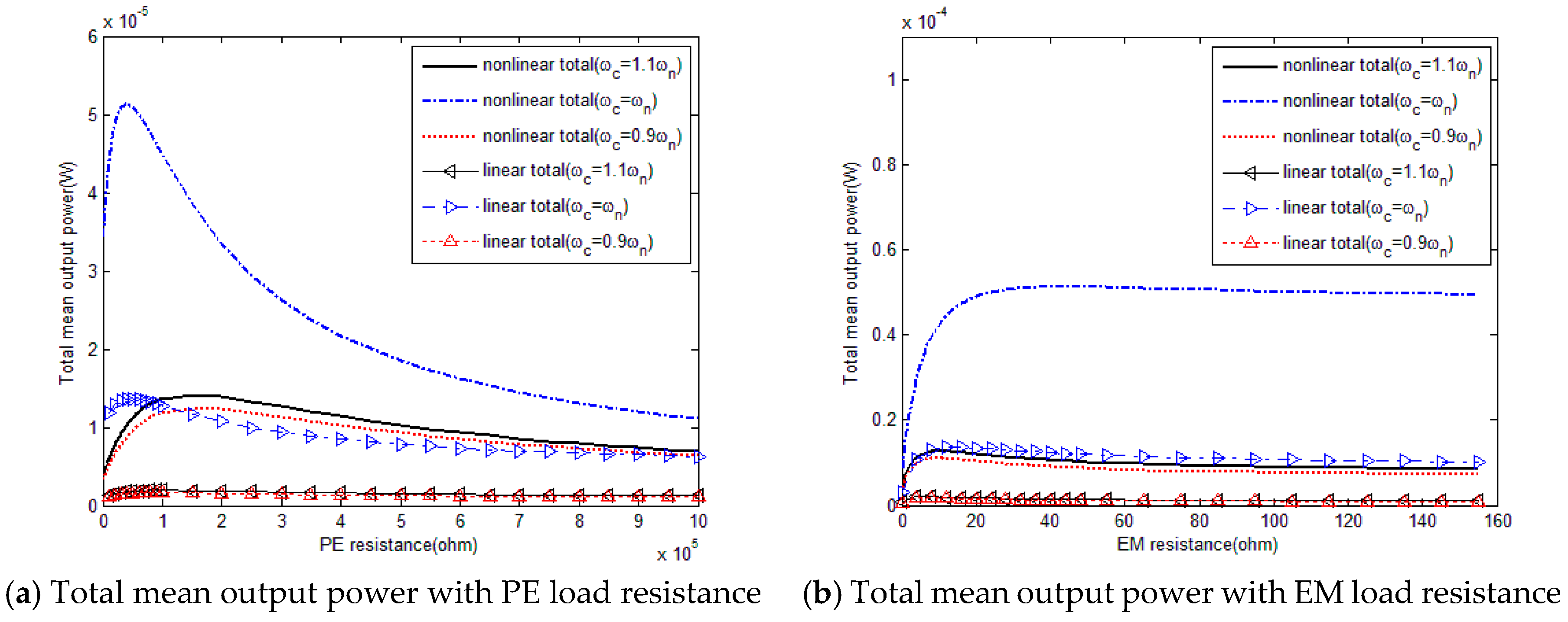
As shown in
Figure 2 and
Table 4, when variables
ωc, γ and
S0 are constant, a nonlinear hybrid piezoelectric and electromagnetic energy harvester could provide much higher output power (5.1243 × 10
−5 W) with respect to the linear counterpart (1.3631 × 10
−5 W). Besides, the natural frequency of the nonlinear hybrid energy harvester is much smaller than that of a linear one, which is beneficial for energy harvesting in the application. Therefore, the nonlinear hybrid PE and EM energy harvester could obviously outperform the linear case. In addition, it also indicates that the optimal values of PE load resistance and optimal EM load resistance for nonlinear and linear hybrid energy harvester are different.
Under colored excitation with
γ = 1 Hz,
ωc =
ωn and
S0 = 0.1 m
2/s
4·Hz, the variation of the output performances of nonlinear and linear hybrid PE and EM energy harvesters with PE load resistance, EM load resistance and acceleration’s spectral density are depicted both theoretically and numerically in
Figure 3,
Figure 4 and
Figure 5. In
Figure 3, EM load resistances are set to optimal values, that is, 45
for a nonlinear hybrid energy harvester and 15
for the linear case. Similarly in
Figure 4, PE load resistances are set to optimal values, 41,000
for the nonlinear configuration and 51,000
for the linear one; In
Figure 5, both the PE load resistances and EM load resistances are the optimum.
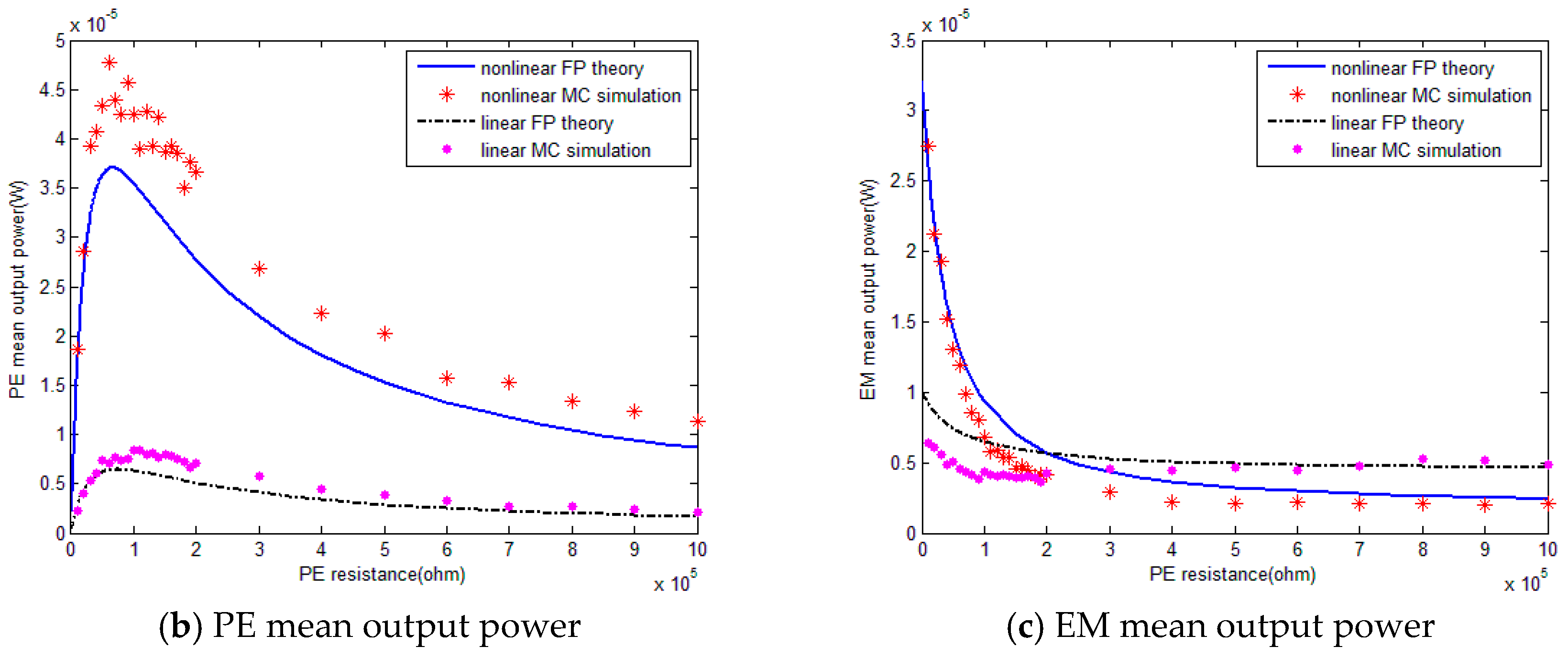
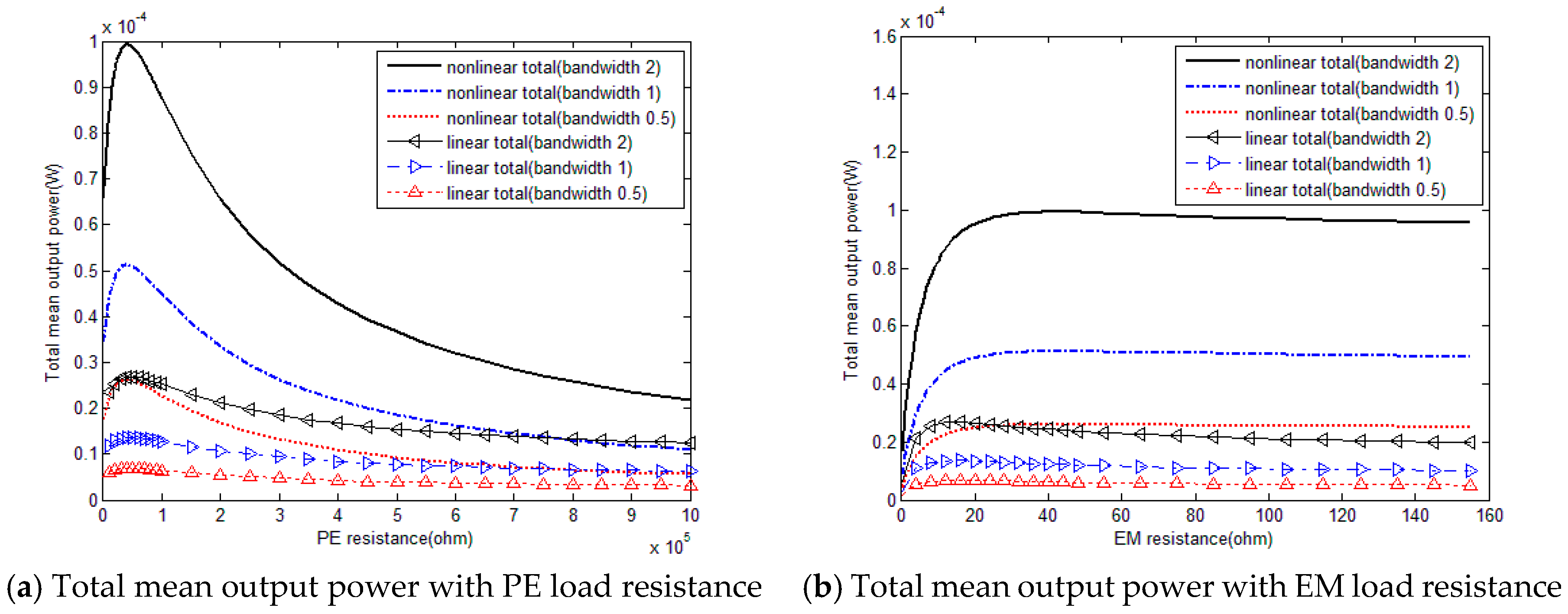
Figure 3 shows that Monte Carlo numerical results verify the effectiveness of the modeling method based on the Fokker-Planck equation for describing the output characteristics of nonlinear hybrid energy harvester under colored excitation. When the EM load resistance is fixed, there exists an optimal PE load resistance value to obtain the maximum of total mean output power. For the PE element of the hybrid energy harvester, the PE mean output power increases with the PE load resistance until it reaches the maximum, after that it decreases with the PE load resistance, while for the EM element, the EM mean output power decreases with the increase of PE load resistance. Moreover, it also demonstrates that the nonlinear hybrid PE and EM energy harvester could provide higher EM mean output power within a certain PE load resistance range compared to the linear configuration. Nevertheless, this improvement decreases with PE load resistance and even with some PE load resistance values, the EM mean output power of nonlinear hybrid energy harvester is a little bit lower than the linear one. However, PE mean output power of nonlinear hybrid energy harvester could improve dramatically with respect to the linear counterpart. Consequently, total mean output power of colored excited nonlinear hybrid PE and EM energy harvester could always outperform the linear one.
As shown in
Figure 4, it could be observed firstly that the theoretical trends of mean output power with the increase of EM resistance are consistent with Monte Carlo simulation, which proves the accuracy and feasibility of using the Fokker-Planck theory to predict output characteristics of nonlinear hybrid PE and EM energy harvester under colored noise again. Secondly, it shows that when the PE load resistance is constant, the total mean output power increases with the increase of EM load resistance, and after it reaches the maximum, it decreases slightly with the EM load resistance. PE mean output power increases with the EM load resistance, while EM mean output power firstly increases then decreases with the EM load resistance. Additionally,
Figure 4 also indicates that total mean output power, PE mean output power and EM mean output power of colored excited nonlinear hybrid PE and EM energy harvester could all increase significantly in comparison of the linear case. The increase of the PE element is much higher than that of the EM element. Accordingly, it reveals again that under colored excitation, nonlinear hybrid PE and EM energy harvester could have better performances than the linear counterpart and hence nonlinear hybrid PE and EM energy harvester is more favorable than linear one for energy harvesting in practical applications.
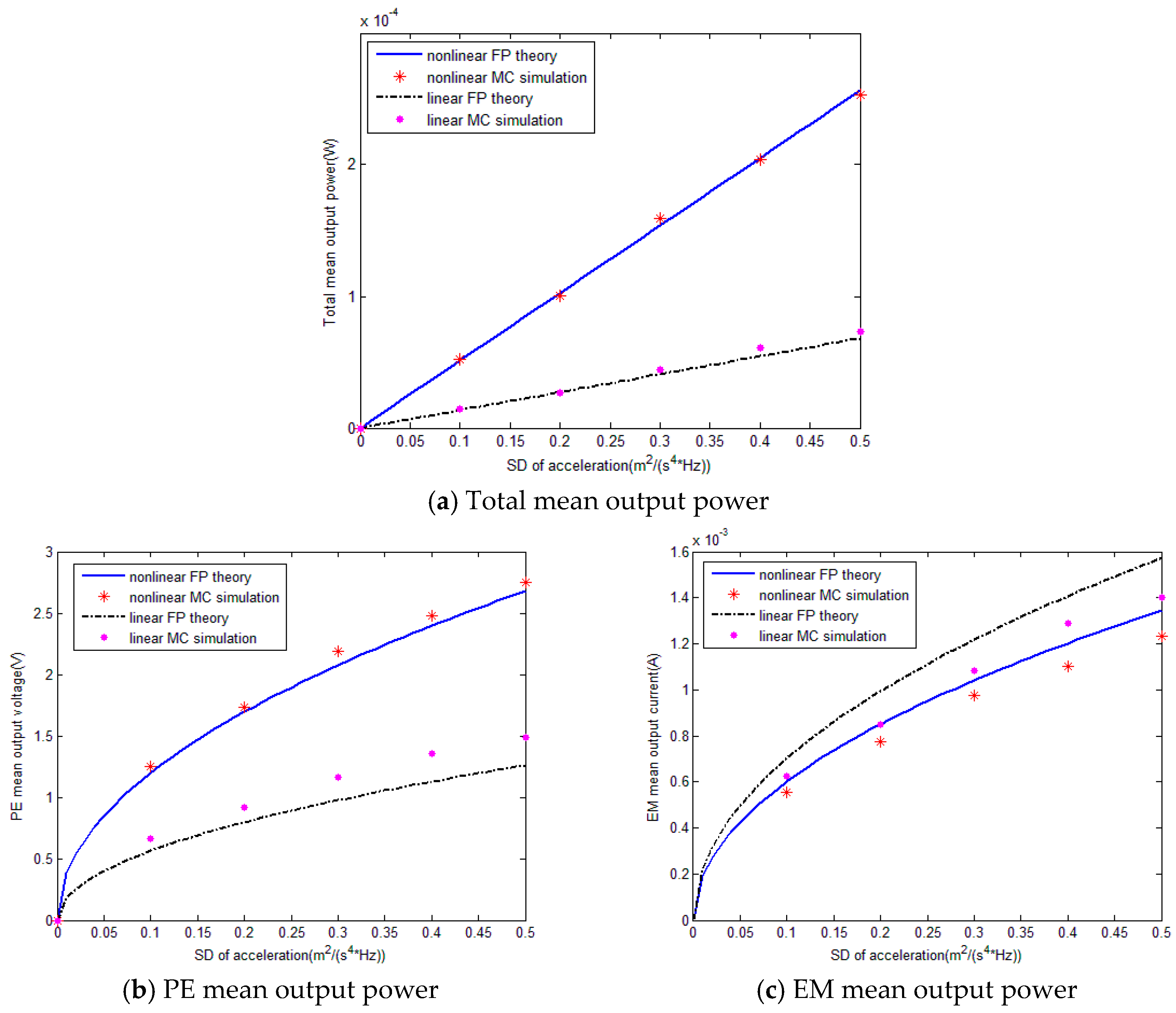
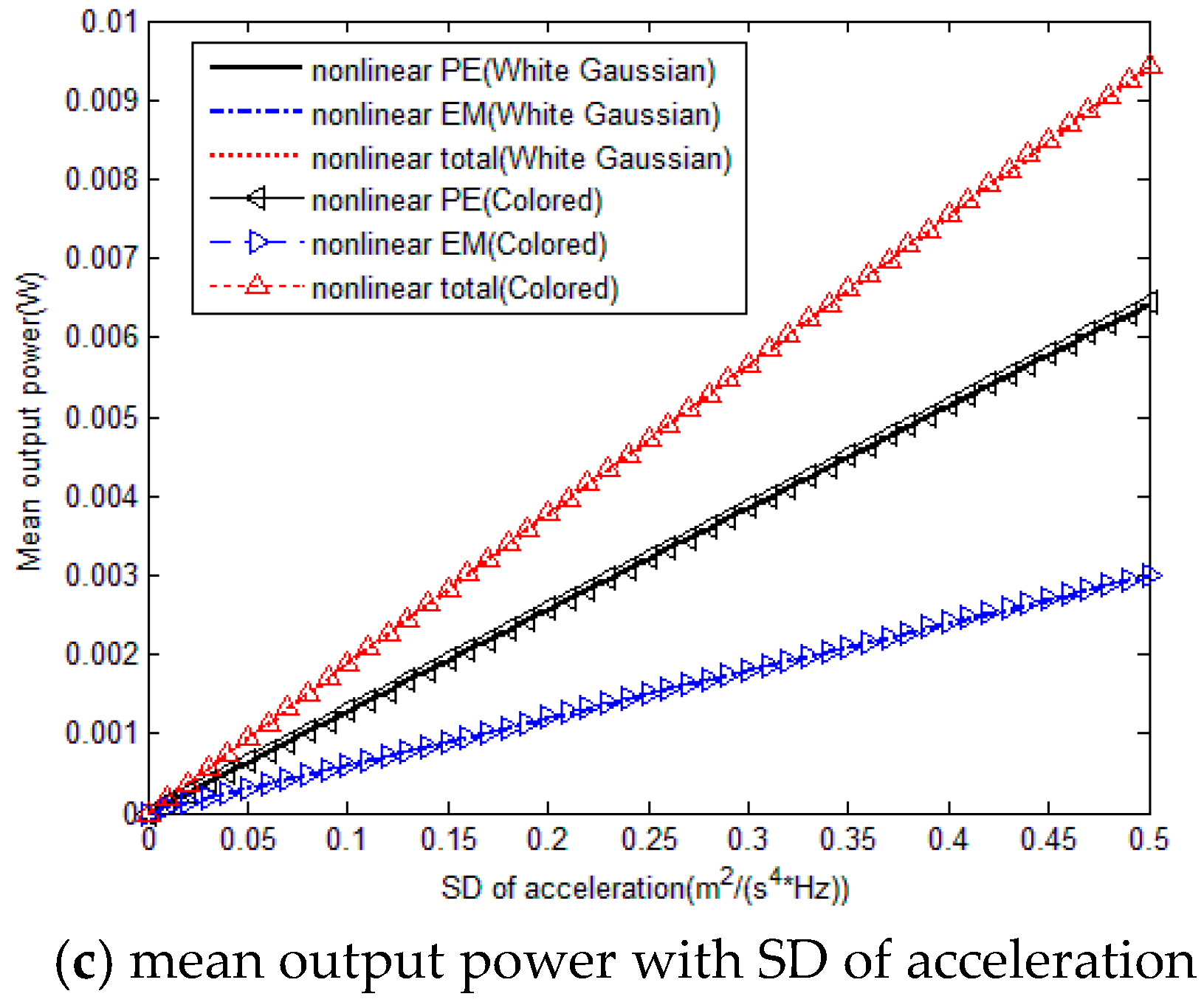
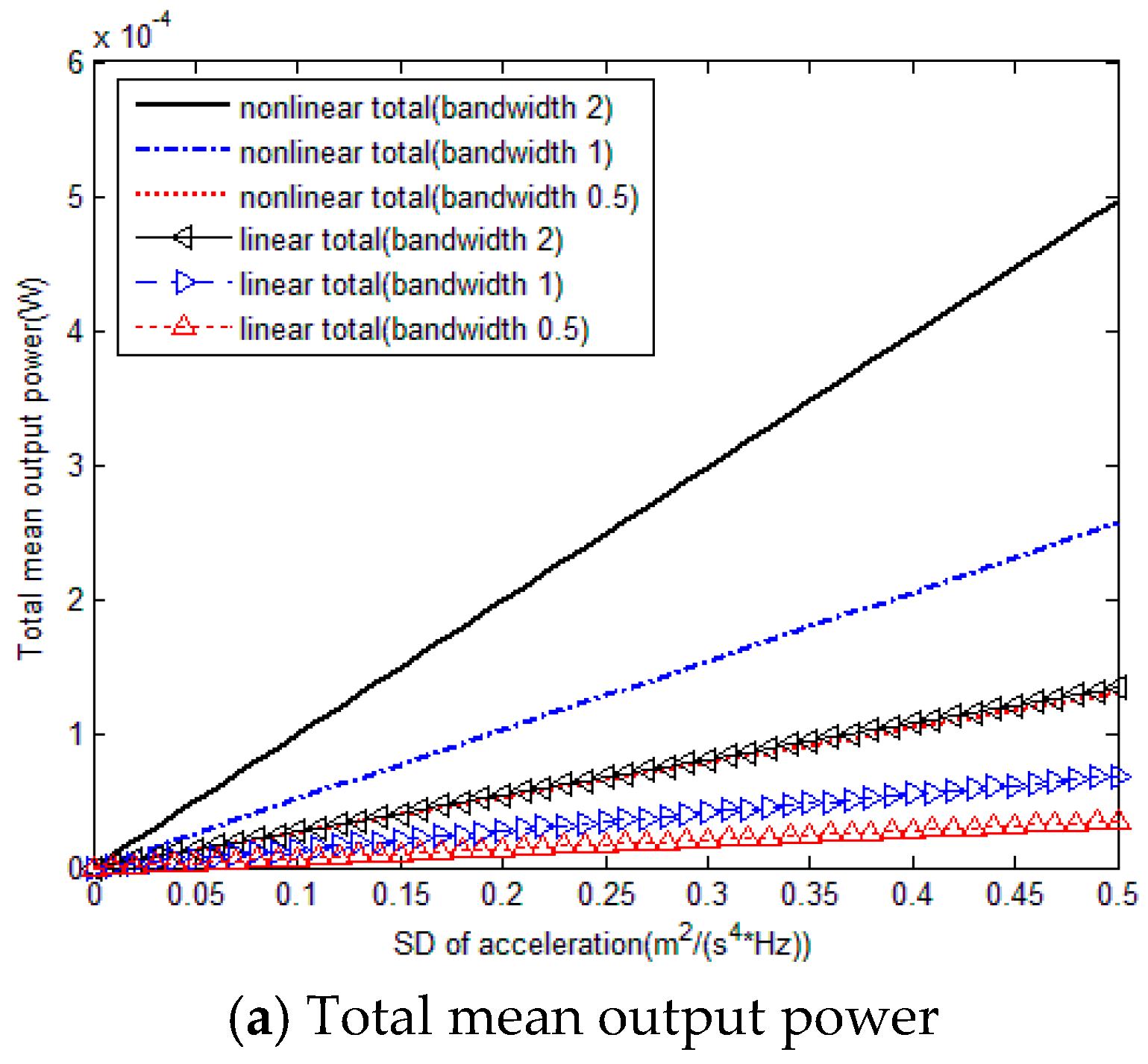
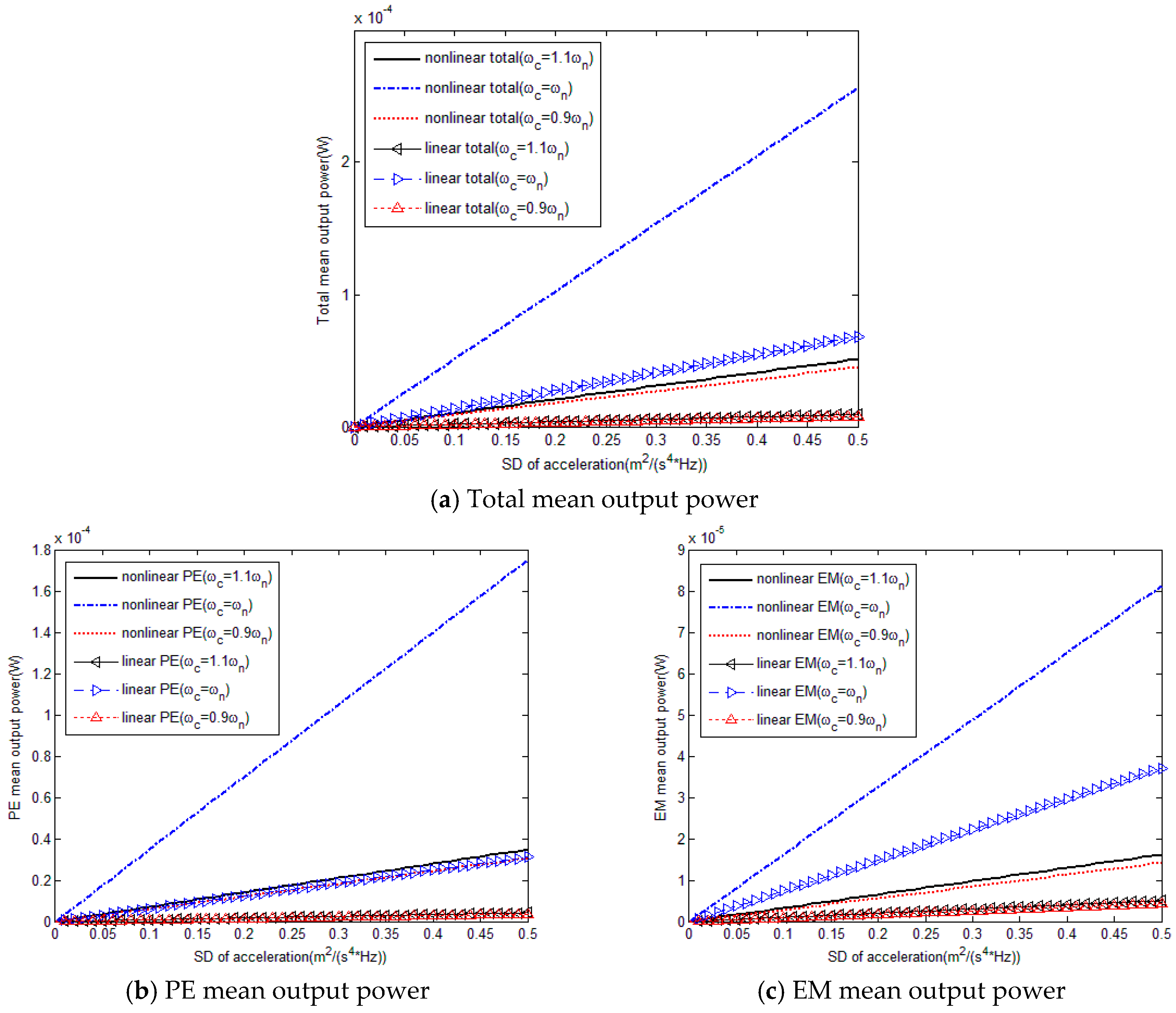
Following the output responses trajectories obtained from the Fokker-Planck theory, it is numerically verified that when the center frequency and bandwidth of colored excitation are constant, total mean output power increases linearly with the increase of acceleration’s spectral density, and both PE mean output voltage and EM mean output current increase with the acceleration’s spectral density. Besides, the slopes of the PE and EM mean output curves become smooth with the increase of acceleration’s spectral density. In addition,
Figure 5 also illustrates that the nonlinear hybrid PE and EM energy harvester under colored excitation could perform much better than the linear one. The PE element has a more significant influence on the output characteristics compared to EM element. Moreover, curvatures of trends of nonlinear hybrid PE and EM energy harvester varying with the acceleration’s spectral density are larger than their linear counterparts. Thus the mean output power of nonlinear hybrid energy harvester could increase rapidly with the acceleration’s spectral density compared to the linear case.
It should be explained that although the theoretical results are successfully validated numerically within a certain error range, it could still be observed that there exists fluctuations in the Monte Carlo simulation data. A plausible reason is that Monte Carlo method uses the average value to simulate the expected value (as shown in Equation (28)). However, the number of data sample is limited and thus data error is inevitably produced. Besides, this error will be reduced when choosing larger data sample.
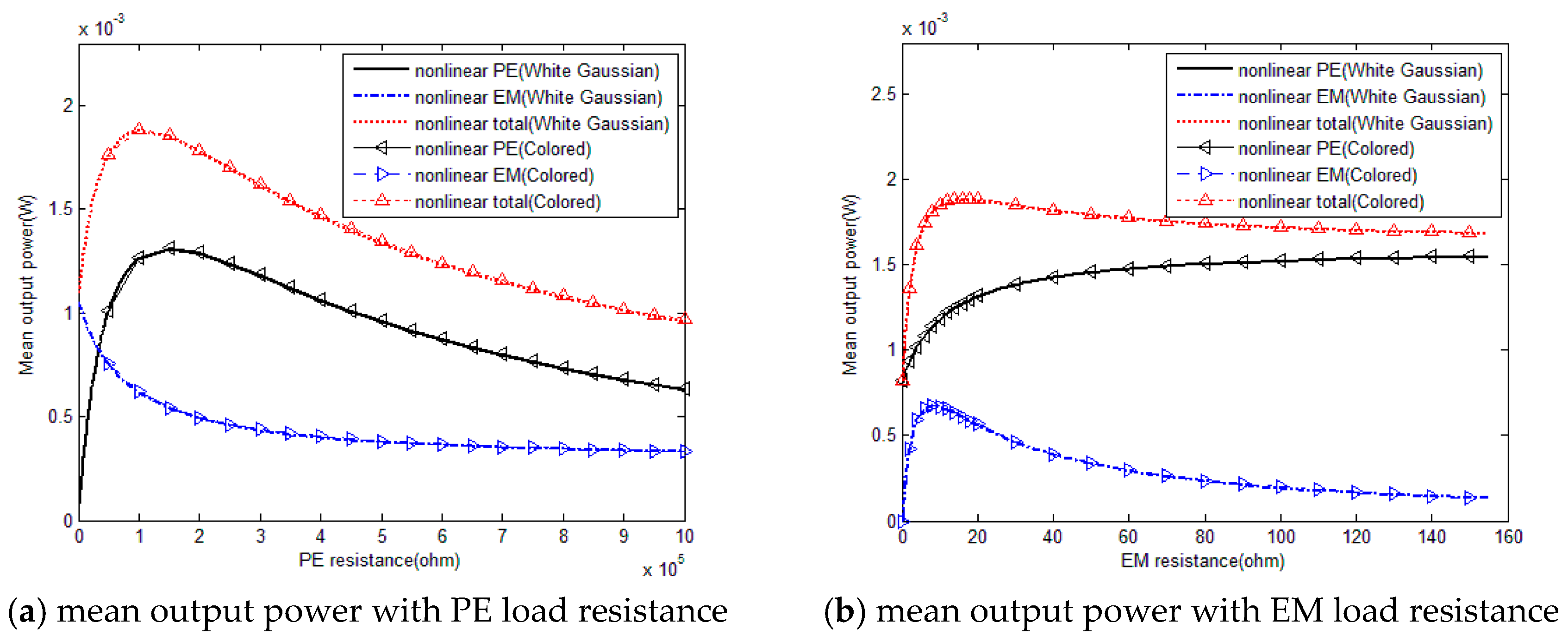
If the bandwidth has an enormously large value, i.e.,
γ = 10,000 Hz, then the colored excitation will approach white Gaussian noise excitation. Under this circumstance, the Fokker-Planck results of the white Gaussian noise excited nonlinear hybrid PE and EM energy harvester based on our previous research [
30] could be used to further verify the correctness of the theoretical method. The output characteristics of the white Gaussian and colored noise excited nonlinear hybrid PE and EM energy harvester (when
γ = 10,000 Hz) are presented in
Figure 6. Here,
ωc =
ωn for colored excitation and for both colored and white noise excitation the spectral density are set as
S0 = 0.1 m
2/s
4·Hz. It should be pointing out that the optimal load resistances are different with the case when
γ = 10,000 Hz, the optimal PE load resistance is 111,000
and optimal EM load resistance is 17
.
As shown in
Figure 6, output performances based on analytical expressions of nonlinear hybrid piezoelectric and electromagnetic energy harvester are consistent with theoretical results through solving 45 linearly coupled equations, the difference between modeling values obtained by two theoretical models is rather small. As a consequence, it demonstrates that it is feasible to predict output characteristics of nonlinear hybrid PE and EM energy harvester under colored excitation using the presented theoretical model again.
In general, different from previous studies for PE or EM energy harvester [
32,
35,
37], nonlinearities generated by additional magnet interactions could be beneficial for hybrid PE and EM energy harvesting because it lowers the natural frequency and provides more efficient transduction under colored excitation.
4.2. Effects of the Excitation’s Bandwidth and Center Frequency
As it presented before, there is a reasonably good match between the analytical results based on Fokker-Planck equations and simulation results obtained from Monte Carlo method. Besides, the feasibility of theory method is also validated by colored excitation case that towards White Gaussian excitation. As a consequence, the theoretical model is capable of accurately predicting output performance of nonlinear hybrid piezoelectric and electromagnetic energy harvester under colored excitation. Furthermore, numerical simulation requires abundant running time. Thus in the following research, we only derive trends with different variables through theoretical method to investigate and discuss relevant results. In this section, effects of excitation’s bandwidth and center frequency on output characteristics of linear and nonlinear hybrid energy harvester have been studied under colored excitation.
Setting that
S0 = 0.1 m
2/s
4·Hz, both PE load resistances and EM load resistances are optimum (41,000
and 45
for
Rp and
Rm of the nonlinear case, 51,000
and 15
for the linear case). The total mean output power variation of the colored noise excited linear and nonlinear hybrid energy harvester with bandwidth and center frequency are illustrated in
Figure 7 and
Figure 8.
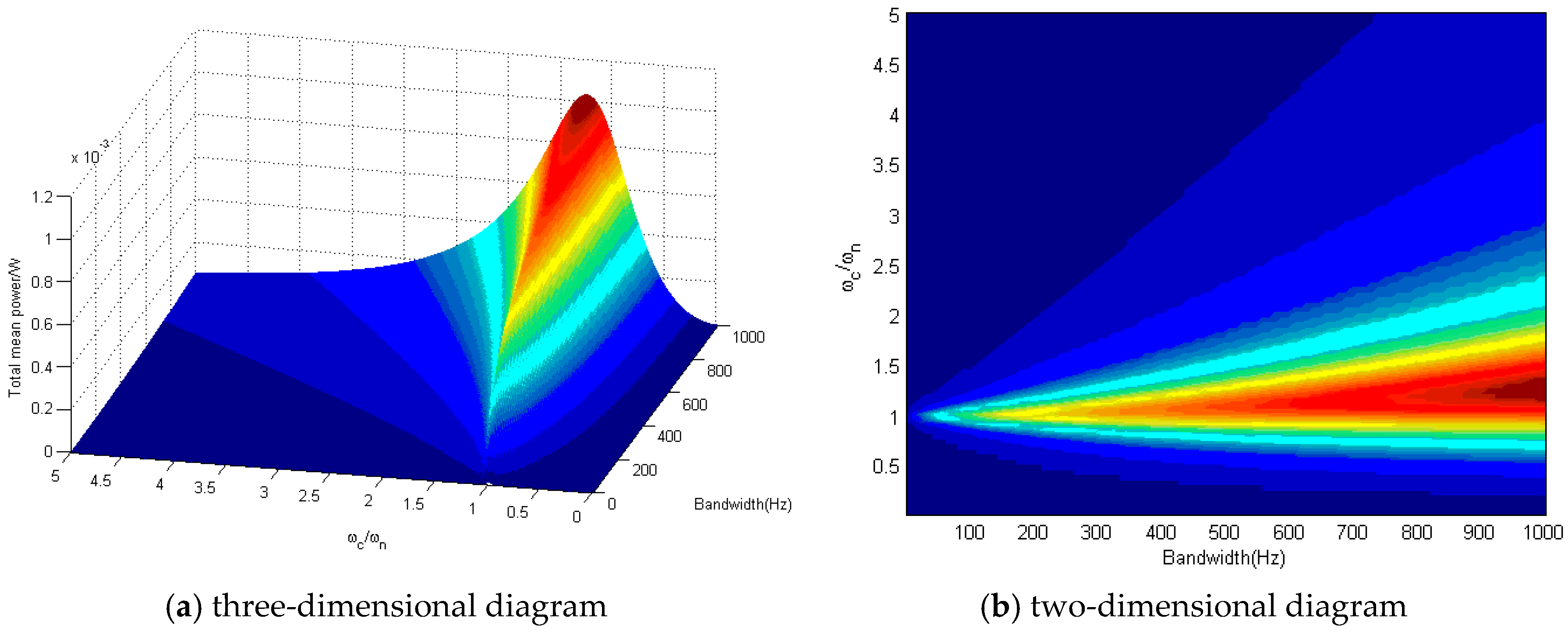
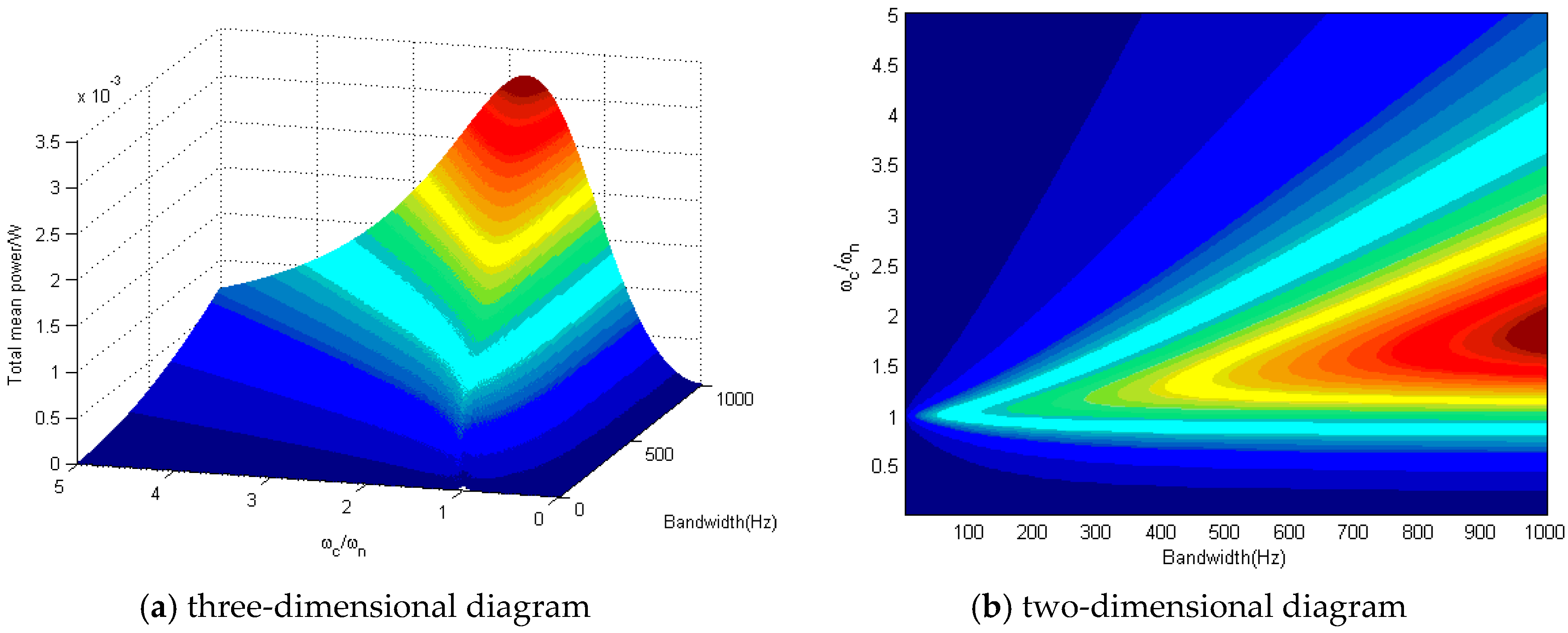
As depicted in
Figure 7 and
Figure 8, firstly it can be observed that the total mean output power of the colored noise excited hybrid energy harvester increases with the increase of bandwidth. Secondly, it reveals that when bandwidth is rather small, the maximum of total mean output power occurs at
ωc =
ωn. With considerably large bandwidth however, the total mean output power is maximized when the center frequency is larger than natural frequency of the system. Finally, it demonstrates that compared to linear hybrid energy harvester, nonlinear hybrid configuration could produce much higher output excited by colored noise varying with bandwidth and center frequency.
The specific changes in the output characteristic variation with bandwidth and center frequency are investigated, respectively, in the following sections.
4.2.1. Effects of the Excitation’s Bandwidth
In this section, when
ωc is a constant, specific mean output powers with the change of bandwidth are shown in
Figure 9 and trends of hybrid energy harvesters varying with load resistances and acceleration’s spectral density under different bandwidths
γ are illustrated in
Figure 10 and
Figure 11. Here, setting that
ωc =
ωn,
S0 = 0.1 m
2/s
4·Hz, EM load resistances are set to optimal values when
γ = 1 Hz, that is, 45
for nonlinear hybrid energy harvester and 15
for linear case in
Figure 10a. Similarly in
Figure 10b, PE load resistances are set to optimal values, 41,000
for the nonlinear configuration and 51,000
for the linear one; In
Figure 9 and
Figure 11, both PE load resistances and EM load resistances are optimum.
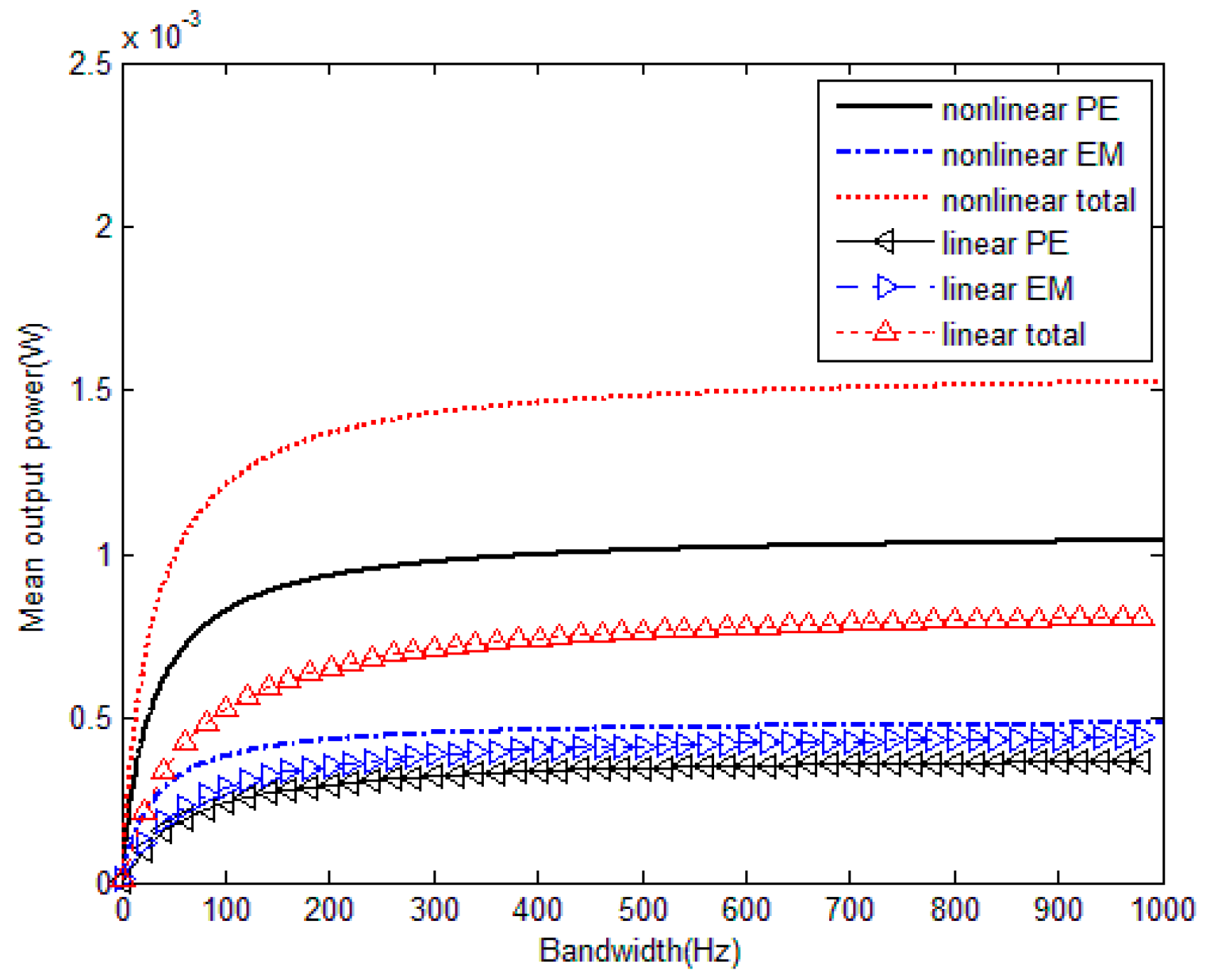
Figure 9 shows that as the bandwidth increases, total, PE and EM mean output power of the hybrid energy harvester all increase. Nevertheless, the growth of the mean output power slows down with the increase of bandwidth. Within the comparatively large bandwidth range, differences among values of total mean output powers are rather small. For the linear hybrid energy harvester, EM mean output power is slightly larger than PE mean output power, while PE mean output power is much higher than that from the EM element for the nonlinear hybrid energy harvester. In addition, it proves that under color excitation with the change of bandwidth, total the mean output power of the nonlinear hybrid energy harvester could always obtain obviously higher output power than the linear one.
As shown in
Figure 10, total mean output power increases as the bandwidth
γ increases. Moreover, it also proves that with same increase of bandwidth, the mean output power of nonlinear hybrid PE and EM energy harvester is greatly improved compared with the linear hybrid energy harvester. Moreover, when the bandwidth is fixed, the output performance of a nonlinear hybrid PE and EM energy harvester could always outperform the linear counterpart. Therefore, the nonlinear energy harvester could always derive much higher total mean output power than the corresponding linear hybrid energy harvester under colored excitation.
According to data in
Figure 11, it reveals that when
ωc =
ωn, load resistances are both set to optimum values, the total mean output power, PE mean output power and EM mean output power are all improved. Furthermore, compared with the EM element, the PE mean output power is more influenced by the change of bandwidth. In addition, when the bandwidth is changed, the output power continues to increase linearly with the spectral density of acceleration. Besides, the larger the bandwidth is, the greater the linear slope of the output power varies with the acceleration spectrum density, and the more obvious the growth trend is.
Figure 11 also shows that mean output power of nonlinear hybrid PE and EM energy harvester are always larger than the linear configuration and trends of nonlinear hybrid energy harvester variation with acceleration’s spectral density are steeper than the linear ones.
Generally, the wider the bandwidth is, the higher the output power for a hybrid PE and EM energy harvester under colored excitation that could be obtained. Besides, the output power of the nonlinear hybrid energy harvester is much higher and could be increased more rapidly with the increase of excitation bandwidth compared to the linear configuration.
4.2.2. Effects of the Excitation’s Center Frequency
In this section, we consider the detailed output characteristics of linear and nonlinear hybrid PE and EM energy harvesters when the center frequency of the excitation changes. According to results in
Figure 7 and
Figure 8, cases with
γ = 1 Hz and
γ = 1000 Hz are chosen for obtaining the influence of center frequency on output characteristics. Here,
S0 = 0.1 m
2/s
4·Hz and load resistances are set as the optima of the case under
γ = 1 Hz excitation. Mean output powers of hybrid energy harvesters with the increase of center frequency for both two selected cases are shown in
Figure 12.
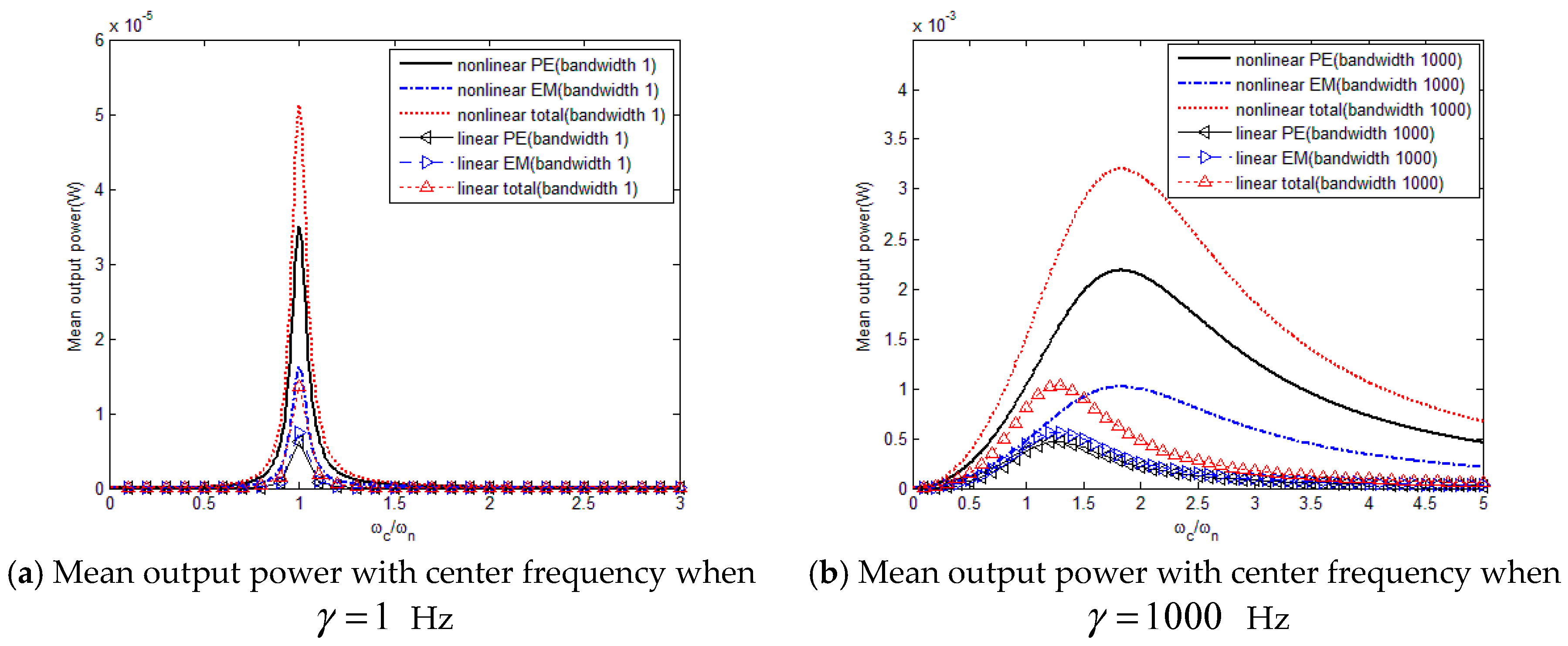
Figure 12 indicates that mean output power of case with
γ = 1 Hz is far less than that of case with
γ = 1000 Hz. Combining the results in
Figure 7,
Figure 8 and
Figure 12, it proves that the optimal value of excitation’s center frequency to perform the best output increases with the increase of excitation’s bandwidth. With smaller bandwidth (
γ = 1 Hz for instance), cases with
ωc =
ωn condition can obtain the best output performance for both linear and nonlinear hybrid energy harvesters. When the value of bandwidth is rather large (
γ = 1000 Hz for instance), tuning the center frequency slightly larger than the natural frequency will derive the highest mean output power for a linear hybrid energy harvester, while for nonlinear hybrid energy harvester with
γ = 1000 Hz, the center frequency should be tuned to approximately 1.8 times larger than the natural frequency for maximizing the output. Besides, it demonstrates that nonlinear hybrid energy harvester seems to be more preferable in energy harvesting under colored excitation again.
It should be highlighted that the results of
Figure 12 are obtained when setting the load resistances at the optima for cases with
γ = 1 Hz. In fact, the optimal load resistances vary with the bandwidth (which can be demonstrated from
Figure 6 of case with
γ = 10,000 Hz. Therefore, the maximum mean output powers for cases
γ = 1000 Hz will be even higher than the data from
Figure 12b.
This research mainly concentrates on output behaviors under narrow-band excitation, accordingly we consider cases with
γ = 1 Hz to observe the output performances of hybrid energy harvesters under different center frequencies (depicted in
Figure 13 and
Figure 14). Similarly,
S0 = 0.1 m
2/s
4·Hz in
Figure 13 and in
Figure 13a, EM load resistances are set as optima, namely, 45
for the nonlinear case and 15
for the linear case. In
Figure 13b, the optimal PE load resistance for the nonlinear hybrid energy harvester is used as 41,000
, and 51,000
for the linear one. In
Figure 14, both PE load resistances and EM load resistances are the optima.
As illustrated in
Figure 13 and
Figure 14, it can be firstly observed that as the center frequency changes, the trends of the mean output powers of the colored excited nonlinear and linear hybrid PE and EM energy harvesters with the variation of load resistances and acceleration’s spectral density remain unchanged. Secondly, it shows that the hybrid energy harvesters under the
ωc =
ωn condition exhibit the highest output power among cases with
γ = 1 Hz. When the center frequency is slightly greater than or less than the natural frequency, the output response of hybrid energy harvesters will be reduced. Besides, reductions of mean output powers obtained in the other two cases are similar. Finally, in comparison with the linear configuration, nonlinear hybrid PE and EM energy harvester could obtain much better output performance. In specific, total mean output power of nonlinear case will be substantially improved and PE element contributes more in the increase of output power compared to EM element. In addition, curves of nonlinear case have larger curvatures, which demonstrates that output of nonlinear hybrid energy harvester will change faster than the linear case when relevant variables increases.
In conclusion, from [
32,
43,
44,
45], researchers arrived that for Duffing-type PE or EM energy harvester under band-limited excitation tuning the natural frequency at a larger or lower frequencies can obtain higher output power according to the value of bandwidth and nonlinearity. Same results have been found for nonlinear hybrid PE and EM energy harvester excited by colored noise with large bandwidth. For nonlinear and linear cases under small bandwidth colored excitation however, the peak in the expected value occurs at the condition that
ωc =
ωn.
5. Conclusions
Validated by Monte Carlo simulation, a theoretical method based on the Fokker–Planck equation corresponding to the hybrid piezoelectric and electromagnetic energy harvester excited by colored excitation is derived. Total mean output power, PE mean output power and EM mean output power of the hybrid oscillator are also obtained. Theoretical results of a nonlinear hybrid PE and EM energy harvester when subjected to colored excitation approaching the white excitation limit are similar to data calculated from white Gaussian noise excited theory, which illustrates the accuracy of the approximation method again. In contrast to the common understanding that stiffness-type nonlinearities hinder the efficiency of the harvester with single harvesting principle under colored excitation, this paper clearly demonstrates that for hybrid piezoelectric and electromagnetic energy harvesters, adding nonlinear magnets to bring linear and nonlinear factors into the governing equations will improve mean output power remarkably. Indeed, when subjected to colored excitation, the designed nonlinear hybrid PE and EM energy harvester can outperform the linear one noticeably. Following is a more detailed summary of the main observations:
For a fixed hybrid piezoelectric and electromagnetic energy harvester under colored excitation, the power output depends on load resistances, spectral density of acceleration within a certain frequency range, bandwidth and center frequency. There exist an optimal PE load resistance and optimal EM load resistance for maximizing the total mean output power of colored noise excited hybrid energy harvester. In addition, the mean output power is increased linearly with the increase of acceleration’s spectral density within a certain frequency range of colored excitation. It is also found that the improvement in output power is mostly pronounced for a wider bandwidth. Moreover, within different bandwidth ranges, optimal ratios of the excitation’s center frequency to the system’s natural frequency for maximizing output are different. Besides, the influence of PE element on the output characteristics is larger than that of EM element.
Under colored excitation, with same conditions a stiffness-type nonlinear hybrid energy harvester could have a fundamental performance advantage over the linear one. Applying nonlinear magnetic forces to a typical hybrid PE and EM harvester to obtain nonlinear hybrid energy harvester will increase the total mean output power significantly. This is due to the fact the introduction of nonlinearities lowers the natural frequency of the vibrator, which will not only affect the damping coefficient but also the value of the so-called equivalent resistance for the capacity of PZT layer.
Trends of nonlinear hybrid PE and EM energy harvester with the change of several variables are similar to the trends of the linear configuration. Nevertheless, the curvatures of the nonlinear curves are larger than those if the linear ones. Thus, with the same change of presented variables, a nonlinear hybrid PE and EM energy harvester will change faster than the linear one and has a higher degree of impact from those variables.
With these observations, it is possible to conclude that a nonlinear hybrid PE and EM energy harvester could always obtain better output performance than the linear counterpart under colored excitation. Therefore, it is more suitable for energy harvesting in a vibrating environment. In order to further improve the output characteristics, the load resistances should be set as optima. The natural frequency should be carefully designed due to the fact it is not only related to the excitation’s center frequency but also the bandwidth, and under a wider bandwidth excitation, the nonlinear hybrid PE and EM energy harvester could perform better.