A Nonparametric Economic Analysis of the US Natural Gas Transmission Infrastructure: Efficiency, Trade-Offs and Emerging Industry Configurations
Abstract
:1. Introduction
- 210 interstate and intrastate gathering and transmission pipelines that extend for more than 320,000 miles around the country (including about 20,000 miles of gathering pipelines);
- more than 1400 compression stations, 11,000 delivery points, 1400 interconnection points, 5000 receiving points, 24 hubs, 400 natural gas storage facilities, and eight liquefied natural gas (LNG) facilities.
2. Literature Review
3. The Measurement of the Economic Efficiency of Gas Transmission Infrastructure
4. Method
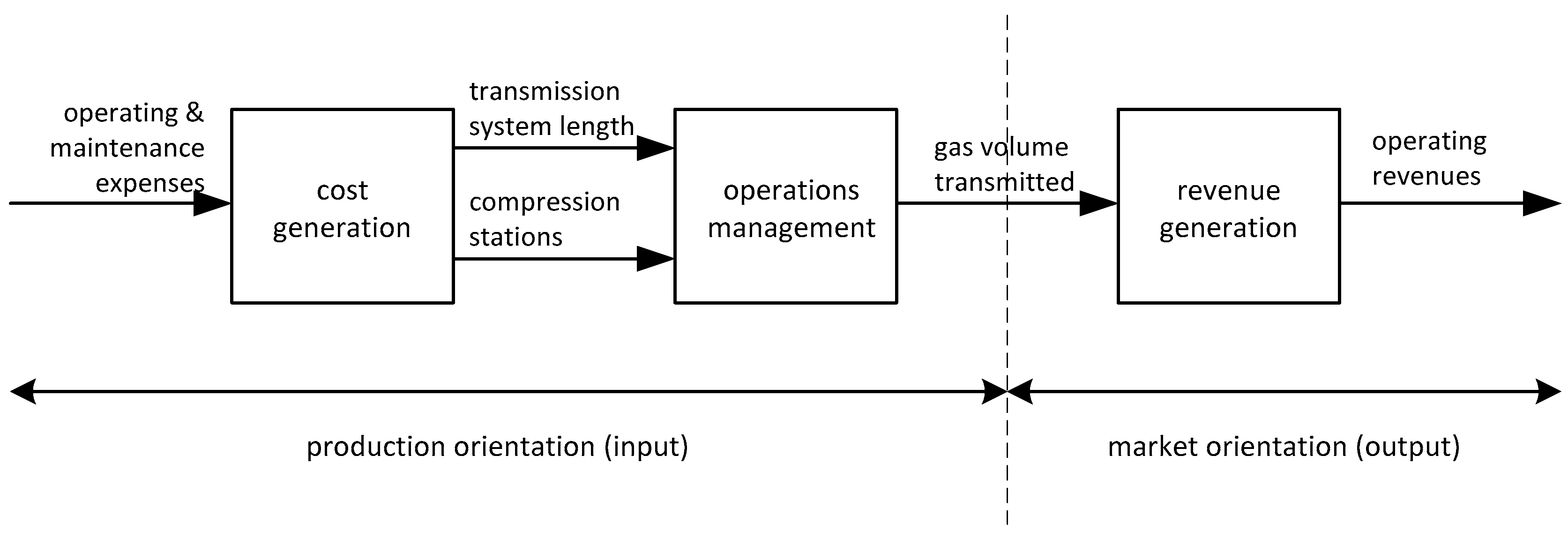
4.1. Production Oriented Segment
- wt is the relative weight of production stage t,
- is an intensity vector related to production stage t (t = 1, …, T)
4.2. Market Oriented Segment
5. Data, Variables and DEA Model Specifications
6. Results
6.1. Efficiency Measurement
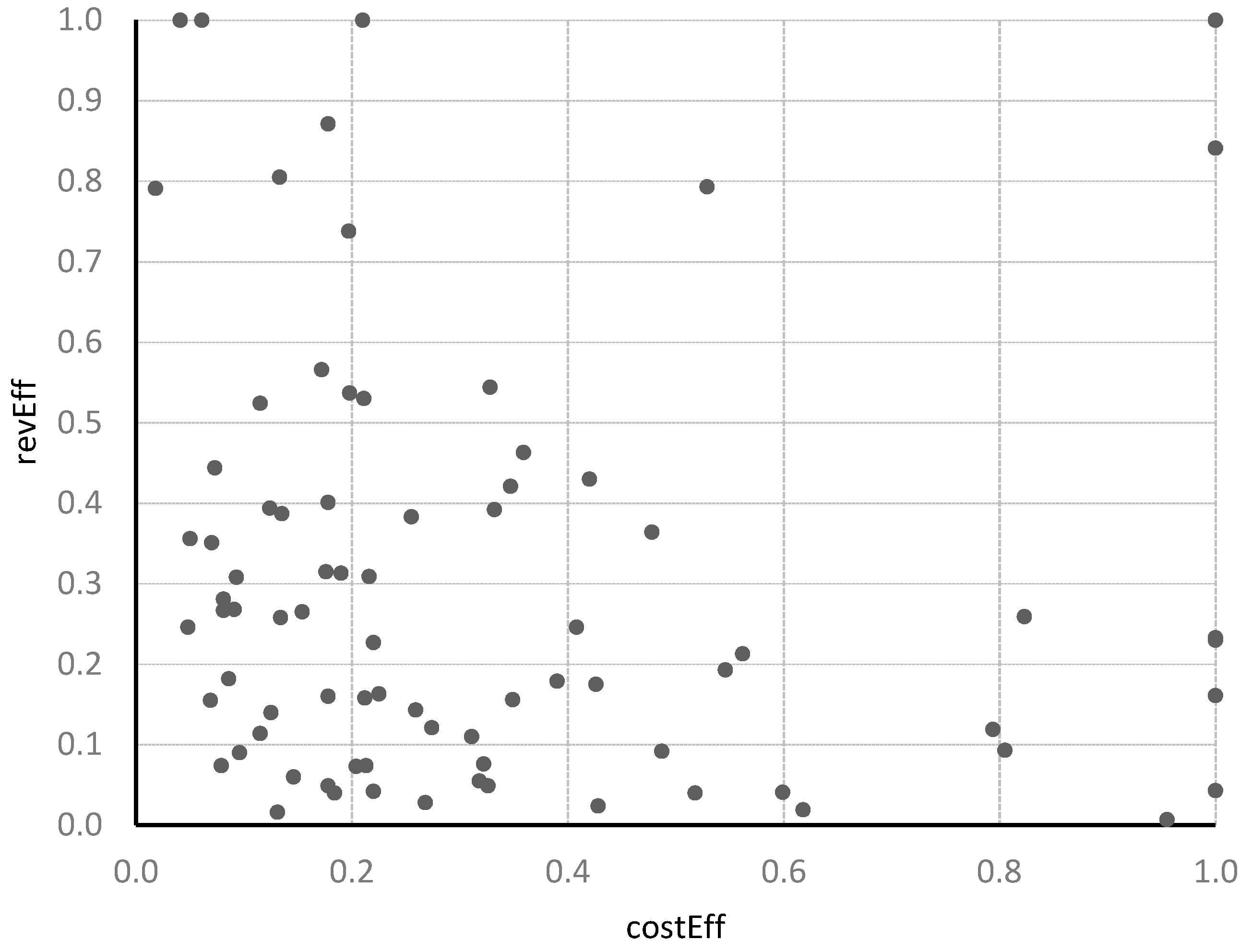
6.2. Relationship between Cost and Revenue-Efficiencies and Trade-Off Analysis
7. Conclusions
Conflicts of Interest
Appendix A
Appendix B
| Name | Configuration | Name | Configuration |
|---|---|---|---|
| Algonquin GAS Transmission LLC | A | Crossroads Pipeline Co | C |
| Alliance Pipeline LP | A | Fayetteville Express Pipeline LLC | C |
| Cheyenne Plains Gas Pipeline Co. LLC | A | Midcontinent Express Pipeline LLC | C |
| Colorado Interstate Gas Co. | A | Northern Border Pipeline Co. | C |
| Dauphin Islands Gathering Partners | A | Ok Tex Pipeline Co. LLC | C |
| East Tennessee Natural Gas LLC | A | Questar Overthrust Pipeline Co. | C |
| Enable Gas Transmission | A | Vector Pipeline LP | C |
| Equitrans LP | A | Wyoming Interstate Co Ltd. | C |
| Gulf Crossing Pipeline LLC | A | American Midstream (Ala Tenn) LLC | D |
| Iroquois Gas Transmission Systems LP | A | Elba Express Co. LLC | D |
| Maritimes & Northeast Pipeline LLC | A | Empire Pipeline Inc | D |
| National Gas Fuel Supply Corp. | A | Garden Banks Gas Pipeline LLC | D |
| Panhandle Eastern Pipe Line Co. LP | A | Gas Transmission Northwest Corp | D |
| Questar Pipeline Co. | A | Horizon Pipeline Co. LLC | D |
| Southern Star Central Gas Pipeline Inc. | A | Millenium Pipeline Co. LLC | D |
| Tallgrass Interstate Gas Transmission LLC | A | Mojave Pipeline Co. | D |
| Transwestern Pipeline Co. LLC | A | North Baja Pipeline LLC | D |
| WBI Energy Transmission Inc. | A | Southeast Suppy Header LLC | D |
| Big Sandy Pipeline LLC | B | Trunkine Gas Co. LLC | D |
| Carolina Gas Transmission Corp. | B | Tennessee Gas Pipeline Co. | E |
| Cimarron River Pipeline LLC | B | Texas Eastern Transmission LP. | E |
| Columbia Gulf Transmission Co | B | Transcontinental Gas Pipe Line Co. LLC | E |
| Destin Pipeline Co. LLC | B | ANR Pipeline Co. | F |
| Discovery Gas Transmission LLC | B | El Paso Natural Gas Co | F |
| Enable Mississippi River Transmission LLC | B | ETC Tiger Pipeline LLC | F |
| Great Lakes Gas Transmission LP | B | Gulf South Pipeline Co. LP | F |
| Guardian Pipeline LLC | B | Gulfstream Natural Gas System LLC | F |
| Midwestern Gas Transmission Co. | B | Natural Gas Pipeline Co. of America | F |
| MIGC Inc | B | Northern Natural Gas Co. | F |
| Ozark Gas Transmission LLC | B | Northwest Pipeline LLC | F |
| Paiute Pipeline Co. | B | Ruby Pipeline LLC | F |
| Petal Gas Storage LLC | B | Southern Natural Gas Co. | F |
| Questar Southern Trails Pipeline Co. | B | Texas Gas Transmission LLC | F |
| Sabine Pipe Line LLC | B | Columbia Gas Transmission LLC | G |
| Sea Robine Pipeline Co. LLC | B | Dominion Cove Point LNG | G |
| TC Offshore LLC | B | Dominion Transmission Inc. | G |
| Trailblazer Pipeline Co. | B | Florida Gas Transmission Co. LLC | G |
| TransColorado Gas Transmission Co. | B | Kern River Gas Transmission Co. | G |
| Tuscarora Gas Tranmission Co. | B | KPC Pipeline LLC | G |
| Viking Gas Transmission Co. | B | Rockies Express Pipeline LLC | G |
Appendix C

References and Notes
- Statistics & Analysis: U.S. Natural Gas Total Consumption. U.S. Energy Information Administration (EIA), 2017. Available online: https://www.eia.gov/dnav/ng/hist/n9140us2A.htm (accessed on 27 December 2017).
- Statistics & Analysis: Natural Gas Consumption by End Use. U.S. Energy Information Administration (EIA), 2017. Available online: https://www.eia.gov/dnav/ng/NG_CONS_SUM_DCU_NUS_A.htm (accessed on 27 December 2017).
- Statistics & Analysis: U.S. Natural Gas Marketed Production. U.S. Energy Information Administration (EIA), 2017. Available online: https://www.eia.gov/dnav/ng/hist/n9050us2a.htm (accessed on 27 December 2017).
- Statistics & Analysis: U.S. Natural Gas Citygate Price. U.S. Energy Information Administration (EIA), 2017. Available online: https://www.eia.gov/dnav/ng/hist/n3050us3a.htm (accessed on 27 December 2017).
- Supervisory Control and Data Acquisition.
- The high interconnection and redundancy of the network makes the natural gas infrastructure particularly resilient and offers a great flexibility in moving gas.
- National Action Plan for Energy Efficiency—Energy Efficiency as a Low-Cost Resource for Achieving Carbon Emissions Reductions. Prepared by William Prindle, ICF International, Inc.; 2009. Available online: https://www.epa.gov/sites/production/files/2015-08/documents/ee_and_carbon.pdf (accessed on 27 December 2017).
- Lo Storto, C.; Ferruzzi, G. Benchmarking Economical Efficiency of Renewable Energy Power Plants: A Data Envelopment Analysis Approach. Adv. Mater. Res. 2013, 772, 699–704. [Google Scholar] [CrossRef]
- Mardani, A.; Zavadskas, E.K.; Streimikiene, D.; Jusoh, A.; Khoshnoudi, M. A comprehensive review of data envelopment analysis (DEA) approach in energy efficiency. Renew. Sustain. Energy Rev. 2017, 70, 1298–1322. [Google Scholar] [CrossRef]
- Sueyoshi, T.; Yuan, Y.; Goto, M. A literature study for DEA applied to energy and environment. Energy Econ. 2017, 62, 104–124. [Google Scholar] [CrossRef]
- Zhou, P.; Ang, B.W.; Poh, K.L. A survey of data envelopment analysis in energy and environmental studies. Eur. J. Oper. Res. 2008, 189, 1–18. [Google Scholar] [CrossRef]
- Hollas, D.R.; Macleod, K.R.; Stansell, S.R. A data envelopment analysis of gas utilities’ efficiency. J. Econ. Financ. 2002, 26, 123–137. [Google Scholar] [CrossRef]
- Hawdon, D. Efficiency, performance and regulation of the international gas industry—A bootstrap DEA approach. Energy Policy 2003, 31, 1167–1178. [Google Scholar] [CrossRef]
- Jamasb, T.; Pollitt, M.; Triebs, T. Productivity and efficiency of US gas transmission companies: A European regulatory perspective. Energy Policy 2008, 36, 3398–3412. [Google Scholar] [CrossRef]
- Erbetta, F.; Rappuoli, L. Optimal scale in the Italian gas distribution industry using data envelopment analysis. Omega 2008, 36, 325–336. [Google Scholar] [CrossRef]
- Goncharuk, A.G. Performance Benchmarking in Gas Distribution Industry. Benchmarking 2008, 15, 548–559. [Google Scholar] [CrossRef]
- Zorić, J.; Hrovatin, N.; Scarsi, G. Gas Distribution Benchmarking of Utilities from Slovenia, the Netherlands and the UK: An Application of Data Envelopment Analysis. South East Eur. J. Econ. Bus. 2009, 4, 113–124. [Google Scholar] [CrossRef]
- Amirteimoori, A.; Kordrostami, S. A Euclidean distance-based measure of efficiency in data envelopment analysis. Optimization 2010, 59, 985–996. [Google Scholar] [CrossRef]
- Nieswand, M.; Cullmann, A.; Neumann, A. Overcoming Data Limitations in Nonparametric Benchmarking: Applying PCA-DEA to Natural Gas Transmission. Rev. Netw. Econ. 2011, 9. [Google Scholar] [CrossRef]
- Ertürk, M.; Türüt-Aşık, S. Efficiency analysis of Turkish natural gas distribution companies by using data envelopment analysis method. Energy Policy 2011, 39, 1426–1438. [Google Scholar] [CrossRef]
- Sadjadi, S.J.; Omrani, H.; Abdollahzadeh, S.; Alinaghian, M.; Mohammadi, H. A robust super-efficiency data envelopment analysis model for ranking of provincial gas companies in Iran. Expert Syst. Appl. 2011, 38, 10875–10881. [Google Scholar] [CrossRef]
- Marques, V.; Almeida, P.; Cunha, M.; Paço, M.; Rocha, M.; Trindade, A. What Drives Efficiency on the Portuguese Gas Distribution? In Proceedings of the 9th International Conference on the European Energy Market, Florence, Italy, 10–12 May 2012. [Google Scholar]
- Lo Storto, C. Gas Distribution in Italy: A Non-Parametric Analysis of Companies Operational Efficiency. Adv. Mater. Res. 2014, 838–841, 1972–1978. [Google Scholar] [CrossRef]
- Yardimci, O.; Karan, M.B. Efficiency and service quality analyses of the natural gas distribution companies: A case study of Turkey. In Energy Technology and Valuation Issues; Part III; Dorsman, A., Westerman, W., Simpson, J.L., Eds.; Springer: Cham, Switzerland, 2015; pp. 165–198. [Google Scholar]
- Goncharuk, A.G.; lo Storto, C. Challenges and policy implications of gas reform in Italy and Ukraine: Evidence from a benchmarking analysis. Energy Policy 2017, 101, 456–466. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.W.; Rhodes, E. Measuring the efficiency of decision making units. Eur. J. Oper. Res. 1978, 2, 429–444. [Google Scholar] [CrossRef]
- Cooper, W.W.; Seiford, L.M.; Tone, K. Data Envelopment Analysis: A Comprehensive Text with Models, Applications, References and DEA-Solver Software; Springer: New York, NY, USA, 2007. [Google Scholar]
- Tone, K. A slacks-based measure of efficiency in data envelopment analysis. Eur. J. Oper. Res. 2001, 130, 498–509. [Google Scholar] [CrossRef]
- Tone, K.; Tsutsui, M. Network DEA: A slacks-based measure approach. Eur. J. Oper. Res. 2009, 197, 243–252. [Google Scholar] [CrossRef]
- Banker, R.D.; Charnes, A.; Cooper, W.W. Some models for estimating technical and scale inefficiencies in data envelopment analysis. Manag. Sci. 1984, 30, 1078–1092. [Google Scholar] [CrossRef]
- PennWell Corporation. Oil & Gas Journal; PennWell Corporation: Houston, TX, USA, 2014; pp. 130–132. [Google Scholar]
- Data were collected by reference [31] from FERC Forms 2 and 2A for major and non-major natural gas pipeline companies, reporting years 2012–13.
- Daraio, C.; Simar, L. Advanced Robust and Nonparametric Methods in Efficiency Analysis: Methodology and Applications; Springer: New York, NY, USA, 2007. [Google Scholar]
- The eigenvalue inertia is 90.28% indicating that the new variable provides a good approximation of the original variables, as the higher the inertia is the higher the information amount of the original variables summarized by the factor.
- Ketchen, D.J.; Shook, C.L. The application of cluster analysis in strategic management research: An analysis and critique. Strateg. Manag. J. 1996, 17, 441–458. [Google Scholar] [CrossRef]
- Everitt, B.S.; Landau, S.; Leese, M.; Stahl, D. Cluster Analysis; John Wiley & Sons: Chichester, UK, 2011. [Google Scholar]
- Calinski, T.; Harabasz, J. A dendrite method for cluster analysis. Commun. Stat. Theory Methods 1974, 3, 1–27. [Google Scholar] [CrossRef]
- Fang, H.; Ciatto, A.; Brock, F. U.S. Natural Gas Storage Capacity and Utilization Outlook. Technical Report Prepared by ICF International for Oak Ridge National Laboratory. ORNL/TM-2016/273; 2016. Available online: https://energy.gov/sites/prod/files/2017/02/f34/U.S.%20Natural%20Gas%20Storage%20Capacity%20and%20Utilization%20Outlook.pdf (accessed on 27 December 2017).
- Lo Storto, C. Ownership structure and the technical, cost, and revenue efficiency of Italian airports. Util. Policy 2018, 50, 175–193. [Google Scholar] [CrossRef]
- Lo Storto, C.; Capano, B. Productivity changes of the renewable energy installed capacity: An empirical study relating to 31 European countries between 2002 and 2011. Energy Educ. Sci. Technol. Part A 2014, 32, 3061–3072. [Google Scholar]
- Milligan, G.W.; Cooper, M. An examination of procedures for determining the number of clusters in a data set. Psychometrika 1985, 50, 159–179. [Google Scholar] [CrossRef]
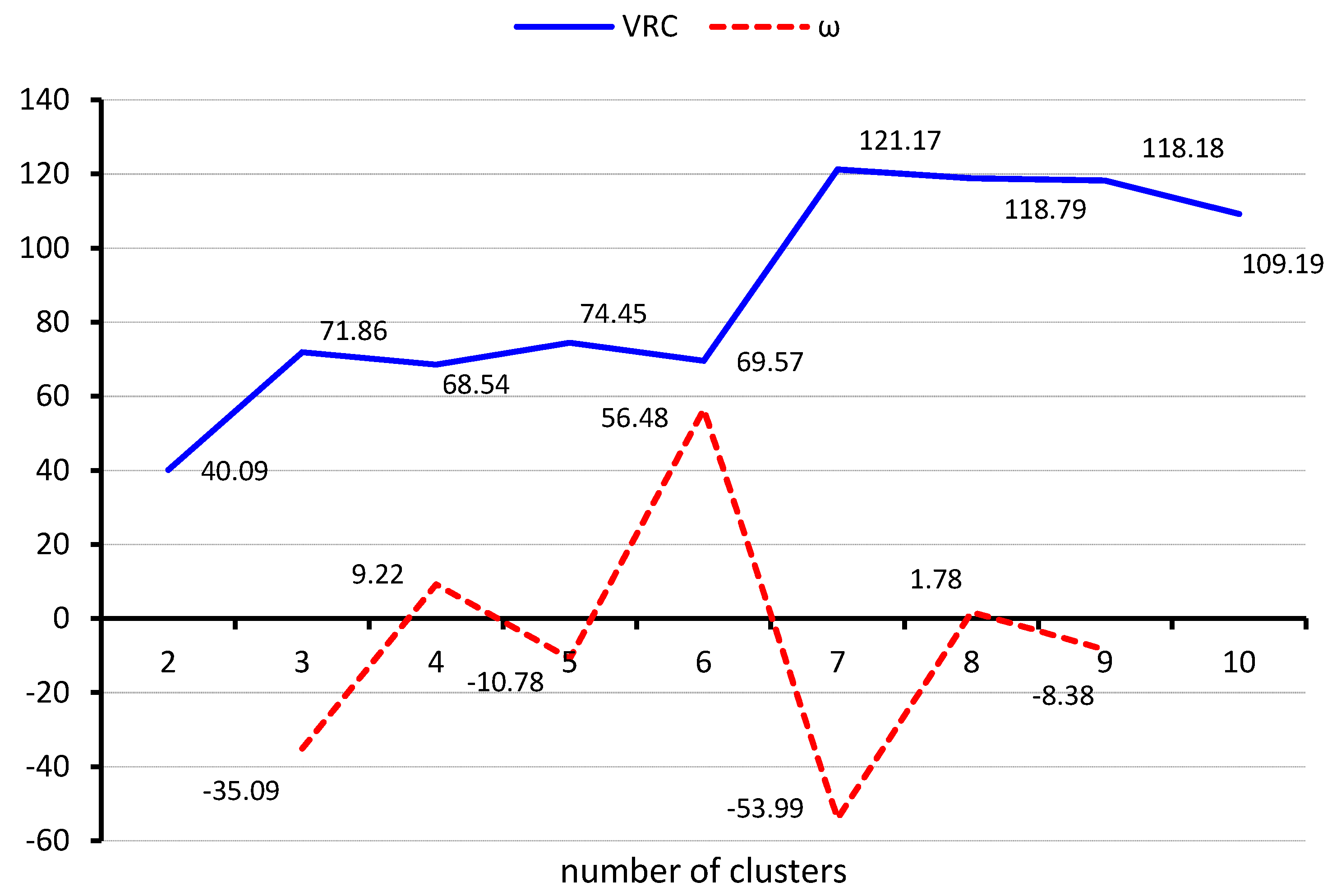

| Variable | Type | Description | Unit | Mean | St.dev. | Max | Min | ||
|---|---|---|---|---|---|---|---|---|---|
| Model 1 | Model 2 | ||||||||
| Stage 1 | Stage 2 | ||||||||
| X1 | input | - | - | operating and maintenance expenses | US$ (× 1000) | 80,134 | 118,987 | 568,156 | 1421 |
| Z1 | output | input | - | transmission system length | miles | 2379 | 3294 | 14,807 | 28 |
| Z2 | output | input | - | no. of compression stations | number | 18 | 23 | 121 | 0 |
| Z3 | - | output | input | gas volume trans. for others | MMcf | 514,760 | 631,797 | 4,043,156 | 11,088 |
| Y1 | - | - | output | operating revenue | US$ (× 1000) | 243,440 | 289,840 | 1,367,655 | 2010 |
| Model | Production Model Segment | Method | Variables | Orientation | ||
|---|---|---|---|---|---|---|
| Input | Output | Intermediate | ||||
| model 1 | production-oriented | NSBM DEA | X1 | Z3 | Z[1, 2] | input |
| model 2 | market-oriented | SBM DEA | Z3 | Y1 | - | output |
| Name | CostEff | RevEff | Name | CostEff | RevEff |
|---|---|---|---|---|---|
| Algonquin GAS Transmission LLC | 0.216 | 0.309 | Millenium Pipeline Co. LLC | 0.408 | 0.246 |
| Alliance Pipeline LP | 0.176 | 0.315 | Mojave Pipeline Co. | 0.599 | 0.041 |
| American Midstream (Ala Tenn) LLC | 0.618 | 0.019 | National Gas Fuel Supply Corp. | 0.081 | 0.267 |
| ANR Pipeline Co. | 0.420 | 0.430 | Natural Gas Pipeline Co. of America | 0.328 | 0.544 |
| Big Sandy Pipeline LLC | 0.274 | 0.121 | North Baja Pipeline LLC | 0.487 | 0.092 |
| Carolina Gas Transmission Corp. | 0.125 | 0.140 | Northern Border Pipeline Co. | 0.823 | 0.259 |
| Cheyenne Plains Gas Pipeline Co. LLC | 0.220 | 0.227 | Northern Natural Gas Co. | 0.198 | 0.537 |
| Cimarron River Pipeline LLC | 0.079 | 0.074 | Northwest Pipeline LLC | 0.115 | 0.524 |
| Colorado Interstate Gas Co. | 0.135 | 0.387 | Ok Tex Pipeline Co. LLC | 0.955 | 0.007 |
| Columbia Gas Transmission LLC | 0.178 | 0.871 | Ozark Gas Transmission LLC | 0.178 | 0.049 |
| Columbia Gulf Transmission Co | 0.225 | 0.163 | Paiute Pipeline Co. | 0.096 | 0.090 |
| Crossroads Pipeline Co | 1.000 | 0.043 | Panhandle Eastern Pipe Line Co. LP | 0.073 | 0.444 |
| Dauphin Islands Gathering Partners | 0.154 | 0.265 | Petal Gas Storage LLC | 0.259 | 0.143 |
| Destin Pipeline Co. LLC | 0.213 | 0.074 | Questar Overthrust Pipeline Co. | 0.805 | 0.093 |
| Discovery Gas Transmission LLC | 0.268 | 0.028 | Questar Pipeline Co. | 0.081 | 0.281 |
| Dominion Cove Point LNG | 0.018 | 0.791 | Questar Southern Trails Pipeline Co. | 0.184 | 0.040 |
| Dominion Transmission Inc. | 0.061 | 1.000 | Rockies Express Pipeline LLC | 0.133 | 0.805 |
| East Tennessee Natural Gas LLC | 0.091 | 0.268 | Ruby Pipeline LLC | 0.172 | 0.566 |
| El Paso Natural Gas Co | 0.359 | 0.463 | Sabine Pipe Line LLC | 0.131 | 0.016 |
| Elba Express Co. LLC | 0.562 | 0.213 | Sea Robine Pipeline Co. LLC | 0.115 | 0.114 |
| Empire Pipeline Inc | 0.349 | 0.156 | Southeast Suppy Header LLC | 0.426 | 0.175 |
| Enable Gas Transmission | 0.178 | 0.401 | Southern Natural Gas Co. | 0.211 | 0.530 |
| Enable Mississippi River Transmission LLC | 0.069 | 0.155 | Southern Star Central Gas Pipeline Inc. | 0.050 | 0.356 |
| Equitrans LP | 0.134 | 0.258 | Tallgrass Interstate Gas Transmission LLC | 0.048 | 0.246 |
| ETC Tiger Pipeline LLC | 0.347 | 0.421 | TC Offshore LLC | 0.146 | 0.060 |
| Fayetteville Express Pipeline LLC | 1.000 | 0.230 | Tennessee Gas Pipeline Co. | 1.000 | 0.841 |
| Florida Gas Transmission Co. LLC | 0.197 | 0.738 | Texas Eastern Transmission LP. | 0.529 | 0.793 |
| Garden Banks Gas Pipeline LLC | 0.428 | 0.024 | Texas Gas Transmission LLC | 0.478 | 0.364 |
| Gas Transmission Northwest Corp | 0.546 | 0.193 | Trailblazer Pipeline Co. | 0.220 | 0.042 |
| Great Lakes Gas Transmission LP | 0.212 | 0.158 | TransColorado Gas Transmission Co. | 0.311 | 0.110 |
| Guardian Pipeline LLC | 0.178 | 0.160 | Transcontinental Gas Pipe Line Co. LLC | 1.000 | 1.000 |
| Gulf Crossing Pipeline LLC | 0.070 | 0.351 | Transwestern Pipeline Co. LLC | 0.093 | 0.308 |
| Gulf South Pipeline Co. LP | 0.255 | 0.383 | Trunkine Gas Co. LLC | 0.390 | 0.179 |
| Gulfstream Natural Gas System LLC | 0.332 | 0.392 | Tuscarora Gas Tranmission Co. | 0.322 | 0.076 |
| Horizon Pipeline Co. LLC | 0.518 | 0.040 | Vector Pipeline LP | 0.794 | 0.119 |
| Iroquois Gas Transmission Systems LP | 0.190 | 0.313 | Viking Gas Transmission Co. | 0.204 | 0.073 |
| Kern River Gas Transmission Co. | 0.041 | 1.000 | WBI Energy Transmission Inc. | 0.086 | 0.182 |
| KPC Pipeline LLC | 0.210 | 1.000 | Wyoming Interstate Co Ltd. | 1.000 | 0.161 |
| Maritimes & Northeast Pipeline LLC | 0.124 | 0.394 | mean | 0.324 | 0.301 |
| Midcontinent Express Pipeline LLC | 1.000 | 0.233 | st.dev | 0.275 | 0.267 |
| Midwestern Gas Transmission Co. | 0.318 | 0.055 | max | 1.000 | 1.000 |
| MIGC Inc | 0.326 | 0.049 | min | 0.018 | 0.007 |
| Between Sum of Squares | df | Within Sum of Squares | df | F | |
|---|---|---|---|---|---|
| costEff | 5.315 | 6 | 0.645 | 73 | 100.226 |
| revEff | 5.222 | 6 | 0.413 | 73 | 154.017 |
| total | 10.538 | 12 | 1.058 | 146 |
| Configuration | CostEff | RevEff | ||||||
|---|---|---|---|---|---|---|---|---|
| Mean | St.dev | Max | Min | Mean | St.dev | Max | Min | |
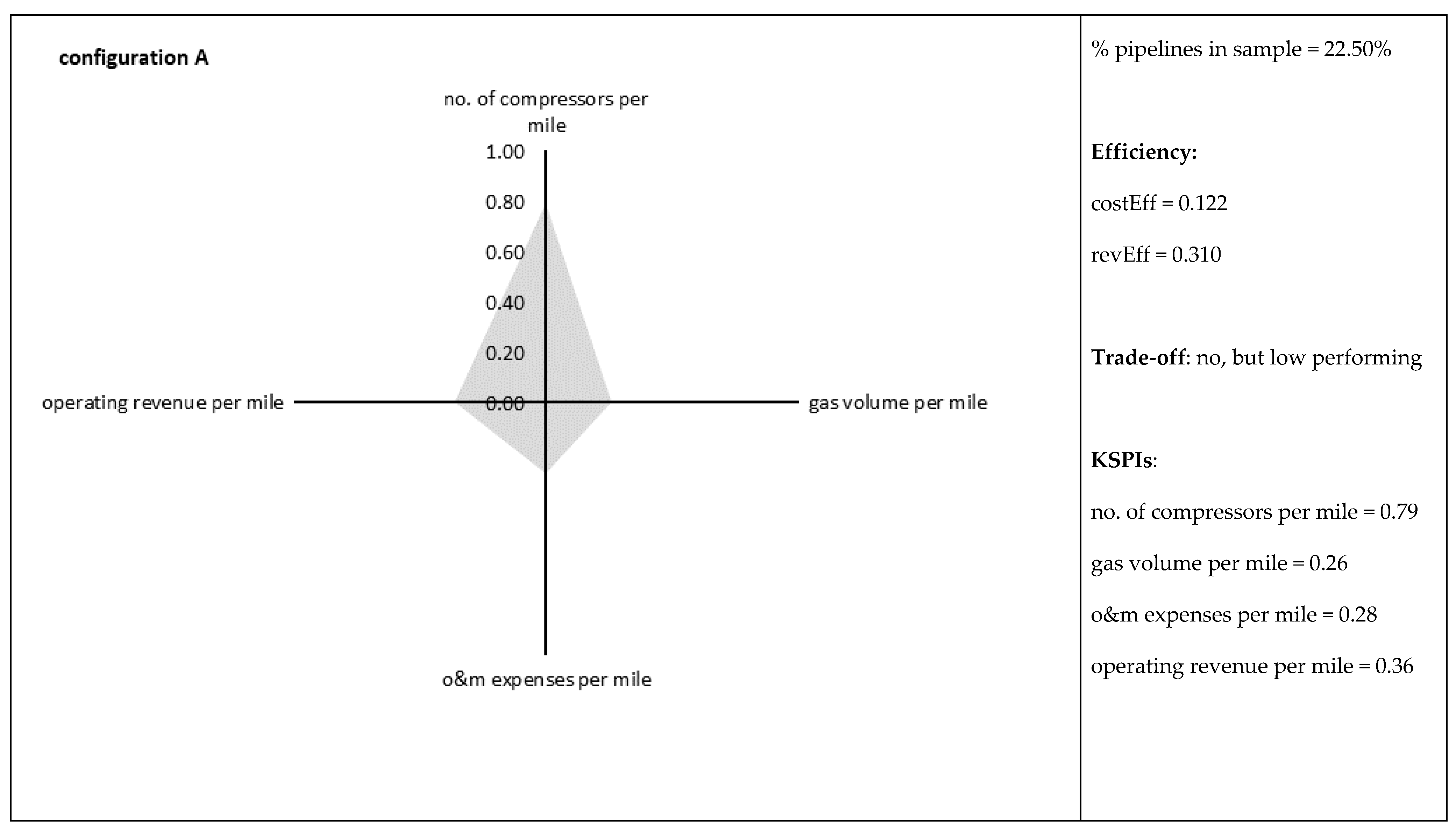
| A (# 18) | 0.122 | 0.056 | 0.220 | 0.048 | 0.310 | 0.068 | 0.444 | 0.182 |
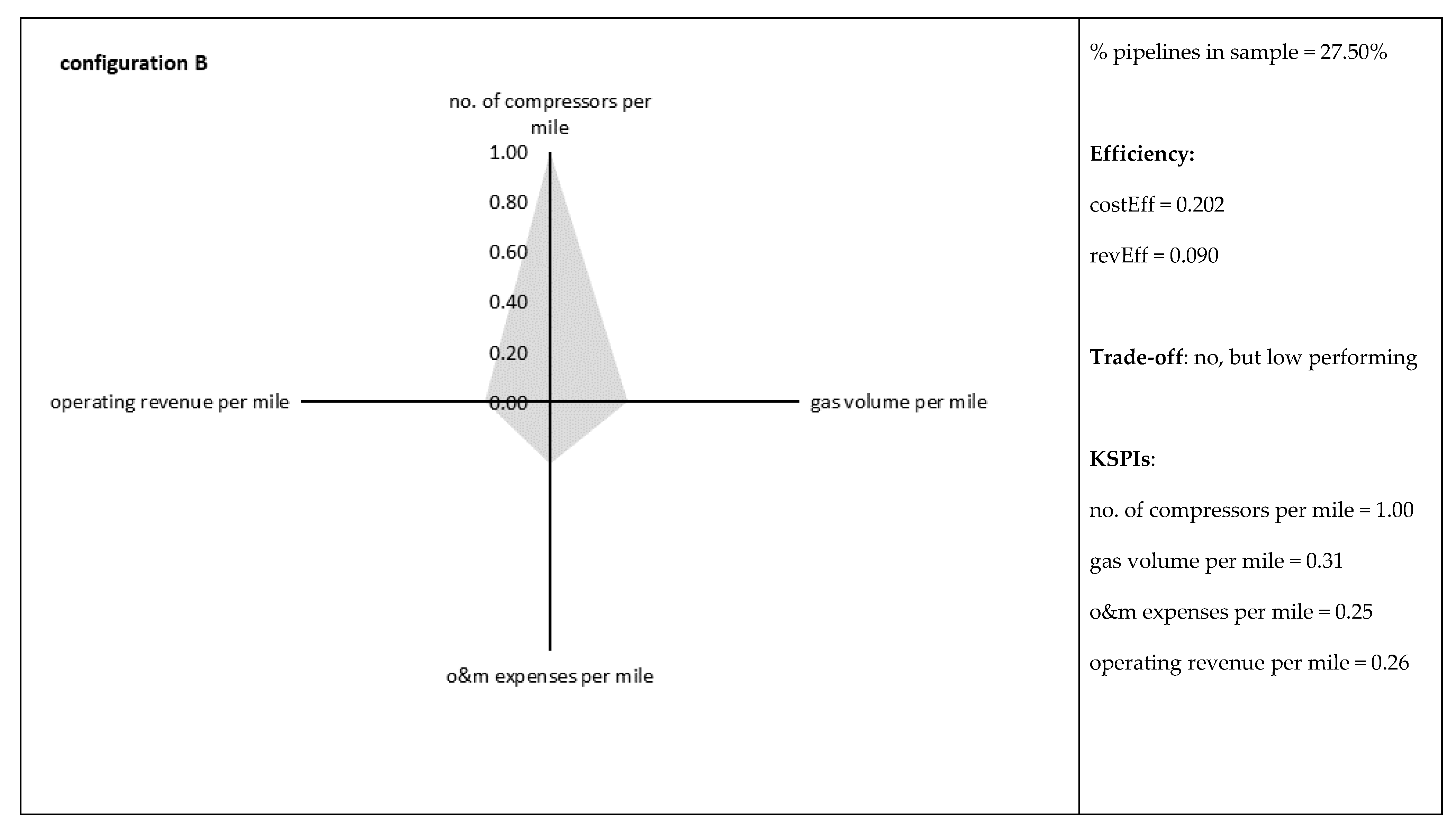
| B (# 22) | 0.202 | 0.081 | 0.326 | 0.069 | 0.090 | 0.047 | 0.163 | 0.016 |
| C (# 8) | 0.922 | 0.097 | 1.000 | 0.794 | 0.143 | 0.093 | 0.259 | 0.007 |
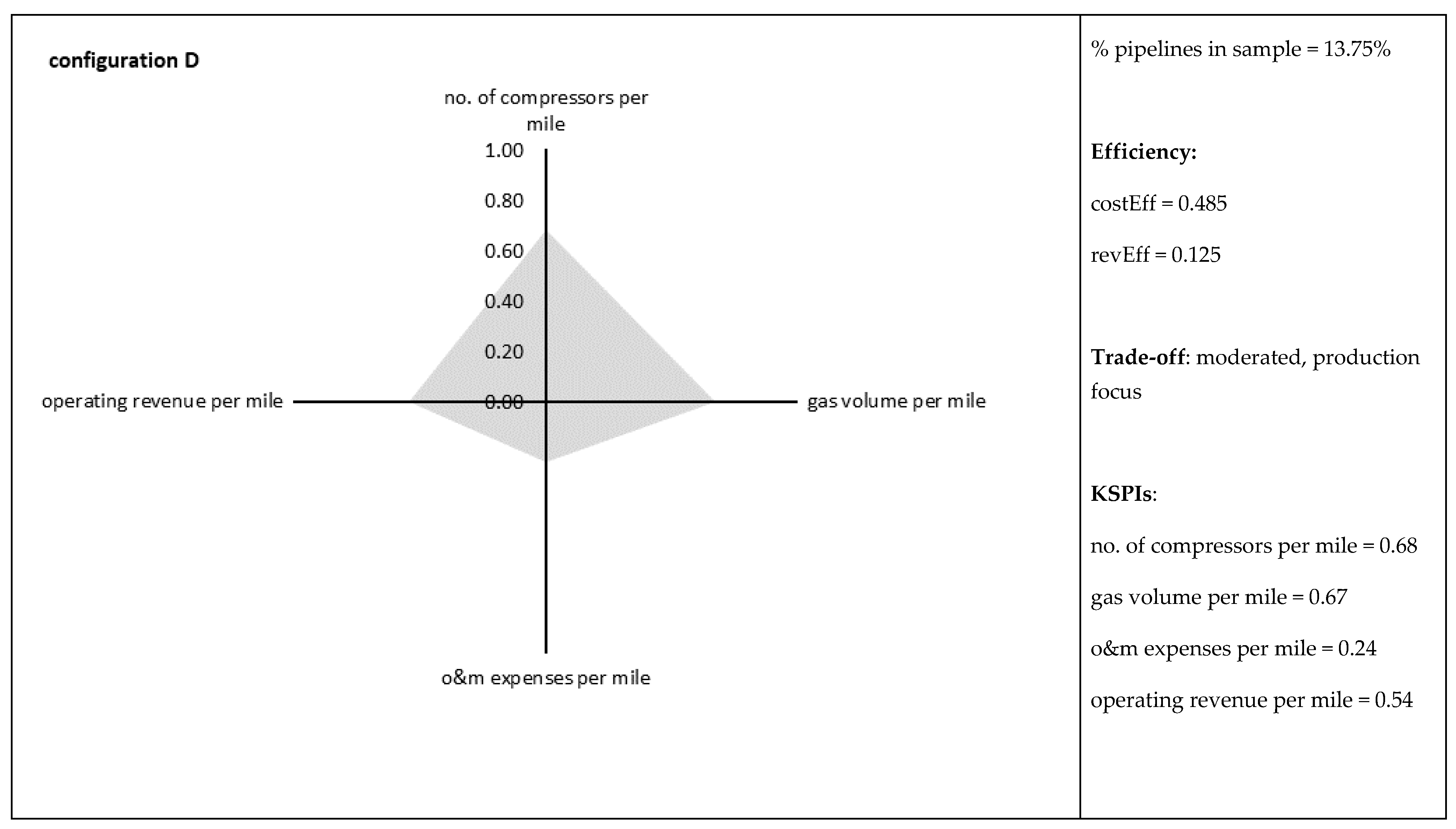
| D (# 11) | 0.485 | 0.090 | 0.618 | 0.349 | 0.125 | 0.084 | 0.246 | 0.019 |
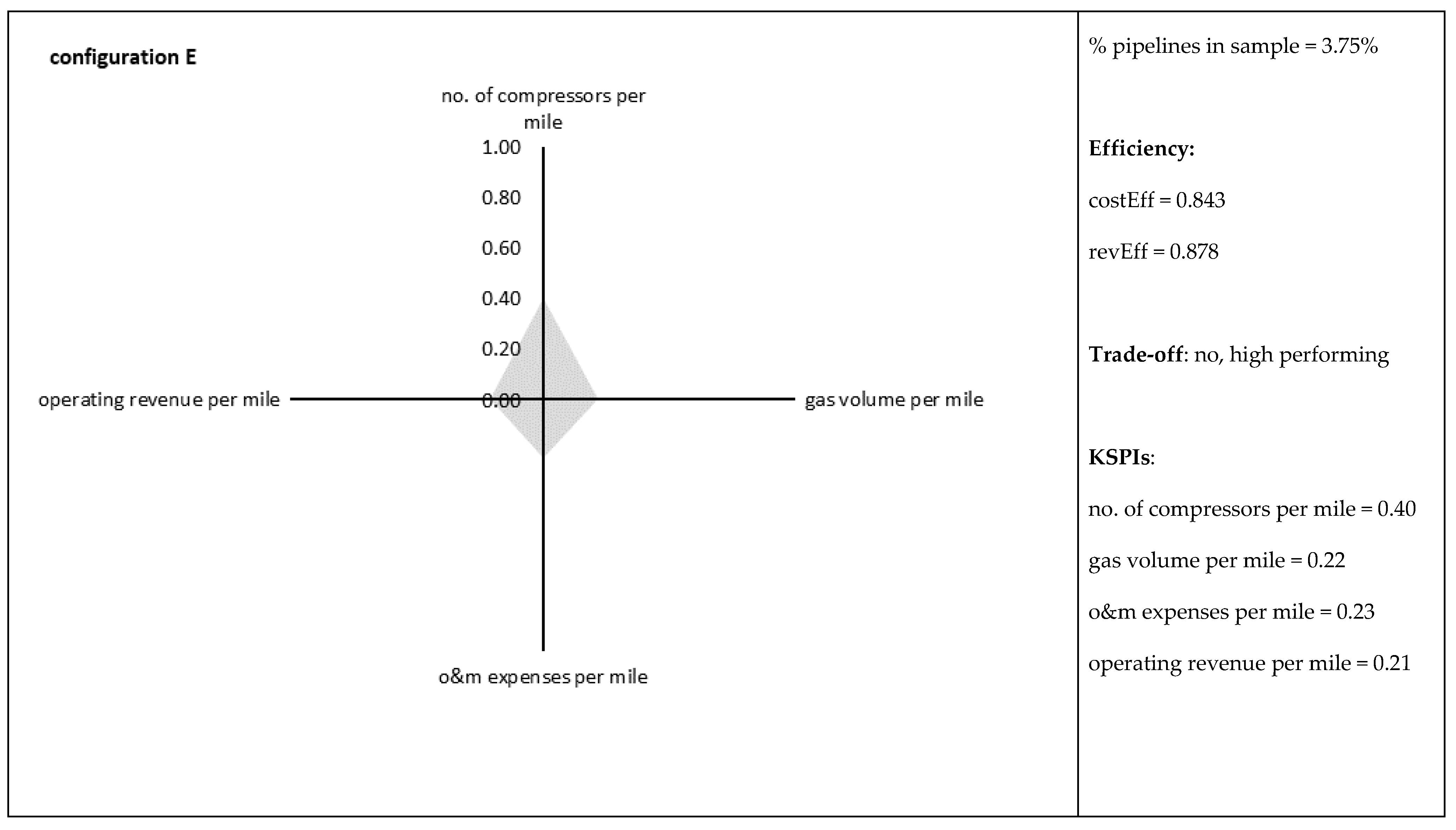
| E (# 3) | 0.843 | 0.272 | 1.000 | 0.529 | 0.878 | 0.108 | 1.000 | 0.793 |
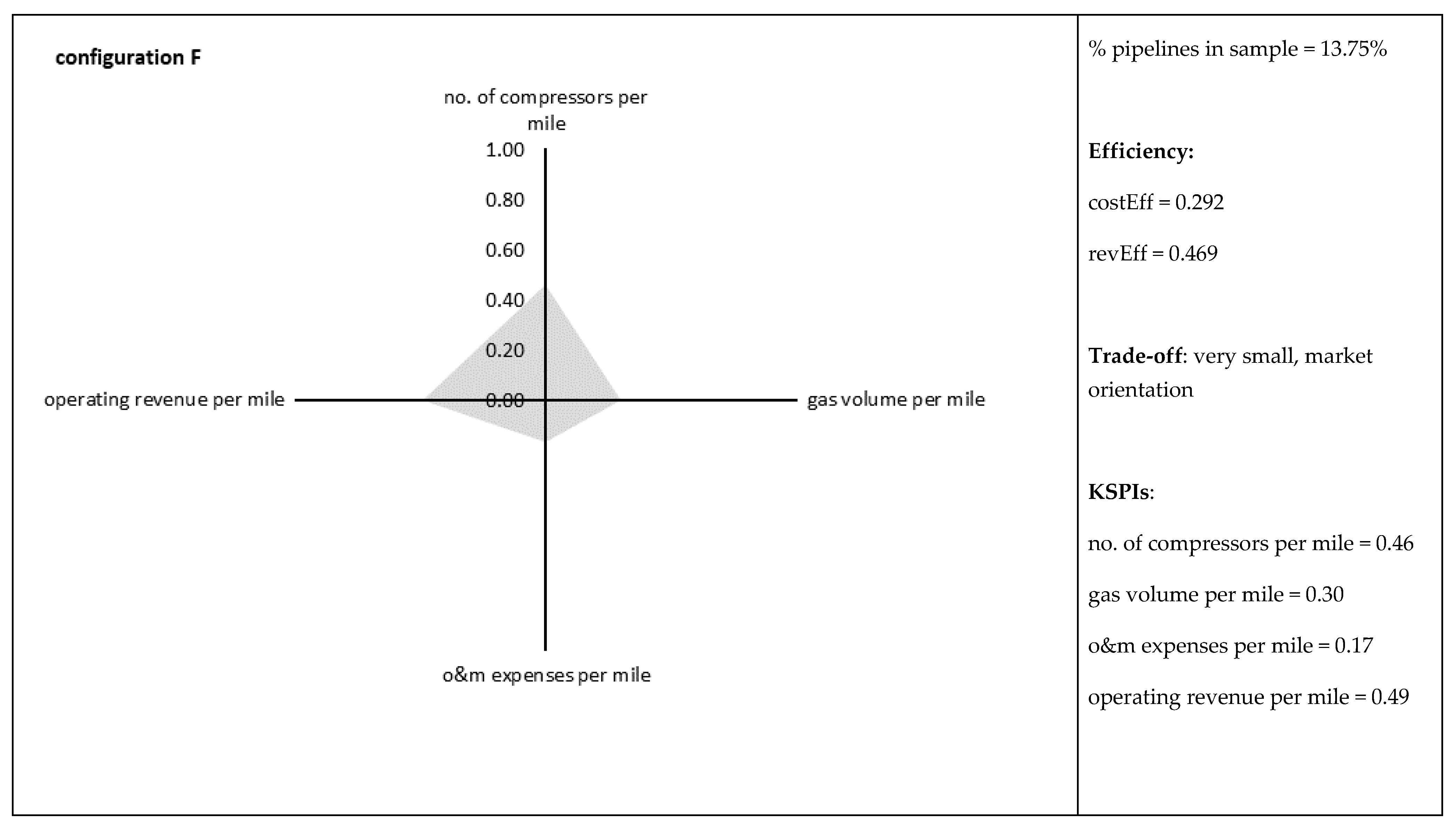
| F (# 11) | 0.292 | 0.111 | 0.478 | 0.115 | 0.469 | 0.074 | 0.566 | 0.364 |
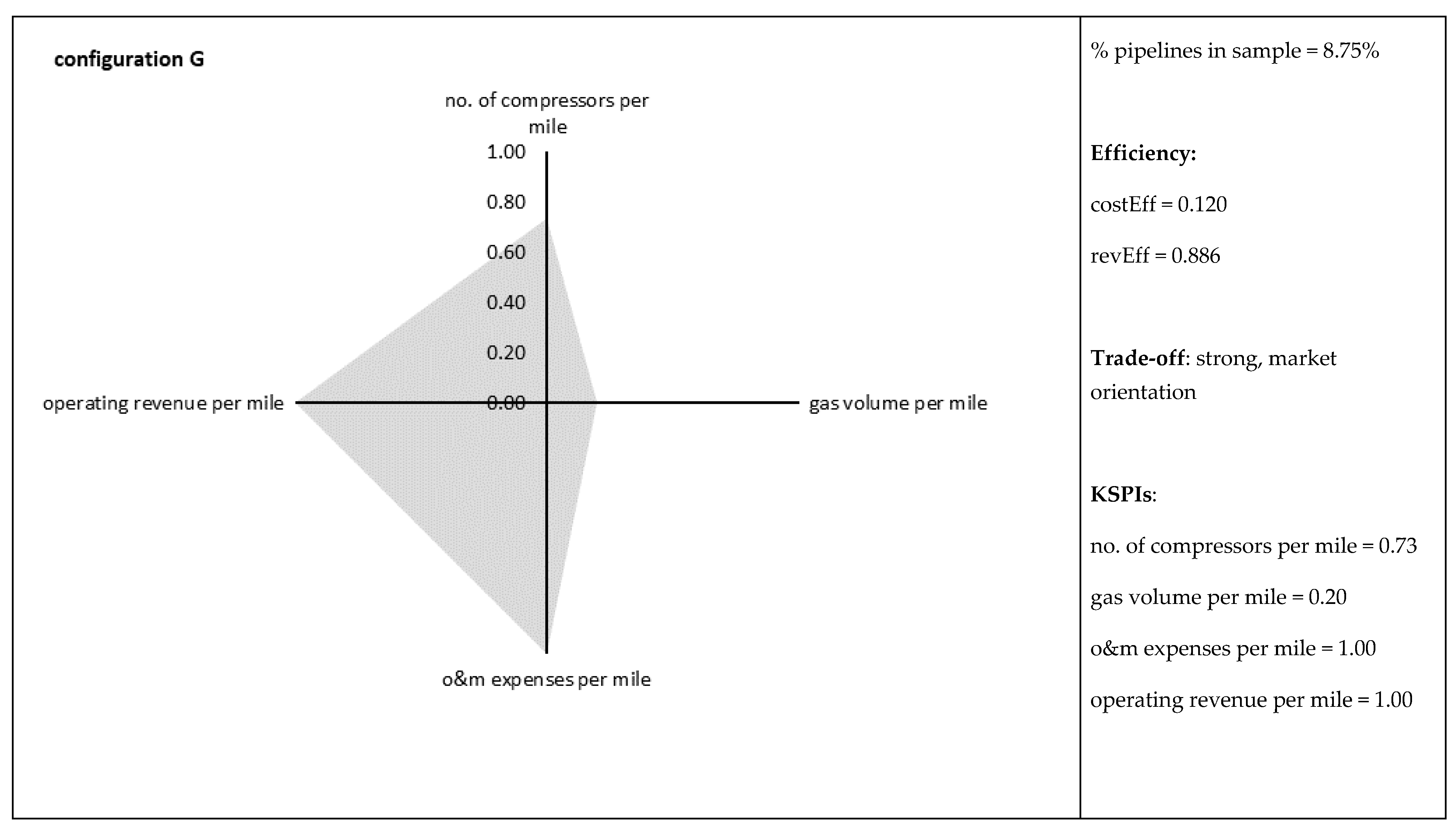
| G (# 7) | 0.120 | 0.079 | 0.210 | 0.018 | 0.886 | 0.113 | 1.000 | 0.738 |
| Variable | Configuration | ||||||
|---|---|---|---|---|---|---|---|
| A | B | C | D | E | F | G | |
| transmission system length | 2346 (2088) | 712 (822) | 483 (442) | 562 (862) | 10,363 (1590) | 6174 (4564) | 3335 (3277) |
| no. of compression stations | 21.28 (14.61) | 6.09 (5.11) | 5.63 (6.02) | 4.00 (5.66) | 66.00 (15.52) | 35.09 (21.88) | 39.00 (47.27) |
| gas volume trans. for others | 415,109 (262,579) | 163,719 (161,739) | 558,976 (392,999) | 261,480 (268,636) | 2,885,485 (1,040,440) | 917,942 (437,683) | 572,162 (523,767) |
| operating&maintenance expenses | 76,801 (57,448) | 19,908 (17,029) | 17,761 (17,436) | 13,231 (15,512) | 412,666 (142,212) | 150,063 (112,134) | 202,006 (198,205) |
| operating revenue | 214,362 (112,622) | 44,210 (35,571) | 132,445 (107,131) | 79,385 (70,067) | 1,118,662 (221,028) | 454,184 (122,353) | 622,754 (395,967) |
| KSPI | Configuration | ||||||
|---|---|---|---|---|---|---|---|
| A | B | C | D | E | F | G | |
| no. of compression stations per mile | 0.79 | 1.00 | 0.65 | 0.68 | 0.40 | 0.46 | 0.73 |
| gas volume trans. for others per mile | 0.26 | 0.31 | 1.00 | 0.67 | 0.22 | 0.30 | 0.20 |
| Operating & maintenance expenses per mile | 0.28 | 0.25 | 0.18 | 0.24 | 0.23 | 0.17 | 1.00 |
| operating revenue per mile | 0.36 | 0.26 | 0.58 | 0.54 | 0.21 | 0.49 | 1.00 |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lo Storto, C. A Nonparametric Economic Analysis of the US Natural Gas Transmission Infrastructure: Efficiency, Trade-Offs and Emerging Industry Configurations. Energies 2018, 11, 519. https://doi.org/10.3390/en11030519
Lo Storto C. A Nonparametric Economic Analysis of the US Natural Gas Transmission Infrastructure: Efficiency, Trade-Offs and Emerging Industry Configurations. Energies. 2018; 11(3):519. https://doi.org/10.3390/en11030519
Chicago/Turabian StyleLo Storto, Corrado. 2018. "A Nonparametric Economic Analysis of the US Natural Gas Transmission Infrastructure: Efficiency, Trade-Offs and Emerging Industry Configurations" Energies 11, no. 3: 519. https://doi.org/10.3390/en11030519
APA StyleLo Storto, C. (2018). A Nonparametric Economic Analysis of the US Natural Gas Transmission Infrastructure: Efficiency, Trade-Offs and Emerging Industry Configurations. Energies, 11(3), 519. https://doi.org/10.3390/en11030519





