A Simplified Design Strategy for Multi-Resonant Current Control of a Grid-Connected Voltage Source Inverter with an LCL Filter
Abstract
:1. Introduction
2. Experimental Setup
2.1. Power Board Hardware Features
2.2. Coupling Inductance and Harmonics Filter
2.3. Control Board Hardware Features
3. Inverter Model
4. Current Controller Design
4.1. Harmonics Gain Definition for the PMR Controller
4.2. Sensitivity Functions and Minimum Distances
4.3. Iterative Design Procedure
4.4. Example of Iterative Design Procedure Results
4.5. Influence of the Optimization Criteria
4.5.1. Influence of η0
4.5.2. Influence of ηz
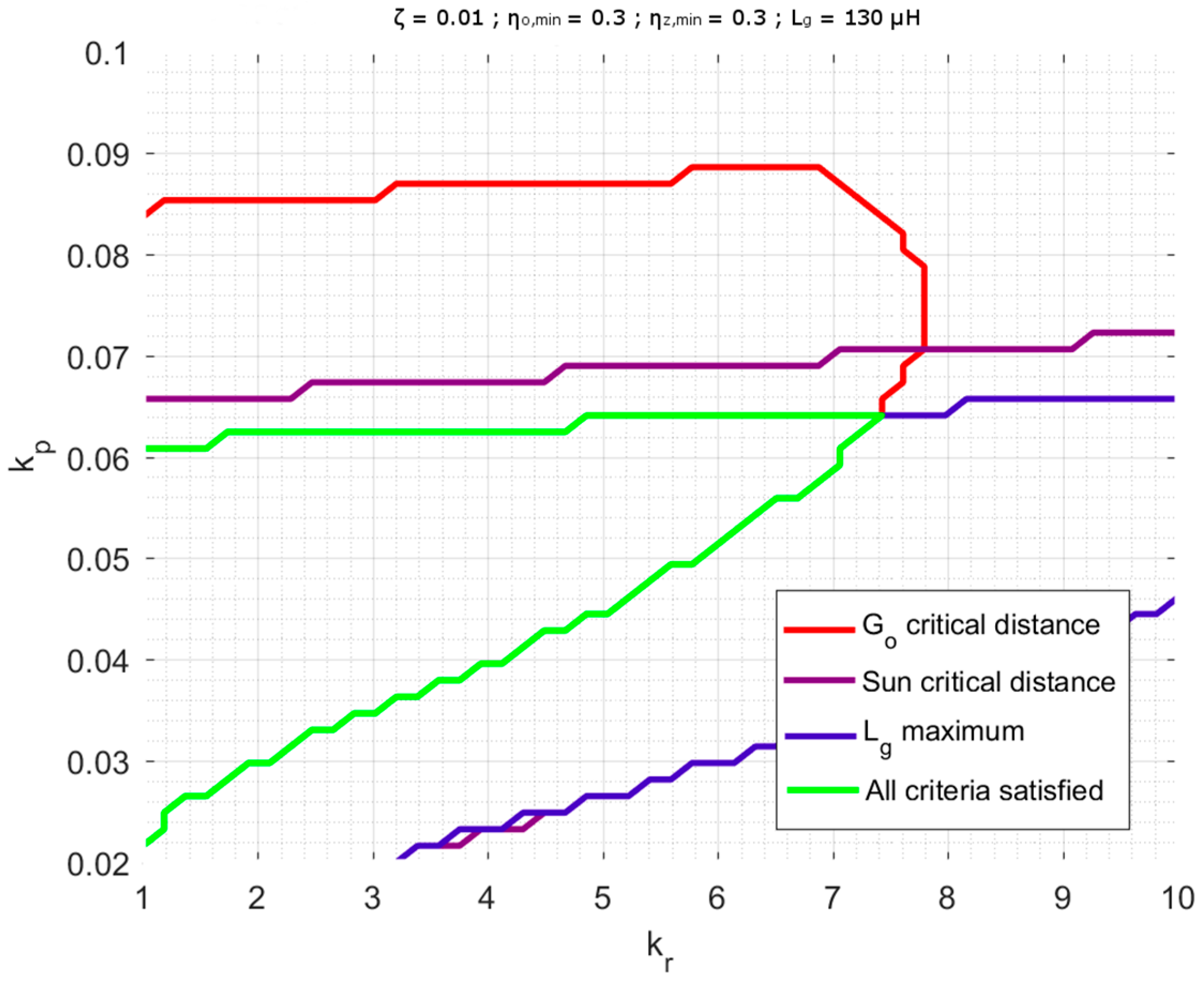
4.5.3. Influence of Lg
5. Experimental Results
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Teodorescu, R.; Liserre, M.; Rodríguez, P. Grid Converters for Photovoltaic and Wind Power Systems; Jon Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Yang, Y.; Zhou, K.; Wang, H.; Blaabjerg, F. Harmonics mitigation of dead time effects in PWM converters using a repetitive controller. In Proceedings of the IEEE Applied Power Electronics Conference and Exposition, Charlotte, NC, USA, 15–19 March 2015. [Google Scholar]
- Castilla, M.; Miret, J.; Matas, J.; de Vicuna, L.G.; Guerrero, J.M. Control Design Guidelines for Single-Phase Grid-Connected Photovoltaic Inverters with Damped Resonant Harmonic Compensators. IEEE Trans. Ind. Electron. 2009, 56, 4492–4501. [Google Scholar] [CrossRef]
- Sato, Y.; Ishizuka, T.; Nezu, K.; Kataoka, T. A new control strategy for voltage-type PWM rectifiers to realize zero steady-state control error in input current. IEEE Trans. Ind. Appl. 1998, 34, 480–486. [Google Scholar] [CrossRef]
- Zmood, D.; Holmes, D. Stationary frame current regulation of PWM inverters with zero steady-state error. IEEE Trans. Power Electron. 2003, 18, 814–822. [Google Scholar] [CrossRef]
- Zmood, D.; Holmes, D.; Bode, G. Frequency-domain analysis of three-phase linear current regulators. IEEE Trans. Ind. Appl. 2001, 37, 601–610. [Google Scholar] [CrossRef]
- Teodorescu, R.; Blaabjerg, F.; Liserre, M.; Loh, P. Proportional-resonant controllers and filters for grid-connected voltage-source converters. IEEE Proc. Electr. Power Appl. 2006, 153, 750–762. [Google Scholar] [CrossRef]
- Teodorescu, R.; Blaabjerg, F.; Borup, U.; Liserre, M. A new control structure for grid-connected LCL PV inverters with zero steady-state error and selective harmonic compensation. In Proceedings of the Applied Power Electronics Conference and Exposition, Anaheim, CA, USA, 22–26 February 2004. [Google Scholar]
- Lee, T.-L.; Hu, S.-H. Resonant current compensator with enhancement of harmonic impedance for LCL-filter based Active rectifiers. In Proceedings of the Twenty-Sixth Annual IEEE Applied Power Electronics Conference and Exposition, Fort Worth, TX, USA, 6–11 March 2011. [Google Scholar]
- Castilla, M.; Miret, J.; Camacho, A.; Matas, J.; de Vicuna, L. Reduction of Current Harmonic Distortion in Three-Phase Grid-Connected Photovoltaic Inverters via Resonant Current Control. IEEE Trans. Ind. Electron. 2013, 60, 1464–1472. [Google Scholar] [CrossRef] [Green Version]
- Cho, Y.; Byen, B.-J.; Lee, H.-S.; Cho, K.-Y. A Single-Loop Repetitive Voltage Controller with an Active Damping Control Technique. Energies 2017, 10, 673. [Google Scholar] [CrossRef]
- Sun, X.; Han, R.; Shen, H.; Wang, B.; Lu, Z.; Chen, Z. A Double-Resistive Active Power Filter System to Attenuate Harmonic Voltages of a Radial Power Distribution Feeder. IEEE Trans. Power Electron. 2016, 31, 6203–6216. [Google Scholar] [CrossRef]
- Nguyen, T.H.; Kim, K.-H. Finite Control Set–Model Predictive Control with Modulation to Mitigate Harmonic Component in Output Current for a Grid-Connected Inverter under Distorted Grid Conditions. Energies 2017, 10, 907. [Google Scholar] [CrossRef]
- Wei, J.; Yongli, L.; Sun, G.; Lizhi, B. H∞ Repetitive Control Based on Active Damping with Reduced Computation Delay for LCL-Type Grid-Connected Inverters. Energies 2017, 10, 586. [Google Scholar]
- Yun, W.; Qiuwei, W.; Wenming, G.; Wenming, G.; Sidoroff, G.M.P. H∞ Robust Current Control for DFIG-Based Wind Turbine Subject to Grid Voltage Distortions. IEEE Trans. Sustain. Energy 2017, 8, 816–825. [Google Scholar]
- Panda, K.P.; Rout, S. Swarm optimization based harmonic elimination in improved H-bridge multilevel inverter. In Proceedings of the International Conference on Inventive Systems and Control (ICISC), Coimbatore, India, 19–20 January 2017. [Google Scholar]
- Duranay, Z.B.; Guldemir, H. Fuzzy logic based harmonic elimination in single phase inverters. In Proceedings of the XXVI International Scientific Conference Electronics, Sozopol, Bulgaria, 13–15 September 2017. [Google Scholar]
- Mehrasa, M.; Pouresmaeil, E.; Zabihi, S.; Rodrigues, E.M.; Catalao, J.P. A control strategy for the stable operation of shunt active power filters in power grids. Energy 2016, 96, 325–334. [Google Scholar] [CrossRef]
- Mehrasa, M.; Pouresmaeil, E.; Akorede, M.; Jørgensen, B.; Catalão, J. Multilevel converter control approach of active power filter for harmonics elimination in electric grids. Energy 2015, 84, 722–731. [Google Scholar] [CrossRef]
- Peng, F.Z. Z-Source Inverter. IEEE Trans. Ind. Appl. 2003, 39, 504–510. [Google Scholar] [CrossRef]
- Zha, X.; Yang, M. A novel active power filter based on injection of α-β current components to power system. In Proceedings of the IEEE Power Electronics Specialists Conference, Jeju, Korea, 18–22 June 2006. [Google Scholar]
- Bai, H.; Wang, X.; Loh, P.C.; Blaabjerg, F. Harmonic analysis and mitigation of low-frequency switching voltage source inverter with series LC filtered VSI. In Proceedings of the Applied Power Electronics Conference and Exposition, Tampa, FL, USA, 26–30 March 2017. [Google Scholar]
- Wasterlain, S.; Parisod, H.; Roggo, D.; Carpita, M. EMC studies on grid integration of Distributed Energy Resources. A 10 kW, IEC-61850 compliant inverter design and preliminary test results. In Proceedings of the 2016 International Symposium on Power Electronics, Electrical Drives, Automation and Motion, Anacapri, Italy, 22–24 June 2016. [Google Scholar]
- Mitsubishi Semiconductors Power Modules MOS, General Considerations for IGBT and Intelligent Power Modules. 1986. Available online: http://www.mitsubishielectric.com/semiconductors/files/manuals/powermos3_0.pdf (accessed on 30 January 2018).
- Kolar, J.; Round, S. Analytical calculation of the RMS current stress on the DC-link capacitor of voltage-PWM converter systems. IEEE Proc. Electr. Power Appl. 2006, 153, 535–543. [Google Scholar] [CrossRef]
- Costa-Castelló, R.; Nebot, J.; Griñó, R. Demonstration of the internal model principle by digital repetitive control of an educational laboratory plant. IEEE Trans. Educ. 2005, 48, 73–80. [Google Scholar] [CrossRef]
- Sun, J. Impedance-Based Stability Criterion for Grid-Connected Inverters. IEEE Trans. Power Electron. 2011, 26, 3075–3078. [Google Scholar] [CrossRef]
- Blaabjerg, F.; Pedersen, J.; Thoegersen, P. Improved modulation techniques for PWM-VSI drives. IEEE Trans. Ind. Electron. 1997, 44, 87–95. [Google Scholar] [CrossRef]
- Wang, X.; Ruan, X.; Liu, S.; Tse, C.K. Full Feedforward of Grid Voltage for Grid-Connected Inverter with LCL Filter to Suppress Current Distortion Due to Grid Voltage Harmonics. IEEE Trans. Power Electron. 2010, 25, 3119–3127. [Google Scholar] [CrossRef]
- Li, W.; Ruan, X.; Pan, D.; Xuehua, W. Full-Feedforward Schemes of Grid Voltages for a Three-Phase LCL-Type Grid-Connected Inverter. IEEE Trans. Ind. Electron. 2013, 60, 2237–2250. [Google Scholar] [CrossRef]
- European Committee for Electrotechnical Standardization. Voltage Characteristic of Electricity Supplied by Public Electricity Networks; EN50160; European Committee for Electrotechnical Standardization: Brussels, Belgium, 2010. [Google Scholar]
- Yepes, A.G.; Freijedo, F.D.; Lopez, Ó.; Doval-Gandoy, J. Analysis and Design of Resonant Current Controllers for Voltage-Source Converters by Means of Nyquist Diagrams and Sensitivity Function. IEEE Trans. Ind. Electron. 2011, 58, 5231–5250. [Google Scholar] [CrossRef]
- Yang, D.; Ruan, X.; Wu, H. Using virtual impedance network to improve the control performances of LCL-type grid-connected inverter under the weak grid condition. In Proceedings of the Applied Power Electronics Conference and Exposition, Fort Worth, TX, USA, 16–20 March 2014. [Google Scholar]
- Germanier, A.; Roggo, D.; Biner, H.-P. AC line voltage controller for grid integration of renewable energy sources. In Proceedings of the Power Electronics and Applications (EPE’15 ECCE-Europe), Geneva, Switzerland, 8–10 September 2015. [Google Scholar]















| Parameter | Symbol | Value |
|---|---|---|
| DC-link voltage | UDC | 700 V |
| Nominal power (overload 200%, 60 s) | P | 10 kW |
| Utility grid nominal voltage (line-to-line) | Vg | 400 V |
| Utility grid nominal frequency | f | 50 Hz |
| Inverter switching frequency | fsw | 15 kHz |
| Switching dead time | Ta | 3.2 µs |
| Inverter side inductor | L1 | 3 mH |
| Grid side inductor | L2 | 600 µH |
| Filter Capacitor | C1 | 1.41 µH |
| Damping resistor | Rf | 1 Ω |
| Inductance of the damping circuit | Lf | 51 µH |
| Parameter | PMR Controller | PR Controller |
|---|---|---|
| kp | 0.064 | 0.054 |
| kr,1 | 7.43 | 38.6 |
| ζ | 0.01 | 0.01 |
| Voltage Distortion | Current Distortion | |
|---|---|---|
| PR | PMR | |
| 2.47% | 2.41% | 1.39% |
| 6.83% | 5.34% | 1.47% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schiesser, M.; Wasterlain, S.; Marchesoni, M.; Carpita, M. A Simplified Design Strategy for Multi-Resonant Current Control of a Grid-Connected Voltage Source Inverter with an LCL Filter. Energies 2018, 11, 609. https://doi.org/10.3390/en11030609
Schiesser M, Wasterlain S, Marchesoni M, Carpita M. A Simplified Design Strategy for Multi-Resonant Current Control of a Grid-Connected Voltage Source Inverter with an LCL Filter. Energies. 2018; 11(3):609. https://doi.org/10.3390/en11030609
Chicago/Turabian StyleSchiesser, Matthias, Sébastien Wasterlain, Mario Marchesoni, and Mauro Carpita. 2018. "A Simplified Design Strategy for Multi-Resonant Current Control of a Grid-Connected Voltage Source Inverter with an LCL Filter" Energies 11, no. 3: 609. https://doi.org/10.3390/en11030609






