Impedance Modelling and Parametric Sensitivity of a VSC-HVDC System: New Insights on Resonances and Interactions
Abstract
:1. Introduction
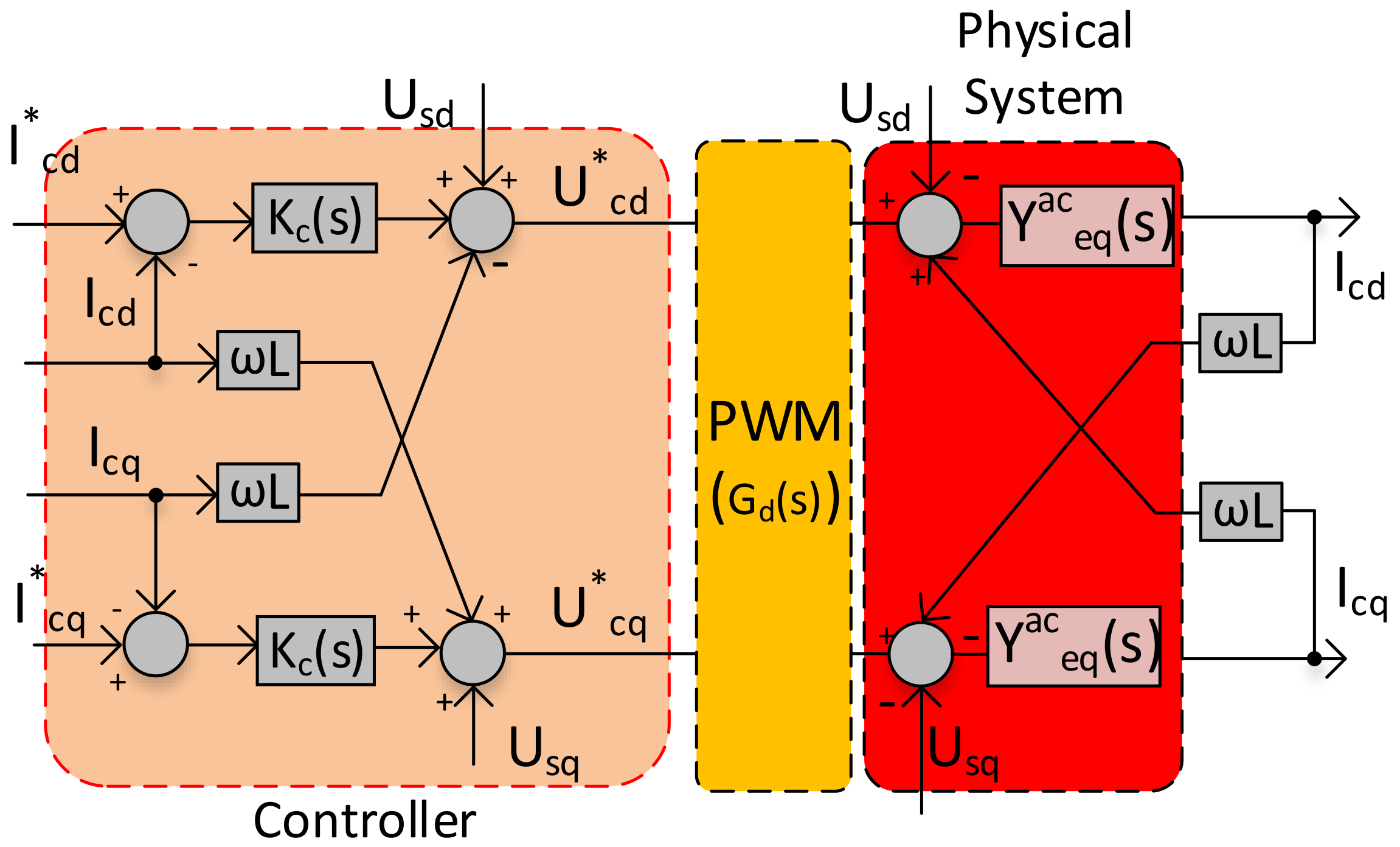
2. System Description and Control System
3. Impedance Modelling of the System
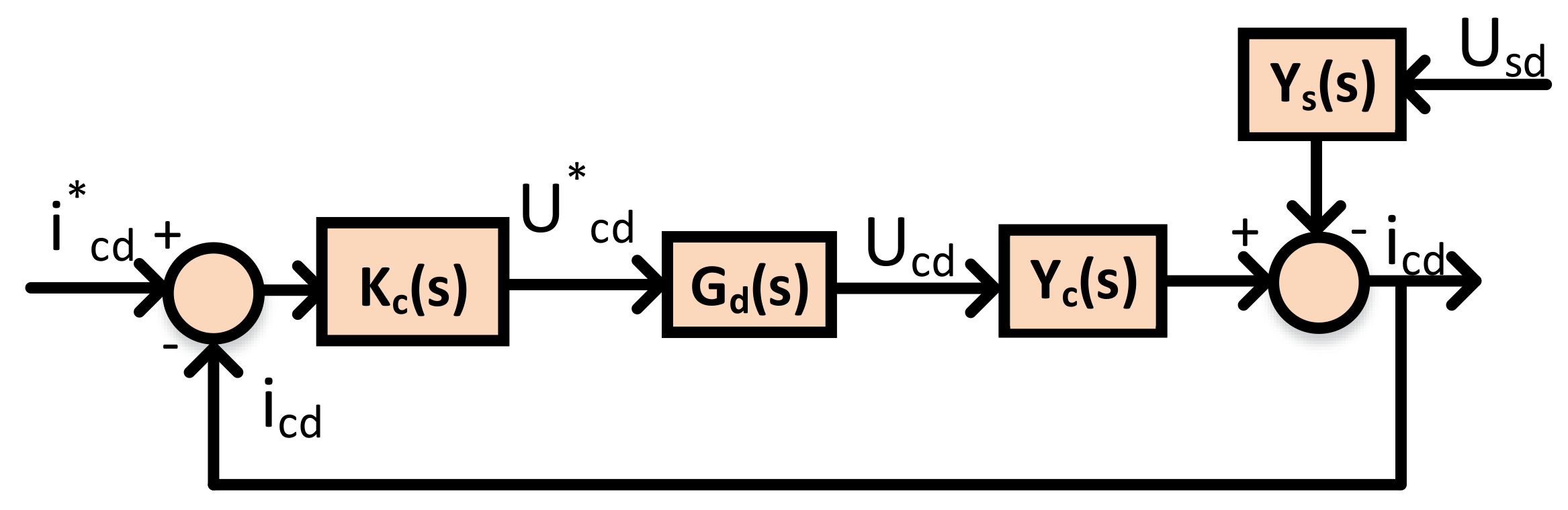
3.1. Analytical Modelling of the Inner Current Controller
3.2. Analytical Modelling of the DC Voltage Controller
3.3. Harmonic Stability Derivation
4. Parametric Sensitivity and Stability Analysis
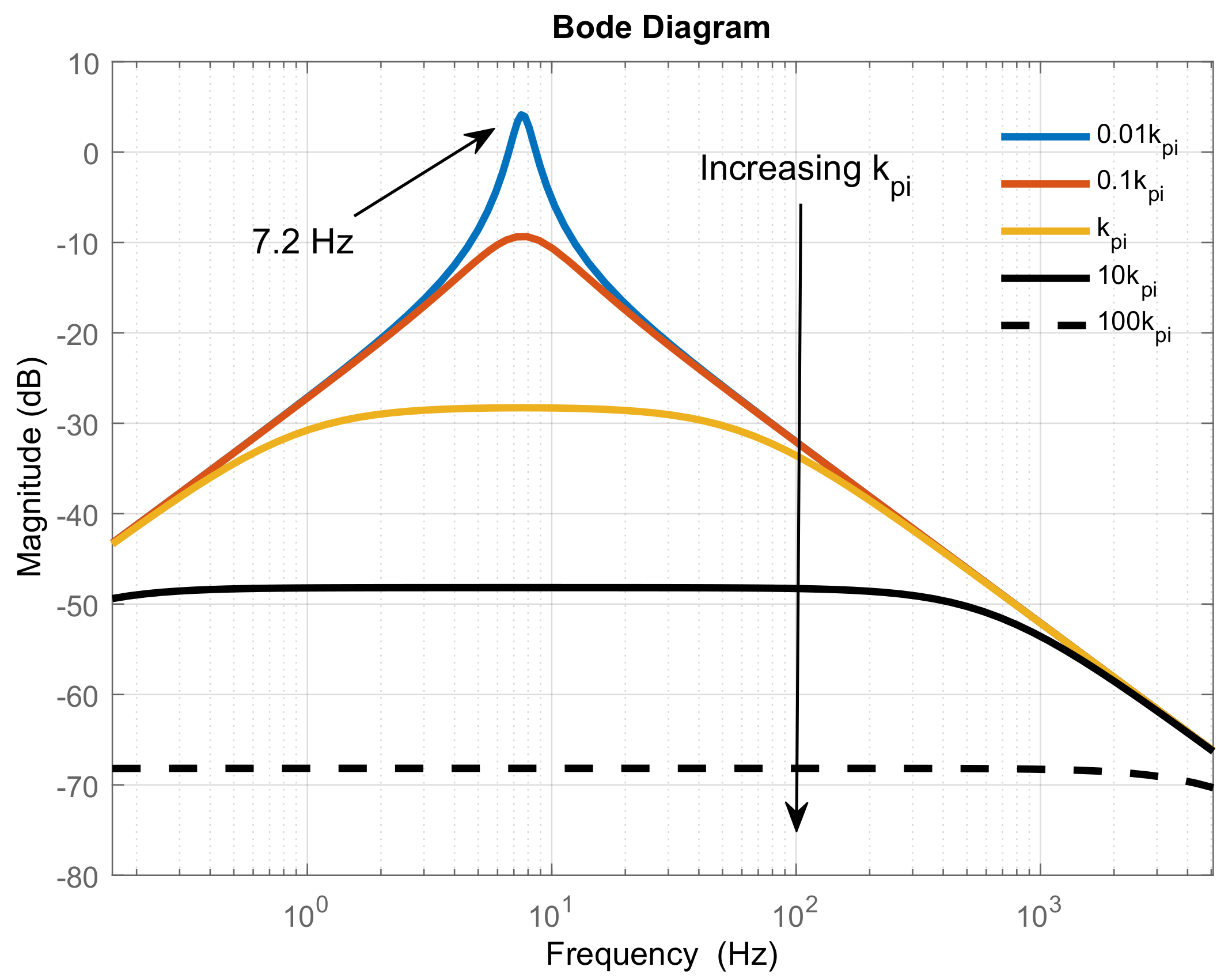
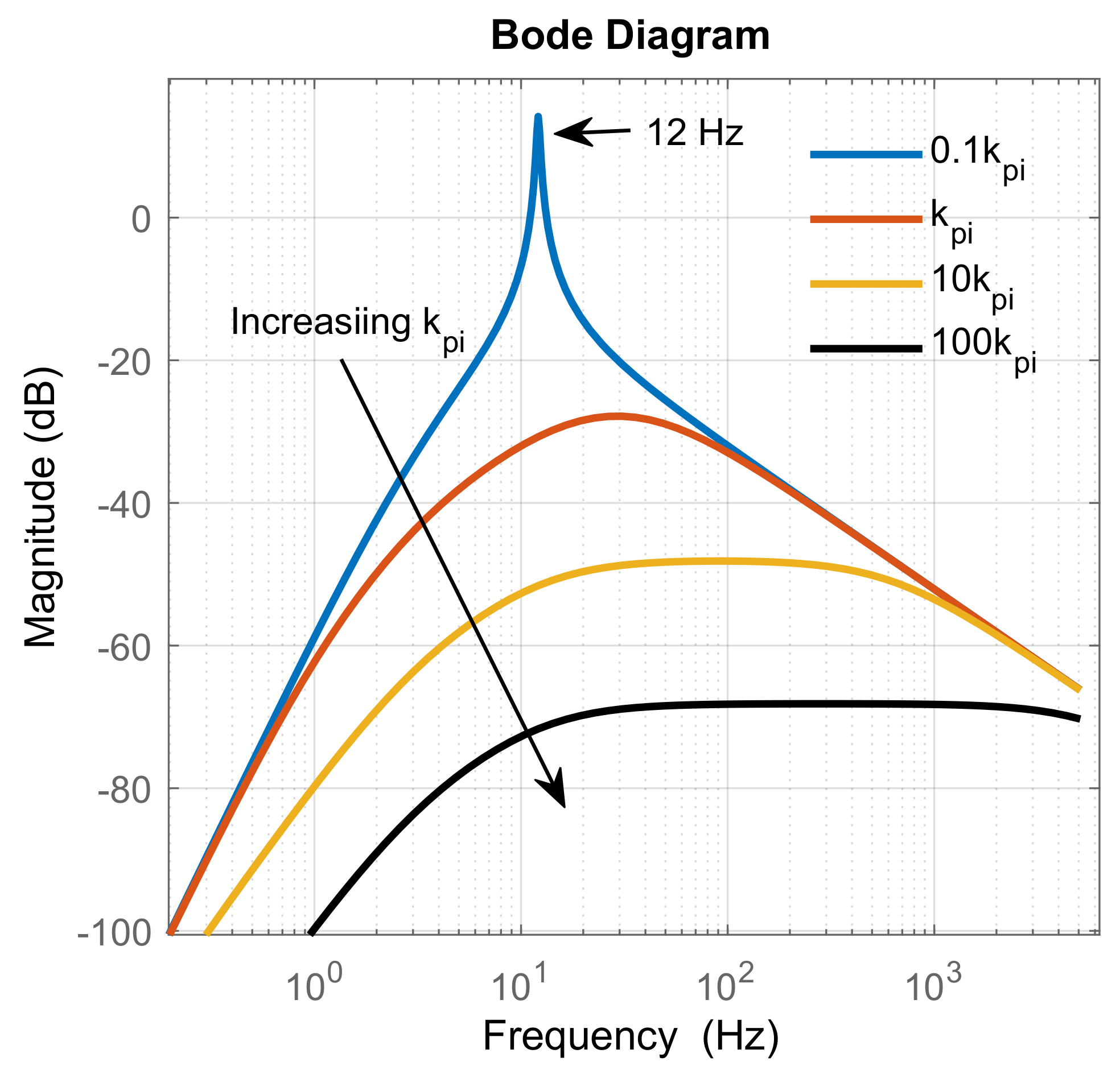
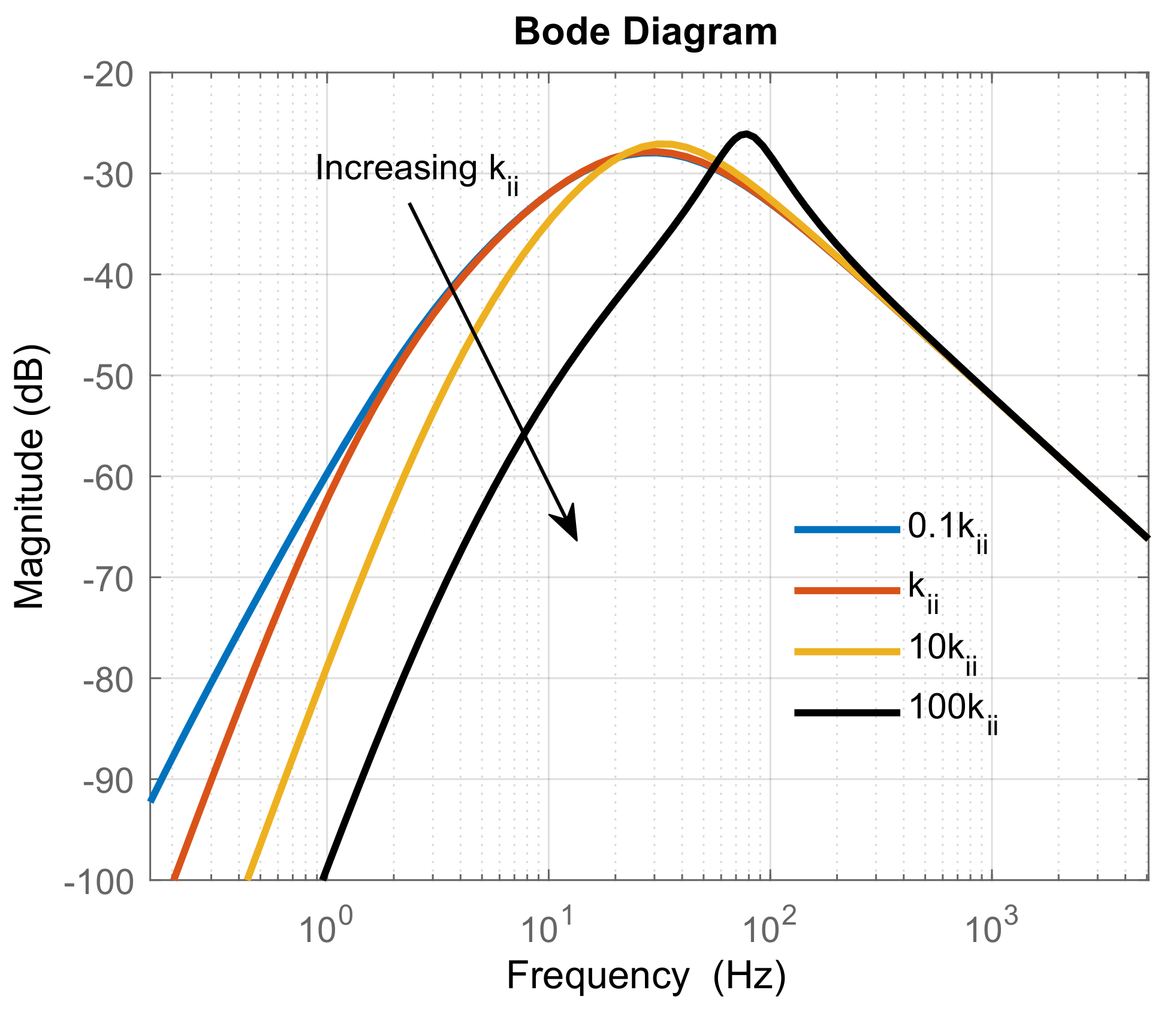
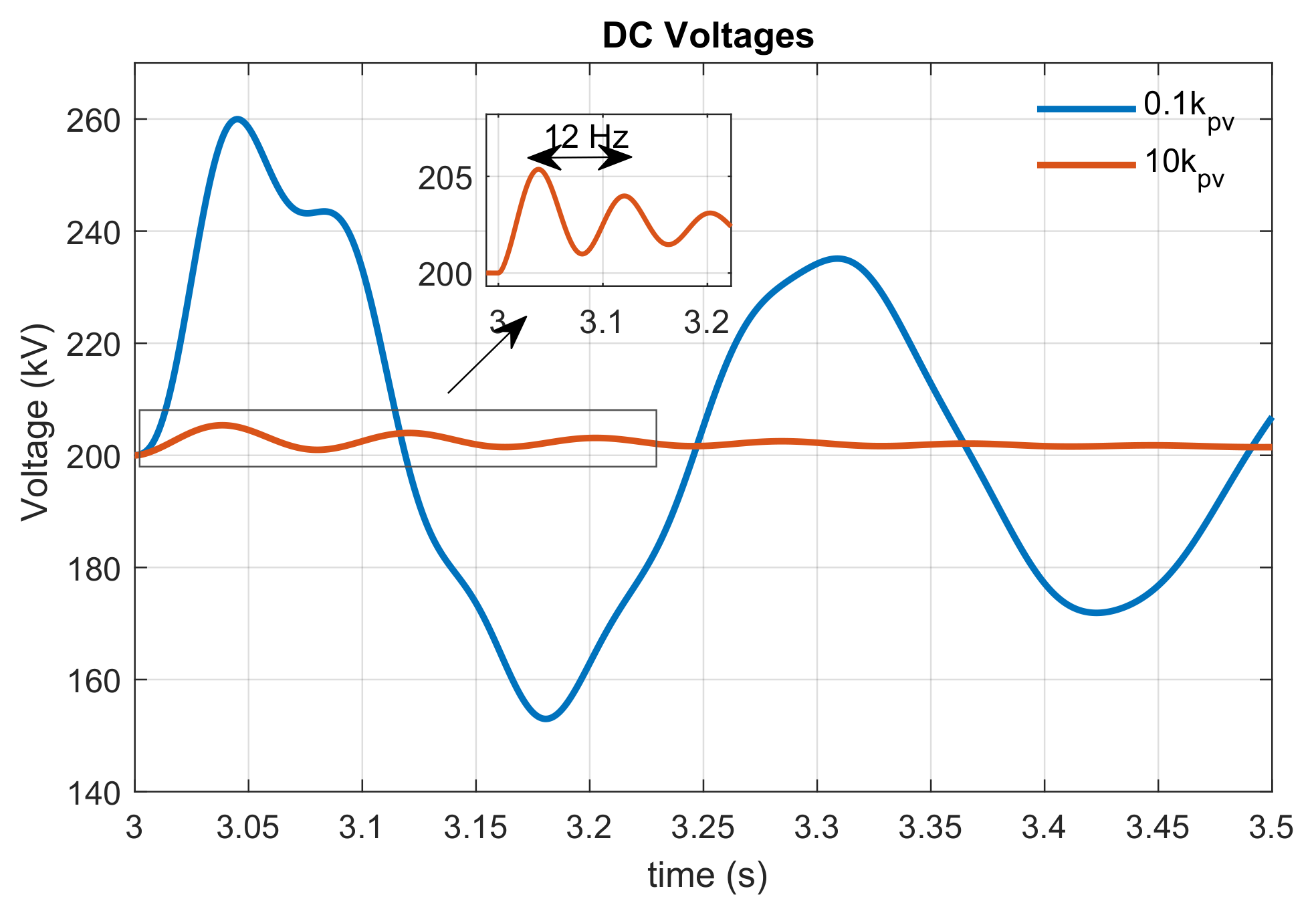
4.1. Sensitivity Analysis to Controller Dynamics
4.1.1. Output Admittance with Current Control Loop
4.1.2. Output Admittance with DC Voltage Control Loop
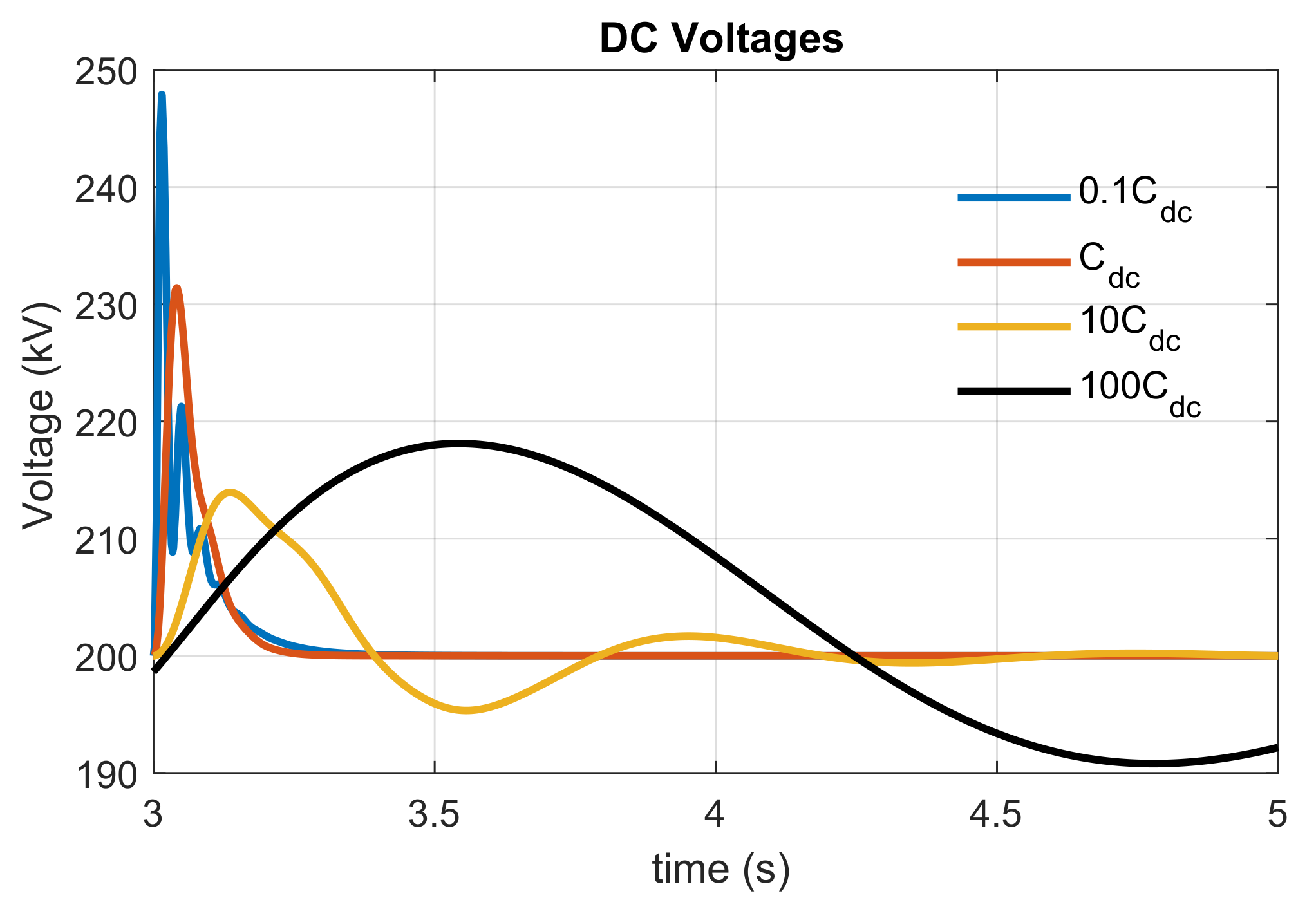
4.2. DC Grid Parameters
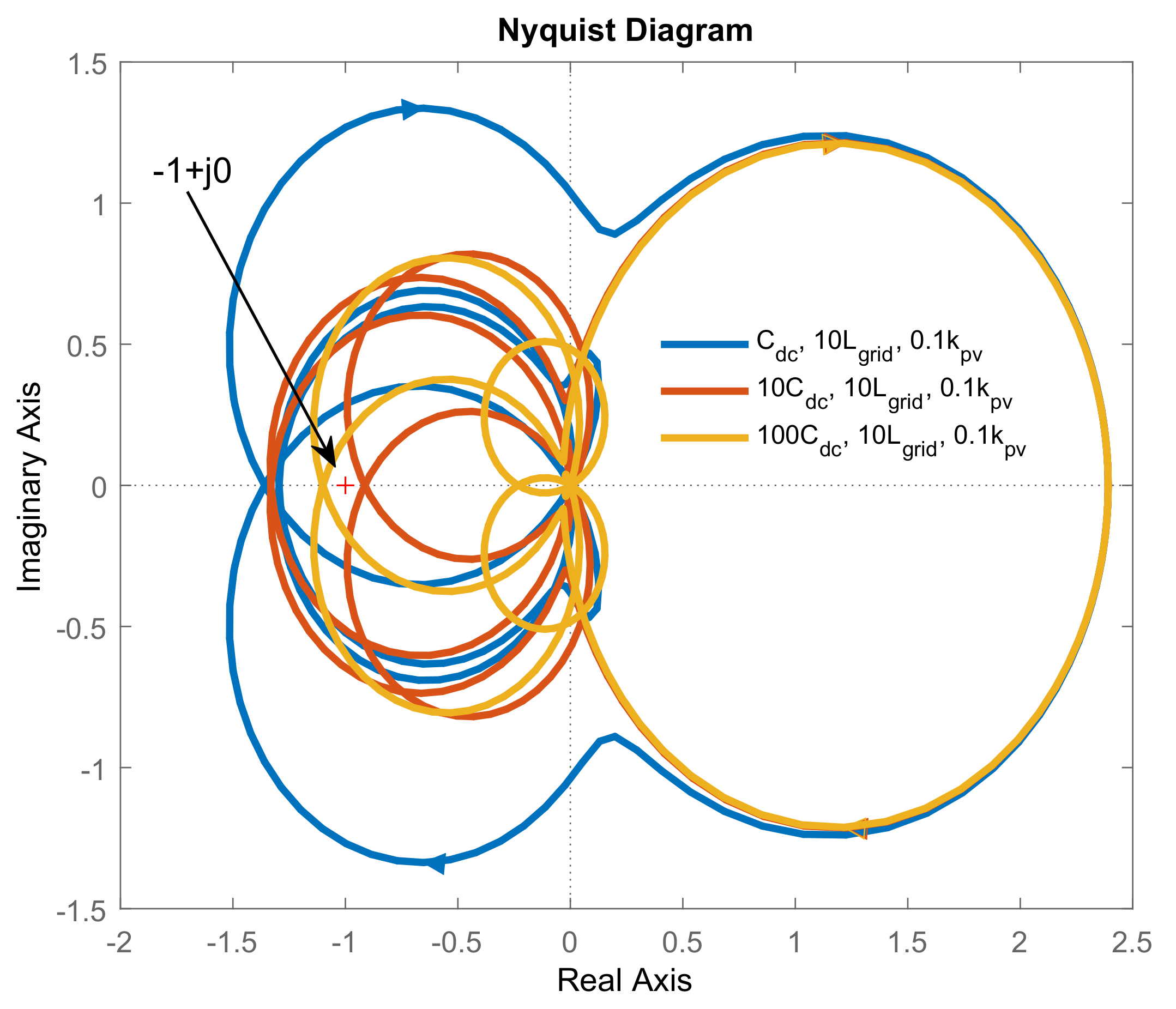
4.3. Harmonic Stability
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| C | Constant |
| Modulation delay | |
| Closed-loop gain of AC to DC side of converter | |
| Closed-loop transfer functions from output to reference of current loop | |
| Closed-loop transfer functions from output to reference of DC voltage loop | |
| Open-loop gain of current loop | |
| Open-loop gain of DC voltage loop | |
| Reference current | |
| Converter AC current in abc frame | |
| Converter AC current in dq frame | |
| DC current injection at nth terminal | |
| Current compensator | |
| Integral gain of current compensator | |
| Integral gain of DC voltage compensator | |
| Proportional gain of current compensator | |
| Proportional gain of DC voltage compensator | |
| DC voltage compensator | |
| Inductance of DC cable | |
| Inductance of filter | |
| Inductance of transformer | |
| AC active power | |
| DC power |
| Transformer resistance | |
| Modulation delay | |
| Inner-loop time constant | |
| Converter AC voltage in dq frame | |
| Converter AC voltage in abc frame | |
| Source AC voltage in dq frame | |
| Source AC voltage in abc frame | |
| DC voltage reference | |
| DC voltage at nth terminal | |
| Current compensator | |
| Converter closed-loop output admittance with current loop | |
| Converter closed-loop output admittance considering influence of DC voltage loop | |
| Admittance as seen from source | |
| DC nodal impedance matrix | |
| Filter capacitor impedance | |
| Impedance of total DC capacitance at nth terminal | |
| Impedance of DC cable | |
| Impedance of filter inductor | |
| Equivalent AC grid impedance | |
| Converter DC input impedance | |
| Converter closed-loop output impedance considering influence of DC voltage loop | |
| Impedance of transformer |
Appendix A. DC Voltage Equation of the HVDC Link

Appendix B. Transfer Functions
- AC admittance with inner-loopwhere , , , ,
- Closed-loop transfer function of the inner-loop,
- Open-loop transfer function of the complete system,wherewhere
- Closed-loop transfer function of the complete system,where
- AC admittance with complete system,
- DC impedance with complete system,
- Characteristic equation of the entire system,
| Parameter | Value |
|---|---|
| Base Power | 800 MVA |
| AC Voltage | 220 kV |
| DC Voltage | 200 kV |
| Frequency | 50 Hz |
| DC Cable Length | 200 km |
| 35 mH | |
| 0.363 | |
| 29 mH | |
| 10–100 F | |
| 4.813 |
| Control Data | Value |
|---|---|
| 25.6 | |
| 145.2 | |
| 0.0192 | |
| 0.272 |
References
- European Wind Energy Association. EU Energy Policy to 2050: Achieving 80–95% Emissions Reductions; EWEA: Brussels, Belgium, 2011. [Google Scholar]
- Meyer, C.; Hoing, M.; Peterson, A.; Doncker, R.W.D. Control and Design of DC Grids for Offshore Wind Farms. IEEE Trans. Ind. Appl. 2007, 43, 1475–1482. [Google Scholar] [CrossRef]
- Yazdani, A.; Iravani, R. Voltage-Sourced Converters in Power Systems: Modeling, Control, and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Dierckxsens, C.; Srivastava, K.; Reza, M.; Cole, S.; Beerten, J.; Belmans, R. A distributed DC voltage control method for VSC-MTDC systems. Electr. Power Syst. Res. 2012, 82, 54–58. [Google Scholar] [CrossRef]
- Yang, S.; Bryant, A.; Mawby, P.; Xiang, D.; Ran, L.; Tavner, P. An Industry-Based Survey of Reliability in Power Electronic Converters. IEEE Trans. Ind. Appl. 2011, 47, 1441–1451. [Google Scholar] [CrossRef]
- Wang, H.; Liserre, M.; Blaabjerg, F. Toward Reliable Power Electronics: Challenges, Design Tools, and Opportunities. IEEE Ind. Electron. Mag. 2013, 7, 17–26. [Google Scholar] [CrossRef]
- Liserre, M.; Teodorescu, R.; Blaabjerg, F. Stability of photovoltaic and wind turbine grid-connected inverters for a large set of grid impedance values. IEEE Trans. Power Electron. 2006, 21, 263–272. [Google Scholar] [CrossRef]
- Enslin, J.H.R.; Heskes, P.J.M. Harmonic interaction between a large number of distributed power inverters and the distribution network. IEEE Trans. Power Electron. 2004, 19, 1586–1593. [Google Scholar] [CrossRef]
- Wang, X.; Blaabjerg, F.; Loh, P.C. Proportional derivative based stabilizing control of paralleled grid converters with cables in renwable power plants. In Proceedings of the 2014 IEEE Energy Conversion Congress and Exposition (ECCE), Pittsburgh, PA, USA, 14–18 September 2014; pp. 4917–4924. [Google Scholar]
- Céspedes, M.; Sun, J. Impedance shaping of three-phase grid-parallel voltage-source converters. In Proceedings of the 2012 Twenty-Seventh Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Orlando, FL, USA, 5–9 Feburary 2012; pp. 754–760. [Google Scholar]
- Harnefors, L.; Wang, X.; Yepes, A.G.; Blaabjerg, F. Passivity-Based Stability Assessment of Grid-Connected VSCs; An Overview. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 116–125. [Google Scholar] [CrossRef]
- Harnefors, L.; Zhang, L.; Bongiorno, M. Frequency-domain passivity-based current controller design. IET Power Electron. 2008, 1, 455–465. [Google Scholar] [CrossRef]
- Vesti, S.; Suntio, T.; Oliver, J.A.; Prieto, R.; Cobos, J.A. Impedance-Based Stability and Transient-Performance Assessment Applying Maximum Peak Criteria. IEEE Trans. Power Electron. 2013, 28, 2099–2104. [Google Scholar] [CrossRef]
- Sun, J. Small-Signal Methods for AC Distributed Power Systems—A Review. IEEE Trans. Power Electron. 2009, 24, 2545–2554. [Google Scholar]
- Sun, J. Impedance-Based Stability Criterion for Grid-Connected Inverters. IEEE Trans. Power Electron. 2011, 26, 3075–3078. [Google Scholar] [CrossRef]
- Chen, M.; Sun, J. Low-Frequency Input Impedance Modeling of Boost Single-Phase PFC Converters. IEEE Trans. Power Electron. 2007, 22, 1402–1409. [Google Scholar] [CrossRef]
- Yang, D.; Ruan, X.; Wu, H. Impedance Shaping of the Grid-Connected Inverter with LCL Filter to Improve Its Adaptability to the Weak Grid Condition. IEEE Trans. Power Electron. 2014, 29, 5795–5805. [Google Scholar] [CrossRef]
- Rygg, A.; Molinas, M.; Zhang, C.; Cai, X. On the Equivalence and Impact on Stability of Impedance Modeling of Power Electronic Converters in Different Domains. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 1444–1454. [Google Scholar] [CrossRef]
- Wang, X.; Harnefors, L.; Blaabjerg, F. Unified Impedance Model of Grid-Connected Voltage-Source Converters. IEEE Trans. Power Electron. 2018, 33, 1775–1787. [Google Scholar] [CrossRef]
- Cespedes, M.; Sun, J. Impedance Modeling and Analysis of Grid-Connected Voltage-Source Converters. IEEE Trans. Power Electron. 2014, 29, 1254–1261. [Google Scholar] [CrossRef]
- Harnefors, L.; Yepes, A.G.; Vidal, A.; Doval-Gandoy, J. Passivity-Based Controller Design of Grid-Connected VSCs for Prevention of Electrical Resonance Instability. IEEE Trans. Ind. Electron. 2015, 62, 702–710. [Google Scholar] [CrossRef]
- Jessen, L.; Fuchs, F.W. Modeling of inverter output impedance for stability analysis in combination with measured grid impedances. In Proceedings of the 2015 IEEE 6th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Aachen, Germany, 22–25 June 2015; pp. 1–7. [Google Scholar]
- Cho, Y.; Hur, K.; Kang, Y.C.; Muljadi, E. Impedance-Based Stability Analysis in Grid Interconnection Impact Study Owing to the Increased Adoption of Converter-Interfaced Generators. Energies 2017, 10, 1355. [Google Scholar] [CrossRef]
- Freijedo, F.D.; Chaudhary, S.K.; Teodorescu, R.; Guerrero, J.M.; Bak, C.L.; Kocewiak, H.; Jensen, C.F. Harmonic resonances in Wind Power Plants: Modeling, analysis and active mitigation methods. In Proceedings of the 2015 IEEE Eindhoven PowerTech, Eindhoven, The Netherlands, 29 June–2 July 2015; pp. 1–6. [Google Scholar]
- Liu, H.; Sun, J. Voltage Stability and Control of Offshore Wind Farms with AC Collection and HVDC Transmission. IEEE J. Emerg. Sel. Top. Power Electron. 2014, 2, 1181–1189. [Google Scholar]
- Amin, M.; Molinas, M. Understanding the Origin of Oscillatory Phenomena Observed between Wind Farms and HVDC Systems. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 378–392. [Google Scholar] [CrossRef]
- Ebrahimzadeh, E.; Blaabjerg, F.; Wang, X.; Bak, C.L. Efficient approach for harmonic resonance identification of large Wind Power Plants. In Proceedings of the 2016 IEEE 7th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Vancouver, BC, Canada, 27–30 June 2016; pp. 1–7. [Google Scholar]
- Kunjumuhammed, L.P.; Pal, B.C.; Oates, C.; Dyke, K.J. Electrical Oscillations in Wind Farm Systems: Analysis and Insight Based on Detailed Modeling. IEEE Trans. Sustain. Energy 2016, 7, 51–62. [Google Scholar] [CrossRef]
- Xu, L.; Fan, L. Impedance-Based Resonance Analysis in a VSC-HVDC System. IEEE Trans. Power Deliv. 2013, 28, 2209–2216. [Google Scholar] [CrossRef]
- Xu, L.; Fan, L.; Miao, Z. DC Impedance-Model-Based Resonance Analysis of a VSC-HVDC System. IEEE Trans. Power Deliv. 2015, 30, 1221–1230. [Google Scholar] [CrossRef]
- Pinares, G.; Bongiorno, M. Modeling and Analysis of VSC-Based HVDC Systems for DC Network Stability Studies. IEEE Trans. Power Deliv. 2016, 31, 848–856. [Google Scholar] [CrossRef]
- Agbemuko, A.J.; Domınguez-Garcıa, J.L.; Prieto-Araujo, E.; Gomis-Bellmunt, O. Harmonic Stability and Interactions in Meshed VSC-HVDC Dominated Power Systems. In Proceedings of the 16th International Wind Integration Workshop, Berlin, Germany, 25–27 October 2017. [Google Scholar]
- Zou, C.; GE, H.R.; Xu, S.; Li, Y.; Li, W.; Chen, J.; Zhao, X.; Yang, Y.; Lei, B. Analysis of Resonance between a VSC-HVDC Converter and the AC Grid. IEEE Trans. Power Electron. 2018. [Google Scholar] [CrossRef]
- Haileselassie, T.M.; Uhlen, K. Impact of DC Line Voltage Drops on Power Flow of MTDC Using Droop Control. IEEE Trans. Power Syst. 2012, 27, 1441–1449. [Google Scholar] [CrossRef]
- Harnefors, L.; Nee, H.P. Model-based current control of AC machines using the internal model control method. IEEE Trans. Ind. Appl. 1998, 34, 133–141. [Google Scholar] [CrossRef]
- Chaudhuri, N.; Chaudhuri, B.; Majumder, R.; Yazdani, A. Multi-Terminal Direct-Current Grids: Modeling, Analysis, and Control; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Wang, X.; Blaabjerg, F.; Wu, W. Modeling and Analysis of Harmonic Stability in an AC Power-Electronics-Based Power System. IEEE Trans. Power Electron. 2014, 29, 6421–6432. [Google Scholar] [CrossRef]
- Amin, M.; Molinas, M.; Lyu, J.; Cai, X. Impact of Power Flow Direction on the Stability of VSC-HVDC Seen From the Impedance Nyquist Plot. IEEE Trans. Power Electron. 2017, 32, 8204–8217. [Google Scholar] [CrossRef]
- Amin, M.; Rygg, A.; Molinas, M. Impedance-based and eigenvalue based stability assessment compared in VSC-HVDC system. In Proceedings of the 2016 IEEE Energy Conversion Congress and Exposition (ECCE), Milwaukee, WI, USA, 18–22 September 2016; pp. 1–8. [Google Scholar]




















© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Agbemuko, A.J.; Domínguez-García, J.L.; Prieto-Araujo, E.; Gomis-Bellmunt, O. Impedance Modelling and Parametric Sensitivity of a VSC-HVDC System: New Insights on Resonances and Interactions. Energies 2018, 11, 845. https://doi.org/10.3390/en11040845
Agbemuko AJ, Domínguez-García JL, Prieto-Araujo E, Gomis-Bellmunt O. Impedance Modelling and Parametric Sensitivity of a VSC-HVDC System: New Insights on Resonances and Interactions. Energies. 2018; 11(4):845. https://doi.org/10.3390/en11040845
Chicago/Turabian StyleAgbemuko, Adedotun J., José Luis Domínguez-García, Eduardo Prieto-Araujo, and Oriol Gomis-Bellmunt. 2018. "Impedance Modelling and Parametric Sensitivity of a VSC-HVDC System: New Insights on Resonances and Interactions" Energies 11, no. 4: 845. https://doi.org/10.3390/en11040845
APA StyleAgbemuko, A. J., Domínguez-García, J. L., Prieto-Araujo, E., & Gomis-Bellmunt, O. (2018). Impedance Modelling and Parametric Sensitivity of a VSC-HVDC System: New Insights on Resonances and Interactions. Energies, 11(4), 845. https://doi.org/10.3390/en11040845








