Influence of Operating Conditions and Crushing Chamber on Energy Consumption of Cone Crusher
Abstract
:1. Introduction
2. Energy Consumption Analysis
3. Prediction Model of Breakage Energy
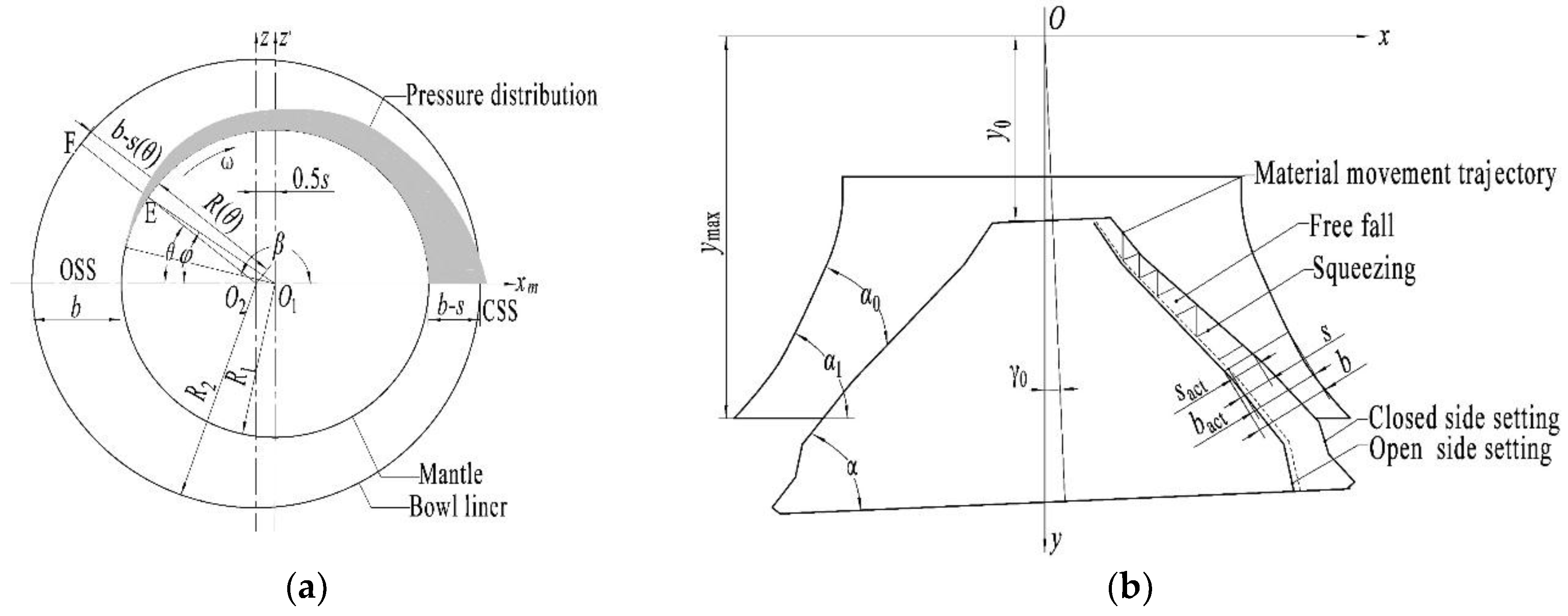
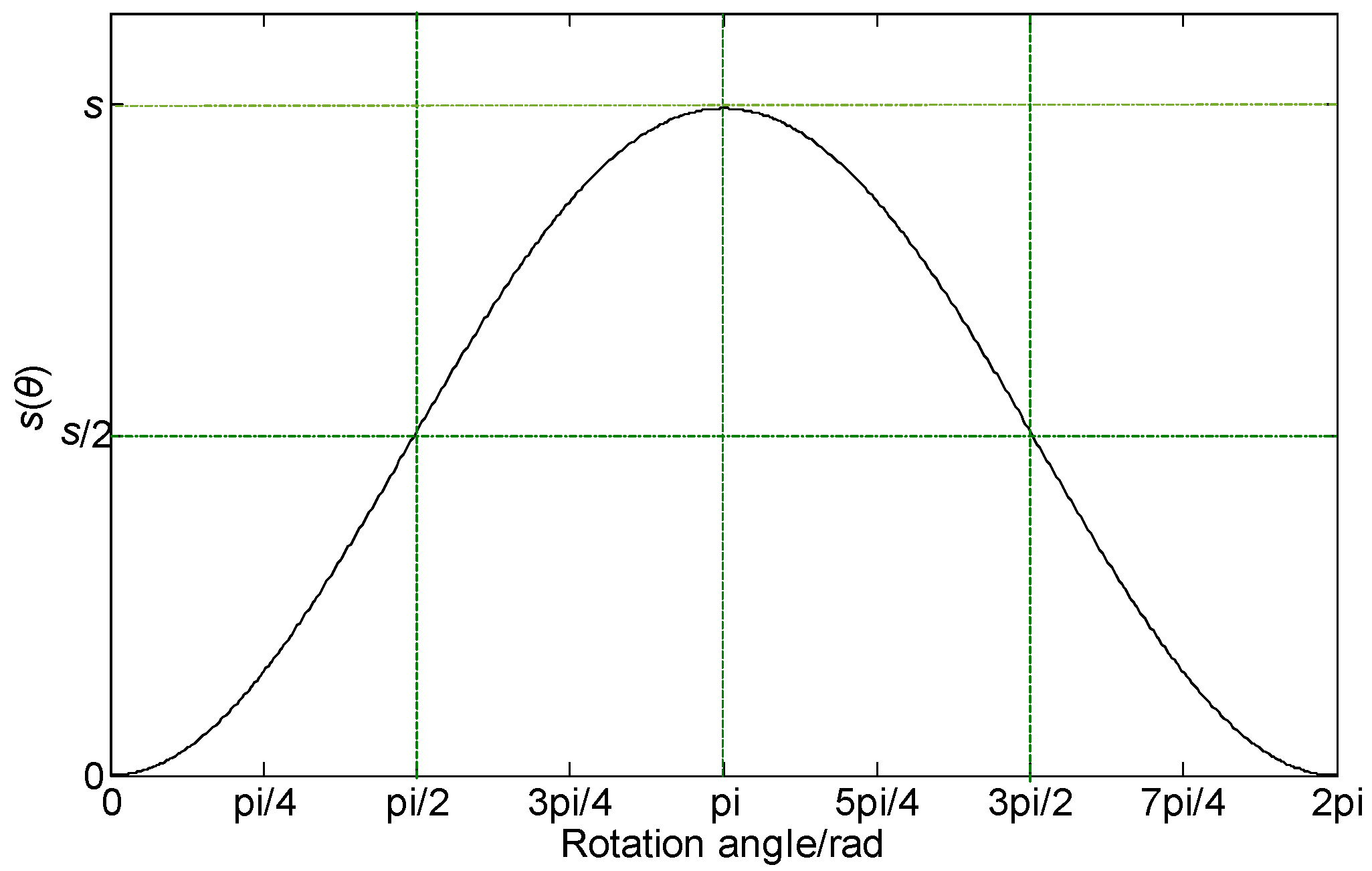
3.1. Crushing Pressure Model of the Liner
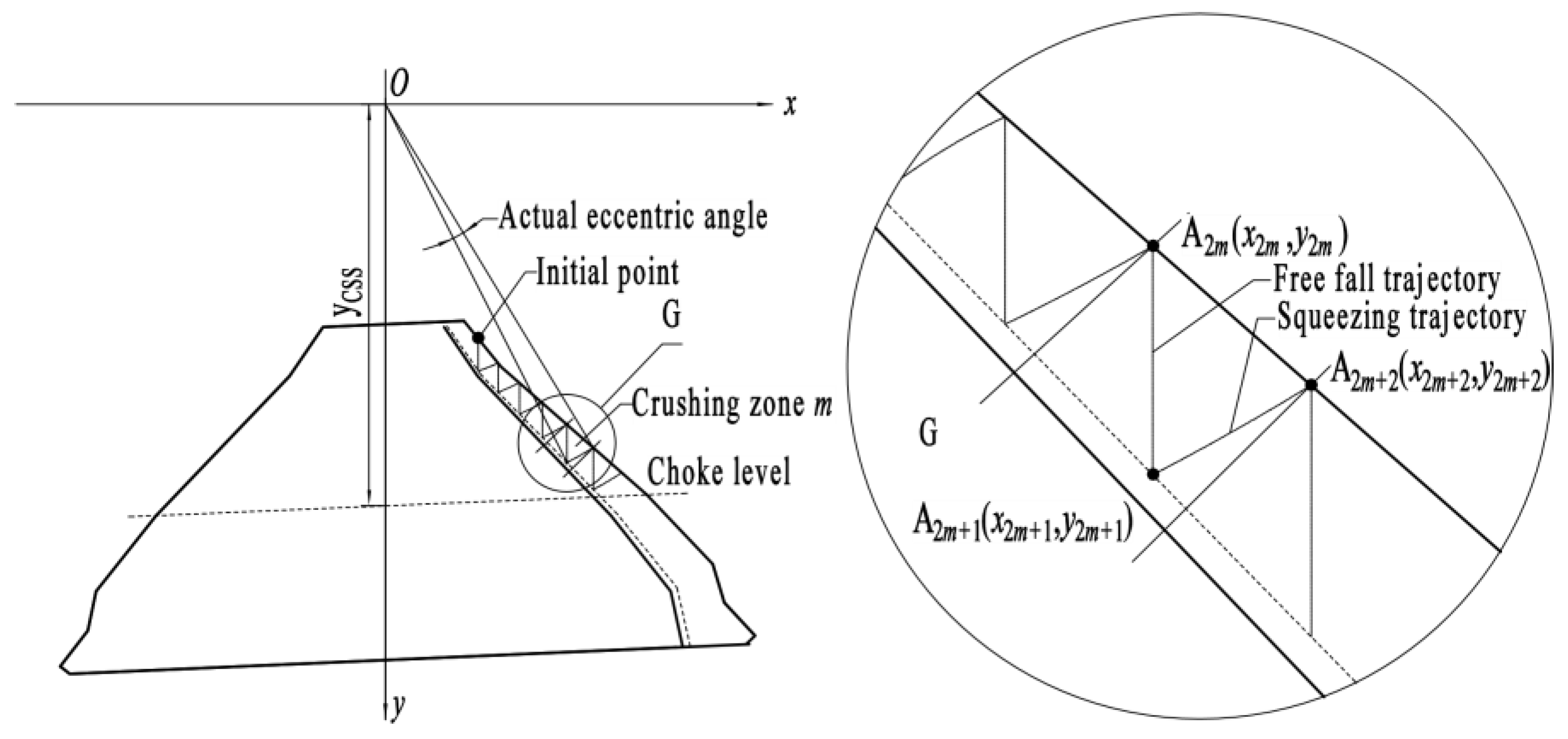
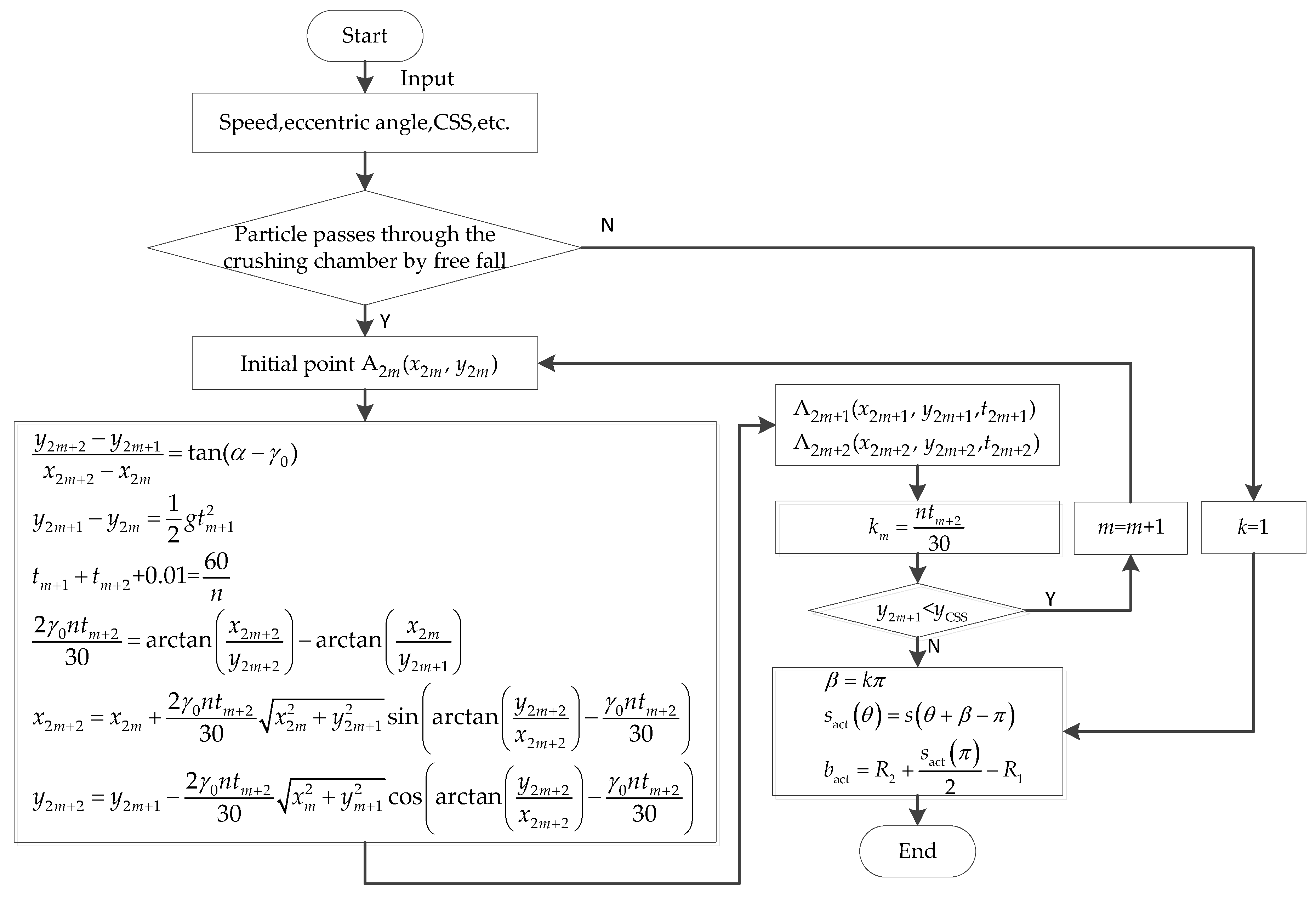
3.2. Modeling of Energy Consumption
4. Example
4.1. Experiment
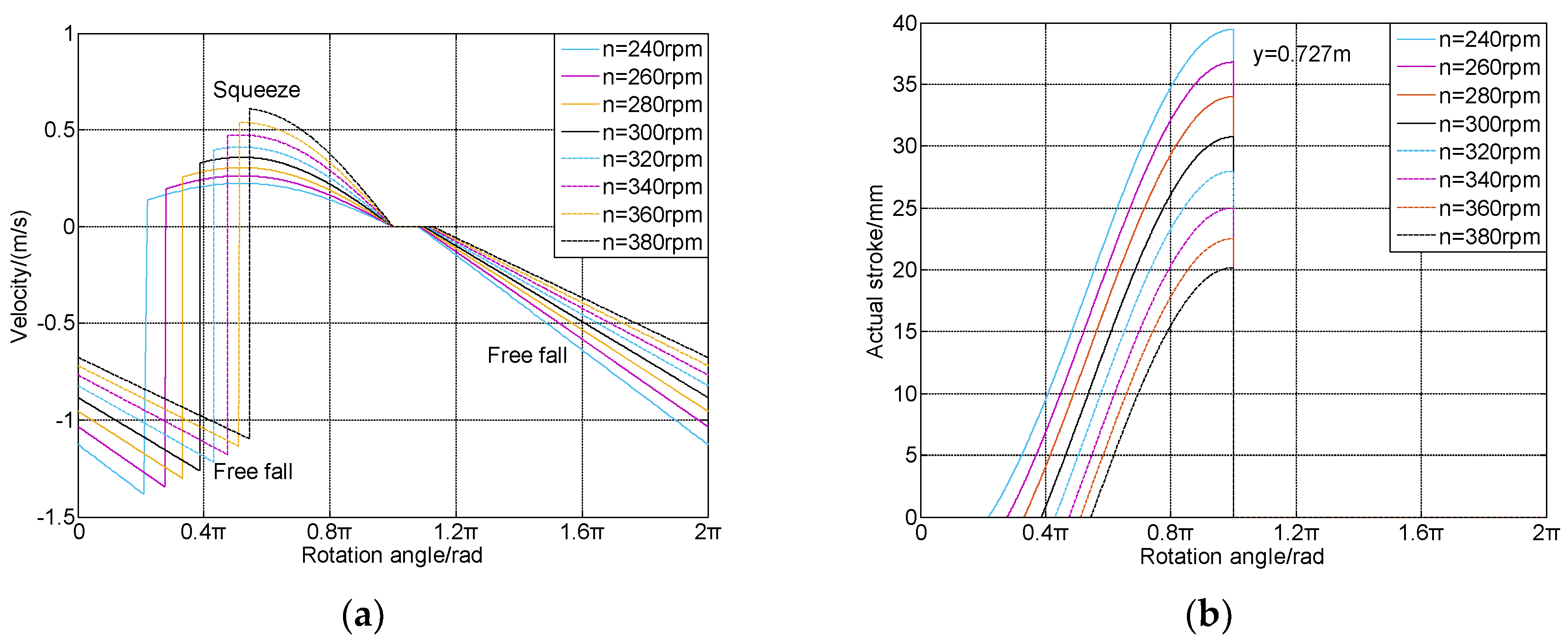
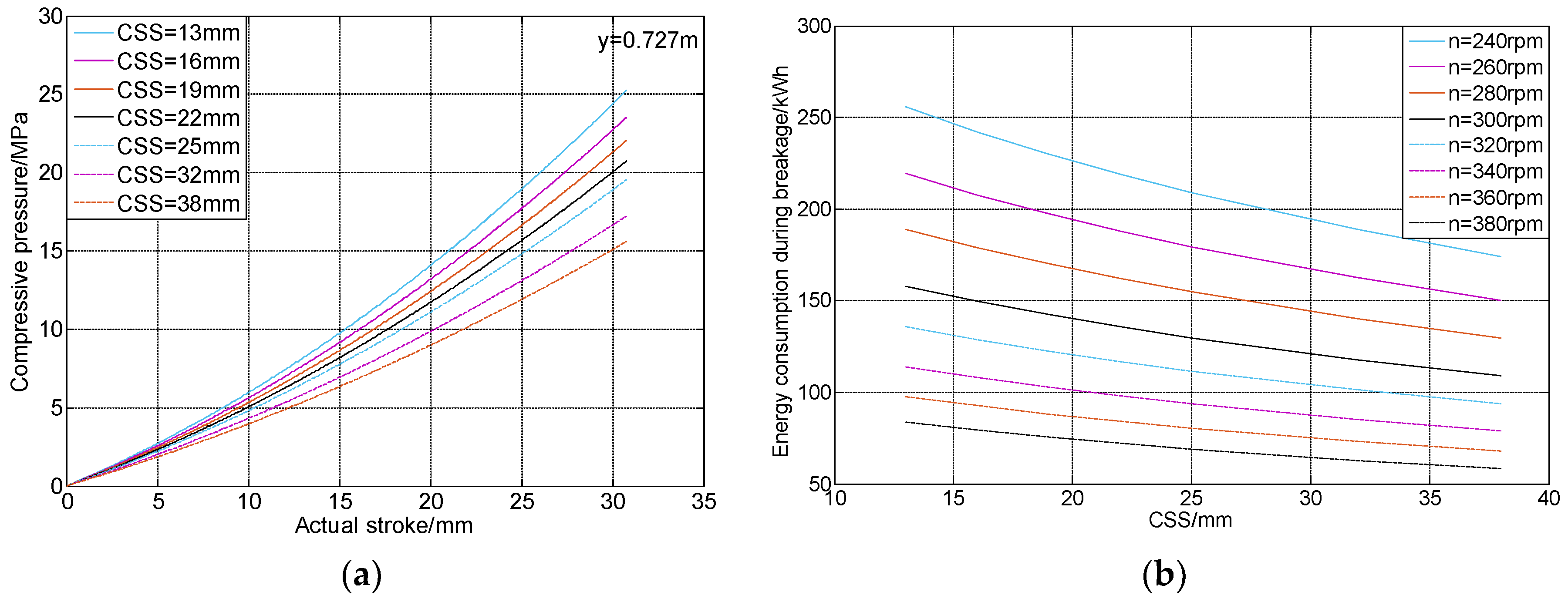
4.2. Results Analysis
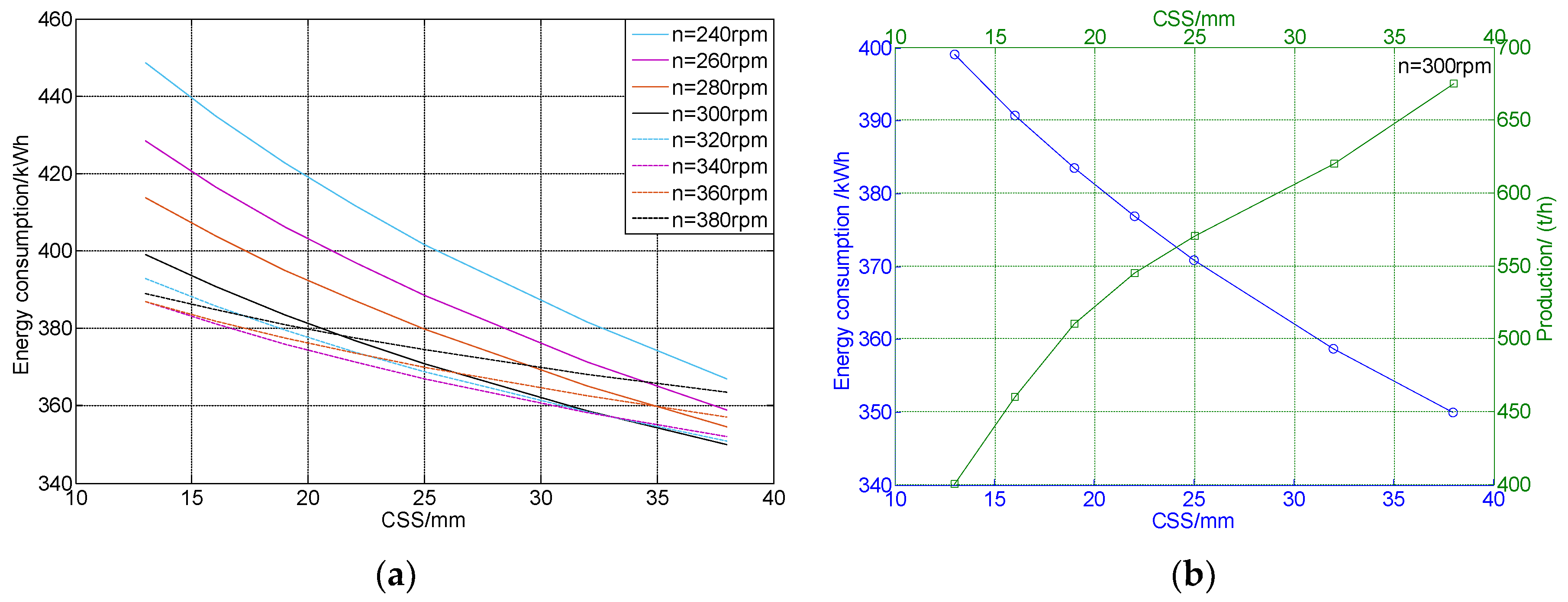
4.3. Influencing Factors of Energy Consumption
5. Discussion
6. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Nomenclature
| A | surface area of liner, m2 |
| b | material height before compression, m |
| bact | actual material height before compression, m |
| CSS | closed side setting |
| the average size of all particles, mm | |
| the mean size of particle j, mm | |
| E | energy consumption of cone crusher, kW·h |
| E0 | no-load mechanical energy, kW·h |
| E1 | energy consumption during breakage, kW·h |
| Fstress | stress on the liner, N |
| i | compression ratio |
| iact | actual compression ratio |
| k | actual stroke coefficient |
| lact | the actual arc length of mantle during squeezing, m |
| l | arc length, m |
| m | crushing zone |
| n | mantle speed, r/min |
| O | suspension point |
| OSS | open side setting |
| O1 | the center of the mantle |
| O2 | the center of the bowl liner |
| p | pressure on the mantle, MPa |
| q | the number of particle sizes |
| Q | production, t/h |
| R1 | radius of the mantle, m |
| R2 | radius of bowl liner, m |
| R(θ) | distance between the center O2 of the bowl liner and the surface of the mantle, m |
| s | stroke, m |
| sact | actual stroke, m |
| s(θ) | the stroke when the mantle rotates angle θ, m |
| tdown | free fall time of choke level, s |
| tup | squeezing time of choke level, s |
| tm+1 | free fall time of crushing zone m, s |
| tm+2 | squeezing time of crushing zone m, s |
| vdown | the free fall velocity of material, m/s |
| vup | the upward speed of material, m/s |
| ycss | ordinate of closed side setting, m |
| ymax | the distance between the suspension point O and the bottom of the bowl, m |
| y0 | the height under the suspension point O, m |
| x2m | abscissa of A2m, m |
| y2m | ordinate of A2m, m |
| x2m+1 | abscissa of A2m+1, m |
| y2m+1 | ordinate of A2m+1, m |
| x2m+2 | abscissa of A2m+2, m |
| y2m+2 | ordinate of A2m+2, m |
| α | base angle of the mantle, ° |
| α0 | nip angle, ° |
| α1 | base angle of the bowl liner, ° |
| β | actual squeezing angle, ° |
| γ0 | eccentric angle, ° |
| θ | rotation angle of mantle around the center of bowl liner, ° |
| λj | the yield of particle size j |
| ρ | material density, kg/m3 |
| σ | feed size distribution |
| φ | rotation angle of mantle around its center, ° |
Appendix A
- (1)
- Stroke
- (2)
- Actual material height and actual stroke
References
- Holmberg, K.; Kivikytö-Reponen, P.; Härkisaari, P.; Valtonen, K.; Erdemir, A. Global energy consumption due to friction and wear in the mining industry. Tribol. Int. 2017, 115, 116–139. [Google Scholar] [CrossRef]
- Legendre, D.; Zevenhoven, R. Assessing the energy efficiency of a jaw crusher. Energy 2014, 74, 119–130. [Google Scholar] [CrossRef]
- Petrakis, E.; Stamboliadis, E.; Komnitsas, K. Evaluation of the relationship between energy input and particle size distribution in comminution with the use of piecewise regression analysis. Part. Sci. Technol. 2016, 35, 479–489. [Google Scholar] [CrossRef]
- Terva, J.; Kuokkala, V.T.; Valtonen, K.; Siitonen, P. Effects of compression and sliding on the wear and energy consumption in mineral crushing. Wear 2018, 398–399, 116–126. [Google Scholar] [CrossRef]
- Lindqvist, M. Energy considerations in compressive and impact crushing of rock. Miner. Eng. 2008, 21, 631–641. [Google Scholar] [CrossRef]
- Deng, Y.; Chen, M.; Jin, Y.; Zou, D. Theoretical analysis and experimental research on the energy dissipation of rock crushing based on fractal theory. J. Nat. Gas Sci. Eng. 2016, 33, 231–239. [Google Scholar] [CrossRef]
- Martins, S. Size-energy relationship in comminution, incorporating scaling laws and heat. Int. J. Miner. Process. 2016, 153, 29–43. [Google Scholar] [CrossRef]
- Xu, Y.; Wang, Y. Size effect on specific energy distribution in particle comminution. Fractals 2017, 25, 1750016. [Google Scholar] [CrossRef]
- Bengtsson, M.; Svedensten, P.; Evertsson, C.M. Characterization of Compressive Breakage Behavior. In Proceedings of the XXIII International Mineral Processing Congress, Istanbul, Turkey, 3–8 September 2006. [Google Scholar]
- Shi, F. A review of the applications of the JK size-dependent breakage model part 2: Assessment of material strength and energy requirement in size reduction. Int. J. Miner. Process. 2016, 157, 36–45. [Google Scholar] [CrossRef]
- Nadolski, S.; Klein, B.; Kumar, A.; Davaanyam, Z. An energy benchmarking model for mineral comminution. Miner. Eng. 2014, 65, 178–186. [Google Scholar] [CrossRef]
- Bonfils, B.; Ballantyne, G.R.; Powell, M.S. Developments in incremental rock breakage testing methodologies and modelling. Int. J. Miner. Process. 2016, 152, 16–25. [Google Scholar] [CrossRef]
- Zhang, C.; Nguyen, G.D.; Kodikara, J. An application of breakage mechanics for predicting energy-size reduction relationships in comminution. Powder Technol. 2016, 287, 121–130. [Google Scholar] [CrossRef]
- Mütze, T. Energy dissipation in particle bed comminution. Int. J. Miner. Process. 2015, 136, 15–19. [Google Scholar] [CrossRef]
- Mütze, T. Modelling the stress behaviour in particle bed comminution. Int. J. Miner. Process. 2016, 156, 14–23. [Google Scholar] [CrossRef]
- Numbi, B.P.; Zhang, J.; Xia, X. Optimal energy management for a jaw crushing process in deep mines. Energy 2014, 68, 337–348. [Google Scholar] [CrossRef]
- Johansson, M.; Bengtsson, M.; Evertsson, C.M.; Hulthén, E. A fundamental model of an industrial-scale jaw crusher. Miner. Eng. 2017, 105, 69–78. [Google Scholar] [CrossRef]
- Quist, J.; Evertsson, C.M. Cone crusher modelling and simulation using DEM. Miner. Eng. 2016, 85, 92–105. [Google Scholar] [CrossRef]
- Johansson, M.; Quist, J.; Evertsson, C.M.; Hulthén, E. Cone crusher performance evaluation using DEM simulations and laboratory experiments for model validation. Miner. Eng. 2017, 103–104, 93–101. [Google Scholar] [CrossRef]
- Cleary, P.W.; Sinnott, M.D.; Morrison, R.D.; Cummins, S.; Delaney, G.W. Analysis of cone crusher performance with changes in material properties and operating conditions using DEM. Miner. Eng. 2017, 100, 49–70. [Google Scholar] [CrossRef]
- Wu, J.; Bai, H.; Li, Q.; Ma, D. Grain size distribution effect on the hydraulic properties of disintegrated coal mixtures. Energies 2017, 10, 612. [Google Scholar] [CrossRef]
- Evertsson, C.M. Cone Crusher Performance. Ph.D. Thesis, Chalmers University of Technology, Gothenburg, Sweden, July 2000. [Google Scholar]
- Ma, Y.; Fan, X.; He, Q. Prediction of cone crusher performance considering liner wear. Appl. Sci. 2016, 6, 404. [Google Scholar] [CrossRef]






| Energy Consumption /(kW·h) | Material Level/% | Energy Consumption /(kW·h) | Material Level/% | Energy Consumption /(kW·h) | Material Level/% |
|---|---|---|---|---|---|
| 235.03 | 0 | 374.28 | 65.51 | 374.03 | 60.45 |
| 235.77 | 0 | 370.20 | 65.80 | 375.03 | 58.33 |
| 235.52 | 0 | 387.50 | 66.98 | 376.69 | 57.64 |
| 235.03 | 0 | 387.33 | 67.82 | 369.04 | 56.60 |
| 239.1 | 0 | 391.90 | 67.45 | 391.15 | 63.14 |
| 245.33 | 0 | 383.42 | 67.68 | 391.15 | 64.06 |
| 245.08 | 0 | 384.67 | 67.77 | 393.82 | 63.40 |
| 244.17 | 0 | 402.71 | 68.50 | 424.33 | 65.36 |
| 245.83 | 0 | 407.03 | 67.13 | 424.33 | 62.85 |
| 242.01 | 0 | 386.58 | 69.21 | 402.71 | 62.38 |
| 244.67 | 0 | 399.30 | 70.23 | 402.71 | 63.72 |
| 241.76 | 0 | 384.67 | 67.13 | 375.03 | 67.25 |
| 244.17 | 0 | 394.48 | 67.91 | 384.67 | 69.36 |
| 242.01 | 0 | 382.51 | 68.00 | 386.58 | 69.21 |
| 376.94 | 70.02 | 396.23 | 68.87 | 375.03 | 67.59 |
| 380.10 | 62.50 | 399.80 | 70.28 | 396.64 | 71.38 |
| 371.45 | 66.29 | 387.08 | 57.06 | 379.85 | 62.64 |
| 370.95 | 66.03 | 372.86 | 53.27 | 373.86 | 61.2 |
| 373.86 | 65.89 | 380.60 | 60.39 | 374.53 | 59.81 |
| 380.35 | 66.72 | 374.53 | 61.89 | 369.29 | 59.03 |
| 383.42 | 67.39 | 379.85 | 62.64 | 387.33 | 67.53 |
| 380.35 | 66.72 | 373.86 | 61.20 | 378.19 | 65.83 |
| Particle Size/mm | Feed Size Distribution/% | ||
|---|---|---|---|
| Test Number | |||
| 1 | 2 | 3 | |
| +100 | 2.51 | 4.13 | 1.87 |
| −100~+66 | 8.69 | 13.25 | 12.05 |
| −66~+42 | 19.42 | 16.73 | 22.03 |
| −42~+30 | 19.39 | 18.34 | 17.92 |
| −30~+24 | 15.13 | 12.72 | 11.35 |
| −24~+12 | 30.31 | 32.17 | 30.77 |
| −12~+7 | 3.34 | 1.97 | 3.52 |
| −7~+5 | 0.27 | 0.13 | 0.29 |
| −5~0 | 0.94 | 0.56 | 0.20 |
| Coefficient | Value |
|---|---|
| Maximum radius of the mantle/m | 0.8039 |
| Maximum radius of the bowl liner/m | 0.917 |
| Abscissa of initial point/m | 0.1878 |
| Ordinate of initial point/m | 0.3333 |
| Ordinate of CSS/m | 0.727 |
| Height under the suspension point O/m | 0.3412 |
| Height of bowl liner/m | 0.8732 |
| Base angle of mantle/° | 50.5 |
| Base angle of bowl liner/° | 48 |
| Nip angle/° | 21 |
| Eccentric angle/° | 2.5 |
| Closed set setting/mm | 19 |
| Speed/(r/min) | 300 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, R.; Shi, B.; Li, G.; Yu, H. Influence of Operating Conditions and Crushing Chamber on Energy Consumption of Cone Crusher. Energies 2018, 11, 1102. https://doi.org/10.3390/en11051102
Liu R, Shi B, Li G, Yu H. Influence of Operating Conditions and Crushing Chamber on Energy Consumption of Cone Crusher. Energies. 2018; 11(5):1102. https://doi.org/10.3390/en11051102
Chicago/Turabian StyleLiu, Ruiyue, Boqiang Shi, Guoguang Li, and Hongjun Yu. 2018. "Influence of Operating Conditions and Crushing Chamber on Energy Consumption of Cone Crusher" Energies 11, no. 5: 1102. https://doi.org/10.3390/en11051102
APA StyleLiu, R., Shi, B., Li, G., & Yu, H. (2018). Influence of Operating Conditions and Crushing Chamber on Energy Consumption of Cone Crusher. Energies, 11(5), 1102. https://doi.org/10.3390/en11051102




