Wavelet Based Denoising for the Estimation of the State of Charge for Lithium-Ion Batteries
Abstract
:1. Introduction
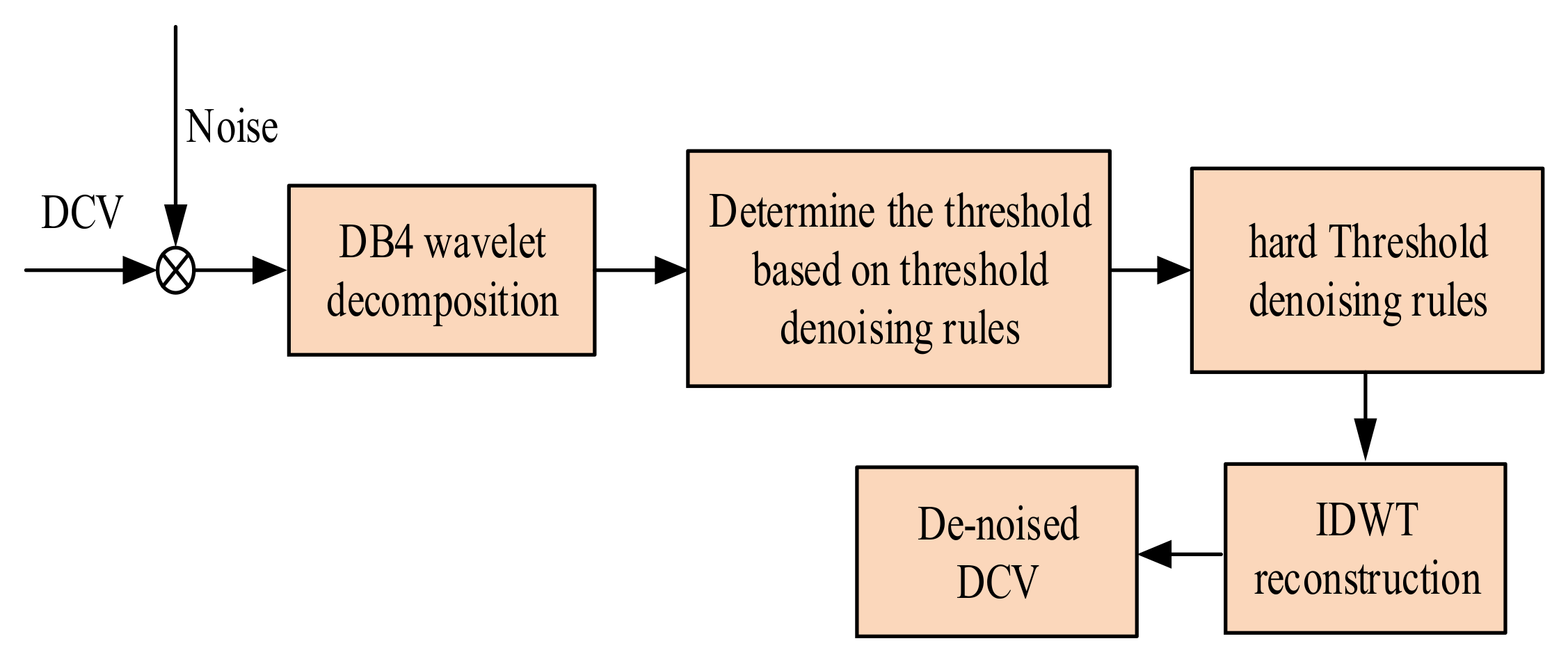
2. DWT-Based Denoising of DCV Signals
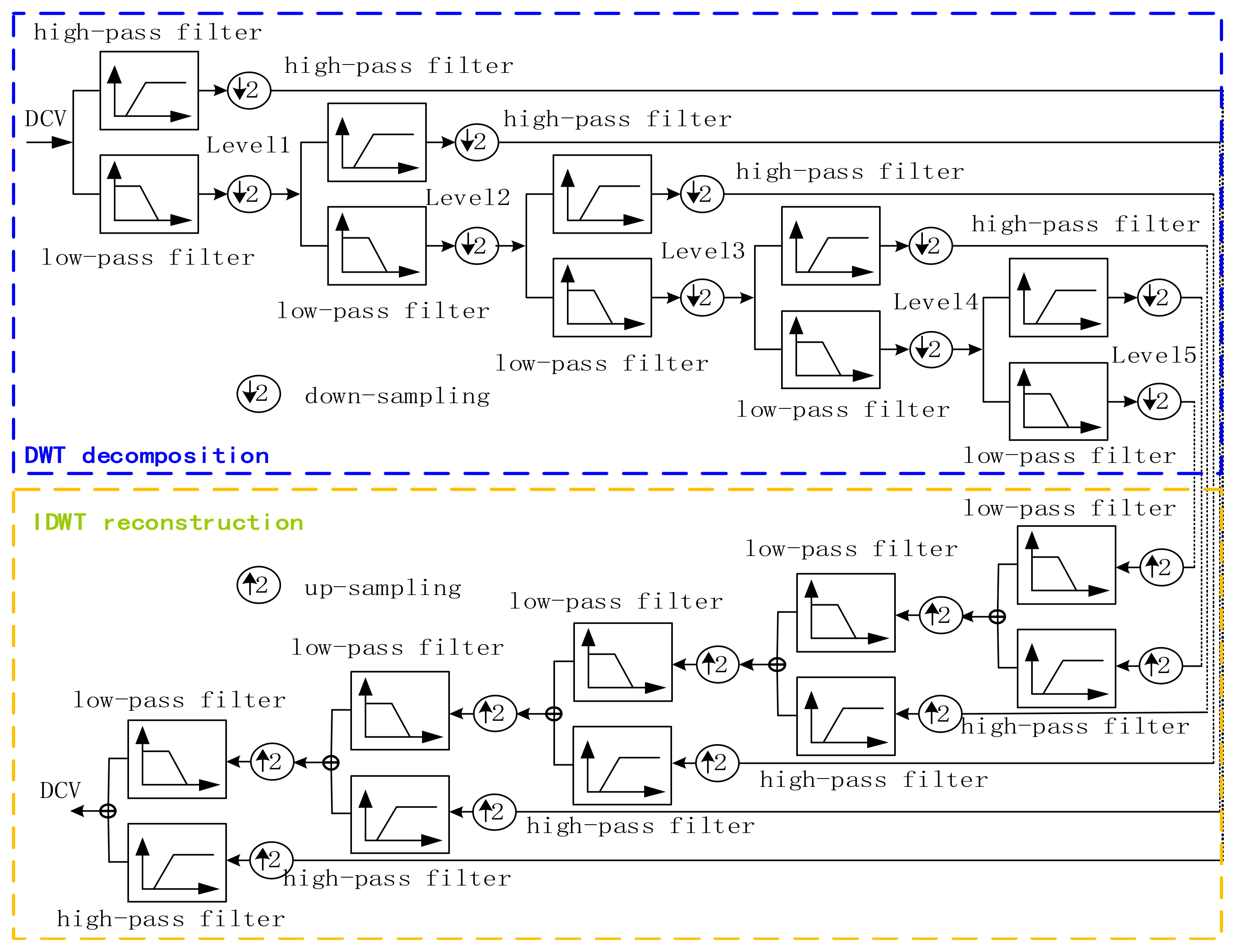
2.1. DWT and the Multi-Resolution Analysis
2.2. Experimental Platform and Processing of DCV Signal
2.3. The Denoised DCV Signal Based on the Thresholding-Based Denoising Rule
3. The ECM of the Battery and the Parameter Identification Method
3.1. AFFRLS Algorithm
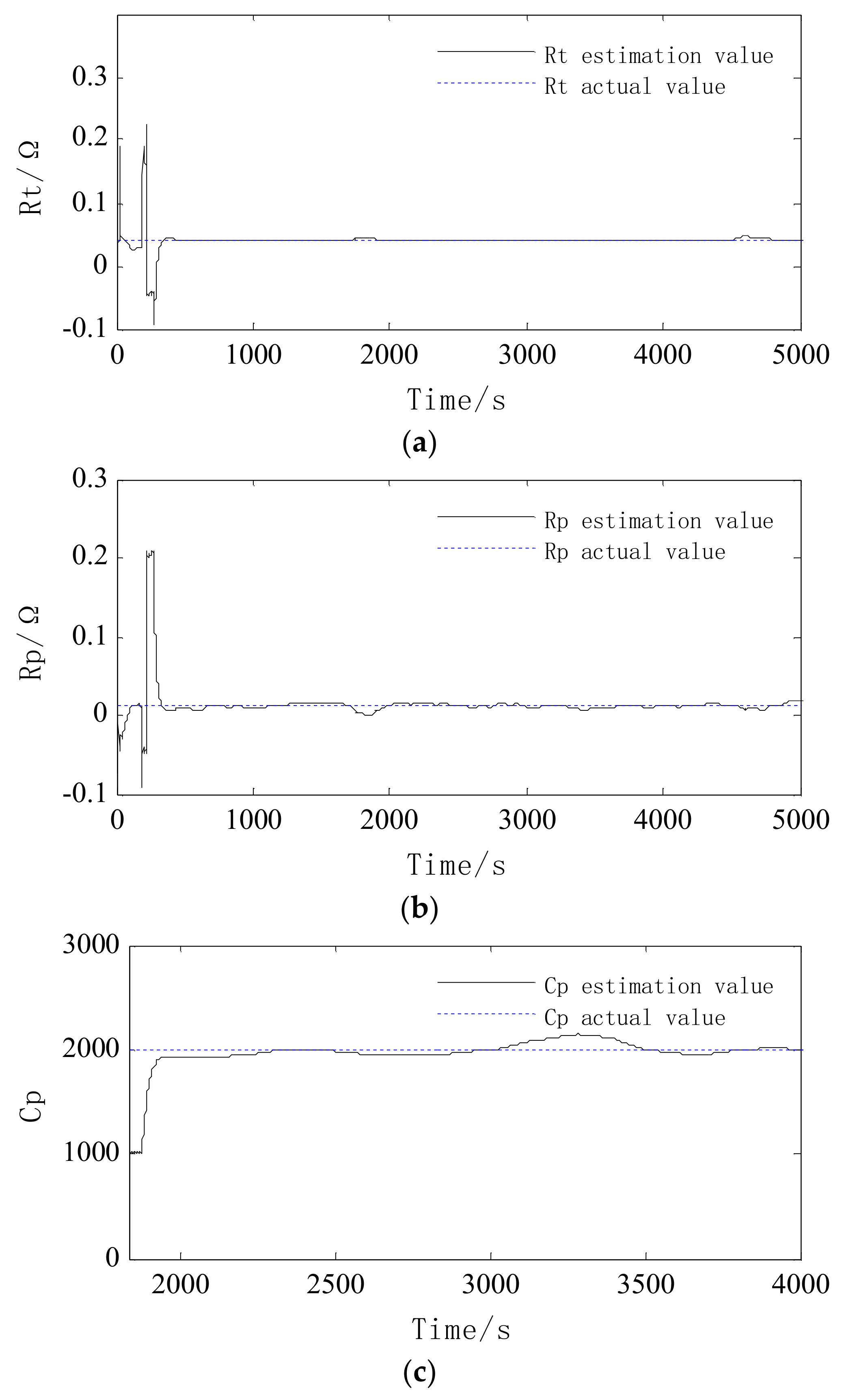
3.2. Parameter Identification
4. The SOC Estimation Based on the AEKF Method
4.1. The AEKF Algorithm
4.2. Simulation and Experimental Validation
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Meng, J.; Ricco, M.; Luo, G.; Swierczynski, M.; Stroe, D.I.; Stroe, A.I.; Teodorescu, R. An overview and comparison of online implementable soc estimation methods for lithium-ion battery. IEEE Trans. Ind. Appl. 2018, 54, 1583–1591. [Google Scholar] [CrossRef]
- Xu, J.; Mi, C.C.; Cao, B.; Cao, J. A new method to estimate the state of charge of lithium-ion batteries based on the battery impedance model. J. Power Sources 2013, 233, 277–284. [Google Scholar] [CrossRef]
- Xiong, R.; Zhang, Y.; He, H.; Zhou, X.; Pecht, M.G. A double-scale, particle-filtering, energy state prediction algorithm for lithium-ion batteries. IEEE Trans. Ind. Electron. 2017, 65, 1526–1538. [Google Scholar] [CrossRef]
- Zheng, Y.; Ouyang, M.; Han, X.; Lu, L.; Li, J. Investigating the error sources of the online state of charge estimation methods for lithium-ion batteries in electric vehicles. J. Power Sources 2018, 377, 161–188. [Google Scholar] [CrossRef]
- Zou, Z.; Xu, J.; Mi, C.; Cao, B.; Chen, Z. Evaluation of model based state of charge estimation methods for lithium-ion batteries. Energies 2014, 7, 5065–5082. [Google Scholar] [CrossRef]
- Xu, J.; Cao, B. Battery Management System for Electric Drive Vehicles: Modelling, State Estimation and Balancing, 1st ed.; InTech: Rijeka, Croatia, 2015; pp. 87–113. [Google Scholar]
- Plett, G.L. Sigma-point kalman filtering for battery management systems of lipb-based hev battery packs: Part 2: Simultaneous state and parameter estimation. J. Power Sources 2006, 161, 1369–1384. [Google Scholar] [CrossRef]
- Plett, G.L. Extended kalman filtering for battery management systems of lipb-based hev battery packs: Part 2. Modeling and identification. J. Power Sources 2004, 134, 262–276. [Google Scholar] [CrossRef]
- Xiong, R.; Sun, F.; Chen, Z.; He, H. A data-driven multi-scale extended kalman filtering based parameter and state estimation approach of lithium-ion olymer battery in electric vehicles. Appl. Energy 2014, 113, 463–476. [Google Scholar] [CrossRef]
- Lim, K.; Bastawrous, H.A.; Duong, V.-H.; See, K.W.; Zhang, P.; Dou, S.X. Fading kalman filter-based real-time state of charge estimation in LiFePO4 battery-powered electric vehicles. Appl. Energy 2016, 169, 40–48. [Google Scholar] [CrossRef]
- Xu, J.; Mi, C.C.; Cao, B.; Deng, J.; Chen, Z.; Li, S. The state of charge estimation of lithium-ion batteries based on a proportional-integral observer. IEEE Trans. Veh. Technol. 2014, 63, 1614–1621. [Google Scholar]
- Zheng, L.; Zhang, L.; Zhu, J.; Wang, G.; Jiang, J. Co-estimation of state-of-charge, capacity and resistance for lithium-ion batteries based on a high-fidelity electrochemical model. Appl. Energy 2016, 180, 424–434. [Google Scholar] [CrossRef]
- Xu, J.; Wang, J.; Li, S.; Cao, B. A method to simultaneously detect the current sensor fault and estimate the state of energy for batteries in electric vehicles. Sensors 2016, 16, 1328. [Google Scholar] [CrossRef] [PubMed]
- Zou, C.; Manzie, C.; Nešić, D.; Kallapur, A.G. Multi-time-scale observer design for state-of-charge and state-of-health of a lithium-ion battery. J. Power Sources 2016, 335, 121–130. [Google Scholar] [CrossRef]
- Sepasi, S.; Ghorbani, R.; Liaw, B.Y. A novel on-board state-of-charge estimation method for aged Li-ion batteries based on model adaptive extended kalman filter. J. Power Sources 2014, 245, 337–344. [Google Scholar] [CrossRef]
- Hu, X.; Sun, F.; Zou, Y. Estimation of state of charge of a lithium-ion battery pack for electric vehicles using an adaptive luenberger observer (vol 3, pg 1586, 2010). Energies 2011, 4, 2132. [Google Scholar] [CrossRef]
- Bouzida, A.; Touhami, O.; Ibtiouen, R.; Belouchrani, A.; Fadel, M.; Rezzoug, A. Fault diagnosis in industrial induction machines through discrete wavelet transform. IEEE Trans. Ind. Electron. 2011, 58, 4385–4395. [Google Scholar] [CrossRef]
- Kim, J.; Cho, B.H. An innovative approach for characteristic analysis and state-of-health diagnosis for a Li-ion cell based on the discrete wavelet transform. J. Power Sources 2014, 260, 115–130. [Google Scholar] [CrossRef]
- Smith, C.M.; Nair, N.C. Comparing discrete wavelet transform (dwt) with discrete fourier transform (dft) implemented for digital relays. In Proceedings of the Power Engineering Conference, AUPEC 2009, Adelaide, Australia, 27–30 September 2009; pp. 1–6. [Google Scholar]
- Muhit, A.A.; Islam, M.S.; Othman, M. Design and analysis of discrete wavelet transform(dwt) for image compression using vhdl. In Proceedings of the International Conference on Parallel and Distributed Processing Techniques and Applications, Pdpta 2005, Las Vegas, NV, USA, 27–30 June 2005; pp. 157–160. [Google Scholar]
- Hwang, B.Y.; Jung, J.H.; Lee, J.M. Advanced sound source localization study using de-noising filter based on the discrete wavelet transform(dwt). J. Inst. Control 2015, 21, 1185–1192. [Google Scholar] [CrossRef]
- Zhang, X.; Mi, C.C.; Masrur, A.; Daniszewski, D. Wavelet-transform-based power management of hybrid vehicles with multiple on-board energy sources including fuel cell, battery and ultracapacitor. J. Power Sources 2008, 185, 1533–1543. [Google Scholar] [CrossRef]
- Maleknejad, K.; Yousefi, M.; Nouri, K. Computational methods for integrals involving functions and daubechies wavelets. Appl. Math. Comput. 2007, 189, 1828–1840. [Google Scholar] [CrossRef]
- Kopsinis, Y.; McLaughlin, S. Development of emd-based denoising methods inspired by wavelet thresholding. IEEE Trans. Signal Process. 2009, 57, 1351–1362. [Google Scholar] [CrossRef]
- Liu, C.-C.; Sun, T.-Y.; Tsai, S.-J.; Yu, Y.-H.; Hsieh, S.-T. Heuristic wavelet shrinkage for denoising. Appl. Soft Comput. 2011, 11, 256–264. [Google Scholar] [CrossRef]
- Wei, W.; Zhang, Y.; Ren, G. Adaptive selection and simulation of optimal decomposition level in threshold de-noising algorithm based on wavelet transform. Chin. J. Sci. Instrum. 2009, 30, 526–530. [Google Scholar]
- Rahimi-Eichi, H.; Chow, M.Y. Adaptive parameter identification and state-of-charge estimation of lithium-ion batteries. In Proceedings of the IECON 2012—38th Annual Conference on IEEE Industrial Electronics Society, Montreal, QC, Canada, 25–28 October 2012; pp. 4012–4017. [Google Scholar]
- Paleologu, C.; Benesty, J.; Ciochina, S. A robust variable forgetting factor recursive least-squares algorithm for system identification. IEEE Signal Process. Lett. 2008, 15, 597–600. [Google Scholar] [CrossRef]
- Yao, L.W.; Aziz, J.A.; Idris, N.R.N.; Alsofyani, I.M. Online battery modeling for state-of-charge estimation using extended kalman filter with busse’s adaptive rule. In Proceedings of the Industrial Electronics Society, IECON 2015—Conference of the IEEE, Yokohama, Japan, 9–12 November 2015; pp. 004742–004747. [Google Scholar]
- He, H.; Xiong, R.; Zhang, X.; Sun, F.; Fan, J. State-of-charge estimation of the lithium-ion battery using an adaptive extended kalman filter based on an improved thevenin model. IEEE Trans. Veh. Technol. 2011, 60, 1461–1469. [Google Scholar]







| Denoising Rules | SNR |
|---|---|
| noisy simulation DCV signal | 25 |
| sqtwolong rule | 29.0315 |
| sure rule | 36.4833 |
| heursure rule | 29.6599 |
| minimaxi rule | 32.2239 |
| SOC | 0.0–0.1 | 0.1–0.2 | 0.2–0.3 | 0.3–0.4 | 0.4–0.5 | 0.5–0.6 | 0.6–0.7 | 0.7–0.8 | 0.8–0.9 | 0.9–1.0 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.323 | 0.387 | 0.468 | 0.552 | 0.62 | 0.465 | 0.478 | 0.586 | 0.604 | 0.534 | |
| 3.565 | 3.558 | 3.542 | 3.517 | 3.49 | 3.567 | 3.559 | 3.484 | 3.469 | 3.532 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Xu, J.; Zhao, Y. Wavelet Based Denoising for the Estimation of the State of Charge for Lithium-Ion Batteries. Energies 2018, 11, 1144. https://doi.org/10.3390/en11051144
Wang X, Xu J, Zhao Y. Wavelet Based Denoising for the Estimation of the State of Charge for Lithium-Ion Batteries. Energies. 2018; 11(5):1144. https://doi.org/10.3390/en11051144
Chicago/Turabian StyleWang, Xiao, Jun Xu, and Yunfei Zhao. 2018. "Wavelet Based Denoising for the Estimation of the State of Charge for Lithium-Ion Batteries" Energies 11, no. 5: 1144. https://doi.org/10.3390/en11051144
APA StyleWang, X., Xu, J., & Zhao, Y. (2018). Wavelet Based Denoising for the Estimation of the State of Charge for Lithium-Ion Batteries. Energies, 11(5), 1144. https://doi.org/10.3390/en11051144





