Local Stability Analysis and Controller Design for Speed-Controlled Wind Turbine Systems in Regime II.5

Abstract

The paper presents a local stability analysis for machine speed control of wind turbine systems (WTS) in regime II.5, where the control objective is set-point reference tracking of the machine speed via a PI-controller. Stability criteria for the controller parameters are derived. Based on these criteria, the controller parameters are chosen by pole placement. Moreover, a model-based tuning rule is proposed which leads (i) to a stable and (ii) to an accurate and fast control performance. The control system is additionally augmented by anti-windup (AWU) and saturation (SAT) strategies to enhance its performance. Simulation results illustrate stability and tracking performance of the closed-loop system.

1. Introduction

The increasing amount of wind power for electrical power generation ($12.4$% in Germany 2016 [1], p. 7) necessitates a detailed understanding of wind turbine systems (WTS) to be capable of fulfilling the increasing requirements [2] (e.g., more strict grid codes) for wind turbine operators.

This paper discusses machine speed control of WTS in regime II.5. Figure 1 shows the (simplified) dependence of machine speed reference ${\omega }_{m,\mathrm{ref}}$ (in $\frac{\mathrm{rad}}{\mathrm{s}}$) on the wind speed $v_w$ (in $\frac{\mathrm{m}}{\mathrm{s}}$) for different operation regimes (for details see e.g., [3,4,5]). Each regime has its own machine speed control system. In regime I, the wind speed $v_w$ is too small to achieve an economic operation of the WTS, whereas, in regime IV, the wind speed $v_w$ is too high and would overload the mechanical structure of the WTS [6]. Hence, in both regimes, the WTS is not operated. In regime I, it is freely floating (without active speed control) to be ready to start its operation as soon as the wind speed exceeds the cut-in wind speed $v_w^{\mathrm{in}}$ (transition to regime II). In regime IV, the WTS is usually at standstill for safety reasons.

In regime II, the machine speed ${\omega }_m$ (in $\frac{\mathrm{rad}}{\mathrm{s}}$) is controlled by a nonlinear controller (see e.g., [7,8]) to achieve an optimal and constant ratio $\frac{{\omega }_m}{v_w}$. This ensures maximal power generation in regime II (i.e., maximum power point tracking, for details see [6,7,8]). In regime II.5, the machine speed ${\omega }_m$ is limited by some ${\omega }_m^{max}$ (in $\frac{\mathrm{rad}}{\mathrm{s}}$) to reduce e.g., acoustic noise (when the WTS is close to buildings). But, then, since nominal power is not yet reached, the machine torque $m_m$ (in $\mathrm{N}\mathrm{m}$) and, hence, the output power can still be increased [9]. Regime III is characterized by a limitation of both, machine speed ${\omega }_m$ and machine torque $m_m$. In this regime, the pitch angle ${\beta }_t$ (in ${}^{\circ }$) controls the machine speed ${\omega }_m$ and compensates for the increasing wind speed $v_w$ and wind power $p_w$ (in $\mathrm{W}$) (see e.g., [10,11]).

This paper focuses on regime II.5. In [12,13], it is explained that reasons for the machine speed limitation are, e.g., “acoustic noise, loads or other design constraints” ([12], p. 488). In regime II.5, neither the nonlinear controller of regime II (see e.g., [6,7]) nor the pitch controller of regime III (see e.g., [2], Chapter 25) can achieve the goals of machine speed control in regime II.5: (a) tracking of the constraint machine speed reference ${\omega }_{m,\mathrm{ref}}$ $(={\omega }_m^{max})$ and (b) maximized power generation of the WTS. A simple method to achieve (a) is “to implement a torque-speed ramp” [13], which is explained in detail in [13,14]. This method has several drawbacks; e.g., the WTS does not operate at its maximally achievable power generation and the “torque demand will be varying rapidly up and down the slope” ([12], p. 489). To overcome these drawbacks, ref. [15] proposes the use of a simple PI-controller, where the (optimal) reference torque $m_{m,\mathrm{ref}}$ (in $\mathrm{N}\mathrm{m}$) is the controller output. Besides the benefit that a PI-controller is a state-of-the-art controller and widely spread in industry, the use of the PI-controller achieves both goals (a) & (b), and, additionally, is able to produce only small torque variations (see [12], p. 489). Therefore, in the following, a PI-controller will be considered to control the machine speed ${\omega }_m$ via the machine torque $m_m$ in regime II.5. To the best knowledge of the authors, there does not exist a (local) stability analysis and model-based tuning rule for a speed PI-controller in regime II.5.

This paper analysis the dynamical system (including mechanical system, speed control system with PI-controller and underlying torque control loop) of a WTS in regime II.5. It will be shown that a bad controller parameter design will cause instability of the closed-loop system. To avoid that, model-based stability criteria for a stable closed-loop system are derived. Based on these criteria, a tuning rule for the controller parameters is proposed which (i) guarantees (local) stability of the closed-loop system and (ii) leads to an accurate and fast tracking of the machine speed reference ${\omega }_{m,\mathrm{ref}}$. Moreover, additional anti-windup (AWU) and saturation (SAT) strategies are applied to enhance the control performance further.

The paper is organized as follows: Section 2 discusses the nonlinear dynamics of the system. These dynamics will be linearized via Taylor series expansion in Section 3. In Section 4 the (linearized) dynamics will be analyzed with respect to closed-loop system stability. Section 5 proposes a tuning rule for PI-controller parameter design including the AWU & SAT strategies. Finally, in Section 6, simulation results illustrate the theoretical results.

2. Dynamics of the System

Control objective is tracking of a machine speed reference ${\omega }_{m,\mathrm{ref}}$ in regime II.5 via a proportional-integral (PI) controller. For the analysis, the machine torque reference $m_{m,\mathrm{ref}}$ is considered as control input, i.e., the control law is given by

$$\begin{array}{c}\hfill m_{m,\mathrm{ref}}\left(t\right)=k_i{x}_i\left(t\right)+k_p\left({\omega }_{m,\mathrm{ref}}\left(t\right)-{\omega }_m\left(t\right)\right)\end{array}$$

(1)

with proportional gain $k_p$ (in $\frac{\mathrm{Nms}}{\mathrm{rad}}$), integral gain $k_i$ (in $\frac{\mathrm{Nm}}{\mathrm{rad}}$) and integral state $x_i$ (in $\mathrm{rad}$). The dynamics of the integral state $x_i$ are

$$\begin{array}{c}\hfill \frac{\mathrm{d}}{\mathrm{d}t}{x}_i\left(t\right)={\omega }_{m,\mathrm{ref}}\left(t\right)-{\omega }_m\left(t\right)=:f_{x_i}\left({\omega }_m,{\omega }_{m,\mathrm{ref}}\right),x_{i,0}=x_i\left(0\right).\end{array}$$

(2)

Hence, the tuning parameters are $k_p$ and $k_i$ which must be chosen carefully and properly to achieve a stable closed-loop system with good tracking performance. Stability analysis and controller design (tuning) are presented in Section 4 and Section 5, respectively.

2.1. Dynamics of the Mechanics

For the dynamics of the machine speed ${\omega }_m$ with initial value ${\omega }_{m,0}={\omega }_m\left(0\right)$ the following holds:

$$\begin{array}{cc}\hfill \frac{\mathrm{d}}{\mathrm{d}t}{\omega }_m\left(t\right)& =\frac{1}{\theta }\left(\frac{m_t\left(t\right)}{g_b}-m_m\left(t\right)\right)\hfill \\ \hfill & =\frac{1}{\theta }\left(\frac{1}{2}{\rho }_w{r}_t^2\pi {v_w\left(t\right)}^3\frac{c_p\left({\lambda }_t({\omega }_m,v_w),{\beta }_t\right)}{{\omega }_m\left(t\right)}-m_m\left(t\right)\right)=:f_{{\omega }_m}\left({\omega }_m,m_m,v_w,{\beta }_t\right),\hfill \end{array}$$

(3)

with total inertia $\theta >0$ (in $\mathrm{k}\mathrm{g} {\mathrm{m}}^2$), turbine torque $m_t$ (in $\mathrm{N}\mathrm{m}$), gear ratio $g_b>0$ (in 1), air density ${\rho }_w>0$ (in $\frac{\mathrm{kg}}{{\mathrm{m}}^3}$), turbine radius $r_t>0$ (in $\mathrm{m}$), wind speed $v_w>0$ (in $\frac{\mathrm{m}}{\mathrm{s}}$) and power factor curve $c_p\in {\mathcal{C}}^1$ (in 1) which depends on tip speed ratio ${\lambda }_t=\frac{r_t{\omega }_m}{g_b{v}_w}>0$ (in 1) and pitch angle ${\beta }_t$. (3) is a standard model of the machine speed dynamics in WTS and can e.g., be found in [16], ([17], Chapter 4).

2.2. Dynamics of the Underlying Control Loop of the Machine Torque

The capability to track the machine torque reference $m_{m,\mathrm{ref}}$ results from an underlying control loop of the machine torque (based on machine current control via a voltage source inverter and pulse-width modulation). The dynamics of the machine torque control are quite fast (compared to those of the mechanics) and are approximated via the first-order lag system (see e.g., [6])

$$\begin{array}{cc}\hfill \frac{\mathrm{d}}{\mathrm{d}t}{m}_m\left(t\right)& \stackrel{\phantom{\left(\right)}}{=}-\frac{1}{T_{cl}}{m}_m\left(t\right)+\frac{V_{cl}}{T_{cl}}{m}_{m,\mathrm{ref}}\left(t\right)\hfill \\ \hfill & \stackrel{\left(1\right)}{=}-\frac{1}{T_{cl}}{m}_m\left(t\right)+\frac{k_i{V}_{cl}}{T_{cl}}{x}_i\left(t\right)+\frac{k_p{V}_{cl}}{T_{cl}}\left({\omega }_{m,\mathrm{ref}}\left(t\right)-{\omega }_m\left(t\right)\right)=:f_{m_m}\left({\omega }_m,m_m,x_i,{\omega }_{m,\mathrm{ref}}\right)\hfill \end{array}$$

(4)

with initial value $m_{m,0}=m_m\left(0\right)$, gain $V_{cl}>0$ (in 1) and time constant $0<T_{cl}\ll 1\mathrm{s}$. A well designed machine torque controller yields $V_{cl}=1$.

2.3. Overall Dynamics

By introducing state vector $\mathit{x}:={\left({\omega }_m,m_m,x_i\right)}^{\top }$, disturbance vector $\mathit{d}:={\left(v_w,{\beta }_t\right)}^{\top }$, reference input $v:={\omega }_{m,\mathrm{ref}}$ and output $y:={\omega }_m$, the overall (nonlinear) system dynamics can be written as

$$\begin{array}{c}\hfill \frac{\mathrm{d}}{\mathrm{d}t}\mathit{x}\left(t\right)=\mathit{f}\left(\mathit{x}\left(t\right),v\left(t\right),\mathit{d}\left(t\right)\right),{\mathit{x}}_0=\mathit{x}\left(0\right)\mathrm{and}y\left(t\right)=\left(\begin{array}{ccc}1& 0& 0\end{array}\right)\mathit{x}\left(t\right)=:{\mathit{c}}^{\top }\mathit{x}\left(t\right)\end{array}$$

(5)

with $\mathit{f}\left(\mathit{x},v,\mathit{d}\right):={\left(f_{{\omega }_m}\left({\omega }_m,m_m,v_w,{\beta }_t\right),f_{m_m}\left({\omega }_m,m_m,x_i,{\omega }_{m,\mathrm{ref}}\right),f_{x_i}\left({\omega }_m,{\omega }_{m,\mathrm{ref}}\right)\right)}^{\top }$.

3. Linearization

The dynamics of system (5) will be linearized via Taylor series expansion around the operation point $\star :=\left({\omega }_m^{\star },m_m^{\star },x_i^{\star },{\omega }_{m,\mathrm{ref}}^{\star },v_w^{\star },{\beta }_t^{\star }\right)$. Hence, the following small-signal approximations are defined:

$${\tilde{\omega }}_m:={\omega }_m-{\omega }_m^{\star },{\tilde{m}}_m:=m_m-m_m^{\star },{\tilde{x}}_i:=x_i-x_i^{\star },{\tilde{\omega }}_{m,\mathrm{ref}}:={\omega }_{m,\mathrm{ref}}-{\omega }_{m,\mathrm{ref}}^{\star },{\tilde{v}}_w:=v_w-v_w^{\star },{\tilde{\beta }}_t:={\beta }_t-{\beta }_t^{\star }.$$

Applying the Taylor series expansion to system (5) yields

$$\begin{array}{cc}\hfill \frac{\mathrm{d}}{\mathrm{d}t}\tilde{\mathit{x}}\left(t\right)& =\frac{\mathrm{d}}{\mathrm{d}t}\left(\mathit{x}\left(t\right)-{\mathit{x}}^{\star }\left(t\right)\right)=\frac{\mathrm{d}}{\mathrm{d}t}\mathit{x}\left(t\right)-\frac{\mathrm{d}}{\mathrm{d}t}{\mathit{x}}^{\star }\left(t\right)\hfill \\ \hfill & =\underset{=\frac{\mathrm{d}}{\mathrm{d}t}{\mathit{x}}^{\star }}{\underbrace{\mathit{f}(\star )}}+\underset{=:{\mathit{A}}^{\star }}{\underbrace{\frac{\partial \mathit{f}\left(\mathit{x},v,\mathit{d}\right)}{\partial \mathit{x}}{|}_{\star }}}\tilde{\mathit{x}}\left(t\right)+\underset{=:\mathit{b}}{\underbrace{\frac{\partial \mathit{f}\left(\mathit{x},v,\mathit{d}\right)}{\partial v}{|}_{\star }}}\tilde{v}\left(t\right)+\underset{=:{\mathit{E}}^{\star }}{\underbrace{\frac{\partial \mathit{f}\left(\mathit{x},v,\mathit{d}\right)}{\partial \mathit{d}}{|}_{\star }}}\tilde{\mathit{d}}\left(t\right)+\delta \left(t\right)-\frac{\mathrm{d}}{\mathrm{d}t}{\mathit{x}}^{\star }\left(t\right)\hfill \end{array}$$

(6)

with initial values ${\tilde{\mathit{x}}}_0=\tilde{\mathit{x}}\left(0\right)$, ${\mathit{A}}^{\star }:=\mathit{A}({\omega }_m^{\star },v_w^{\star },{\beta }_t^{\star })$ and ${\mathit{E}}^{\star }:=\mathit{E}({\omega }_m^{\star },v_w^{\star },{\beta }_t^{\star })$. The term $\delta \left(t\right):=\delta (\tilde{\mathit{x}}\left(t\right),\tilde{v}\left(t\right),\tilde{\mathit{d}}\left(t\right),\star )$ characterizes the higher order terms of the Taylor series. Imposing the following

Assumption 1.

The higher order terms of the Taylor series are neglected, i.e., $\delta \left(t\right)=0$

Allows to approximate the nonlinear system (5) by its small signal (linearized) dynamics

$$\begin{array}{c}\hfill \frac{\mathrm{d}}{\mathrm{d}t}\tilde{\mathit{x}}\left(t\right)={\mathit{A}}^{\star }\tilde{\mathit{x}}\left(t\right)+\mathit{b}\tilde{v}\left(t\right)+{\mathit{E}}^{\star }\tilde{\mathit{d}}\left(t\right),{\tilde{\mathit{x}}}_0=\tilde{\mathit{x}}\left(0\right)\mathrm{and}\tilde{y}\left(t\right)={\mathit{c}}^{\top }\tilde{\mathit{x}}\left(t\right)\end{array}$$

(7)

where system matrix ${\mathit{A}}^{\star }$, input vector $\mathit{b}$ and disturbance matrix ${\mathit{E}}^{\star }$ are given by

$$\begin{array}{c}\hfill {\mathit{A}}^{\star }=\left[\begin{array}{ccc}{\mathsf{\Omega }}_{{\omega }_m}^{\star }& -\frac{1}{\theta }& 0\\ -\frac{k_p{V}_{cl}}{T_{cl}}& -\frac{1}{T_{cl}}& \frac{k_i{V}_{cl}}{T_{cl}}\\ -1& 0& 0\end{array}\right],\mathit{b}=\left(\begin{array}{c}0\\ \frac{k_p{V}_{cl}}{T_{cl}}\\ 1\end{array}\right)\mathrm{and}{\mathit{E}}^{\star }=\left[\begin{array}{cc}{\mathsf{\Omega }}_{v_w}^{\star }& {\mathsf{\Omega }}_{{\beta }_t}^{\star }\\ 0& 0\\ 0& 0\end{array}\right]\end{array}$$

(8)

and the following definition holds: ${\mathsf{\Omega }}_{\alpha }^{\star }:={\mathsf{\Omega }}_{\alpha }({\omega }_m^{\star },v_w^{\star },{\beta }_t^{\star }):=\frac{\partial f_{{\omega }_m}\left({\omega }_m,m_m,v_w,{\beta }_t\right)}{\partial \alpha }{|}_{\star },\alpha \in \{{\omega }_m,v_w,{\beta }_t\}$.

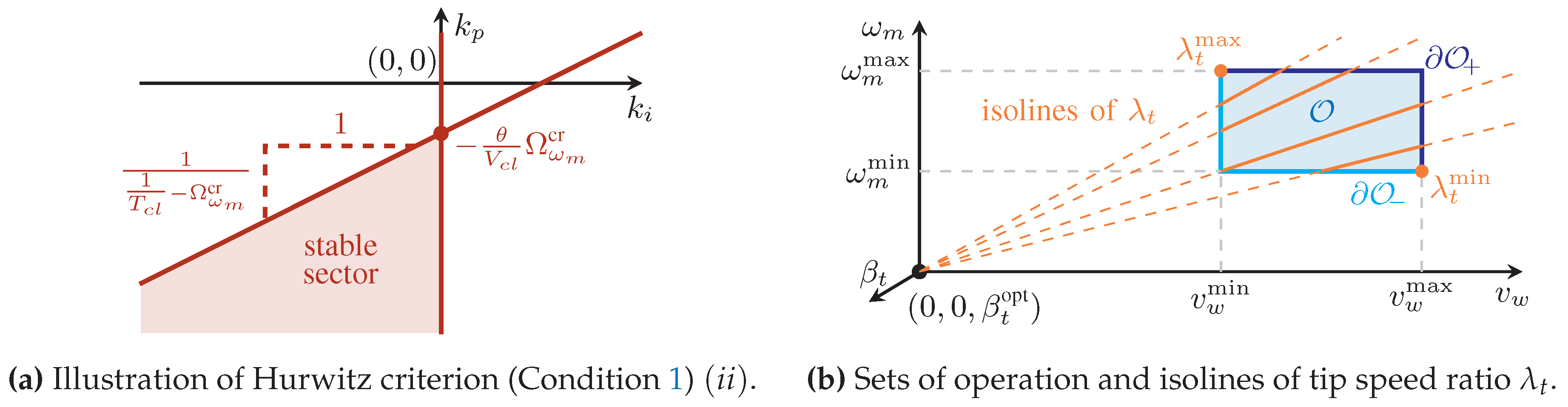
4. Stability Analysis

In this section, based on the linearization above, a local stability analysis is performed. One obtains the following stability condition:

Condition 1.

The linearized closed-loop system (7), (8) of the machine speed control is stable, if and only if the following holds:

$$\left(i\right){\mathsf{\Omega }}_{{\omega }_m}^{\star }<\frac{1}{T_{cl}}\wedge \left(ii\right)k_p<-\frac{\theta }{V_{cl}}{\mathsf{\Omega }}_{{\omega }_m}^{\star }+\frac{k_i}{\frac{1}{T_{cl}}-{\mathsf{\Omega }}_{{\omega }_m}^{\star }}\wedge \left(iii\right)k_i<0.$$

Proof of Condition 1.

The characteristic polynomial ${\chi }_{{\phantom{x}}_{{\mathit{A}}^{\star }}}$ of the system matrix ${\mathit{A}}^{\star }$ of system (7), (8) is given by

$$\begin{array}{cc}\hfill {\chi }_{{\phantom{x}}_{{\mathit{A}}^{\star }}}(\lambda ,\star )& \stackrel{\left(8\right)}{=}det\left(\lambda {\mathit{I}}_3-{\mathit{A}}^{\star }\right)=det\left[\begin{array}{ccc}\lambda -{\mathsf{\Omega }}_{{\omega }_m}^{\star }& \frac{1}{\theta }& 0\\ \frac{k_p{V}_{cl}}{T_{cl}}& \lambda +\frac{1}{T_{cl}}& -\frac{k_i{V}_{cl}}{T_{cl}}\\ 1& 0& \lambda \end{array}\right]\hfill \\ \hfill & \stackrel{\phantom{\left(\right)}}{=}{\lambda }^3+{\lambda }^2\underset{=:a_2({\omega }_m^{\star },v_w^{\star },{\beta }_t^{\star })=:a_2^{\star }}{\underbrace{\left(\frac{1}{T_{cl}}-{\mathsf{\Omega }}_{{\omega }_m}^{\star }\right)}}+{\lambda }^1\underset{=:a_1({\omega }_m^{\star },v_w^{\star },{\beta }_t^{\star })=:a_1^{\star }}{\underbrace{\left(-\frac{{\mathsf{\Omega }}_{{\omega }_m}^{\star }}{T_{cl}}-\frac{k_p{V}_{cl}}{\theta T_{cl}}\right)}}+{\lambda }^0\underset{=:a_0}{\underbrace{\left(-\frac{k_i{V}_{cl}}{\theta T_{cl}}\right)}}.\hfill \end{array}$$

(9)

In view of Hurwitz’s theorem (see e.g., ([18], Chapter 8), ([19], Chapter 1)), system (7), (8) is stable, if and only if (a) $a_2^{\star }>0\wedge a_1^{\star }>0\wedge a_0>0$ and (b) $a_2^{\star }{a}_1^{\star }-a_0>0$ hold. Clearly, because of $\theta >0$, $V_{cl}>0$ and $T_{cl}>0$, the inequalities $a_2^{\star }>0$ and $a_0>0$ result in $\left(i\right)$ and $\left(iii\right)$ of Condition 1. $a_1^{\star }>0$ necessitates the condition $k_p<-\frac{\theta }{V_{cl}}{\mathsf{\Omega }}_{{\omega }_m}^{\star }$ which is already satisfied if $\left(ii\right)$ holds, since

$$\begin{array}{c}\hfill k_p\stackrel{\left(ii\right)}{<}-\frac{\theta }{V_{cl}}{\mathsf{\Omega }}_{{\omega }_m}^{\star }+\frac{k_i}{\frac{1}{T_{cl}}-{\mathsf{\Omega }}_{{\omega }_m}^{\star }}\stackrel{\left(i\right),\left(iii\right)}{<}-\frac{\theta }{V_{cl}}{\mathsf{\Omega }}_{{\omega }_m}^{\star }\end{array}$$

(10)

The term $a_2^{\star }{a}_1^{\star }-a_0$ is given by

$$\begin{array}{c}\hfill 0<a_2^{\star }{a}_1^{\star }-a_0\stackrel{\left(9\right)}{=}\frac{1}{T_{cl}}{\left({\mathsf{\Omega }}_{{\omega }_m}^{\star }\right)}^2-\left(\frac{1}{T_{cl}^2}-\frac{k_p{V}_{cl}}{\theta T_{cl}}\right){\mathsf{\Omega }}_{{\omega }_m}^{\star }-\frac{k_p{V}_{cl}}{\theta T_{cl}^2}+\frac{k_i{V}_{cl}}{\theta T_{cl}}.\end{array}$$

(11)

Multiplying (11) by $\frac{\theta T_{cl}}{V_{cl}}>0$ yields

$$\begin{array}{cc}\hfill \frac{\theta }{V_{cl}}{\left({\mathsf{\Omega }}_{{\omega }_m}^{\star }\right)}^2-\left(\frac{\theta }{T_{cl}{V}_{cl}}-k_p\right){\mathsf{\Omega }}_{{\omega }_m}^{\star }-\frac{k_p}{T_{cl}}+k_i& \stackrel{\left(11\right)}{>}0,\hfill \end{array}$$

(12)

which results in $\left(ii\right)$, since rearranging (12) leads to

$$\begin{array}{c}\hfill k_p<\frac{-\frac{\theta }{V_{cl}}{\left({\mathsf{\Omega }}_{{\omega }_m}^{\star }\right)}^2+\frac{\theta }{V_{cl}{T}_{cl}}{\mathsf{\Omega }}_{{\omega }_m}^{\star }-k_i}{{\mathsf{\Omega }}_{{\omega }_m}^{\star }-\frac{1}{T_{cl}}}=-\frac{\theta }{V_{cl}}{\mathsf{\Omega }}_{{\omega }_m}^{\star }+\frac{k_i}{\frac{1}{T_{cl}}-{\mathsf{\Omega }}_{{\omega }_m}^{\star }}.\end{array}$$

(13)

 ☐

Remark 1.

A physical interpretation of Condition 1 is the following: $\left(iii\right)$ must hold, since the integral gain $x_i$ has to act with correct sign. Moreover, the underlying machine torque control loop has to be faster than the outer control loop of the machine speed. This results in $\left(i\right)$ where the time constant $T_{cl}$ of the torque control loop leads to an upper bound on $\frac{1}{T_{cl}}$ for ${\mathsf{\Omega }}_{{\omega }_m}^{\star }$. $\left(ii\right)$ characterizes the impact of integral $k_i$ and proportional $k_p$ gain on closed-loop stability.

Sub-conditions $\left(i\right)$ and $\left(ii\right)$ depend on ${\mathsf{\Omega }}_{{\omega }_m}^{\star }$ and, consequently, on the operation point $({\omega }_m^{\star },v_w^{\star },{\beta }_t^{\star })$. Since it is necessary that $\left(i\right)$ and $\left(ii\right)$ are fulfilled for all possible operation points $({\omega }_m^{\star },v_w^{\star },{\beta }_t^{\star })$, the most critical operation point $({\omega }_m^{\mathrm{cr}},v_w^{\mathrm{cr}},{\beta }_t^{\mathrm{cr}})$ needs to be considered for the design of the controller parameters $k_p$ and $k_i$ (worst-case analysis). Figure 2a illustrates the sector of all feasible $k_p$ and $k_i$ which yield a (locally) stable closed-loop system (7), (8).

Condition 2.

For the critical operation point the following holds:

$$\begin{array}{c}\hfill {\mathsf{\Omega }}_{{\omega }_m}^{cr}:=\underset{({\omega }_m^{\star },v_w^{\star },{\beta }_t^{\star })}{max}{\mathsf{\Omega }}_{{\omega }_m}({\omega }_m^{\star },v_w^{\star },{\beta }_t^{\star })\iff ({\omega }_m^{cr},v_w^{cr},{\beta }_t^{cr}):=\underset{({\omega }_m^{\star },v_w^{\star },{\beta }_t^{\star })}{argmax}{\mathsf{\Omega }}_{{\omega }_m}({\omega }_m^{\star },v_w^{\star },{\beta }_t^{\star })\end{array}$$

(14)

Thus, the maximal value ${\mathsf{\Omega }}_{{\omega }_m}^{\mathrm{cr}}$ of all possible ${\mathsf{\Omega }}_{{\omega }_m}^{\star }$ is the most critical one.

Proof of Condition 2.

The calculation of the derivative of the right term of $\left(ii\right)$ with respect to ${\mathsf{\Omega }}_{{\omega }_m}^{\star }$ yields

$$\begin{array}{c}\hfill \frac{\partial }{\partial {\mathsf{\Omega }}_{{\omega }_m}^{\star }}\left(-\frac{\theta }{V_{cl}}{\mathsf{\Omega }}_{{\omega }_m}^{\star }+\frac{k_i}{\frac{1}{T_{cl}}-{\mathsf{\Omega }}_{{\omega }_m}^{\star }}\right)=-\frac{\theta }{V_{cl}}+\frac{k_i}{{\left(\frac{1}{T_{cl}}-{\mathsf{\Omega }}_{{\omega }_m}^{\star }\right)}^2}\stackrel{\left(iii\right)}{<}-\frac{\theta }{V_{cl}}<0\end{array}$$

(15)

Thus, the derivative in (15) is strictly negative and, accordingly, the greater ${\mathsf{\Omega }}_{{\omega }_m}^{\star }$ the smaller is the right term of $\left(ii\right)$. Hence, for the most critical choice of ${\mathsf{\Omega }}_{{\omega }_m}^{\mathrm{cr}}$, the inequalities $k_p<-\frac{\theta }{V_{cl}}{\mathsf{\Omega }}_{{\omega }_m}^{\mathrm{cr}}+\frac{k_i}{\frac{1}{T_{cl}}-{\mathsf{\Omega }}_{{\omega }_m}^{\mathrm{cr}}}<-\frac{\theta }{V_{cl}}{\mathsf{\Omega }}_{{\omega }_m}^{\star }+\frac{k_i}{\frac{1}{T_{cl}}-{\mathsf{\Omega }}_{{\omega }_m}^{\star }}$ and ${\mathsf{\Omega }}_{{\omega }_m}^{\star }<{\mathsf{\Omega }}_{{\omega }_m}^{\mathrm{cr}}\stackrel{\left(i\right)}{<}\frac{1}{T_{cl}}$ hold for any operation point. ☐

In regime II.5—where the PI-controller is used—the pitch angle ${\beta }_t$ is controlled to its optimal (but constant) value, i.e., ${\beta }_t^{\star }={\beta }_t^{\mathrm{opt}}={\beta }_t^{\mathrm{cr}}$. Consequently, in regime II.5, the following holds: $({\omega }_m^{\star },v_w^{\star },{\beta }_t^{\star })\in \mathcal{O}=[{\omega }_m^{min},{\omega }_m^{max}]\times [v_w^{min},v_w^{max}]\times \left\{{\beta }_t^{\mathrm{opt}}\right\}$. By defining the boundary $\partial \mathcal{O}:=\partial {\mathcal{O}}_{+}\vee \partial {\mathcal{O}}_{-}$ with $\partial {\mathcal{O}}_{+}:=\left\{{\omega }_m^{max}\right\}\times [v_w^{min},v_w^{max}]\times \left\{{\beta }_t^{\mathrm{opt}}\right\}\vee [{\omega }_m^{min},{\omega }_m^{max}]\times \left\{v_w^{max}\right\}\times \left\{{\beta }_t^{\mathrm{opt}}\right\}$ and $\partial {\mathcal{O}}_{-}:=\left\{{\omega }_m^{min}\right\}\times [v_w^{min},v_w^{max})\times \left\{{\beta }_t^{\mathrm{opt}}\right\}\vee [{\omega }_m^{min},{\omega }_m^{max})\times \left\{v_w^{min}\right\}\times \left\{{\beta }_t^{\mathrm{opt}}\right\}$, as illustrated in Figure 2b, the following holds:

Condition 3.

The set—where the critical operation point $({\omega }_m^{cr},v_w^{cr},{\beta }_t^{cr})$ is located in—is given by

$$\begin{array}{c}\hfill ({\omega }_m^{cr},v_w^{cr},{\beta }_t^{cr})\in \left\{\begin{array}{cc}\partial {\mathcal{O}}_{+}\hfill & ,if\exists ({\omega }_m^{\star },v_w^{\star },{\beta }_t^{\star })\in \mathcal{O}suchthat{\mathsf{\Omega }}_{{\omega }_m}^{\star }\ge 0\hfill \\ \partial {\mathcal{O}}_{-}\hfill & ,if{\mathsf{\Omega }}_{{\omega }_m}^{\star }<0\forall ({\omega }_m^{\star },v_w^{\star },{\beta }_t^{\star })\in \mathcal{O}\hfill \end{array}\right.\end{array}$$

(16)

Proof of Condition 3.

In regime II.5, the set Λ of all possible operation points of the tip speed ratio ${\lambda }_t^{\star }:={\lambda }_t({\omega }_m^{\star },v_w^{\star })$ results in $\mathsf{\Lambda }=[{\lambda }_t^{min},{\lambda }_t^{max}]$ with ${\lambda }_t^{min}:=\frac{r_t{\omega }_m^{min}}{g_b{v}_w^{max}}$ and ${\lambda }_t^{max}:=\frac{r_t{\omega }_m^{max}}{g_b{v}_w^{min}}$. Hence, both $\partial {\mathcal{O}}_{+}$ and $\partial {\mathcal{O}}_{-}$ cover all ${\lambda }_t^{\star }\in \mathsf{\Lambda }$ (see Figure 2b). By taking ${\beta }_t^{\star }={\beta }_t^{\mathrm{opt}}$ and ${\lambda }_t^{\mathrm{cr}}:=\frac{r_t{\omega }_m^{\mathrm{cr}}}{g_b{v}_w^{\mathrm{cr}}}\in \mathsf{\Lambda }$ into account, ${\mathsf{\Omega }}_{{\omega }_m}^{\star }$ is finally given by

$$\begin{array}{cc}\hfill {\mathsf{\Omega }}_{{\omega }_m}^{\star }& \stackrel{\left(3\right)}{=}{v}_w^{\star }\stackrel{=:F_{v_w}\left({\lambda }_t^{\star }\right)}{\overbrace{\frac{{\rho }_w{r}_t^4\pi }{2g_b^2\theta }\frac{{\lambda }_t^{\star }\frac{\partial c_p\left({\lambda }_t^{\star },{\beta }_t^{\mathrm{opt}}\right)}{\partial {\lambda }_t^{\star }}-c_p\left({\lambda }_t^{\star },{\beta }_t^{\star }\right)}{{\left({\lambda }_t^{\star }\right)}^2}}}={\omega }_m^{\star }\stackrel{=:F_{{\omega }_m}\left({\lambda }_t^{\star }\right)}{\overbrace{\frac{{\rho }_w{r}_t^5\pi }{2g_b^3\theta }\frac{{\lambda }_t^{\star }\frac{\partial c_p\left({\lambda }_t^{\star },{\beta }_t^{\mathrm{opt}}\right)}{\partial {\lambda }_t^{\star }}-c_p\left({\lambda }_t^{\star },{\beta }_t^{\star }\right)}{{\left({\lambda }_t^{\star }\right)}^3}}}\hfill \\ \hfill & \le \left\{\begin{array}{l}\begin{array}{cc}{v}_w^{max}{F}_{v_w}\left({\lambda }_t^{\mathrm{cr}}\right)\hfill & ,\mathrm{if}{F}_{v_w}\left({\lambda }_t^{\mathrm{cr}}\right)\ge 0\wedge {\lambda }_t^{\mathrm{cr}}\in [{\lambda }_t^{min},\frac{r_t{\omega }_m^{max}}{g_b{v}_w^{max}}]\hfill \\ {\omega }_m^{max}{F}_{{\omega }_m}\left({\lambda }_t^{\mathrm{cr}}\right)\hfill & ,\mathrm{if}{F}_{{\omega }_m}\left({\lambda }_t^{\mathrm{cr}}\right)\ge 0\wedge {\lambda }_t^{\mathrm{cr}}\in (\frac{r_t{\omega }_m^{max}}{g_b{v}_w^{max}},{\lambda }_t^{max}]\hfill \end{array}\}\equiv \mathrm{line}1\mathrm{in}(16)\\ \begin{array}{cc}{v}_w^{min}{F}_{v_w}\left({\lambda }_t^{\mathrm{cr}}\right)\hfill & ,\mathrm{if}{F}_{v_w}\left({\lambda }_t^{\mathrm{cr}}\right)<0\wedge {\lambda }_t^{\mathrm{cr}}\in [\frac{r_t{\omega }_m^{min}}{g_b{v}_w^{min}},{\lambda }_t^{max}]\hfill \\ {\omega }_m^{min}{F}_{{\omega }_m}\left({\lambda }_t^{\mathrm{cr}}\right)\hfill & ,\mathrm{if}{F}_{{\omega }_m}\left({\lambda }_t^{\mathrm{cr}}\right)<0\wedge {\lambda }_t^{\mathrm{cr}}\in [{\lambda }_t^{min},\frac{r_t{\omega }_m^{min}}{g_b{v}_w^{min}})\hfill \end{array}\}\equiv \mathrm{line}2\mathrm{in}(16).\end{array}\right.\hfill \end{array}$$

(17)

Consequently, (17) is equivalent to (Condition 3). ☐

5. Controller Design

In this section, the stability condition is translated into a simple tuning rule for the PI-controller parameters.

5.1. Controller Parameter Tuning

The following tuning rule for the parameters $k_p$ and $k_i$ of the PI-controller is based on pole placement. The closed-loop poles of the (linearized) system (7), (8) are specified by some desired (real and negative) poles ${\lambda }_1\le {\lambda }_2\le {\lambda }_3<0$ which leads to the desired polynomial

$$\begin{array}{c}\hfill {\chi }_{\mathrm{des}}\left(\lambda \right):=(\lambda -{\lambda }_1)(\lambda -{\lambda }_2)(\lambda -{\lambda }_3)={\lambda }^3-{\lambda }^2\left({\lambda }_1+{\lambda }_2+{\lambda }_3\right)+\lambda ({\lambda }_1{\lambda }_2+{\lambda }_1{\lambda }_3+{\lambda }_2{\lambda }_3)-{\lambda }_1{\lambda }_2{\lambda }_3.\end{array}$$

(18)

Note that the closed-loop poles of (7), (8) can not be chosen independently; since, comparing the coefficients of the characteristic ${\chi }_{{\phantom{x}}_{{\mathit{A}}^{\star }}}$ and desired ${\chi }_{\mathrm{des}}$ polynomial (see (9) and (18)) yields the following overdetermined equation system with three equations but only two free design parameters $k_p$ and $k_i$:

$$\begin{array}{c}\hfill \left.\begin{array}{cc}\hfill -{\lambda }_1-{\lambda }_2-{\lambda }_3& =\frac{1}{T_{cl}}-{\mathsf{\Omega }}_{{\omega }_m}^{\mathrm{cr}}\hfill \\ \hfill {\lambda }_1{\lambda }_2+{\lambda }_1{\lambda }_3+{\lambda }_2{\lambda }_3& =-\frac{{\mathsf{\Omega }}_{{\omega }_m}^{\mathrm{cr}}}{T_{cl}}-\frac{k_p{V}_{cl}}{\theta T_{cl}}\hfill \\ \hfill -{\lambda }_1{\lambda }_2{\lambda }_3& =-\frac{k_i{V}_{cl}}{\theta T_{cl}}\hfill \end{array}\right\}.\end{array}$$

(19)

To guarantee (local) stability for all possible operation points, the comparison of the coefficients in (19) is accomplished for the critical operation point $({\omega }_m^{\mathrm{cr}},v_w^{\mathrm{cr}},{\beta }_t^{\mathrm{cr}})$. For the tuning of the parameters $k_p$ and $k_i$, ${\lambda }_1\le {\lambda }_2\le {\lambda }_3<0$ and (19) have to be fulfilled. Therefore, the following tuning rule

$$\begin{array}{c}\begin{array}{c}{k}_p=-\left(1-\kappa \right)\left(\frac{3}{4}\kappa +\frac{1}{4}\right)\frac{\theta T_{cl}}{V_{cl}}{\left(\frac{1}{T_{cl}}-{\mathsf{\Omega }}_{{\omega }_m}^{\mathrm{cr}}\right)}^2-\frac{\theta {\mathsf{\Omega }}_{{\omega }_m}^{\mathrm{cr}}}{V_{cl}}\hfill \\ k_i=-\frac{1}{4}\kappa {\left(1-\kappa \right)}^2\frac{\theta T_{cl}}{V_{cl}}{\left(\frac{1}{T_{cl}}-{\mathsf{\Omega }}_{{\omega }_m}^{\mathrm{cr}}\right)}^3\hfill \end{array}\hfill \end{array}\}\mathrm{with}\kappa \in (0,1).$$

(20)

for $k_p$ and $k_i$ is proposed, where $\kappa \in (0,1)$ is a single free design parameter which assures local stability and can be adjusted to achieve good tracking performance.

Remark 2.

The choice of the control parameters $k_p$ and $k_i$ as in (20) gives the closed-loop poles ${\lambda }_1=-\kappa \left(\frac{1}{T_{cl}}-{\mathsf{\Omega }}_{{\omega }_m}^{\mathrm{cr}}\right)\stackrel{\left(i\right)}{<}0$ and ${\lambda }_2={\lambda }_3=-\frac{1}{2}\left(1-\kappa \right)\left(\frac{1}{T_{cl}}-{\mathsf{\Omega }}_{{\omega }_m}^{\mathrm{cr}}\right)\stackrel{\left(i\right)}{<}0$, which are clearly negative.

Proof of Remark 2.

Inserting the closed-loop poles of (Remark 2) into (19) yields

$$\begin{array}{c}\hfill \left.\begin{array}{ccc}\hfill -{\lambda }_1-{\lambda }_2-{\lambda }_3=& \left(\kappa +\frac{1}{2}\left(1-\kappa \right)+\frac{1}{2}\left(1-\kappa \right)\right)\left(\frac{1}{T_{cl}}-{\mathsf{\Omega }}_{{\omega }_m}^{\mathrm{cr}}\right)& =\frac{1}{T_{cl}}-{\mathsf{\Omega }}_{{\omega }_m}^{\mathrm{cr}}\hfill \\ \hfill {\lambda }_1{\lambda }_2+{\lambda }_1{\lambda }_3+{\lambda }_2{\lambda }_3=& \left(\kappa \frac{1}{2}\left(1-\kappa \right)+\kappa \frac{1}{2}\left(1-\kappa \right)+\frac{1}{4}{\left(1-\kappa \right)}^2\right){\left(\frac{1}{T_{cl}}-{\mathsf{\Omega }}_{{\omega }_m}^{\mathrm{cr}}\right)}^2& =-\frac{{\mathsf{\Omega }}_{{\omega }_m}^{\mathrm{cr}}}{T_{cl}}-\frac{k_p{V}_{cl}}{\theta T_{cl}}\hfill \\ \hfill -{\lambda }_1{\lambda }_2{\lambda }_3=& \kappa \frac{1}{4}{\left(1-\kappa \right)}^2{\left(\frac{1}{T_{cl}}-{\mathsf{\Omega }}_{{\omega }_m}^{\mathrm{cr}}\right)}^3& =-\frac{k_i{V}_{cl}}{\theta T_{cl}}\hfill \end{array}\right\}.\end{array}$$

(21)

The first equation of (21) is automatically fulfilled. The second and third equation of (21) result in $\left(1-\kappa \right)\left(\frac{3}{4}\kappa +\frac{1}{4}\right){\left(\frac{1}{T_{cl}}-{\mathsf{\Omega }}_{{\omega }_m}^{\mathrm{cr}}\right)}^2\stackrel{!}{=}-\frac{{\mathsf{\Omega }}_{{\omega }_m}^{\mathrm{cr}}}{T_{cl}}-\frac{k_p{V}_{cl}}{\theta T_{cl}}$ and $\frac{1}{4}\kappa {\left(1-\kappa \right)}^2{\left(\frac{1}{T_{cl}}-{\mathsf{\Omega }}_{{\omega }_m}^{\mathrm{cr}}\right)}^3\stackrel{!}{=}-\frac{k_i{V}_{cl}}{\theta T_{cl}}$, respectively. This leads to the choice of $k_p$ and $k_i$ as in (20) with which (local) stability of system (7), (8) is guaranteed. ☐

5.2. Anti-Wind Up and Saturation

To enhance the PI-controller control performance, it is augmented by an additional anti-wind up (AWU) and saturation (SAT) block as shown in Figure 3, where the following holds (the idea of (22) is taken from [20], Chapter 14):

$$\begin{array}{cc}\left(\mathrm{AWU}\right)\hfill & \frac{\mathrm{d}}{\mathrm{d}t}{x}_i={\alpha }_i\left(t\right)\left({\omega }_{m,\mathrm{ref}}\left(t\right)-{\omega }_m\left(t\right)\right)\mathrm{with}{\alpha }_i\left(t\right)=\left\{\begin{array}{cc}0\hfill & ,\mathrm{if}{m}_{m,\mathrm{ref}}\left(t\right)\notin [m_m^{min},m_m^{max}]\hfill \\ 1\hfill & ,\mathrm{if}{m}_{m,\mathrm{ref}}\left(t\right)\in [m_m^{min},m_m^{max}]\hfill \end{array}\right.\hfill \\ \left(\mathrm{SAT}\right)\hfill & m_{m,\mathrm{ref}}^{\mathrm{sat}}\left(t\right)=max\left(m_m^{min},min\left(m_{m,\mathrm{ref}}\left(t\right),m_m^{max}\right)\right)\hfill \end{array}\}$$

(22)

where $m_m^{min}/m_m^{max}$ (in $\mathrm{N}\mathrm{m}$) are the minimal/maximal machine torque available in regime II.5. (AWU) and (SAT) take the saturated (available) machine torque in regime II.5 into account in order to avoid (i) unfeasible torques and (ii) windup effects (which would deteriorate the tracking performance, see [20], Chapter 14).

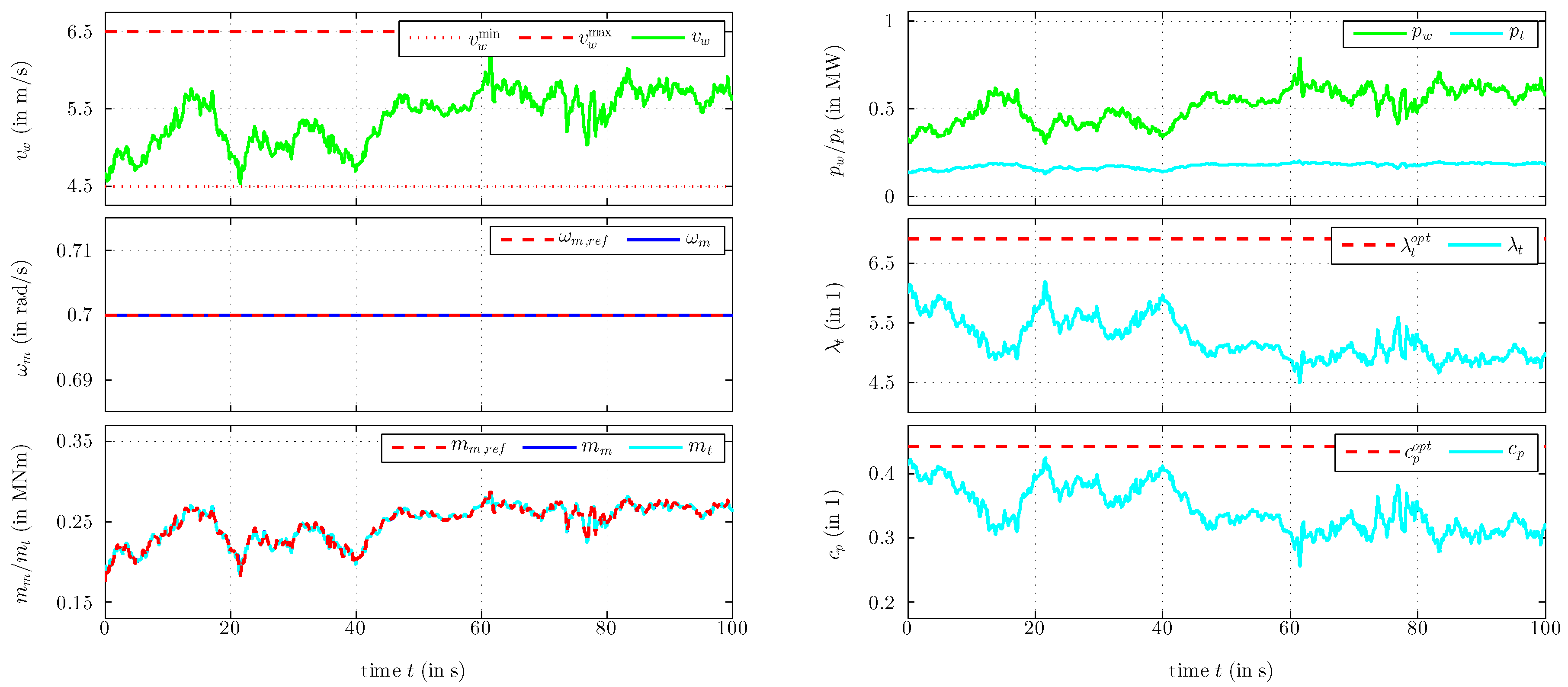
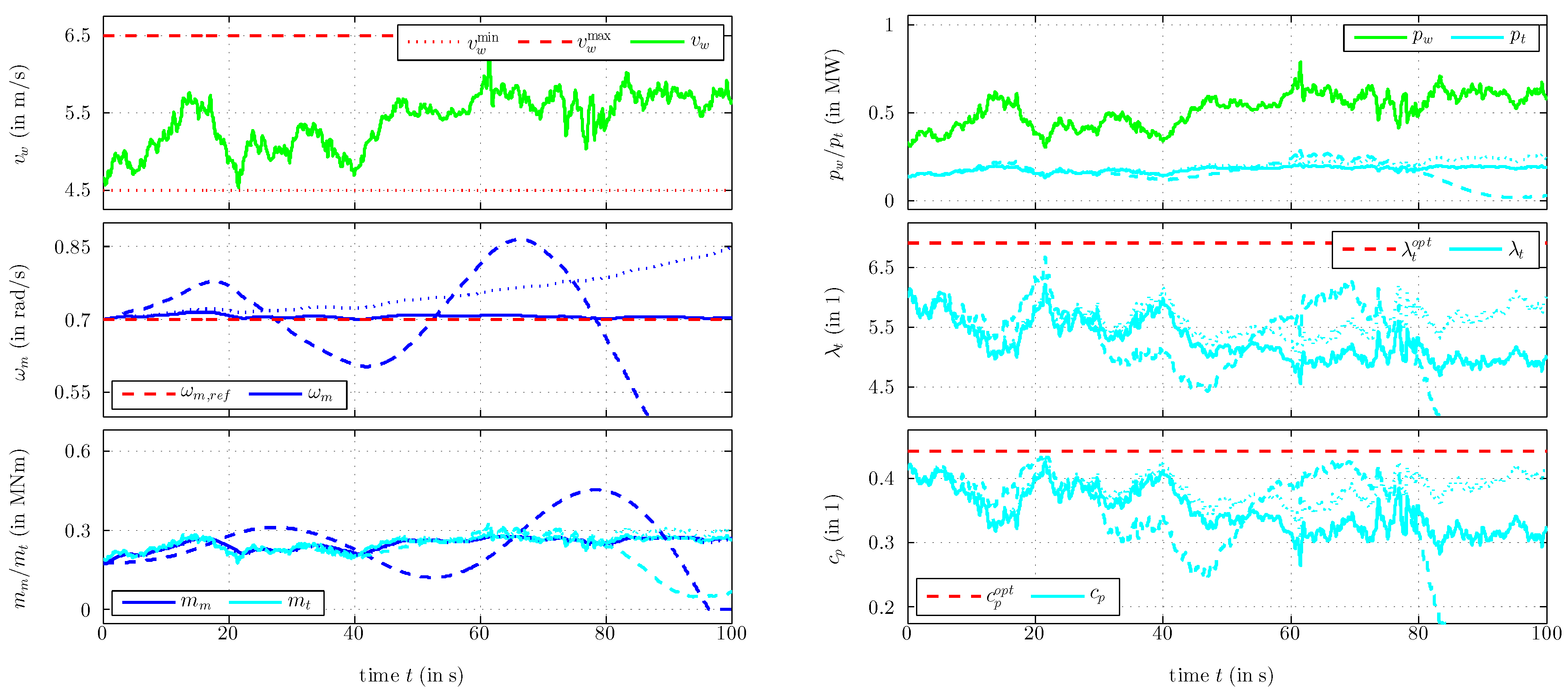
6. Simulation Results

In this section, the theoretical findings are illustrated by simulation results for four different scenarios:

• Scenario 1: Control performance for a constant but maximal speed reference to illustrate stability and set-point tracking control performance.
• Scenario 2: Control performance for an arbitrarily time-varying speed reference to illustrate stability and reference tracking control performance at different operation points.
• Scenario 3: Control performance for a constant but maximal speed reference for three different controller tunings to illustrate the effect of tuning on stability and set-point tracking control performance.
• Scenario 4: Control performance for an arbitrarily time-varying speed reference for three different controller tunings to illustrate the effect of tuning on stability and reference tracking control performance at different operation points.

All scenarios are fed by the same realistic wind speed profile. The control performance of all four scenarios is evaluated by the integral absolute error (IAE) performance measure. The IAE performance measure is computed by [20]

$$\begin{array}{c}\hfill \mathrm{IAE}\left(e\left(·\right)\right):={\int }_{t_{\mathrm{start}}}^{t_{\mathrm{end}}}\left|e\left(\tau \right)\right|\mathrm{d}\tau ={\int }_{0 \mathrm{s}}^{100 \mathrm{s}}|{\omega }_{m,\mathrm{ref}}\left(\tau \right)-{\omega }_m\left(\tau \right)|\mathrm{d}\tau .\end{array}$$

(23)

Figure 3 shows the implementation block diagram of controller and physical system in Matlab/Simulink. Simulation data is collected in

Table 1. System, implementation and controller data.

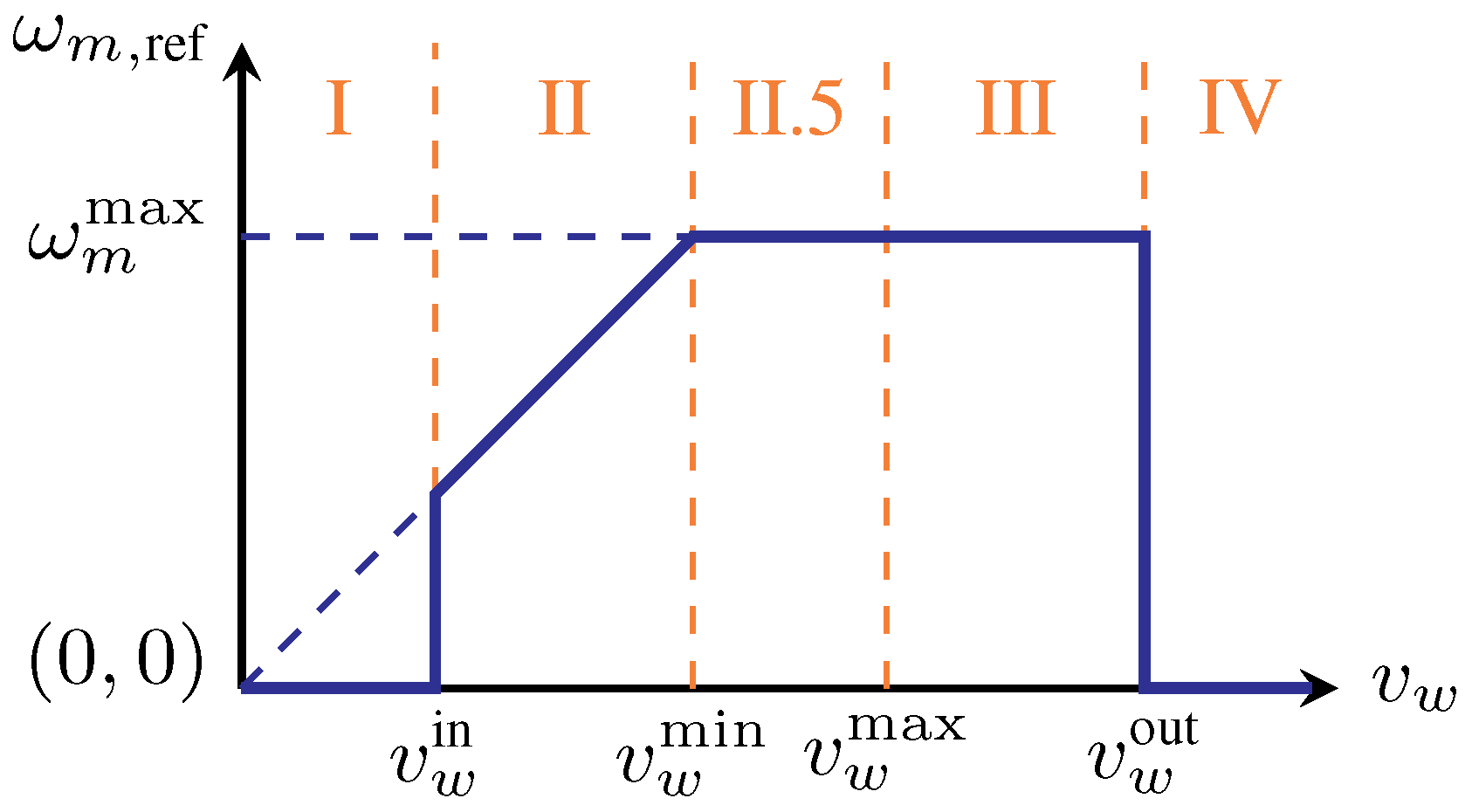
Description	Symbols & Values with Unit
Matlab/Simulink	solver (fixed step): ode4, sampling time $=5\times {10}^{-5} \mathrm{s}$ for model
	sampling time $=1\times {10}^{-3} \mathrm{s}$ for (discretized) controller implementation
WTS parameter	$r_t=40 \mathrm{m}$, $g_b=1$, ${\rho }_w=1.293\frac{\mathrm{kg}}{{\mathrm{m}}^3}$, $\theta =8.6\times {10}^6 \mathrm{k}\mathrm{g} {\mathrm{m}}^2$, $V_{cl}=1$, $T_{cl}=0.5\times {10}^{-3} \mathrm{s}$
Power factor	$c_1=0.73$, $c_2=151$, $c_3=0.58$, $c_4=0.002$, $c_5=13.2$, $c_6=18.4$, $c_7=2.14$
	$h({\lambda }_t({\omega }_m,v_w),{\beta }_t)=\frac{1}{{\lambda }_t({\omega }_m,v_w)-0.02}-\frac{0.003}{{\beta }_t^3+1}$, ${\beta }_t={\beta }_t^{\mathrm{opt}}=0{}^{\circ }$
Controller	$v_w^{min}=4.5\frac{\mathrm{m}}{\mathrm{s}}$, $v_w^{max}=6.5\frac{\mathrm{m}}{\mathrm{s}}$, ${\omega }_m^{min}=0.35\frac{\mathrm{rad}}{\mathrm{s}}$, ${\omega }_m^{max}=0.75\frac{\mathrm{rad}}{\mathrm{s}}$, $m_m^{min}=0 \mathrm{N}\mathrm{m}$,
parameter	$m_m^{max}=1\times {10}^6 \mathrm{N}\mathrm{m}$, $\kappa =0.5$⇒$k_p=-5.38\times {10}^9\frac{\mathrm{Nms}}{\mathrm{rad}}$, $k_i=-1.25\times {10}^5\frac{\mathrm{Nm}}{\mathrm{rad}}$, ${\mathsf{\Omega }}_{{\omega }_m}^{\mathrm{cr}}=0.107\frac{1}{\mathrm{s}}$

. The power factor $c_p$ of the WTS is approximated by (for details see [21])

$$\begin{array}{c}\hfill c_p\left({\lambda }_t({\omega }_m,v_w),{\beta }_t\right)=c_1\left(c_{2}h\left({\lambda }_t({\omega }_m,v_w),{\beta }_t\right)-c_3{\beta }_t-c_4{\beta }_t^{c_7}-c_5\right)exp\left(-c_{6}h\left({\lambda }_t({\omega }_m,v_w),{\beta }_t\right)\right)\end{array}$$

(24)

with $c_1,\dots ,c_6>0$, $c_7\ge 0$ and $h\left({\lambda }_t({\omega }_m,v_w),{\beta }_t\right)$ as in Table 1. Figure 4 depicts the power factor $c_p$ and additionally ${\mathsf{\Omega }}_{{\omega }_m}^{\star }$. For the critical operation point of the considered system, the following holds: $({\omega }_m^{\mathrm{cr}},v_w^{\mathrm{cr}},{\beta }_t^{\mathrm{cr}})=(0.55\frac{\mathrm{rad}}{\mathrm{s}},6.5\frac{\mathrm{m}}{\mathrm{s}},0{}^{\circ })\in \partial {\mathcal{O}}_{+}$.

Scenario 1:Figure 5 shows the simulation result for Scenario 1, where the machine speed ${\omega }_m$ is controlled to its maximal value, i.e., ${\omega }_{m,\mathrm{ref}}={\omega }_m^{max}$. To point out the impact of variations of the wind speed $v_w$, real wind data (The authors are deeply grateful to the FINO-Project (BMU, PTJ, BSH, DEWI GmbH) for providing the wind data.) is used. The simulation illustrates the stable and good control performance of the controller design as in (20), since the control performance is characterized by an accurate tracking of the machine speed reference ${\omega }_{m,\mathrm{ref}}$. The IAE value of $0.001\mathrm{rad}$ verifies the accurate reference tracking (see

Table 2. Simulation results—Control performance evaluation with IAE performance measure.

	Figure 5	Figure 6	Figure 7			Figure 8
${\mathbf{\omega }}_{\mathit{m},\mathbf{ref}}$	Constant	Varying	Constant			Varying
			(a)	(b)	(c)	(a)	(b)	(c)
$k_p$ (in $\frac{\mathrm{Nms}}{\mathrm{rad}}$)	$-5.38\times {10}^9$	$-5.38\times {10}^9$	$-5\times {10}^6$	$-5\times {10}^2$	$-5\times {10}^6$	$-5\times {10}^6$	$-5\times {10}^2$	$-5\times {10}^6$
$k_i$ (in $\frac{\mathrm{Nm}}{\mathrm{rad}}$)	$-1.25\times {10}^5$	$-1.25\times {10}^5$	$-1.25\times {10}^5$	$-1.25\times {10}^5$	$1.25\times {10}^5$	$-1.25\times {10}^5$	$-1.25\times {10}^5$	$1.25\times {10}^5$
IAE (in $\mathrm{rad}$)	0.001	0.290	0.618	9.967	5.173	1.425	17.791	5.196

). The right hand-side of Figure 5 shows the wind $p_w$ and turbine $p_t$ power (with $p_t=c_p{p}_w=m_t\frac{{\omega }_m}{g_b}$), the tip speed ratio ${\lambda }_t$ and the power factor $c_p$. As expected for regime II.5, the WTS operates below the optimal tip speed ratio ${\lambda }_t^{\mathrm{opt}}$ and consequently does not reach the optimal power factor $c_p^{\mathrm{opt}}$.

Scenario 2:Figure 6 illustrates the control performance under a time-varying machine speed reference ${\omega }_{m,\mathrm{ref}}$, where significant changes in ${\omega }_{m,\mathrm{ref}}$ are allowed. Again, the control performance achieves an accurate and fast tracking of the machine speed reference ${\omega }_{m,\mathrm{ref}}$ with an IAE value of $0.290\mathrm{rad}$. The IAE value of this scenario is also small but larger than the IAE value of Scenario 1 due to the rapidly changing reference and the actuator constraint (SAT) which activates the anti-windup strategy as in (22). The machine torque reference $m_{m,\mathrm{ref}}$ is upper and lower bounded by $m_m^{max}$ and $m_m^{min}$, respectively. Clearly, the jumps in the machine speed reference $m_{m,\mathrm{ref}}$ cause rapid changes in the machine torque $m_m$ and accordingly strong loads on the mechanical components. Since the normal operation in regime II.5 is characterized by a fixed (constant) machine speed reference ${\omega }_{m,\mathrm{ref}}={\omega }_m^{max}$, the peaks in the machine torque $m_m$ in Figure 6 at $t=25\mathrm{s}$ and $85\mathrm{s}$ would not occur and stress the mechanical components (as shown in Figure 5).

Scenario 3: To illustrate the impact of badly tuned controller parameters $k_p$ and $k_i$ on stability and set-point tracking control performance, Scenario 1 is repeated for three different controller tunings; see controller tunings (a), (b) & (c) in Table 2. The simulation results for Scenario 3 are shown in Figure 7: (a) — shows a stable but slow control performance. Even for the constant machine speed reference ${\omega }_{m,\mathrm{ref}}$, the controller is not able to compensate for the changes in the wind speed $v_w$ and turbine torque $m_t$. The IAE value of $0.618\mathrm{rad}$ is much greater than the value $0.001\mathrm{rad}$ of Scenario 1. The selected parameters of tuning (b) - - - violate sub-condition (ii) of the stability condition (Condition 1) whereas the selected parameters of tuning (c) ⋯ violate sub-condition (iii) of (Condition 1). Hence, for the cases (b) and (c), the closed-loop systems are unstable and their IAE values of $9.967\mathrm{rad}$ and $5.173\mathrm{rad}$ are extremely large (see Table 2).

Scenario 4: Scenario 4 is similar to Scenario 2 and uses a time-varying speed reference to illustrate the reference tracking control performance for different operation points. The simulation results are shown in Figure 8. The impact of the badly tuned controller parameters (a) —, (b) - - - and (c) ⋯ is obvious. The control performance of the stable but slow tuning (a) results in an IAE value of $1.425\mathrm{rad}$, which is not acceptable and even worse than that in Figure 7 (Scenario 3). Moreover, the tunings (b) - - - and (c) ⋯ yield again an unstable closed-loop system with extremely high IAE values of $17.791\mathrm{rad}$ and $5.196\mathrm{rad}$, respectively.

7. Conclusions

The paper presented a local stability analysis for a machine speed PI-controller design for wind turbine systems operated in regime II.5. The proportional gain $k_p$ and integral gain $k_i$ of the PI-controller must be chosen properly to guarantee a (locally) stable closed-loop system. Therefore—based on the derived stability criteria—a tuning rule for the controller parameters via pole placement was proposed, which can achieve both: a stable closed-loop system and accurate and fast reference tracking. Four simulation scenarios have been implemented in Matlab/Simulink to demonstrate the achievable control performance of the proposed controller design and the effect of badly tuned controller designs on stability and tracking accuracy. The tracking control performance of all scenarios was compared and evaluated by the integral absolute error (IAE) performance measure. The simulation results showed that even, if the derived stability criteria is satisfied, a wrong controller tuning may give a slow and bad control performance leading to high IAEs values. Finally, the simulation results also demonstrated that, if the stability criteria is violated, then the closed-loop system becomes (as expected) unstable.