Electromagnetic Characteristics Analysis of a High-Temperature Superconducting Field-Modulation Double-Stator Machine with Stationary Seal
Abstract
:1. Introduction
2. Topology and Operating Principle
2.1. Topology
2.2. Operating Principle
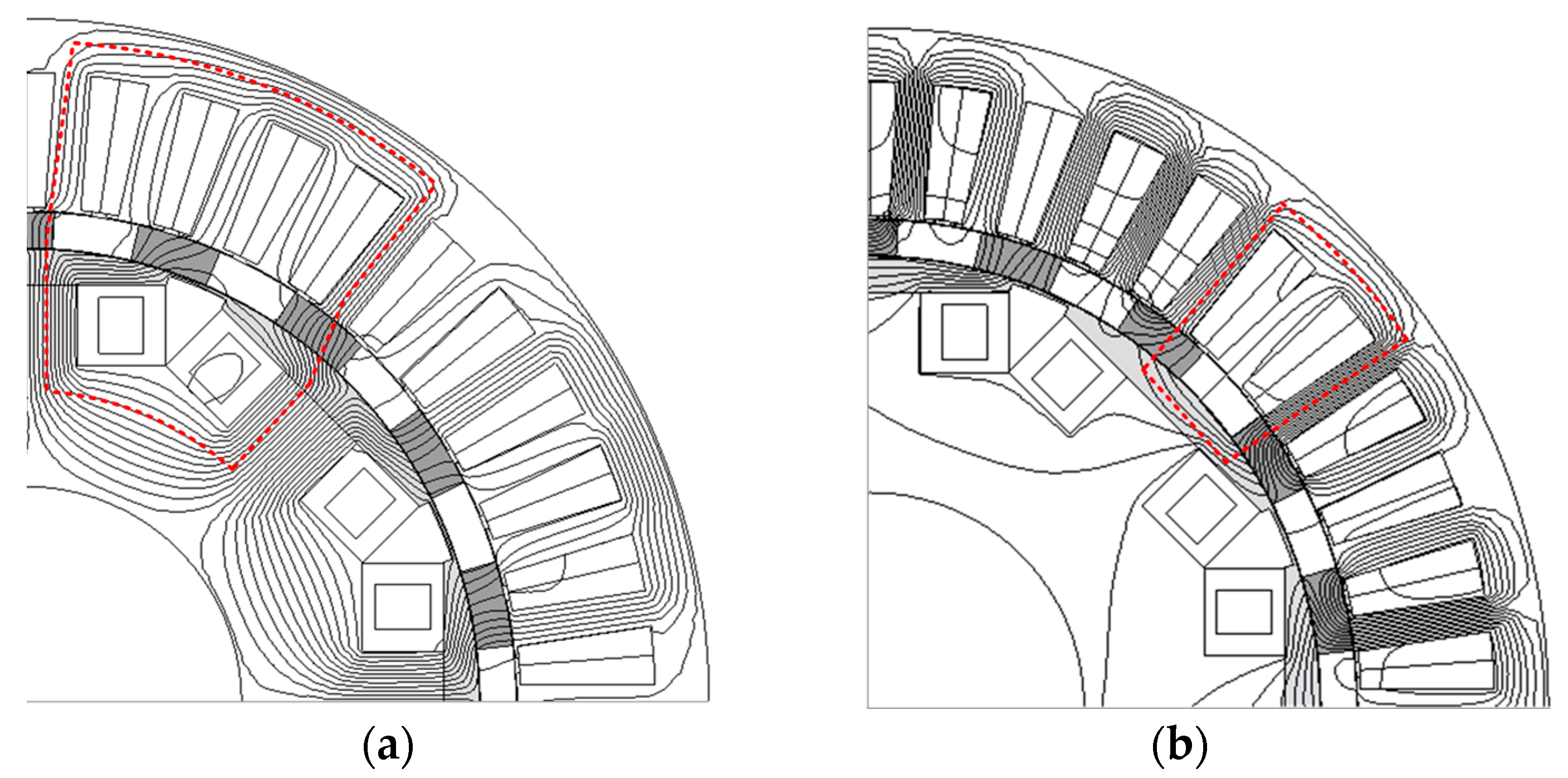
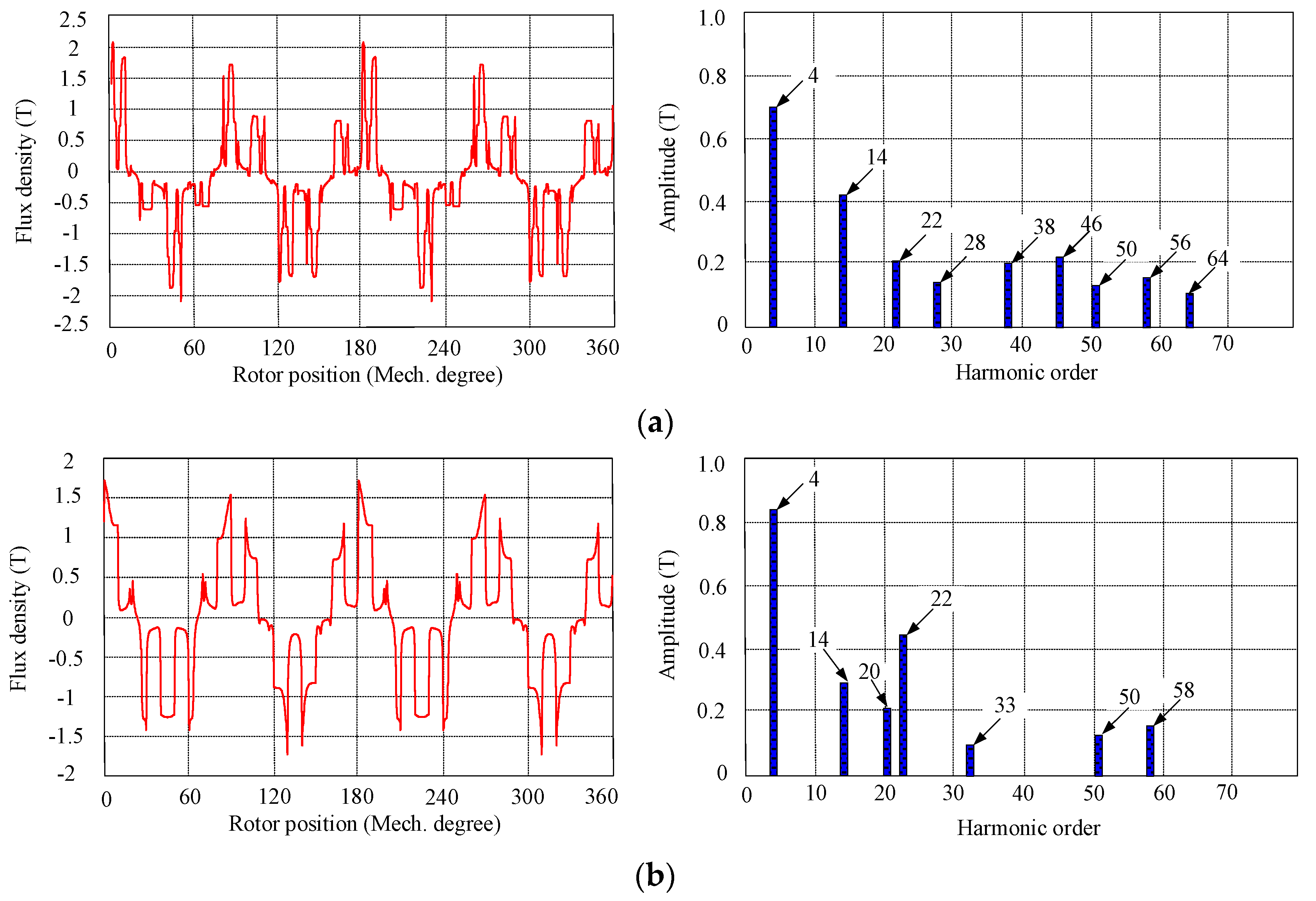
3. Influence of Armature-Reaction Magnetic-Field on the Critical Current
4. Electromagnetic Characteristics Analysis
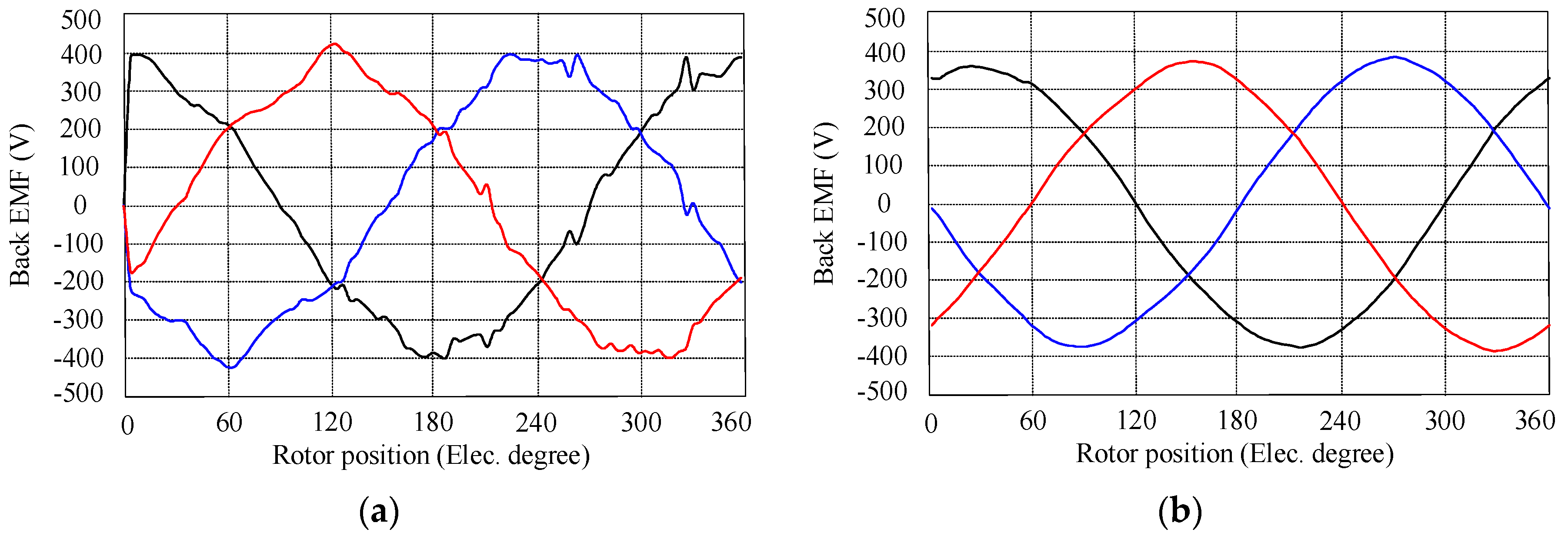
4.1. Back EMF
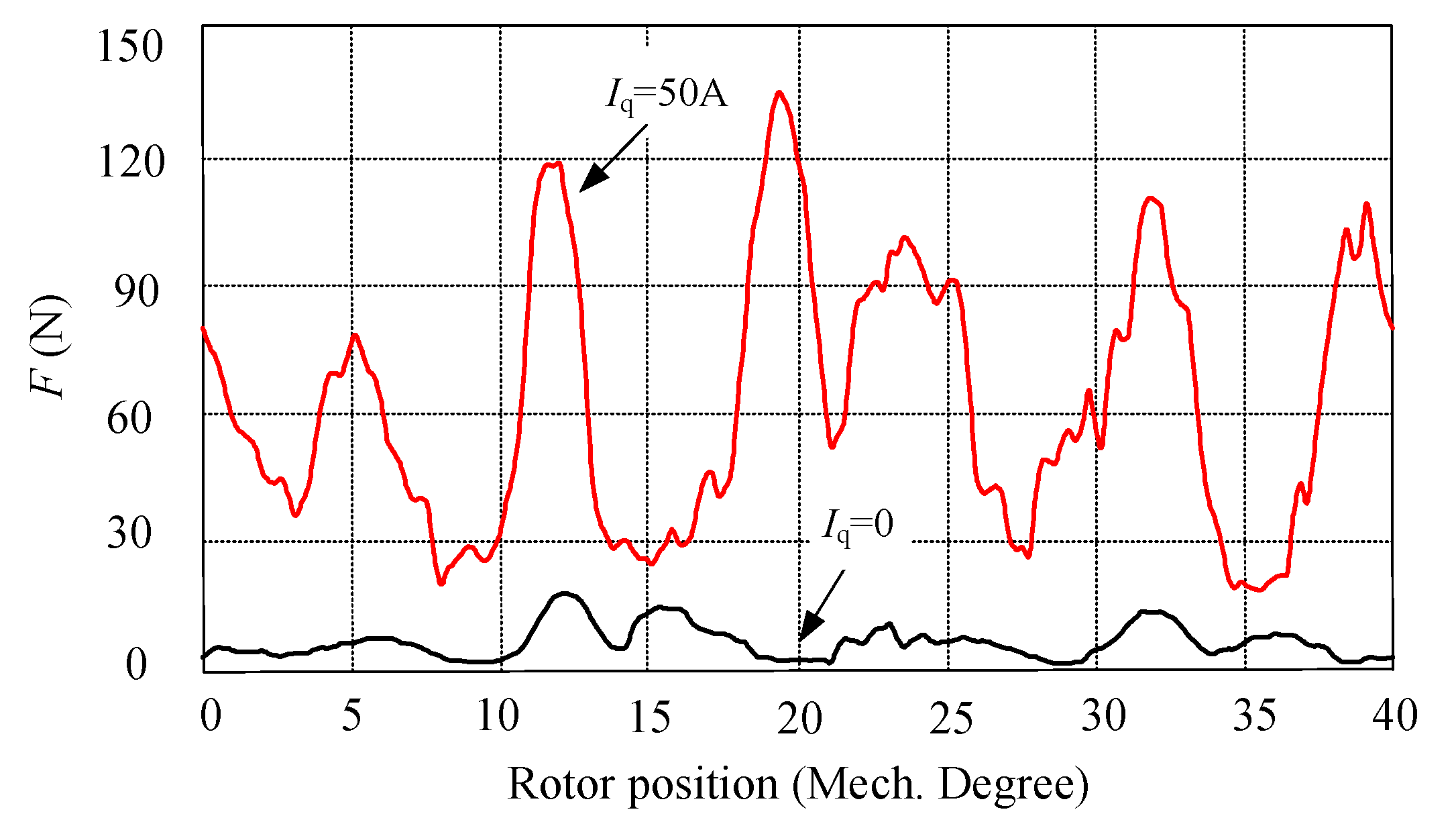
4.2. Unbalanced Magnetic Force
4.3. Electromagnetic Torque
4.4. Efficiency
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Polinder, H.; Ferreira, J.A.; Jensen, B.B.; Abrahamsen, A.B.; Atallah, K.; McMahon, R.A. Trends in wind turbine generator systems. IEEE J. Emerg. Sel. Top. Power Electron. 2013, 1, 174–185. [Google Scholar] [CrossRef]
- Yanamoto, T.; Izumi, M.; Yokoyama, M.; Umemoto, K. Electric propulsion motor development for commercial ships in Japan. Proc. IEEE 2015, 103, 2333–2343. [Google Scholar] [CrossRef]
- Shafaie, R.; Amirkhanloo, F.; Kalantar, M. Toward an optimum design of large-scale HTS synchronous generator for wind turbine applications. IEEE Trans. Appl. Supercond. 2016, 26, 5201408. [Google Scholar] [CrossRef]
- Kalsi, S.S.; Weeber, K.; Takesue, H.; Lewis, C.; Neumueller, H.W.; Blaugher, R.D. Development status of rotating machines employing superconducting field windings. Proc. IEEE 2004, 92, 1688–1704. [Google Scholar] [CrossRef]
- Klaus, G.; Wilke, M.; Frauenhofer, J.; Nick, W.; Neumuller, H.W. Design challenges and benefits of HTS synchronous machines. In Proceedings of the 2007 IEEE Power Engineering Society General Meeting, Tampa, FL, USA, 24–28 June 2007. [Google Scholar]
- Kalsi, S.S. Development status of superconducting rotating machines. In Proceedings of the 2002 IEEE Power Engineering Society Winter Meeting, New York, NY, USA, 27–31 January 2002. [Google Scholar]
- Gamble, B.; Snitchler, G.; Kalsi, S.S. HTS generator topologies. In Proceedings of the 2006 IEEE Power Engineering Society General Meeting, Montreal, QC, Canada, 18–22 June 2006. [Google Scholar]
- Cheng, M.; Hua, W.; Zhang, J.; Zhao, W. Overview of stator-permanent magnet brushless machines. IEEE Trans. Ind. Electron. 2011, 58, 5087–5101. [Google Scholar] [CrossRef]
- Cheng, M.; Han, P.; Hua, W. General airgap field modulation theory for electrical machines. IEEE Trans. Ind. Electron. 2017, 64, 6063–6074. [Google Scholar] [CrossRef]
- Zhu, X.; Xiang, Z.; Zhang, C.; Quan, L.; Du, Y.; Gu, W. Co-reduction of torque ripple for outer rotor flux-switching PM motor using systematic multi-level design and control schemes. IEEE Trans. Ind. Electron. 2017, 64, 1102–1112. [Google Scholar] [CrossRef]
- Xiang, Z.; Zhu, X.; Quan, L.; Du, Y.; Zhang, C.; Fan, D. Multilevel design optimization and operation of a brushless double mechanical port flux-switching permanent-magnet motor. IEEE Trans. Ind. Electron. 2016, 63, 6042–6054. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, C.; Feng, Q.; Li, X.; Ching, T.W. Fabrication and experiment of racetrack HTS coil for stator field-excitation HTS machine. IEEE Trans. Appl. Supercond. 2017, 27, 5201605. [Google Scholar] [CrossRef]
- Wang, Y.; Feng, Q.; Li, X.; Ma, W. Design, analysis, and experimental test of a segmented-rotor high temperature superconducting generator with stationary seal. IEEE Trans. Ind. Electron. 2018. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, C.; Feng, Q.; Li, X. Design and experiment of an HTS flux-switching machine with stationary seal. IEEE Trans. Appl. Supercond. 2017, 27, 5201405. [Google Scholar] [CrossRef]
- Toba, A.; Lipo, T.A. Generic torque-maximizing design methodology of surface permanent-magnet vernier machine. IEEE Trans. Ind. Appl. 2000, 36, 1539–1546. [Google Scholar] [CrossRef]
- Zheng, P.; Song, Z.Y.; Bai, J.G.; Tong, C.D.; Yu, B. Research on an axial magnetic-field-modulated brushless double rotor machine. Energies 2013, 6, 4799–4829. [Google Scholar] [CrossRef]
- Li, X.; Chau, K.T.; Cheng, M. Analysis, design and experimental verification of a field-modulated permanent-magnet machine for direct-drive wind turbines. IET Electr. Power Appl. 2015, 9, 150–159. [Google Scholar] [CrossRef]
- Wang, Q.; Niu, S. A novel hybrid-excited dual-PM machine with bidirectional flux modulation. IEEE Trans. Energy Convers. 2017, 32, 424–435. [Google Scholar] [CrossRef]
- Wang, Q.; Niu, S.; Yang, L. Design optimization and comparative study of novel dual-PM excited machines. IEEE Trans. Ind. Electron. 2017, 64, 9924–9933. [Google Scholar] [CrossRef]
- Wu, Z.Z.; Zhu, Z.Q. analysis of air-gap field modulation and magnetic gearing effects in switched flux permanent magnet machines. IEEE Trans. Magn. 2015, 51, 1–12. [Google Scholar] [CrossRef]
- Luo, X.; Niu, S.X. Maximum power point tracking sensorless control of an axial-flux permanent magnet vernier wind power generator. Energies 2016, 9, 581. [Google Scholar] [CrossRef]
- Du, Y.; Xiao, F.; Hua, W.; Zhu, X.; Cheng, M.; Quan, L.; Chau, K.T. Comparison of flux-switching pm motors with different winding configurations using magnetic gearing principle. IEEE Transa. Magn. 2016, 52, 8201908. [Google Scholar] [CrossRef]
- Li, F.; Chau, K.T.; Liu, C. Pole-changing flux-weakening DC-excited dual-memory machines for electric vehicles. IEEE Trans. Energy Convers. 2016, 31, 27–36. [Google Scholar] [CrossRef]
- Lee, C.H.T.; Chau, K.T.; Liu, C.; Ching, T.W.; Chen, M. A new magnetless flux-reversal HTS machine for direct-drive application. IEEE Trans. Appl. Supercond. 2015, 25, 5203105. [Google Scholar] [CrossRef]
- Lee, C.H.T.; Chau, K.T.; Liu, C.; Qiu, C. Design and analysis of a new multitoothed magnetless doubly-salient machine. IEEE Trans. Appl. Supercond. 2014, 24, 5200804. [Google Scholar] [CrossRef]
- Gong, Y.; Chau, K.T.; Jiang, J.Z.; Yu, C.; Li, W. Design of doubly salient permanent magnet motors with minimum torque ripple. IEEE Trans. Magn. 2009, 45, 4704–4707. [Google Scholar] [CrossRef] [Green Version]
- Lee, C.H.T.; Chau, K.T.; Liu, C.; Ching, T.W.; Li, F. Mechanical offset for torque ripple reduction for magnetless double-stator doubly salient machine. IEEE Trans. Magn. 2014, 50, 1–4. [Google Scholar] [CrossRef]
- Chau, K.T. Electric Vehicle Machines and Drives—Design, Analysis and Application; Wiley-IEEE Press: Hoboken, NJ, USA, 2015. [Google Scholar]












| Parameters | Value |
|---|---|
| Ic @ 77 K, 0 T | 120 A |
| Max. tensile strength | 100 MPa @ 77 K |
| Critical bending radius | 30 mm |
| Thickness | 0.25 mm |
| Width | 4.2 mm |
| Parameters | Value |
|---|---|
| Number of outer stator teeth | 42 |
| Number of inner stator teeth | 8 |
| Number of pole pairs of armature windings | 14 |
| Number of pole pairs of field-excitation windings | 4 |
| Number of modulation-ring rotor teeth | 18 |
| Stator outside diameter of outer stator (mm) | 760 |
| Stator inside diameter of outer stator (mm) | 546.4 |
| Stator outside diameter of inner stator (mm) | 504 |
| Stator inside diameter of inner stator (mm) | 240 |
| Rotor outside diameter (mm) | 42 |
| Stack length (mm) | 100 |
| Inner air-gap length (mm) | 0.6 |
| Outer air-gap length (mm) | 0.6 |
| Number of phases | 3 |
| Rated speed (rpm) | 167 |
| Rated power (kW) | 25 |
| HTS material | Bi-2223 |
| Number of turns of each HTS winding (turn) | 80 |
| Consumption of total HTS wires (m) | 373 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Yang, G.; Zhu, X.; Li, X.; Ma, W. Electromagnetic Characteristics Analysis of a High-Temperature Superconducting Field-Modulation Double-Stator Machine with Stationary Seal. Energies 2018, 11, 1269. https://doi.org/10.3390/en11051269
Wang Y, Yang G, Zhu X, Li X, Ma W. Electromagnetic Characteristics Analysis of a High-Temperature Superconducting Field-Modulation Double-Stator Machine with Stationary Seal. Energies. 2018; 11(5):1269. https://doi.org/10.3390/en11051269
Chicago/Turabian StyleWang, Yubin, Guangyong Yang, Xinkai Zhu, Xianglin Li, and Wenzhong Ma. 2018. "Electromagnetic Characteristics Analysis of a High-Temperature Superconducting Field-Modulation Double-Stator Machine with Stationary Seal" Energies 11, no. 5: 1269. https://doi.org/10.3390/en11051269





