Abstract
This paper is concerned with bump-less transfer of parameterized disturbance observer based controller with individual pitch control strategy to reduce cyclic loads of wind turbine in full load operation. Cyclic loads are generated due to wind shear and tower shadow effects. Multivariable disturbance observer based linear controllers are designed with objective to reduce output power fluctuation, tower oscillation and drive-train torsion using optimal control theory. Linear parameterized controllers are designed by using a smooth scheduling mechanism between the controllers. The proposed parameterized controller with individual pitch was tested on nonlinear Fatigue, Aerodynamics, Structures, and Turbulence (FAST) code model of National Renewable Energy Laboratory (NREL)’s 5 MW wind turbine. The closed-loop system performance was assessed by comparing the simulation results of proposed controller with a fixed gain and parameterized controller with collective pitch for full load operation of wind turbine. Simulations are performed with step wind to see the behavior of the system with wind shear and tower shadow effects. Then, turbulent wind is applied to see the smooth transition of the controllers. It can be concluded from the results that the proposed parameterized control shows smooth transition from one controller to another controller. Moreover, 3p and 6p harmonics are well mitigated as compared to fixed gain DOBC and parameterized DOBC with collective pitch.
1. Introduction
This paper proposes multivariable linear parameter varying controller based on disturbance observer based control (DOBC) technique to reduce the effect of cyclic loads using individual pitch control (IPC) strategy. Pitch-regulated variable-speed wind turbines have two operational modes: partial load and full load. In partial load operation, maximum aerodynamic efficiency is achieved by controlling the generator torque. However, in full load operation, nominal electrical power is produced by controlling the blade pitch angle. During operation of wind turbine, different types of aerodynamic loads are acting on its components, i.e., steady, periodic and random fluctuating. Mean wind is the source of steady load and wind gust generate random fluctuating loads. Cyclic or periodic loads are generated due to wind shear and tower shadow effects, which reduce the life time and add harmonics in the output power. DOBC is widely used controller to mitigate the effect of know disturbance. We modeled the disturbance with step and periodic effects then designed a controller to reject these disturbances. Parameterized controller based on DOBC with IPC is used to reduce the fluctuations in the output power and minimize the fatigue of drive train, tower and pitch system for full load operation of wind turbine.
Disturbance accommodation control (DAC) was used to model and simulate system with known disturbance waveform. DAC was used [1] to mitigate the effect of disturbances by using collective pitch control of wind turbine. Then, multivariable DAC was developed [2] to mitigate the effect of periodic loads (wind shear and tower shadow) with multiple objectives using pitch control of wind turbine. Multivariable control algorithm used in [3,4] are based on proportional-Integral (PI) control for regulating generator speed and independent pitch control to reduce structural loads. Nonlinear state feedback torque control was used [5] for the above-rated power operating condition of wind turbine and DOBC strategies were reviewed [6]. Ostergaard et al. observed that the operation of wind turbines at different wind speeds require some kind of gain scheduling, so they have applied linear parameter varying control to develop robust controllers that cater for a both partial load and full load conditions [7,8].
Various linear and nonlinear control schemes have been used for partial and full load operation of wind turbine. Nonlinear control strategies have intensive mathematical computations and the controller takes longer time as compared to linear control. Adaptive control is designed for the system with known and unknown aerodynamic torque. Arbitrary steady state and transient performance are achieved for both cases [9]. A three-fold controller has also been designed: the first parameter is the independent current controller in the inner loop, the second is stabilizing PI gain in the outer loop and the third is adaptive DOBC to predict one state ahead to compensate the time delay in the input [10]. A novel adaptive controller is designed to tack the reference torque for Maximum power point (MPPT) and reactive power controller to manicure the desired reactive power determined by the grid [11]. Some of the methods are developed on the basis of incremental state model of the plant for zero steady state error. Multivariable optimal control based on incremental state model is presented [12] and fuzzy linear quadratic regulator is designed for better robustness [13].
DOBC, a linear controller based on state space model of plant, was used to solve multivariable problems. High gain DOBC was used to regulate load frequency to nominal value [14] and active disturbance rejection control tuned by particle swarm optimization algorithm [15]. A comparison of the results of observer based controller designed on the basis of one-state, seven-state and nine-state model has been presented [16]. Asymptotic stability of DOBC is guaranteed [17] in the presence of anti-disturbance by combined approach of back stepping and linear matrix inequality. Multivariable control techniques are used to reduce the fatigue of wind turbine components with CPC and IPC. Linear Quadratic Gaussian controller was developed to mitigate the effect of sensor noise [18], DAC with optimal control theory was designed to get better stability of output power [1] and 3p harmonics generated due to periodic loads were reduced using CPC [2,19].
This paper presents a systematic approach to design a linear parameter varying with individual pitch control for full load operation of wind turbine with objectives to regulate output power and reduce fatigue under periodic loads. Five-state disturbance linear model and five-state wind turbine linear model were used for DOBC design. Kalman filter was used for the state estimation and optimal control was used to choose the feedback matrices to meet the multiple objectives. Multivariable linear controllers were developed based on [19] at 18 m/s and 19 m/s wind speed and bump-less transfer between controllers was accomplished by interpolation of covariance of linear controllers. Proposed controller was designed based on the linear plant model and then tested on Fatigue, Aerodynamics, Structures, and Turbulence (FAST) Code [20] with the nonlinear model of National Renewable Energy Laboratory (NREL)’s 5 MW wind turbine by enabling the drive-train rotational-flexibility degree of freedom (DOF), generator DOF, and first and second fore–aft bending mode DOF with actuator dynamics.
The closed loop performance was evaluated by simulation of fixed gain disturbance-observer-based control with CPC (FixedGain-CPC), linear parameter varying with CPC (LPV-CPC) and proposed linear parameter varying with IPC (LPV-IPC) under same testing conditions. Simulation of the proposed controller was performed with step changing to see the mitigation to periodic loads and turbulent wind was used to see the bump-less transfer between the family of controllers in full load operation of wind turbine. Standard deviation of the generator speed, drive-train torsion and tower fore–aft moments were analyzed. This paper is organized as follows. Section 2 describes the wind turbine model. Section 3 describes the control methodology. Section 4 is the problem formulation. Simulation results are found in Section 5. Conclusions are drawn in Section 6.
2. Wind Turbine Model
The nonlinear model of wind energy conversion system (WECS) [19] is shown in Figure 1 and its equations are summarized in Table 1.
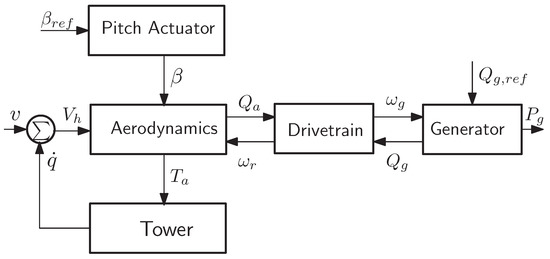
Figure 1.
Wind energy conversion system.

Table 1.
Nonlinear model equations summary.
is the power coefficient and thrust coefficient is of rotor. Length is R. Tip speed ratio is of the rotor of wind turbine. Air density is and relative wind speed is v. is rotor and shaft inertia, is stiffness and is damping coefficients of the drive train. is inertia of rotor of the generator, high-speed shaft and gearbox. is the generator torque, is generator speed and is the gear ratio.The relative wind speed is , is the absolute wind speed measured at hub height of the tower. is the model mass of the first fore–aft bending mode, is structural damping coefficient and is the stiffness coefficient of the tower. is the commanded generator torque, is the time constant for the generator, is the efficiency of the generator and is the output power.
Five-state linear model with tower dynamics [21] can be represented as
where is the input vector, is state vector, is the output and is the disturbance vector. A, B, , C, and D are state transition, control input, disturbance input, measured state and output matrices of the plant, respectively. is the wind speed (m·), is the rotor speed (rad·), is the blade pitch angle (rad), is drive-train torsion (rad), and q is the fore–aft bending displacement of the tower (m).
Parameters of the NREL’s 5 MW wind turbine [22] linear model are summarized in Table 2.

Table 2.
Parameters of Linear Model.
3. Control Methodology
3.1. Disturbance Observer Based Control (DOBC)
Five-state disturbance model for step, 3rd and 6th harmonic mitigation [1,2] is the following:
where is state of the disturbance, is step disturbance, is 3p disturbance and is for 6p disturbance. F is the state transition matrix and is the output matrix of the disturbance waveform. is the 3p frequency and is 6p frequency, where p is the rotational speed of the rotor for full load operation.
Control law is:
If the system (A,B) is controllable, then can be calculated by minimizing the fitness function for optimal performance as:
Full state feedback matrix value depends upon the weighing matrices: Q is symmetric positive semi definite and R is symmetric positive definite matrix, i.e., , . Control performance depends upon the selection of Q and R matrices [23,24]. is disturbance feedback matrix, which is calculated independently [1].
Kalman estimator is used to estimate the states of the plant as:
is estimated state of the plant and is estimated state of the disturbance, , and are estimated input, disturbance and output, respectively. It is also used to estimate the state of the disturbance as:
is the plant and is the disturbance state estimation matrices, respectively. Estimator gain matrices are calculated using pole placement technique for disturbance augmented plant. DOBC with CPC [21] can be represented as:
is the fixed gain disturbance observer based controller with generator speed is the input and collective pitch angle.
3.2. Parameterized DOBC with CPC
Wind turbine is a nonlinear and time varying system. Operating locus of wind turbine is generated using classical linearization around operating points [22] and linear controllers are designed to get optimum performance [19]. is the family of linear plants in Equation (14) of detectable and stablizable parameter varying plants [8] and is the scheduling parameter. is the estimated wind speed used for the scheduling of parameterized controller. and are linearized model of nonlinear plant generated at two operating points can be scheduled as:
Let and are linear controllers tuned at operating points to satisfy the desired performance [19]. , , and are the plant state estimation, disturbance state estimation, plant state feedback and disturbance feedback matrices, respectively, for the first controller. , , and are the plant state estimation, disturbance state estimation, plant state feedback and disturbance feedback matrices, respectively, for the second controller. Then, is the parameterized disturbance accommodated observer based controller with CPC, which can be represented as:
where
State feedback and observer gain matrices for the family of interpolated controllers can be written
, , , , and are state transition, control input, disturbance input, measured state and output matrices of the interpolated plant between the operating points, respectively.
3.3. Parameterized DOBC with IPC
Proposed parameterized controller with individual pitch [19] can be written as:
where is the disturbance feedback to mitigate the periodic disturbance and is for step mitigation. Disturbance feedback is the sum of periodic and step feedback matrices. is the parameterized controller [21] with output to mitigate the effect of periodic disturbances and output to mitigate the step disturbance. In the NREL’s 5 MW wind turbine, rotor blades are spanned at apart and the individual blade pitch [25] can be implemented as:
, and are the pitch angle for blade 1, 2 and 3, respectively. is the azimuth angle of the rotor. Then, the closed loop system with proposed DOBC controller is shown in Figure 2.
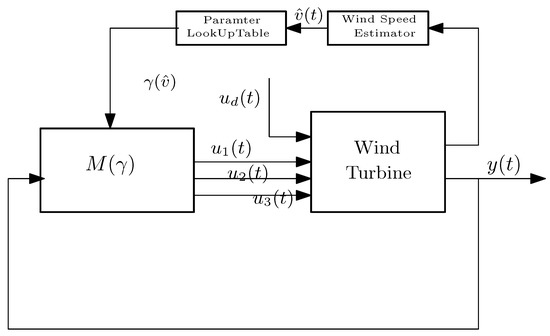
Figure 2.
Closed loop System with Controller.
4. Problem Formulation
There are main two operational regions of control [19,21]: partial load region and full load region. In partial load operation region, control objective is to extract maximum power by keeping track of maximum power coefficient. In full load operation region, control objective is to regulate the generator speed at its rated value and blade pitch angle are controlled to reduce load on wind turbine components. In this paper, full load operation region is considered. Therefore, generator power is regulated at its rated value as well as cyclic loads generated due to wind shear and tower shadow effects [2] are mitigated using IPC. NREL’s 5 MW wind turbine is used as research object and its characteristics are in Table 3.

Table 3.
NREL’s 5 MW wind turbine parameters [22].
DOBC are tuned using the following definite symmetric matrices to meet the desired performance:
Then, states of the disturbance accommodated plant are estimated by placing the observer poles at to make closed loop system stable.
Stability of the multivariable observer based controller is discussed in [26,27].
5. Simulation Results
The proposed controller (LPV-IPC) in Equation (24) is designed based on the family of LPV plant model in Equation (14) and tested on NREL’s 5MW wind turbine [22] FAST code model with wind shear and tower shadow effect. Operating points are chosen based on Refs. [7,22]. is the controller at operating point (18 m/s, 14.92 deg) and is the linear controller at operating point of (19 m/s, 16.23 deg) with rated generator torque for full load operation of wind turbine. State feedback matrices and estimator gain matrices are chosen using optimal control theory [1,2]. (FixedGain-CPC) represented by Equation (13) is the fixed gain controller at 18 m/s wind speed and (LPV-CPC) is the parameterized controller with collective pitch represented by Equation (15). Then, same parameters are used for the tuning of parameterized controllers and and smooth transition from one to another controller is accomplished by interpolation of linear controllers. Wind speed used for the scheduling of controller can be estimated following Ref. [28] and the closed loop system with proposed controller for wind turbine with actuator dynamics is shown in Figure 2. The proposed controller performance is evaluated by applying step changing wind to see the behavior of the system and then turbulent wind generated with mean of mid wind speed is used to see the smooth transition of the controller in full load operation of wind turbine. The closed-loop performance was assessed by the simulations of proposed LPV-IPC with FixedGain-CPC and LPV-CPC. The performance was analyzed by measuring the standard deviation in generator speed, drive-train torsion and tower moment.
For step analysis of the system, a step changing wind from 17 m/s to 21 m/s was applied to the wind turbine with wind shear and tower shadow effect. From the comparison of the results in Figure 3, it can seen that LPV-IPC (proposed controller) has less fluctuation in the generator speed at step change and periodic loads are well mitigated as compared to fixed gain-CPC and LPV-CPC. Drive-train torsion and tower fore–aft moment are better reduced for step with wind shear and tower shadow effects.
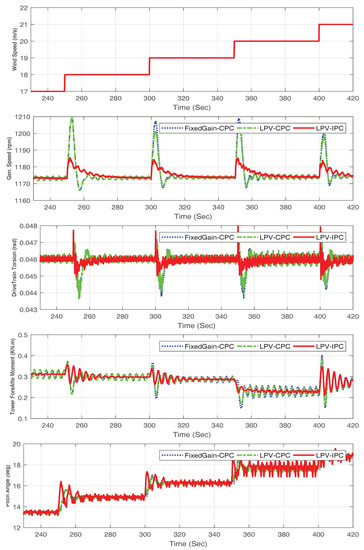
Figure 3.
Step Wind. Blueline: FixedGain-CPC, Greenline: LPV-CPC, Redline: LPV-IPC.
Finally, the scheduling of the proposed controller was tested by performing a simulation with turbulent wind with mean of 18 m/s and turbulence value of 10 generated from TurbSim [29] for above rated wind speed condition. The purpose of this simulation was to investigate the controller transitions along the operating trajectory. The results are shown in Figure 4. It can be seen that the controller provides a glitch free transfer of controller for above rated wind speed condition. In addition, fatigue of drive-train is reduced, and there are less pitching activity and better power regulation as compared to fixed gain and LPV DOBC controllers with CPC.
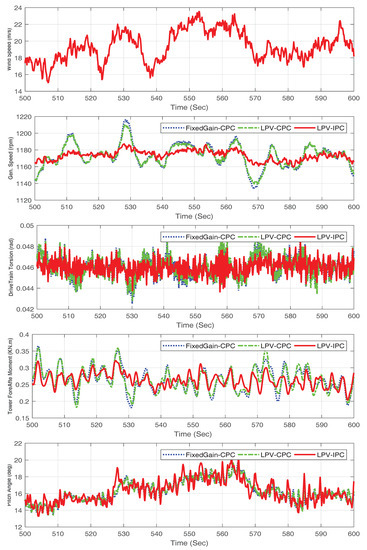
Figure 4.
Turbulent Wind. Blueline: FixedGain-CPC, Greenline: LPV-CPC, Redline: LPV-IPC.
Results of turbulent wind simulation are summarized in Table 4. It can be inferred from the results that percentage improvement in the standard deviation of the generator speed, drive-train torsion and tower moments are simultaneously , and , respectively, compared to fixed gain-CPC. Furthermore, , and improvement in the standard deviation of the generator speed, drive-train torsion and tower moments, respectively, are observed compared to fixed gain-CPC. However, better performance can be achieved by the tuning of the multivariable controller at the operating points to do better mitigation to loads of components, regulation of output power and reduced pitching activity.

Table 4.
Standard deviation of parameters.
6. Conclusions
This paper has presented a systematic method for designing a parameterized DOBC with IPC for full load operations of wind turbine. The proposed controller is based on the LPV design method that provides a smooth transition between two multivariable DOBC. Controllers are interpolated between the two operating points without any bump. This was tested with step changing wind and then switching between the controllers was checked by applying turbulent wind. Analysis of the simulation results shows that the proposed controller reduced load of drive train, gearbox and tower moment in the presence of wind shear and tower shadow effect and provided better regulation to the produced power. It should be noted that model uncertainty is not directly handled in the design formulation. The performance can be increased by retuning of controller with objectives to reduce tower oscillations, drive train torsion, mitigate periodic aerodynamic loads and individual pitch controller can also be accommodated in the controller design for the full load operation of wind turbine.
Author Contributions
All the authors contributed to this work. Raja M. Imran designed the system model, performed the algorithm and wrote this paper. D. M. Akbar Hussain and Bhawani Shanker Chowdhry set the simulation environment and checked the results of this work.
Funding
This paper is not supported by any funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Imran, R.M.; Akbar Hussain, D.M.; Soltani, M. DAC with LQR control design for pitch regulated variable speed wind turbine. In Proceedings of the 2014 IEEE 36th International Telecommunications Energy Conference (INTELEC), Vancouver, BC, Canada, 28 September–2 October 2014. [Google Scholar]
- Imran, R.M.; Akbar Hussain, D.M.; Soltani, M. DAC to mitigate the effect of periodic disturbances on drive train using collective pitch for variable speed wind turbine. In Proceedings of the 2015 IEEE International Conference on Industrial Technology (ICIT), Seville, Spain, 17–19 March 2015. [Google Scholar]
- Johansson, K.H.; James, B.; Bryant, G.F.; Astrom, K.J. Multivariable controller tuning. In Proceedings of the 1998 American Control Conference, Philadelphia, PA, USA, 24–26 June 1998; Volume 6. [Google Scholar]
- Njiri, J.G.; Liu, Y.; Söffker, D. Multivariable control of large variable-speed wind turbines for generator power regulation and load reduction. IFAC-PapersOnLine 2015, 48, 544–549. [Google Scholar] [CrossRef]
- Boukhezzar, B.; Lupu, L.; Siguerdidjane, H.; Hand, M. Multivariable control strategy for variable speed, variable pitch wind turbines. Renew. Energy 2007, 32, 1273–1287. [Google Scholar] [CrossRef]
- Chen, W.H.; Yang, J.; Guo, L.; Li, S. Disturbance observer-based control and related methods: An overview. IEEE Trans. Ind. Electron. 2016, 63, 1083–1095. [Google Scholar] [CrossRef]
- Østergaard, K.Z.; Stoustrup, J.; Brath, P. Linear parameter varying control of wind turbines covering both partial load and full load conditions. Int. J. Robust Nonlinear Control 2009, 19, 92–116. [Google Scholar] [CrossRef]
- Hangstrup, M.E.; Stoustrup, J.; Andersen, P.; Pedersen, T.S. Gain-scheduled control of a fossil-fired power plant boiler. In Proceedings of the 1999 IEEE International Conference on Control Applications, Kohala Coast, HI, USA, 22–27 August 1999; Volume 2. [Google Scholar]
- Meng, W.; Yang, Q.; Ying, Y.; Sun, Y.; Yang, Z.; Sun, Y. Adaptive power capture control of variable-speed wind energy conversion systems with guaranteed transient and steady-state performance. IEEE Trans. Energy Convers. 2013, 28, 716–725. [Google Scholar] [CrossRef]
- Kim, S.-K.; Song, H.; Lee, J.-H. Adaptive disturbance observer-based parameter-independent speed control of an uncertain permanent magnet synchronous machine for wind power generation applications. Energies 2015, 8, 4496–4512. [Google Scholar] [CrossRef]
- Meng, W.; Yang, Q.; Sun, Y. Guaranteed performance control of DFIG variable-speed wind turbines. IEEE Trans. Control Syst. Technol. 2016, 24, 2215–2223. [Google Scholar] [CrossRef]
- Adánez, J.M.; Al-Hadithi, B.M.; Jiménez, A. Wind Turbine Multivariable Optimal Control Based on Incremental State Model. Asian J. Control 2017. [Google Scholar] [CrossRef]
- Al-Hadithi, B.M.; Jiménez, A.; Perez-Oria, J. New incremental Takagi–Sugeno state model for optimal control of multivariable nonlinear time delay systems. Eng. Appl. Artif. Intell. 2015, 45, 259–268. [Google Scholar] [CrossRef]
- Rosyiana, F.I.; Kim, J.-S.; Song, H. High-Gain Disturbance Observer-Based Robust Load Frequency Control of Power Systems with Multiple Areas. Energies 2017, 10, 595. [Google Scholar]
- Qi, X.; Bai, Y. Improved Linear Active Disturbance Rejection Control for Microgrid Frequency Regulation. Energies 2017, 10, 1047. [Google Scholar] [CrossRef]
- Menezes, E.J.N.; Araujo, A.M.; Rohatgi, J.S.; del Foyo, P.M.G. Active load control of large wind turbines using state-space methods and disturbance accommodating control. Energy 2018, 150, 310–319. [Google Scholar] [CrossRef]
- Wu, K.; Zhang, Z.; Sun, C. Disturbance-observer-based output feedback control of non-linear cascaded systems with external disturbance. IET Control Theory Appl. 2017, 12, 738–744. [Google Scholar] [CrossRef]
- Imran, R.M.; Akbar Hussain, D.M.; Chen, Z. LQG controller design for pitch regulated variable speed wind turbine. In Proceedings of the 2014 IEEE International Energy Conference (ENERGYCON), Cavtat, Croatia, 13–16 May 2014. [Google Scholar]
- Imran, R.M.; Akbar Hussain, D.M.; Soltani, M.; Rafaq, R.M. Optimal Tuning of Multivariable Disturbance-Observer-Based Control for Flicker Mitigation Using IPC of Wind Turbine. J. IET Renew. Power Gener. 2017, 11, 1121–1128. [Google Scholar] [CrossRef]
- Jonkman, J.M.; Buhl, M.L., Jr. FAST User’S Guide; Technical Report No. NREL/EL-500-38230; National Renewable Energy Laboratory: Golden, CO, USA, 2005. [Google Scholar]
- Imran, R.M. Multivariable Control for Load Mitigation of Wind Turbine. Ph.D. Thesis, Aalborg University, Esbjerg, Denmark, 2016. [Google Scholar]
- Jonkman, J.; Butterfield, S.; Musial, W.; Scott, G. Definition of a 5-MW Reference Wind Turbine for Offshore System Development; National Renewable Energy Laboratory: Golden, CO, USA, 2009. [Google Scholar]
- Anderson, B.; Moore, J.B. Optimal Control: Linear Quadratic Methods; Courier Corporation: North Chelmsford, MA, USA, 2007. [Google Scholar]
- Pintea, A.; Wang, H.; Christov, N.; Borne, P.; Popescu, D.; Badea, A. Optimal control of variable speed wind turbines. In Proceedings of the 2011 19th Mediterranean Conference on Control & Automation (MED), Corfu, Greece, 20–23 June 2011. [Google Scholar]
- Bossanyi, E.A. Individual blade pitch control for load reduction. Wind Energy 2003, 6, 119–128. [Google Scholar] [CrossRef]
- Goodwin, G.C.; Graebe, S.F.; Salgado, M.E. Control System Design; Prentice Hall: Upper Saddle River, NJ, USA, 2001; Volume 13. [Google Scholar]
- Yuan, Y.; Chen, X.; Tang, J. Disturbance Observer-Based Pitch Control of Wind Turbines for Enhanced Speed Regulation. J. Dyn. Syst. Meas. Control 2017, 139, 071006. [Google Scholar] [CrossRef]
- Soltani, M.N.; Knudsen, T.; Svenstrup, M.; Wisniewski, R.; Brath, P.; Ortega, R.; Johnson, K. Estimation of rotor effective wind speed: A comparison. IEEE Trans. Control Syst. Technol. 2013, 21, 1155–1167. [Google Scholar] [CrossRef]
- Kelley, N.D.; Jonkman, B.J. Overview of the TurbSim Stochastic Inflow Turbulence Simulator; Technical Report, NREL/TP-500-41137; National Renewable Energy Laboratory: Golden, CO, USA, 2007. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).