Aerodynamic Design Optimization of a Micro Radial Compressor of a Turbocharger
Abstract
:1. Introduction
2. Geometry Parameterization
2.1. Parameterization of the Main Blade by the Beta Distribution
2.2. Parameterization of Splitter Blade by LE Location
3. Numerical Analysis
4. Surrogate Method with Single-Objective Optimization and Results
4.1. Optimization of Main Blade
4.2. Optimization of Splitter Blade
5. Results and Discussion
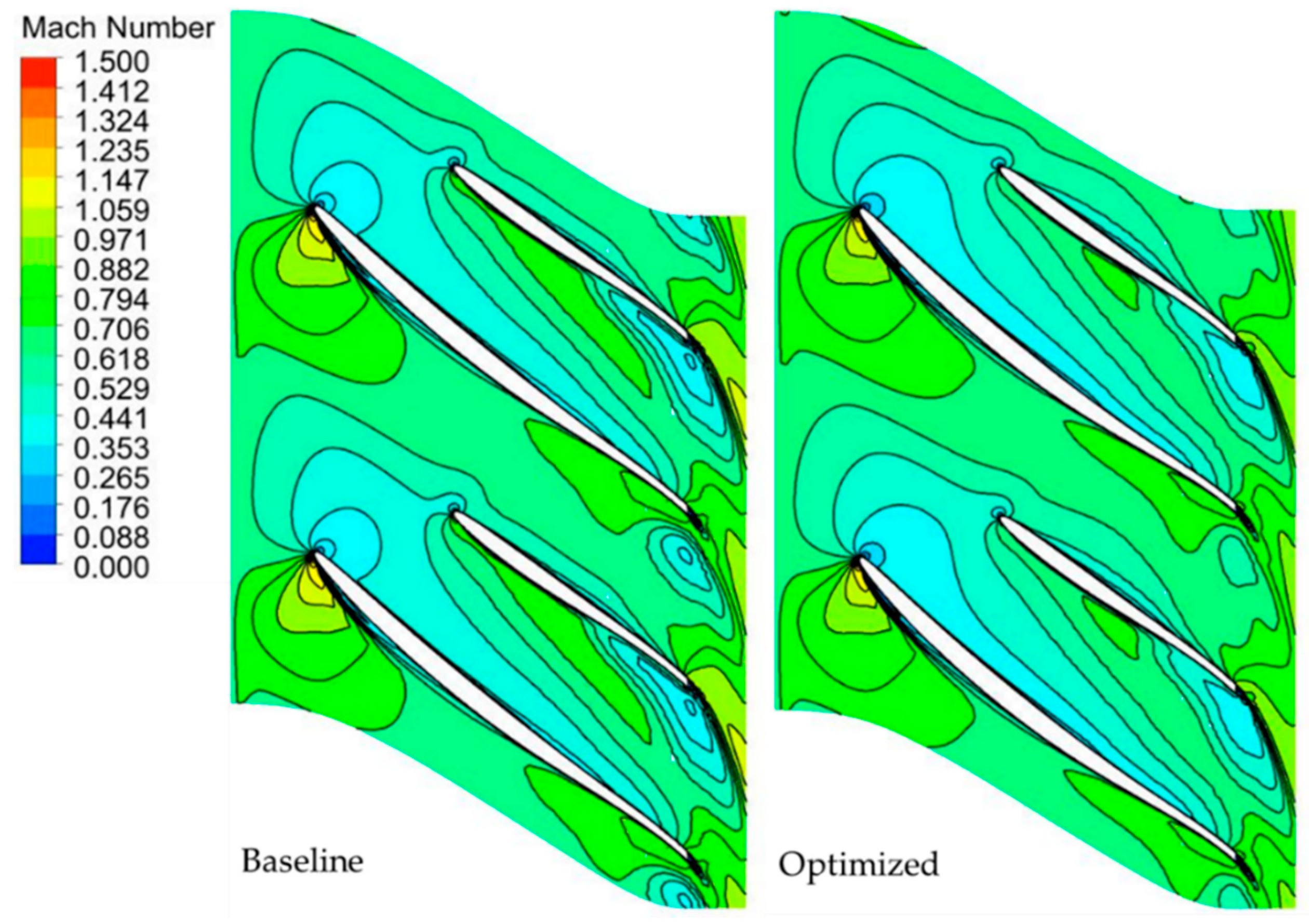
5.1. Comparison of the Baseline (Base Main-Base Splitter) and Optimized Impeller (Optimized Main-Base Splitter)
5.2. Comparison of the Baseline Splitter (Optimized Main-Base Splitter) and Optimized Splitter Impeller (Optimized Main-Optimized Splitter)
6. Conclusions
- After two consecutive optimization processes, a 2.2% efficiency improvement (1.8% based on main blade optimization, 0.4% based on LE location optimization of splitter blade) was observed at the design point as well as the near-choke point. However, similar improvements were not seen in the near-surge region.
- Beta distribution of the main blade and LE location of the splitter blade are adequate parameters to achieve dramatic aerodynamic performance by the optimization process.
- Significant aerodynamic improvement in the micro impeller after the main blade focused optimization procedure indicated that splitter blades could be independently investigated; it was not necessary to assume they were short versions of the main blade.
- Considering different parameterization method on the beta distribution could reduce design points on the fourth and higher-order Bezier curves in comparison to conventional method. Therefore, optimization performance would be increased.
- The LE location of the splitter blade is also an important parameter that enables researchers to better capture the flow and provide better blade loading at the LE, even though it does not have significant impact on the efficiency.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Trigg, M.A.; Tubby, G.R.; Sheard, A.G. Automatic genetic optimization approach to two-dimensional blade profile design for steam turbines. ASME J. Turbomach. 1999, 121, 11–17. [Google Scholar] [CrossRef]
- Casey, M.; Gersbach, F.; Robinson, C. An optimization technique for radial compressor impellers. In Proceedings of the ASME Turbo: Power for Land, Sea, and Air, Berlin, Germany, 9–13 June 2008; pp. 2401–2411. [Google Scholar]
- Benini, E. Optimal Navier-Stokes design of compressor impellers using evolutionary computation. Int. J. Comput. Fluid Dyn. 2003, 17, 357–369. [Google Scholar] [CrossRef]
- Cho, S.-Y.; Ahn, K.-Y.; Lee, Y.-D.; Kim, Y.-C. Optimal design of a centrifugal compressor impeller using evolutionary algorithms. Math. Probl. Eng. 2012, 1–22. [Google Scholar] [CrossRef]
- Kim, J.H.; Choi, J.H.; Husain, A.; Kim, K.Y. Multi-objective optimization of a centrifugal compressor impeller through evolutionary algorithms. Proc. Inst. Mech. Eng. Part A J. Power Energy 2010, 224, 711–721. [Google Scholar] [CrossRef]
- Li, X.; Liu, Z.; Lin, Y. Multipoint and multiobjective optimization of a centrifugal compressor impeller based on genetic algorithm. Math. Probl. Eng. 2017. [Google Scholar] [CrossRef]
- Kim, J.-H.; Choi, J.-H.; Kim, K.-Y. Surrogate modeling for optimization of a centrifugal compressor impeller. Int. J. Fluid Mach. Syst. 2010, 3, 29–38. [Google Scholar] [CrossRef]
- Kim, J.; Choi, J.; Kim, K. Design optimization of a centrifugal compressor impeller using radial basis neural network method. ASME Turbo Expo 2009, 443–451. [Google Scholar] [CrossRef]
- Pierret, S.; Van Den Braembussche, R.A. Turbomachinery blade design using a Navier-Stokes solver and artificial neural network. ASME J. Turbomach. 1999, 121, 326–332. [Google Scholar] [CrossRef]
- Okui, H.; Verstraete, T.; Van Den Braembussche, R.A.; Alsalihi, Z. Three dimensional design and optimization of a Transonic Rotor in axial flow compressors. In Proceedings of the ASME 2011 Turbo Expo: Turbine Technical Conference and Exposition, Vancouver, BC, Canada, 6–10 June 2011; pp. 77–88. [Google Scholar]
- Verstraete, T.; Alsalihi, Z.; Van Den Braembussche, R.A.; Alsalihi, Z. Multidisciplinary optimization of a radial compressor for micro gas turbine applications. In Proceedings of the ASME Turbo: Power for Land, Sea, and Air, Montreal, QC, Canada, 14–17 May 2007. [Google Scholar]
- Whitfield, A.; Baines, N.C. Design of Radial Turbomachines; Long-man Scientific & Technical: Harlow, UK; New York, NY, USA, 1990. [Google Scholar]
- Dixon, S.L. Fluid Mechanics, and Thermodynamics of Turbomachinery, 5th ed.; Elsevier Butterworth-Heinemann: Oxford, UK, 1998. [Google Scholar]
- Chen, H.; Baines, N. Analytical optimization design of radial and mixed flow turbines. J. Power Energy 1992, 206, 177–187. [Google Scholar] [CrossRef]
- Moussavi, S.A.; Hajilouy Benisi, A.; Durali, M. Effect of splitter leading edge location on performance of an automotive turbocharger compressor. Energy 2017, 123, 511–520. [Google Scholar] [CrossRef]
- Van Den Braembussche, R.A.; Alsalihi, Z.; Verstraete, T.; Matsuo, A.; Ibaraki, S.; Sugimoto, K.; Tomita, I. Multidisciplinary Multipoint Optimization of a Transonic Turbocharger Compressor. In Proceedings of the ASME Turbo Expo: Turbine Technical Conference and Exposition, Copenhagen, Denmark, 11–15 June 2012. [Google Scholar]
- Farin, G. Curves and Surfaces for Computer Aided Geometric Design; Elsevier Inc.: New York, NY, USA, 1993. [Google Scholar]
- Montgomery, D.C. Design and Analysis of Experiments; Wiley: New York, NY, USA, 2006. [Google Scholar]
- Hazelton, M.L. Nonparametric Regression, 2nd ed.; Elsevier Wright JDBT-IE of the S& BS: Oxford, UK, 2015; pp. 867–877. [Google Scholar] [CrossRef]
- Fan, J. Design-adaptive nonparametric regression. J. Am. Stat. Assoc. 1992, 87, 998–1004. [Google Scholar] [CrossRef]
- Chagny, G.; Roche, A. Adaptive estimation in the functional nonparametric regression model. J. Multivar. Anal. 2016, 146, 105–118. [Google Scholar] [CrossRef] [Green Version]
- Miyamoto, H.; Nakashima, Y.; Ohba, H. Effect of splitter blades on the flows and characteristics in centrifugal impeller. JSME Int. J. 1992, 35. [Google Scholar] [CrossRef]
- ANSYS Inc. ANSYS Bladegen User’s Guide; ANSYS Inc.: Canonsburg, PA, USA, 2011. [Google Scholar]
- ANSYS Inc. ANSYS TurboGrid User’s Guide; ANSYS Inc.: Canonsburg, PA, USA, 2011. [Google Scholar]
- Menter, F.R.; Kuntz, M.; Langtry, R. Ten Years of Industrial Experience with SST Turbulence Model. In Proceedings of the Fourth International Symposium on Turbulence, Heat Transfer, Antalya, Turkey, 12–17 October 2003. [Google Scholar]
- ANSYS Inc. ANSYS CFX User’s Guide; ANSYS Inc.: Canonsburg, PA, USA, 2011. [Google Scholar]
- ANSYS Inc. ANSYS DesignXplorer User’s Guide; ANSYS Inc.: Canonsburg, PA, USA, 2011. [Google Scholar]
- Li, Z.; Zheng, X. Review of design optimization methods for turbomachinery aerodynamics. Prog. Aerosp. Sci. 2017, 93, 1–23. [Google Scholar] [CrossRef]
- Pinto, J.M.; Gut, J.A.W. A screening method for the optimal selection of plate heat exchanger configurations. Braz. J. Chem. Eng. 2002, 19, 433–439. [Google Scholar] [CrossRef] [Green Version]
- Xu, C.; Amano, R.S. Meridional Considerations of the centrifugal compressor development. Int. J. Rotat. Mach. 2012. [Google Scholar] [CrossRef]























| Geometric Specifications | Value |
|---|---|
| Impeller inlet hub diameter | 9 mm |
| Impeller inlet tip diameter | 24 mm |
| Impeller exit tip diameter | 32.5 mm |
| Impeller exit width | 2.4 mm |
| Number of blades main/splitter | 5/5 |
| Design Parameters | Boundary Values |
|---|---|
| 55° ≤ ≤ 65° | |
| 30° ≤ ≤ 60° | |
| 70° ≤ ≤ 76° | |
| 50° ≤ ≤ 60° | |
| 25° ≤ ≤ 35° | |
| 0° ≤ ≤ 5° | |
| 45° ≤ ≤ 55° | |
| 35° ≤ ≤ 50° | |
| 0% ≤ ≤ 55% | |
| 0% ≤ ≤ 55% |
| Size Factor in Mesh Size Tab | Total Element Size | Computational Time | Iteration | Isentropic Efficiency | Pressure Ratio |
|---|---|---|---|---|---|
| 1.1 | 1,272,054 | 364 min | 670 | 74.64% | 1.99 |
| 1 | 952,786 | 301 min | 570 | 74.15% | 1.98 |
| 0.9 | 680,744 | 282 min | 635 | 73.58% | 1.97 |
| 0.8 | 408,109 | 184 min | 528 | 73.02% | 1.96 |
| 0.7 | 300,372 | 176 min | 571 | 72.8% | 1.95 |
| Design Parameters | ||||||||
|---|---|---|---|---|---|---|---|---|
| Optimal Values | 55.3° | 53.8° | 71.9° | 54.6° | 25.6° | 2.3° | 52.9° | 45.9° |
| Design Parameters | Baseline Impeller | Optimized Impeller |
|---|---|---|
| 58° | 55.3° | |
| 44° | 53.8° | |
| 71° | 71.9° | |
| 54° | 54.6° | |
| 28° | 25.6° | |
| 3° | 2.3° | |
| 48° | 52.9° | |
| 42.5° | 45.9° |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Atac, O.F.; Yun, J.-E.; Noh, T. Aerodynamic Design Optimization of a Micro Radial Compressor of a Turbocharger. Energies 2018, 11, 1827. https://doi.org/10.3390/en11071827
Atac OF, Yun J-E, Noh T. Aerodynamic Design Optimization of a Micro Radial Compressor of a Turbocharger. Energies. 2018; 11(7):1827. https://doi.org/10.3390/en11071827
Chicago/Turabian StyleAtac, Omer Faruk, Jeong-Eui Yun, and Taehyun Noh. 2018. "Aerodynamic Design Optimization of a Micro Radial Compressor of a Turbocharger" Energies 11, no. 7: 1827. https://doi.org/10.3390/en11071827
APA StyleAtac, O. F., Yun, J.-E., & Noh, T. (2018). Aerodynamic Design Optimization of a Micro Radial Compressor of a Turbocharger. Energies, 11(7), 1827. https://doi.org/10.3390/en11071827




