Abstract
Modeling is an integral part of fuel cell design and development. This paper identifies a long-standing inaccuracy in the fuel cell modeling literature. Specifically, it discusses an inexact insertion, in popular models, of cell/stack current into Nernst’s equation in the derivation of output (load) voltage. The origin of the inaccuracy is traced to the nature of reversible and irreversible potentials (equilibrium and non-equilibrium states) in the cell. The significance of the inaccuracy is explained in the context of the electrochemistry and thermodynamics of the fuel cell.
1. Introduction
Modeling the operation of fuel cells is an indispensable part of fuel cell research. In many papers in the literature involving the modeling of solid oxide fuel cells (SOFCs) and proton exchange membrane fuel cells (PEMFCs), an inaccuracy is found in the cell/stack voltage expression (see, for example, references [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30]). We argue that the problem arises because of an inexact intermediate step in the derivation of the output voltage. The origin of this inaccuracy can be traced to the substitution in the Nernst equation of activity (or concentration or partial pressure) with a function of the load current. An analysis of the flaw is presented in the remainder of this paper.
2. Background: The Nernst Equation
The Nernst equation, which is the cornerstone of fuel cell thermodynamics, provides an expression for the reversible thermodynamic potential, also known as the equilibrium voltage or the open-circuit electromotive force (EMF), of the fuel cell [31]:
where is the reference (standard) EMF at unit activity and atmospheric pressure; i and j are the numbers of reactant and product species; a represents the activity; is the stoichiometric coefficient of species i; R is the universal gas constant; F is Faraday’s constant; n is the number of electrons transferred for each molecule of the fuel participating in the reaction; and T is the temperature. For a hydrogen–oxygen fuel cell (e.g., solid oxide fuel cell or proton exchange membrane fuel cell), hydrogen and oxygen are the reactants, and the product is water (or steam). The reference EMF, , depends on the temperature, T:
where is the standard EMF at temperature , and is the change in entropy. The activity, a, of an ideal gas is expressed in terms of its pressure (or partial pressure), p:
where is the standard-state pressure (1 atm). At high temperatures, such as 1000 °C (as in solid oxide fuel cells), steam can be assumed to behave as an ideal gas, and therefore,
Using = 1 atm, and noting that for a hydrogen fuel cell, we have the following version of the Nernst equation for solid oxide fuel cells:
If the fuel cell is operated below 100 °C so that liquid water is produced (as in proton exchange membrane fuel cells), the activity of water can be taken to be unity ( = 1). In that case, the Nernst equation takes the form
3. The Inaccuracy in the Model
Drawing inspiration from the pioneering work in reference [1] where an elegant dynamic model for an SOFC plant was developed, many later papers (e.g., references [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30]) re-derived and/or built upon the model, expressing the partial pressures of the reactants and products as functions of the cell current (not to be confused with the exchange current [31] or the fuel crossover/internal current [31]), before inserting those partial pressure expressions into the Nernst equation.
Reference [1], in its “dynamic behaviour algorithm” (Figure 2 on p. 497 of that paper), expressed (i) the partial pressures of the reactants and products in terms of the corresponding molar flow rates, and (ii) the molar flow rates taking part in the reaction in terms of cell (load) current, and inserted the resulting expressions of , and into Equation (6).
Building upon reference [1], other papers (e.g., references [6,7,12,14,15,16,19,20]) obtained essentially the same core model with the following fallacious form of the Nernst equation:
where , , and are valve molar constants [1]; [1,12,13]; is the ratio of the input molar flow rates of hydrogen and oxygen [2,6]; u is the fuel utilization ratio [2,6]; and is the load current [6]. A detailed derivation of Equation (8) is given in the following sub-section.
Derivation of the Fallacious Expression
A derivation of the fallacious form of the Nernst voltage expression (Equation (8)) is presented here. This derivation follows the treatment in references [1,6,12]. A single cell is considered here; the extension of the derivation to a stack is trivially easy.
Assuming perfect gas properties for hydrogen at the anode channel, we have
where is the partial pressure of hydrogen in the anode channel; is the number of moles of hydrogen in the anode channel; and is the anode volume. Taking the derivative with respect to time, we can express the rate of change of partial pressure in terms of the molar flow rate:
with defined as
Splitting into its three components, namely, the input flow rate, the flow rate that takes part in the reaction, and the output flow rate, we have
and thus (omitting the t for simplicity)
The process of oxygen inflow–reaction–outflow at the cathode channel can be described by
In SOFCs, water vapor (steam) forms at the anode:
In PEMFCs, water forms at the cathode. Of course, when liquid water is produced in a fuel cell (as in PEMFCs), we have
Assuming that “the molar flow of any gas through the valve is proportional to its partial pressure inside the channel” [1], we have for an SOFC
and
at the anode and
at the cathode, with , , and being constants.
From electrochemistry we know that
where is the cell current. Upon the introduction of a constant [1,13],
Now, inserting Equations (17) and (22) into Equation (13) and taking the Laplace transform (we use the notation that the transform of is ), we get [12]
which, upon the substitution of and
becomes
Similarly, for oxygen, Equations (14), (19) and (23) yield
which, with the substitution of and
gives
Now, applying the inverse Laplace transform to Equation (26) allows us go from the s-domain back to the time domain:
The steady-state partial pressure, then, is obtained from the above equation as
(A simpler derivation of Equation (33) is given in Appendix A.1) The steady-state partial pressures of oxygen and steam are obtained similarly:
and
Now, plugging the above three Equations (33)–(35), as well as the definitions of u and (Equations (A4) and (A5), respectively, from Appendix A.2) into the Nernst EMF expression (Equation (6) of Section 2), we obtain, after some algebra (see Appendix A.2), our familiar Equation (8).
4. Analysis of the Inaccuracy
The terminal (load) voltage is generally obtained by subtracting the following types of losses (or “irreversibilities”) from :
- activation loss;
- concentration loss;
- ohmic loss; and
- losses due to fuel crossover and internal current.
Equation (8), or one of its many (implicit or explicit) variants, has been the mainstay of a line of fuel cell modeling research for about two decades now (examples abound; a few representative articles are listed in the References section). Not all of the models in references [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30] show the explicit form of Equation (8), but they all use some form of this equation, by expressing—directly or indirectly—the Nernst voltage as a function of, among other variables, current.
The problem with Equation (8) is that it mixes equilibrium and non-equilibrium expressions. The Nernst voltage (EMF) is the reversible thermodynamic potential that applies only to the equilibrium condition of the cell; the equilibrium is lost when current is drawn from the cell. In other words, the Nernst voltage is, by definition, the open-circuit EMF and cannot therefore be expressed in terms of the cell (load) current or current density.
That the use of in Equation (8) is questionable can also be seen from the fact that setting
causes the right side to be mathematically undefined.
The effect of Equation (8) on the output voltage can be seen in the SOFC polarization curve (Figure 1) obtained from the following relationship:
where V is the output (load) voltage; is given by Equation (8); and r is the ohmic resistance of the cell (cell parameter values, taken from references [1,6,12], are given in Table 1). The upper curve (red) in Figure 1 shows the Nernst voltage, , computed from Equation (8), while the lower one plots the output voltage, V. Equation (36), like Equation (12) of reference [1] and Equation (6) of reference [6], considers only the ohmic loss out of the four types of losses mentioned earlier.
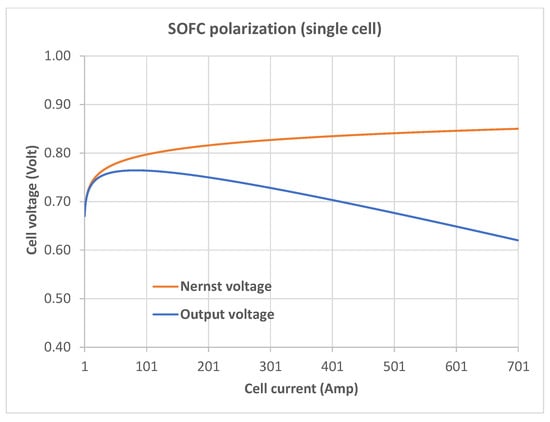
Figure 1.
Solid oxide fuel cell (SOFC) polarization obtained with given by Equation (8).

Table 1.
Numerical values of parameters and constants.
Figure 1 has the horizontal (current) axis starting at 1 A, not zero, because in Equation (8), the Nernst voltage is undefined at .
Figure 1 shows an increase in the Nernst voltage with an increasing load current. At first sight, it may not be immediately clear how the model represented by Equation (8) produces the V-values in this figure (it may not be impossible for the polarization characteristics in Figure 1 to be obtained from actual measurements of a physical fuel cell stack under specific operating conditions; much depends on fuel flow, fuel utilization, thermal effects, diffusion, back-diffusion, load current and voltage requirements, and not all complex interactions are fully understood). It can, however, be argued that Equation (8) produces this polarization curve by holding both u and constant to mimic a constant fuel utilization ratio and a constant hydrogen–oxygen ratio of input flow rates. We need to account for the changes in the V-values without having to make a function of current.
For a head-to-head comparison of the polarization produced by Equation (8) with the “correct” polarization, we need the “correct” Nernst voltage (that is, the Nernst voltage at open circuit), which, unfortunately, cannot be obtained from Equation (8). (We could, of course, obtain the correct Nernst voltage by assuming reasonable values for , and and plugging those values, along with the relevant parameter values from Table 1, into Equation (6), but the resulting Nernst voltage would have no connection to Equation (8).) We circumvent this difficulty by extrapolating the open-circuit Nernst voltage from values produced by Equation (8). Specifically, we use a trivial extrapolation where we obtain the point where the line joining the first two points—(1 A, 0.670472 V) and (2 A, 0.689471 V)—meets the = 0 line. This gives us an extrapolated
which is used in Figure 2 to show the “correct” polarization behavior. The upper plot (red) in Figure 2 represents the (constant) Nernst voltage, and the lower one shows the output values from Equation (36) (obviously, both the plots in this figure are straight lines). For ease of comparison with Figure 1, the current axis in Figure 2 starts from 1 A.
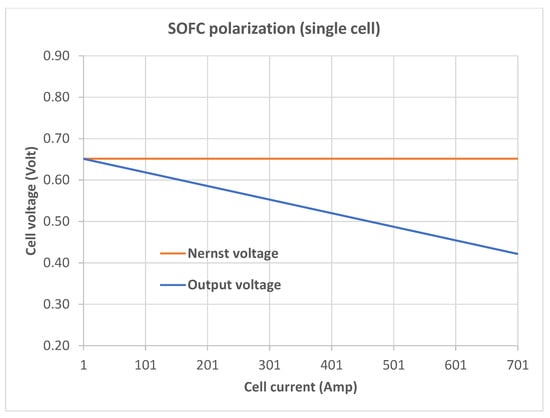
Figure 2.
SOFC polarization obtained with = 0.651473 V.
5. Discussion
If a non-zero current is to be considered, the proper equation to use is the Butler–Volmer equation, not the Nernst equation. The current–voltage relationship at a non-zero current (away from equilibrium) is perhaps best investigated using reaction kinetic expressions with microscopic reversibility. When modeling specific polarization behaviors, it is important to distinguish between the “reversible” potential and the “irreversibilities”.
The difference between reversible and irreversible potentials and its connection to the Nernst equation are important in the study of solid oxide electrolysis cells (e.g., [32]), too.
In reference [33], the partial pressures of hydrogen and oxygen of a proton exchange membrane fuel cell are expressed (in Equations (2) and (3) of that paper [33]) in terms of current, but before these partial pressures are plugged into the Nernst equation Equation (1) of that paper [33]) to obtain the reversible potential, the current, correctly, is set to zero. Reference [33] also reported using non-zero values of current in the Nernst equation.
Reference [12] used Equation (8) to generate both training and test data, and therefore, none of the conclusions in that paper are invalidated by the inaccuracy discussed here.
6. Conclusions
An inaccuracy in the fuel cell modeling literature involving the nature of the reversible thermodynamic potential was identified in this paper. An analysis of the inaccuracy was provided and its significance explained. To summarize, there is nothing wrong with the Nernst equation that provides the reversible (equilibrium) voltage of a fuel cell; what is wrong is the mixing up of equilibrium and non-equilibrium conditions by inserting cell (load) current into the Nernst voltage expression. It can be argued that expressing the Nernst voltage as a function of current is a “quick-and-dirty” trick that makes modeling easy for us. However, by taking such a shortcut, we compromise scientific rigor for the sake of practical convenience.
Funding
This research was funded, in part, by the United States National Science Foundation Grant IIS-1115352.
Acknowledgments
Three anonymous reviewers provided detailed comments on an earlier version of this paper.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| SOFC | Solid oxide fuel cell |
| PEMFC | Proton exchange membrane fuel cell |
| EMF | Electromotive force |
| Nernst potential (open-circuit EMF) of a single cell, V | |
| Standard (reference) EMF of a single cell, V | |
| Standard (reference) EMF of a single cell at temperature , V | |
| V | Output terminal voltage of a single cell, V |
| T | Temperature, K |
| n | Number of electrons transferred |
| a | Activity |
| Activity of hydrogen | |
| Activity of oxygen | |
| Activity of water vapor (steam) | |
| Change in entropy, J/(mol K) | |
| p | Pressure or partial pressure, atm |
| Standard-state pressure, atm | |
| Partial pressure of hydrogen, atm | |
| Partial pressure of oxygen, atm | |
| Partial pressure of water vapor, atm | |
| Fuel cell current, A | |
| u | Fuel utilization ratio |
| Ratio of hydrogen-to-oxygen input flow rates | |
| Valve molar constant for hydrogen, mol/(s atm) | |
| Valve molar constant for oxygen, mol/(s atm) | |
| Valve molar constant for water vapor, mol/(s atm) | |
| Modeling constant, mol/(s A) | |
| Anode compartment volume, m | |
| Cathode compartment volume, m | |
| t | Time, s |
| Amount of hydrogen in the anode channel, mol | |
| Rate of change of the quantity of hydrogen in the anode channel, mol/s | |
| Hydrogen input flow rate, mol/s | |
| Hydrogen output flow rate, mol/s | |
| Hydrogen flow rate that takes part in the reaction, mol/s | |
| Rate of change of the amount of oxygen in the cathode channel, mol/s | |
| Oxygen input flow rate, mol/s | |
| Oxygen output flow rate, mol/s | |
| Oxygen reacting flow rate, mol/s | |
| Rate of change of the amount of water vapor in the anode channel, mol/s | |
| Water vapor output flow rate, mol/s | |
| Water vapor flow rate produced in the reaction, mol/s | |
| Hydrogen flow response time constant, s | |
| Oxygen flow response time constant, s | |
| Water vapor flow response time constant, s | |
| r | Ohmic resistance of a single cell, Ohm |
| Notation (used in the subscript) to indicate steady-state values | |
| Laplace transform of | |
| R | Universal gas constant, J/(mol K) |
| F | Faraday’s constant, Coulombs/mol |
Appendix A
Appendix A.1. Equation (33)
At steady state, there are no changes in the input/output flow rates or the current, and the partial pressures of hydrogen, oxygen and water vapor have fixed (unchanging) values. Of course, corresponding to a load change, the cell (stack) may move from one fixed (steady) state to another fixed (steady) state. The steady-state partial pressure of a reactant or product can be obtained by setting the time derivative of its partial pressure to zero and solving for the partial pressure. From Equation (13), setting
we have at steady state
which, by Equations (17) and (22), becomes
which, after rearrangement of terms, yields Equation (33).
Appendix A.2. Equation (8)
We will need the definitions of the fuel utilization ratio [2,6],
and the ratio of hydrogen-to-oxygen input flow rates [2,6]:
References
- Padulles, J.; Ault, G.W.; McDonald, J.R. An integrated SOFC plant dynamic model for power systems simulation. J. Power Sources 2000, 86, 495–500. [Google Scholar] [CrossRef]
- Zhu, Y.; Tomsovic, K. Development of models for analyzing the load-following performance of microturbines and fuel cells. Electr. Power Syst. Res. 2002, 62, 1–11. [Google Scholar] [CrossRef]
- El-Sharkh, M.Y.; Rahman, A.; Alam, M.S.; Byrne, P.C.; Sakla, A.A.; Thomas, T. A dynamic model for a stand-alone PEM fuel cell power plant for residential applications. J. Power Sources 2004, 138, 199–204. [Google Scholar] [CrossRef]
- Jurado, F.; Valverde, M. Multiobjective genetic algorithms for fuzzy inverter in solid oxide fuel cell system. In Proceedings of the IEEE International Symposium on Industrial Electronics (ISIE), Dubrovnik, Croatia, 20–23 June 2005. [Google Scholar]
- Jurado, F.; Valverde, M. Genetic fuzzy control applied to the inverter of solid oxide fuel cell for power quality improvement. Electr. Power Syst. Res. 2005, 76, 93–105. [Google Scholar] [CrossRef]
- Li, Y.H.; Choi, S.S.; Rajakaruna, S. An analysis of the control and operation of a solid oxide fuel-cell power plant in an isolated system. IEEE Trans. Energy Convers. 2005, 20, 381–387. [Google Scholar] [CrossRef]
- Li, Y.H.; Rajakaruna, S.; Choi, S.S. Control of a solid oxide fuel cell power plant in a grid-connected system. IEEE Trans. Energy Convers. 2007, 22, 405–413. [Google Scholar] [CrossRef]
- Wang, C.; Nehrir, M.H.; Shaw, S.R. Dynamic models and model validation for PEM fuel cells using electrical circuits. IEEE Trans. Energy Convers. 2005, 20, 442–451. [Google Scholar] [CrossRef]
- Wang, C.; Nehrir, M.H. A physically based dynamic model for solid oxide fuel cells. IEEE Trans. Energy Convers. 2007, 22, 887–897. [Google Scholar] [CrossRef]
- Huo, H.-B.; Zhong, Z.-D.; Zhu, X.-J.; Tu, H.-Y. Nonlinear dynamic modeling for a SOFC stack by using a Hammerstein model. J. Power Sources 2008, 175, 441–446. [Google Scholar] [CrossRef]
- Wu, X.-J.; Zhu, X.-J.; Cao, G.-Y.; Tu, H.-Y. Predictive control of SOFC based on a GA-RBF neural network. J. Power Sources 2008, 179, 232–239. [Google Scholar] [CrossRef]
- Chakraborty, U.K. Static and dynamic modeling of solid oxide fuel cell using genetic programming. Energy 2009, 34, 740–751. [Google Scholar] [CrossRef]
- Chakraborty, U.K. An error in solid oxide fuel cell stack modeling. Energy 2011, 36, 801–802. [Google Scholar] [CrossRef]
- Nayeripour, M.; Hoseintabar, M.; Niknam, T. A new method for dynamic performance improvement of a hybrid power system by coordination of converter’s controller. J. Power Sources 2011, 196, 4033–4043. [Google Scholar] [CrossRef]
- Nayeripour, M.; Hoseintabar, M.; Niknam, T.; Adabi, J. Power management, dynamic modeling and control of wind/FC/battery-bank based hybrid power generation system for stand-alone application. Eur. Trans. Electr. Power 2012, 22, 271–293. [Google Scholar] [CrossRef]
- Radisavljevic, V. On controllability and system constraints of the linear models of proton exchange membrane and solid oxide fuel cells. J. Power Sources 2011, 196, 8549–8552. [Google Scholar] [CrossRef]
- Torreglosa, J.P.; García, P.; Fernández, L.M.; Jurado, F. Predictive control for the energy management of a fuel-cell–battery–supercapacitor tramway. IEEE Trans. Ind. Inform. 2014, 10, 276–285. [Google Scholar] [CrossRef]
- Fedakar, S.; Bahceci, S.; Yalcinoz, T. Modeling and simulation of grid connected solid oxide fuel cell using PSCAD. J. Renew. Sustain. Energy 2014, 6, 053118. [Google Scholar] [CrossRef]
- Taghizadeh, M.; Hoseintabar, M.; Faiz, J. Frequency control of isolated WT/PV/SOFC/UC network with new control strategy for improving SOFC dynamic response. Int. Trans. Electr. Energy Syst. 2015, 25, 1748–1770. [Google Scholar] [CrossRef]
- Chettibi, N.; Mellit, A.; Sulligoi, G.; Massi Pavan, A. Fuzzy-based power control for distributed generators based on solid oxide fuel cells. In Proceedings of the IEEE International Conference on Clean Electrical Power (ICCEP), Taormina, Italy, 16–18 June 2015; pp. 580–585. [Google Scholar] [CrossRef]
- Barelli, L.; Bidini, G.; Ottaviano, A. Solid oxide fuel cell modelling: Electrochemical performance and thermal management during load-following operation. Energy 2016, 115, 107–119. [Google Scholar] [CrossRef]
- Vigneysh, T.; Kumarappan, N. Autonomous operation and control of photovoltaic/solid oxide fuel cell/battery energy storage based microgrid using fuzzy logic controller. Int. J. Hydrogen Energy 2016, 41, 1877–1891. [Google Scholar] [CrossRef]
- Wu, Z.; Shi, W.; Li, D.; He, T.; Xue, Y.; Han, M.; Zheng, S. The disturbance rejection design based on physical feedforward for solid oxide fuel cell. In Proceedings of the 17th IEEE International Conference on Control, Automation and Systems (ICCAS), Jeju, Korea, 18–21 October 2017. [Google Scholar]
- Pan, L.; Xue, Y.; Sun, L.; Li, D.; Wu, Z. Multiple model predictive control for solid oxide fuel cells. In Proceedings of the ASME 2017 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference (IDETC/CIE 2017), Cleveland, OH, USA, 6–9 August 2017. [Google Scholar]
- Wu, G.; Sun, L.; Lee, K.Y. Disturbance rejection control of a fuel cell power plant in a grid-connected system. Control Eng. Pract. 2017, 60, 183–192. [Google Scholar] [CrossRef]
- Sun, L.; Hua, Q.; Shen, J.; Xue, Y.; Li, D.; Lee, K.Y. A combined voltage control strategy for fuel cell. Sustainability 2017, 9, 1517. [Google Scholar] [CrossRef]
- Darjat; Sulistyo; Triwiyatno, A.; Thalib, H. The design of connection solid oxide fuel cell (SOFC) integrated grid with three-phase inverter. IOP Conf. Ser. Mater. Sci. Eng. 2018, 316, 012057. [Google Scholar] [CrossRef]
- Sun, L.; Wu, G.; Xue, Y.; Shen, J.; Li, D.; Lee, K.Y. Coordinated control strategies for fuel cell power plant in a microgrid. IEEE Trans. Energy Convers. 2018, 33, 1–9. [Google Scholar] [CrossRef]
- Chettibi, N.; Mellit, A. Intelligent control strategy for a grid connected PV/SOFC/BESS energy generation system. Energy 2018, 147, 239–262. [Google Scholar] [CrossRef]
- Safari, A.; Shahsavari, H.; Salehi, J. A mathematical model of SOFC power plant for dynamic simulation of multi-machine power systems. Energy 2018, 149, 397–413. [Google Scholar] [CrossRef]
- Larminie, J.; Dicks, A. Fuel Cell Systems Explained, 2nd ed.; Wiley: Chichester, UK, 2003. [Google Scholar]
- Udagawa, J.; Aguiar, P.; Brandon, N.P. Hydrogen production through steam electrolysis: Model-based steady state performance of a cathode-supported intermediate temperature solid oxide electrolysis cell. J. Power Sources 2007, 166, 127–136. [Google Scholar] [CrossRef]
- Chakraborty, U.K.; Abbott, T.; Das, S.K. PEM fuel cell modeling using differential evolution. Energy 2012, 40, 387–399. [Google Scholar] [CrossRef]
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).