A Bottom-Up Model for Household Load Profile Based on the Consumption Behavior of Residents
Abstract
:1. Introduction
- A forecasting framework is proposed for the household load profile with the bottom-up modelling method considering the consumption behavior of residents.
- A similar day extraction model is formulated to choose similar days by comparing external environmental factors and household internal influence factors on the energy consumption in order to enhance the prediction accuracy of residents’ consumption behavior.
- A case study is conducted based on the measured data in a residential community containing 64 households. Furthermore, load profiles of families in different categories (i.e., worker family, senior family, and senior + worker family) are forecasted separately to verify the effectiveness of proposed approach in different family categories.
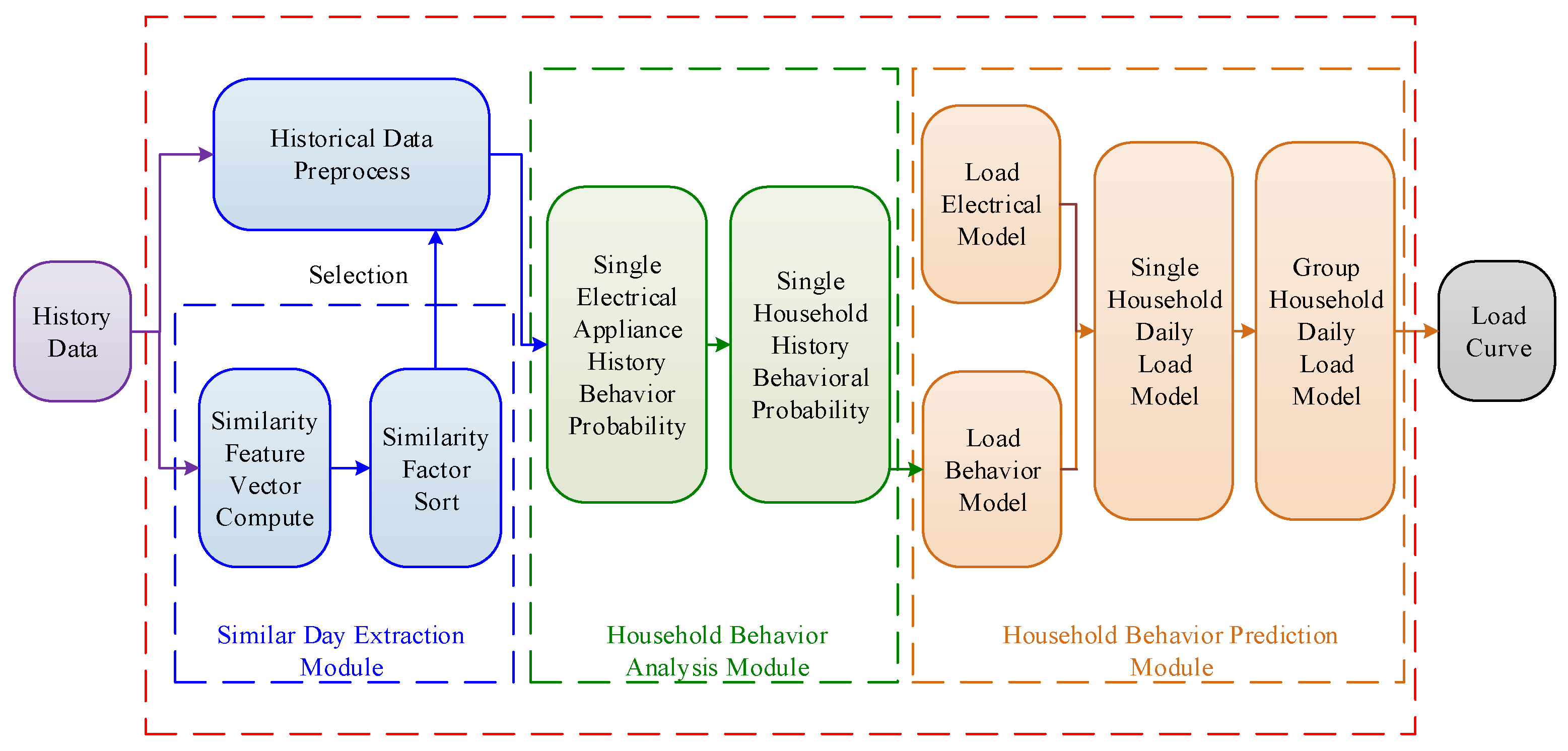
2. Electricity Forecasting Framework
3. Data Acquisition and Processing
3.1. Data Acquisition
3.2. Data Processing
4. Bottom-Up Forecasting Model for Group Household
4.1. Similar Day Extraction Module
4.1.1. Similarity Feature Vector Computing Module
- (1)
- Human comfort factor
- (2)
- Time gap factor
- (3)
- Weekday type factor
- (4)
- Major event factor
- (5)
- Family category index
4.1.2. Similarity Factor Sorting Module
4.2. Load Profile for Group Household
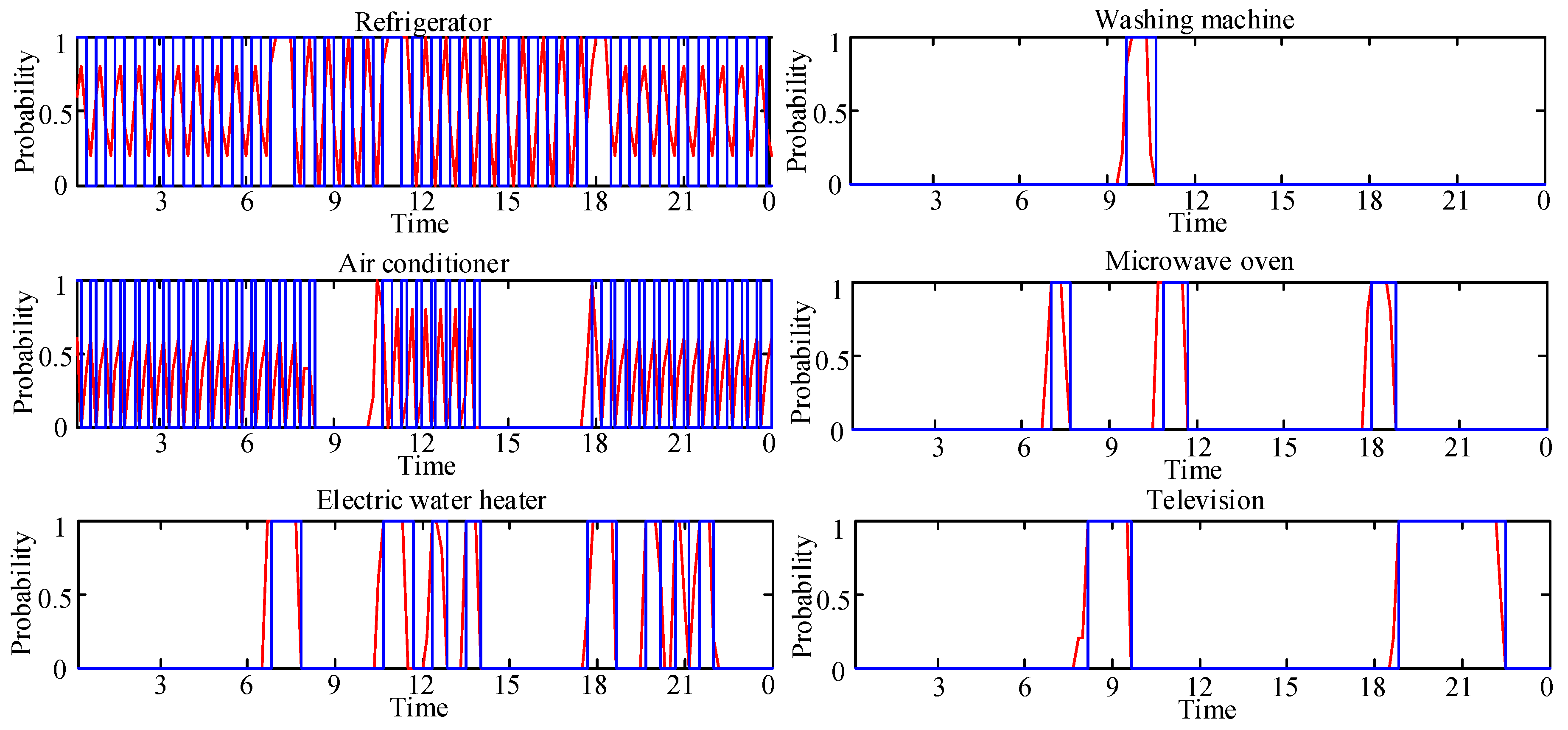
4.2.1. Household Behavior Analysis Module
4.2.2. Household Behavior Prediction Module
5. Case Study
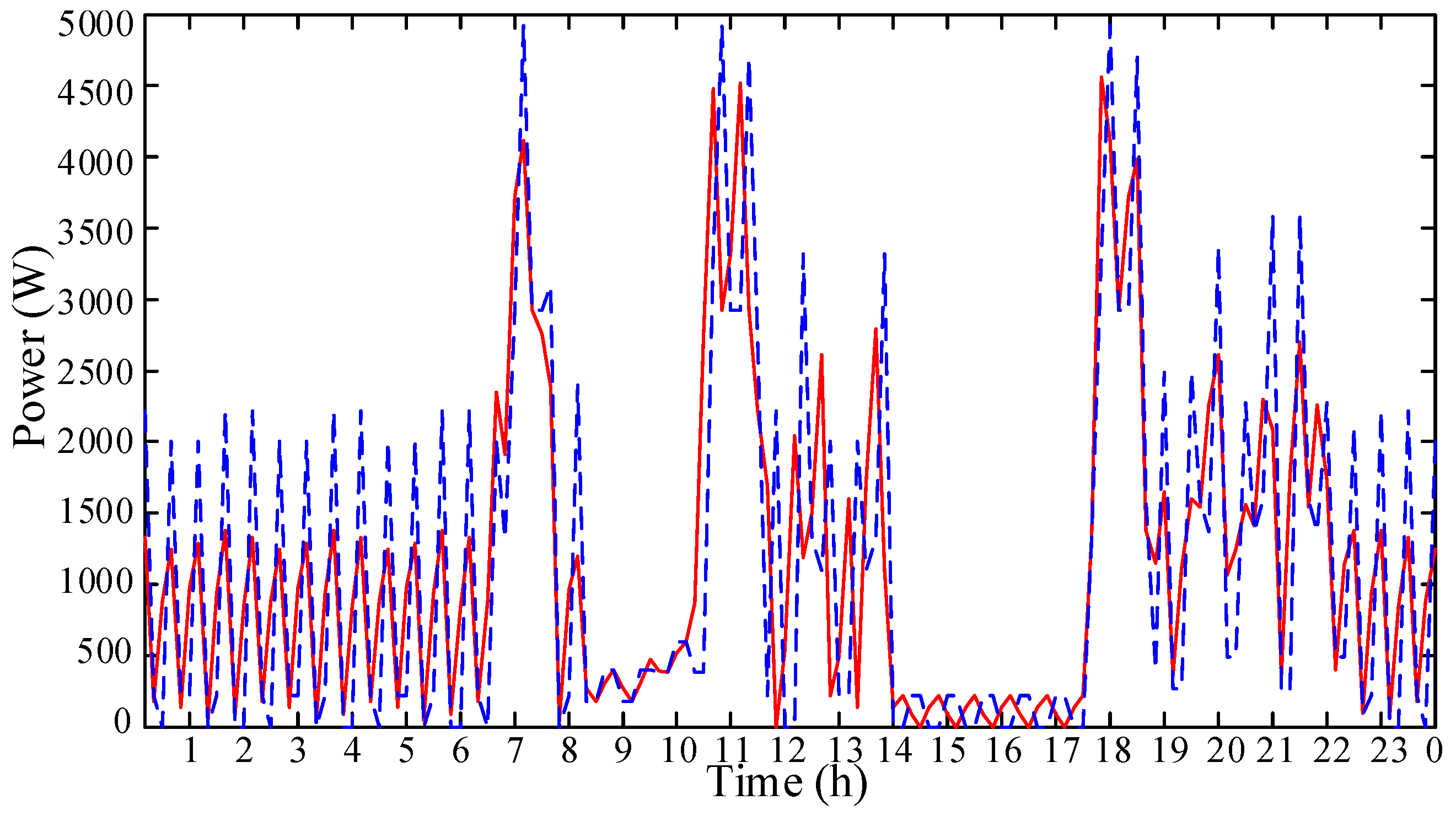
5.1. Forecasting Result for a Single Household
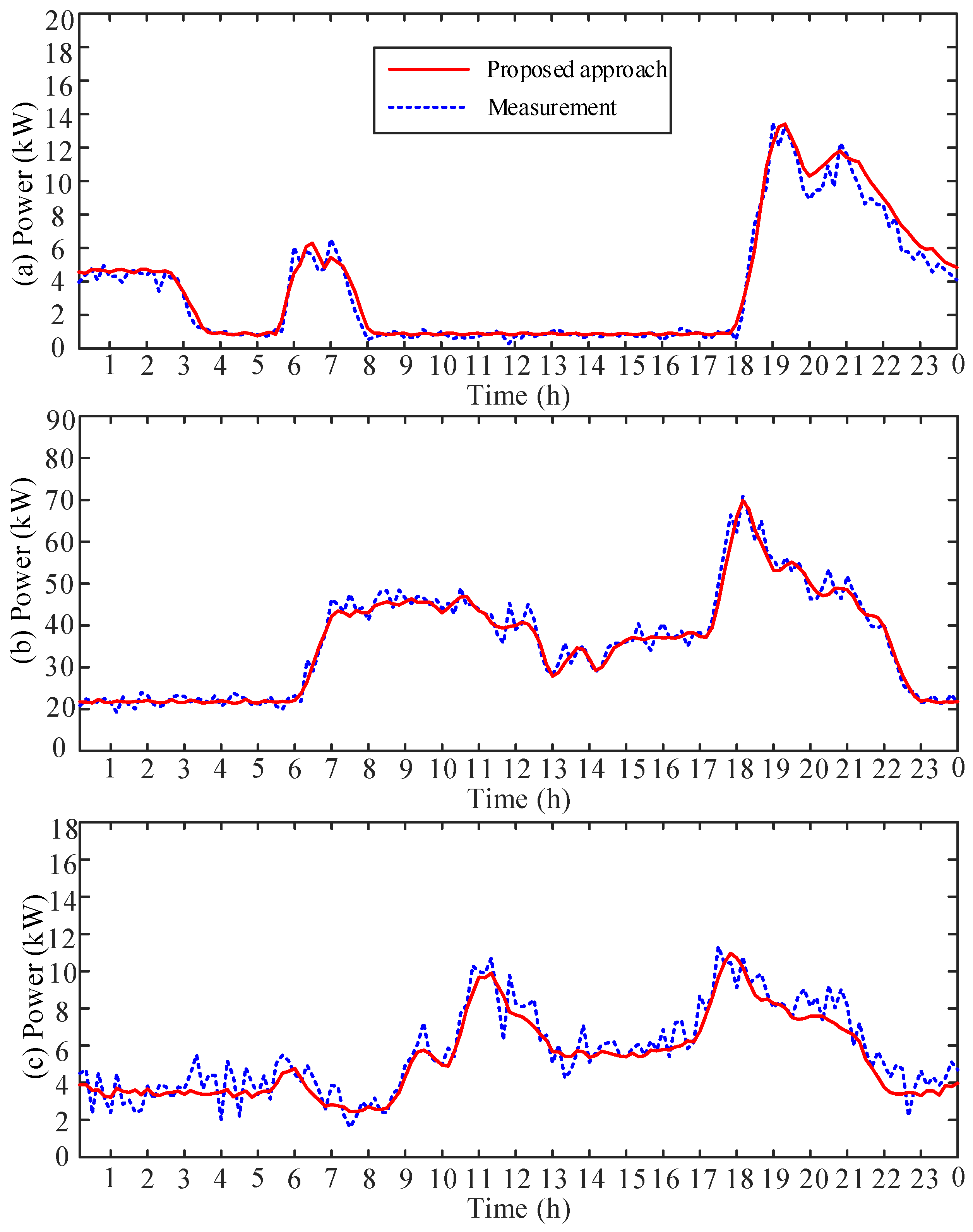
5.2. Forecasting Result for Group Household
5.3. Discussion on the Application of Proposed Approach
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Date | Humidity | Temperature | Wind Speed | Weekday Type | Major Event |
|---|---|---|---|---|---|
| 1 July 2017 | 45 | 28 | 6 | 6 | 0 |
| 2 July 2017 | 70 | 33 | 12 | 7 | 0 |
| 3 July 2017 | 47 | 26 | 8 | 1 | 0 |
| 4 July 2017 | 48 | 28 | 6 | 2 | 0 |
| 5 July 2017 | 51 | 30 | 10 | 3 | 0 |
| 6 July 2017 | 33 | 30 | 7 | 4 | 0 |
| 7 July 2017 | 40 | 32 | 8 | 5 | 0 |
| 8 July 2017 | 45 | 32 | 8 | 6 | 0 |
| 9 July 2017 | 72 | 30 | 7 | 7 | 0 |
| 10 July 2017 | 81 | 34 | 12 | 1 | 0 |
| 11 July 2017 | 65 | 32 | 8 | 2 | 0 |
| 12 July 2017 | 75 | 30 | 12 | 3 | 0 |
| 13 July 2017 | 73 | 30 | 10 | 4 | 0 |
| 14 July 2017 | 71 | 30 | 10 | 5 | 0 |
| 15 July 2017 | 60 | 32 | 5 | 6 | 0 |
| 16 July 2017 | 61 | 32 | 3 | 7 | 0 |
| 17 July 2017 | 60 | 32 | 9 | 1 | 0 |
| 18 July 2017 | 52 | 32 | 8 | 2 | 0 |
| 19 July 2017 | 60 | 32 | 7 | 3 | 0 |
| 20 July 2017 | 78 | 30 | 11 | 4 | 0 |
| 21 July 2017 | 65 | 30 | 8 | 5 | 0 |
| 22 July 2017 | 61 | 34 | 7 | 6 | 0 |
| 23 July 2017 | 47 | 34 | 8 | 7 | 0 |
| 24 July 2017 | 71 | 35 | 11 | 1 | 0 |
| 25 July 2017 | 60 | 34 | 10 | 2 | 0 |
| 26 July 2017 | 43 | 32 | 9 | 3 | 0 |
| 27 July 2017 | 48 | 34 | 6 | 4 | 0 |
| 28 July 2017 | 84 | 36 | 12 | 5 | 0 |
| 29 July 2017 | 77 | 36 | 11 | 6 | 0 |
| 30 July 2017 | 79 | 32 | 12 | 7 | 0 |
| 31 July 2017 | 60 | 33 | 8 | 1 | 0 |
| Family | Morning | Noon | Evening | Wake | Bed | Family | Morning | Noon | Evening | Wake | Bed |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 42 | 65 | 108 | 37 | 138 | 33 | 37 | 65 | 106 | 34 | 126 |
| 2 | 41 | 64 | 109 | 39 | 139 | 34 | 42 | 63 | 110 | 38 | 135 |
| 3 | 44 | 0 | 113 | 42 | 143 | 35 | 44 | 62 | 111 | 39 | 137 |
| 4 | 43 | 70 | 113 | 42 | 141 | 36 | 41 | 68 | 115 | 39 | 137 |
| 5 | 43 | 69 | 112 | 43 | 142 | 37 | 45 | 63 | 109 | 39 | 139 |
| 6 | 44 | 0 | 113 | 42 | 142 | 38 | 45 | 63 | 109 | 39 | 137 |
| 7 | 37 | 69 | 108 | 35 | 126 | 39 | 44 | 0 | 112 | 42 | 144 |
| 8 | 44 | 66 | 113 | 35 | 137 | 40 | 43 | 62 | 110 | 40 | 139 |
| 9 | 44 | 62 | 107 | 41 | 137 | 41 | 42 | 64 | 107 | 40 | 135 |
| 10 | 43 | 63 | 109 | 40 | 135 | 42 | 37 | 68 | 107 | 35 | 125 |
| 11 | 45 | 0 | 111 | 43 | 142 | 43 | 43 | 65 | 112 | 40 | 137 |
| 12 | 35 | 65 | 106 | 31 | 130 | 44 | 45 | 0 | 114 | 42 | 144 |
| 13 | 43 | 66 | 109 | 36 | 134 | 45 | 42 | 64 | 112 | 40 | 137 |
| 14 | 42 | 65 | 108 | 40 | 137 | 46 | 34 | 64 | 107 | 33 | 120 |
| 15 | 42 | 68 | 115 | 41 | 142 | 47 | 43 | 67 | 108 | 39 | 136 |
| 16 | 43 | 64 | 110 | 40 | 137 | 48 | 40 | 67 | 111 | 38 | 134 |
| 17 | 45 | 0 | 114 | 43 | 144 | 49 | 42 | 64 | 113 | 40 | 138 |
| 18 | 44 | 64 | 110 | 35 | 135 | 50 | 45 | 0 | 115 | 43 | 143 |
| 19 | 38 | 68 | 108 | 35 | 126 | 51 | 37 | 68 | 109 | 35 | 124 |
| 20 | 43 | 64 | 107 | 40 | 136 | 52 | 40 | 63 | 109 | 39 | 136 |
| 21 | 43 | 65 | 109 | 39 | 138 | 53 | 39 | 66 | 112 | 40 | 135 |
| 22 | 39 | 70 | 110 | 38 | 125 | 54 | 43 | 67 | 111 | 39 | 134 |
| 23 | 44 | 65 | 107 | 41 | 136 | 55 | 44 | 0 | 118 | 42 | 143 |
| 24 | 44 | 0 | 112 | 42 | 143 | 56 | 43 | 64 | 110 | 40 | 133 |
| 25 | 43 | 63 | 107 | 41 | 132 | 57 | 43 | 0 | 116 | 43 | 144 |
| 26 | 43 | 64 | 107 | 39 | 133 | 58 | 44 | 65 | 109 | 40 | 135 |
| 27 | 45 | 0 | 115 | 42 | 144 | 59 | 43 | 66 | 110 | 40 | 134 |
| 28 | 36 | 68 | 107 | 34 | 122 | 60 | 44 | 0 | 113 | 41 | 141 |
| 29 | 44 | 0 | 118 | 41 | 140 | 61 | 36 | 66 | 107 | 34 | 127 |
| 30 | 42 | 67 | 114 | 40 | 138 | 62 | 44 | 64 | 108 | 41 | 132 |
| 31 | 43 | 64 | 108 | 40 | 134 | 63 | 41 | 69 | 110 | 38 | 133 |
| 32 | 45 | 64 | 109 | 40 | 132 | 64 | 35 | 65 | 111 | 34 | 124 |
References
- Shi, J.; Lee, W.; Liu, X. Generation scheduling optimization of wind-energy storage system based on wind power output fluctuation features. IEEE Trans. Ind. Appl. 2018, 54, 10–17. [Google Scholar] [CrossRef]
- Capozzoli, A.; Piscitelli, M.; Brandi, S. Mining typical load profiles in buildings to support energy management in the smart city context. Energy Procedia 2017, 134, 865–874. [Google Scholar] [CrossRef]
- Mediwaththe, C.; Stephens, E.; Smith, D. Competitive energy trading framework for demand-side management in neighborhood area networks. IEEE Trans. Smart Grid 2017, 1–10. [Google Scholar] [CrossRef]
- Gajowniczek, K.; Zabkowski, T. Electricity forecasting on the individual household level enhanced based on activity patterns. PLoS ONE 2017, 12, e0174098. [Google Scholar] [CrossRef] [PubMed]
- Chuan, L.; Ukil, A. Modeling and validation of electrical load profiling in residential buildings in Singapore. IEEE Trans. Power Syst. 2015, 30, 2800–2809. [Google Scholar] [CrossRef]
- Swan, L.G.; Ugursal, V.I. Modeling of end-use energy consumption in the residential sector: A review of modeling techniques. Renew. Sustain. Energy Rev. 2009, 13, 1819–1835. [Google Scholar] [CrossRef]
- Jardini, J.A.; Tahan, C.M.V.; Gouvea, M.R. Daily load profiles for residential, commercial and industrial low voltage consumers. IEEE Trans. Power Deliv. 2000, 15, 375–380. [Google Scholar] [CrossRef]
- Hoverstad, B.A.; Tidemann, A.; Langseth, H. Short-term load forecasting with seasonal decomposition using evolution for parameter tuning. IEEE Trans. Smart Grid 2015, 6, 1904–1913. [Google Scholar] [CrossRef]
- Thouvenot, V.; Pichavant, A.; Goude, Y. Electricity forecasting using multi-stage estimators of nonlinear additive models. IEEE Trans. Power Syst. 2016, 31, 3665–3673. [Google Scholar] [CrossRef]
- McLoughlin, F.; Duffy, A.; Conlon, M. Characterising domestic electricity consumption patterns by dwelling and occupant socio-economic variables: An Irish case study. Energy Build. 2012, 48, 240–249. [Google Scholar] [CrossRef]
- Wang, C.; Grozev, G.; Seo, S. Decomposition and statistical analysis for regional electricity demand forecasting. Energy 2012, 41, 313–325. [Google Scholar] [CrossRef]
- Dordonnat, V.; Koopman, S.J.; Ooms, M. An hourly periodic state space model for modelling French national electricity load. Int. J. Forecast. 2008, 24, 566–587. [Google Scholar] [CrossRef] [Green Version]
- Stephen, B.; Mutanen, A.J.; Galloway, S. Enhanced load profiling for residential network customers. IEEE Trans. Power Deliv. 2014, 29, 88–96. [Google Scholar] [CrossRef]
- Nagbe, K.; Cugliari, J.; Jacques, J. Short-Term Electricity Demand Forecasting Using a Functional State Space Model. Energies 2018, 11, 1120. [Google Scholar] [CrossRef]
- Capasso, A.; Grattieri, W.; Lamedica, R. A bottom-up approach to residential load modeling. IEEE Trans. Power Syst. 1994, 9, 957–964. [Google Scholar] [CrossRef]
- Marszal-Pomianowska, A.; Heiselberg, P.; Larsen, O.K. Household electricity demand profiles-A high-resolution load model to facilitate modelling of energy flexible buildings. Energy 2016, 103, 487–501. [Google Scholar] [CrossRef]
- Widen, J.; Nilsson, A.M.; Wackelgard, E. A combined Markov-chain and bottom-up approach to modelling of domestic lighting demand. Energy Build. 2009, 41, 1001–1012. [Google Scholar] [CrossRef]
- Paatero, J.V.; Lund, P.D. A model for generating household electricity load profiles. Int. J. Energy Res. 2006, 30, 273–290. [Google Scholar] [CrossRef] [Green Version]
- Fischer, D.; Hartl, A.; Wille-Haussmann, B. Model for electric load profiles with high time resolution for German households. Energy Build. 2015, 92, 170–179. [Google Scholar] [CrossRef]
- Fischer, D.; Wolf, T.; Scherer, J. A stochastic bottom-up model for space heating and domestic hot water load profiles for German households. Energy Build. 2016, 124, 120–128. [Google Scholar] [CrossRef]
- Singh, S.; Yassine, A. Big data mining of energy time series for behavioral analytics and energy consumption forecasting. Energies 2018, 11, 452. [Google Scholar] [CrossRef]
- Richardson, I.; Thomson, M.; Infield, D. Domestic electricity use: A high-resolution energy demand model. Energy Build. 2010, 42, 1878–1887. [Google Scholar] [CrossRef] [Green Version]
- Widen, J.; Wackelgard, E. A high-resolution stochastic model of domestic activity patterns and electricity demand. Appl. Energy 2010, 87, 1880–1892. [Google Scholar] [CrossRef]
- Lin, S.; Huang, N.; Zhao, L. Domestic daily load curve modeling based on user behavior. Electr. Power Constr. 2016, 37, 114–121. [Google Scholar]
- Wei, H.; Su, Z.; Yao, G. The Short-Term Load Forecasting Based on Similar Day and PSO-NN Model with Human Body Comfortable Indicator Vector. Power Syst. Clean Energy 2016, 32, 135–139. [Google Scholar]
- Angelos, E.W.S.; Saavedra, O.R.; Cortes, O.A.C. Detection and identification of abnormalities in customer consumptions in power distribution systems. IEEE Trans. Power Deliv. 2011, 26, 2436–2442. [Google Scholar] [CrossRef]
- Ma, Z.; Yan, Z.R.; Nord, N. A variation focused cluster analysis strategy to identify typical daily heating load profiles of higher education buildings. Energy 2017, 134, 90–102. [Google Scholar] [CrossRef]
- Chicco, G.; Napoli, R.; Piglione, F. Comparisons among clustering techniques for electricity customer classification. IEEE Trans. Power Syst. 2006, 21, 933–940. [Google Scholar] [CrossRef]
- Ferraro, P.; Crisostomi, E.; Tucci, M. Comparison and clustering analysis of the daily electrical load in eight European countries. Electr. Power Syst. Res. 2016, 141, 114–123. [Google Scholar] [CrossRef]
- Panapakidis, I.; Asimopoulos, N.; Dagoumas, A. An Improved Fuzzy C-Means Algorithm for the Implementation of Demand Side Management Measures. Energies 2017, 10, 1407. [Google Scholar] [CrossRef]


| Appliance | Power (W) | Appliance | Power (W) |
|---|---|---|---|
| Fluorescent lamp | 90 | Air conditioner | 2000 |
| Washing machine | 380 | Electric water heater | 1100 |
| Microwave oven | 900 | Television | 180 |
| Refrigerator | 220 | Rice cooker | 500 |
| Parameter | |||
|---|---|---|---|
| Measurement (W) | 85,760 | 24,188 | 45,824 |
| Proposed approach (W) | 88,794 | 25,348 | 46,366 |
| Comparison approach (W) | 95,605 | 26,362 | 47,946 |
| Proposed approach error (%) | 3.5 | 4.8 | 1.2 |
| Comparison approach error (%) | 11.5 | 9.0 | 4.6 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, B.; Liu, X.; Zhu, Z. A Bottom-Up Model for Household Load Profile Based on the Consumption Behavior of Residents. Energies 2018, 11, 2112. https://doi.org/10.3390/en11082112
Gao B, Liu X, Zhu Z. A Bottom-Up Model for Household Load Profile Based on the Consumption Behavior of Residents. Energies. 2018; 11(8):2112. https://doi.org/10.3390/en11082112
Chicago/Turabian StyleGao, Bingtuan, Xiaofeng Liu, and Zhenyu Zhu. 2018. "A Bottom-Up Model for Household Load Profile Based on the Consumption Behavior of Residents" Energies 11, no. 8: 2112. https://doi.org/10.3390/en11082112
APA StyleGao, B., Liu, X., & Zhu, Z. (2018). A Bottom-Up Model for Household Load Profile Based on the Consumption Behavior of Residents. Energies, 11(8), 2112. https://doi.org/10.3390/en11082112





