Multi-Time Scale Rolling Economic Dispatch for Wind/Storage Power System Based on Forecast Error Feature Extraction
Abstract
:1. Introduction
2. WPFE Estimation Based on Optimal Factor Features Extraction
2.1. Analysis on the Method to Extract Probabilistic Optimal Factor Features
2.2. WPFE Estimation Based on Optimal Correlation Weights
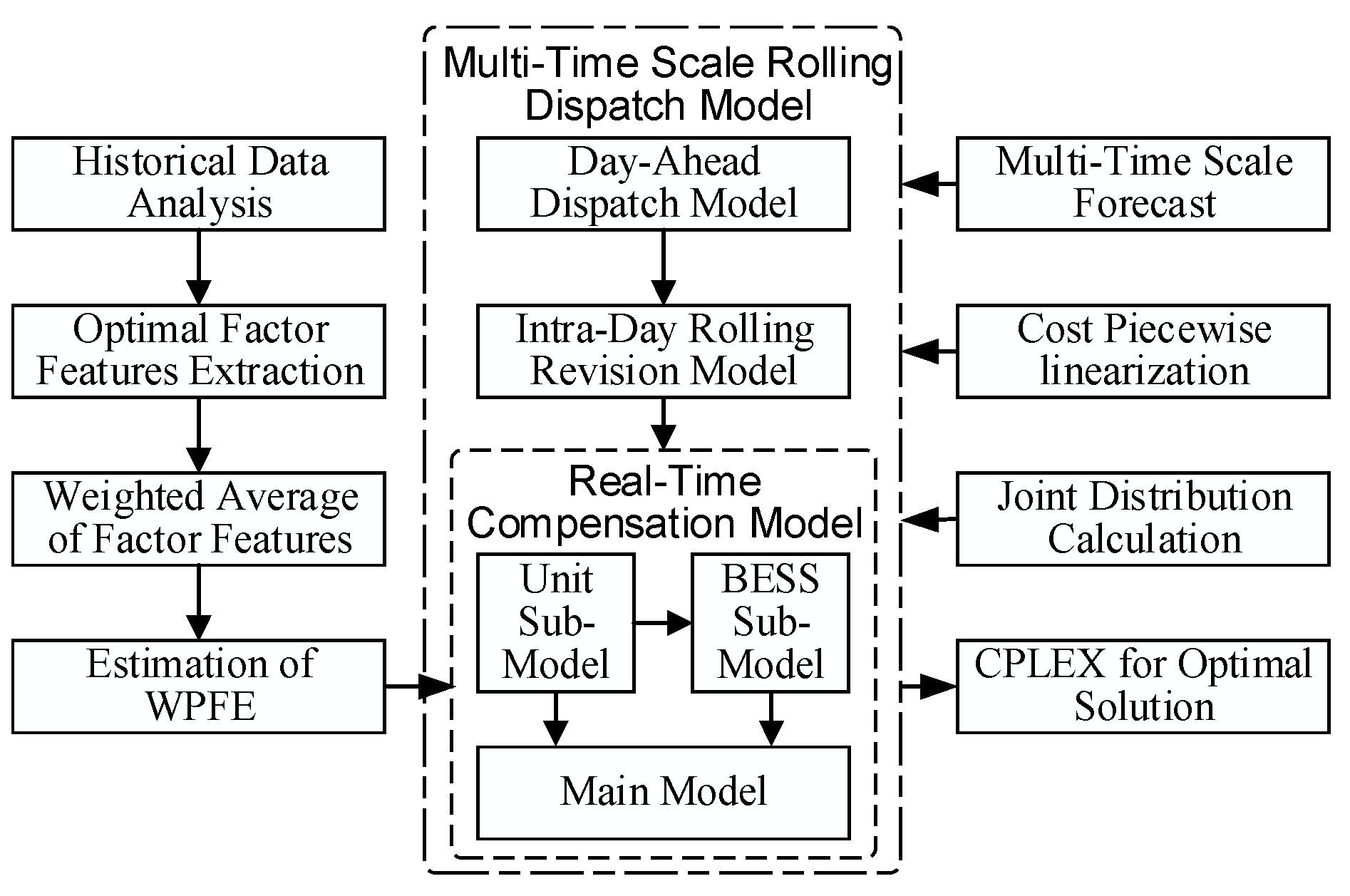
3. Power System Multi-Time Scale Rolling Dispatch Model Based on Real-time Error Compensation
3.1. The Overall Idea of the Dispatch Model
3.2. Day-Ahead Dispatch Model
3.2.1. Objective Functions
3.2.2. Constraints of the Model
3.3. Intra-Day Rolling Revision Model
3.3.1. Objective Functions
3.3.2. Constraints of the Model
3.4. Real-Time Error Compensation Model
3.4.1. The Compensation Sub-Model of the Units
3.4.2. The Compensation Sub-Model of BESS
3.4.3. Real-Time Compensation Main Model
3.5. The Transformation and Solving Method for the Model
3.5.1. Piecewise Linearization of Coal Consumption Cost
3.5.2. Simplification of Chance Constraints
3.5.3. The Overall Flowchart of the Proposed Method and Model
4. Case Study
4.1. Case Analysis
- Case 1: The dispatch model consists of day-ahead dispatch model and intra-day rolling revision model. According to the chance constraint based on probability distribution of intra-day model, the spinning reserve (SR) are set to provide compensation. Real-time compensation section is not taken into consideration.
- Case 2: The dispatch model consists of day-ahead dispatch model, intra-day rolling revision model, real-time compensation sub-model of units and real-time compensation main model. Real-time estimation of WPFE is compensated only by the units.
- Case 3: The dispatch model consists of day-ahead dispatch model, intra-day rolling revision model, real-time compensation sub-model of BESS and real-time compensation main model. Real-time estimation of WPFE is compensated only by the BESS.
- Case 4: The dispatch model consists of day-ahead dispatch model, intra-day rolling revision model, real-time compensation sub-model of unit, real-time compensation sub-model of BESS and real-time compensation main model. Real-time estimation of WPFE is compensated by the units and the BESS.
4.2. Simulation and Analysis in IEEE 39-Bus System
4.2.1. Estimation of Wind Power Forecast Error
4.2.2. Analysis of Case 1
4.2.3. Analysis of Case 2
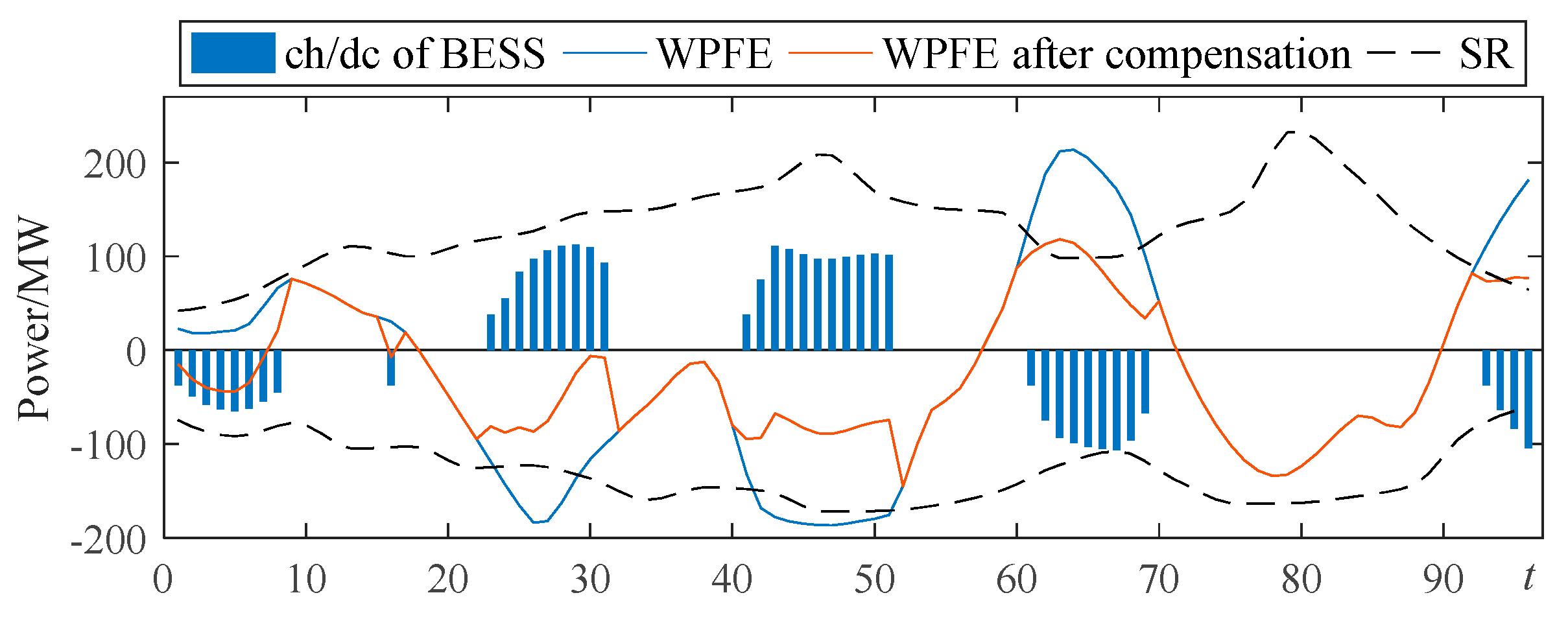
4.2.4. Analysis of Case 3
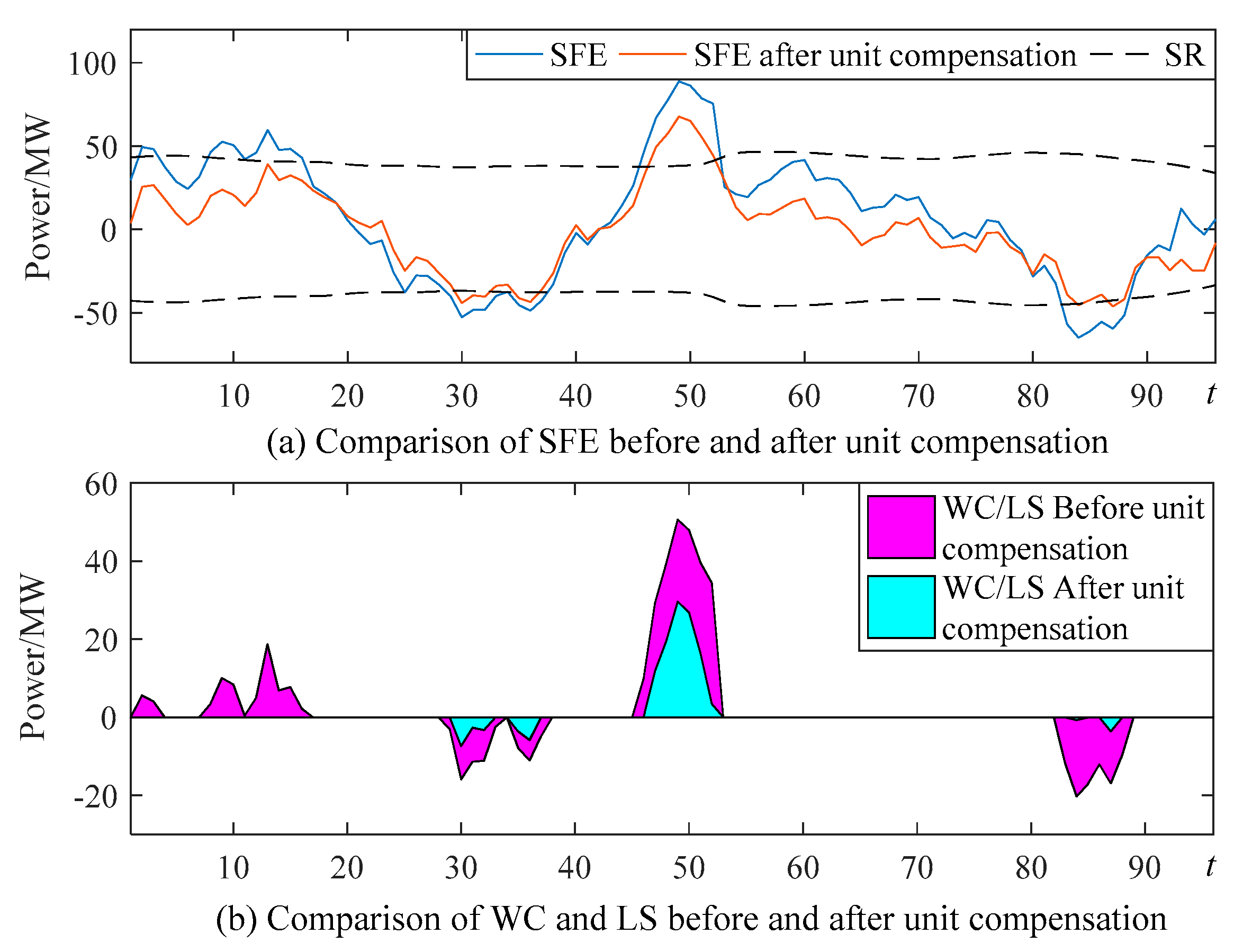
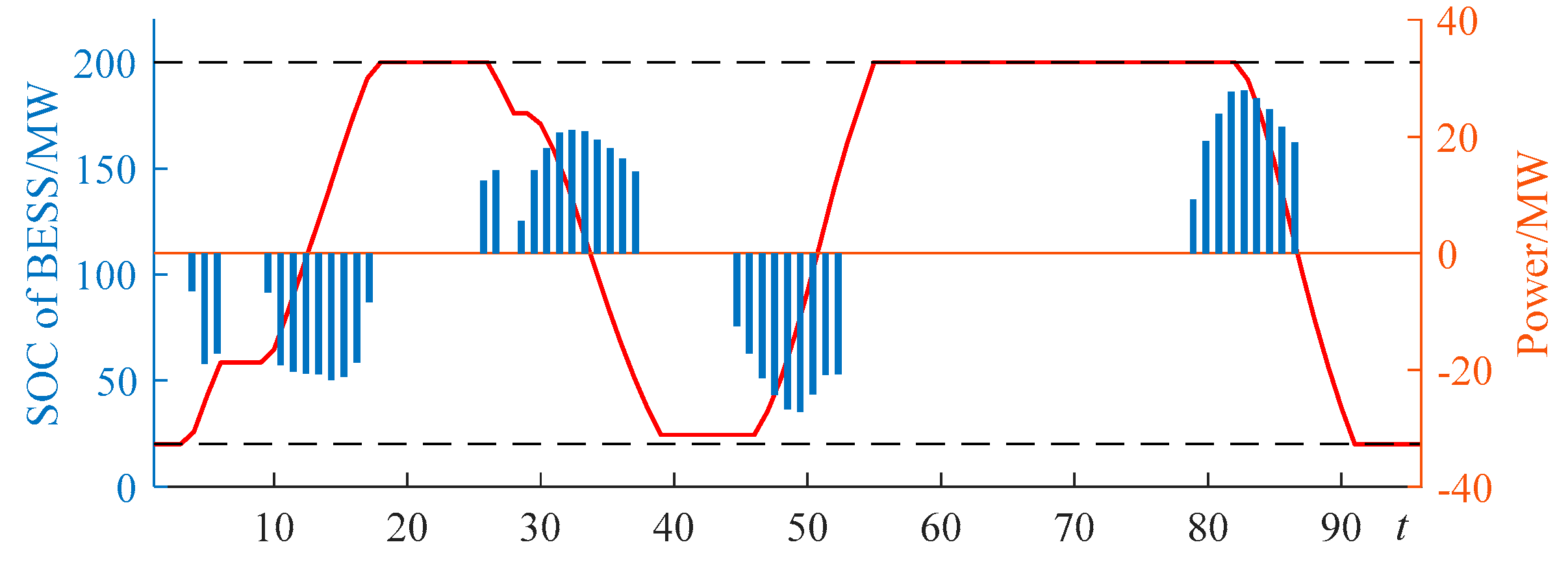
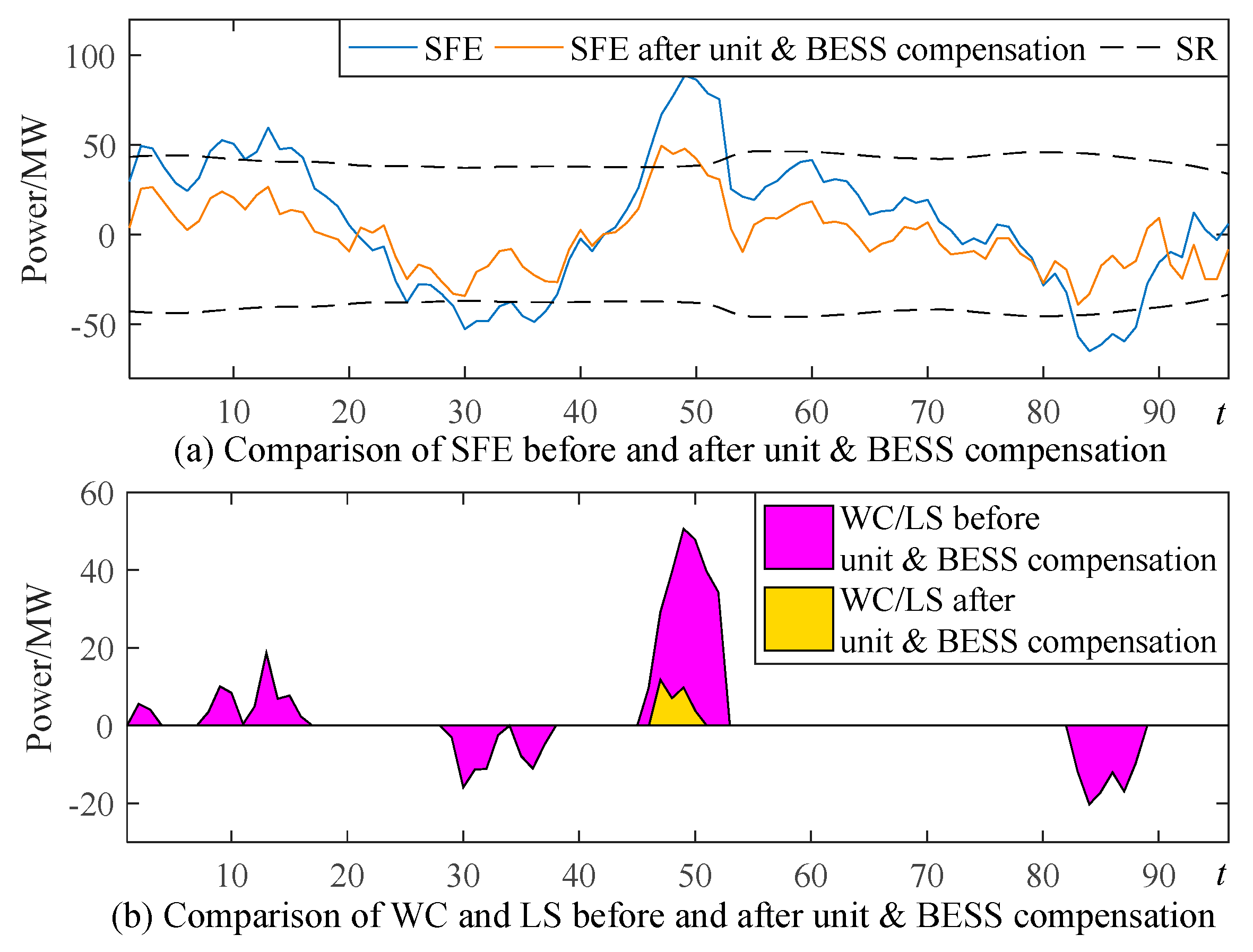
4.2.5. Analysis of Case 4
4.2.6. Comprehensive Comparison of Cases
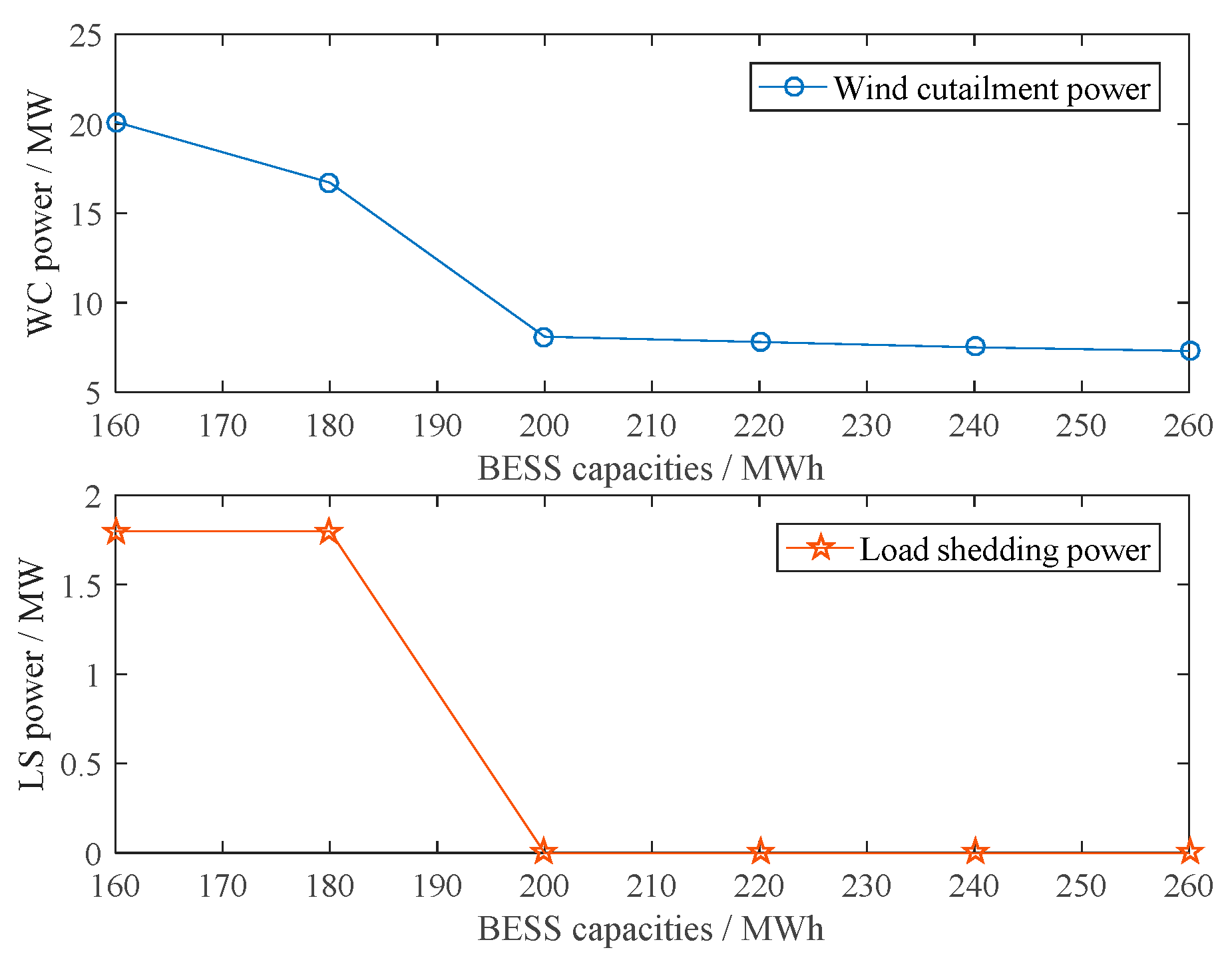
4.2.7. Analysis for Different BESS Capacities
4.3. Simulation and Analysis in IEEE 118-Bus System
4.3.1. The Estimation of WPFE
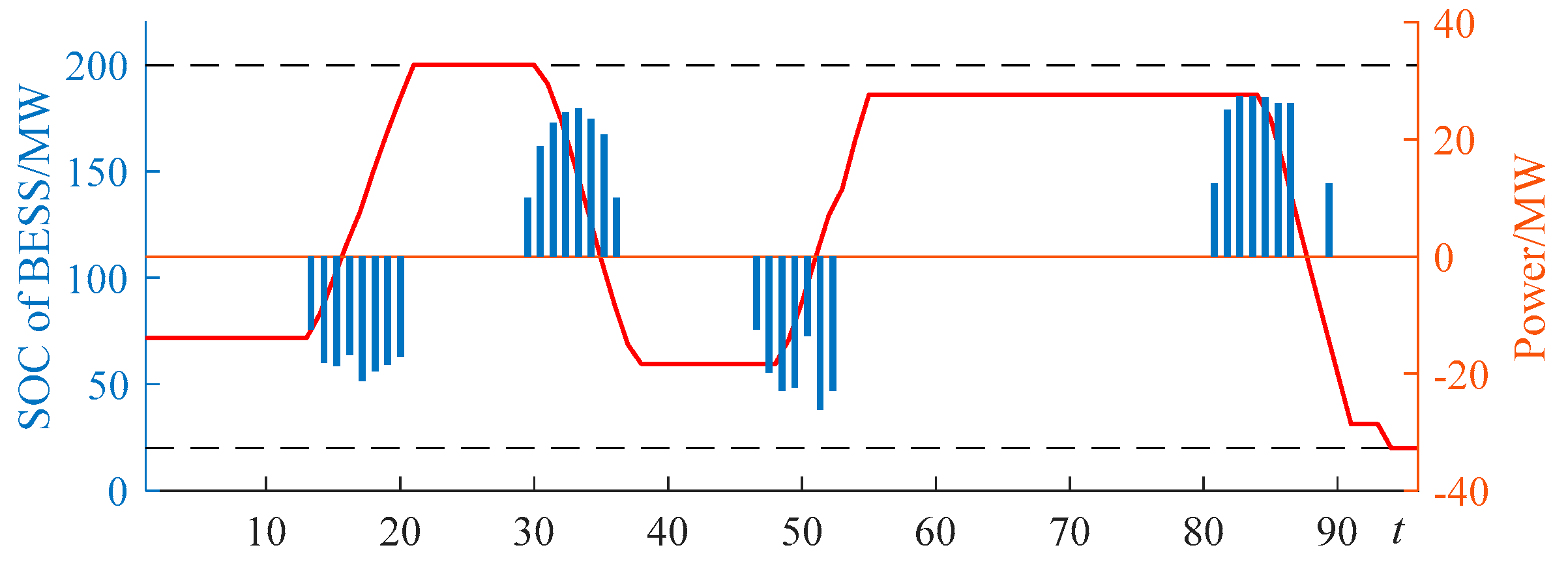
4.3.2. Analysis of Dispatch Results of Case 4
4.3.3. Analysis for Different Charge/Discharge Threshold of BESS
4.3.4. Analysis and Comparison with Alternative Models
5. Conclusions and Discussion
- According to wind power forecast output fluctuation, short-term wind power output stability, wind power output amplitude and short-term wind power forecast output accuracy, a weighted average indicator is obtained to estimate the WPFE. The estimation of WPFE can measure the actual WPFE accurately.
- The estimation of WPFE obtained by this method is introduced, and a multi-time scale rolling dispatch model based on day-ahead dispatch model, intra-day rolling revision model and real-time error compensation model is established. The model can arrange the compensation plan of units and BESS in real-time, thereby increase the adjustable space of the SR set by probability model.
- The case study of 10-units power system with wind farms, and BESS, verifies that the WPFE estimation method and dispatch model proposed in this paper are reasonable and effective. The obtained dispatch plan can maximally track the actual wind power, minimize the wind curtailment and load shedding. Therefore, the security and economic results can be obtained.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A

| Time | PG/MW | Ru,a/MW | Rd,a/MW | wa/MW | PB,ch/MW | PB,dc/MW | PWC/MW | PLS/MW | Ptotal/MW | La/MW |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 620.7 | 0.0 | −3.9 | 302.6 | 0.0 | 0.0 | 0.0 | 0.0 | 919.4 | 919.4 |
| 2 | 595.3 | 0.0 | −25.6 | 324.1 | 0.0 | 0.0 | 0.0 | 0.0 | 893.9 | 893.9 |
| 3 | 571.5 | 0.0 | −26.5 | 324.6 | 0.0 | 0.0 | 0.0 | 0.0 | 869.6 | 869.6 |
| 4 | 549.5 | 0.0 | −18.1 | 315.4 | 0.0 | 0.0 | 0.0 | 0.0 | 846.8 | 846.8 |
| 5 | 529.5 | 0.0 | −9.4 | 305.4 | 0.0 | 0.0 | 0.0 | 0.0 | 825.5 | 825.5 |
| 6 | 510.5 | 0.0 | −2.7 | 297.1 | 0.0 | 0.0 | 0.0 | 0.0 | 804.9 | 804.9 |
| 7 | 491.7 | 0.0 | −7.5 | 300.4 | 0.0 | 0.0 | 0.0 | 0.0 | 784.5 | 784.5 |
| 8 | 475.2 | 0.0 | −20.2 | 311.2 | 0.0 | 0.0 | 0.0 | 0.0 | 766.2 | 766.2 |
| 9 | 463.3 | 0.0 | −23.9 | 312.5 | 0.0 | 0.0 | 0.0 | 0.0 | 751.8 | 751.8 |
| 10 | 457.2 | 0.0 | −20.6 | 304.6 | 0.0 | 0.0 | 0.0 | 0.0 | 741.2 | 741.2 |
| 11 | 455.6 | 0.0 | −14.1 | 289.8 | 0.0 | 0.0 | 0.0 | 0.0 | 731.3 | 731.3 |
| 12 | 457.4 | 0.0 | −22.0 | 288.1 | 0.0 | 0.0 | 0.0 | 0.0 | 723.5 | 723.5 |
| 13 | 461.4 | 0.0 | −26.6 | 296.9 | −12.5 | 0.0 | 0.0 | 0.0 | 719.2 | 719.2 |
| 14 | 469.1 | 0.0 | −11.5 | 282.2 | −18.1 | 0.0 | 0.0 | 0.0 | 721.7 | 721.7 |
| 15 | 488.2 | 0.0 | −13.8 | 281.2 | −18.7 | 0.0 | 0.0 | 0.0 | 737.0 | 737.0 |
| 16 | 515.7 | 0.0 | −12.5 | 274.6 | −16.8 | 0.0 | 0.0 | 0.0 | 761.1 | 761.1 |
| 17 | 547.4 | 0.0 | −1.9 | 265.0 | −21.3 | 0.0 | 0.0 | 0.0 | 789.2 | 789.2 |
| 18 | 581.0 | 0.5 | 0.0 | 256.6 | −19.6 | 0.0 | 0.0 | 0.0 | 818.5 | 818.5 |
| 19 | 625.2 | 2.6 | 0.0 | 247.5 | −18.4 | 0.0 | 0.0 | 0.0 | 856.8 | 856.8 |
| 20 | 675.5 | 9.4 | 0.0 | 233.5 | −17.2 | 0.0 | 0.0 | 0.0 | 901.2 | 901.2 |
| 21 | 724.9 | 0.0 | −4.0 | 225.4 | 0.0 | 0.0 | 0.0 | 0.0 | 946.3 | 946.3 |
| 22 | 767.6 | 0.0 | −1.1 | 221.3 | 0.0 | 0.0 | 0.0 | 0.0 | 987.8 | 987.8 |
| 23 | 811.6 | 0.0 | −5.2 | 226.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1032.4 | 1032.4 |
| 24 | 854.4 | 12.3 | 0.0 | 209.9 | 0.0 | 0.0 | 0.0 | 0.0 | 1076.5 | 1076.5 |
| 25 | 889.1 | 24.7 | 0.0 | 198.9 | 0.0 | 0.0 | 0.0 | 0.0 | 1112.7 | 1112.7 |
| 26 | 909.4 | 16.7 | 0.0 | 207.9 | 0.0 | 0.0 | 0.0 | 0.0 | 1134.0 | 1134.0 |
| 27 | 920.7 | 18.9 | 0.0 | 205.8 | 0.0 | 0.0 | 0.0 | 0.0 | 1145.3 | 1145.3 |
| 28 | 929.0 | 26.2 | 0.0 | 198.2 | 0.0 | 0.0 | 0.0 | 0.0 | 1153.3 | 1153.3 |
| 29 | 936.7 | 33.0 | 0.0 | 191.6 | 0.0 | 0.0 | 0.0 | 0.0 | 1161.3 | 1161.3 |
| 30 | 946.1 | 34.1 | 0.0 | 182.1 | 0.0 | 10.0 | 0.0 | 0.0 | 1172.4 | 1172.4 |
| 31 | 957.4 | 20.7 | 0.0 | 191.5 | 0.0 | 18.9 | 0.0 | 0.0 | 1188.4 | 1188.4 |
| 32 | 970.2 | 17.5 | 0.0 | 197.7 | 0.0 | 22.9 | 0.0 | 0.0 | 1208.3 | 1208.3 |
| 33 | 986.0 | 9.2 | 0.0 | 210.9 | 0.0 | 24.6 | 0.0 | 0.0 | 1230.7 | 1230.7 |
| 34 | 1006.3 | 7.9 | 0.0 | 214.8 | 0.0 | 25.3 | 0.0 | 0.0 | 1254.3 | 1254.3 |
| 35 | 1035.0 | 17.8 | 0.0 | 204.9 | 0.0 | 23.4 | 0.0 | 0.0 | 1281.1 | 1281.1 |
| 36 | 1071.5 | 22.5 | 0.0 | 196.9 | 0.0 | 20.9 | 0.0 | 0.0 | 1311.8 | 1311.8 |
| 37 | 1109.6 | 26.1 | 0.0 | 196.8 | 0.0 | 10.1 | 0.0 | 0.0 | 1342.5 | 1342.5 |
| 38 | 1142.8 | 26.4 | 0.0 | 199.9 | 0.0 | 0.0 | 0.0 | 0.0 | 1369.0 | 1369.0 |
| 39 | 1167.9 | 8.2 | 0.0 | 213.1 | 0.0 | 0.0 | 0.0 | 0.0 | 1389.3 | 1389.3 |
| 40 | 1189.4 | 0.0 | −2.6 | 219.6 | 0.0 | 0.0 | 0.0 | 0.0 | 1406.4 | 1406.4 |
| 41 | 1209.5 | 6.2 | 0.0 | 206.6 | 0.0 | 0.0 | 0.0 | 0.0 | 1422.2 | 1422.2 |
| 42 | 1230.4 | 0.0 | −0.3 | 208.6 | 0.0 | 0.0 | 0.0 | 0.0 | 1438.8 | 1438.8 |
| 43 | 1255.5 | 0.0 | −1.4 | 205.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1459.1 | 1459.1 |
| 44 | 1285.7 | 0.0 | −6.6 | 205.4 | 0.0 | 0.0 | 0.0 | 0.0 | 1484.5 | 1484.5 |
| 45 | 1312.8 | 0.0 | −14.3 | 209.7 | 0.0 | 0.0 | 0.0 | 0.0 | 1508.2 | 1508.2 |
| 46 | 1328.0 | 0.0 | −32.9 | 227.8 | 0.0 | 0.0 | 0.0 | 0.0 | 1522.9 | 1522.9 |
| 47 | 1322.4 | 0.0 | −37.7 | 248.0 | 0.0 | 0.0 | −11.8 | 0.0 | 1520.8 | 1520.8 |
| 48 | 1294.6 | 0.0 | −37.9 | 262.1 | −12.5 | 0.0 | −7.1 | 0.0 | 1499.3 | 1499.3 |
| 49 | 1254.1 | 0.0 | −38.1 | 280.3 | −19.8 | 0.0 | −9.8 | 0.0 | 1466.7 | 1466.7 |
| 50 | 1210.5 | 0.0 | −38.4 | 286.9 | −22.9 | 0.0 | −3.8 | 0.0 | 1432.2 | 1432.2 |
| 51 | 1171.8 | 0.0 | −33.1 | 287.4 | −22.3 | 0.0 | 0.0 | 0.0 | 1403.7 | 1403.7 |
| 52 | 1128.4 | 0.0 | −30.8 | 292.5 | −13.6 | 0.0 | 0.0 | 0.0 | 1376.5 | 1376.5 |
| 53 | 1082.5 | 0.0 | −3.3 | 296.0 | −26.1 | 0.0 | 0.0 | 0.0 | 1349.1 | 1349.1 |
| 54 | 1039.5 | 9.7 | 0.0 | 296.2 | −23.0 | 0.0 | 0.0 | 0.0 | 1322.3 | 1322.3 |
| 55 | 1004.7 | 0.0 | −5.6 | 297.7 | 0.0 | 0.0 | 0.0 | 0.0 | 1296.9 | 1296.9 |
| 56 | 975.8 | 0.0 | −9.3 | 307.3 | 0.0 | 0.0 | 0.0 | 0.0 | 1273.8 | 1273.8 |
| 57 | 949.2 | 0.0 | −9.1 | 311.4 | 0.0 | 0.0 | 0.0 | 0.0 | 1251.6 | 1251.6 |
| 58 | 923.0 | 0.0 | −12.9 | 318.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1228.0 | 1228.0 |
| 59 | 894.6 | 0.0 | −16.7 | 322.8 | 0.0 | 0.0 | 0.0 | 0.0 | 1200.7 | 1200.7 |
| 60 | 857.9 | 0.0 | −18.5 | 324.3 | 0.0 | 0.0 | 0.0 | 0.0 | 1163.7 | 1163.7 |
| 61 | 816.6 | 0.0 | −6.4 | 311.2 | 0.0 | 0.0 | 0.0 | 0.0 | 1121.4 | 1121.4 |
| 62 | 779.2 | 0.0 | −7.3 | 310.8 | 0.0 | 0.0 | 0.0 | 0.0 | 1082.7 | 1082.7 |
| 63 | 754.0 | 0.0 | −5.8 | 308.1 | 0.0 | 0.0 | 0.0 | 0.0 | 1056.3 | 1056.3 |
| 64 | 738.6 | 0.8 | 0.0 | 299.2 | 0.0 | 0.0 | 0.0 | 0.0 | 1038.6 | 1038.6 |
| 65 | 727.1 | 9.4 | 0.0 | 286.6 | 0.0 | 0.0 | 0.0 | 0.0 | 1023.2 | 1023.2 |
| 66 | 720.6 | 5.2 | 0.0 | 286.2 | 0.0 | 0.0 | 0.0 | 0.0 | 1012.0 | 1012.0 |
| 67 | 720.2 | 3.2 | 0.0 | 283.9 | 0.0 | 0.0 | 0.0 | 0.0 | 1007.3 | 1007.3 |
| 68 | 731.8 | 0.0 | −4.3 | 287.7 | 0.0 | 0.0 | 0.0 | 0.0 | 1015.2 | 1015.2 |
| 69 | 757.6 | 0.0 | −3.0 | 282.7 | 0.0 | 0.0 | 0.0 | 0.0 | 1037.3 | 1037.3 |
| 70 | 788.9 | 0.0 | −6.9 | 283.9 | 0.0 | 0.0 | 0.0 | 0.0 | 1065.9 | 1065.9 |
| 71 | 817.4 | 4.7 | 0.0 | 271.1 | 0.0 | 0.0 | 0.0 | 0.0 | 1093.2 | 1093.2 |
| 72 | 837.5 | 10.9 | 0.0 | 266.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1114.3 | 1114.3 |
| 73 | 853.9 | 10.2 | 0.0 | 269.5 | 0.0 | 0.0 | 0.0 | 0.0 | 1133.6 | 1133.6 |
| 74 | 870.9 | 9.1 | 0.0 | 273.9 | 0.0 | 0.0 | 0.0 | 0.0 | 1153.9 | 1153.9 |
| 75 | 892.6 | 13.5 | 0.0 | 272.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1178.1 | 1178.1 |
| 76 | 927.9 | 2.1 | 0.0 | 284.3 | 0.0 | 0.0 | 0.0 | 0.0 | 1214.3 | 1214.3 |
| 77 | 984.9 | 1.9 | 0.0 | 285.7 | 0.0 | 0.0 | 0.0 | 0.0 | 1272.6 | 1272.6 |
| 78 | 1044.1 | 10.5 | 0.0 | 278.2 | 0.0 | 0.0 | 0.0 | 0.0 | 1332.8 | 1332.8 |
| 79 | 1083.9 | 14.6 | 0.0 | 274.4 | 0.0 | 0.0 | 0.0 | 0.0 | 1372.9 | 1372.9 |
| 80 | 1087.7 | 26.9 | 0.0 | 261.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1375.5 | 1375.5 |
| 81 | 1071.4 | 14.8 | 0.0 | 269.7 | 0.0 | 0.0 | 0.0 | 0.0 | 1356.0 | 1356.0 |
| 82 | 1043.5 | 19.5 | 0.0 | 261.2 | 0.0 | 0.0 | 0.0 | 0.0 | 1324.2 | 1324.2 |
| 83 | 1009.4 | 39.0 | 0.0 | 238.7 | 0.0 | 0.0 | 0.0 | 0.0 | 1287.1 | 1287.1 |
| 84 | 972.9 | 32.9 | 0.0 | 231.9 | 0.0 | 12.5 | 0.0 | 0.0 | 1250.2 | 1250.2 |
| 85 | 927.0 | 17.3 | 0.0 | 234.5 | 0.0 | 25.0 | 0.0 | 0.0 | 1203.9 | 1203.9 |
| 86 | 875.4 | 11.6 | 0.0 | 237.0 | 0.0 | 27.4 | 0.0 | 0.0 | 1151.5 | 1151.5 |
| 87 | 825.3 | 18.7 | 0.0 | 228.9 | 0.0 | 27.4 | 0.0 | 0.0 | 1100.4 | 1100.4 |
| 88 | 783.4 | 14.7 | 0.0 | 232.2 | 0.0 | 27.2 | 0.0 | 0.0 | 1057.5 | 1057.5 |
| 89 | 744.3 | 0.0 | −3.6 | 251.2 | 0.0 | 26.2 | 0.0 | 0.0 | 1018.2 | 1018.2 |
| 90 | 707.4 | 0.0 | −9.3 | 257.1 | 0.0 | 26.2 | 0.0 | 0.0 | 981.4 | 981.4 |
| 91 | 676.3 | 16.7 | 0.0 | 256.8 | 0.0 | 0.0 | 0.0 | 0.0 | 949.8 | 949.8 |
| 92 | 654.6 | 24.5 | 0.0 | 247.1 | 0.0 | 0.0 | 0.0 | 0.0 | 926.2 | 926.2 |
| 93 | 641.1 | 5.6 | 0.0 | 247.9 | 0.0 | 12.5 | 0.0 | 0.0 | 907.1 | 907.1 |
| 94 | 633.9 | 24.7 | 0.0 | 231.9 | 0.0 | 0.0 | 0.0 | 0.0 | 890.5 | 890.5 |
| 95 | 633.5 | 24.7 | 0.0 | 219.5 | 0.0 | 0.0 | 0.0 | 0.0 | 877.7 | 877.7 |
| 96 | 640.3 | 8.2 | 0.0 | 221.6 | 0.0 | 0.0 | 0.0 | 0.0 | 870.1 | 870.1 |
| Total | 20,593.1 | 186.6 | −166.9 | 6216.1 | −70.7 | 85.1 | −8.1 | 0.0 | 26,835.1 | 26,835.1 |
References
- Zhao, X.; Liu, S.; Yan, F.; Yuan, Z.; Liu, Z. Energy conservation, environmental and economic value of the wind power priority dispatch in China. Renew. Energy 2017, 111, 666–675. [Google Scholar] [CrossRef]
- Denny, E.; O’Malley, M. Wind generation, power system operation, and emissions reduction. IEEE Trans. Power Syst. 2006, 21, 341–347. [Google Scholar] [CrossRef]
- Lujano-Rojas, J.M.; Osório, G.J.; Matias, J.C.O.; Catalão, J.P.S. A heuristic methodology to economic dispatch problem incorporating renewable power forecasting error and system reliability. Renew. Energy 2016, 87, 731–743. [Google Scholar] [CrossRef]
- Archer, C.L.; Simão, H.P.; Kempton, W.; Powell, W.B.; Dvorak, M.J. The challenge of integrating offshore wind power in the U.S. electric grid. Part I: Wind forecast error. Renew. Energy 2017, 103, 346–360. [Google Scholar] [CrossRef]
- Zhao, X.; Wu, L.; Zhang, S. Joint environmental and economic power dispatch considering wind power integration: Empirical analysis from Liaoning Province of China. Renew. Energy 2013, 52, 260–265. [Google Scholar] [CrossRef]
- Wang, Z.; Shen, C.; Liu, F. A Conditional Model of Wind Power Forecast Errors and Its Application in Scenario Generation. Appl. Energy 2018, 212, 771–785. [Google Scholar] [CrossRef]
- Ummels, B.C.; Gibescu, M.; Pelgrum, E.; Kling, W.L.; Brand, A.J. Impacts of Wind Power on Thermal Generation Unit Commitment and Dispatch. IEEE Trans. Energy Convers. 2007, 22, 44–51. [Google Scholar] [CrossRef] [Green Version]
- Tuohy, A.; Meibom, P.; Denny, E.; O’Malley, M. Unit Commitment for Systems with Significant Wind Penetration. IEEE Trans. Power Syst. 2009, 24, 592–601. [Google Scholar] [CrossRef] [Green Version]
- Hetzer, J.; Yu, D.C.; Bhattarai, K. An Economic Dispatch Model Incorporating Wind Power. IEEE Trans. Energy Convers. 2008, 23, 603–611. [Google Scholar] [CrossRef]
- Zhou, W.; Peng, Y.; Sun, H.; Wei, Q. Dynamic Economic Dispatch in Wind Power Integrated System. Proc. CSEE 2009, 29, 13–18. [Google Scholar]
- Zhu, Y.S.; Wang, J.; Qu, B.Y; Suganthan, P.N. Multi-Objective Dynamic Economic Emission Dispatching of Power Grid Containing Wind Farms. Power Syst. Technol. 2015, 39, 1315–1322. [Google Scholar]
- Narimani, H.; Razavi, S.E.; Azizivahed, A.; Ehsan, N.; Mehdi, F.; Ateai, M.H.; Narimani, M.R. A Multi-Objective Framework for Multi-Area Economic Emission Dispatch. Energy 2018, 154, 126–142. [Google Scholar] [CrossRef]
- Naderi, E.; Azizivahed, A.; Narimani, H.; Faith, M.; Narimani, M.R. A Comprehensive Study of Practical Economic Dispatch Problems by a New Hybrid Evolutionary Algorithm. Appl. Soft Comput. 2017, 61, 1186–1206. [Google Scholar] [CrossRef]
- Ortega-Vazquez, M.A.; Kirschen, D.S. Estimating the Spinning Reserve Requirements in Systems with Significant Wind Power Generation Penetration. IEEE Trans. Power Syst. 2009, 24, 114–124. [Google Scholar] [CrossRef]
- Zhou, B.; Geng, G.; Jiang, Q. Hierarchical Unit Commitment with Uncertain Wind Power Generation. IEEE Trans. Power Syst. 2015, 31, 94–104. [Google Scholar] [CrossRef]
- Tang, C.; Xu, J.; Sun, Y.; Liu, J.; Li, X.; Ke, D.; Yang, J.; Peng, X. Look-Ahead Economic Dispatch with Adjustable Confidence Interval Based on a Truncated Versatile Distribution Model for Wind Power. IEEE Trans. Power Syst. 2018, 33, 1755–1767. [Google Scholar] [CrossRef]
- Li, Y.Z.; Jiang, L.; Wu, Q.H.; Wang, P.; Gooi, H.B.; Li, K.C.; Liu, Y.Q.; Lu, P.; Cao, M.; Imura, J. Wind-thermal power system dispatch using MLSAD model and GSOICLW algorithm. Knowl. Based Syst. 2017, 116, 94–101. [Google Scholar] [CrossRef]
- Xiong, P.; Jirutitijaroen, P.; Singh, C.A. Distributionally Robust Optimization Model for Unit Commitment Considering Uncertain Wind Power Generation. IEEE Trans. Power Syst. 2017, 33, 39–49. [Google Scholar] [CrossRef]
- Zhai, J.Y.; Ren, J.W.; Zhou, M.; Li, Z. Multi-Time Scale Fuzzy Chance Constrained Dynamic Economic Dispatch Model for Power System with Wind Power. Power Syst. Technol. 2016, 40, 1094–1099. [Google Scholar]
- Safta, C.; Chen, L.Y.; Najm, H.N.; Pinar, A.; Watson, J. Efficient Uncertainty Quantification in Stochastic Economic Dispatch. IEEE Trans. Power Syst. 2017, 32, 2535–2546. [Google Scholar] [CrossRef]
- Wang, Q.; Guan, Y.; Wang, J. A Chance-Constrained Two-Stage Stochastic Program for Unit Commitment with Uncertain Wind Power Output. IEEE Trans. Power Syst. 2012, 27, 206–215. [Google Scholar] [CrossRef]
- Uçkun, C.; Botterud, A.; Birge, J.R. An Improved Stochastic Unit Commitment Formulation to Accommodate Wind Uncertainty. IEEE Trans. Power Syst. 2016, 31, 2507–2517. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, S.; Zhou, Z.; Botterud, A.; Xu, Y.; Chen, R. Risk Adjustable Day Ahead Unit Commitment with Wind Power Based on Chance Constrained Goal Programming. IEEE Trans. Sustain. Energy 2017, 8, 530–541. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Yang, J.Q.; Zhang, X.J. Dynamic economic dispatch incorporating multiple wind farms based on FFT simplified chance constrained programming. J. Zhejiang Univ. 2017, 51, 976–983. [Google Scholar]
- Wen, Y.; Li, W.; Huang, G.; Liu, X. Frequency Dynamics Constrained Unit Commitment with Battery Energy Storage. IEEE Trans. Power Syst. 2016, 31, 5115–5125. [Google Scholar] [CrossRef]
- Zhang, X.S.; Yuan, Y.; Cao, Y. Modeling and Scheduling for Battery Energy Storage Station with Consideration of Wearing Costs. Power Syst. Technol. 2017, 41, 1541–1548. [Google Scholar]
- Andervazh, M.R.; Javadi, S. Emission-economic dispatch of thermal power generation units in the presence of hybrid electric vehicles and correlated wind power plants. IET Gener. Transm. Distrib. 2017, 11, 2232–2243. [Google Scholar] [CrossRef]
- Narimani, M.R.; Maigha; Joo, J.Y.; Crow, M. Multi-Objective Dynamic Economic Dispatch with Demand Side Management of Residential Loads and Electric Vehicles. Energies 2017, 10, 624. [Google Scholar] [CrossRef]
- Alham, M.H.; Elshahed, M.; Ibrahim, D.K.; Zahab, E.E. A dynamic economic emission dispatch considering wind power uncertainty incorporating BESS and demand side management. Renew. Energy 2016, 96, 800–811. [Google Scholar] [CrossRef]
- Narimani, M.R.; Joo, J.Y.; Crow, M.L. Dynamic economic dispatch with demand side management of individual residential loads. In Proceedings of the North American Power Symposium, Charlotte, NC, USA, 4–6 October 2015. [Google Scholar]
- Jiang, Y.; Xu, J.; Sun, Y.; Wei, C.; Wang, J.; Ke, D.; Li, X.; Yang, J.; Peng, X.; Tang, B. Day-ahead stochastic economic dispatch of wind integrated power system considering demand response of residential hybrid energy system. Appl. Energy 2017, 190, 1126–1137. [Google Scholar] [CrossRef]
- Ye, Y.D.; Wei, L.J.; Qiao, Y.; Li, Y.; Lu, Z. Optimal Method of Improving Wind Power Accommodation by Nonparametric Conditional Probabilistic Forecasting. Power Syst. Technol. 2017, 41, 1443–1450. [Google Scholar]
- Zhang, K.F.; Yang, G.Q.; Chen, H.Y.; Wang, Y.; Ding, Q. An Estimation Method for Wind Power Forecast Errors Based on Numerical Feature Extraction. Autom. Electr. Power Syst. 2014, 16, 22–27. [Google Scholar]
- Elia. Wind-Power Generation Data. Available online: http://www.elia.be/en/grid-data/power-generation/wind-power (accessed on 1 April 2017).
- Carrion, M.; Arroyo, J.M. A computationally efficient mixed-integer linear formulation for the thermal unit commitment problem. IEEE Trans. Power Syst. 2006, 21, 1371–1378. [Google Scholar] [CrossRef]
- Morales-España, G.; Lorca, Á.; de Weerdt, M.M. Robust unit commitment with dispatchable wind power. Electr. Power Syst. Res. 2018, 155, 58–66. [Google Scholar] [CrossRef]
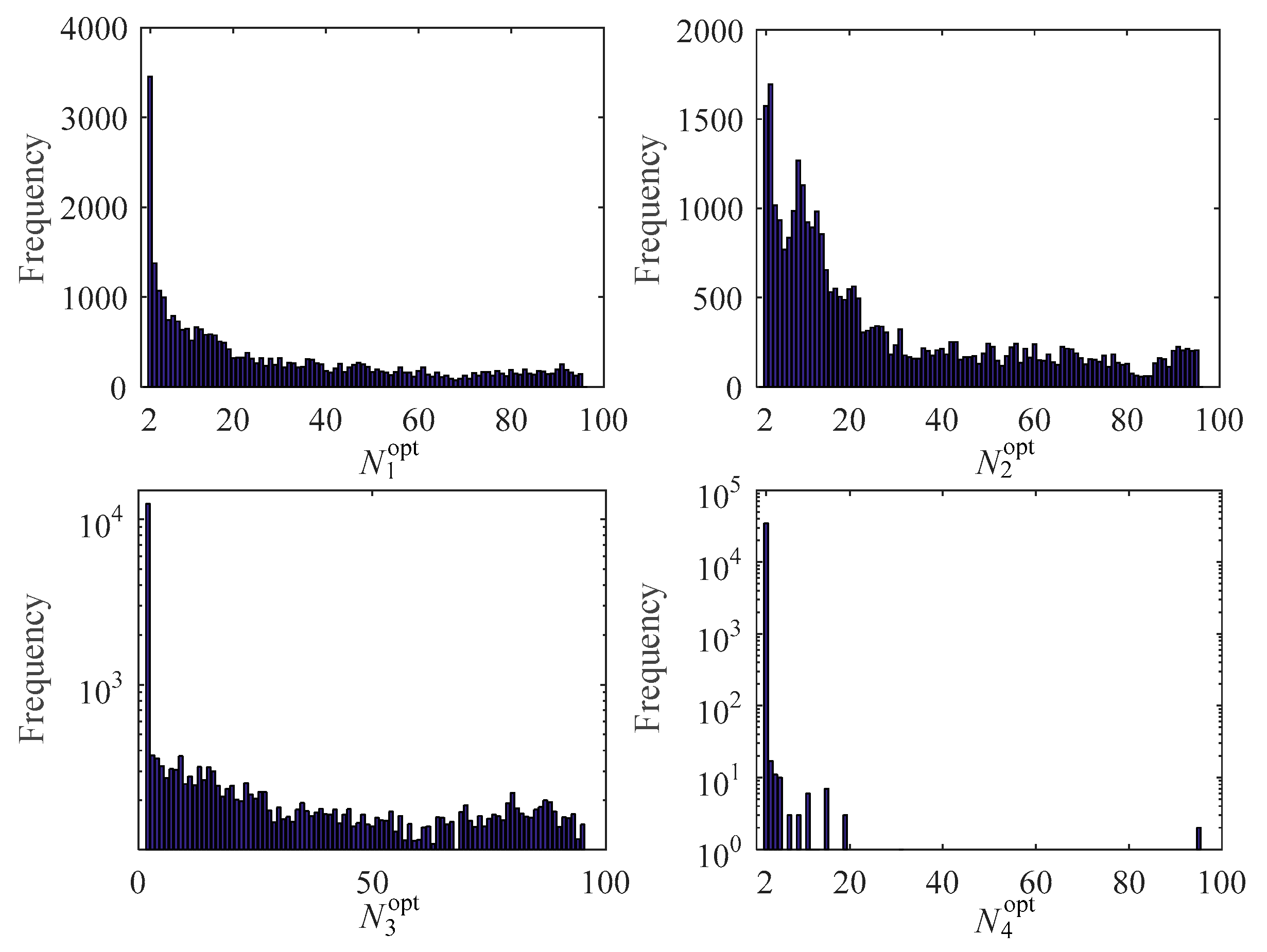
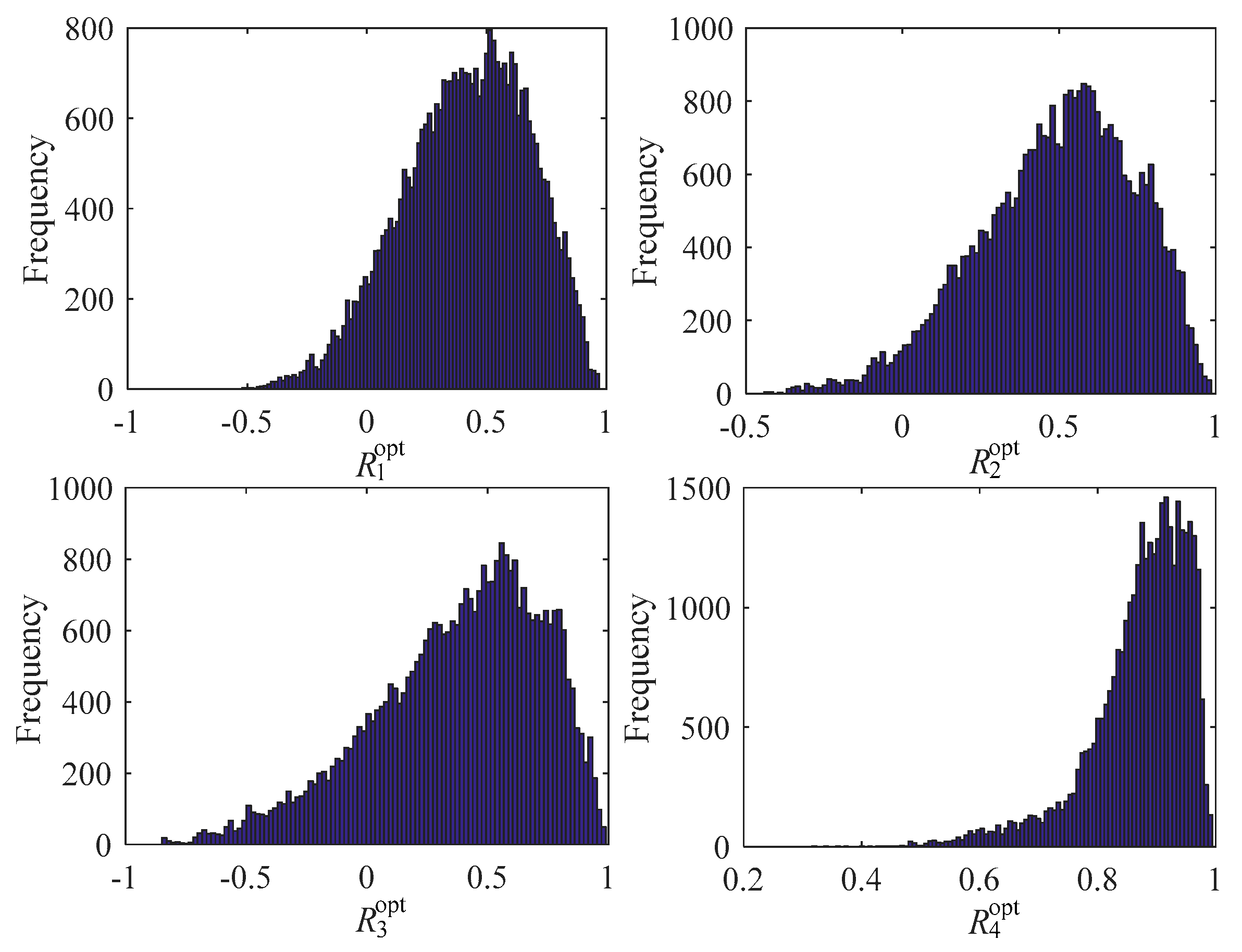







| Wind Power Data | N1opt | N2opt | N3opt | N4opt | R1mean | R2mean | R3mean | R4mean |
|---|---|---|---|---|---|---|---|---|
| Spring | 2 | 3 | 2 | 2 | 0.4049 | 0.5122 | 0.3684 | 0.8688 |
| Summer | 2 | 2 | 2 | 2 | 0.4067 | 0.4973 | 0.4188 | 0.8843 |
| Autumn | 2 | 5 | 2 | 2 | 0.4559 | 0.5064 | 0.3708 | 0.8677 |
| Winter | 2 | 3 | 2 | 2 | 0.3913 | 0.4513 | 0.3500 | 0.8643 |
| A whole year | 2 | 3 | 2 | 2 | 0.4152 | 0.4932 | 0.3778 | 0.8716 |
| EB,min | EB,max | PB,min | PB,max | ηB,ch | ηB,dc | CI | ntotal |
| 20 MW·h | 200 MW·h | 0 MW | 50 MW | 0.9 | 0.9 | 7.7 × 105 $ | 2 × 104 |
| kch | kch | ku | kd | kw | kl | αu | αd |
| 0.8 | 0.8 | 20 $/MW | 15 $/MW | 0.4 | 0.02 | 0.9 | 0.9 |
| R1 | R2 | R3 | R4 | Re |
|---|---|---|---|---|
| 0.0831 | 0.3094 | 0.2060 | 0.5336 | 0.8775 |
| Cases | Unit Power Generation Costs | BESS Costs | Operation Risk Penalty Costs | Total | |||||
|---|---|---|---|---|---|---|---|---|---|
| CP+CS/$ | CU/$ | CD/$ | CU+CD/$ | CB/$ | CWC/$ | CLS/$ | CR/$ | Ctotal/$ | |
| Case1 | 430,496.7 | 5033.5 | 5571.0 | 10,604.5 | - | 8100.0 | 2917.5 | 11,017.5 | 452,118.7 |
| Case2 | 427,267.3 | 5123.0 | 3151.0 | 8274.0 | - | 2690.0 | 510.0 | 3200.0 | 438,741.3 |
| Case3 | 430,496.7 | 3845.8 | 4894.5 | 8740.3 | 1655.5 | 2820.0 | 30.0 | 2850.0 | 443,742.5 |
| Case4 | 427,267.3 | 3731.7 | 2502.8 | 6234.5 | 1232.0 | 810.0 | 0.0 | 810.0 | 435,543.8 |
| Case 1 | Case 2 | Case 3 | Case 4 |
|---|---|---|---|
| 4.67 s | 10.92 s | 9.07 s | 14.03 s |
| EB,min | EB,max | PB,min | PB,max | ηB,ch | ηB,dc | CI | ntotal |
| 50 MW·h | 500 MW·h | 0 MW | 150 MW | 0.9 | 0.9 | 1.3 × 106 $ | 2 × 104 |
| kch | kch | ku | kd | kw | kl | αu | αd |
| 0.8 | 0.8 | 16.5 $/MW | 16.5 $/MW | 0.4 | 0.02 | 0.9 | 0.9 |
| kchkdc | ch/dc Times | Cost of BESS/$ | Wind Curtail/MW | Wind Curtailment Rate (%) | Load Shedding/MW |
|---|---|---|---|---|---|
| 1.00 | 16 | 1040.0 | 293.7 | 1.19% | 177.5 |
| 0.95 | 20 | 1300.0 | 181.2 | 0.74% | 119.9 |
| 0.90 | 29 | 1885.0 | 108.8 | 0.44% | 96.3 |
| 0.85 | 32 | 2080.0 | 108.8 | 0.44% | 29.8 |
| 0.80 | 42 | 2730.0 | 67.9 | 0.28% | 0.0 |
| 0.75 | 44 | 2860.0 | 11.4 | 0.05% | 0.0 |
| 0.70 | 46 | 2990.0 | 0.0 | 0.00% | 0.0 |
| CP + CS | CSR | CB | CWC | CLS | Ctotal |
|---|---|---|---|---|---|
| 661,442.8 | 100,671.5 | 2730.0 | 1697.5 | 0.0 | 766,541.8 |
| Models | Parameter Settings | Total Cost /k$ | Computational Times/s | Wind Curtail Rate (%) |
|---|---|---|---|---|
| SO (stochastic) | SC = 30 | 763.80 | 980.6 | 0.16 |
| RO (robust) | SC = 1 | 813.16 | 13.8 | 1.05 |
| ROB (robust) | SC = 1 | 816.78 | 184.4 | 1.11 |
| SR (unified robust–stochastic) | SC = 20 | 764.47 | 289.6 | 0.14 |
| SRB (unified robust–stochastic) | SC = 10 | 765.23 | 654.8 | 0.17 |
| M-T SDM | kch = kdc = 0.80 | 766.54 | 94.91 | 0.28 |
| M-T SDM | kch = kdc = 0.75 | 765.26 | 93.28 | 0.05 |
| M-T SDM | kch = kdc = 0.70 | 765.10 | 95.01 | 0.00 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, L.; Zhang, R.; Wang, X.; Dong, Y. Multi-Time Scale Rolling Economic Dispatch for Wind/Storage Power System Based on Forecast Error Feature Extraction. Energies 2018, 11, 2124. https://doi.org/10.3390/en11082124
Han L, Zhang R, Wang X, Dong Y. Multi-Time Scale Rolling Economic Dispatch for Wind/Storage Power System Based on Forecast Error Feature Extraction. Energies. 2018; 11(8):2124. https://doi.org/10.3390/en11082124
Chicago/Turabian StyleHan, Li, Rongchang Zhang, Xuesong Wang, and Yu Dong. 2018. "Multi-Time Scale Rolling Economic Dispatch for Wind/Storage Power System Based on Forecast Error Feature Extraction" Energies 11, no. 8: 2124. https://doi.org/10.3390/en11082124
APA StyleHan, L., Zhang, R., Wang, X., & Dong, Y. (2018). Multi-Time Scale Rolling Economic Dispatch for Wind/Storage Power System Based on Forecast Error Feature Extraction. Energies, 11(8), 2124. https://doi.org/10.3390/en11082124





