Numerical Simulation and Analysis on Spray Drift Movement of Multirotor Plant Protection Unmanned Aerial Vehicle
Abstract
1. Introduction
2. Computational Fluid Dynamics Model and Experimental Verification for Downwash Airflow
2.1. Working Principle of the SLK-5 Six-Rotor UAV
2.2. Wind Speed Test and Verification of Downwash Airflow Model
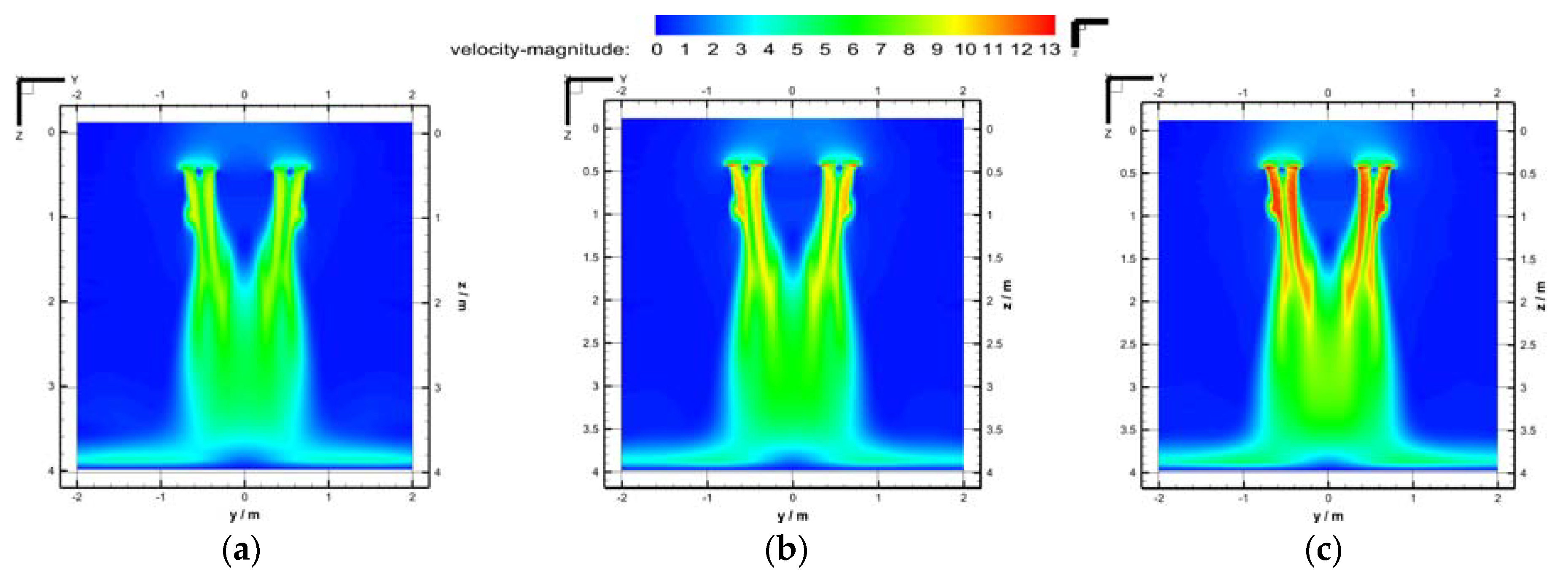
2.3. Effect of Load on Downwash Airflow Distribution in Hover
3. Two-Phase Computational Fluid Dynamics Model and Experimental Verification
3.1. Droplet Particle Size and Spray Width Test
3.2. Two-Phase Numerical Calculation of Discrete Droplet Motion Law
4. Droplet Movement Law of the Six-Rotor Plant Protection UAV Spraying
4.1. Influence of Downwash Airflow on Droplet Movement in Hover
4.2. Droplet Drift Model
5. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Wang, C.; Song, J.; He, X.; Wang, Z.; Wang, S.; Meng, Y. Effect of flight parameters on distribution characteristics of pesticide spraying droplets deposition of plant-protection unmanned aerial vehicle. Trans. Chin. Soc. Agric. Eng. 2017, 33, 109–116. [Google Scholar]
- Qin, W.; Xue, X.; Zhou, L.; Zhang, S.; Sun, Z.; Kong, W.; Wang, B. Effects of spraying parameters of unmanned aerial vehicle on droplets deposition distribution of maize canopies. Trans. Chin. Soc. Agric. Eng. 2014, 30, 50–56. [Google Scholar]
- Bradley, K.F. Role of atmospheric stability in drift and deposition of aerially applied sprays-preliminary results. ASAE 2004, 58, 742–755. [Google Scholar]
- Ivan, W.K.; Bradley, K.F.; Wesley, C.H. Aerial methods for increasing spray deposits on wheat heads. ASAE 2004, 58, 716–729. [Google Scholar]
- Kirk, L.W.; Teske, M.E.; Thistle, H.W. What about upwind buffer zones for aerial applications? J. Agric. Saf. Health 2002, 8, 333–336. [Google Scholar] [CrossRef] [PubMed]
- Xue, X.Y.; Lan, Y.B. Agricultural aviation application in USA. Trans. Chin. Soc. Agric. Mach. 2012, 44, 194–201. [Google Scholar]
- Dumbauld, R.K.; Bjorklund, J.R.; Saterlie, S.F. Computer Models for Predicting Aircraft Spray Dispersion and Deposition above and within Forest Canopies: User’s Manual for the FSCBG Computer Program Report; No 80–11; US Forest Service: Davis, CA, USA, 1980. [Google Scholar]
- Teske, M.E.; Thistle, H.W.; Schou, W.C.; Miller, P.C.H.; Strager, J.M.; Richardson, B.; Butler-Ellis, M.C.; Barry, J.M.; Twardus, D.B.; Thompson, D.G. A review of computer models for pesticide deposition prediction. Trans. ASABE 2011, 54, 789–801. [Google Scholar] [CrossRef]
- Reed, W.H. An Analytical Study of the Effect of Airplane Wake on the Lateral Dispersion of Aerial Sprays; Langley Aeronautical Laboratory: Hampton, VA, USA, 1953. [Google Scholar]
- Bilanin, A.J.; Teske, M.E.; Barry, J.W.; Ekblad, R.B. AGDISP: The aircraft spray dispersion model, code development and experimental validation. Trans. ASABE 1989, 32, 327–334. [Google Scholar] [CrossRef]
- Teske, M.E.; Bird, S.L.; Esterly, D.M.; Curbishley, T.B.; Ray, S.L.; Perry, S.G. AgDrift®: A model for estimating near-field spray drift from aerial applications. Environ. Toxicol. Chem. 2002, 21, 659–671. [Google Scholar] [CrossRef] [PubMed]
- Hewitt, A.J. Spray drift: Impact of requirements to protect the environment. Crop Prot. 2000, 19, 623–627. [Google Scholar] [CrossRef]
- Hewitt, A.J.; Johnson, D.R.; Fish, J.D.; Hermansky, C.G.; Valcore, D.L. Development of the spray drift task force database for aerial applications. Environ. Toxicol. Chem. 2002, 21, 648–658. [Google Scholar] [CrossRef] [PubMed]
- Teske, M.E.; Thistle, H.W.; Riley, C.M.; Hewitt, A.J. Initial laboratory measurements of the evaporation rate of droplets inside a spray cloud. Trans. ASABE 2016, 59, 487–493. [Google Scholar]
- Teske, M.E; Thistle, H.W.; Riley, C.M.; Hewitt, A.J. Laboratory measurements on the sensitivity of evaporation rate of droplets inside a spray cloud. Trans. ASABE 2017, 60, 361–366. [Google Scholar]
- States, U. Unmanned Flight: The Drones Come Home-Pictures. National Geographic. March 2013. Available online: https://www.nationalgeographic.com/magazine/2013/03/drones-come-home/ (accessed on 18 June 2018).
- Yang, F.B.; Xue, X.Y.; Zhang, L.; Zhu, S. Numerical simulation and experimental verification on downwash air flow of six-rotor agricultural unmanned aerial vehicle in hover. Int. J. Agric. Biol. Eng. 2017, 10, 41–53. [Google Scholar]
- Duga, A.T.; Dekeyser, D.; Ruysen, K.; Bylemans, D.; Nuyttens, D.; Nicolai, B.; Verboven, P. Challenges for CFD modeling of drift from air assisted orchard sprayers. In Proceedings of the 13th Workshop on Spray Application Techniques in Fruit Growing, Lindau, Germany, 15–18 July 2015; pp. 34–35. [Google Scholar]
- Endalew, A.M.; Debaer, C.; Rutten, N.; Vercammen, J.; Delele, M.A.; Ramon, H.; Nicolaï, B.M.; Verboven, P. A new integrated CFD modelling approach towards air-assisted orchard spraying. Part I. Model development and effect of wind speed and direction on sprayer airflow. Comput. Electron. Agric. 2010, 71, 128–136. [Google Scholar] [CrossRef]
- Endalew, A.M.; Debaer, C.; Rutten, N.; Vercammen, J.; Delele, M.A.; Ramon, H.; Nicolaï, B.M.; Verbovena, P. Modelling pesticide flow and deposition from air-assisted orchard spraying in orchards: A new integrated CFD approach. Agric. Forest Meteorol. 2010, 150, 1383–1392. [Google Scholar] [CrossRef]
- Salcedo, R.; Vallet, A.; Granell, R.; Garcerá, C.; Moltó, E.; Chueca, P. Euleriane Lagrangian model of the behaviour of droplets produced by an air-assisted sprayer in a citrus orchard. Biosyst. Eng. 2017, 154, 76–91. [Google Scholar] [CrossRef]
- Ryan, S.D.; Gerber, A.G.; Holloway, A.G.L. A computational study on spray dispersal in the wake of an aircraft. Trans. ASABE 2013, 56, 847–868. [Google Scholar]
- Zhang, B.; Tang, Q.; Chen, L.P.; Xu, M. Numerical simulation of wake vortices of crop spraying aircraft close to the ground. Biosyst. Eng. 2016, 145, 52–64. [Google Scholar] [CrossRef]
- Zhang, B.; Tang, Q.; Chen, L.P.; Zhang, R.R.; Xu, M. Numerical simulation of spray drift and deposition from a crop spraying aircraft using a CFD approach. Biosyst. Eng. 2018, 166, 184–199. [Google Scholar] [CrossRef]
- Roberts, T.W.; Murman, E.M. Solution method for a hovering helicopter rotor using the Euler equations. In Proceedings of the 23rd Aerospace Sciences Meeting, Reno, NV, USA, 14–17 January 1985. [Google Scholar]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method; Wiley Press: New York, NY, USA, 1995. [Google Scholar]
- Crowe, C.T.; Sharma, M.P.; Stock, D.E. The particle-source-in cell (PSI-CELL) model for gas-droplet flow. J. Fluids Eng. 1977, 99, 325–332. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Rigoni, E. Latin Square DOE; ModeFRONTIER: Yasist, Italy, 2005. [Google Scholar]
- McKay, M.D.; Beckman, R.J.; Conover, W.J. Comparison of three methods for selecting values of input variables in the analysis of output from a computer code. Technometrics 1979, 21, 239–245. [Google Scholar]
- Jin, R.; Chen, W.; Simpson, T.W. Comparative studies of metamodeling techniques under multiple modeling criteria. Struct. Multidiscip. Optim. 2011, 23, 1–11. [Google Scholar] [CrossRef]



















| Height (m) | Rotor 1 | Rotor 2 | Rotor 3 | ||||||
| CFD (m/s) | Test (m/s) | Error(%) | CFD (m/s) | Test (m/s) | Error(%) | CFD (m/s) | Test (m/s) | Error(%) | |
| 2.55 | 9.50 | 9.10 | 4.4 | 9.6 | 9.30 | 3.8 | 9.56 | 9.00 | 6.2 |
| 1.55 | 6.52 | 6.10 | 6.9 | 6.7 | 6.30 | 7.1 | 6.63 | 6.40 | 3.6 |
| Height(m) | Rotor 4 | Rotor 5 | Rotor 6 | ||||||
| CFD (m/s) | Test (m/s) | Error(%) | CFD (m/s) | Test (m/s) | Error(%) | CFD (m/s) | Test (m/s) | Error(%) | |
| 2.55 | 9.70 | 9.10 | 6.6 | 9.70 | 9.10 | 6.6 | 9.70 | 9.10 | 6.6 |
| 1.55 | 6.35 | 5.90 | 7.6 | 6.35 | 5.90 | 7.6 | 6.35 | 5.90 | 7.6 |
| Sample Number | Vw/(m/s) | Dd/μm | LP Actual/m | LP Prediction/m |
|---|---|---|---|---|
| 1 | 0.50 | 190.000 | 1.10 | 0.92 |
| 2 | 2.00 | 283.333 | 2.95 | 3.18 |
| 3 | 1.50 | 323.333 | 2.45 | 2.15 |
| 4 | 2.33 | 176.667 | 3.65 | 3.64 |
| 5 | 0.67 | 256.667 | 1.40 | 1.44 |
| 6 | 1.83 | 230.000 | 2.85 | 2.93 |
| 7 | 1.67 | 163.333 | 2.50 | 2.47 |
| 8 | 2.17 | 336.667 | 3.05 | 3.43 |
| 9 | 1.00 | 150.000 | 1.45 | 1.57 |
| 10 | 2.67 | 296.667 | 4.50 | 4.31 |
| 11 | 1.17 | 216.667 | 2.10 | 2.03 |
| 12 | 1.33 | 270.000 | 2.25 | 2.23 |
| 13 | 0.83 | 310.000 | 1.50 | 1.63 |
| 14 | 2.83 | 350.000 | 4.50 | 4.60 |
| 15 | 3.00 | 203.333 | 5.30 | 5.71 |
| 16 | 2.50 | 243.333 | 4.30 | 4.10 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, F.; Xue, X.; Cai, C.; Sun, Z.; Zhou, Q. Numerical Simulation and Analysis on Spray Drift Movement of Multirotor Plant Protection Unmanned Aerial Vehicle. Energies 2018, 11, 2399. https://doi.org/10.3390/en11092399
Yang F, Xue X, Cai C, Sun Z, Zhou Q. Numerical Simulation and Analysis on Spray Drift Movement of Multirotor Plant Protection Unmanned Aerial Vehicle. Energies. 2018; 11(9):2399. https://doi.org/10.3390/en11092399
Chicago/Turabian StyleYang, Fengbo, Xinyu Xue, Chen Cai, Zhu Sun, and Qingqing Zhou. 2018. "Numerical Simulation and Analysis on Spray Drift Movement of Multirotor Plant Protection Unmanned Aerial Vehicle" Energies 11, no. 9: 2399. https://doi.org/10.3390/en11092399
APA StyleYang, F., Xue, X., Cai, C., Sun, Z., & Zhou, Q. (2018). Numerical Simulation and Analysis on Spray Drift Movement of Multirotor Plant Protection Unmanned Aerial Vehicle. Energies, 11(9), 2399. https://doi.org/10.3390/en11092399




