Demand-Side Management of Smart Distribution Grids Incorporating Renewable Energy Sources
Abstract
:1. Introduction
2. Methodology
2.1. Objective Function
2.2. Problem Restrictions
2.2.1. First-Stage Restrictions
2.2.2. Demand Response Strategies
2.2.3. Second-Stage Restrictions
3. Case Studies and Results Analysis
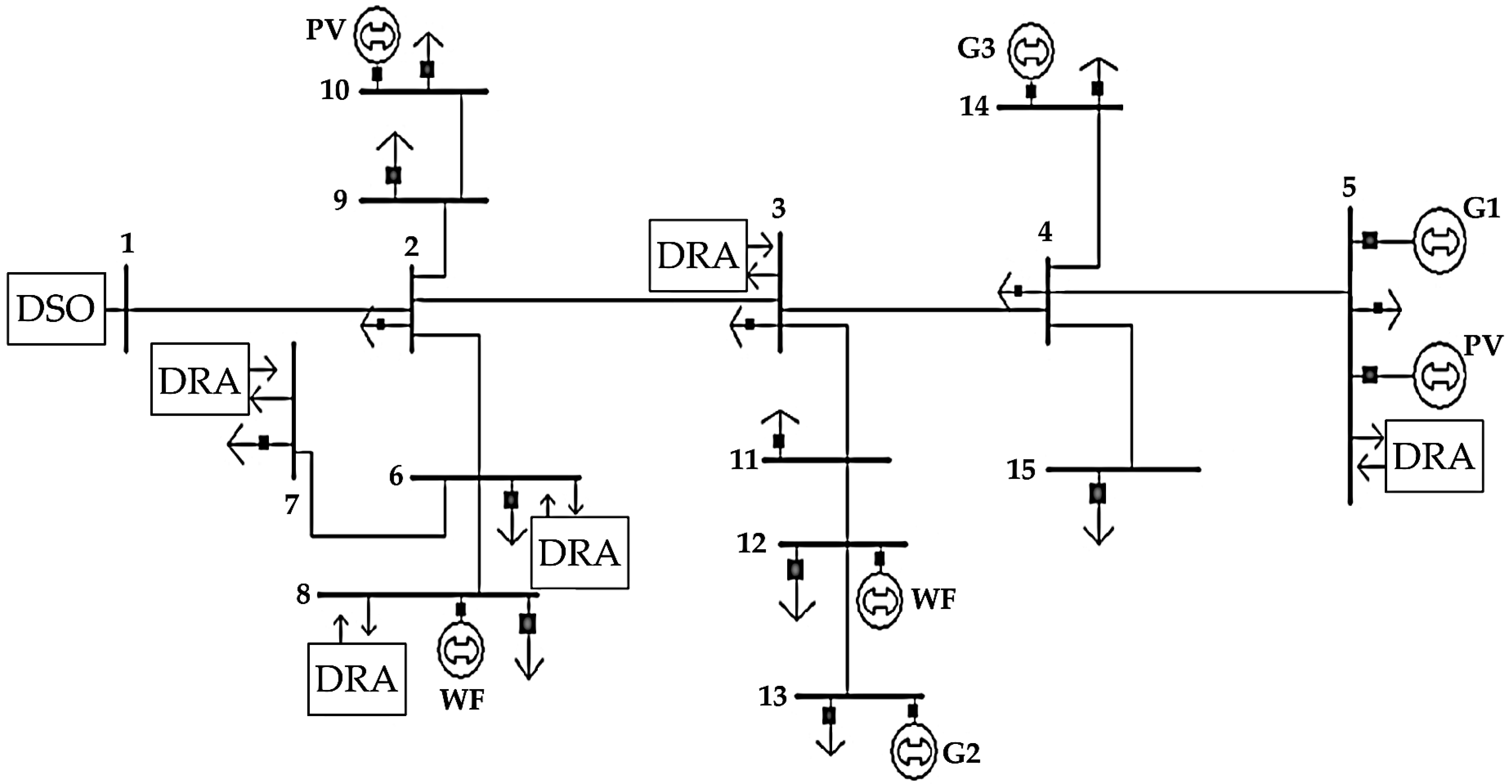
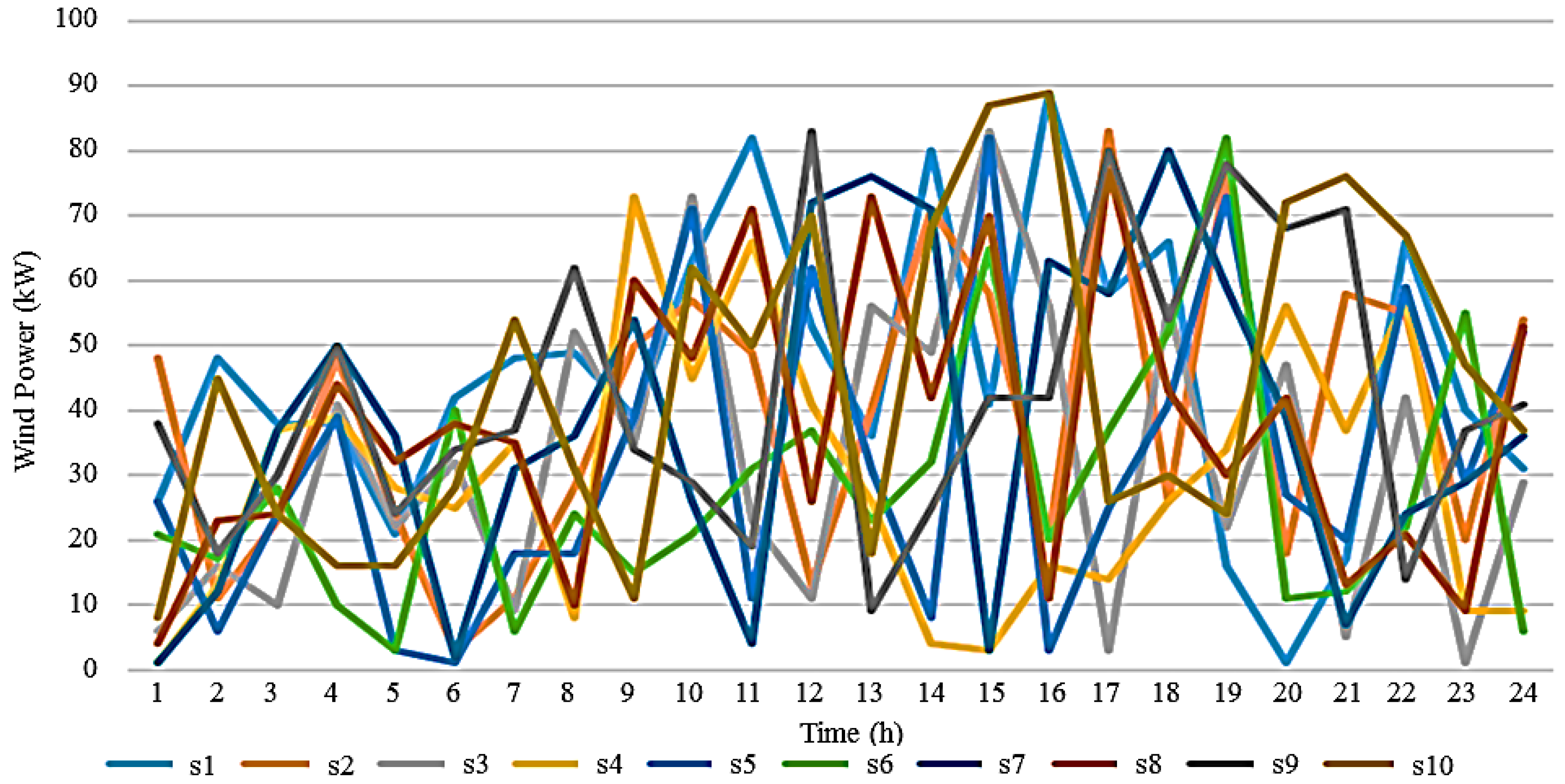
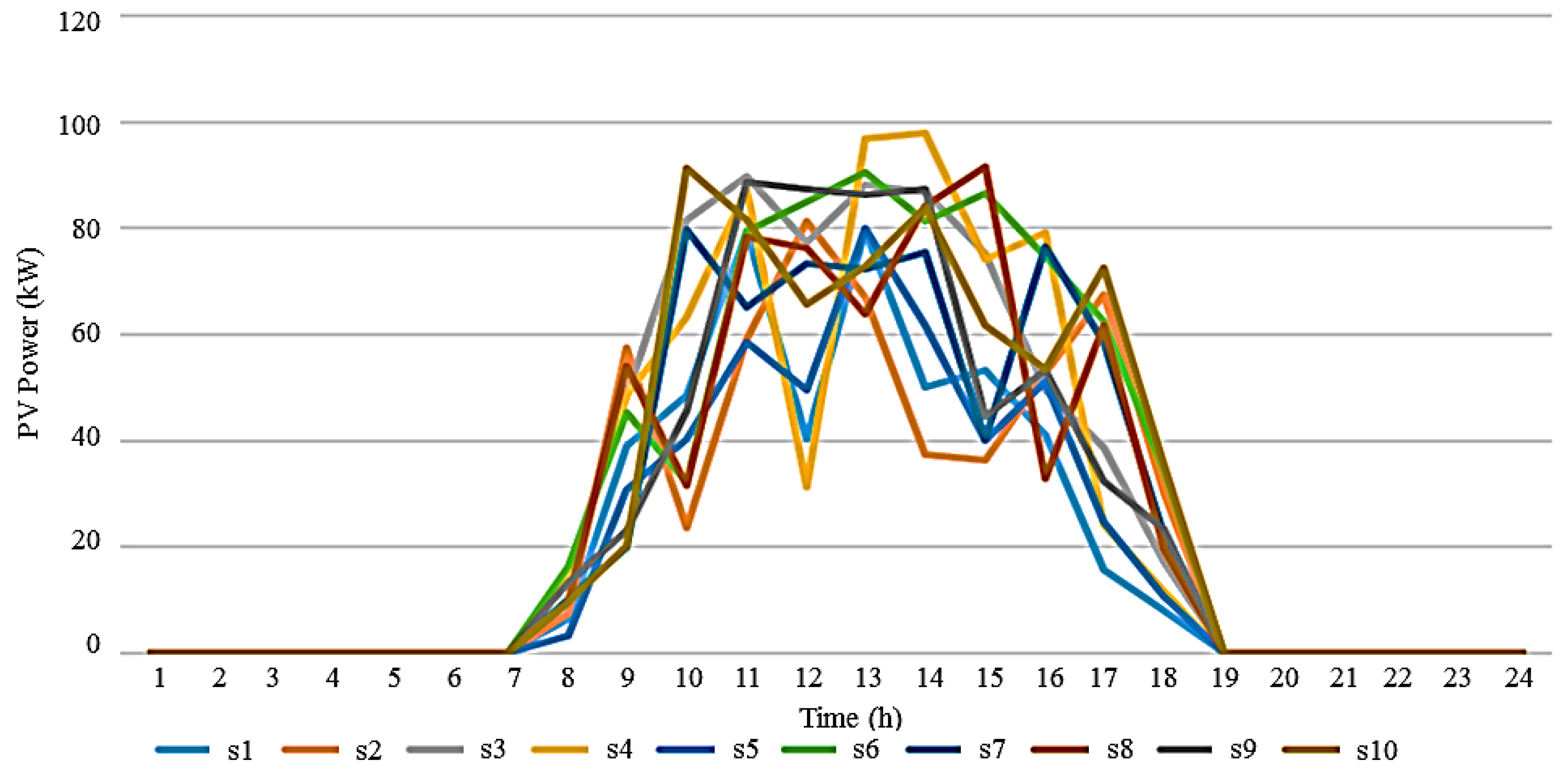
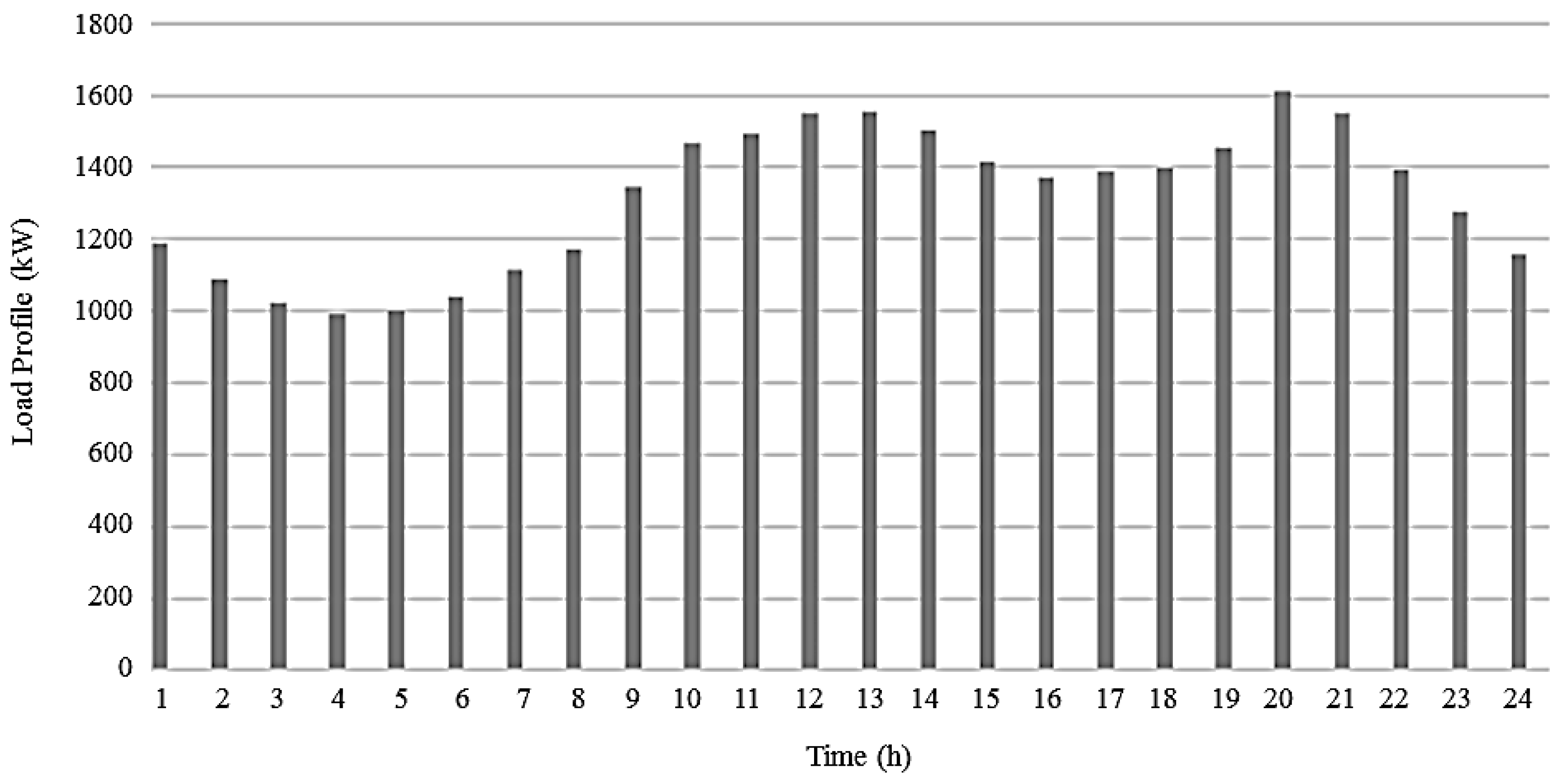
3.1. Details, Data, and System Considered
3.2. Case Studies
3.3. Results Analysis
3.3.1. Base Case Comparison with Cases 2 and 3
3.3.2. Base Case Comparison with Cases 4, 5, and 6
3.3.3. Base Case Comparison with Cases 7, 8, and 9
3.3.4. Comparison between Case 4 and Case 7
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations and Nomenclature
| Abbreviations | |
| A/S | Ancillary services. |
| CAP | Capacity market programs. |
| CES | Conventional energy sources. |
| CPP | Critical peak pricing. |
| DB | Demand bidding/buyback. |
| DG | Distributed generation. |
| DGs | Distribution grids. |
| DLC | Direct load control. |
| DR | Demand response. |
| DRA | Demand response aggregators. |
| DSM | Demand-side management. |
| DSO | Distribution System Operator. |
| EDRP | Emergency demand response programs. |
| EVs | Electric vehicles. |
| I/C | Interruptible/Curtailable. |
| IBDRs | Incentive-based demand response. |
| ISO | Independent System Operator. |
| MG | Microgrid. |
| PBDRs | Price-based demand response. |
| PS | Power systems. |
| PTR | Peak tariff reduction. |
| PV | Photovoltaic system. |
| RES | Renewable energy resources. |
| RTP | Real-time pricing. |
| SG | Smart grid. |
| TOU | Time-of-use. |
| VPP | Variable peak prices. |
| Indexes | |
| Distributed generation index. | |
| Contract index . | |
| Bus index . | |
| Connection points index with the upstream network | |
| Solar system index. | |
| Scenario index . | |
| Time index . | |
| Linear partition index from the linearization process. | |
| Time interval set index for strategy . | |
| Power index . | |
| Wind farm index. | |
| Load shifting (LS), load curtailment (LC), and load recovery (LR) strategy. | |
| Parameter | |
| Unit generation cost. | |
| Regulation cost for the day-ahead market and real-time market. | |
| Higher limit of the quadratic discretization flow (kVA) | |
| Maximum current in the bus. | |
| Predicted active and reactive power, respectively. | |
| Maximum/minimum time for the contract from the strategy . | |
| Market clearing price. | |
| Daily maximum number usage of the strategy . | |
| Contract cost from each strategy . | |
| Maximum power capacity for each . | |
| Transferred load quantity in each contract from the strategy . | |
| Regulation for the day-ahead market and real-time market. | |
| Resistance and inductance in each bus. | |
| Maximum, minimum, and nominal voltage, respectively. | |
| Probability of occurrence of each scenario. | |
| Binary Variables | |
| Load reduction indicator state, from the contract from the strategy . | |
| Relative starting load reduction indicator state, from the contract from the strategy . | |
| Relative finish load reduction indicator state, from the contract from the strategy . | |
| Variables and Functions | |
| Total reduction cost of scheduled load from strategy . | |
| Cost function. | |
| Current flow and quadratic current flow for the day-ahead market (A). | |
| Scheduled load reduction for each strategy . | |
| Active and reactive power flow from the downstream day-ahead market (kW). | |
| Active and reactive power flow from the upstream day-ahead market (kW). | |
| Active power for each in the day-ahead and real-time market. | |
| Reactive power for each in the day-ahead and real-time market. | |
| Power factor. | |
| Voltage and quadratic voltage for the day-ahead market (V). | |
- Foster, E.; Contestabile, M.; Blazquez, J.; Manzano, B.; Workman, M.; Shah, N. The Unstudied Barriers to Widespread Renewable Energy Deployment: Fossil Fuel Price Responses. Energy Policy 2017, 103, 258–264. [Google Scholar] [CrossRef]
- U.S. Energy Information Administration. International Energy Outlook 2017; EIA: Washington, DC, USA, 2017.
- Hepbasli, A. A Key Review on Exergetic Analysis and Assessment of Renewable Energy Resources for a Sustainable Future. Renew. Sustain. Energy Rev. 2008, 12, 593–661. [Google Scholar] [CrossRef]
- Ghaderi, A.; Parsa Moghaddam, M.; Sheikh-El-Eslami, M.K. Energy Efficiency Resource Modeling in Generation Expansion Planning. Energy 2014, 68, 529–537. [Google Scholar] [CrossRef]
- Kiani, A.; Annaswamy, A. Equilibrium in Wholesale Energy Markets: Perturbation Analysis in the Presence of Renewables. IEEE Trans. Smart Grid 2014, 5, 177–187. [Google Scholar] [CrossRef]
- Laureri, F.; Puliga, L.; Robba, M.; Delfino, F.; Bulto, G.O. An Optimization Model for the Integration of Electric Vehicles and Smart Grids: Problem Definition and Experimental Validation. In Proceedings of the 2016 IEEE International Smart Cities Conference (ISC2), Trento, Italy, 12–15 September 2016; pp. 1–6. [Google Scholar]
- Siano, P. Demand Response and Smart grids—A Survey. Renew. Sustain. Energy Rev. 2014, 30, 461–478. [Google Scholar] [CrossRef]
- Amrollahi, M.H.; Bathaee, S.M.T. Techno-Economic Optimization of Hybrid Photovoltaic/wind Generation Together with Energy Storage System in a Stand-Alone Micro-Grid Subjected to Demand Response. Appl. Energy 2017, 202, 66–77. [Google Scholar] [CrossRef]
- Aghajani, G.R.; Shayanfar, H.A.; Shayeghi, H. Demand Side Management in a Smart Micro-Grid in the Presence of Renewable Generation and Demand Response. Energy 2017, 126, 622–637. [Google Scholar] [CrossRef]
- Hossain, M.S.; Madlool, N.A.; Rahim, N.A.; Selvaraj, J.; Pandey, A.K.; Khan, A.F. Role of Smart Grid in Renewable Energy: An Overview. Renew. Sustain. Energy Rev. 2016, 60, 1168–1184. [Google Scholar] [CrossRef]
- Rahmani-andebili, M. Modeling Nonlinear Incentive-Based and Price-Based Demand Response Programs and Implementing on Real Power Markets. Electr. Power Syst. Res. 2016, 132, 115–124. [Google Scholar] [CrossRef]
- Thakur, J.; Chakraborty, B. Demand Side Management in Developing Nations: A Mitigating Tool for Energy Imbalance and Peak Load Management. Energy 2016, 114, 895–912. [Google Scholar] [CrossRef]
- Hu, Z.; Kim, J.; Wang, J.; Byrne, J. Review of Dynamic Pricing Programs in the U.S. and Europe: Status Quo and Policy Recommendations. Renew. Sustain. Energy Rev. 2015, 42, 743–751. [Google Scholar] [CrossRef]
- Heydarian-Forushani, E.; Moghaddam, M.P.; Sheikh-El-Eslami, M.K.; Shafie-khah, M.; Catalão, J.P.S. A Stochastic Framework for the Grid Integration of Wind Power Using Flexible Load Approach. Energy Convers. Manag. 2014, 88, 985–998. [Google Scholar] [CrossRef]
- Aalami, H.A.; Moghaddam, M.P.; Yousefi, G.R. Modeling and Prioritizing Demand Response Programs in Power Markets. Electr. Power Syst. Res. 2010, 80, 426–435. [Google Scholar] [CrossRef]
- Nikzad, M.; Mozafari, B. Reliability Assessment of Incentive- and Priced-Based Demand Response Programs in Restructured Power Systems. Int. J. Electr. Power Energy Syst. 2014, 56, 83–96. [Google Scholar] [CrossRef]
- Babar, M.; Nguyen, P.H.; Cuk, V.; Kamphuis, I.G. The Development of Demand Elasticity Model for Demand Response in the Retail Market Environment. In Proceedings of the 2015 IEEE Eindhoven PowerTech, Eindhoven, The Netherlands, 29 June–2 July 2015; pp. 1–6. [Google Scholar]
- Fan, W.; Liu, N.; Zhang, J.; Fan, W.; Liu, N.; Zhang, J. An Event-Triggered Online Energy Management Algorithm of Smart Home: Lyapunov Optimization Approach. Energies 2016, 9, 381. [Google Scholar] [CrossRef]
- Babar, M.; Grela, J.; Ożadowicz, A.; Nguyen, P.; Hanzelka, Z.; Kamphuis, I.; Babar, M.; Grela, J.; Ożadowicz, A.; Nguyen, P.H.; et al. Energy Flexometer: Transactive Energy-Based Internet of Things Technology. Energies 2018, 11, 568. [Google Scholar] [CrossRef]
- Liu, Z.; Wu, Q.; Huang, S.; Zhao, H. Transactive Energy: A Review of State of the Art and Implementation. In Proceedings of the 2017 IEEE Manchester PowerTech, Manchester, UK, 18–22 June 2017; pp. 1–6. [Google Scholar]
- Chen, S.; Liu, C.-C. From Demand Response to Transactive Energy: State of the Art. J. Mod. Power Syst. Clean Energy 2017, 5, 10–19. [Google Scholar] [CrossRef]
- Parvania, M.; Fotuhi-Firuzabad, M.; Shahidehpour, M. Optimal Demand Response Aggregation in Wholesale Electricity Markets. IEEE Trans. Smart Grid 2013, 4, 1957–1965. [Google Scholar] [CrossRef]
- O’Connell, N.; Pinson, P.; Madsen, H.; O’Malley, M. Benefits and Challenges of Electrical Demand Response: A Critical Review. Renew. Sustain. Energy Rev. 2014, 39, 686–699. [Google Scholar] [CrossRef]
- Guo, P.; Li, V.O.K.; Lam, J.C.K. Smart Demand Response in China: Challenges and Drivers. Energy Policy 2017, 107, 1–10. [Google Scholar] [CrossRef]
- Nolan, S.; O’Malley, M. Challenges and Barriers to Demand Response Deployment and Evaluation. Appl. Energy 2015, 152, 1–10. [Google Scholar] [CrossRef]
- Siano, P.; Sarno, D. Assessing the Benefits of Residential Demand Response in a Real Time Distribution Energy Market. Appl. Energy 2016, 161, 533–551. [Google Scholar] [CrossRef]
- Talari, S.; Shafie-khah, M.; Wang, F.; Aghaei, J.; Catalao, J.P.S. Optimal Scheduling of Demand Response in Pre-Emptive Markets Based on Stochastic Bilevel Programming Method. IEEE Trans. Ind. Electron. 2019, 66, 1453–1464. [Google Scholar] [CrossRef]
- Selin Kocaman, A.; Abad, C.; Troy, T.J.; Tim Huh, W.; Modi, V. A Stochastic Model for a Macroscale Hybrid Renewable Energy System. Renew. Sustain. Energy Rev. 2016, 54, 688–703. [Google Scholar] [CrossRef]
- Kwon, S.; Ntaimo, L.; Gautam, N. Optimal Day-Ahead Power Procurement With Renewable Energy and Demand Response. IEEE Trans. Power Syst. 2017, 32, 3924–3933. [Google Scholar] [CrossRef]
- GAMS Development Corp. GAMS Software GmbH. General Algebraic Modeling System (GAMS)—Cutting Edge Modeling. Available online: https://www.gams.com/ (accessed on 2 November 2018).
- ESIOS Electricity. Available online: https://www.esios.ree.es/en (accessed on 21 December 2018).




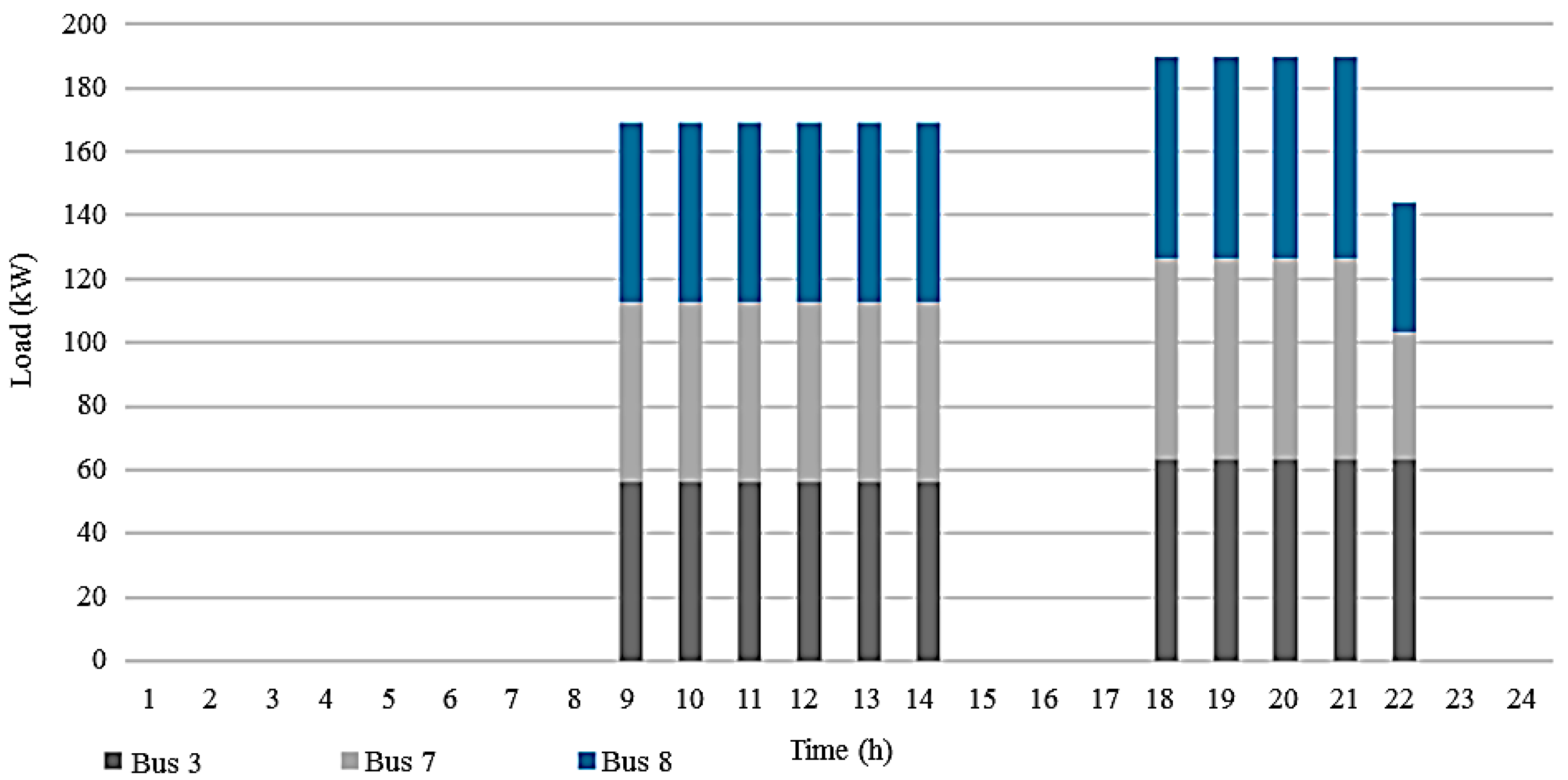



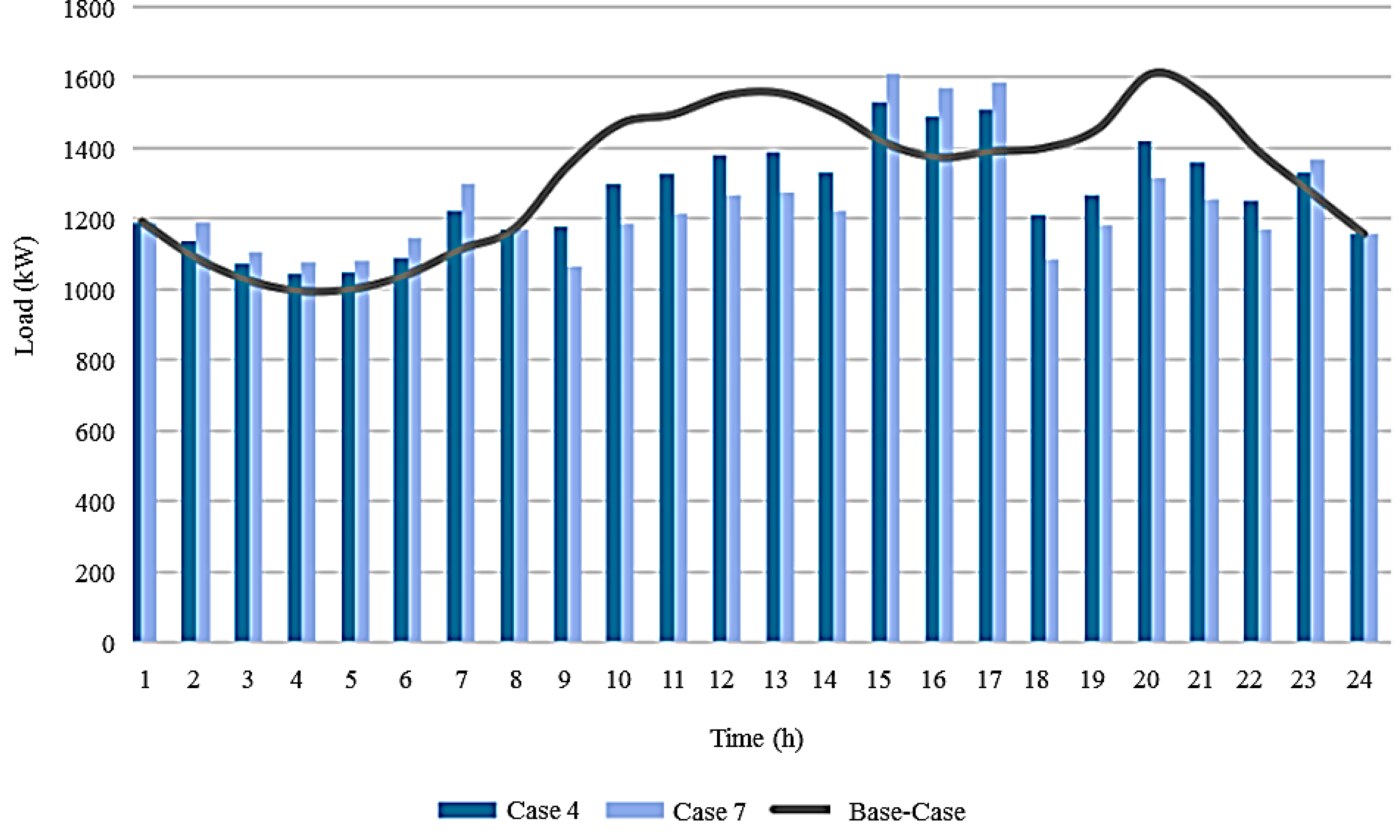
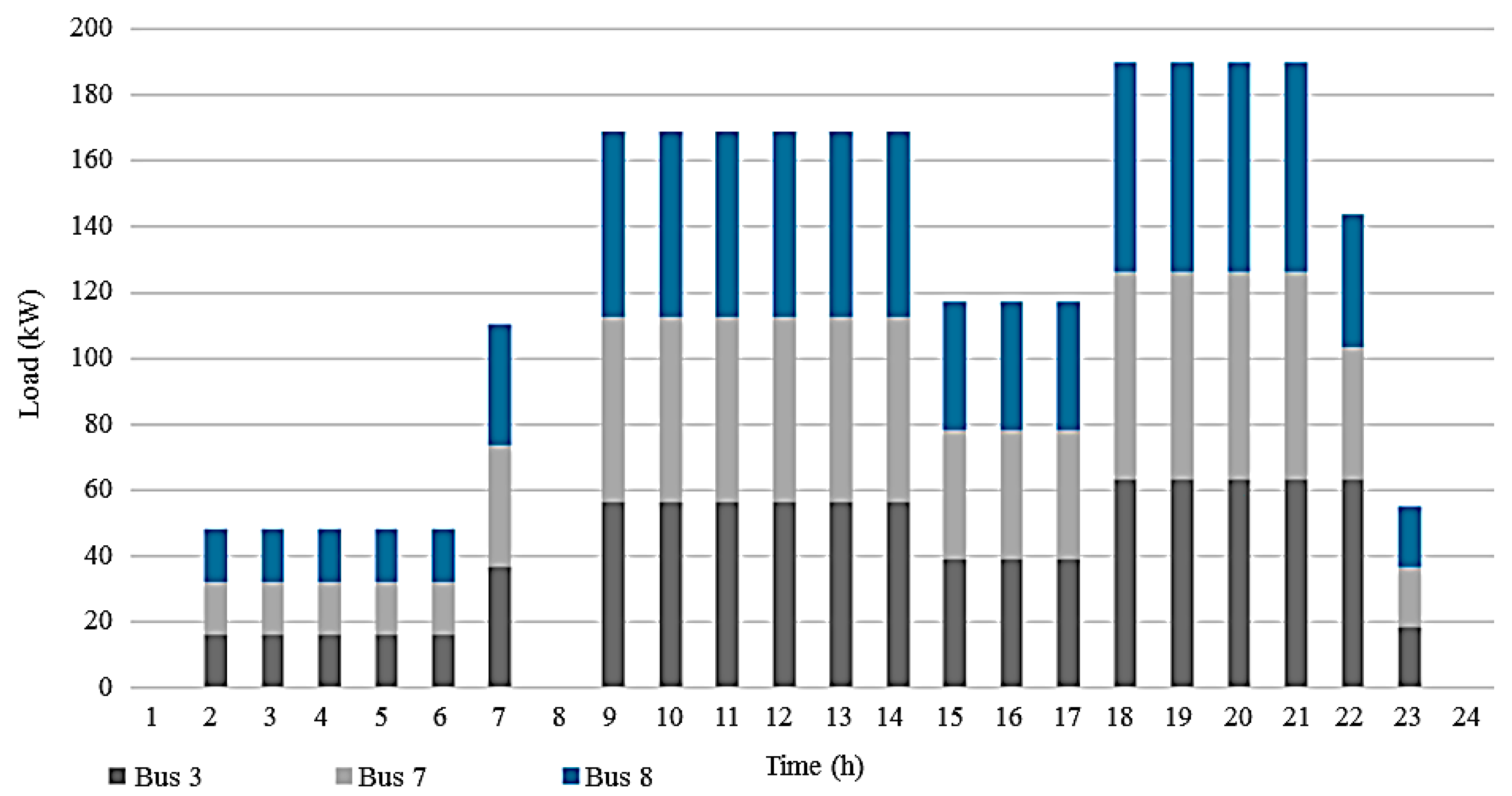
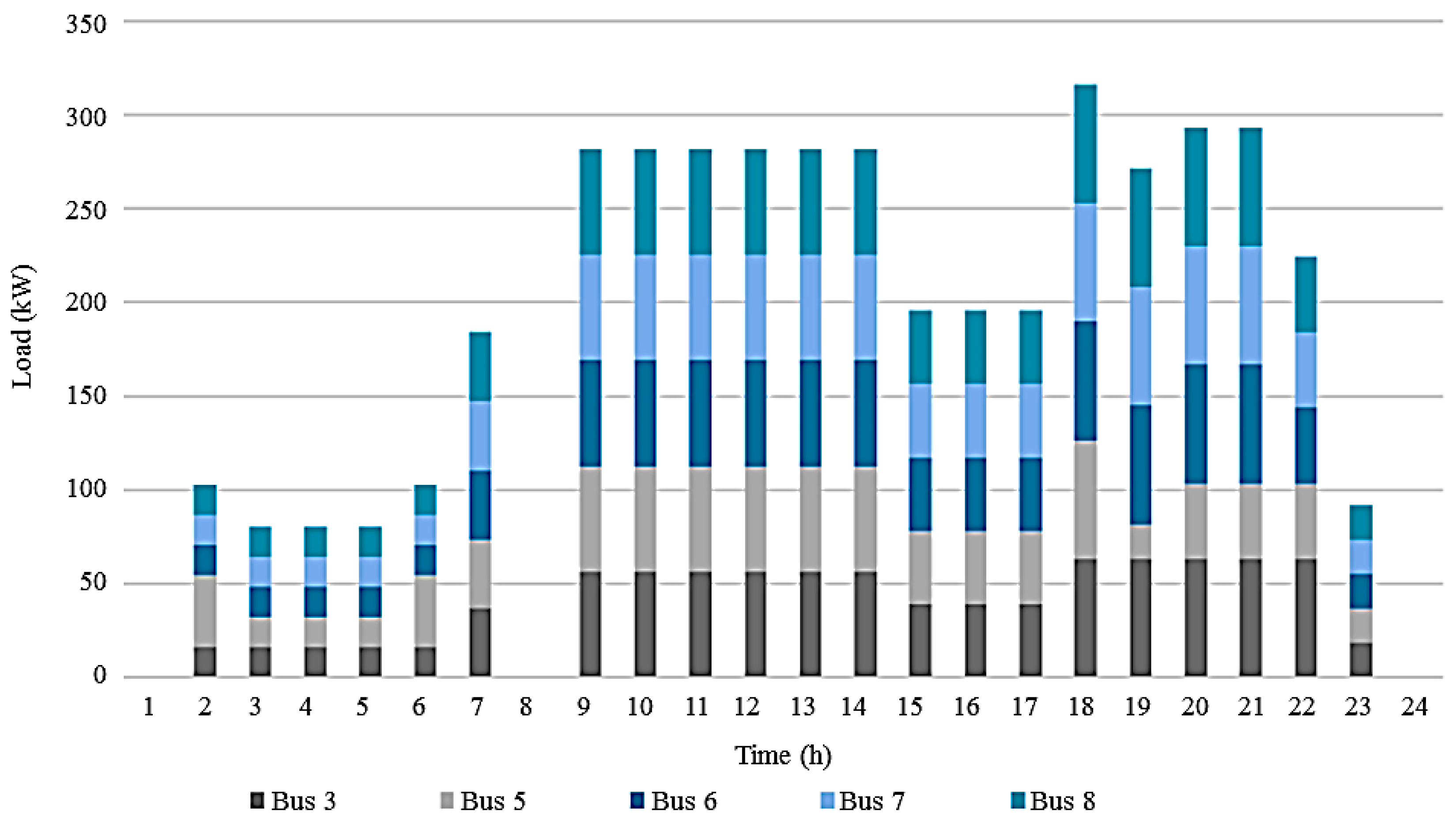
| CES Unit (Bus #) | Power (kW) | |
|---|---|---|
| 1 (Bus 05) | 23.00 | 230.00 |
| 2 (Bus 13) | 69.00 | 690.00 |
| 3 (Bus 14) | 46.00 | 460.00 |
| Scenario | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Probability (%) | 10.90 | 9.60 | 12.40 | 14.40 | 2.80 | 6.40 | 5.20 | 17.70 | 17.80 | 2.80 |
| Scenario | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Probability (%) | 13.30 | 6.70 | 4.60 | 8.10 | 16.30 | 14.20 | 9.40 | 14.20 | 4.20 | 9.00 |
| Case | Case Description | DR Contract Type | Tariffs | DRA Buses |
|---|---|---|---|---|
| 1 | No DR (Base Case) | - | - | - |
| 2 | DRA in 3 buses with LC contracts. | LC | +0% | 3 |
| 3 | DRA in 5 buses with LC contracts. | LC | +0% | 5 |
| 4 | DRA in 3 buses with LS contracts and normal electricity tariffs. | LS | +0% | 3 |
| 5 | DRA in 3 buses with LS contracts and 30% electricity tariffs higher. | LS | +30% | 3 |
| 6 | DRA in 3 buses with LS contracts and 30% electricity tariffs lower. | LS | −30% | 3 |
| 7 | DRA in 5 buses with LS contracts and normal electricity tariffs. | LS | +0% | 5 |
| 8 | DRA in 5 buses with LS contracts and 30% electricity tariffs higher. | LS | +30% | 5 |
| 9 | DRA in 5 buses with LS contracts and 30% electricity tariffs lower. | LS | −30% | 5 |
| Case | Total Operation Cost (€) | DR Cost (€) |
|---|---|---|
| 1 | 1014.30 | 0 |
| 2 | 1053.40 | 67.80 |
| 3 | 1307.30 | 107.90 |
| 4 | 1046.50 | 90.20 |
| 5 | 1064.90 | 71.90 |
| 6 | 1016.60 | 69.90 |
| 7 | 1023.50 | 146.80 |
| 8 | 1055.70 | 105.70 |
| 9 | 977.50 | 117.70 |
| Contract | LC Period (h) | Quantity (kW) | Price (€/kW) |
|---|---|---|---|
| K1 | 09:00–14:00 18:00–22:00 | 16.10 18.40 | 0.02 0.03 |
| K2 | 09:00–14:00 18:00–22:00 | 18.40 21.85 | 0.03 0.04 |
| K3 | 09:00–14:00 18:00–22:00 | 21.85 23.00 | 0.04 0.05 |
| Contract | Maximum LC per Day | Maximum Time of Load Reduction (h) | Minimum Time of Load Reduction (h) |
|---|---|---|---|
| K1 | 1 | 9 | 4 |
| K2 | 1 | 9 | 4 |
| K3 | 1 | 9 | 4 |
| Contract | K1 | K2 | K3 |
|---|---|---|---|
| LS period (h) | 09:00–14:00 18:00–22:00 | 09:00–14:00 18:00–22:00 | 09:00–14:00 18:00–22:00 |
| LR period (h) | 02:00–07:00 | 15:00–17:00 23:00–00:00 | 02:00–07:00 15:00–17:00 |
| Quantity (kW) | 16.10 | 18.40 | 20.70 |
| Normal Price (€/kW) | 0.020 | 0.030 | 0.040 |
| Price 30% higher (€/kW) | 0.026 | 0.039 | 0.052 |
| Price 30% lower (€/kW) | 0.014 | 0.021 | 0.028 |
| Maximum LS per day | 1 | 1 | 1 |
| Maximum time of load reduction (h) | 9 | 9 | 9 |
| Minimum time of load reduction (h) | 4 | 4 | 4 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Osório, G.J.; Shafie-khah, M.; Lotfi, M.; Ferreira-Silva, B.J.M.; Catalão, J.P.S. Demand-Side Management of Smart Distribution Grids Incorporating Renewable Energy Sources. Energies 2019, 12, 143. https://doi.org/10.3390/en12010143
Osório GJ, Shafie-khah M, Lotfi M, Ferreira-Silva BJM, Catalão JPS. Demand-Side Management of Smart Distribution Grids Incorporating Renewable Energy Sources. Energies. 2019; 12(1):143. https://doi.org/10.3390/en12010143
Chicago/Turabian StyleOsório, Gerardo J., Miadreza Shafie-khah, Mohamed Lotfi, Bernardo J. M. Ferreira-Silva, and João P. S. Catalão. 2019. "Demand-Side Management of Smart Distribution Grids Incorporating Renewable Energy Sources" Energies 12, no. 1: 143. https://doi.org/10.3390/en12010143
APA StyleOsório, G. J., Shafie-khah, M., Lotfi, M., Ferreira-Silva, B. J. M., & Catalão, J. P. S. (2019). Demand-Side Management of Smart Distribution Grids Incorporating Renewable Energy Sources. Energies, 12(1), 143. https://doi.org/10.3390/en12010143








