Natural Convection of Non-Newtonian Power-Law Fluid in a Square Cavity with a Heat-Generating Element

Abstract

Development of modern technology in microelectronics and power engineering necessitates the creation of effective cooling systems. This is made possible by the use of the special fins technology within the cavity or special heat transfer liquids in order to intensify the heat removal from the heat-generating elements. The present work is devoted to the mathematical modeling of thermogravitational convection of a non-Newtonian fluid in a closed square cavity with a local source of internal volumetric heat generation. The behavior of the fluid is described by the Ostwald-de Waele power law model. The defining Navier–Stokes equations written using the dimensionless stream function, vorticity and temperature are solved using the finite difference method. The effects of the Rayleigh number, power-law index, and thermal conductivity ratio on heat transfer and the flow structure are studied. The obtained results are presented in the form of isolines of the stream function and temperature, as well as the dependences of the average Nusselt number and average temperature on the governing parameters.

1. Introduction

The use of liquids in various technical applications is well known, but there is a greater special interest of researchers in the study of non-Newtonian fluids because of the realization that they are now very common in everyday life [1,2,3]. For example, most polymeric liquids, including melts and solutions, foams, emulsions, suspensions, worm-like micelles, antifreezes, porcelain clay, sewage sludge, pharmaceutical formulations, cosmetics and toiletries, paints and synthetic lubricants, biological fluids (blood, synovial fluid, sage) and food products (butter, jams, jellies, soups, marmalade) show non-Newtonian properties according to flow characteristics [4,5,6,7,8].

The main feature of non-Newtonian fluids is the nonlinear dependence of shear stress on shear rate. Since dynamic viscosity changes with shear stress, the fluidity of such a fluid, and thus heat transfer, becomes more complex. Therefore, the analysis of non-Newtonian fluids behavior warrants special attention [1,2,3,4,5,6,7,8,9].

Many papers have been devoted to the analysis of non-Newtonian fluids flow in various configurations. The peristaltic transport of non-Newtonian fluids in a diverging tube with various forms of near-wall waves was studied by Hariharan et al. [10]. Comparison of ink exhibiting Newtonian and non-Newtonian character for laser printing was carried out by Kalaitzis et al. [11]. The rheological properties of the TiO₂/ZnO/EG nanofluid were studied by Nafchi et al. [12]. Hundertmark-Zausková and Lukácová-Medvid’ová [13] considered blood flow as a pseudoplastic fluid circulating inside elastic vessels. A three-dimensional simulation of the human cardiovascular system was performed by Janela et al. [14], where the authors compared the Newtonian and non-Newtonian models for blood.

Along with the hydrodynamics of non-Newtonian fluid, the process of natural convection is being actively studied, since it is the most common method of electronic components cooling. This technique is of great interest due to its simplicity, minimal cost, low noise, smaller size and reliability [15]. In addition, cooling by natural convection in enclosures is very popular due to various areas of applicability, such as cooling systems for electronic gadgets, high-performance insulation of buildings, multi-layer structures, various furnaces, solar heat collectors, polymer processing, oil product recovery, transportation of suspensions, production of chemical substances and fertilizers, medicine and food industry, paper making, production and packaging of paints and emulsions, etc. [16,17]. The process of natural convection is also considered in various cavities and with various heat exchange agents, for example, natural convection cooling of a heat source by a nanofluid was studied by Aminossadati and Ghasemi [18]. Heat transfer using natural convection during the melting of a material with a phase transition in a closed rectangular cavity with three heaters on the left vertical wall was studied by El Qarnia et al. [19]. Laminar natural convection in a square cavity heated through side walls at small Prandtl numbers with large differences in density has been numerically studied by Pesso and Piva [20]. Aly and Raizahan [21] proposed a hydrodynamic method for incompressible particles for natural convection in a cavity filled with nanofluid, including numerous solid structures. Laminar unsteady free convection in a closed region with a heat source of various shapes was numerically studied by Gibanov and Sheremet [22]. A numerical study of natural convection in a closed cavity, in the center of which a heat source is located, was carried out by Mahalakshmi et al. [23].

Despite the active use of various nanofluids, water and air in such processes, non-Newtonian power law fluids are also assigned a significant role. For example, Sasmal et al. [24] studied the laminar natural convection of a non-Newtonian fluid in a closed square cavity with an isothermal rotating cylinder. Kiyasatfar [25] performed the analysis of convective heat exchange of a sliding flow of non-Newtonian fluid through a parallel plate and round microchannels. A numerical study of the natural convection of power law fluids in a vertical open finite channel was carried out by Zhou and Bayazitoglu [26]. Double-diffusive natural convection of a Bingham fluid was studied by Kefayati [27] taking into account the Soret and Dufour effects. Laminar natural convection in a closed trapezoidal cavity filled with a non-Newtonian nanofluid was studied numerically by Alsabery et al. [28]. Kefayati and Tang [29] investigated the natural convection of a non-Newtonian nanofluid in a cavity with a uniform magnetic field. An experimental study of the convective heat transfer of a stream of a non-Newtonian solution of Xanthan gum in a micropipe was carried out by Shojaeian et al. [30].

Based on the review of literature, it can be concluded that natural convection of a non-Newtonian fluid in a closed cavity has a great deal of significance in modern research. In this regard, the aim of the present work is the mathematical modeling of the natural convection of a power-law fluid in a closed square cavity with a heat-generating and heat-conducting element.

2. Governing Equations and Numerical Technique

In this paper, we study the process of thermogravitational convection in a closed square cavity as shown in Figure 1. Horizontal walls are heat insulated. Vertical walls are maintained at low temperature T_c. The energy source is located in the center of the bottom wall and this source has a constant internal volumetric heat generation Q. Gravity force is directed vertically down.

The cavity under investigation is filled with a non-Newtonian fluid that follows the Ostwald-de Waele power law model:

$${\tau }_{ij}=2{\mu }_{eff}{D}_{ij}=2K{\left(2D_{kl}{D}_{kl}\right)}^{\frac{n-1}{2}}{D}_{ij}$$

(1)

Here τ_ij-is the shear stress, ${\mu }_{eff}$-is the effective viscosity, $D_{ij}$-is the component of the strain rate tensor, K-is the flow consistency index, n-is the power law index.

The process of natural convection is described by the following time-dependent system of partial differential equations:

$$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0$$

(2)

$$\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=-\frac{1}{\rho }\frac{\partial p}{\partial x}+\frac{1}{\rho }\left(\frac{\partial {\tau }_{xx}}{\partial x}+\frac{\partial {\tau }_{xy}}{\partial y}\right)$$

(3)

$$\frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}=-\frac{1}{\rho }\frac{\partial p}{\partial y}+\frac{1}{\rho }\left(\frac{\partial {\tau }_{xy}}{\partial x}+\frac{\partial {\tau }_{yy}}{\partial y}\right)+g\beta \left(T-T_c\right)$$

(4)

$$\frac{\partial T}{\partial t}+u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\alpha \left(\frac{{\partial }^{2}T}{\partial x^2}+\frac{{\partial }^{2}T}{\partial y^2}\right)$$

(5)

The heat conduction equation for the local heater is

$$\left(\rho c\right)\frac{\partial T}{\partial t}=k_{hs}\left(\frac{{\partial }^{2}T}{\partial x^2}+\frac{{\partial }^{2}T}{\partial y^2}\right)+Q$$

(6)

For ease of calculation, the problem was reduced to a transformed dimensionless form. The non-primitive variables such as the stream function $u=\frac{\partial \psi }{\partial y},v=-\frac{\partial \psi }{\partial x}$ and vorticity $\omega =\frac{\partial v}{\partial x}-\frac{\partial u}{\partial y}$ were introduced. Further, dimensionless variables were included into the equations using the following parameters L is the length of the cavity; X = x/L, Y = y/L are the coordinates; $\tau =t\sqrt{g\beta \Delta T/L}$ is the dimensionless time; $\Psi =\psi /\sqrt{g\beta \Delta T{L}^3}$ is the dimensionless stream function; $\Omega =\omega /\sqrt{L/g\beta \Delta T}$ is the dimensionless vorticity; $\Theta =\left(T-T_c\right)/\Delta T$ is the dimensionless temperature; $\Delta T=Q{L}^2/k_{hs}$ is the temperature difference.

The basic equations in non-dimensional form using the stream function, vorticity and temperature variables take a new form (7)–(10):

$$\frac{{\partial }^2\Psi }{\partial X^2}+\frac{{\partial }^2\Psi }{\partial Y^2}=-\Omega$$

(7)

$$\frac{\partial \Omega }{\partial \tau }+\frac{\partial \Psi }{\partial Y}\frac{\partial \Omega }{\partial X}-\frac{\partial \Psi }{\partial X}\frac{\partial \Omega }{\partial Y}={\left(\frac{Ra}{Pr}\right)}^{\frac{n-2}{2}}\left[{\nabla }^2\left(\tilde{M}\Omega \right)+S_{\Omega }\right]+\frac{\partial \Theta }{\partial X}$$

(8)

$$\frac{\partial \Theta }{\partial \tau }+\frac{\partial \Psi }{\partial Y}\frac{\partial \Theta }{\partial X}-\frac{\partial \Psi }{\partial X}\frac{\partial \Theta }{\partial Y}=\frac{1}{\sqrt{Ra\cdot Pr}}\left(\frac{{\partial }^2\Theta }{\partial X^2}+\frac{{\partial }^2\Theta }{\partial Y^2}\right)$$

(9)

In the case of internal heat-generating element we have the following heat conduction equation

$$\frac{\partial {\Theta }_{hs}}{\partial \tau }=\frac{Ar}{\sqrt{Ra\cdot Pr}}\left(\frac{{\partial }^2{\Theta }_{hs}}{\partial X^2}+\frac{{\partial }^2{\Theta }_{hs}}{\partial Y^2}+1\right)$$

(10)

Here $\tilde{M}={\left[4{\left(\frac{{\partial }^2\Psi }{\partial X\partial Y}\right)}^2+{\left(\frac{{\partial }^2\Psi }{\partial Y^2}-\frac{{\partial }^2\Psi }{\partial X^2}\right)}^2\right]}^{\frac{n-1}{2}}$, $S_{\Omega }=2\left[\frac{{\partial }^2\tilde{M}}{\partial X^2}\frac{{\partial }^2\Psi }{\partial Y^2}+\frac{{\partial }^2\tilde{M}}{\partial Y^2}\frac{{\partial }^2\Psi }{\partial X^2}-2\frac{{\partial }^2\tilde{M}}{\partial X\partial Y}\frac{{\partial }^2\Psi }{\partial X\partial Y}\right]$, $Pr=\frac{\tilde{\nu }}{\alpha }$ is the Prandtl number; $Ra=\frac{g\beta \Delta T{L}^3}{\tilde{\nu }\alpha }$ is the Rayleigh number, $\tilde{\nu }={\left(\frac{K}{\rho }\right)}^{\frac{1}{2-n}}{L}^{\frac{2\left(1-n\right)}{2-n}}$ is the effective kinematic viscosity.

Initial conditions for the considered problem are $\Omega =\Psi =\Theta =0$.

Boundary conditions:

$$\begin{array}{c}X=0\mathrm{and}X=1,0\le Y\le 1,\Psi =0,\frac{\partial \Psi }{\partial X}=0,\Theta =0;\\ Y=0\mathrm{and}Y=1,0\le X\le 1,\Psi =0,\frac{\partial \Psi }{\partial Y}=0,\frac{\partial \Theta }{\partial Y}=0;\end{array}$$

at the heat source surface: $\Psi =0,\Omega =-\frac{{\partial }^2\Psi }{\partial {\overline{n}}^2},\{\begin{array}{l}{\Theta }_{hs}={\Theta }_f\\ \frac{k_{hs}}{k_f}\frac{\partial {\Theta }_{hs}}{\partial \overline{n}}=\frac{\partial {\Theta }_f}{\partial \overline{n}}\end{array}$.

The main numerical technique used to solve the considered problem is the finite difference method. The differential Equation (7) for the stream function was discretized using the central differences and the obtained difference equation was solved by the successive over-relaxation method [31,32]. The optimal value of the relaxation parameter was selected on the basis of numerical experiments. The convective terms in parabolic Equations (8) and (9) were approximated using the “donor cell” difference scheme. It should be noted that this scheme is known also as the second upstream scheme. This scheme is based on one-sided differences in spatial variables and has the property of transport and conservatism. The point is that when the velocities are positive, the difference is used backwards, and vice versa. The diffusion terms were discretized by central differences. The numerical solution of parabolic Equations (8)–(10) was performed using the locally one-dimensional Samarskii scheme [31,32]. This scheme allows transformation of a two-dimensional problem to a one-dimensional problem. The obtained linear algebraic equations were solved by the Thomas algorithm [31,32].

The developed algorithm for solving the problem was implemented by a computational code using the C++ programming language. Before carrying out the basic calculations, the developed in-house code was tested in detail using some problems for verification. The first benchmark problem was the natural convection of a non-Newtonian fluid in a differentially heated cavity. The horizontal walls were heat insulated. The vertical left wall was maintained at a constant temperature T_h, while the vertical right wall had a constant temperature T_c (T_h > T_c). The diagram of the test problem solution area is shown in Figure 2.

Figure 3 shows the comparison of streamlines at Ra = 10⁵, Pr = 100, n = 1.0 and 1.4, obtained using the developed in-house computational code and numerical data of Khezzar et al. [33]. As a result of this validation study, an analysis was obtained for the values of the average Nusselt number at the left isothermal wall of the cavity in comparison with the results [33,34].

Table 1. The value of the average Nusselt number depending on the power law index.

n	Nuavg in This Work	Nuavg in [33]	Nuavg in [34]
0.6	7.3823	6.9345	7.020
0.8	5.6201	5.5127	–
1.0	4.7662	4.6993	4.741
1.2	4.2227	4.1709	–
1.4	3.8464	3.7869	3.770

shows the obtained comparison for the average Nusselt number. Thus, the results of testing the computational code showed that the data obtained are in good agreement with the data of other authors. The numerical algorithm and developed computational code are operable and may be applicable in further studies.

In the case of thermogravitational convection of a power law fluid in a cavity with an energy source, preliminary estimation of the influence of the grid parameters and the time step on the process under study was carried out. Figure 4 shows the time dependences of the average Nusselt number (a) and average heater temperature (b). Dependencies are plotted at n = 0.6, Ra = 10⁵, k = k_hs/k_f = 1, Pr = 10² with the following grid parameters: 50 × 50, 100 × 100, 150 × 150.

Based on this dependence, we chose a grid of 100 × 100 nodes, since it does not lead to strong discrepancies and it does not affect the process under study. In addition, in the course of the study it was revealed that the final value of dimensionless time τ = 200 is not enough, so the calculations were carried out at τ = 2000.

3. Results

As a result of numerical simulation of thermogravitational convection of a non-Newtonian power law fluid in a closed square cavity with a heat source, an analysis was made to understand the effects of governing parameters on the process. The Rayleigh number Ra is varied in the range 10⁴–10⁵, the power law index n is changed from 0.8 to 1.4, the thermal conductivity ratio is k = 1, 10, 10², 10³. The Prandtl number was fixed at Pr = 10². Streamlines, isotherms and distributions of the average Nusselt number and mean temperature within the heater are shown in Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10.

Figure 5 shows the effect of the Rayleigh number on the distribution of streamlines Ψ (a) and isotherms Θ (b) for n = 0.8, Pr = 10², k = 10². In Figure 5a, the distribution of the streamlines shows that with the increasing of the Rayleigh number, the flow structure does not change. Namely, two convective cells are formed in the cavity, and these cells are symmetrical to each other relative to the central axis. The shape of the cells varies slightly from elliptical to more rectangular with a pronounced flow around the source. Moreover, the convective cells cores are displaced to the central vertical axis and the streamlines density increases in this central part. Such behavior can be explained by a growth of convective flow intensity due to high values of the buoyancy force magnitude and as a result, the thickness of the central thermal plume decreases that reflects intensive liquid motion in this narrow zone. The temperature field in Figure 5b with Ra = 10⁴ indicates the predominance of the conductive mechanism of heat transfer in the cavity, since the isotherms are located almost parallel to the cooling walls. Consequently, the heat transfer in the cavity is very weak. With an increase in Ra, the convective heat exchange is enhanced, which corresponds to the formation of a two-dimensional heat plume above the heat source. It is seen that an upward flow is formed above the source due to the temperature difference between the heater and the liquid near this element. The hot ascending flow reaches the upper adiabatic wall. After that, this flow separates and descends along the cooling vertical walls, which corresponds to the expansion of the thermal plume cap and an appearance of cold temperature wave in the bottom part of the cavity from the left and right sides of the heater. Similar relationship between streamlines and isotherms can be observed for all considered cases.

Figure 6 shows the time dependence of the average Nusselt number Nu_avg (a) and mean heater temperature Θ_avg (b) for different Rayleigh numbers. Dependencies are plotted for n = 0.8, Pr = 10², k = 10². The average Nusselt number at the heat source surface was calculated as follows $N{u}_{avg}=\frac{1}{0.6}{\displaystyle \underset{0}{\overset{0.6}{\int }}\left(-\frac{\partial \Theta }{\partial \overline{n}}\right)}d\varsigma$. Figure 6a shows that as the Rayleigh number increases, the average Nusselt number also rises. This suggests that convective heat transfer is enhanced in the cavity. In addition, it can be seen that the considered modes are unsteady, because Nu_avg continues to change with time. It is worth noting that for Ra = 10⁴ the mean Nusselt number decreases during the conduction regime and increases during the weak convective regime, while for Ra = 10⁵ and 10⁶ Nu_avg reduces. Figure 6b shows the dependence of the average temperature within the source on the time and Rayleigh number. One can see that this dependence fully corresponds to the dependence of the average Nusselt number on the Rayleigh number, namely, the mean temperature decreases with time for Ra = 10⁵ and 10⁶, while it increases with time for Ra = 10⁴.

An analysis of the effect of the power law index on the liquid circulation and thermal transmission can be observed in Figure 7 and Figure 8. It should be noted that n describes the character of the relationship between the components of the stress tensor and the strain rate tensor. The case n < 1 describes a pseudoplastic fluid, whose viscosity reduces with increasing strain rate. The case n = 1 describes a Newtonian fluid. The case n > 1 characterizes the behavior of the dilatant fluid, the viscosity of which rises with increasing strain rate.

The weakening of the convective heat transfer is well reflected with the distribution of streamlines and isotherms, shown in Figure 7a,b, respectively. It should be noted that with an increase in the power law index, the number of streamlines decreases, which also corresponds to a slowdown of the convective flow. The structure of the distribution of streamlines does not tolerate changes. One can find also a growth of the dynamic boundary layer thickness near the vertical walls.

The distribution of isotherms is also not subject to significant changes (see Figure 7b). The two-dimensional heat plume is located above the heat source, which reflects the formation of temperature stratification zones to the left and right of the energy source. As a result, it is possible to conclude that a growth of the power law index characterizes less intensive cooling of the cavity from the vertical cooled walls. Therefore, the temperature gradient within the cavity diminishes with increasing n and liquid circulation becomes weaker.

Moreover, velocity field behavior is related to the temperature field considering the natural convection problem where there is no any external dynamic influence. This relation can be described as follows; the presence of the non-slip effect at solid walls characterizes an appearance of high velocity gradients in these zones and as a result a growth of the power law index leads to a rise of the effective viscosity. The latter illustrates the attenuation of convective flow circulation and a formation of heat conduction dominated mode near the walls. Therefore, for high n one can find less intensive cooling of the cavity from the vertical walls.

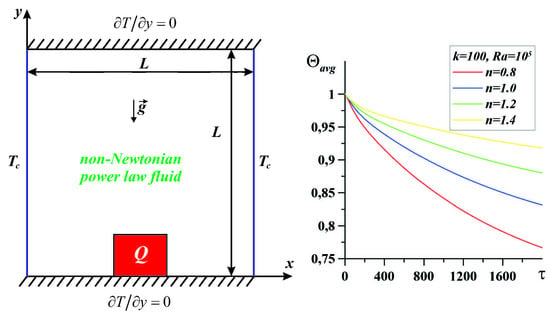
In Figure 8a, the average Nusselt number decreases slightly with increasing n at k = 100, Pr = 100, Ra = 10⁵. This suggests that convective heat transfer slows down with an increase in the power law index, which corresponds to a growth in temperature inside the source, as illustrated in Figure 8b. Moreover, the average Nusselt number reaches the constant value for high values of the power law index, while low values require more time for reaching steady state. At the same time, the mean heater temperature rises with n, which reflects less intensive heat removal from the heater for the case of dilatant liquid, while in the case of the pseudoplastic liquid it is possible to intensify the heater cooling.

For the considered problem, a key parameter is the thermal conductivity ratio. Figure 9 and Figure 10 demonstrate the impacts of the thermal conductivity ratio on the flow structures and heat transfer patterns. Thus, streamlines and isotherms are presented in Figure 9 for n = 0.8, Pr = 10², Ra = 10⁵.

It should be noted that the considered thermal conductivity ratio is a relation between the thermal conductivity of the heater material and liquid thermal conductivity. Therefore, growth of k illustrates an increase in the heater material thermal conductivity. A growth of this parameter reflects more intensive heating of the cavity and a growth of the circulation rate due to a formation of high temperature gradient. It is worth noting that a growth of the heater material thermal conductivity illustrates more intensive heating of this local element considering the internal volumetric heat generation and as a result the liquid near the heater warms rapidly for high k. Therefore, high k illustrates less cooling, while for low values of k heat conduction is a dominating heat transfer mechanism.

Figure 10 shows the average Nusselt number at the heater surface and the mean heater temperature depending on the thermal conductivity ratio and dimensionless time. It follows that an increase in k indicates a more heat-conducting material of the energy source or a less heat-conducting non-Newtonian medium. Therefore, with a growth of k, the average temperature in the source increases, which leads to a rise in the temperature gradient inside the cavity, and thus, one can find an augmentation of the average Nusselt number. It should be noted that for k = 1 and 10 the considered time range is enough for reaching the steady state, while for k ≥ 100 the time range should be increased for the steady state. As a result, one can conclude that more cooling of the local heater can be organized by the passive cooling system (from the cooled vertical walls) in the case of low values of the thermal conductivity ratio k ≤ 100.

4. Conclusions

In the present work, the mathematical simulation of the thermogravitational convection of a non-Newtonian fluid within a closed square cavity in the presence of a local heat-generating element was carried out. Governing partial differential equations formulated using the non-primitive variables and Ostwald-de Waele power law were solved by the finite difference method. An analysis of the key parameters influence on the process under investigation was performed based on the obtained distributions of streamlines and isotherms, as well as dependences of the average Nusselt number and average temperature inside the energy source. Taking into account the obtained results the following conclusions can be formulated:

-

The influence of the Rayleigh number was considered in the range between 10⁴ and 10⁶. It has been established that with increasing Ra the heat transport mechanism changes from conductive to convective, and the average Nusselt number increases, which corresponds to the intensification of heat removal from the heater surface. At the same time, a rise of Ra characterizes a growth of time for reaching the steady state. Moreover, a rise of the Rayleigh number characterizes a reduction of the thermal boundary layers thickness not only near the vertical walls but also for the central formed thermal plume.

-

The power law index is varied within the limits 0.8 and 1.4. It has been found that the growth of n slows down the flow and heat transfer in the cavity, therefore, for a pseudoplastic fluid, heat removal from the energy source occurs more intensively. It should be noted that at a large n faster stationary mode is achieved.

-

Analysis of the flow and heat transfer as a result of an increase in the thermal conductivity ratio from 1 to 1000 showed that as the flow rate and time for reaching the steady state are increased, the cavity warms up more intensively, and therefore the heat removal from the heater surface is weakened.