Simulation-Based Comparison Between the Thermal Behavior of Coaxial and Double U-Tube Borehole Heat Exchangers
Abstract
:1. Introduction
2. Method
2.1. Case Study
2.2. Test Measurements
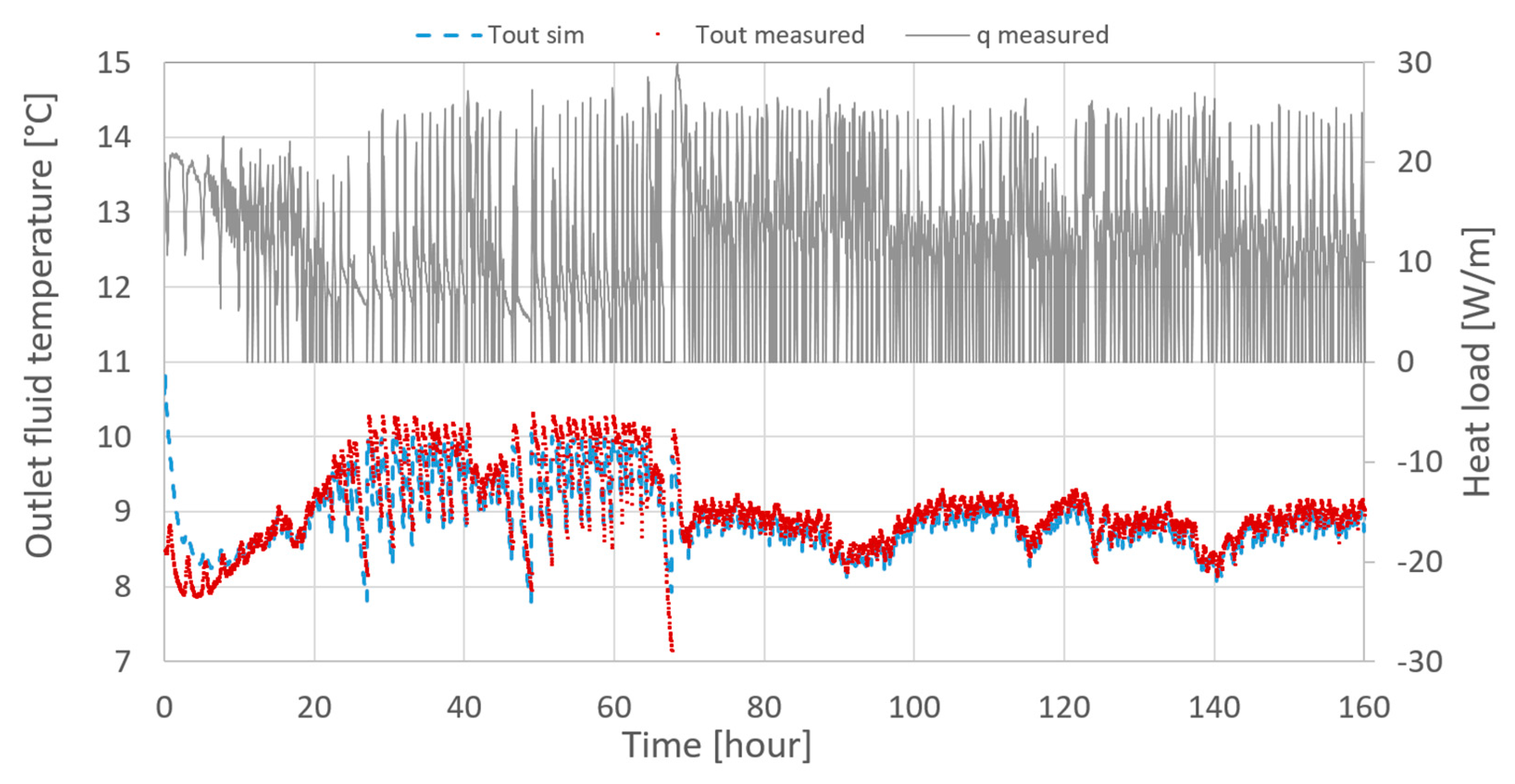
2.2.1. Thermal Response Test (TRT)
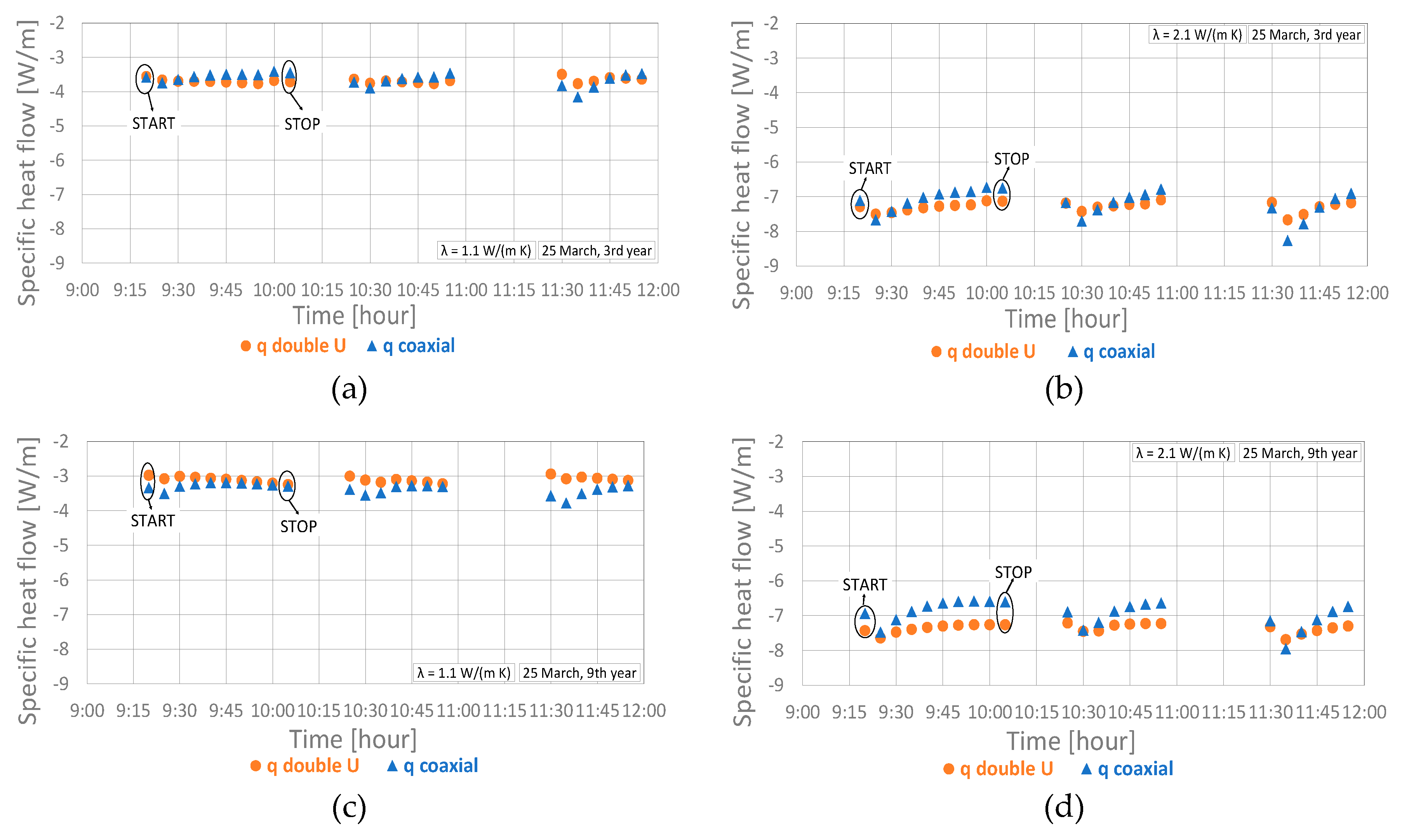
2.2.2. Weekly Test
2.3. Computer Simulations
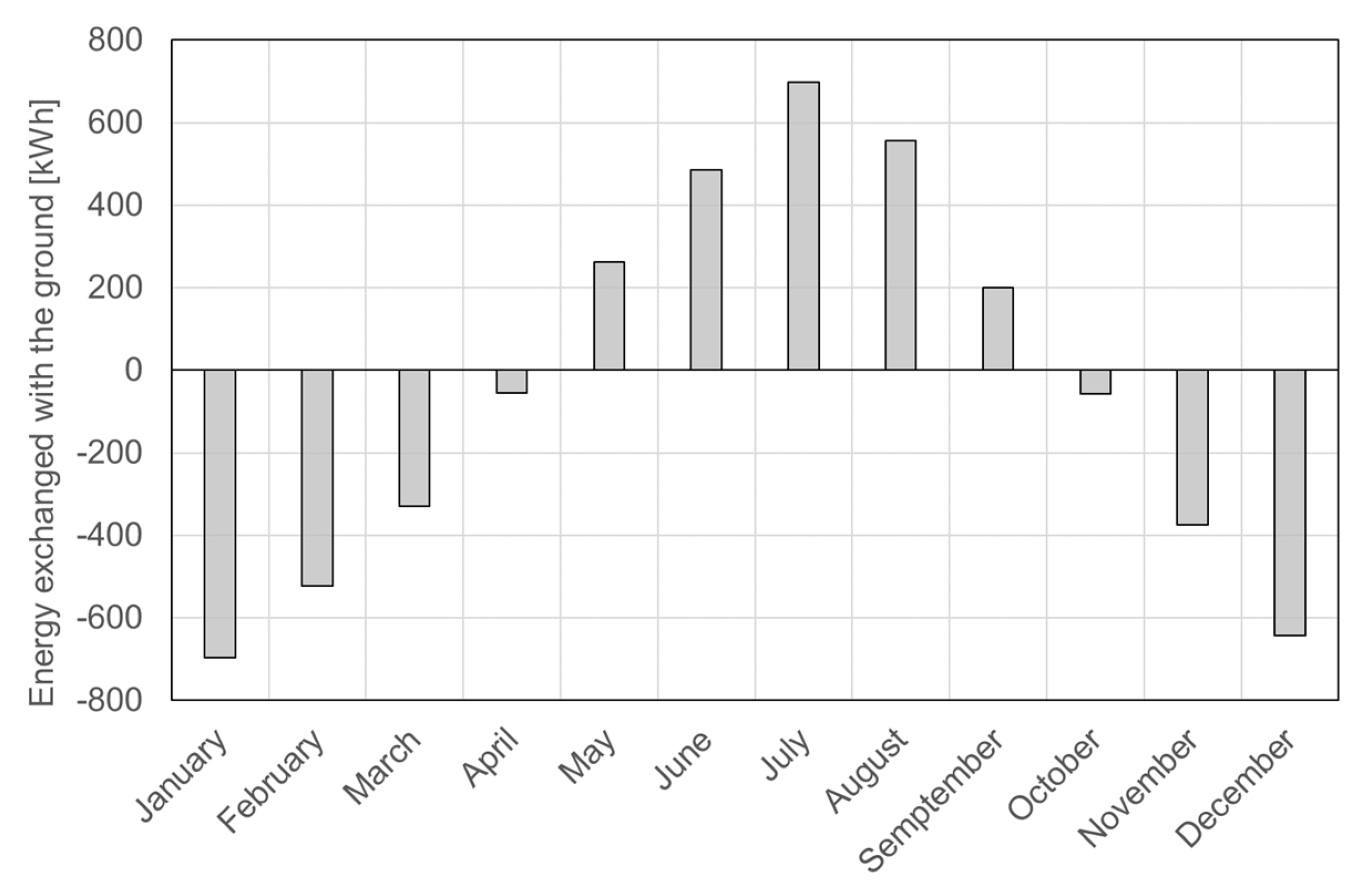
2.3.1. Long-Term Analysis
- (1)
- The mass flow rate of the heat-carrier fluid (pure water) was 0.23 kg/s. This flow develops a transient flow regime for both the double U-tube (since the Reynolds number is 5602) and the coaxial pipes (Re = 2696 in the annulus).
- (2)
- As main ground characteristics: the ground thermal conductivity (λ) was assumed to be 2.1 W/(m∙K) and the volumetric heat capacity (C) was 2.42 MJ/(m3∙K).
- (3)
- With regards to the mesh parameters, to model the borehole heat exchangers: (1) in the surface zone and the deep zone, the ground was split into vertical sub-regions with a thickness of 0.25 m each, whereas in the ground surrounding the borehole, the sub-regions were 1 m thick. (2) Each vertical sub-region of the borehole zone was divided into 20 annular regions from the borehole axis to the maximum radius (rmax) of 10 m.
- (4)
- At the ground level, the following values were applied and assumed to be constant for the entire simulation time: absorptance (a) was 0.7, emittance (ε) was 0.9, and specific surface convective thermal resistance (Rext) was 0.04 (m2∙K)/W.
2.3.2. Short-Term Analysis
3. Results and Discussion
3.1. Long-Term Analysis
- (1)
- Period A: During the heating mode when the inlet fluid temperature at the head of the probe is equal to the minimum value (a critical condition because the absorption of energy has minimized the ground temperature).
- (2)
- Period B: During the end of the winter when the external air temperature starts to increase.
- (3)
- Period C: In cooling mode when the inlet fluid temperature at the head of the probe is equal to the maximum value (a critical condition because the heat injection into the ground has maximized the ground temperature).
3.1.1. Comparison BHEs in Heating Mode
3.1.2. Comparison BHEs in Cooling Mode
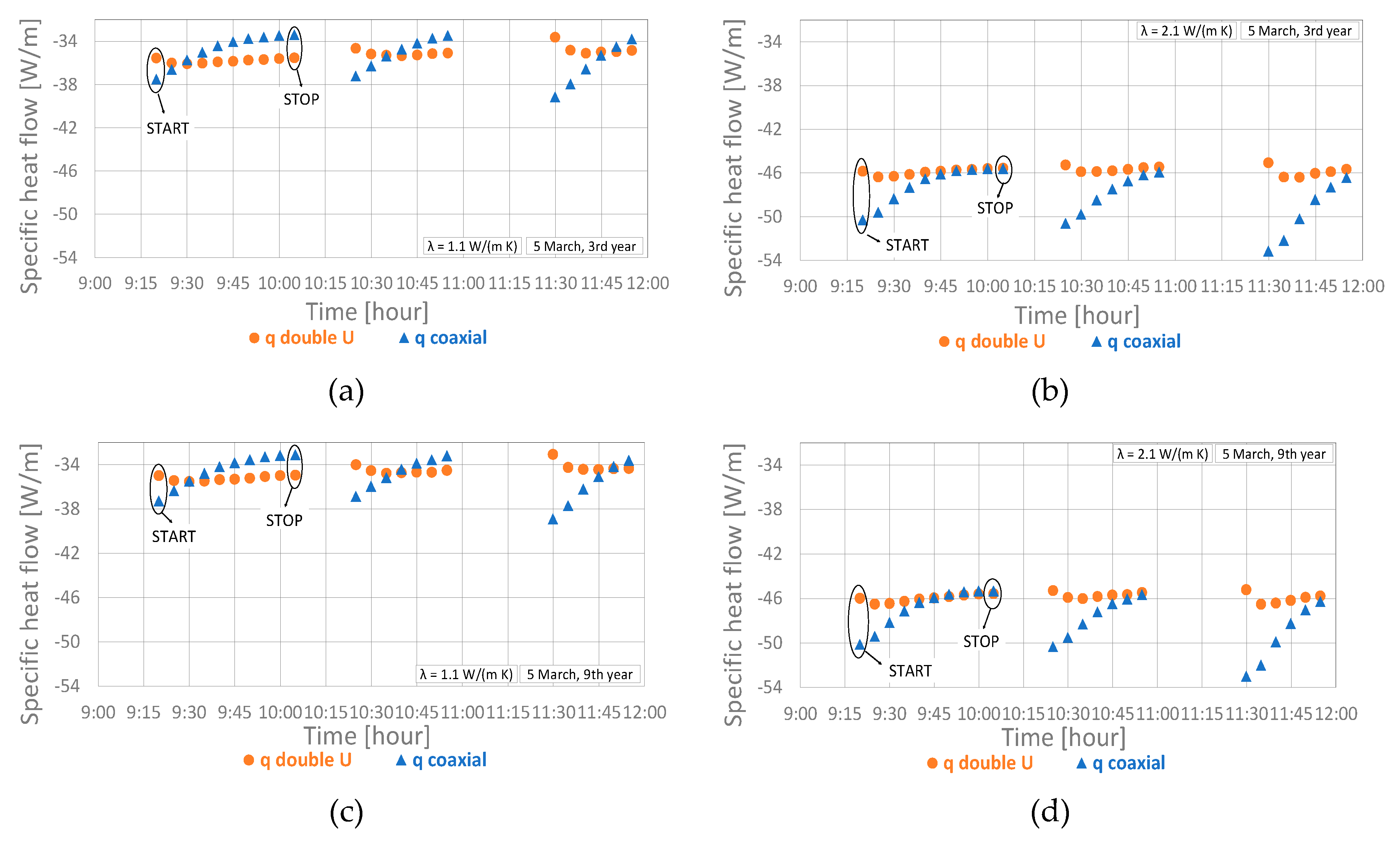
3.2. Short-Term Analysis
- (1)
- At the start of the heat pump (first period) for the first six time steps (i.e., 30 min), the coaxial borehole heat exchanger is characterized by a higher outlet fluid temperature than that of the double U. This occurs due to the larger fluid volume of the coaxial probe (237 L). As a consequence, the thermal capacitance of its stationary transfer fluid is greater than that of the double U-tube, which has a volume of 168 L. This means that when the heat pump is switched on in the two BHEs, the same inlet fluid temperature solicits two different thermal capacitances (i.e., that of the heat-carrier fluid), and the coaxial probe, which has the greater capacitance, has a higher outlet fluid temperature. The thermal capacitance of the transfer fluid inside the probe is a key parameter for the first 30 minutes. Notably, the coaxial BHE shows a flatter pattern in the first time steps than the double U-tube because the transit time of the entire coaxial probe is longer (17 min vs. 12 min for the double U-tube). To better understand the difference between the performance of the BHEs, the outlet fluid temperatures are plotted against the natural logarithm of time in Figure 18.
- (2)
- In the second period (from the 30th minute until 1.5 h of operation) the thermal capacitance of the grouting material is the main factor affecting the thermal performance of the BHEs. The double U probe, with a grouting material volume (0.71 m3) greater than that of the coaxial probe (0.27 m3), has a higher outlet fluid temperature in this period.
- (3)
- In the third period, the thermal behavior of the coaxial borehole heat exchanger is better than that of the double U-tube. This occurs due to its lower borehole thermal resistance Rb of 0.03 (K∙m)/W, which is about half that of the double U-tube.
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| a | Surface absorptance (-) | Subscripts | |
| C | Volumetric heat capacity (MJ/m3 K) | exp | Experimental |
| COP | Coefficient of performance in heating mode (-) | in | Inlet |
| Lbore | Borehole length (m) | out | Outlet |
| nstep | Number of the steps (-) | sim | Simulation |
| rmax | Radius from axis borehole beyond which the undisturbed ground is considered (m) | ||
| Rb | Borehole thermal resistance (m∙K/W) | Abbreviations | |
| Rext | Convection thermal resistance at ground level per unit area (m2∙K/W) | BHE | Borehole heat exchanger |
| T | Temperature (°C) | CaRM | Capacitance Resistance Model |
| GHE | Ground heat exchanger | ||
| Greek symbols | GSHP | Ground source heat pump | |
| ε | Surface emittance (-) | MEW | Final value of the measuring range |
| λ | Thermal conductivity (W/(m∙K)) | MS | Set measuring span |
| MW | Measured value | ||
| PE-Xa | Cross-linked polyethylene | ||
| RMSE | Root mean square error | ||
| TRT | Thermal Response Test | ||
References
- Oliver, H.; Braud, J. Thermal exchange to earth with concentric well pipes. Trans. ASAE 1981, 24, 906–910. [Google Scholar] [CrossRef]
- Mei, V.C.; Fischer, S.K. Vertical Concentric Tube Ground Couoled Heat Exchangers. ASHRAE Trans. 1983, 89, 391–406. [Google Scholar]
- Hellström, G. Ground Heat Storage, Thermal Analyses of Duct Storage Systems. Ph.D. Thesis, University of Lund, Lund, Sweden, 1991. [Google Scholar]
- Zanchini, E.; Lazzari, S.; Priarone, A. Effects of flow direction and thermal short-circuiting on the performance of small coaxial ground heat exchangers. Renew. Energy 2010, 35, 1255–1265. [Google Scholar] [CrossRef]
- Acuña, J.; Palm, B. Distributed thermal response tests on pipe-in-pipe borehole heat exchangers. Appl. Energy 2013, 109, 312–320. [Google Scholar] [CrossRef]
- Wood, C.J.; Liu, H.; Riffat, S.B. Comparative performance of ‘U-tube’ and ‘coaxial’ loop designs for use with a ground source heat pump. Appl. Therm. Eng. 2012, 37, 190–195. [Google Scholar] [CrossRef]
- Zarrella, A.; Scarpa, M.; de Carli, M. Short time-step performances of coaxial and double U-tube borehole heat exchangers: Modeling and measurements. HVAC R Res. 2011, 17, 959–976. [Google Scholar]
- Raymond, J.; Mercier, S.; Nguyen, L. Designing coaxial ground heat exchangers with a thermally enhanced outer pipe. Geotherm. Energy 2015, 3, 7. [Google Scholar] [CrossRef] [Green Version]
- Aresti, L.; Christodoulides, P.; Florides, G. A review of the design aspects of ground heat exchangers. Renew. Sustain. Energy Rev. 2018, 92, 757–773. [Google Scholar] [CrossRef]
- Conti, P. Dimensionless Maps for the Validity of Analytical Ground Heat Transfer Models for GSHP Applications. Energies 2016, 9, 890. [Google Scholar] [CrossRef]
- Zeng, H.Y.; Diao, N.R.; Fang, Z.H. A Finite Line-Source Model for Boreholes in Geothermal Heat Exchangers. Heat Trans. Asian Res. 2002, 31, 558–567. [Google Scholar] [CrossRef]
- Carslaw, J.C.; Jaeger, H.S. Conduction of Heat in Solids, 2nd ed.; Clarendon Press: Oxford, UK; Oxford University Press: New York, NY, USA, 1959. [Google Scholar]
- Zanchini, E.; Lazzari, S.; Priarone, A. Improving the thermal performance of coaxial borehole heat exchangers. Energy 2010, 35, 657–666. [Google Scholar] [CrossRef]
- Marcotte, D.; Pasquier, P. On the estimation of thermal resistance in borehole thermal conductivity test. Renew. Energy 2008, 33, 2407–2415. [Google Scholar] [CrossRef]
- Pasquier, P. Ghe3d: A 3d Transient Ground Heat Exchanger Numerical Model; Internal Technical Report; Golder Associates: Montreal, QC, Canada, 2007. [Google Scholar]
- Zanchini, E.; Jahanbin, A. Finite-element analysis of the fluid temperature distribution in double U-tube Borehole Heat Exchangers Ground-coupled heat pump systems View project. Artic. J. Phys. Conf. Ser. 2016, 745, 032002. [Google Scholar] [CrossRef]
- Zeng, H.; Diao, N.; Fang, Z. Heat transfer analysis of boreholes in vertical ground heat exchangers. Int. J. Heat Mass Transf. 2003, 46, 4467–4481. [Google Scholar] [CrossRef]
- Zarrella, A.; Scarpa, M.; de Carli, M. Short time step analysis of vertical ground-coupled heat exchangers: The approach of CaRM. Renew. Energy 2011, 36, 2357–2367. [Google Scholar] [CrossRef]
- Cheap-GSHPs. Cheap and Efficient Application of Reliable Ground Source Heat Exchangers and Pumps. Available online: https://cheap-gshp.eu/ (accessed on 17 April 2019).
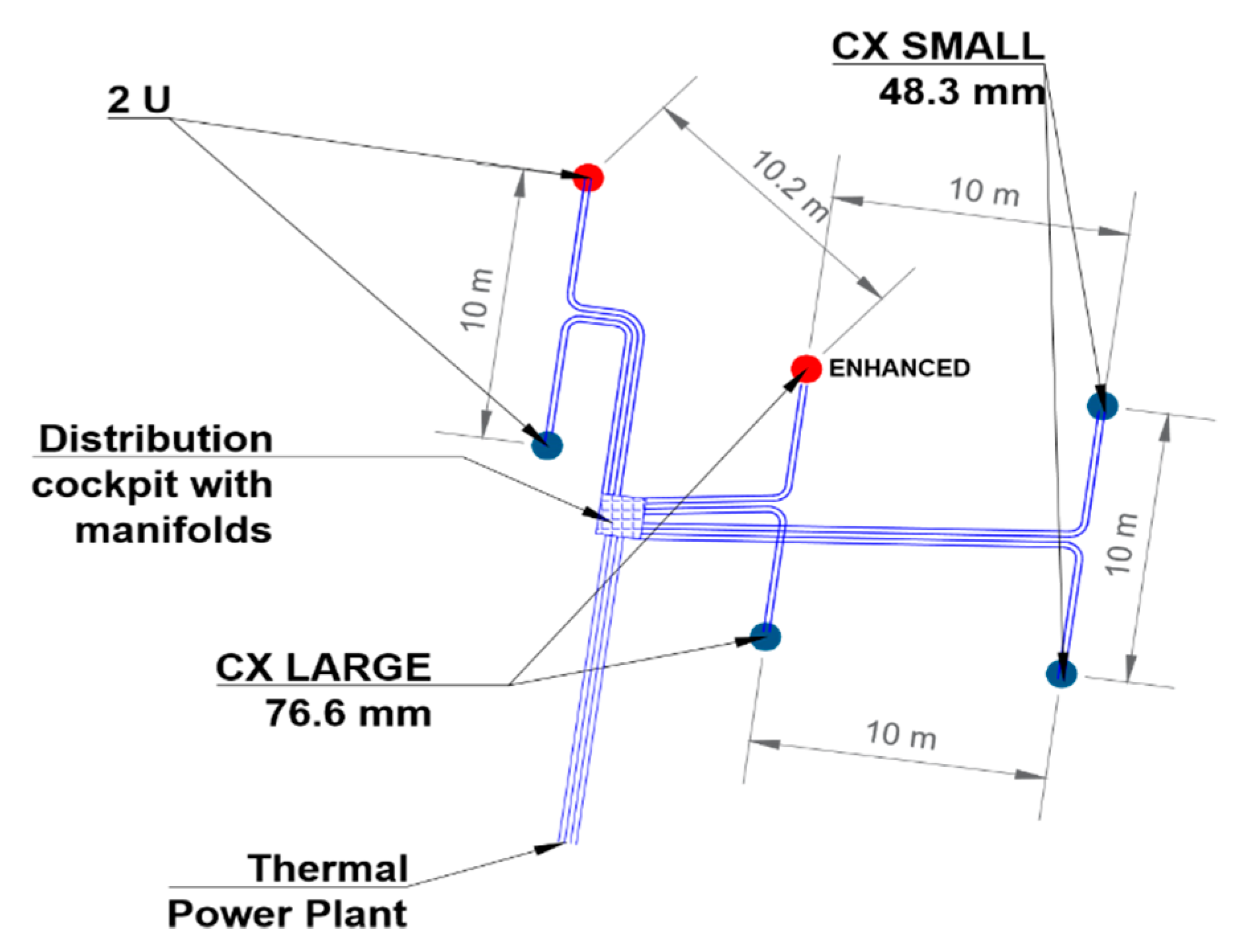














| Description | Value |
|---|---|
| Inner pipe (1) | |
| Inside diameter of pipe (mm) | 26.8 |
| Outside diameter of pipe (mm) | 40 |
| Thermal conductivity of pipe (W/(m∙K)) | 0.14 |
| Outer pipe (2) | |
| Inside diameter of pipe (mm) | 68.9 |
| Outside diameter of pipe (mm) | 76.1 |
| Thermal conductivity of pipe (W/(m∙K)) | 15.0 |
| Borehole diameter (m) | 0.101 |
| Inlet pipe | inner pipe |
| Grouting material | |
| Thermal conductivity (W/(m∙K)) | 1.5 |
| Specific heat (J/(kg K)) | 2500.0 |
| Density (kg/m3) | 1400.0 |
| Description | Value |
|---|---|
| Inside diameter of pipe (mm) | 26.2 |
| Outside diameter of pipe (mm) | 32.0 |
| Spacing between the pipes (mm) | 82.6 |
| Borehole diameter (m) | 0.125 |
| Thermal resistance between adjacent pipes (m∙K/W) | 0.59 |
| Thermal resistance between opposite pipes (m∙K/W) | 0.8 |
| Thermal resistance between the pipe and the bore wall (m∙K/W) | 0.25 |
| Grouting material | |
| Thermal conductivity (W/(m∙K)) | 1.5 |
| Specific heat (J/(kg∙K)) | 2500.0 |
| Density (kg/m3) | 1400.0 |
| Connection 2 U | Parallel |
| BHE | Borehole Thermal Resistance, Rb ((m∙K)/W) | Ground Thermal Conductivity, λ (W/(m∙K)) |
|---|---|---|
| Double U-tube | 0.076 | 2.16 |
| Coaxial pipes | 0.036 | 2.06 |
| BHE | Average Flow Rate (L/min) | Re | Re in | Re out |
|---|---|---|---|---|
| Double U-tube | 8.68 | 2603 | - | - |
| Coaxial pipes | 4.79 | - | 2832 | 688 |
| Simulation Year | Energy Exchanged with the Ground (kWh) | |||
|---|---|---|---|---|
| Heating | Cooling | |||
| Coaxial | Double U | Coaxial | Double U | |
| 1st | –2222 | –2159 | 1742 | 1715 |
| 3rd | –2173 | –2099 | 1768 | 1751 |
| 9th | –2139 | –2027 | 1794 | 1808 |
| Simulation Year | Energy Exchanged with the Ground (kWh) | |||
|---|---|---|---|---|
| Heating | Cooling | |||
| Coaxial | Double U | Coaxial | Double U | |
| 1st | –3043 | -–2863 | 2432 | 2307 |
| 3rd | –3036 | –2876 | 2443 | 2304 |
| 9th | –3009 | –2884 | 2465 | 2297 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Quaggiotto, D.; Zarrella, A.; Emmi, G.; De Carli, M.; Pockelé, L.; Vercruysse, J.; Psyk, M.; Righini, D.; Galgaro, A.; Mendrinos, D.; et al. Simulation-Based Comparison Between the Thermal Behavior of Coaxial and Double U-Tube Borehole Heat Exchangers. Energies 2019, 12, 2321. https://doi.org/10.3390/en12122321
Quaggiotto D, Zarrella A, Emmi G, De Carli M, Pockelé L, Vercruysse J, Psyk M, Righini D, Galgaro A, Mendrinos D, et al. Simulation-Based Comparison Between the Thermal Behavior of Coaxial and Double U-Tube Borehole Heat Exchangers. Energies. 2019; 12(12):2321. https://doi.org/10.3390/en12122321
Chicago/Turabian StyleQuaggiotto, Davide, Angelo Zarrella, Giuseppe Emmi, Michele De Carli, Luc Pockelé, Jacques Vercruysse, Mario Psyk, Davide Righini, Antonio Galgaro, Dimitrios Mendrinos, and et al. 2019. "Simulation-Based Comparison Between the Thermal Behavior of Coaxial and Double U-Tube Borehole Heat Exchangers" Energies 12, no. 12: 2321. https://doi.org/10.3390/en12122321






