Thermal Effect of Different Laying Modes on Cross-Linked Polyethylene (XLPE) Insulation and a New Estimation on Cable Ampacity
Abstract
:1. Introduction
2. Experimental
2.1. Preparation of XLPE Specimens
2.2. Cable Thermal Parameters and Ampacity Measurement
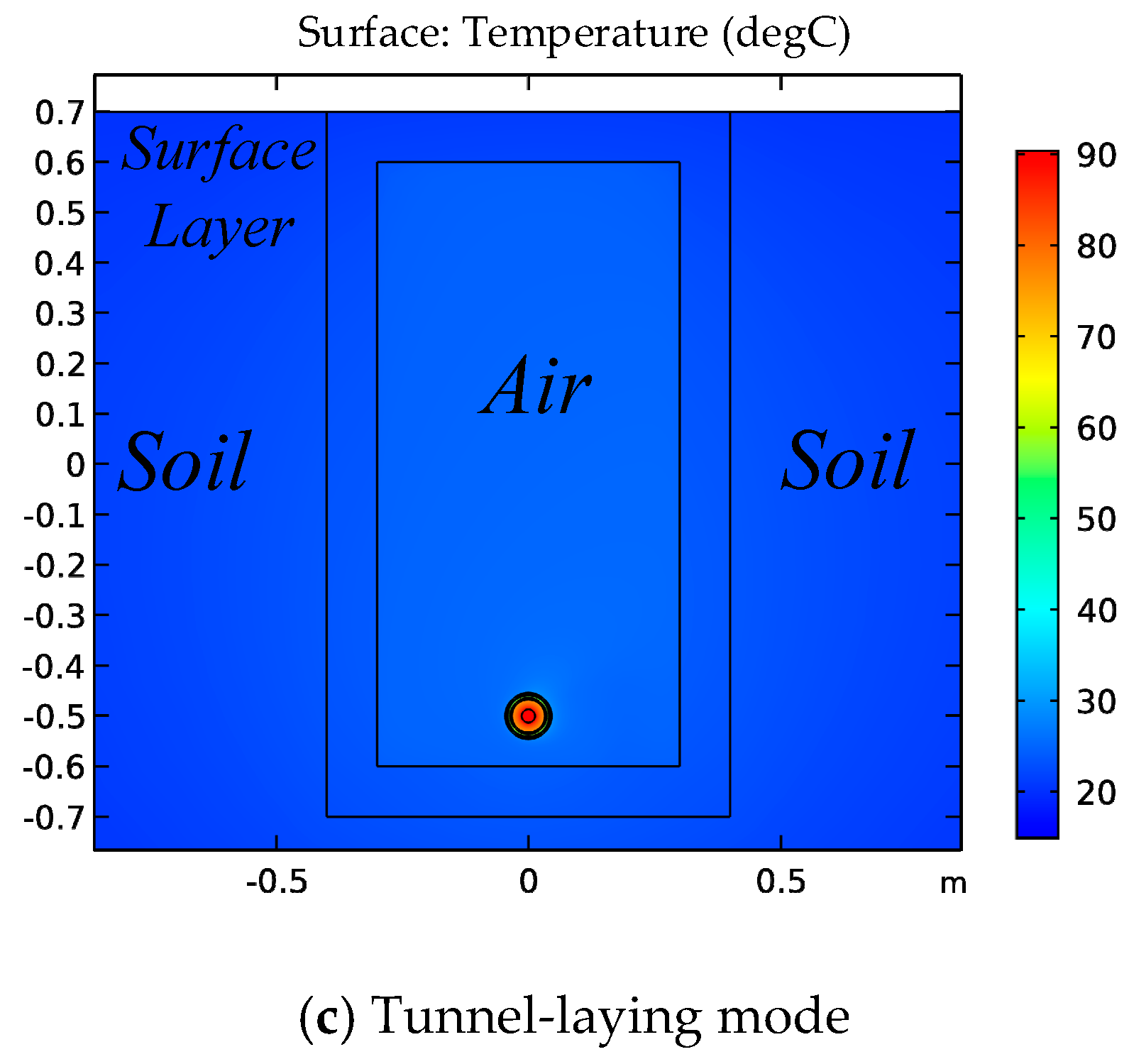
2.3. Simulation of Different Laying Modes of Cables
2.4. Thermal Aging
2.5. Diagnostic Measurements
3. Results and Discussions
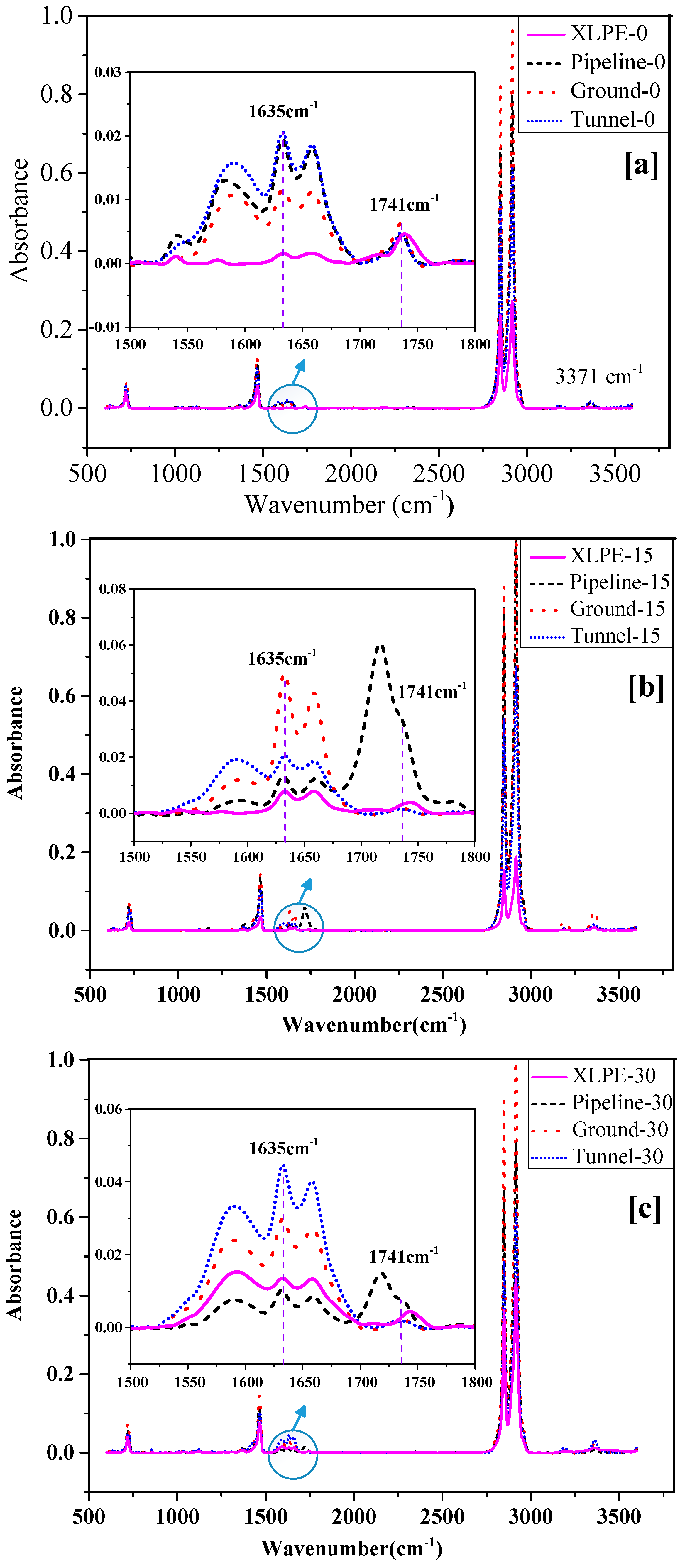
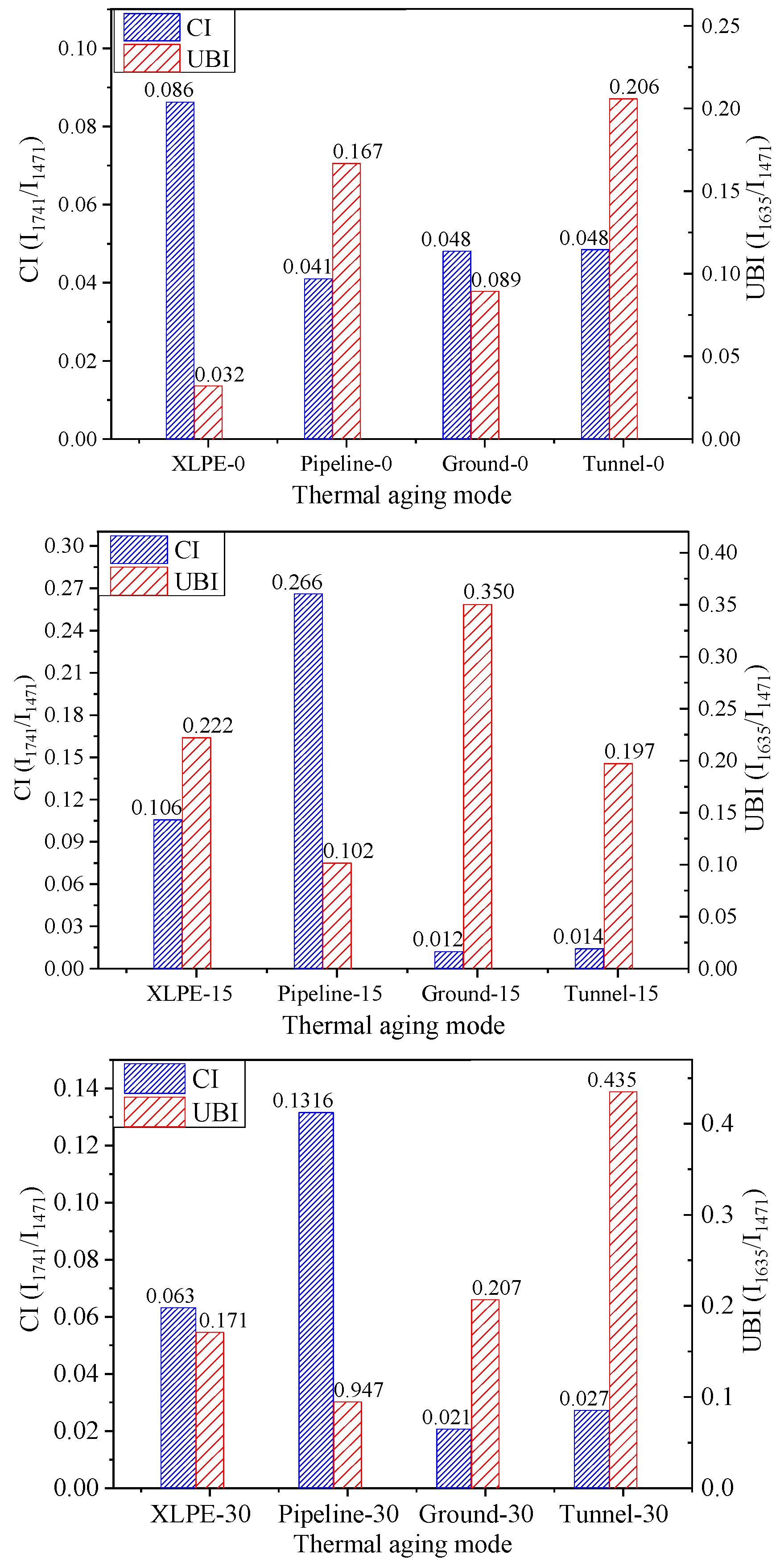
3.1. Result of FTIR Spectroscopy Measurement
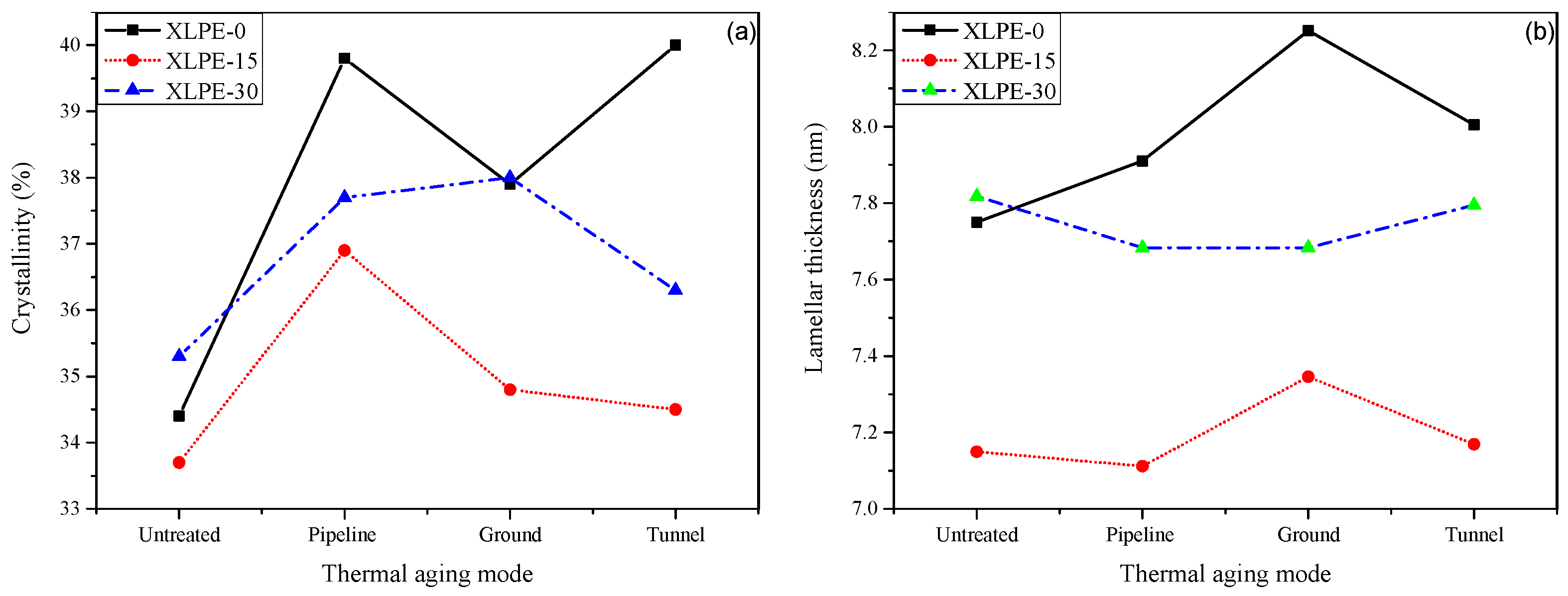
3.2. Result of DSC Measurement
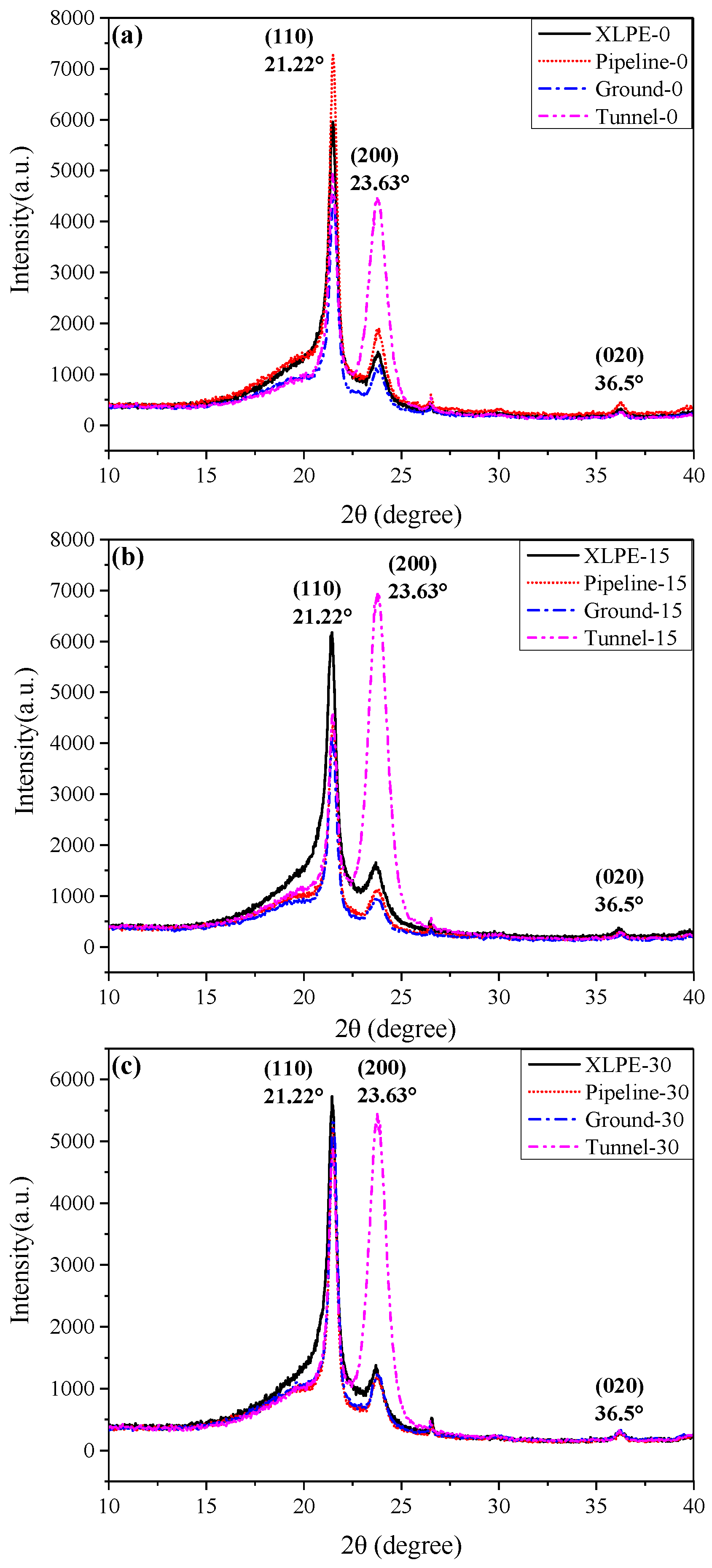
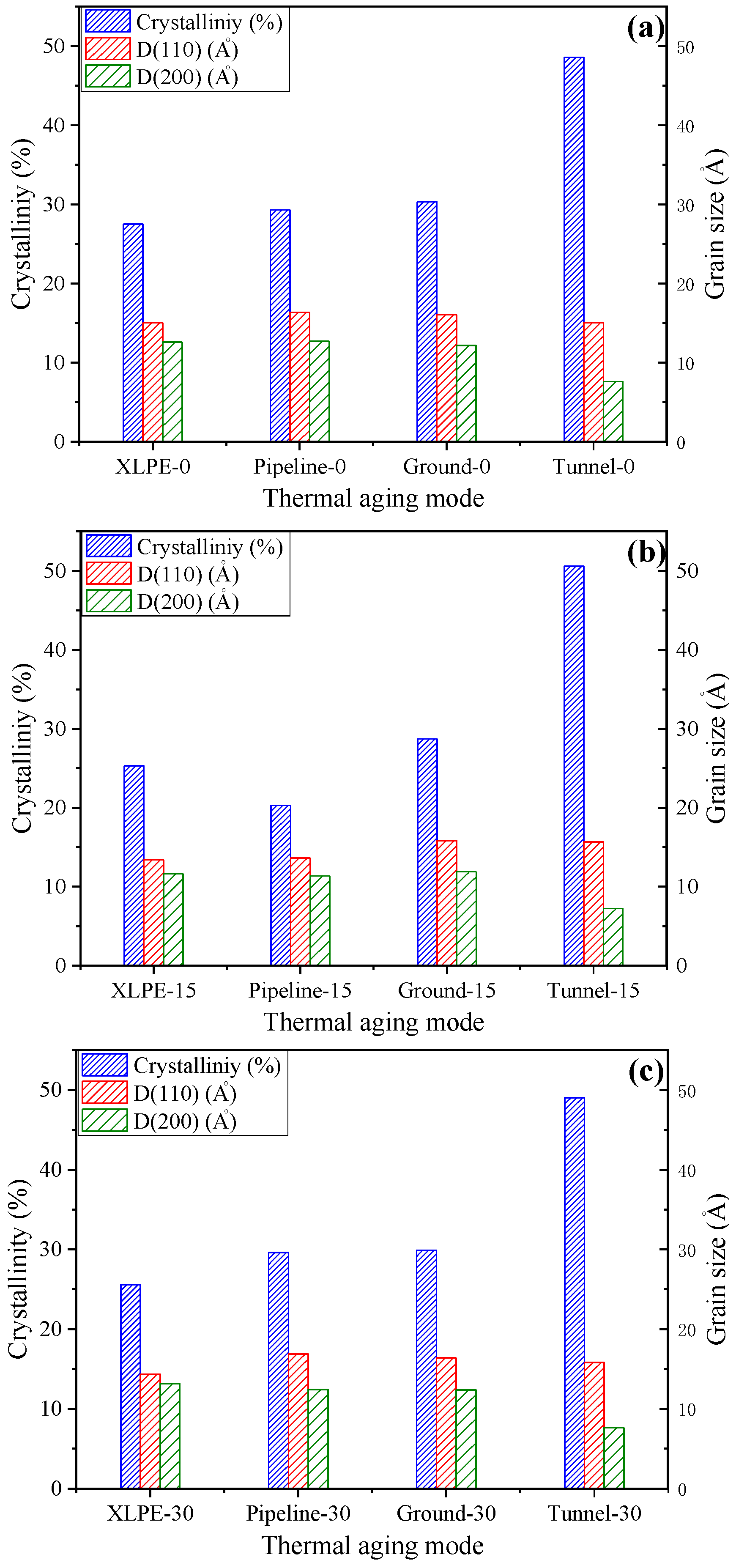
3.3. Result of XRD Measurement
3.4. Results of the Breakdown Field Strength Measurement
3.5. Assessment of the Structural and Electrical Properties of XLPE under Thermal Effects
3.6. A Proposal of New Estimation on Cable Ampacity
4. Conclusions
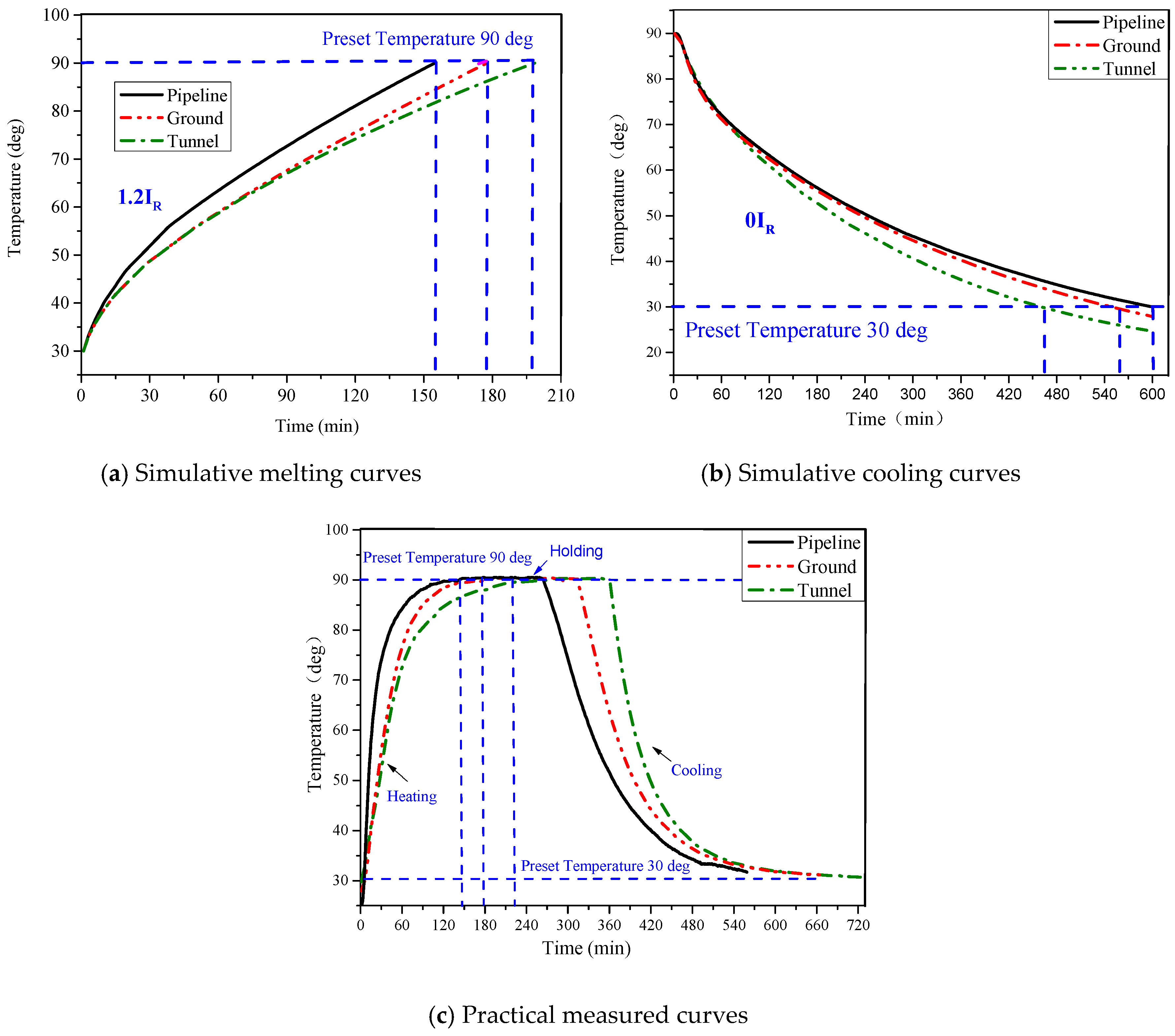
- For the spare cable, it has a high potential to adapt to thermal effect of the three laying modes, so the margin of ampacity can be elevated to 1.2 IR.
- For the cable which had operated for 15 years, the margin of ampacity can be elevated to 1.2 IR in the tunnel, should not be lifted to 1.2 IR for a long time in ground mode, and should be decreased properly in the pipeline based on IR.
- For the cable which had operated for 30 years, the margin of ampacity can be elevated to 1.2 IR in ground mode, should be reduced from 1.2 IR in tunnel mode, but the margin of ampacity should not be elevated in the pipeline based on IR.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| function y = XLPE-0() | |
| global k dki dko Rk Ck Rk1 Ck1 l p i A B P T1u E To I h2 R12 number number1 T1 number2 C0 Tou r0p R11 | |
| load('XLPE-0.mat'); | %introduce the matrix (column 1: conductor temperature; column 2: current) |
| I = XLPE(:,2); | %reading the current in the matrix |
| T1 = XLPE(:,1); | %reading the temperature in the matrix |
| t1 = 0:60:54900; | %calculating time range (total data volume in the matric) |
| hold on | %keeping the drawing interface |
| number = 30; | %insulation hierarchical Number |
| number1 = number + 1; | %lapped covering |
| number2 = number + 2; | %outer-sheath |
| d1 = 26.6*10^-3; | %conductor diameter |
| d2 = 65.6*10^-3; | %insulation diameter |
| d6 = 92.0*10^-3; | %outer-sheath diameter |
| h1 = (d2-d1)/(2*number); | %insulation hierarchical thickness |
| h2 = 3.0*10^-3; | %outer-sheath thickness |
| a = 0.00393; | %resistance temperature coefficient of copper conductor |
| p1 = 3.23; | %thermal resistance coefficient of insulation layer |
| p6 = 3.5; | %thermal resistance coefficient of outer-sheath |
| Dc = 344.312*10^4; | %volumetric thermal capacity of Cu |
| DPE = 194.12*10^4; | %volumetric thermal capacity of XLPE |
| D6 = 242.54*10^4; | %volumetric thermal capacity of outer-sheath |
| r0p = 3.482e-5; | %DC Resistance of Conductor at 20 °C |
| R11 = 0.1095; | %thermal resistance of lapped covering |
| dki = zeros(1,number); | %inner diameter array of each insulation layer |
| dko = zeros(1,number); | %outer diameter array of each insulation layer |
| Rk = zeros(1,number); | %thermal resistance array of each insulation layer |
| Ck = zeros(1,number); | %thermal capacity array of each insulation layer |
| Rk1 = zeros(1,number2); | %thermal resistance array |
| Ck1 = zeros(1,number2); | %thermal capacity array |
| A = zeros(number2,number2); | %A matrix |
| B = zeros(number2,number2); | %A matrix |
| P = zeros(number2,1); | %P matrix |
| E = zeros(1,number2); | %temperature initial matrix |
| T1c = zeros(1,915); | %calculating point number |
| R12 = 0.0299; | %outer-sheath thermal resistance |
| C0 = Dc*pi*0.25*d1*d1; | %conductor thermal capacity |
| C12 = D6*pi*0.25*(d6^2-(d6-2*h2)^2); | % outer-sheath thermal capacity |
| for k = 1:number | |
| dki(k) = d1 + 2*h1*(k-1); | |
| dko(k) = d1 + 2*h1*k; | |
| Rk(k) = p1/(2*pi)*log(1 + 2*h1/dki(k)); | %thermal resistance of each insulation layer |
| Ck(k) = DPE*pi*0.25*(dko(k)^2-dki(k)^2); | %thermal capacity of each insulation layer |
| end | |
| C11 = 5549.4; | %lapped covering thermal capacity |
| for n = 1:number2 | %array of initial cable internal temperature |
| E(n) = 17.7; | |
| end | |
| T1u = 17.7; | %initial conductor temperature |
| for u = 0:60:54900; | %time horizon |
| for l = 1:number2 | |
| if(l==1) | |
| Rk1(l) = Rk(l); | |
| Ck1(l) = Ck(l) + C0; | |
| else if(l==number1) | |
| Rk1(l) = R11; | |
| Ck1(l) = C11; | |
| else if(l==number2) | |
| Rk1(l) = R12; | |
| Ck1(l) = C12; | |
| else | |
| Rk1(l) = Rk(l); | |
| Ck1(l) = Ck(l); | |
| end | |
| end | |
| for i = 1:number2 | |
| for j = 1:number2 | |
| if(j==i) | |
| if(j==1) | |
| A(i,j) = -(Ck1(i)*Rk1(i))^-1;B(i,j)=Ck1(i)^-1; | |
| else | |
| A(i,j) = -Ck1(i)^-1*(Rk1(i-1)^-1+Rk1(i)^-1);B(i,j)=Ck1(i)^-1; | |
| end | |
| else if(j==I + 1) | |
| A(i,j) = (Ck1(i)*Rk1(i))^-1;B(i,j)=0; | |
| else if(j==i-1) | |
| A(i,j) = (Ck1(i)*Rk1(j))^-1;B(i,j)=0; | |
| else | |
| A(i,j) = 0;B(i,j) = 0; | |
| end | |
| end | |
| end | |
| tt = [u,u+60]; | |
| Tou = To(u/60+1); | %initial surface temperature |
| i = I(u/60 + 1); | %initial current |
| T1c(u/60 + 1) = E(1); | %calculating conductor temperature |
| rp = r0p*(1+a*(T1u-20)); | %DC resistance of conductor |
| x = pi*400e-7/rp; | |
| Y = x^2/(192 + 0.8*x^2); | %skin effect factor of conductor |
| r = rp.*(1 + Y); | %AC resistance of conductor |
| p = i^2*r; | %heating power of conductor |
| [t,x] = ode23t(@odefun3,tt,E); | %solution of differential equation |
| E = x(end,:); | %updating the initial temperature array for the next period |
| T1u = E(end,1); | % updating the conductor temperature array for the next period |
| end | |
| y = T1c'; | %calculating conductor temperature |
| plot(t1,y,'g') | %plotting curves |
| hold on | |
| end | |
| function dx = odefun3(t,x) | %P array solution |
| global A B P p Tou R12 number2 | |
| dx = zeros(number2,1); | |
| for m = 1:number2 | |
| if(m==1) | |
| P(m) = p; | |
| else if(m==number2) | |
| P(m) = Tou/R12; | |
| else | |
| P(m) = 0; | |
| end | |
| end | |
| dx = A*x + B*P; | |
| end | |

References
- Orton, H. Power cable technology review. High Volt. Eng. 2015, 41, 1057–1067. [Google Scholar] [CrossRef]
- Shwehdi, M.H.; Morsy, M.A.; Abugurain, A. Thermal aging tests on XLPE and PVC cable insulation materials of Saudi Arabia. In Proceedings of the IEEE Conference on Electrical Insulation and Dielectric Phenomena, Albuquerque, NM, USA, 19 November 2003; pp. 176–180. [Google Scholar] [CrossRef]
- Liu, X.; Yu, Q.; Liu, M.; Li, Y.; Zhong, L.; Fu, M. DC electrical breakdown dependence on the radial position of specimens within HVDC XLPE cable insulation. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 1476–1486. [Google Scholar] [CrossRef]
- Ouyang, B.; Li, H.; Li, J. The role of micro-structure changes on space charge distribution of XLPE during thermo-oxidative ageing. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 3849–3859. [Google Scholar] [CrossRef]
- Diego, J.A.; Belana, J.; Orrit, J.; Cañadas, J.C.; Mudarra, M.; Frutos, F.; Acedo, M. Annealing effect on the conductivity of xlpe insulation in power cable. IEEE Trans. Dielectr. Electr. Insul. 2011, 18, 1554–1561. [Google Scholar] [CrossRef]
- Xie, Y.; Zhao, Y.; Liu, G.; Huang, J.; Li, L. Annealing Effects on XLPE Insulation of Retired High-Voltage Cable. IEEE Access. 2019. [Google Scholar] [CrossRef]
- Xie, Y.; Liu, G.; Zhao, Y. Rejuvenation of Retired Power Cables by Heat Treatment. IEEE Trans. Dielectr. Electr. Insul. 2019, 26, 668–670. [Google Scholar] [CrossRef]
- Celina, M.; Gillen, K.T.; Clough, R.L. Inverse temperature and annealing phenomena during degradation of crosslinked polyolefins. Polym. Degrad. Stab. 1998, 61, 231–244. [Google Scholar] [CrossRef]
- Kalkar, A.K.; Deshpande, A.A. Kinetics of isothermal and non-isothermal crystallization of poly (butylene terephthalate) liquid crystalline polymer blends. Polym. Eng. Sci. 2010, 41, 1597–1615. [Google Scholar] [CrossRef]
- Wang, Y.; Shen, C.; Li, H.; Qian, L.; Chen, J. Nonisothermal melt crystallization kinetics of poly (ethylene terephthalate)/clay nanocomposites. J. Appl. Polym. Sci. 2010, 91, 308–314. [Google Scholar] [CrossRef]
- Xie, A.S.; Zheng, X.Q.; Li, S.T.; Chen, G. The conduction characteristics of electrical trees in XLPE cable insulation. J. Appl. Polym. Sci. 2010, 114, 3325–3330. [Google Scholar] [CrossRef]
- Xie, A.; Li, S.; Zheng, X.; Chen, G. The characteristics of electrical trees in the inner and outer layers of different voltage rating XLPE cable insulation. J. Phys. D Appl. Physic 2009, 42, 125106–125115. [Google Scholar] [CrossRef]
- Insulated Conductors Committee of the IEEE Power Engineering Society. IEEE GUIDE for Soil Thermal Resistivity Measurements; IEEE Std 442, Reaffirmed 2003; IEEE: Piscataway, NJ, USA, 1981. [Google Scholar]
- Frank, D.W.; Jos, V.R.; George, A.; Bruno, B.; Rusty, B.; James, P.; Marcio, C.; Georg, H. A Guide for Rating Calculations of Insulated Cables; Cigré TB # 640; Cigré: Paris, France, 2015. [Google Scholar]
- International Electrotechnical Commission. Calculation of the Current Rating of Electric Cables; IEC Press: Geneva, Switzerland, 2006. [Google Scholar]
- Wang, P.; Liu, G.; Ma, H. Investigation of the Ampacity of a Prefabricated Straight-Through Joint of High Voltage Cable. Energies 2017, 10, 2050. [Google Scholar] [CrossRef]
- Meng, X.K.; Wang, Z.Q.; Li, G.F. Dynamic analysis of core temperature of low-voltage power cable based on thermal conductivity. Can. J. Electr. Comput. Eng. 2006, 39, 59–65. [Google Scholar] [CrossRef]
- Del Pino Lopez, J.C.; Romero, P.C. Thermal effects on the design of passive loops to mitigate the magnetic field generated by underground power cables. IEEE Trans. Power Deliv. 2011, 26, 1718–1726. [Google Scholar] [CrossRef]
- Sharad, P.A.; Kumar, K.S. Application of surface-modified XLPE nanocomposites for electrical insulation- partial discharge and morphological study. Nanocomposites 2017, 3, 30–41. [Google Scholar] [CrossRef] [Green Version]
- Andjelkovic, D.; Rajakovic, N. Influence of accelerated aging on mechanical and structural properties of cross-linked polyethylene (XLPE) insulation. Electr. Eng. 2001, 83, 83–87. [Google Scholar] [CrossRef]
- Fu, Q.; Liu, J.P.; He, T.B. Non-isothermal Crystallization Behavior and Kinetics of Metallocene Short Chain Branched Polyethylen. Chem. Res. 2002, 6, 1183–1188. [Google Scholar] [CrossRef]
- Olsen, R.; Anders, G.J.; Holboell, J.; Gudmundsdottir, U.S. Modelling of dynamic transmission cable temperature considering soil-specific heat, thermal resistivity, and precipitation. IEEE Trans. Power Deliv. 2013, 28, 1909–1917. [Google Scholar] [CrossRef]
- Han, Y.J.; Lee, H.M.; Shin, Y.J. Thermal aging estimation with load cycle and thermal transients for XLPE-insulated underground cable. In Proceedings of the IEEE Conference on Electrical Insulation and Dielectric Phenomenon (CEIDP), Fort Worth, TX, USA, 1 October 2017; pp. 205–208. [Google Scholar] [CrossRef]
- Xiaobin, C.; Zhixing, Y.I.; Kui, C.; Xianyi, Z.; Jia, Y. Laying mode and laying spacing for single-core feeder cable of high speed railway. China Railw. Sci. 2015, 85–90. [Google Scholar] [CrossRef]
- Chen, Y.; Duan, P.; Cheng, P.; Yang, F. Numerical calculation of ampacity of cable laying in ventilation tunnel based on coupled fields as well as the analysis on relevant factors. In Proceedings of the IEEE Conference on Intelligent Control and Automation, Shenyang, China, 29 June–4 July 2014; pp. 3534–3538. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, R.; Li, J.; Grzybowski, S.; Jiang, T. Analysis of influential factors on the underground cable ampacity. In Proceedings of the IEEE Conference on Electrical Insulation Conference, Annapolis, MD, USA, 5–8 June 2011; pp. 430–433. [Google Scholar] [CrossRef]
- Wang, P.; Ma, H.; Liu, G. Dynamic Thermal Analysis of High-Voltage Power Cable Insulation for Cable Dynamic Thermal Rating. IEEE Access. 2019, 7, 56095–56106. [Google Scholar] [CrossRef]
- Xu, Y.; Luo, P.; Xu, M.; Sun, T. Investigation on insulation material morphological structure of 110 and 220 kv xlpe retired cables for reusing. IEEE Trans. Dielectr. Electr. Insul. 2014, 21, 1687–1696. [Google Scholar] [CrossRef]
- Bin, Y.; Adachi, R.; Tong, X. Small-angle HV light scattering from deformed spherulites with orientational fluctuation of optical axes. Colloid Polym. Sci. 2004, 282, 544–554. [Google Scholar] [CrossRef]
- Li, J.; Li, H.; Wang, Q. Accelerated inhomogeneous degradation of XLPE insulation caused by copper-rich impurities at elevated temperature. IEEE Trans. Dielectr. Electr. Insul. 2016, 23, 1789–1797. [Google Scholar] [CrossRef]
- He, K.; Chen, N.; Wang, C.; Wei, L.; Chen, J. Method for determining crystal grain size by X-ray diffraction. Cryst. Res. Technol. 2018, 53, 1700157. [Google Scholar] [CrossRef]
- Rabello, M.S.; White, J.R. The role of physical structure and morphology in the photodegradation behavior of polypropylene. Polym. Degrad. Stab. 1997, 56, 55–73. [Google Scholar] [CrossRef]
- Martini, H.; Zhao, S.; Friberg, A.; Jabri, Z. Influence of electron beam irradiation on electrical properties of engineering thermoplastics. In Proceedings of the IEEE Conference on Electrical Insulation Conference (EIC), Montreal, QC, Canada, 19–22 June 2016; pp. 305–308. [Google Scholar] [CrossRef]






| Cable | VL | MI | MC | dI | OP |
|---|---|---|---|---|---|
| XLPE-0 | 110/63.5 | XLPE | Cu | 18.5 | 1998- |
| XLPE-15 | 110/63.5 | XLPE | Cu | 18.5 | 1999–2015 |
| XLPE-30 | 110/63.5 | XLPE | Cu | 18.5 | 1985–2015 |
| Cable | (J/K·m3) | (K·m/W) | (W/K·m) | (°C) | (°C) | (A) |
|---|---|---|---|---|---|---|
| XLPE-0 | 1.94 106 | 3.23 | 0.31 | 17.7 | 89.6 | 1244.07 |
| XLPE-15 | 1.96 106 | 3.45 | 0.29 | 17.7 | 89.7 | 1222.99 |
| XLPE-30 | 2.07 106 | 5.26 | 0.19 | 17.7 | 90.2 | 1096.47 |
| Specimen | Pipeline | Ground | Tunnel |
|---|---|---|---|
| XLPE-0 | Improved | Improved | Improved |
| XLPE-15 | Degraded | Maintained | Improved |
| XLPE-30 | Degraded | Improved | Maintained |
| Specimen | (°C) | (J/g) | (°C) | (J/g) | (°C) |
|---|---|---|---|---|---|
| XLPE-0 | 91.8 | −99.0 | 106.9 | 100.8 | 15.1 |
| Pipeline-0 | 92.0 | −108.8 | 107.6 | 116.6 | 15.6 |
| Ground-0 | 89.7 | −102.8 | 109.0 | 111.1 | 19.3 |
| Tunnel-0 | 90.0 | −110.8 | 108.0 | 117.2 | 18.0 |
| XLPE-15 | 89.0 | −93.4 | 104.0 | 98.7 | 15.0 |
| Pipeline-15 | 88.2 | −99.6 | 103.8 | 108.1 | 15.6 |
| Ground-15 | 86.9 | −93.4 | 105.0 | 101.9 | 18.1 |
| Tunnel-15 | 87.8 | −99.1 | 104.1 | 101.1 | 16.3 |
| XLPE-30 | 89.5 | −103.9 | 107.2 | 103.4 | 17.7 |
| Pipeline-30 | 90.6 | −103.0 | 106.6 | 110.5 | 16.0 |
| Ground-30 | 90.9 | −105.1 | 106.6 | 111.3 | 15.7 |
| Tunnel-30 | 89.8 | −104.5 | 107.1 | 106.4 | 17.0 |
| Specimen | Pipeline | Ground | Tunnel |
|---|---|---|---|
| XLPE-0 | Improved | Improved | Improved |
| XLPE-15 | Degraded | Improved | Improved |
| XLPE-30 | Degraded | Improved | Maintained |
| Specimen | Pipeline | Ground | Tunnel |
|---|---|---|---|
| XLPE-0 | Improved | Improved | Improved |
| XLPE-15 | Degraded | Improved | Improved |
| XLPE-30 | Maintained | Maintained | Improved |
| Specimen | Untreated | Pipeline | Ground | Tunnel |
|---|---|---|---|---|
| XLPE-0 | 66.106 | 69.273 | 68.860 | 71.325 |
| XLPE-15 | 73.489 | 63.941 | 75.640 | 81.650 |
| XLPE-30 | 68.382 | 65.463 | 67.609 | 69.600 |
| Specimen | Pipeline | Ground | Tunnel |
|---|---|---|---|
| XLPE-0 | Improved (greatly) | Improved (greatly) | Improved (greatly) |
| XLPE-15 | Degraded (severely) | Maintained | Improved (greatly) |
| XLPE-30 | Degraded (slightly) | Improved (slightly) | Maintained |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, W.; Zhao, Y.; Han, Z.; Wang, X.; Wang, Y.; Liu, G.; Xie, Y.; Zhu, N. Thermal Effect of Different Laying Modes on Cross-Linked Polyethylene (XLPE) Insulation and a New Estimation on Cable Ampacity. Energies 2019, 12, 2994. https://doi.org/10.3390/en12152994
Zhu W, Zhao Y, Han Z, Wang X, Wang Y, Liu G, Xie Y, Zhu N. Thermal Effect of Different Laying Modes on Cross-Linked Polyethylene (XLPE) Insulation and a New Estimation on Cable Ampacity. Energies. 2019; 12(15):2994. https://doi.org/10.3390/en12152994
Chicago/Turabian StyleZhu, WenWei, YiFeng Zhao, ZhuoZhan Han, XiangBing Wang, YanFeng Wang, Gang Liu, Yue Xie, and NingXi Zhu. 2019. "Thermal Effect of Different Laying Modes on Cross-Linked Polyethylene (XLPE) Insulation and a New Estimation on Cable Ampacity" Energies 12, no. 15: 2994. https://doi.org/10.3390/en12152994






