The Spatial Spillover Effects of Environmental Regulation on China’s Industrial Green Growth Performance
Abstract
:1. Introduction
2. Method and Data
2.1. Stochastic Frontier Production Function
2.2. Spatial Econometric Model
2.2.1. Global Spatial Autocorrelation
2.2.2. Spatial Econometric Models
2.3. Variables and Data Description
2.3.1. Variables for the Calculation of IGGP
- (1)
- Output (): the industrial value added (IVA) is taken as the output. To ensure the comparability of the data, the original data of IVA are deflated to 2000 constant price by using the regional industrial producer price indexes.
- (2)
- Inputs: capital stock (), labor force (), energy consumption (), and carbon emissions () are selected as the inputs (because the natural environment itself has a certain metabolic function of absorbing and digesting pollutants, resources and environmental elements are considered as social resources that do not need to pay for costs, in this study, carbon emission is regarded as environmental cost for industrial output). The industrial capital stock is approximated using the net value of industrial fixed assets, being deflated to 2000 constant price level by deflating the fixed asset price index. The number of industrial employees at the end of every year in each province represents labor force. This study adopt the overall energy consumption to denote energy input. Because of the official data on carbon emission from regional industry is not available in China, this paper adopts Equation (9) to calculate carbon emissions from the industry sector in province i:where m refers to the category of energy (to obtain more accurate results, this study selected 15 kinds of fossil fuels reported in the statistical yearbooks, including raw coal, cleaned coal, coke, coke oven gas, other gases, crude oil, petrol, kerosene, diesel, fuel oil, liquefied petroleum gas, refinery gas, natural gas, other petroleum products, and other coking products); q stands for the amount of consumption of a certain energy product; s denotes the net calorific value of a certain energy product; ξ represents the carbon emission coefficient, η is the carbon oxidation factor, and 44 and 12 stand for the molecular weights of CO2 and , respectively.
2.3.2. Variables for ER
- (1)
- AER: the annual investment of pollution control projects in each region is used to measure the intensity of AER. To eliminate the impact of price factors, the original data are deflated to 2000 constant price through the price indexes.
- (2)
- MER: the revenue from sewage charges in various regions is applied to measure the intensity of MER and the original data are converted to 2000 constant price.
- (3)
- VER: the total quantity of environmental letters and visits in various regions is used to measure the intensity of VER.
2.3.3. The Controlled Variables
- (1)
- Foreign direct investment (FDI): the level of FDI in each region is measured by the proportion of FDI to GDP. It should be noted that FDI is converted by the average price of the RMB exchange rate during the sample period.
- (2)
- Energy consumption structure (ESC): taking the share of coal consumption in overall energy consumption in industrial sector as ESC. As a carbon-intensive energy source, coal accounts for an overwhelming majority of the energy consumption in China [28].
- (3)
- Technology level (TL): using the number of patent applications in each region to present the scientific and technical level in each area.
3. Results and Discussion
3.1. Static Time-Series Change Characters of Provincial IGGP
3.2. Estimation Results of the Spatial Autocorrelation
3.3. Spatial Econometric Analysis
4. Conclusions and Policy Implications
- Rationally use AER instruments to promote the process of regional integration. Because of the different economic patterns in different regions, the applicability of policies is not identical. Therefore, in formulating specific AER policies, “one size fits all” should be avoided. Local governments should formulate corresponding AER based on the different characteristics of industries in each region. On this basis, multi-target performance appraisal mechanisms should be introduced so that local governments no longer focus on economic development but ignore the environment. We must also work hard to promote the regional cooperation, achieve the sharing of benefits, eliminate various trade barriers and market barriers, and remove obstacles to promote the flow of funds, talent, and technology among different regions. In addition, it is necessary to increase supervision over administrative controls to ensure that environmental protection investment is used compliantly and efficiently and prevent rent-seeking behaviors.
- Complete MER tools and establish environmental compensation mechanisms. It is crucial to promote the process of replacing the green taxes sewage charges with the environmental taxes, and strength the intensity of MER, so as to force the elimination of backward production capacity. Meanwhile, it should also actively learn from the developed countries and continuously enrich MER tools in accordance with China’s national conditions. In view of the different attitudes between the central government and local governments toward MER, in order to prevent the emergence of environmental competition among regions, appropriate environmental compensation mechanisms should be established. At the same time, policy-makers may as well make clear provisions on compensation standards and actively coordinate regional environmental compensation.
- Strengthen government supervision and exert the role of VER in maximize extent. Related departments should encourage and guide public to take part in environmental protection. First of all, it is necessary to strengthen advocating to improve the public awareness of environmental protection. Then, relevant departments should complete legislation as soon as possible to provide legal protection for citizens to exercise the right to know and supervise. Furthermore, government should publish relevant environmental construction projects through the media in time, and fully listen to public opinions through seminars, hearings, questionnaires.
- Additionally, FDI has a significant role in promoting China’s IGGP. China’s government should further improve the policies of FDI inflow. For example, strictly restricting the entry of low-tech foreign-funded companies, positively encouraging the introduction of high-tech foreign-funded companies and related advanced technologies. Moreover, given the imbalance in development of various regions in China, the underdeveloped regions should think highly of improving the quality of foreign investment. In addition, the underdeveloped areas should strengthen infrastructure construction and enhance the human capital level to reduce the disadvantageous technology spillover effects of FDI on the quality of environment.
- Furthermore, it is vital to improve the ratio of non-fossil energy to the overall energy consumption. Given the difference of energy endowments in various regions, ECS is diverse. The government should positively push forward the market-oriented reform of energy pricing mechanism according to the differentiated features of ESC of industrial sectors in various areas.
- Finally, the conclusions also indicate that higher TL is beneficial to IGGP and social environmental protection to a certain extent, IGGP could be stimulated if industrial sector input in technology. According to the results, we suggest that under strengthening technology introduction and independent innovation, we must pay special attention to technology absorption and application promotion related to energy-saving and environmental protection, improve government related investment, guide and encourage private capital to enter emission reduction, transform and upgrade traditional industries while actively develop modern manufacturing technologies, and promote the extension of manufacturing and its products to the high end of the technology chain.
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Variables | Coefficient | T-Ratio | Variables | Coefficient | T-Ratio |
|---|---|---|---|---|---|
| 3.294 *** | 3.047 | 1.061 *** | 3.769 | ||
| 0.388 *** | 8.722 | 0.277 ** | 2.130 | ||
| 0.003 | 1.278 | −0.107 *** | -2.926 | ||
| 0.624 ** | 2.165 | 0.034 | 0.166 | ||
| 0.332 ** | 2.245 | −0.084 | −0.409 | ||
| −2.128 *** | −3.291 | −0.142 | −0.882 | ||
| 1.573 *** | 2.794 | 0.217 ** | 1.972 | ||
| 0.017 *** | −2.612 | −1.192 ** | −2.379 | ||
| 0.006 | 0.778 | σ² | 0.299 *** | 10.327 | |
| −0.095 *** | −5.636 | γ | 0.952 *** | 142.714 | |
| 0.069 *** | 4.948 | mu | 1.068 *** | 9.372 | |
| 0.012 | 0.202 | eta | −0.029 *** | −7.504 | |
| -0.034 | −0.588 | LR | 541.901 | ||
References
- NBSC (National Bureau of Statistics of China). China Statistical Yearbook 2017; China Statistics Press: Beijing, China, 2017.
- OECD. Towards Green Growth: Monitoring Progress; OECD: Paris, Frnace, 2011. [Google Scholar]
- Gunningham, N.; Grabosky, P.N.; Sinclair, D. Smart Regulation: Designing Environmental Policy; Socio-Legal Studies: Oxford, UK, 1998. [Google Scholar]
- Huang, J.H.; Yang, X.G.; Cheng, G.; Wang, S.Y. A comprehensive eco-efficiency model and dynamics of regional eco-efficiency in China. J. Clean. Prod. 2014, 67, 228. [Google Scholar] [CrossRef]
- Zhang, N.; Kong, F.B.; Yu, Y.N. Measuring ecological total-factor energy efficiency incorporating regional heterogeneities in China. Ecol. Indic. 2015, 51, 165. [Google Scholar] [CrossRef]
- CIIGBC (Confederation of Indian Industry-Sohrabji Godrej Green Business Centre). Green Company Rating System. 2012. Available online: http://www.greenbusinesscentre.com/ CII-Publication/greenco.html (accessed on 5 July 2016).
- Li, X.X.; Pan, J.C. China Green Development Index Report 2011; Springer-Verlag: Heidelberg, Germany, 2013. [Google Scholar]
- Shi, G.M.; Bi, J.; Wang, J.N. Chinese regional industrial energy efficiency evaluation based on a DEA model of fixing non-energy inputs. Energy Policy 2010, 38, 6172. [Google Scholar] [CrossRef]
- Zhang, J.X.; Liu, Y.M.; Chang, Y.; Zhang, L.X. Industrial eco-efficiency in China: A provincial quantification using three-stage data envelopment analysis. J. Clean. Prod. 2017, 143, 238. [Google Scholar] [CrossRef]
- Wu, J.; Zhu, Q.; Chu, J.; Liang, L. Two-stage network structures with undesirable intermediate outputs reused: A DEA based approach. Comput. Econ. 2015, 46, 455. [Google Scholar] [CrossRef]
- Aigner, D.; Lovell, C.A.K.; Schmit, P. Formulation and estimation of stochastic frontier production function models. J. Econom. 1977, 6, 21. [Google Scholar] [CrossRef]
- Lin, B.Q.; Yang, L.S. The potential estimation and factor analysis of China’s energy conservation on thermal power industry. Energy Policy 2013, 62, 354. [Google Scholar] [CrossRef]
- Ouyang, X.L.; Sun, C.W. Energy savings potential in China’s industrial sector: From the perspectives of factor price distortion and allocative inefficiency. Energy Econ. 2015, 48, 117. [Google Scholar] [CrossRef]
- Gray, W.B. The cost of regulation: OSHA, EPA and the productivity slowdown. Am. Econ. Rev. 1987, 77, 998. [Google Scholar]
- Jorgenson, D.W.; Wilcoxen, P.J. Environmental Regulation and U.S. Economic Growth. Rand J. Econ. 1990, 21, 314. [Google Scholar] [CrossRef]
- Wu, M.Q.; Zhou, S.M.; Chen, J.C. Can environmental regulation and economic growth be a win-win situation? Based on the empirical research of China’s “two control areas”. Contemp. Econ. Sci. 2016, 38, 44. [Google Scholar]
- Lu, K.J.; Cheng, Y.; Fan, B.J. The Impact of Environmental Regulation on Green Total Factor Productivity of Chinese Manufacturing Industry. Ecol. Econ. 2017, 33, 49. [Google Scholar]
- Wang, J.; Liu, B. Environmental Regulation and Corporate Total Factor Productivity: Empirical Analysis Based on Chinese Industrial Enterprise Data. China Ind. Econ. 2014, 3, 44. [Google Scholar]
- Yan, Y.G.; Chang, R. Environmental Regulation and Industrial Total Factor Productivity: Empirical Study Based on Dynamic Panel Data of 280 Prefecture-level Cities. Econ. Issues 2016, 11, 18. [Google Scholar]
- Zhao, X.; Yin, H.; Zhao, Y. Impact of environmental regulations on the efficiency and CO2 emissions of power plants in China. Appl. Energy 2015, 149, 238. [Google Scholar] [CrossRef]
- Zhao, X.; Zhao, Y.; Zeng, S.; Zhang, S. Corporate behavior and competitiveness: Impact of environmental regulation on Chinese firms. J. Clean. Prod. 2015, 86, 311. [Google Scholar] [CrossRef]
- Ren, S.; Li, X.; Yuan, B.; Li, D.; Chen, X. The effects of three types of environmental regulation on eco-efficiency: A cross-region analysis in China. J. Clean. Prod. 2018, 173, 245. [Google Scholar] [CrossRef]
- Tobler, W. A computer movie simulating urban growth in the Detroit region. Econ. Geogr. 1970, 46, 234. [Google Scholar] [CrossRef]
- Kumbhakar, S.C. Estimation and decomposition of productivity change when production is not efficient: A panel data approach. Econom. Rev. 2000, 19, 425. [Google Scholar] [CrossRef]
- Shao, B.B.M.; Lin, W.T. Assessing output performance of information technology service industries: Productivity, innovation and catch-up. Int. J. Prod. Econ. 2016, 172, 43–53. [Google Scholar] [CrossRef]
- Shao, S.; Luan, R.R.; Yang, Z.B.; Li, C.Y. Does directed technological change get greener: Empirical evidence from Shanghai’s industrial green development transformation. Ecol. Indic. 2016, 69, 758. [Google Scholar] [CrossRef]
- Lesage, J.P.; Pace, R.K. Introduction to Spatial Econometrics; Press/Taylor & Francis: Boca Raton, FL, USA, 2009; p. 20. [Google Scholar]
- National Bureau of Statistics of China. China Energy Statistical Yearbook; China Statistic Press: Beijing, China, 2012.
- Yang, Z.B.; Shao, S.; Yang, L.L.; Miao, Z. Improvement pathway of energy consumption structure in China’s industrial sector: From the perspective of directed technical change. Energy Econ. 2018, 72, 166. [Google Scholar] [CrossRef]


| Variables | Mean | Std. dev. | Min. | Max. | Sample Size |
|---|---|---|---|---|---|
| lnY | 7.6465 | 1.1741 | 4.2550 | 10.2529 | 450 |
| lnK | 7.8205 | 0.9509 | 4.9237 | 10.8480 | 450 |
| lnL | 4.9304 | 1.0216 | 2.2807 | 7.2833 | 450 |
| lnE | 8.5513 | 0.8422 | 5.2902 | 10.2531 | 450 |
| lnC | 8.8380 | 0.8667 | 7.2204 | 10.6099 | 450 |
| lnAER | 0.0047 | 0.0037 | 0.0004 | 0.0273 | 450 |
| lnMER | 0.0213 | 0.0028 | 0.0148 | 0.0268 | 450 |
| lnVER | 0.0126 | 0.0065 | 0.0015 | 0.0491 | 450 |
| FDI | 0.0201 | 0.0201 | 0.0005 | 0.1356 | 450 |
| ESC | 0.8100 | 0.1400 | 0.2800 | 0.9700 | 450 |
| lnTL | 0.0128 | 0.0102 | 0.0014 | 0.0601 | 450 |
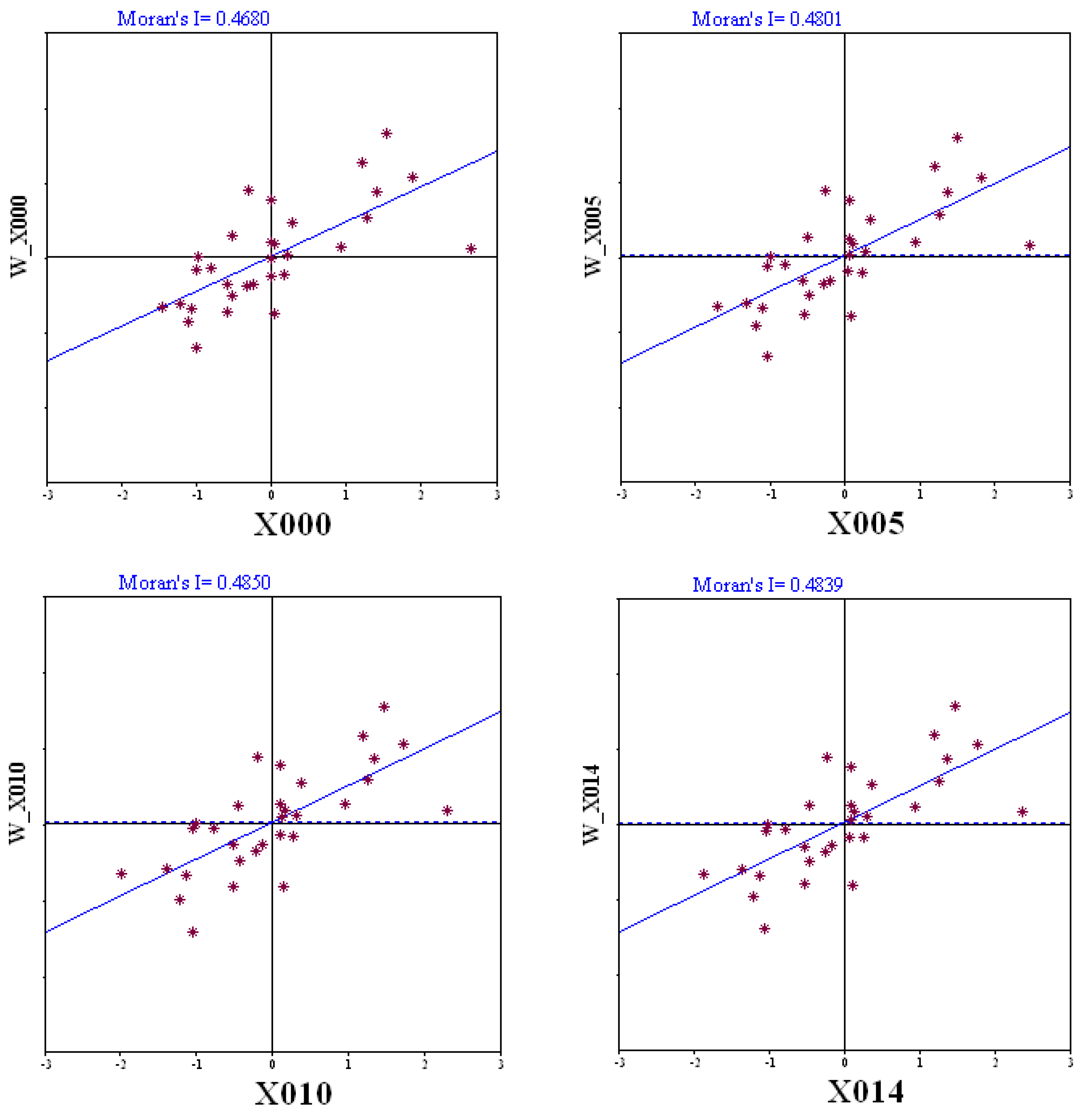
| Year | Moran’I | Year | Moran’I |
|---|---|---|---|
| 2000 | 0.4680 *** | 2008 | 0.4839 *** |
| 2001 | 0.4710 *** | 2009 | 0.4846 *** |
| 2002 | 0.4737 *** | 2010 | 0.4850 *** |
| 2003 | 0.4761 *** | 2011 | 0.4851 *** |
| 2004 | 0.4782 *** | 2012 | 0.4849 *** |
| 2005 | 0.4801 *** | 2013 | 0.4844 *** |
| 2006 | 0.4816 *** | 2014 | 0.4839 *** |
| 2007 | 0.4829 *** | Average | 0.4802 *** |
| Independent Variables | SLM | SEM | SDM |
|---|---|---|---|
| InAER | −0.0536 *** (3.3574) | −0.0912 *** (−2.9735) | −0.0792 ** (−2.2627) |
| InMER | −0.0924 *** (2.9641) | −0.1017 *** (5.6491) | −0.1274 * (−1.9519) |
| InVER | 0.0001 ***(2.9719) | 0.0001 *** (2.7896) | 0.0002 *** (6.2815) |
| FDI | −0.0163 *** (−5.1382) | −0.0125 *** (8.1257) | −0.0216 *** (2.8916) |
| ESC | −0.0635 *** (3.1972) | −0.0826 *** (4.3671) | −0.1104 *** (5.1467) |
| InTL | 0.0392 *** (3.1764) | 0.0347 *** (6.1253) | 0.0874 *** (−4.0734) |
| W·InAER | −0.9761 *** (5.1206) | ||
| W·InMER | 1.0813 *** (−2.7638) | ||
| W·InVER | 0.0001 *** (11.4251) | ||
| W·FDI | 0.1769 *** (3.2483) | ||
| W·ESC | −0.0152*** (−3.1152) | ||
| W·InTL | 0.3157*** (4.1657) | ||
| ρ or δ | 0.172 *** (−3.1728) | 0.1692 *** (4.2136) | 0.1786 *** (2.9334) |
| Adj-R2 | 0.6137 | 0.6923 | 0.7911 |
| Log-L | 718.6123 | 798.2151 | 1207.9126 |
| Observation value | 450 | 450 | 450 |
| Independent Variables | Direct Effects | Indirect Effects | Total Effects |
|---|---|---|---|
| InAER | −0.2224 *** (5.7152) | −0.9278 *** (2.9364) | −1.1502 *** (−3.1726) |
| InMER | −0.2499 *** (−3.1128) | 1.4316 *** (3.6271) | 1.1817 *** (2.9714) |
| InVER | 0.001 *** (7.2314) | 0.0002 *** (4.3716) | 0.0012 *** (4.1268) |
| FDI | 0.2884 *** (3.7714) | −0.0572 *** (3.6812) | 0.2312 *** (−2.9714) |
| ESC | −0.1316 *** (2.9617) | −0.1197 *** (3.1293) | −0.2513 *** (3.1292) |
| InTL | 0.7440 *** (6.1273) | −0.1146 *** (4.3274) | 0.6294 *** (4.2791) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Li, M. The Spatial Spillover Effects of Environmental Regulation on China’s Industrial Green Growth Performance. Energies 2019, 12, 267. https://doi.org/10.3390/en12020267
Wang X, Li M. The Spatial Spillover Effects of Environmental Regulation on China’s Industrial Green Growth Performance. Energies. 2019; 12(2):267. https://doi.org/10.3390/en12020267
Chicago/Turabian StyleWang, Xiping, and Moyang Li. 2019. "The Spatial Spillover Effects of Environmental Regulation on China’s Industrial Green Growth Performance" Energies 12, no. 2: 267. https://doi.org/10.3390/en12020267
APA StyleWang, X., & Li, M. (2019). The Spatial Spillover Effects of Environmental Regulation on China’s Industrial Green Growth Performance. Energies, 12(2), 267. https://doi.org/10.3390/en12020267




