Modelling of the Bearing Breakdown Resistance in Bearing Currents Problem of AC Motors
Abstract
:1. Introduction
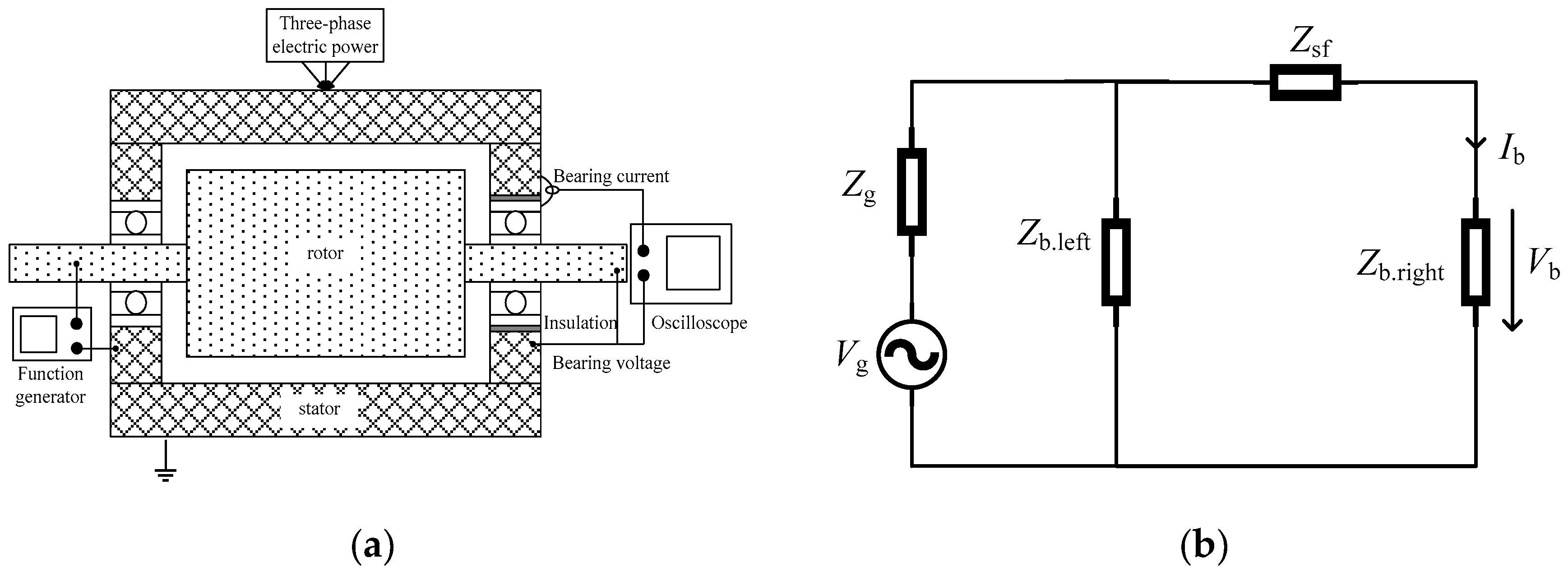
2. Experiment of Electrical Properties of the Bearing
3. Bearing Breakdown Equivalent Model
4. Determination the Electrical Parameters in the Bearing Breakdown Model
4.1. Capacitance in Bearing Breakdown Model
4.2. Variable Breakdown Resistance in Bearing Breakdown Model
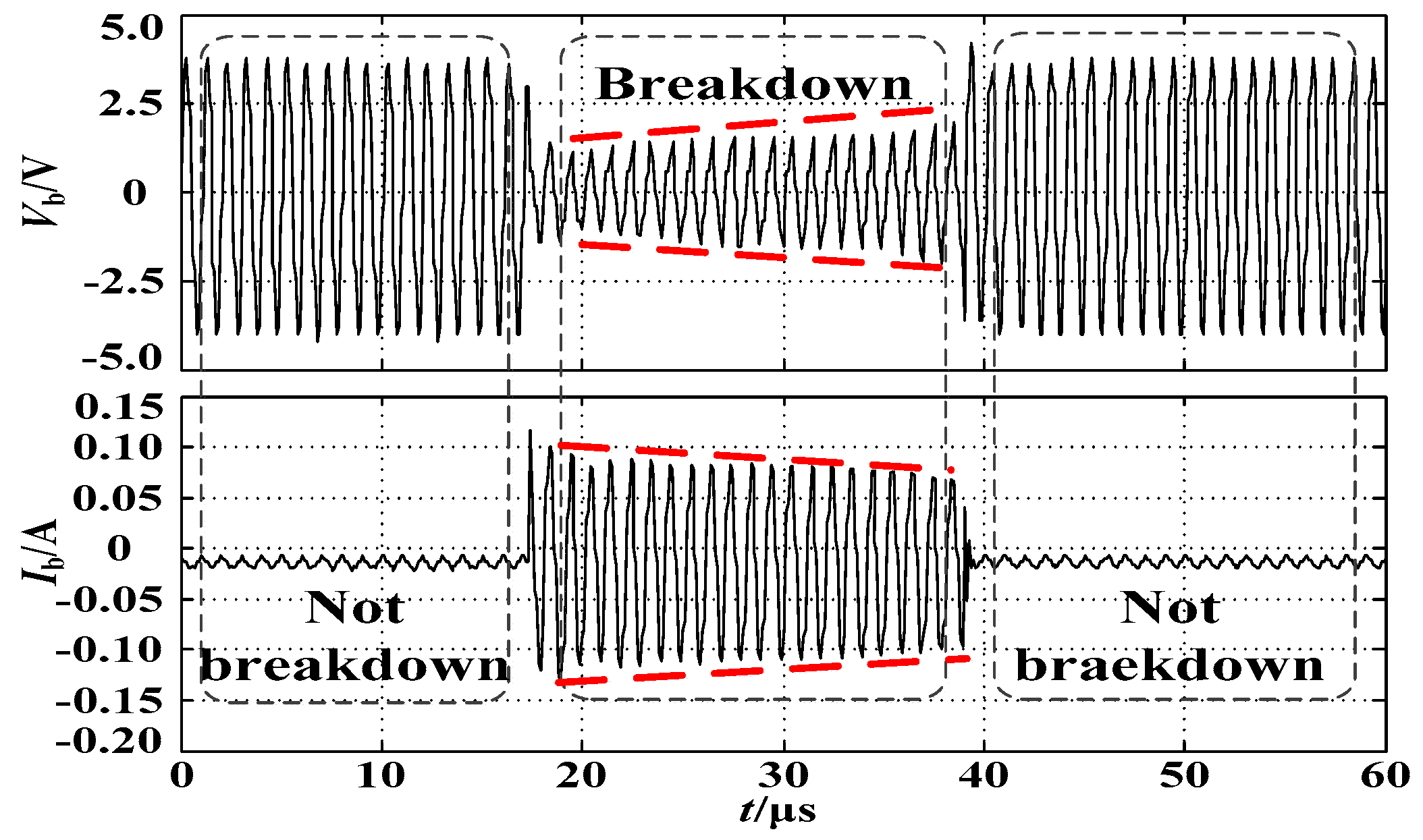
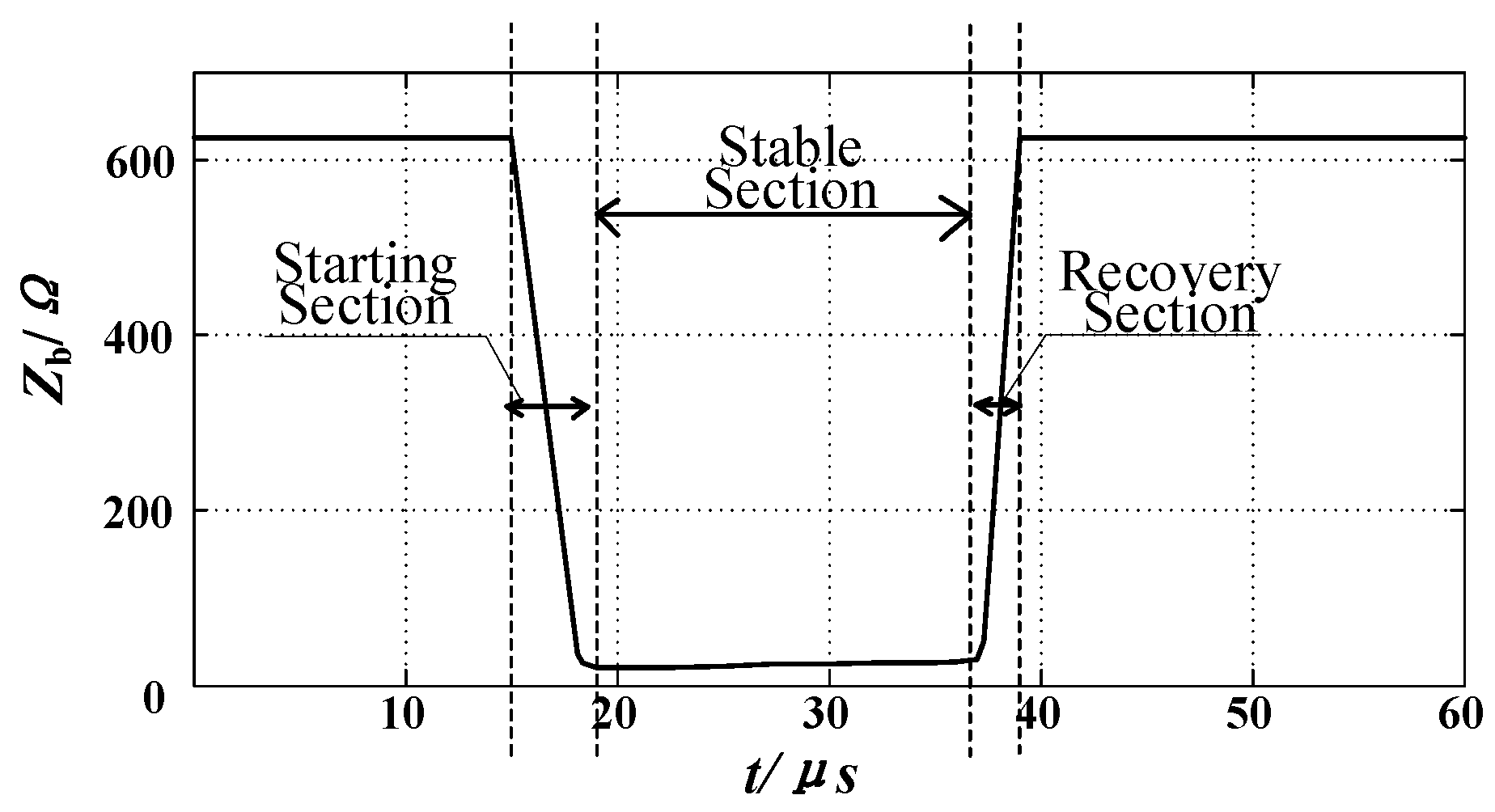
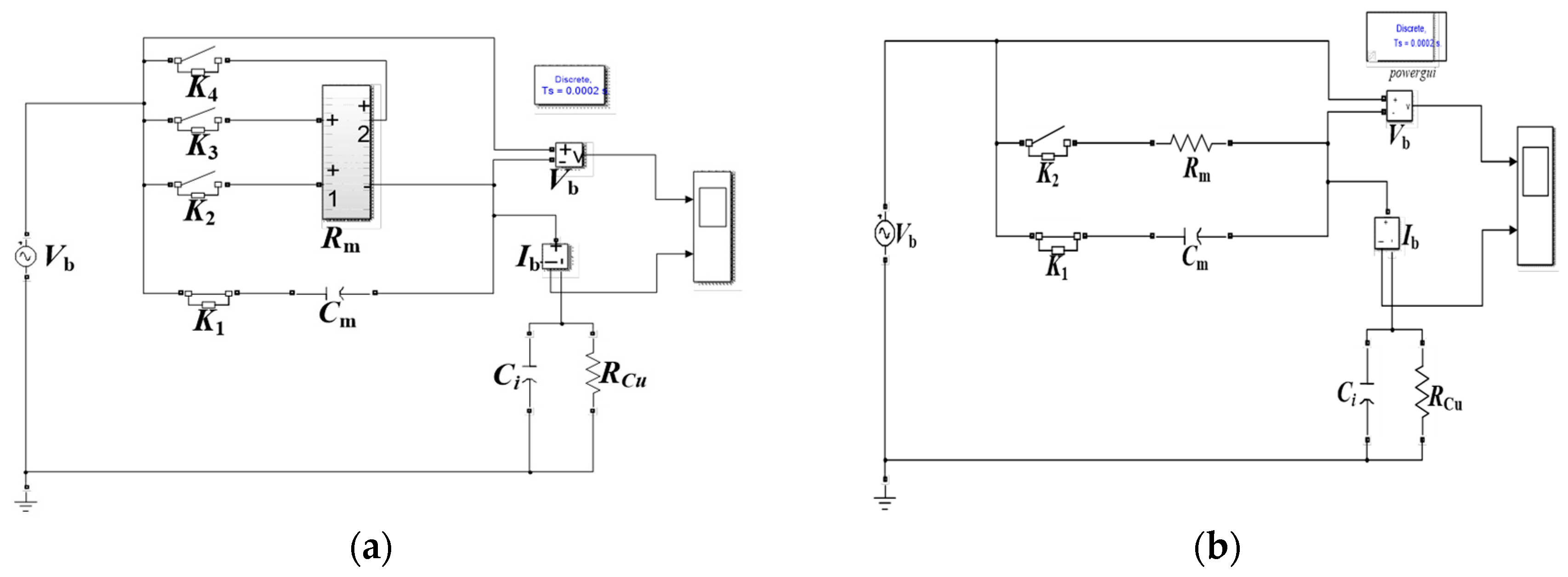
5. Verification and Simulation of the Variable Breakdown Resistance Model
5.1. Verification of the Variable Breakdown Resistance Model
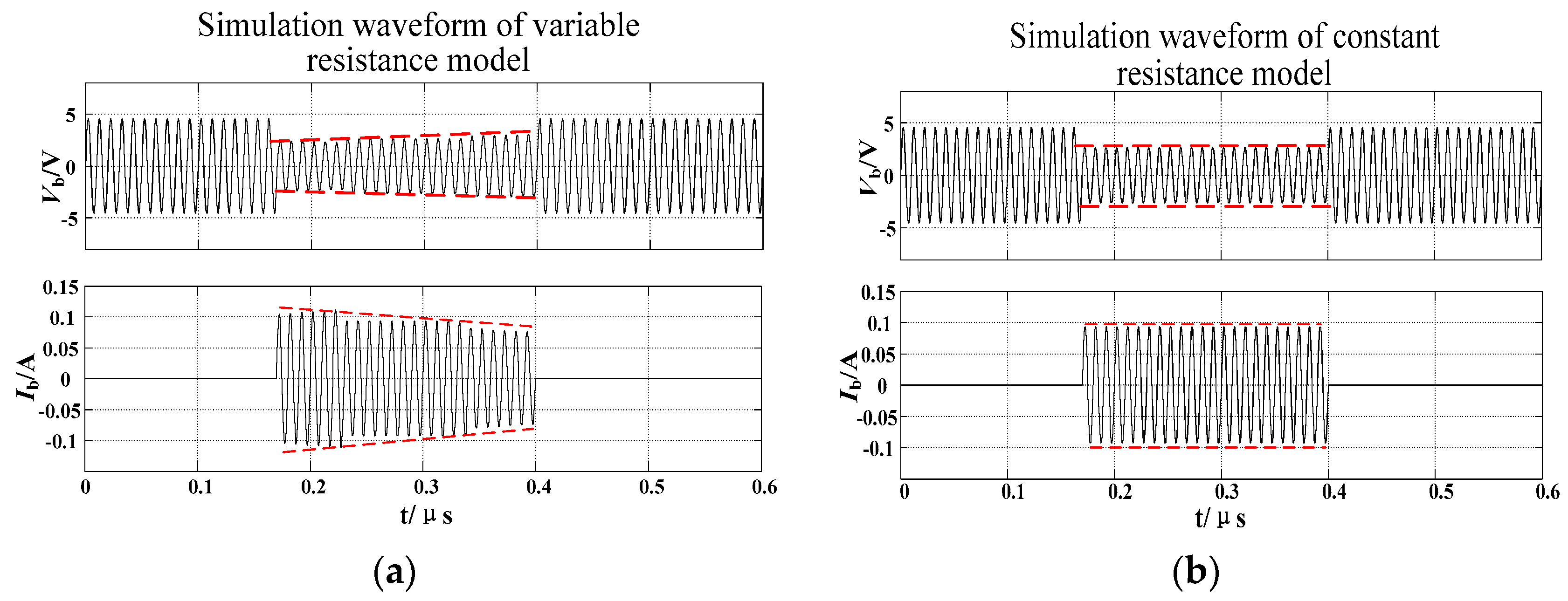
5.2. Simulation of the Variable Resistance Model and the Constant Resistance Model
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Plazenet, T.; Boileau, T.; Caironi, C.; Nahid-Mobarakeh, B. An overview of shaft voltages and bearing currents in rotating machines. In Proceedings of the 2016 IEEE Industry Applications Society Annual Meeting, Portland, OR, USA, 2–6 October 2016. [Google Scholar]
- Liu, R.; Ma, X.; Ren, X. Comparative Analysis of Bearing Current in Wind Turbine Generators. Energies 2018, 11, 1305. [Google Scholar] [CrossRef]
- Schiferl, R.F.; Melfi, M.J. Bearing current remediation options. IEEE Ind. Appl. Mag. 2004, 10, 40–50. [Google Scholar] [CrossRef]
- Muetze, A. Bearing Currents in Inverter-Fed AC-Motors. Ph.D. Thesis, Darmstadt University of Technology, Aachen, Germany, 2004. [Google Scholar]
- Sang, B. Analysis and Measurement of Bearing Current of Variable Frequency Power Supply AC Motor. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2016. [Google Scholar]
- Chaves, C.S.; Camacho, J.R.; De Paula, H.; Chaves, M.L.; Saraiva, E. Capacitances calculation using FEM for transient overvoltage and common mode currents prediction in inverter-driven induction motors. In Proceedings of the 2011 IEEE Trondheim PowerTech, Trondheim, Norway, 19–23 June 2011. [Google Scholar]
- Muetze, A.; Binder, A. Calculation of motor capacitances for prediction of discharge bearing currents in machines of inverter-based drive systems. In Proceedings of the IEEE International Conference on Electric Machines and Drives, San Antonio, TX, USA, 15 May 2005. [Google Scholar]
- Wellawatta, T.; Park, J.K.; Kim, H.M.; Hur, J. New Equivalent Circuit of the IPM-Type BLDC Motor for Calculation of Shaft Voltage by Considering Electric and Magnetic Fields. In Proceedings of the IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 20–24 September 2015. [Google Scholar]
- Wang, Y.; Bai, B.; Liu, W.; Wang, X. Determination of key parameters of common parameters equivalent circuit of distributed parameters and calculation of bearing current. Trans. China Electrotech. Soc. 2014, 29, 124–131. [Google Scholar]
- Ruifang, L.; Zhuofu, L.; Xiping, M. Modeling of Bearing Capacitance and Resistance in Motor Bearing Current Problem. Proc. CSEE 2014, 34, 2430–2437. [Google Scholar]
- Prashad, H. Tribology in Electrical Environments; Elsevier: Hyderabad, India, 2006. [Google Scholar]
- Bartz, M. Lubricant Film Formation in Grease Lubricated High Speed Spindle Bearings. Ph.D. Thesis, University of Hannover, Hannover, Germany, 1996. [Google Scholar]
- Busse, D.; Erdman, J.; Kerkman, R.J.; Schlegel, D.; Skibinski, G. System Electrical Parameters and Their Effects On Bearing Currents. IEEE Trans. Ind. Appl. 1997, 33, 577–584. [Google Scholar] [CrossRef]
- Busse, D.; Erdman, J.; Kerkman, R.J.; Schlegel, D.; Skibinski, G. Bearing Currents and Their Relationship to PWM Drives. IEEE Trans. Power Electron. 1997, 12, 243–252. [Google Scholar] [CrossRef]
- Niskanen, V.; Muetze, A.; Ahola, J. Study on bearing impedance properties at several hundred kilohertz for different electric machine operating parameters. IEEE Trans. Ind. Appl. 2014, 50, 3438–3447. [Google Scholar] [CrossRef]
- Rui, X. Theoretical Analysis of Electrical Discharge Channel and Research of Gap Distance Testing. Master’s Thesis, Shanghai JiaoTong University, Shanghai, China, 2011. [Google Scholar]
- Zhan, H.; Duan, S.; Li, C.; Yao, L.; Zhao, L. A Novel Arc Model for Very Fast Transient Overvoltage Simulation in a 252-kV Gas-Insulated Switchgear. IEEE Trans. Plasma Sci. 2014, 42, 3423–3429. [Google Scholar] [CrossRef]



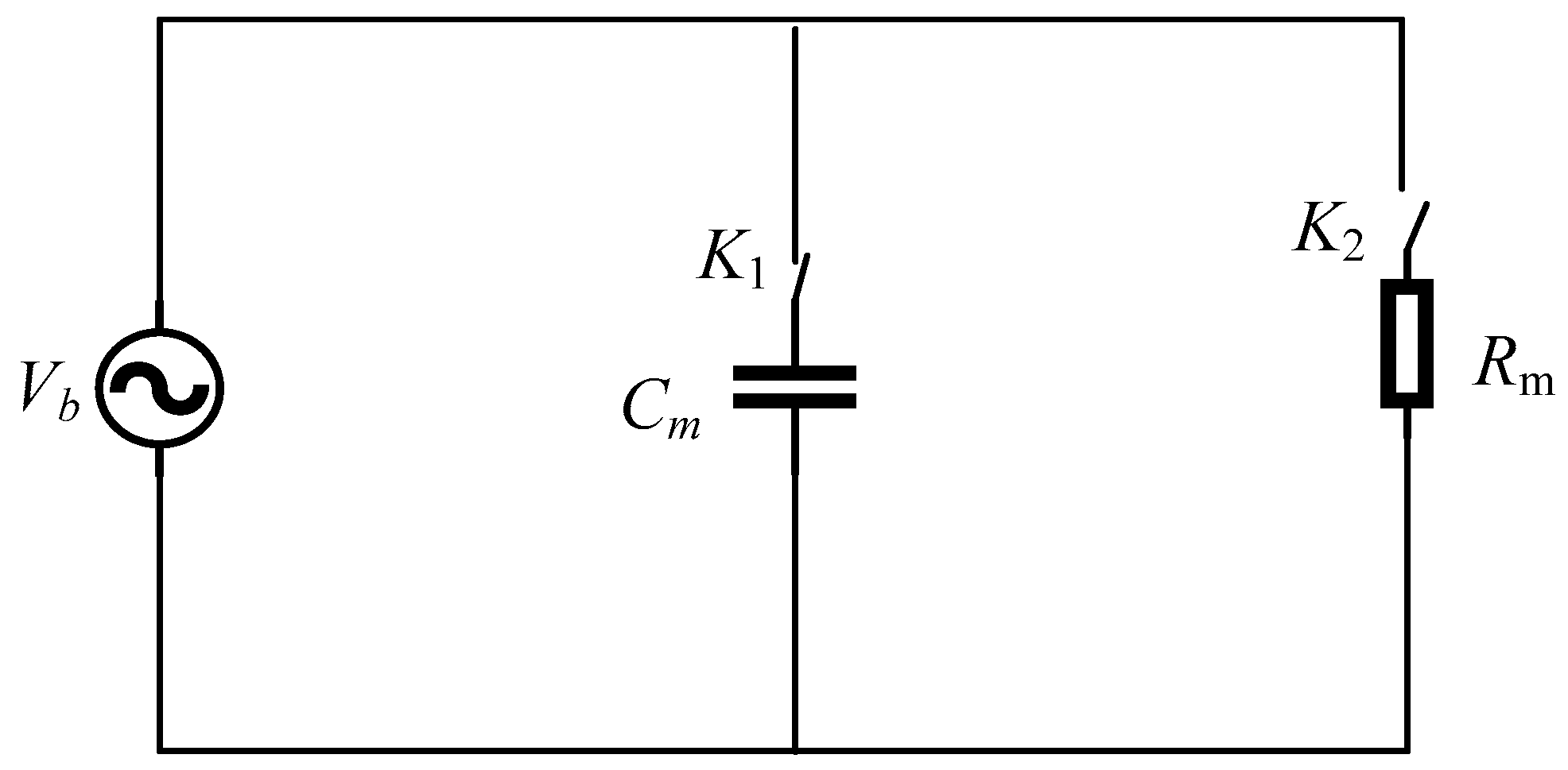

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, X.; Liu, R.; Yang, E. Modelling of the Bearing Breakdown Resistance in Bearing Currents Problem of AC Motors. Energies 2019, 12, 1121. https://doi.org/10.3390/en12061121
Ren X, Liu R, Yang E. Modelling of the Bearing Breakdown Resistance in Bearing Currents Problem of AC Motors. Energies. 2019; 12(6):1121. https://doi.org/10.3390/en12061121
Chicago/Turabian StyleRen, Xuejiao, Ruifang Liu, and Erle Yang. 2019. "Modelling of the Bearing Breakdown Resistance in Bearing Currents Problem of AC Motors" Energies 12, no. 6: 1121. https://doi.org/10.3390/en12061121




